Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника. — КиберПедия
Задание B6 (№ 27895)
Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.
Задание B6 (№ 27896)
Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.
Задание B6 (№ 27897)
Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника.
Задание B6 (№ 27898)
В треугольнике ABC , , угол C равен . Найдите радиус описанной окружности этого треугольника.
Задание B6 (№ 27899)
В треугольнике ABC , угол C равен . Радиус описанной окружности этого треугольника равен 5. Найдите AC.
Радиус описанной окружности этого треугольника равен 5. Найдите AC.
Задание B6 (№ 27900)
Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен . Найдите диаметр описанной окружности этого треугольника.
Задание B6 (№ 27901)
Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 3 и 4.
Задание B6 (№ 27902)
Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
Задание B6 (№ 27903)
Найдите радиус окружности, описанной около квадрата со стороной, равной .
Задание B6 (№ 27904)
Найдите сторону квадрата, вписанного в окружность радиуса .
Задание B6 (№ 27905)
Меньшая сторона прямоугольника равна 6. Угол между диагоналями равен . Найдите радиус описанной окружности этого прямоугольника.
Задание B6 (№ 27906)
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Задание B6 (№ 27907)
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Задание B6 (№ 27908)
Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
Задание B6 (№ 27909)
Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задание B6 (№ 27910)
Радиус окружности, вписанной в правильный треугольник, равен . Найдите сторону этого треугольника.
Найдите сторону этого треугольника.
Задание B6 (№ 27911)
Найдите радиус окружности, вписанной в квадрат со стороной 4.
Задание B6 (№ 27912)
Найдите сторону квадрата, описанного около окружности радиуса 4.
Задание B6 (№ 27913)
Сторона ромба равна 1, острый угол равен . Найдите радиус вписанной окружности этого ромба.
Задание B6 (№ 27914)
Острый угол ромба равен . Радиус вписанной в этот ромб окружности равен 2.
Найдите сторону ромба.
Задание B6 (№ 27915)
Найдите высоту трапеции, в которую вписана окружность радиуса 1.
Задание B6 (№ 27916)
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .
Задание B6 (№ 27917)
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Задание B6 (№ 27918)
Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.
Задание B6 (№ 27919)
Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.
Задание B6 (№ 27920)
Угол C треугольника ABC, вписанного в окружность радиуса 3, равен . Найдите сторону AB этого треугольника.
Задание B6 (№ 27921)
Сторона AB треугольника ABC равна 1.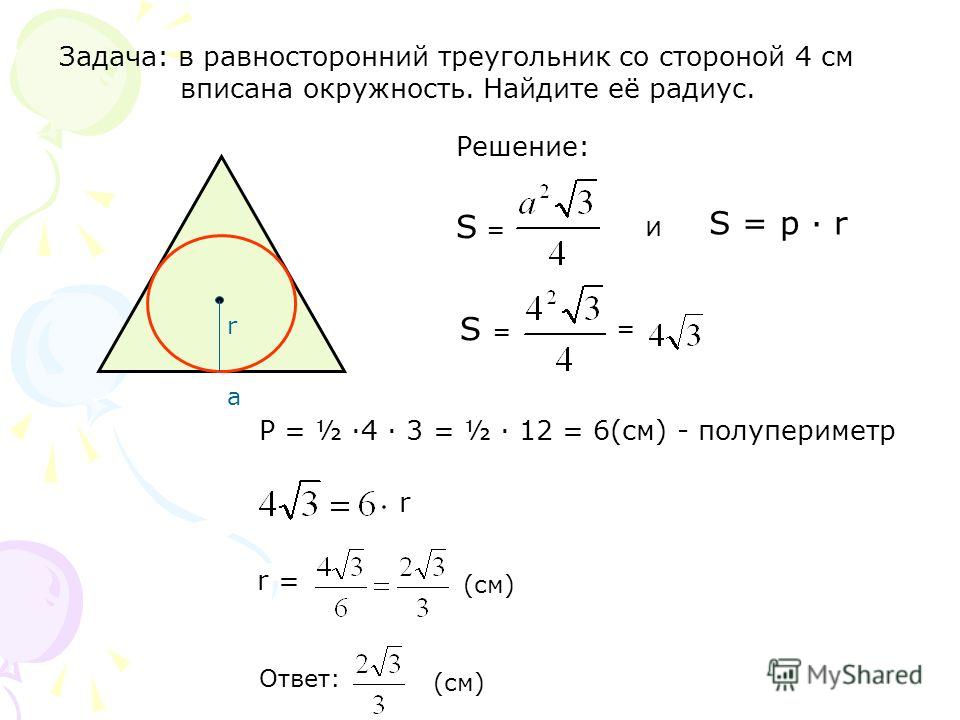 Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.
Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.
Задание B6 (№ 27922)
Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.
Задание B6 (№ 27923)
ЕГЭ Профиль №3. Описанные окружности — math200.ru
Skip to contentЕГЭ Профиль №3. Описанные окружностиadmin2022-08-01T16:07:25+03:00
Скачать файл в формате pdf.
ЕГЭ Профиль №3. Описанные окружности
| Задача 1. Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах. Ответ ОТВЕТ: 122. | |
Задача 2. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95°, 49°, 71°, 145°. Найдите угол B этого четырехугольника. Ответ дайте в градусах. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95°, 49°, 71°, 145°. Найдите угол B этого четырехугольника. Ответ дайте в градусах.Ответ ОТВЕТ: 108. | |
| Задача 3. Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги Ответ ОТВЕТ: 60. | |
| Задача 4. Четырехугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в градусах. Ответ ОТВЕТ: 70. | |
Задача 5. Четырехугольник ABCD вписан в окружность.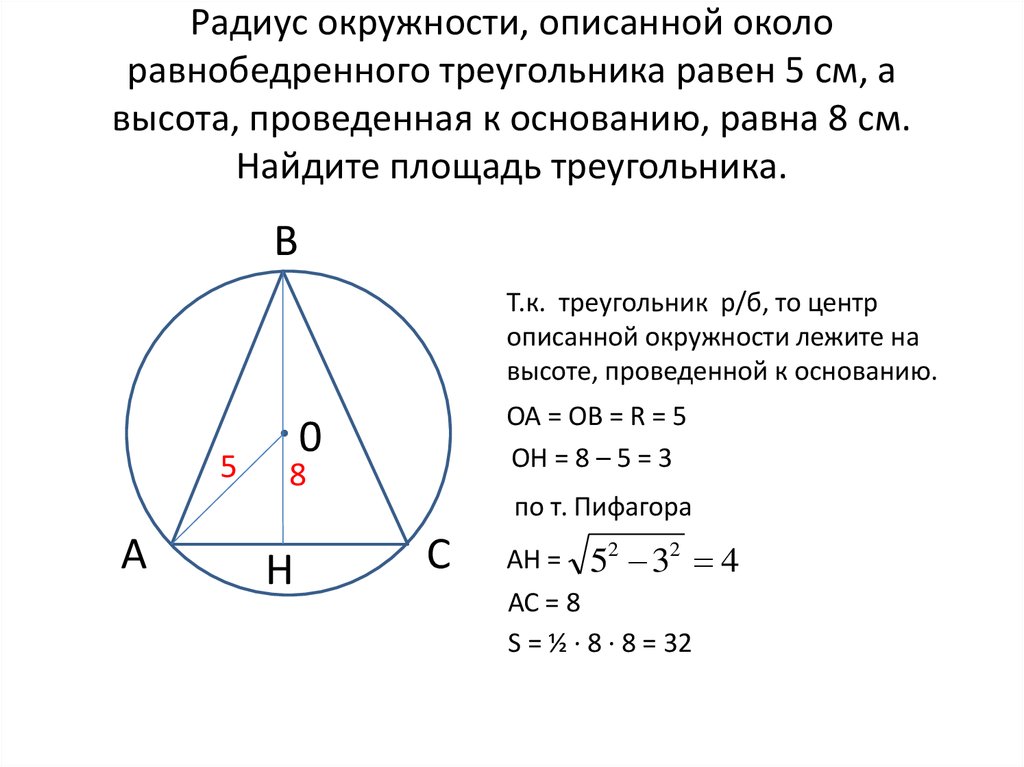 Угол Угол Ответ ОТВЕТ: 110. | |
| Задача 6. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах. Ответ ОТВЕТ: 40. | |
| Задача 7. Сторона правильного треугольника равна \(\sqrt 3 \). Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 1. | |
| Задача 8. Радиус окружности, описанной около правильного треугольника, равен \(\sqrt 3 \). Найдите сторону этого треугольника. ОТВЕТ: 3. | |
| Задача 9. Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 2. | |
Задача 10.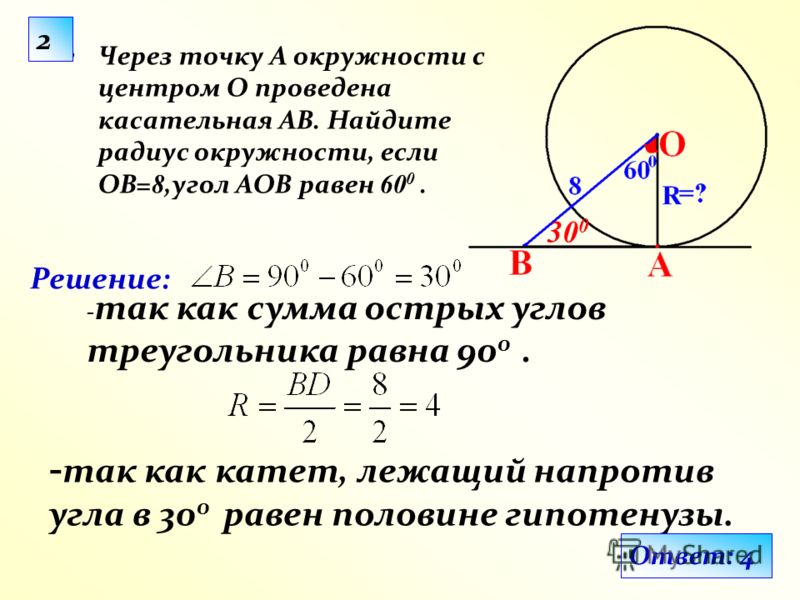 Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.Ответ ОТВЕТ: 4,5. | |
| Задача 11. Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника. Ответ ОТВЕТ: 6. | |
| Задача 12. Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника. Ответ ОТВЕТ: 8. | |
| Задача 13. В треугольнике ABC угол С равен 90°, \(AC = 4,\;\;BC = 3.\) Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 2,5. |
Задача 14. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника. Ответ ОТВЕТ: 2. | |
| Задача 15. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6? Ответ ОТВЕТ: 6. | |
| Задача 16. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 30°. Найдите радиус окружности, описанной около этого треугольника. Ответ ОТВЕТ: 1. | |
| Задача 17. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах. ОТВЕТ: 30. | |
| Задача 18. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30°. Найдите сторону AB этого треугольника. Ответ ОТВЕТ: 3. | |
Задача 19. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 150°. Найдите радиус окружности, описанной около этого треугольника. Противолежащий ей угол C равен 150°. Найдите радиус окружности, описанной около этого треугольника.Ответ ОТВЕТ: 1. | |
| Задача 20. Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол Ответ ОТВЕТ: 150. | |
| Задача 21. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника. Ответ ОТВЕТ: 25. | |
| Задача 22. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции. Ответ ОТВЕТ: 6. | |
Задача 23. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции. Ответ ОТВЕТ: 6. | |
| Задача 24. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции. Ответ ОТВЕТ: 7. | |
| Задача 25. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах. Ответ ОТВЕТ: 122. | |
| Задача 26. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности. ОТВЕТ: 24. | |
| Задача 27. Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 108°. Найдите число вершин многоугольника. Ответ ОТВЕТ: 5. | |
Реклама
Поддержать нас
Как найти площадь равностороннего треугольника
Все математические ресурсы GRE
13 Диагностические тесты 452 практических теста Вопрос дня Карточки Learn by Concept
GRE Math Help » Геометрия » Плоская геометрия » Треугольники » Равнобедренные треугольники » Как найти площадь равностороннего треугольника
Какова площадь равностороннего треугольника с основанием ?
Возможные ответы:
Правильный ответ:
Пояснение:
Равносторонний треугольник можно рассматривать как 2 одинаковых треугольника 30-60-90, что дает треугольнику высоту . Отсюда используйте формулу площади треугольника:
Отсюда используйте формулу площади треугольника:
Сообщить об ошибке
Равносторонний треугольник вписан в окружность радиусом 10. Какова площадь треугольника?
Ответ не может быть определен из предоставленной информации.
Правильный ответ:
Объяснение:
Чтобы решить это уравнение, сначала обратите внимание, что линия, проведенная из начала координат в вершину равностороннего треугольника, делит пополам угол вершины. При этом длина этой линии равна радиусу:
Это, в свою очередь, создает прямоугольный треугольник 30-60-90. Напомним, что отношение сторон треугольника 30-60-90 задается как:
Следовательно, длина стороны может быть равна
Это также половина основания треугольника , поэтому можно найти основание треугольника:
Кроме того, длина стороны равна:
Вертикальный участок, восходящий от начала координат, представляет собой длину радиуса, который в сочетании с более коротким раздел выше дает высоту треугольника:
Площадь треугольника равна половине основания, умноженной на высоту, поэтому мы можем найти ответ следующим образом:
Сообщить об ошибке Равенство 4.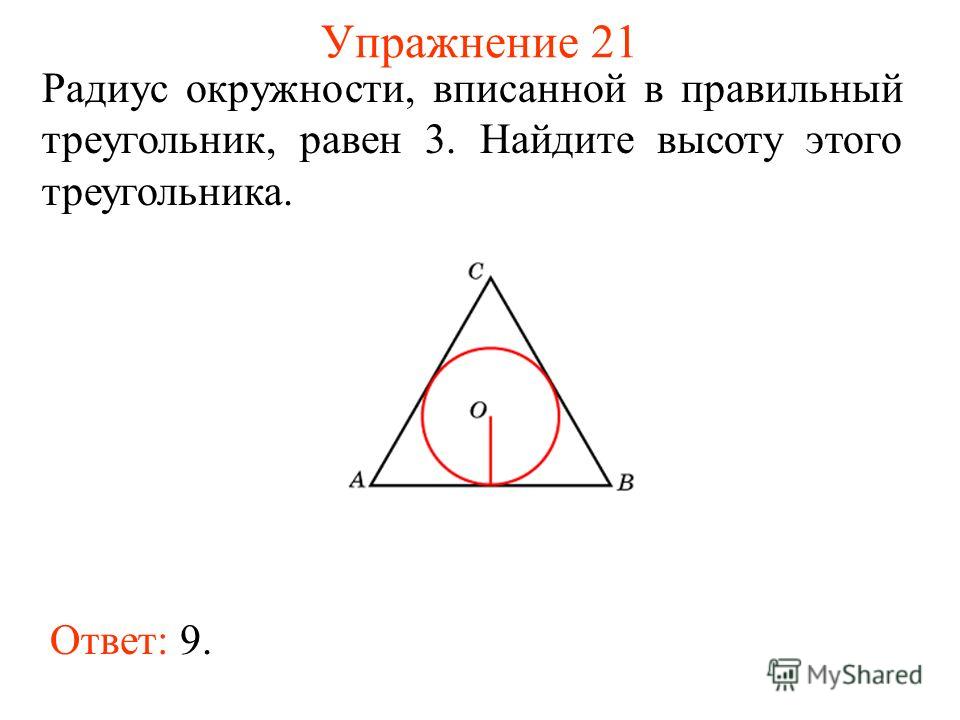
Возможные ответы:
4√3
8
2√3
4
Правильный ответ:
4√3
Пояснение:
Все стороны равностороннего треугольника равны, поэтому все стороны этого треугольника равны 4.
Площадь = 1/2 основания * высота, поэтому нам нужно вычислить высоту: это легко для равностороннего треугольника, поскольку любой такой треугольник можно разделить пополам на два одинаковых треугольника 30:60:90.
Отношение длин треугольника 30:60:90 равно 1:√3:2. Сторона равностороннего треугольника равна 4, и мы разделили основание пополам, когда делили треугольник пополам, так что длина равна 2, поэтому наш треугольник должен иметь стороны 2, 4 и 2√3; таким образом, мы имеем нашу высоту.
Один из наших 30:60:90 треугольников будут иметь основание 2 и высоту 2√3. Половина основания равна 1, поэтому 1 * 2√3 = 2√3.
У нас есть два таких треугольника, так как мы разделили исходный треугольник, поэтому общая площадь равна 2 * 2√3 = 4√3.
Вы также можете найти площадь любого равностороннего треугольника, применив формулу (s 2 √3)/4, где s = длина любой стороны.
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы GRE
13 Диагностические тесты 452 практических теста Вопрос дня Карточки Учитесь по концепции
геометрия — Площадь замкнутых перекрывающихся кругов внутри равностороннего треугольника
Задавать вопрос
спросил
Изменено 5 лет, 3 месяца назад
Просмотрено 647 раз
$\begingroup$
Рассмотрим равносторонний треугольник длины $\sqrt{6}$, как показано на рисунке ниже.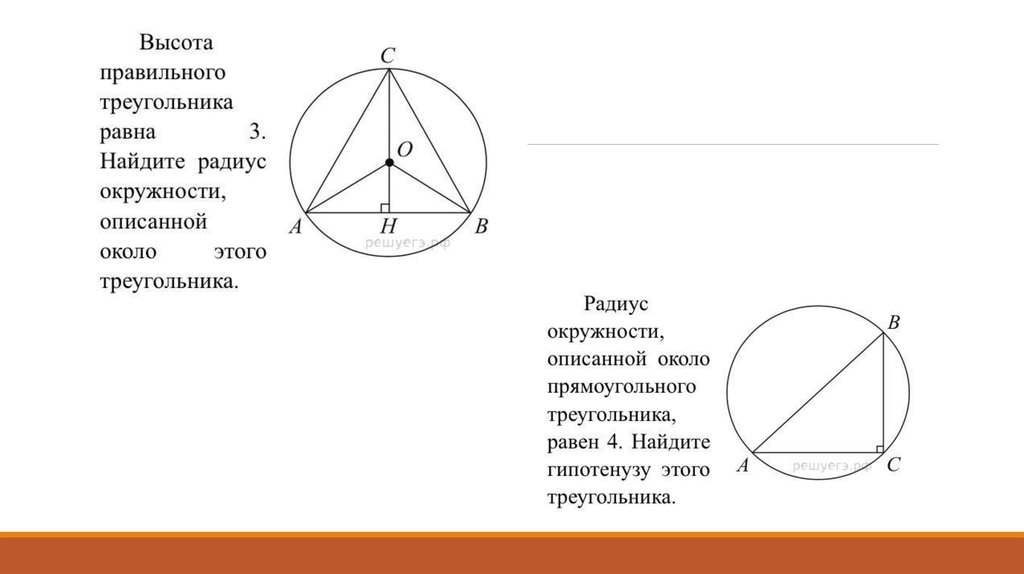 Найдите площадь заштрихованной области.
Найдите площадь заштрихованной области.
Моя попытка: Поскольку сторона треугольника дана, следовательно, высота = $\frac{3}{\sqrt{2}}$.
Так как это равносторонний треугольник, то в силу симметрии три окружности должны пересекаться в центре тяжести.
Отсюда inradius = $\frac{1}{\sqrt{2} }$ и Радиус окружности = $\frac{2}{\sqrt{2} }$.
Пожалуйста, подскажите, как действовать дальше. Любая помощь будет оценена.
- геометрия
- круги
- треугольники
$\endgroup$
$\begingroup$
Обратите внимание, что вы можете разрезать каждый лепесток вдоль пополам, а затем переставить половинки лепестков перемещением, чтобы увидеть, что заштрихованная область имеет ту же площадь, что и часть круга с радиусом описанной окружности равностороннего треугольника минус вписанный правильный шестиугольник. . Поскольку вы вычислили радиус описанной окружности, $r=\sqrt{2}$, площадь круга равна $\pi r^2=2\pi$, а площадь шестиугольника равна $6r^2\sqrt{ 3}/4=3\sqrt{3}$.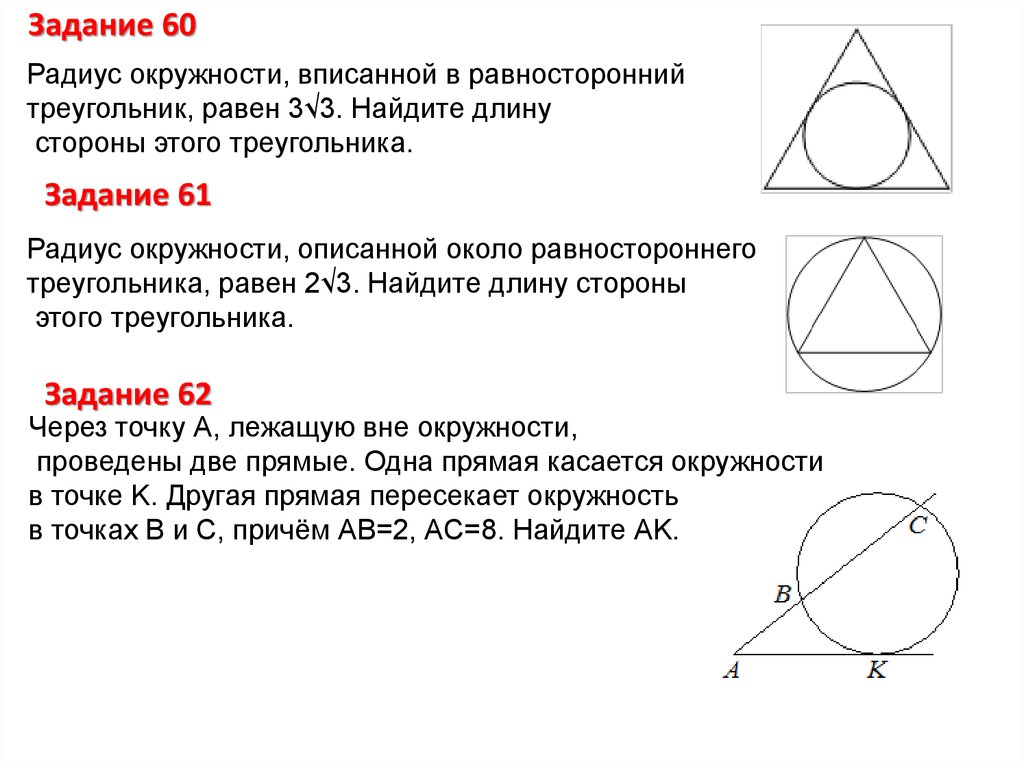

Leave A Comment