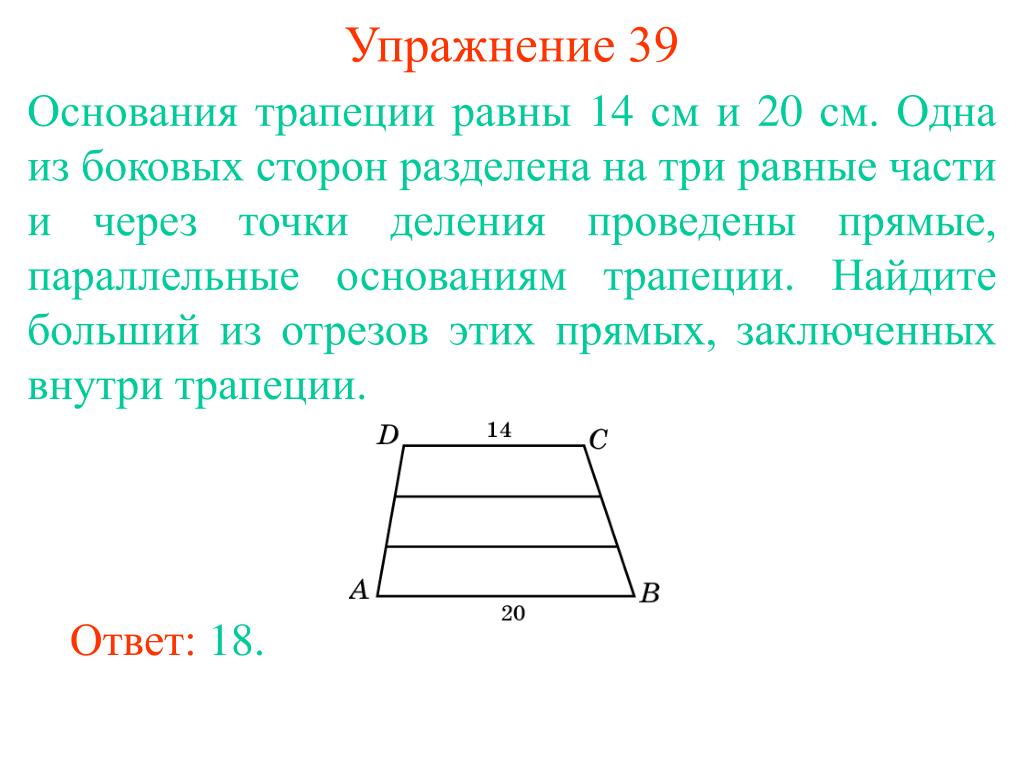
Трапеция, Средняя линия трапеции, треугольник
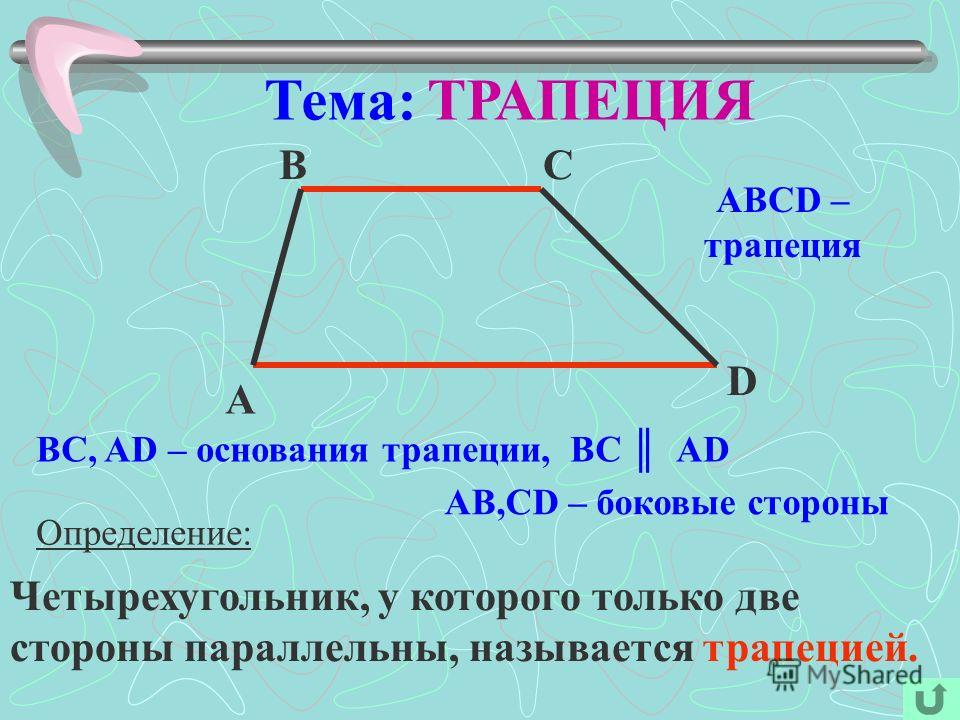
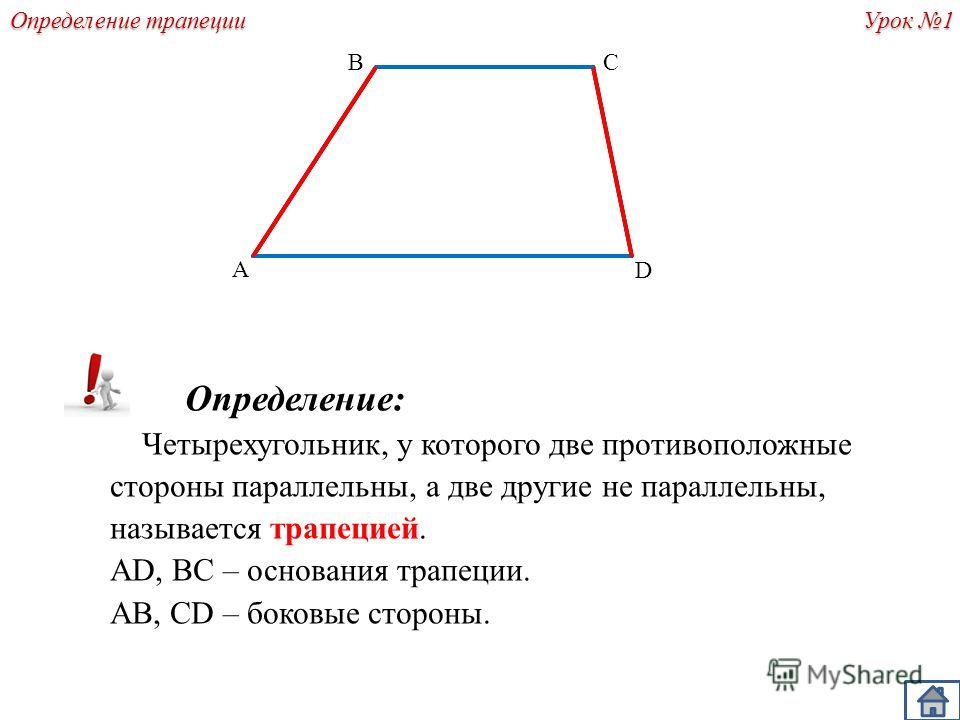
Четырёхугольник, у которого только две стороны параллельны называются трапецией.
Параллельные стороны трапеции называются её основаниями, а те стороны, которые не параллельны, называются боковыми сторонами. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC =>
MN || AB
MN = AB/2
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA1 = A1A2 = A2A3 = A3A4 = A4A5
Мы соединяем A5 с B и проводим такие прямые через A4, A3, A2 и A1, которые параллельны A5B.
 Они пересекают AB соответственно в точках B4, B3, B2 и B1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB
Они пересекают AB соответственно в точках B4, B3, B2 и B1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB В то время как из трапеции B3B1A1A3, B3B2 = B2B1.
Тогда из B2AA2 следует, что B2B1 = B1A. В заключении получаем :
AB1 = B1B2 = B2B3 = B3B4 = B4
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
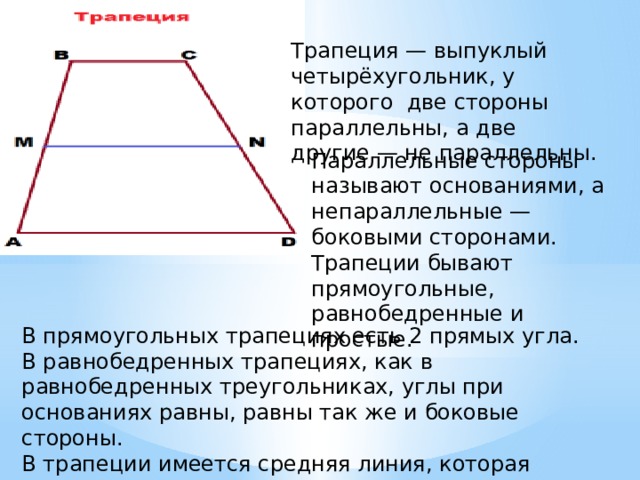
Диагонали трапеции
Свойства диагоналей трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.
Данный отрезок параллелен основаниям трапеции.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
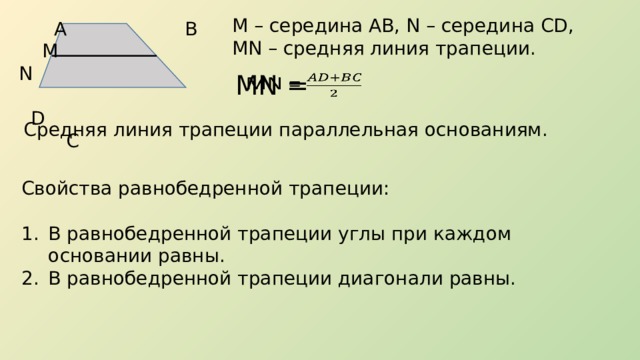
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны

Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание.
 В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ: 16 см
Задача.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
h2 + (24 — a)2 = (5√17)2
и
h2 + (24 — b)2 = 132
Учтем, что a = 16 — b , тогда в первом уравнении
h2 + (24 — 16 + b)2 = 425
h2 = 425 — (8 + b)2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
Получим:
425 — (8 + b)2 + (24 — b)2 = 169
-(64 + 16b + b)2 + (24 — b)2 = -256
-64 — 16b — b2 + 576 — 48b + b2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h2 = 425 — (8 + b)2 = 425 — (8 + 12)2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см2
Ответ: площадь трапеции равна 80 см2.
0
Трапеция (задачи про основания) | Описание курса | Прямоугольная трапеция
Определение, Форма, Площадь, Формулы, Свойства, Факты
Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны, с одной парой параллельных сторон.
Параллельные стороны трапеции называются основаниями, а ее непараллельные стороны называются катетами. Трапеция также может иметь параллельные стороны. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными.
2. Равнобедренная трапеция : Имеет одинаковую длину непараллельных сторон. На изображении стороны AD и BC равны.
Медиана трапеции — это отрезок, соединяющий середины двух непараллельных сторон трапеции.
Площадь трапеции = $\frac{1}{2}$ × (сумма параллельных сторон) × (расстояние между ними)
Следовательно, для показанной выше трапеции со сторонами AB, BC, CD и DA Периметр можно записать как
. Мы можем найти трапеции во многих реальных объектах, например, в лампе, коробке из-под попкорна, сумочке и так далее.
Медиана = $\frac{1}{2}\times (\text{сумма базиса}) = \frac{AD + BC}{2} = \frac{8 + 30}{2} см = 19см$
Площадь = $\frac{1}{2}\times (\text{сумма параллельных сторон})\times (\text{высота})$
1 Высота относится к какой размер трапеции?Высота Ширина Угол Диагональ Правильный ответ: Высота 2 Сколько прямых углов в прямой трапеции?Один Две Три Четыре Правильный ответ: Два 3 В чем разница между трапецией и параллелограммом?Трапеция имеет 2 пары параллельных сторон, а параллелограмм имеет 1 пару параллельных сторон. Трапеция имеет 1 пару параллельных сторон, а параллелограмм имеет 2 пары параллельных сторон. Трапеция имеет 2 стороны, а параллелограмм — 4 стороны. Трапеция имеет 4 равных угла, а параллелограмм имеет все 4 неравных угла. Правильный ответ: Трапеция имеет 1 пару параллельных сторон, а параллелограмм имеет 2 пары параллельных сторон. 4 Как мы называем стороны, которые не параллельны в трапеции?Диагонали трапеции Основания трапеции Катеты трапеции Высота трапеции Правильный ответ: Катеты трапеции |
Все ли трапеции четырехугольники?
Так как трапеции являются замкнутыми фигурами с 4 сторонами, мы также можем называть их четырехугольниками.
Чем трапеция отличается от трапеции?
По определению и трапеция, и трапеция являются четырехугольниками с одной парой параллельных сторон. Но трапеция соответствует американскому английскому, а трапеция соответствует британскому английскому.
Может ли трапеция иметь 4 прямых угла?
Нет, трапеция может иметь либо 2 прямых угла, либо вообще не иметь прямых углов.
Все ли ромбы также трапеции?
Нет, трапеция — это четырехугольник только с одной парой параллельных сторон, тогда как у ромба две пары параллельных сторон, и все они равны друг другу.
Является ли трапеция параллелограммом?
Нет, трапеция не может быть параллелограммом. У трапеции только одна пара параллельных сторон, а у параллелограмма две пары параллельных сторон.
Форма, свойства, формула, определение, примеры
Трапеция очаровательна, потому что она определяется на основе географии, к которой вы принадлежите. Если вы посещаете Великобританию по обмену и просите студента нарисовать для вас трапецию, то он нарисует ее как трапецию. Трапецию также называют трапецией в некоторых частях мира, и это тип четырехугольника с одной парой противоположных сторон, параллельных друг другу.
| 1. | Что такое трапеция? |
2. | Свойства трапеции |
| 3. | Типы трапеций |
| 4. | Формула трапеции |
| 5. | Часто задаваемые вопросы о трапеции |
Что такое трапеция?
Трапеция, также известная как трапеция, представляет собой многоугольник с четырьмя сторонами или четырехугольник. Он имеет один набор противоположных сторон, которые параллельны, и набор непараллельных сторон. Параллельные стороны известны как основания, а непараллельные стороны известны как катеты трапеции.
Определение трапеции
Трапеция — это четырехсторонняя замкнутая двумерная фигура, имеющая площадь и периметр. Две стороны фигуры параллельны друг другу и называются основаниями трапеции. Непараллельные стороны известны как стороны или боковые стороны трапеции. Кратчайшее расстояние между двумя параллельными сторонами называется высотой. Поскольку противоположные стороны параллельны друг другу, вычислить площадь трапеции несложно.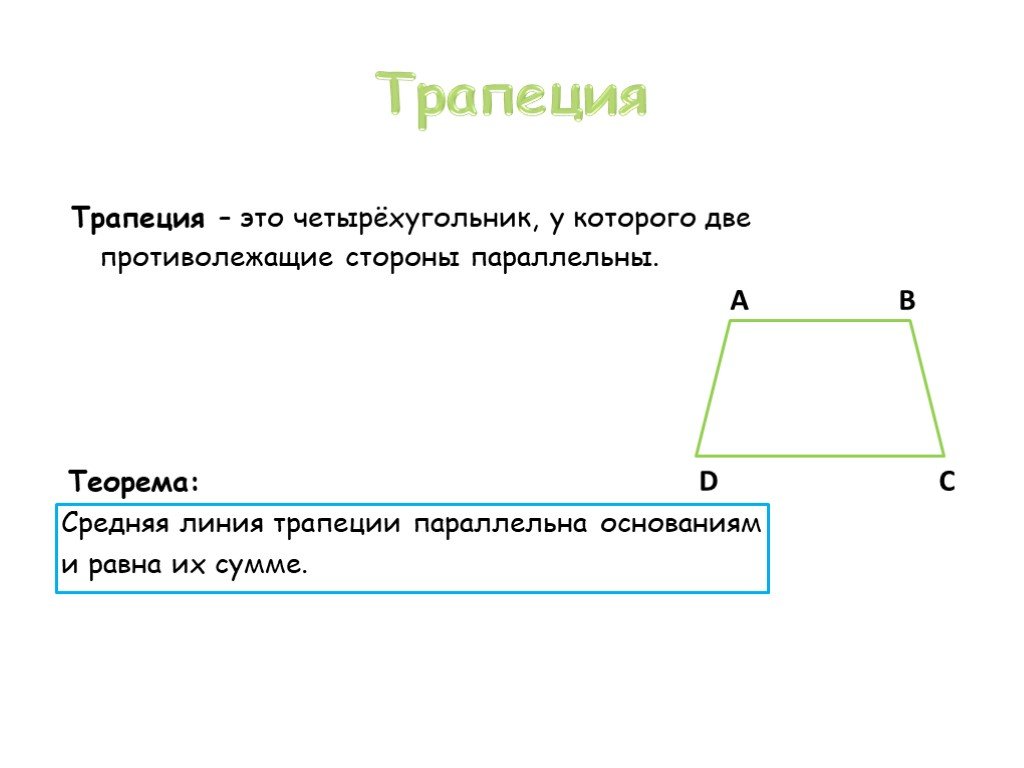
Свойства трапеции
Эти свойства трапеции отличают ее от других четырехугольников:
- Основания (верхнее и нижнее) параллельны друг другу
- Противоположные стороны равнобедренной трапеции имеют одинаковую длину
- Углы рядом друг с другом в сумме дают 180°
- Медиана параллельна обоим основаниям
- Длина медианы равна среднему значению обоих оснований, т.е. (a +b)/2
- Если обе пары противоположных сторон трапеции параллельны, она считается параллелограммом
- Если обе пары противоположных сторон параллельны, все стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то трапецию можно рассматривать как квадрат
- Если обе пары противоположных сторон параллельны, ее противоположные стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то трапецию можно рассматривать как прямоугольник
Типы трапеций
Существует три типа трапеций, они приведены ниже:
- Равнобедренная трапеция
- Трапециевидная трапециевидная форма
- Правая трапеция
Равнобедренная трапеция
Если катеты или непараллельные стороны трапеции равны по длине, то она называется равнобедренной трапецией. Углы параллельных сторон (основания) в равнобедренной трапеции равны между собой. У равнобедренной трапеции есть линия симметрии и обе диагонали равны по длине.
Углы параллельных сторон (основания) в равнобедренной трапеции равны между собой. У равнобедренной трапеции есть линия симметрии и обе диагонали равны по длине.
В приведенной ниже равнобедренной трапеции XYZW, XY и WZ называются основаниями трапеции. WX и YZ называются катетами трапеции, так как они не параллельны друг другу.
Разносторонняя трапеция
Если ни стороны, ни углы трапеции не равны, то это разносторонняя трапеция. В приведенной ниже разносторонней трапеции все четыре стороны, то есть AB, BC, CD и DA, имеют разную длину. Основания, то есть DC и AB, параллельны друг другу, но имеют разную длину.
Прямоугольная трапеция
Прямоугольная трапеция, также называемая прямоугольной, имеет пару прямых углов. Эти виды трапеций используются для оценки площадей под кривой. В приведенной ниже прямой трапеции или прямоугольной трапеции есть два прямых угла, один в D, а другой в A. Одна пара противоположных сторон, то есть DC и AB, параллельны друг другу.
Формула трапеции
Есть две основные формулы трапеции, это:
- Площадь трапеции
- Периметр трапеции
Площадь трапеции
Площадь трапеции вычисляется путем измерения среднего значения параллельных сторон и умножения его на высоту. Чтобы найти площадь трапеции, нужно знать длины двух ее параллельных сторон и расстояние (высоту) между ними. Это количество единичных квадратов, которое может поместиться внутри фигуры, и измеряется в квадратных единицах, таких как см 2 , m 2 , in 2 и т. д. Формула площади (A) трапеции вычисляется по основаниям, т.е. a и b, высота которых равна h, что является перпендикулярным расстоянием между a и b .
Отсюда площадь трапеции вычисляется по следующей формуле:
Площадь = [(AB + CD)/2] × h
A = [(a + b)/2] × h
Где,
- AB и CD = параллельные стороны
- а = короткая база
- b = удлиненная база
- h = высота или высота над уровнем моря
Периметр трапеции
Периметр трапеции определяется как общая длина границы формы, т.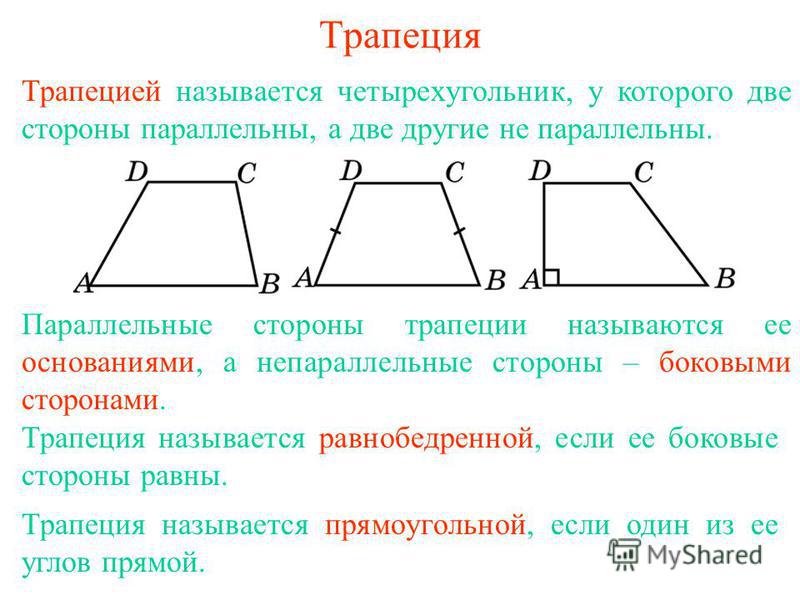 е. сумма всех ее сторон. Так как трапеция является двумерной фигурой, то и периметр будет лежать только в двумерной плоскости. Рассмотрим трапецию ABCD, как показано ниже, с размерами сторон a, b, c и d. Давайте рассмотрим формулу трапеций. Формула периметра трапеции вычисляется путем нахождения суммы всех сторон, т. Е. AB + BC + CD + DA
е. сумма всех ее сторон. Так как трапеция является двумерной фигурой, то и периметр будет лежать только в двумерной плоскости. Рассмотрим трапецию ABCD, как показано ниже, с размерами сторон a, b, c и d. Давайте рассмотрим формулу трапеций. Формула периметра трапеции вычисляется путем нахождения суммы всех сторон, т. Е. AB + BC + CD + DA
Периметр трапеции = сумма всех сторон = a + b + c + d
, где a, b, c и d — стороны трапеции.
☛Связанные темы о трапеции
Ниже перечислены некоторые темы, связанные с трапецией.
- Рабочие листы трапеций
- Калькулятор периметра трапеции
- Ромб
- Квадрат
- 3D-фигуры
Примеры трапеций
Пример 1: Если площадь трапеции 128 дюймов, а длины оснований 12 дюймов и 20 дюймов, какова будет высота трапеции?
Решение:
Предположим, что основания равны a и b, а высота трапеции равна h.
 Используя данную информацию,
Используя данную информацию,Мы должны найти h, который является расстоянием или высотой между основаниями. Подставим все эти значения в площадь трапеции по формуле:
A = [(a + b)/2] × h
128 = [(20 + 12)/2] × h
256 = 32 × h
h = 8 дюймов
Следовательно, высота трапеция равна 8 дм.
Пример 2: Сару попросили найти площадь трапеции со сторонами 13, 8, 17 и 8 единиц. Вы можете помочь ей?
Решение:
Предположим, что a и b — основания, а h — высота данной трапеции.
Вышеприведенная трапеция может быть представлена следующим образом:
13 + х + х = 17
13 + 2х = 17
2х = 4
Следовательно, х = 2
. из треугольников,
8 2 = 2 2 + H 2
64 = 4 + H 2
H 2 = 60
H =
9000 2 9000 2 9000 2 9000 29000 2
9000 2
9000 2
H =
9 2
9000 2
H 2 = 60
H .
 ×15
×15h=2√15
Наконец, мы воспользуемся формулой площади трапеции, чтобы найти ее площадь:
A = [(a + b)/2] × h
A = [(13 + 17)/2] × 2√15
A = (60√15)/2
A=30√15 квадратных единиц
Следовательно, площадь данной трапеции равна 30√15 квадратных единиц
Пример 3: Четыре стороны трапеции имеют размеры 10 единиц, 7 единиц, 5 единиц и 9 единиц. Чему равен периметр трапеции?
Решение: Периметр трапеции равен сумме всех сторон.
Периметр = 10 + 7 + 5 + 9
= 31 единица
Следовательно, периметр данной трапеции равен 31 единице.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Запись на бесплатный пробный урок
Практические вопросы по трапеции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о трапеции
Что такое трапеция?
Трапеция — это четырехсторонняя замкнутая 2D-форма, имеющая площадь и периметр. Его также называют трапецией. Стороны трапеции параллельны друг другу и называются основаниями трапеции. Непараллельные стороны известны как стороны или боковые стороны трапеции. Кратчайшее расстояние между двумя параллельными сторонами называется высотой.
Его также называют трапецией. Стороны трапеции параллельны друг другу и называются основаниями трапеции. Непараллельные стороны известны как стороны или боковые стороны трапеции. Кратчайшее расстояние между двумя параллельными сторонами называется высотой.
Какие бывают трапеции?
Трапеции классифицируются на основе характера их сторон. Основные типы трапеций перечислены ниже:
- Равнобедренная трапеция
- Трапециевидная трапециевидная форма
- Правая трапеция
Каковы основные свойства трапеции?
Существует много свойств трапеции, некоторые из них перечислены ниже:
- Верхнее и нижнее основания трапеции параллельны.
- Равнобедренная трапеция состоит из равных по длине противоположных сторон.
- Смежные углы в сумме дают 180°.
Как найти площадь трапеции?
Площадь трапеции вычисляется путем вычисления среднего значения двух параллельных сторон и умножения его на высоту.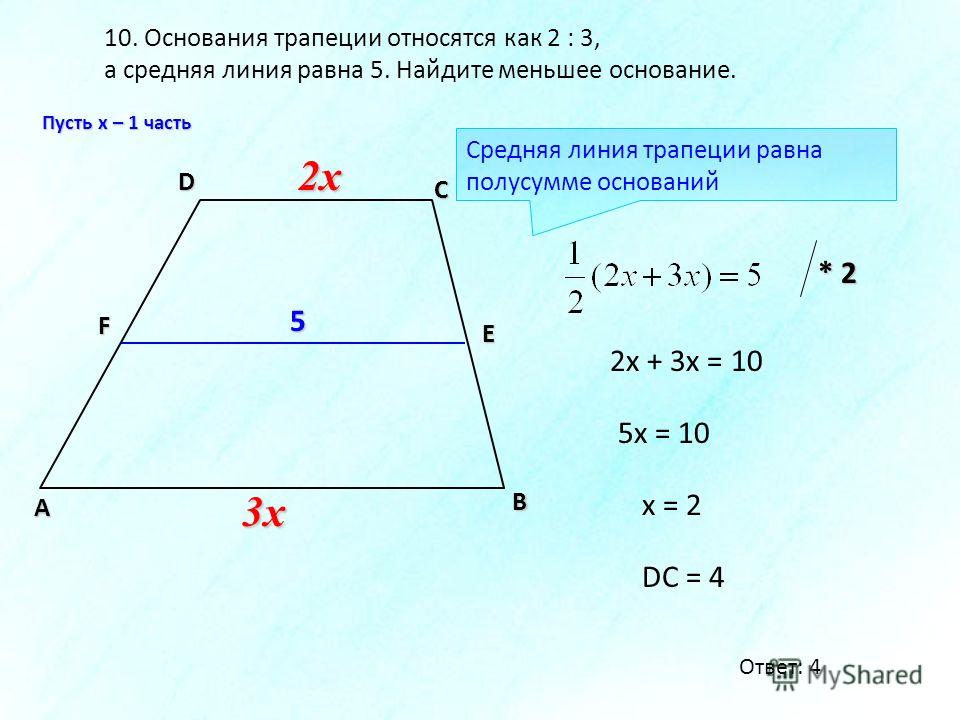
Площадь = [(a + b)/2] × h, где a и b — длины оснований, а h — высота.
Какое уравнение трапеции?
Есть два уравнения трапеции. Одно уравнение вычисляет его площадь; другой — его периметр. Периметр трапеции PQRS определяется как Периметр = PQ + QR + RS + PS. Площадь трапеции = [(a + b)/2] x h, где a и b — длины оснований, а h — высота.
Является ли трапеция четырехугольником?
Поскольку у трапеции четыре стороны, она автоматически становится четырехугольником. У него есть две стороны, которые параллельны, и две стороны, которые не параллельны.
Каковы три атрибута трапеции?
Тремя основными атрибутами трапеции являются следующие
- Углы при основании и диагонали равны, если трапеция равнобедренная
- Точка пересечения диагоналей лежит на одной прямой с серединами двух противоположных сторон
- Противоположные стороны равнобедренной трапеции конгруэнтны
Как найти недостающую сторону трапеции?
Недостающую сторону трапеции можно определить по предоставленной вам информации.

 Используя данную информацию,
Используя данную информацию,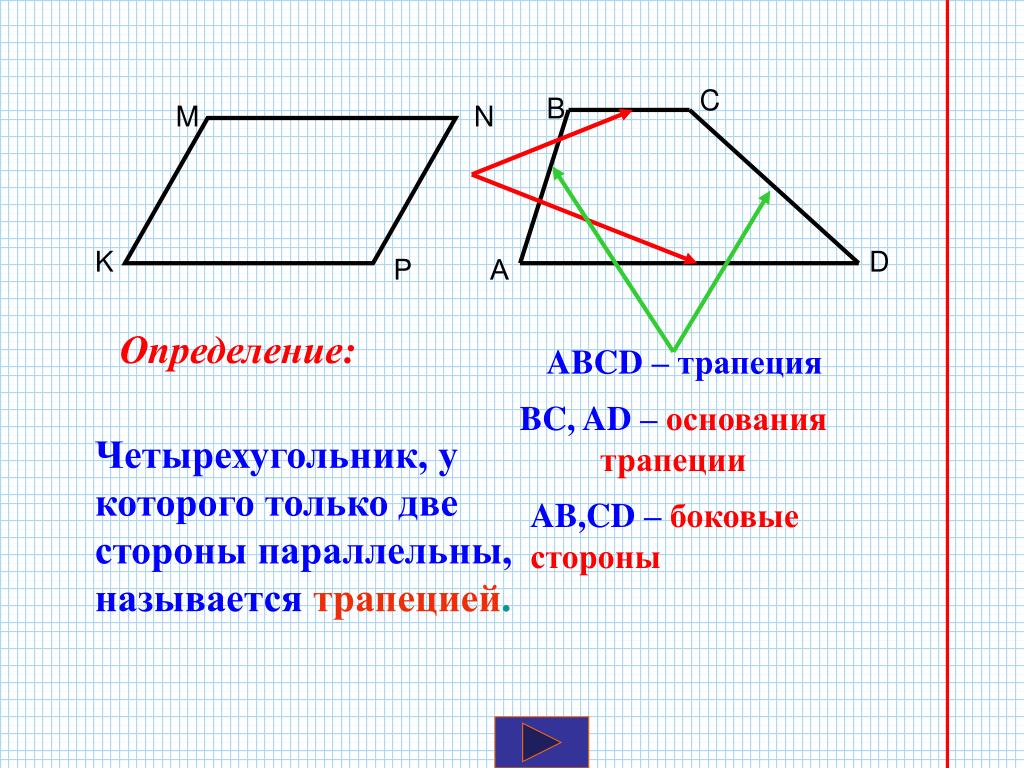 ×15
×15
Leave A Comment