Вписанная в ромб окружность | Треугольники
Какими свойствами обладает вписанная в ромб окружность? Как найти её радиус?
Центр вписанной в ромб окружности — точка пересечения его диагоналей.
Радиус вписанной в ромб окружности можно найти по общей формуле
где S — площадь ромба, p — его полупериметр.
Так как полупериметр ромба равен p=2a, где a — сторона ромба, эту формулу можно записать как
С учётом формул для нахождения площади ромба:
где α — угол ромба (причем α может быть как острым, так и тупым).
где d1и d2 — диагонали ромба.
Таким образом, еще две формулы радиуса вписанной в ромб окружности:
Так как диаметр вписанной окружности равен высоте ромба, радиус равен половине высоты ромба:
Если известно, что точка касания вписанной окружности делит сторону ромба на отрезки, то радиус можно выразить через длины этих отрезков.
Так как диагонали ромба взаимно перпендикулярны и радиус, проведённый в точку касания, перпендикулярен стороне, то по свойству высоты прямоугольного треугольника из треугольника AOD имеем
Следовательно, радиус вписанной в ромб окружности есть среднее пропорциональное между отрезками, на которые делит сторону точка касания:
Радиус вписанной окружности в ромб
Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:

- Диагонали ромба взаимно перпендикулярны.
- Диагонали ромба являются биссектрисами его внутренних углов.
Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами
1 способ. Радиуса вписанной окружности в ромб через высоту
Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.
Следовательно формула радиуса вписанной окружности в ромб через высоту:

2 способ. Радиус вписанной окружности в ромб через диагонали
Площадь ромба можно выразить через радиус вписанной окружности , где Р– периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P=4×а. Тогда
, где Р– периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P=4×а. Тогда 
Но площадь ромба также равна половине произведения его диагоналей 
Прировняв правые части формул площади, имеем следующее равенство

В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали

 Пример расчета радиуса окружности вписанной в ромб, если известны диагонали
Пример расчета радиуса окружности вписанной в ромб, если известны диагоналиНайти радиус окружности вписанной в ромб, если известно, что длина диагоналей 30 см и 40 см
Пусть ABCD-ромб, тогда AC и BD его диагонали. AC=30 см, BD=40 см
Пусть точка О – это центр вписанной в ромб ABCD окружности, тогда она будет также являться и точкой пересечения его диагоналей, делящих их пополам.


т.к диагонали ромба пересекаются под прямым углом, то треугольник AOB прямоугольный. Тогда по теореме Пифагора
 , подставляем в формулу ранее полученные значения
, подставляем в формулу ранее полученные значения
AB = 25 см
Применив ранее выведенную формулу для радиуса описанной окружности в ромб, получаем

3 способ. Радиус вписанной окружности в ромб через отрезки m и n

Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом. , т.к. является радиусом, проведенным в точку касания окружности . Следовательно OF – высота треугольника AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
, т.к. является радиусом, проведенным в точку касания окружности . Следовательно OF – высота треугольника AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.
Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности

 Пример расчета радиуса окружности вписанной в ромб, если известны отрезки m и n
Пример расчета радиуса окружности вписанной в ромб, если известны отрезки m и nНайдите радиус описанной окружности в ромб, если точка касания делит сторону ромба на 9 и 4
Пусть ABCD-ромб, тогда AC и BD его диагонали.
Пусть точка O – это центр вписанной в ромб ABCD окружности.
Пусть точка F – точка касания окружности со стороной ромбаAB. Тогда. AF=9, BF=4
Применив ранее полученную формулу, получаем

Радиус вписанной окружности в ромб
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :


Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :


2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :

- Подробности
- Автор: Administrator

-
В ромб вписана окружность
Когда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений.
Точка касания вписанной в ромб окружности делит его сторону на отрезки
В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике.
Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны).
— как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда
Высота ромба через радиус вписанной окружности
Радиус вписанной в ромб окружности
Радиус вписанной окружности можно найти по формуле
S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба).
Соответственно, площадь ромба через радиус вписанной в него окружности
Поскольку площадь ромба также равна
Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как
Ромб — Формулы | Свойства
Для расчёта всех основных параметров ромба воспользуйтесь калькулятором.
Свойства ромба
- Противолежащие стороны ромба параллельны и равны.
- Диагонали ромба перпендикулярны.
- Точка пересечения диагоналей делит их пополам.
- Диагонали ромба являются биссектрисами его углов.
- Диагонали образуют из ромба 4 прямоугольных треугольника.
- Любой ромб может содержать окружность с центром в точке пересечения его диагоналей.
- Сумма квадратов диагоналей равна квадрату одной из сторон ромба умноженному на четыре
Признаки ромба
- Параллелограмм с перпендикулярными диагоналями является ромбом.
- Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то эта фигурой будет ромб.
Примечание: Не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом, так как прежде всего ромб это частный случай параллелограмма, а следовательно должен иметь все его признаки - Если в параллелограмм можно вписать круг, то он является ромбом
Формулы стороны ромба
Длина стороны ромба через площадь (S) и высоту (AE)
$$ AB = {S \over AE} $$Длина стороны ромба через площадь (S) и синус угла
$$ AB = {\sqrt{S} \over \sqrt{sin(∠CDA)}} = {\sqrt{S} \over \sqrt{sin(∠DAB)}} $$Длина стороны ромба через диагонали
$$ AB = {\sqrt{AC^2 + DB^2} \over 2} $$Длина стороны ромба через диагональ и угол
$$ AB = {BD \over 2 * cos(∠CDA)} = {AC \over 2 * cos(∠DAB)} $$Длина стороны ромба через периметр
$$ AB = {P \over 4} $$Формулы диагоналей ромба
Длина большой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
$$ BD = AB * \sqrt{2 + 2 * cos(∠CDA)} $$ $$ BD = AB * \sqrt{2 — 2 * cos(∠DAB)} $$Длина малой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
$$ AC = AB * \sqrt{2 — 2 * cos(∠CDA)} $$ $$ AC = AB * \sqrt{2 + 2 * cos(∠DAB)} $$Длина диагонали ромба через сторону и другую диагональ
$$ BD = \sqrt{4 * AB^2 + AC^2} $$ $$ AC = \sqrt{4 * AB^2 + BD^2} $$Длина диагонали ромба через площадь и другую диагональ
$$ BD = {2 * S \over AC} $$ $$ AC = {2 * S \over BD} $$Длина диагонали ромба через тангенс острого tg(∠CDA) или тупого tg(∠DAB) угла и другую диагональ
$$ BD = AC * tg({∠DAB \over 2 }) $$ $$ AC = BD * tg({∠CDA \over 2 }) $$Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
$$ S = AB * AE $$Площадь ромба через сторону и синус любого угла
$$ S = AB^2 * sin(∠CDA) = AB^2 * sin(∠DAB) $$Площадь ромба через две диагонали
$$ S = {1 \over 2} * AC * BD $$Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
$$ S = {1 \over 2} * BD^2 * tg({∠CDA \over 2}) $$ $$ S = {1 \over 2} * AC^2 * tg({∠DAB \over 2}) $$Формулы радиуса круга вписанного в ромб
Радиус вписанного круга в ромб через высоту ромба (AE)
$$ R = {AE \over 2} $$Радиус вписанного круга в ромб через площадь и сторону ромба
$$ R = {S \over 2 * AB} $$Радиус вписанного круга в ромб через сторону и синус любого угла
$$ R = {AB * sin(∠CDA) \over 2} = {AB * sin(∠DAB) \over 2} $$Радиус вписанного круга в ромб через диагональ и синус угла
$$ R = {BD * sin(∠CDA / 2) \over 2} $$ $$ R = {AC * sin(∠DAB / 2) \over 2} $$Радиус вписанного круга в ромб через две диагонали
$$ R = {BD * AC \over 2 * \sqrt{BD^2 + AC^2}} $$Формулы высоты ромба
Высота ромба через сторону и угол
$$ AE = AB * sin(∠CDA) = AB * sin(∠DAB) $$Высота ромба через диагональ и угол
$$ AE = BD * sin({∠CDA \over 2}) $$ $$ AE = AC * sin({∠DAB \over 2}) $$Высота ромба через диагонали
$$ AE = {BD * AC \over \sqrt{BD^2 + AC^2}} $$Высота ромба через диагонали и сторону
$$ AE = {BD * AC \over 2 * AB} $$Формулы углов ромба
Косинус углов через диагональ и сторону
$$ cos(∠CDA) = {BD \over 2 * AB^2} — 1 = 1 — {AC \over 2 * AB^2} $$ $$ cos(∠DAB) = {AC \over 2 * AB^2} — 1 = 1 — {BD \over 2 * AB^2} $$Синусы углов через диагонали
$$ sin(∠CDA) = sin(∠DAB) = {2 * BD * AC \over BD^2 + AC^2} $$Синусы углов через площадь и сторону
$$ sin(∠CDA) = sin(∠DAB) = {S \over AB^2} $$Тангенс половинных углов через диагонали
$$ tg(∠CDA) = {AC \over BD} $$ $$ tg(∠DAB) = {BD \over AC} $$Радиус вписанной окружности в ромб
Радиус вписанной окружности в ромб
Существует свойство окружности, которую можно вписать в четырехугольник. Для этого должно выполняться всего одно условие: сумма одной пары противоположных сторон должна быть равна сумме другой пары противоположных сторон.
Поскольку для ромба это условие выполняется, то окружность можно вписать в любой ромб. Центр вписанной окружности и точка пересечения диагоналей ромба совпадают.
Рассмотрим несколько способов вычисления радиуса вписанной в ромб окружности
1 вариант. Вычислить радиус вписанной окружности через высоту.
Поскольку высота ромба и диаметр вписанной окружности равны, что следует из свойств прямоугольника, образованного диаметром вписанной окружности и высотой ромба.
Запишем формулу радиуса вписанной окружности:
2 вариант. Вычислить радиус вписанной окружности через диагонали.
Рассмотрим формулу площади ромба через радиус вписанной окружности:
С другой стороны площадь ромба можно найти через диагонали:
Приравняем правые части записанных формул площадей и получим:
Из этого равенства выразим радиус:
Вписанная окружность | Треугольники
Что такое вписанная окружность?Какими свойствами она обладает?
Определение.
Вписанная в выпуклый многоугольник окружность — это окружность, которая касается всех сторон этого многоугольника (то есть каждая из сторон многоугольника является для окружности касательной).
Центр вписанной окружности лежит внутри многоугольника.
Многоугольник, в который вписана окружность, называется описанным.
В выпуклый многоугольник можно вписать окружность, если биссектрисы всех его внутренних углов пересекаются в одной точке.
Центр вписанной в многоугольник окружности — точка пересечения его биссектрис.
Центр вписанной окружности равноудален от сторон многоугольника. Расстояние от центра до любой стороны равно радиусу вписанной окружности (По свойству касательной, сторона описанного многоугольника перпендикулярна радиусу, проведённому в точку касания).
По свойству касательных, проведённых из одной точки, любая вершина описанного многоугольника равноудалена от точек касания, лежащих на сторонах, выходящих из этой вершины.
Пример.
Окружность с центром в точке O и радиусом r вписана в пятиугольник ABCDE.
ABCDE — описанный пятиугольник.
O — точка пересечения биссектрис ABCD, то есть ∠EAO=∠BAO, ∠ABO=∠CBO, ∠BCO=∠DCO, ∠CDO=∠EDO, ∠AEO=∠DEO.
Точка O равноудалена от точек касания. Расстояние от точки O до любой из сторон равно радиусу: OK=OL=ON=OM=OP=r.
Вершины ABCDE равноудалены от соответствующих точек касания:
AM=AN, BN=BL, CL=CK, DK=DP, EP=EM.
В любой треугольник можно вписать окружность. Центр вписанной в треугольник окружности называется инцентром.
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. В частности, в трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон.
В любой правильный многоугольник можно вписать окружность. Около любого правильного многоугольника можно также описать окружность. Центр вписанной и описанной окружностей лежат в центре правильного многоугольника.
Для любого описанного многоугольника радиус вписанной окружности может быть найден по формуле
где S — площадь многоугольника, p — его полупериметр.
Кроме основной, существуют формулы для нахождения радиуса вписанной окружности в частных случаях (для правильных многоугольников, отдельных видов треугольников, трапеции, ромба и т.д.).
Урок Круг, вписанный в ромб
Круг, вписанный в ромб
Этот урок посвящен одной проблеме.
Задача
Для данного ромба постройте окружность, вписанную в ромб .Чтобы решить эту проблему, мы подразделяем ее на более мелкие подзадачи.
Проблема 1
Где находится центр круга, вписанного в ромб?
| Решение — Мммм… Он расположен в центре ромба. — ОК. Тогда где же находится центр ромба? — Мммм … На пересечении его диагоналей. — ОК. Это верно. Теперь ответьте на вопрос: почему центр вписанной окружности — Мммм … | Рисунок 1 .К проблеме 1 |
Если круг вписан в ромб, он вписан в каждый из четырех внутренних углов ромба.
Следовательно, центр вписанной окружности расположен на биссектрисах внутренних углов ромба. Но биссектриса ромба — это его диагональ.
Следовательно, центр вписанной окружности лежит в точке пересечения диагоналей ромба.
— Очень хорошо. Вам пришла основная идея решить эту строительную задачу.
Чтобы завершить эту часть урока, я хотел бы дать ссылки на уроки, где были доказаны соответствующие геометрические факты.
То, что центр вписанной в угол окружности находится под биссектрисой угла, был доказан на уроке Свойства биссектрисы угла в теме
Треугольники раздела Геометрия на этом сайте.
То, что диагонали ромба являются биссектрисами, было доказано на уроке «Диагонали ромба, делят пополам его углы» в теме Параллелограммы
раздела Геометрия на этом сайте.
Задача 2
Постройте радиус круга, вписанного в данный ромб.
| Решение Если окружность вписана в ромб, то сторона ромба касательная к окружности. Это визуально видно из Рисунок 2 . Примем его сейчас без формальных доказательств. (Это будет доказано позже в одном из следующих уроков). Следовательно, чтобы построить радиус вписанной окружности | Рисунок 2 . К проблеме 2 |
Другими словами, мы должны построить перпендикуляр от центра ромба, который является точкой диагонального пересечения, до стороны ромба.
Алгоритм построения перпендикуляра от точки вне прямой к прямой с помощью линейки и циркуля был описан в уроке
Как разделить отрезок пополам с помощью циркуля и линейки. Этот урок находится в теме Треугольники раздела Геометрия на этом сайте.
Итак, у вас есть алгоритм для построения радиуса вписанной окружности в ромб.
Конструкция Задача 2 решена.
В качестве последнего шага этого урока я бы хотел, чтобы вы решили следующие
Задача 3
Вычислить радиус окружности, вписанной в данный ромб.
Ромб имеет размер стороны, размер диагонали и.
| Решение Как мы договорились выше при решении Задачи 2 , радиус окружности, вписанной в данный ромб, — это перпендикуляр , проведенный от центра окружности (который является точкой пересечения диагоналей) в сторону от ромб в точке касания. Диагонали ромба перпендикулярны и делят друг друга пополам. | Рисунок 3 . К проблеме 3 |
Итак, наша исходная задача сводится к следующей:
найти высоту прямоугольного треугольника, проведенного из прямой угловой вершины к гипотенузе .
Параметры этого прямоугольного треугольника: размеры его катетов a и b и мера гипотенузы c (, рис. 4 ), связанные с параметрами исходного ромба равенствами
| ,,. Пусть x и y — это размеры отрезков, на которых высота отсекает Мы хотим вывести формулу, выражающую z через a , b и c . Существует несколько способов вывести такую формулу. | Рисунок 4 .Высота прямоугольного треугольника |
и получить из него, что
.
Но я не думаю, что в этом уроке вы знакомы с понятием площади треугольников.
Поступая иначе, можно заметить, что треугольник ACD подобен треугольнику ABC ( Рисунок 4 ), чтобы получить пропорцию из этого факта
и, наконец, получить ту же формулу из пропорции
.
Но я не думаю, что в этом уроке вы знакомы с понятием подобия треугольников.
На этом уроке я действительно хочу получить формулу для z из «первых принципов».
Добавим уравнения (1) и (2) (обе части). Мы получили
, г.
или
(5),
потому что
по теореме Пифагора для прямоугольного треугольника ABC .
Сравнивая уравнения (4) и (5), получаем
.(6)
Возвести в квадрат обе части уравнения (6). Ты получаешь
. (7)
Подставить выражения
и
в уравнение (7). (Обратите внимание, что эти выражения представляют собой переписанные уравнения (1) и (2)). Ты получаешь
.
Раскройте квадратные скобки и отмените подобные условия. Ты получаешь
, г.
или
.
Теперь извлеките квадратный корень из обеих частей. Ты получаешь
, г.
, что является нашей целью.
Теперь, возвращаясь к нашему первоначальному ромбу, формула для радиуса вписанной окружности имеет вид
.
Сводка
Из этого урока вы узнали, что центр круга, вписанного в ромб, находится на пересечении его диагоналей.
Вы узнали, как построить радиус вписанного круга, используя линейку и циркуль.
Вы научились рассчитывать радиус круга, вписанного в ромб.
Вы узнали, что есть разные способы получить целевую формулу, и узнали, как получить эту формулу, исходя из «первых принципов».
По пути вы узнали, как вычислить высоту прямоугольного треугольника, проведенного к гипотенузе, с помощью его катетов и мер гипотенузы.
Ниже приведены несколько примеров, показывающих, как работает формула.
Пример 1
Ромб имеет размеры диагонали 40 см и 30 см.
Найдите радиус круга, вписанного в ромб.
Решение
Давайте сначала найдем длину стороны ромба.
Обратите внимание, что диагонали ромба перпендикулярны и делят друг друга пополам. Итак, диагонали ромба делят его на четыре равных прямоугольных треугольника
с размерами ног и, где и — размеры диагоналей ромба.
Найдите размер стороны ромба как длину гипотенузы прямоугольного треугольника с катетами 40/2 = 20 см и 30/2 = 15 см:
.
Получается длина стороны 25 см.
Или вы можете напрямую применить формулу из урока Длина диагоналей ромба, который находится в текущей теме Геометрия раздела Задачи Word
, г.
где и — размеры диагоналей ромба, а — длина его стороны.
Подставьте диагонали ромба в эту формулу.
, г.
и вы получите те же 25 см для длины стороны ромба.
Итак, теперь вы знаете, что размеры диагонали ромба составляют 40 см и 30 см, а длина стороны — 25 см.
Хорошо, очень хорошо.
Теперь используйте формулу теоремы из этого урока, чтобы вычислить радиус окружности, вписанной в ромб:
.
Получаем 12 см для радиуса круга, вписанного в ромб.
Ответ . Радиус круга, вписанного в ромб, составляет 12 см.
Пример 2
Ромб имеет одну диагональ длиной 18 см и периметр 60 см.
Решение
Давайте сначала найдем длину стороны ромба.
Равен одной четвертой периметра, то есть 60/4 = 15 см.
Обратите внимание, что диагонали ромба перпендикулярны и делят друг друга пополам.Итак, диагонали ромба делят его на четыре равных прямоугольных треугольника. Для этих треугольников вам известна длина гипотенузы, которая равна длине стороны ромба, равной 15 см, и длина одной ноги, которая составляет половину известной длины диагонали 18/2 = 9 см.
Найдите неизвестную длину катета одного из этих прямоугольных треугольников, применив формулу Пифагора к треугольнику с гипотенузой 15 см и длиной катета 9 см:
.
Получаем длину второй ножки прямоугольного треугольника 12 см.
Так как это половина размера диагонали ромба, весь размер диагонали равен 2 * 12 см = 24 см.
Или вы можете применить формулу, полученную в уроке Длина диагоналей ромба, которая находится в текущей теме Геометрия раздела Задачи Word на этом сайте:
, г.
где — заданная, а — неизвестная величина диагоналей ромба, а — длина его стороны.
Подставьте данные для ромба в эту формулу
, г.
, и вы получите те же 24 см для длины второй диагонали ромба.
Итак, теперь вы знаете, что размеры диагонали ромба составляют 18 см и 24 см, а длина стороны — 15 см.
Хорошо, очень хорошо.
Теперь используйте формулу теоремы из этого урока, чтобы вычислить радиус окружности, вписанной в ромб:
.
Вы получите радиус круга, вписанного в ромб, в 7,2 см.
Ответ . Радиус круга, вписанного в ромб, равен 7,2 см.
Мои другие уроки ромбов на этом сайте
— Диагонали ромба перпендикулярны
— Диагонали ромба делят его углы пополам
— Длина диагоналей ромба
— КАК решать задачи по сторонам ромба и размерам диагоналей — Примеры,
— Длина диагоналей ромба
— СВОЙСТВА РОМБИСА
Для навигации по всем темам / урокам Онлайн-учебника по геометрии используйте этот файл / ссылку ГЕОМЕТРИЯ — ВАШ ОНЛАЙН-УЧЕБНИК.
.вписанных и описанных окружностей и многоугольников в GMAT
вписанных и описанных
Еще один сложный тип геометрической диаграммы включает многоугольники «внутри» окружностей или окружности «внутри» многоугольников. Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на окружности:
На этой диаграмме неправильный пятиугольник ABCDE равен , вписанному в круг , а круг — , описанному вокруг пятиугольника, .Мы также можем сказать: круг ограничивает пятиугольник. Слово «вписанный» описывает внутреннюю форму, а слово «ограниченный» описывает внешнюю форму. Вот еще одна диаграмма с многоугольником снаружи.
Обратите внимание, что каждая сторона этого неправильного пятиугольника составляет касательной к окружности. Теперь пятиугольник — это , описанный по окружности, а круг — это , вписанный в в пятиугольник .В обоих случаях внешняя форма описывается, а внутренняя форма вписывается.
Треугольники
Как это часто бывает при обсуждении многоугольников, треугольники являются особым случаем при обсуждении вписанного и описанного. Каждый возможный треугольник может быть вписан в один круг и описывать другой круг . Это «универсальное двойное членство» верно ни для каких других многоугольников более высокого порядка — оно верно только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой.
Обратите внимание, что, когда один угол особенно тупой, близкий к 180 °, разница в размерах между описанной окружностью и вписанной окружностью становится довольно большой. Также обратите внимание: в случае прямоугольного треугольника, второго изображения, гипотенуза треугольника — это диаметр описанной окружности. Мы вернемся к этому моменту.
Четырехугольники
Многие четырехугольники нельзя ни вписать в круг, ни описать кругом: то есть невозможно построить круг, проходящий через все четыре вершины, а также невозможно построить круг, к которому все четыре стороны касаются друг друга.
Некоторые четырехугольники, например продолговатый прямоугольник, можно вписать в круг, но нельзя описать круг. Другие четырехугольники, такие как наклонный ромб, описывают круг, но не могут быть вписаны в него.
Несколько элитных четырехугольников могут описывать один круг и вписываться в другой круг. Конечно, квадрат (внизу слева), самый элитный из четырехугольников, обладает этим свойством. Другой пример — «правый воздушный змей» (внизу справа), воздушный змей с парой противоположных прямых углов:
Хотя это «двойное членство» верно для всех треугольников, оно ограничено некоторыми особыми случаями с четырехугольниками.
Высшие многоугольники
То, что было верно для четырехугольников, верно и для всех высших многоугольников.
а. Большинство, подавляющее большинство, не могут ни описать круг, ни вписать круг.
г. Некоторые можно вписать в круг, но нельзя описать круг.
г. Некоторые могут описать круг, но не могут быть вписаны в круг.
г. Некоторые избранные могут как описать круг, так и быть вписанными в него.
Последняя категория, элитные члены, всегда включает правильный многоугольник.Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники. Вот галерея правильных многоугольников, как с вписанной, так и с описанной окружностью.
Очевидно, что с увеличением количества сторон размеры двух окружностей становятся все ближе и ближе.
Вопросы GMAT о вписанных и описанных многоугольниках встречаются редко и могут проверить как ваше понимание терминологии, так и ваши навыки визуализации, описывая геометрическую ситуацию (например,грамм. «Прямоугольник JKLM вписан в круг») и , а не , что дает вам диаграмму.
Особый случай: треугольник, вписанный в полукруг.
Это особый случай, который нравится GMAT. Он появляется в OG13 (DS # 118) и может легко появиться где-нибудь в разделе Quant вашего настоящего GMAT.
Если все, что вы знаете, это то, что KL — это диаметр окружности, этого достаточно, чтобы установить, что ∠J = 90 ° и что треугольник JKL является прямоугольным треугольником с KL в качестве гипотенузы.С другой стороны, если все, что вам известно, это то, что треугольник JKL является прямоугольным с KL в качестве гипотенузы, этого достаточно, чтобы установить, что дуга KJL является полукругом, а KL — диаметром. Это мощный набор идей, потому что выводы работают в обоих направлениях и потому, что он неразрывно связывает две, казалось бы, несопоставимые идеи.
Кстати, этот пост — четвертый в серии из пяти статей. Вот вся серия.
1) Введение в окружности в GMAT
2) Геометрия GMAT: круги и углы
3) Круговые и линейные диаграммы в GMAT
4) Вписанные и замкнутые круги и многоугольники в GMAT
5) Разбиение на части Круги GMAT: длина дуги, секторы и число Пи
Практический вопрос
1) На диаграмме выше буква S — центр круга.Если QS = 5 и QR = 6, что такое PQ?
A. 7
B. 8
C. 9
D. 10
E. 11
Практическое объяснение вопроса
1) Прежде всего, QS — это радиус, поэтому если QS = 5 , это означает, что PS = SR = 5 и диаметр PR = 10. Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR является прямоугольным треугольником с QPQR = 90 °. Нам известны две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.2 = 100 — 36 = 64
PQ = sqrt {64} = 8
Ответ = B
Самые популярные ресурсы
О Майке Мэгэрри
Майк создает уроки экспертов и практические вопросы для руководства GMAT студенты к успеху. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания в области математики, естественных наук и стандартизированных экзаменов. Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидных черепных дефектов, он настаивает на том, чтобы болеть за Нью-Йорк Метс..подписанных и подписанных кругов
В этом уроке мы покажем, какие вписанные и описанные круги используют треугольник и квадрат. Круги можно размещать внутри многоугольника или вне многоугольника.
Вписанные круги
Когда круг помещается внутри многоугольника, мы говорим, что круг вписан в многоугольник. Ниже показаны два примера окружностей, вписанных в треугольник и квадрат.
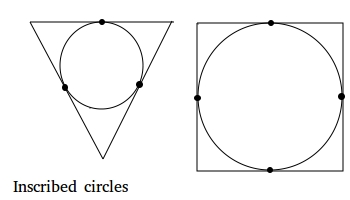
Обратите внимание, как каждая сторона треугольника касается окружности ровно в одной точке.Точно так же каждая сторона квадрата касается круга ровно в одной точке.
Также обратите внимание, что у треугольника есть 3 точки касания, так как у квадрата 3 стороны и 4 точки касания, так как у него 4 стороны.
Вообще говоря, когда окружность вписана в многоугольник с n сторонами, будет n точек касания.
Описанные окружности
Когда окружность помещается вне многоугольника и каждая вершина многоугольника лежит на окружности, мы говорим, что круг описан вокруг многоугольника.Ниже показаны два примера окружностей, описанных вокруг треугольника и квадрата.
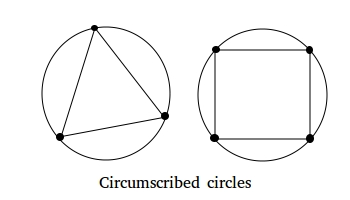
Обратите внимание, как каждая вершина треугольника или круга лежит на окружности. Также обратите внимание, что на окружности треугольника лежат 3 точки, поскольку у треугольника 3 вершины.
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
,Радиус круга, вписанного в ромб
- Детали
- Написал Администратор

1. Радиус круга, вписанного в ромб, если вы знаете диагональ, сторону и угол.

 ,
,  — диагонали ромба
— диагонали ромба
 — сторона
— сторона
 — острый угол ромба
— острый угол ромба
 — центр окружности
— центр окружности






2. Радиус круга, вписанного в ромб, если известна высота

 — высота ромба
— высота ромба
 — сторона ромба
— сторона ромба
 — центр окружности
— центр окружности
Формула для расчета радиуса вписанной окружности ромба при заданной высоте ( r ):

,



Leave A Comment