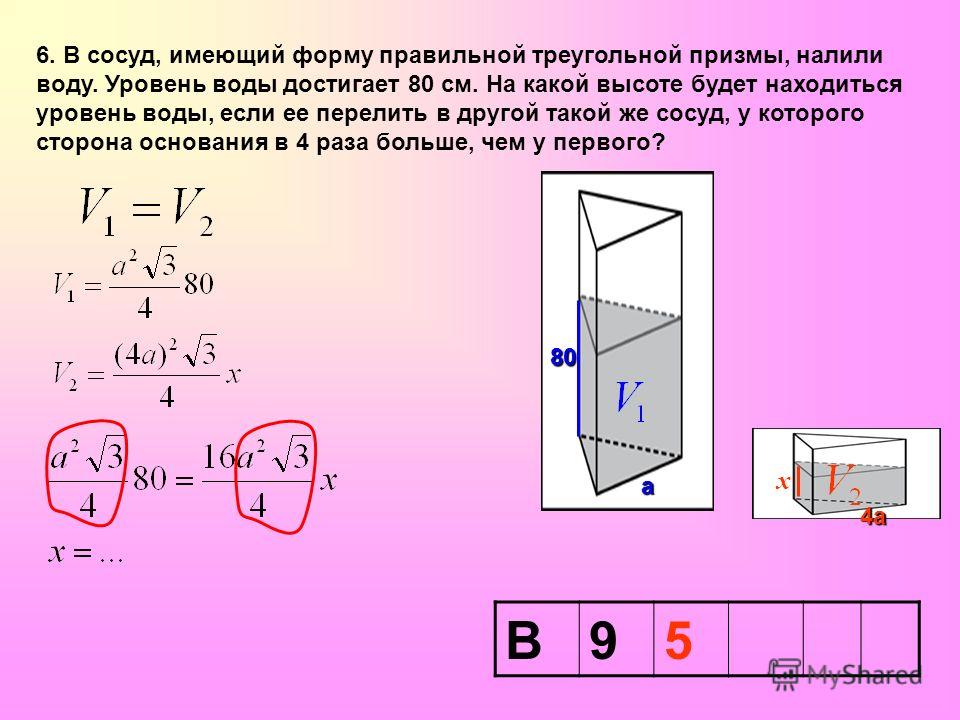
Задание №13 ЕГЭ по математике базового уровня с решением
В 13 задании ЕГЭ базового уровня мы будем иметь дело с задачами по стереометрии, но не абстрактными, а наглядными примерами. Это могут быть задачи на уровень жидкости в сосудах, которую я разобрал ниже, или же задачи на модификации фигуры — например, у которой отрезали вершины. Нужно быть готовым к решению простых задач по стереометрии — они обычно сводятся сразу к задачам на плоскости, необходимо только правильно посмотреть на чертеж.
Разбор типовых вариантов заданий №13 ЕГЭ по математике базового уровня
Вариант 13МБ1
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
Алгоритм выполнения:
- Записать формулу объема цилиндра.
- Подставить значения для цилиндра с жидкостью в первом и во втором случае.

- Объем жидкости не изменялся, следовательно, можно приравнять объемы.
- Полученное уравнение решить относительно второй высоты h2.
- Подставить данные и вычислить искомую величину.
Решение:
Запишем формулу объема цилиндра.
Если вы забыли формулу объема цилиндра, то напомню, как ее можно легко вывести. Объем простых фигур, таких как куб и цилиндр, можно вычислить умножив площадь основания на высоту. Площадь основания в случае с цилиндром равна площади окружности, которую, вы, наверняка помните: π • r2.
Следовательно, объем цилиндра равен π • r2 • h
Подставим значения для цилиндра с жидкостью в первом и во втором случае.
V1 = π r1
V2 = π r2 2 h2
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
Левые части равны, значит можно приравнять и правые.
π r1 2 h1 = π r2 2 h2
Полученное уравнение решим относительно второй высоты h2.
h2 – неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
h2 =( π r1 2 h1)/ π r2
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 .
Подставим r2 = 4 r1 в выражение для h1.
Получим: h2 =( π r1 2 h1)/ π (4 r1) 2
Полученную дробь сократим на π, получим h2 =( r1 2 h1)/ 16 r1 2
Полученную дробь сократим на r1, получим h2 = h1/ 16.
Подставим известные данные: h2 = 80/ 16 = 5 см.
Ответ: 5.
Вариант 13МБ2
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй),
b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a
Объем первой коробочки в 2 раза меньше объема второй.
Ответ: 2.
Вариант 13МБ3
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 1,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 1,5c2)/ ( 9a
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
Получим:
V1 / V2 = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2) = 1,5/9 = 15/(10 · 9) = 3/(2 · 9) = 1/ (2 · 3) = 1/6.
Объем первой коробочки в 6 раза меньше объема второй.
Ответ: 6.
Вариант 13МБ4
От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?
Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
Вариант 13МБ5
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
Алгоритм выполнения
- Записываем ф-лу для вычисления объема цилиндра.
- Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
- Формируем формулы для объема 1-го и 2-го цилиндров.
- Вычисляем отношение объемов.
Решение:
Объем цилиндра равен: V=πR2H. Обозначим радиус основания 1-го цилиндра через R1, а его высоту – через Н1. Соответственно, радиус основания 2-го цилиндра обозначим через R2, а высоту – через Н2.
Отсюда получим: V1=πR12H1, V2=πR22H2.
Запишем искомое отношение объемов:
.
Подставляем в полученное отношение числовые данные:
.
Вывод: объем 2-го цилиндра больше объема 1-го в 6 раз.
Вариант 13МБ6
В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
Алгоритм выполнения
- Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V1 и V2.
- Фиксируем значение для V1. Выражаем V2 через V1. Находим значение V2.
- Переводим результат, полученный в литрах, в куб.см.
Решение:
Объем бака до погружения V1=5 (л). Т.к. после погружения детали объем стал равным V2. Согласно условию, увеличение составило 1,4 раза, поэтому V2=1,4V1.
Отсюда получаем: V2=1,4·5=7 (л).
Т.о., разница объемов, которая и составляет объем детали, равна:
V2–V1=7–5=2 (л).
2 л=2·1000=2000 (куб.см).
Вариант 13МБ7
Вода в сосуде цилиндрической формы находится на уровне h=80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.
Алгоритм выполнения
- Записываем ф-лу для расчета объема цилиндра.
- На основании этой формулы записываем 2 уравнения – для вычисления объема воды в 1-м и 2-м сосудах. Для этого используем в формуле соответствующие индексы 1 и 2.
- Поскольку воду просто переливают их одного сосуда в другой, то ее объем не изменяется. Поэтому приравниваем полученные уравнения. Из полученного единственного уравнения находим уровень воды во 2-м сосуде, выраженный высотой h2.

Решение:
Объем цилиндра равен: V=Sоснh=πR2h.
Объем воды в 1-м сосуде: V1=πR12h1.
Объем во 2-м сосуде: V2=πR22h2.
Приравниваем V1 и V2: πR12h1=πR22h2.
Сокращаем на π, выражаем h2:
.
По условию R2=2R1. Отсюда:
.
Вариант 13МБ8
От деревянной правильной треугольной призмы отпилили все ее вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые ребра на рисунке не изображены)?
Алгоритм выполнения
- Определяем количество вершин у треугольной призмы.
- Анализируем изменения, которые произойдут при отпиливании всех вершин. Подсчитываем кол-во вершин у нового многогранника.

Решение:
Вершины призмы формируют вершины оснований (верхнего и нижнего). Поскольку основаниями правильной треугольной призмы являются правильные треугольники, то вершин у такой призмы 3·2=6 штук.
Спилив вершины призмы, получим вместо них небольшие (по сравнению с размерами самой призмы) треугольники. Это отображено и на рисунке. То есть вместо каждой вершины образуется 3 новых. Следовательно, их кол-во станет равным: 6·3=18.
Вариант 13МБ9
Даны две коробки, имеющие форму правильной четырехугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза ниже второй, а вторая второе уже первой. Во сколько раз объем первой коробки больше объема второй?
Алгоритм выполнения
- Вводим обозначения для линейных параметров коробок и их объемов.
- Определяем зависимость линейных параметров согласно условию.
- Записываем формулу для вычисления объема призмы.
- Адаптируем эту формулу для объемов коробок.

- Находим отношение объемов.
Решение:
Т.к. форма коробок – правильная призма, то в их основании лежат квадраты. Поэтому можем обозначить длину и ширину каждой коробки одинаково. Пусть для первой коробки это а1, а для второй а2. Высоты коробок обозначим соответственно h1 и h2. Объемы – V1 и V2.
Согласно условию, h2=4,5h1, а1=3а2.
Объем призмы равен: V=Sоснh. Т.к. в основании коробок лежит квадрат, то Sосн=а2. Отсюда: V=a2h.
Для 1-й коробки имеем: V1=a12h1. Для 2-й коробки: V2=a22h2.
Тогда получаем отношение:
Ответ: 2
Вариант 13МБ10
В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
Алгоритм выполнения
- Доказываем, что данные в условии конусы подобны.
- Определяем коэффициент подобия.
- Используя свойство для объемов подобных тел, находим объем жидкости.
Решение:
Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.
По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.
Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V1, малого – V2. Получим:
Получим:
.
Поскольку по условию V1=1600 мл, то V2=1600/8=200 мл.
Вариант 13МБ11
Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?
Алгоритм выполнения
- Записываем формулу для вычисления объема шара.
- Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
- Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.
Решение:
Объем шара вычисляется по ф-ле: .
Отсюда объем 1-го (большего) шара равен , 2-го (меньшего) шара – .
Составим отношение объемов:
Подставляем в полученную формулу числовые данные из условия:
Вывод: объем большего шара в 64 раза больше.
Вариант 13МБ12
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Алгоритм выполнения
- Записываем формулу для определения площади бок.
 поверхности цилиндра.
поверхности цилиндра. - Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
- Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.
Решение:
Площадь бок.поверхности цилиндра вычисляется так: S=2πRH.
Для 1-го цилиндра имеем: S1=2πR1H1. Для 2-го цилиндра: S2=2πR2H2.
Составим отношение этих площадей:
Найдем числовое значение полученного отношения:
Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.
Вариант 13МБ13
Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
Алгоритм выполнения
- Записываем формулу для определения массы большего шаров через плотность и объем.
- Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).

- Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
- Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.
Решение:
Масса большего (1-го) шара равна: m1=ρV1. Объем этого шара составляет V1=(4/3)πR13. Отсюда получаем: m1=(4/3)πρR13. Из этого уравнения выразим плотность: .
Масса меньшего (2-го) шара равна: m2=ρV2. Объем шара: V2=(4/3)πR23. В ур-ние для m2 подставим выражения для ρ и V2. Получаем:
Вычисляем m2:
Вариант 13МБ14
В бак, имеющий форму правильной четырехугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объем детали сложной формы, ее полностью погружают в эту жидкость. Найдите объем детали, если после ее погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Чтобы измерить объем детали сложной формы, ее полностью погружают в эту жидкость. Найдите объем детали, если после ее погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
Алгоритм выполнения
- Определяем часть призмы, соответствующую объему погруженной детали.
- Вычисляем объем детали на основании формулы для определения объема прямой призмы с квадратом в основании.
Решение:
Погруженная в жидкость деталь занимает объем, соответствующий столбу жидкости, высота которого равна 10 см, т.е. разнице, возникшей между начальной высотой жидкости и конечной (после погружения). Это означает, что деталь имеет объем, равный части жидкости, занимающей объем 40х40х10 (см).
Найдем этот объем:
V=40·40·10=16000 (см3).
Цилиндр — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
№16
Цилиндр
№16.
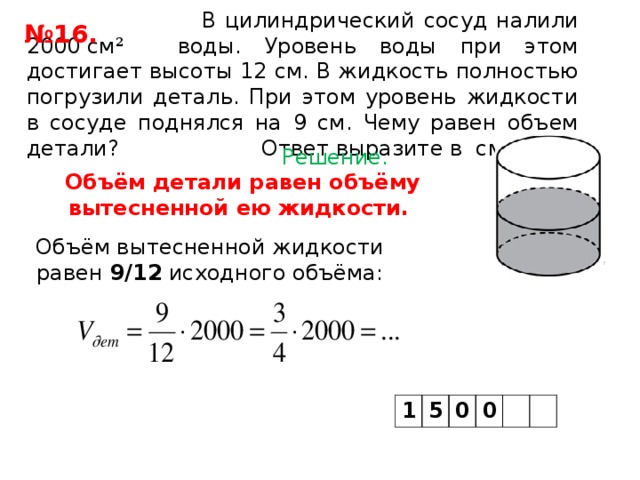
В цилиндрический сосуд налили 2000 см² воды.
Уровень воды при этом достигает высоты 12 см. В жидкость
полностью погрузили деталь. При этом уровень жидкости в
сосуде поднялся на 9 см. Чему равен объем детали?
Ответ выразите в см²
Решение.
Объём детали равен объёму вытесненной ею
жидкости.
Объём вытесненной жидкости равен
9/12 исходного объёма:
Vдет
9
3
2000 2000 …
12
4
1 5 0 0
В цилиндрическом сосуде уровень жидкости
достигает 16 см. На какой высоте будет находиться уровень
жидкости, если ее перелить во второй сосуд, диаметр которого
в 2 раза больше первого?
Ответ выразите в см. Решение.
Решение.
V1 V2
№16.
Vц S H
Отсюда высота
Vц R H
Vц
Vц 1
H
2
2
R
R
2
Число π — это величина постоянная, объем жидкости
V в данной задаче тоже не изменяется.
То есть, высота уровня жидкости обратно пропорциональна
радиусу основания сосуда.
Так как радиус увеличился в 2 раза, то высота
уменьшится в 4 раза. ( 2²= 4 )
4
Н1 16
h3
…(см)
4
4
№16. Объем первого цилиндра равен 12 м3. У второго
цилиндра высота в три раза больше, а радиус основания —
в два раза меньше, чем у первого. Найдите объем второго
цилиндра. Ответ дайте в кубических метрах.
Решение.
Пусть объём первого цилиндра равен
объём второго
V2 R2 H 2
2
V1 R1 h2
2
где R₁ R₂ — радиусы оснований цилиндров, H₁ H₂ — их высоты.
Т.к.
Н 2 3Н1 , R2 0,5R2 ,
то выразим объём второго цилиндра через объём первого:
2
3
3
2
R1
V2 R2 H 2 3h2 R1 h2 V1
4
4
2
3
3
V2 V1 12 . ..
..
9
4
4
2
№16. Одна цилиндрическая кружка вдвое выше второй, зато
вторая в полтора раза шире. Найдите отношение объема второй
кружки к объему первой.
Решение.
Пусть объёмы первой и второй кружек равны
V1 R1 h2
2
V2 R2 H 2
2
R2 2
Н1 2 Н 2 , R1
R2 ,
1,5 3
2
2
2
V1 R1 h2 R2 2 H 2
3
2
2
V2 R2 H 2
R2 H 2
2
V1 R1 h2
4 2
R2 2 H 2
9
Т.к.
9
…
8
1 ,
1 2 5
№16.Даны две кружки цилиндрической формы. Первая
кружка вдвое выше второй, а вторая в четыре раза шире
первой. Во сколько раз объём второй кружки больше
объёма первой?
Решение.
Пусть объёмы первой и второй кружек равны
V1 R1 h2
V2 R2 H 2
1
Т.к. Н 2 Н 2 , R2 4 R1 ,
2
2
2
V2 4 R1 0,5h2
2
V2 R2 H 2 4 R1 0,5h2
…
2
2
V1 R1 h2
R1 h2
2
2
8
№16.
Радиус основания цилиндра равен 2, высота равна 3.
Найдите площадь боковой поверхности цилиндра,
деленную на π
Решение.
Площадь боковой поверхности цилиндра
S 2 R H
поэтому
S 2 2 3 12
S 12
…
1 2
Длина окружности основания цилиндра равна 3,
высота равна 2. Найдите площадь боковой поверхности
цилиндра.
Решение.
№16.
Площадь боковой поверхности цилиндра
S 2 R H
S С H
C– длина окружности основания.
Поэтому S = 2·3 = 6
6
№16. Длина окружности основания цилиндра равна 3. Площадь
боковой поверхности равна 6. Найдите высоту цилиндра.
Решение.
S С H
S
Н
…
С
2
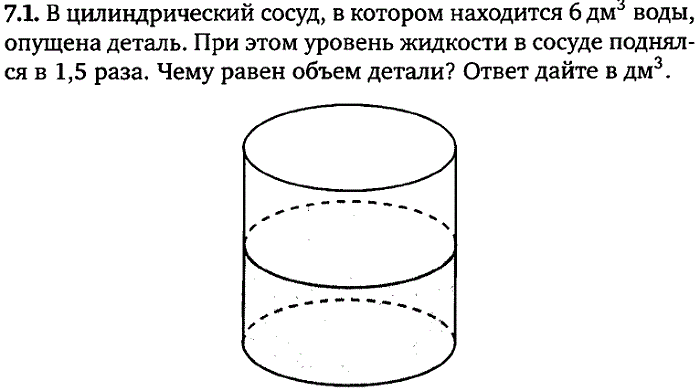
№16. В бак, имеющий форму цилиндра, налито 5 л воды.
После полного погружения в воду детали, уровень воды в
баке поднялся в 1,2 раза. Найдите объём детали.
Ответ дайте в кубических сантиметрах, зная, что в одном
литре 1000 кубических сантиметров.
Решение.
Объём детали равен объёму вытесненной ею
жидкости.
После погружения детали в воду объём стал равен
5 · 1,2 = 6 литров,
поэтом объём детали равен 6 − 5 = 1 л = 1000 см3.
1 0 0 0
№16.
Вода в сосуде цилиндрической формы находится на
уровне h = 40cм. На каком уровне окажется вода, если её
перелить в другой цилиндрический сосуд, у которого радиус
основания вдвое больше, чем у первого? Ответ дайте в
сантиметрах.
Решение.
Объём воды, налитой в цилиндр, высотой h и радиусом R равен
V = πR²h
Следовательно, при увеличении радиуса цилиндра
в 2 раза, при неизменном объёме,
высота стола воды окажется в 2²= 4 раза меньше,
значит, вода во втором цилиндре достигнет уровня
h₂= 40 : 4= 10 см.
1 0
№16. В сосуд цилиндрической формы налили воду до уровня
80 см. Какого уровня достигнет вода, если её перелить в другой
цилиндрический сосуд, у которого радиус основания в 4 раза
больше, чем у первого? Ответ дайте в см.
Решение.
Объём воды, налитой в цилиндр, высотой h и радиусом R равен
V = πR²h
Следовательно, при увеличении радиуса цилиндра
в 4 раза, при неизменном объёме,
высота стола воды окажется в 4²= 16 раза меньше,
значит, вода во втором цилиндре достигнет уровня
h₂= 80 : 16 = 5 см.
5
English Русский Правила
Уровень жидкости в цилиндрическом сосуде поддерживается постоянным на уровне 30см. Он состоит из трех одинаковых горизонтальных трубок А, В и С длиной по 40 см, каждая из которых выходит на высоте 0, 5 и 10 см соответственно. Вычислите длину одной переливной трубки того же радиуса, что и у таких же трубок, которая может заменить три, если их расположить горизонтально на дне цилиндра.
PRADEEP-СВОЙСТВА ОБЪЕМНОГО ВЕЩЕСТВА-Задачи для практики
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке!
Обновлено на: 27-06-2022
लिखित उत्तर
Ответ
Правильный ответ-16 см
Решение
Давление на давление для труб трубка B,h3=30−5=25см
Напор для трубки C,h4=30−10=20см
Длина каждой трубки, l=40см
Скорость течения жидкости по разным трубкам
Q2=πh3ρgr48ηl
Q3=πh4ρgr48ηl
Общий объем вытекающей жидкости Q=Q1+Q2+Q3
=πρgr48ηl[h2+h3+h4]
Пусть l’ – длина сигнальной трубки, через которую вытекает такой же объем жидкости. Тогда
Тогда
Q=πh2ρgr48ηl’
Из (i) и (ii) имеем
πh2ρgr48ηl’=πρgr48ηl[h2+h3+h4]
или h2l’=1l[h2+h3+h4
или 30l’=140[30]. +25+20]=7540=158
или l’=30×815=16 см
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
संबंधित वीडियो
На следующем рисунке показано течение жидкости через горизонтальную трубу. К трубе подсоединены три трубки А, В и С. Радиусы трубок А, В и С в месте соединения равны соответственно 2 см, 1 см и 2 см. Можно сказать, что
11796601
Три капиллярные трубки одинакового радиуса r, но длины l1, l2 и l3 установлены горизонтально на дне длинного цилиндра, содержащего жидкость с постоянным напором, протекающую по этим трубкам. Найдите длину одной переливной трубки того же радиуса r, которой можно заменить три капилляра.
12008068
Три капиллярные трубки одинакового радиуса 1 см, но длиной 1 м, 2 м и 3 м прикреплены горизонтально ко дну длинного сосуда, содержащего жидкость при постоянном давлении и протекающую через них. Какова длина одной трубки, которая может заменить три капилляра?
Какова длина одной трубки, которая может заменить три капилляра?
13077232
Уровень жидкости в сосуде поддерживается постоянным на уровне 50 см. он состоит из трех одинаковых горизонтальных трубок длиной 60 см каждая, выходящих на высоты 5, 10 и 15 см соответственно. Если одна трубка того же радиуса, что и три трубки, может заменить три трубки, если ее положить горизонтально на дно сосуда, то длина этой трубки равна
13077461
В сосуде есть вода до высоты 40 см. он имеет три горизонтальные капиллярные трубки одинакового диаметра, каждая длиной 15 см, выходящие на высоте 10 см, 15 см, 20 см. Длина одной трубки того же диаметра, что и у трех трубок, которые могут заменить их при горизонтальном расположении на дно сосуда:
13077490
Две капиллярные трубки одинакового радиуса r, но длины l_(1) и l_(2) установлены параллельно дну сосуда. Давление на дно сосуда. Напор равен P. Какова должна быть длина одной трубы того же радиуса, которая может заменить две трубы, чтобы скорость потока была такой же, как и раньше?
13077655
Уровень жидкости в цилиндрическом сосуде поддерживается постоянным на уровне 30 см. Он состоит из трех одинаковых горизонтальных трубок длиной 39 см, каждая из которых выходит на высоту 0,4 и 8 см соответственно. Вычислите длину одной переливной трубы того же радиуса, что и у идентичных труб, которая может заменить три, если их расположить горизонтально на дне цилиндра.
Он состоит из трех одинаковых горизонтальных трубок длиной 39 см, каждая из которых выходит на высоту 0,4 и 8 см соответственно. Вычислите длину одной переливной трубы того же радиуса, что и у идентичных труб, которая может заменить три, если их расположить горизонтально на дне цилиндра.
17463853
चित्र में दिखाए गए उपक выполнительный मध्य की दोनों ऊर्ध्व नलियों , B व C में प्रत्येक का की की कथसेमी है | दोनों बाहरी ऊर्ध्व नलियाँ, A व D वायुमणडल में खुही वD A व C नलियों को 95∘c के स्थिर तापमान पर रखा गया है, जबकि b व d को 5∘c पर | A व d नलियों द द्रव की ऊँचाइयाँ, तल रेखा से क्रमशः 52,8 सेमी व 51 सेमी है | द्रव का रेखीय ऊष्मीय प्रसार गुणांक गयकाट कीजिए |
307547079
Три капиллярные трубки одинакового радиуса r, но длины l1, l2 и l3 прикреплены горизонтально ко дну высокого сосуда, содержащего жидкость при постоянном напоре и протекающую по этим трубкам. Вычислите длину одной отводной трубки того же радиуса r, которая может заменить три капилляра.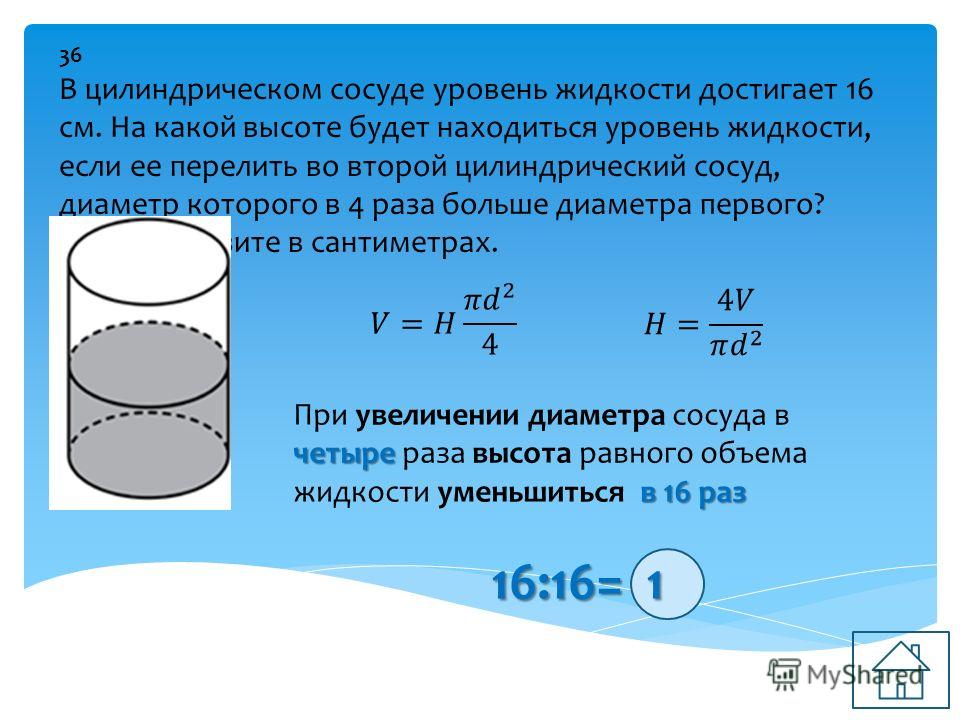
320271486
Три капиллярные трубки одинакового радиуса r, но длины l1, l2 и l3 прикреплены горизонтально ко дну высокого сосуда, содержащего жидкость при постоянном напоре и протекающую по этим трубкам. Вычислите длину одной отводной трубки того же радиуса r, которая может заменить три капилляра.
320285827
Цилиндрический сосуд имеет три одинаковые горизонтальные трубки длиной 40 см, каждая из которых выходит на высоте 0, 5 и 9 см соответственно. Какова будет длина одной переливной трубки того же радиуса, что и у таких же трубок, которая может заменить три трубки, если ее поместить на дно сосуда, если уровень жидкости в цилиндрическом сосуде поддерживать постоянным на уровне 20 см?
415573648
Текст Решение
Две капиллярные трубки радиусами r и 4r и длинами l, 3l установлены горизонтально ко дну сосуда с напором p параллельно друг другу. Вычислите радиус одиночной трубки той же длины l, которая может заменить два капилляра так, что скорость потока не изменится.
415573925
Text Solution
Три капиллярные трубки одинакового радиуса 1 см, но длиной 1 м, 2 м и 3 м прикреплены горизонтально ко дну длинного сосуда с жидкостью, находящейся под постоянным давлением и протекающей по этим трубкам. Какова длина одной трубки, которая может заменить три капилляра?
642693750
Text Solution
Три капиллярные трубки радиусом 1 см и длиной 1 м, 2 м и 3 м горизонтально прикреплены ко дну длинного сосуда, содержащего жидкость, протекающую по этим трубкам при постоянном давлении. Какова длина одной трубки, которая может заменить три капилляра?
642716232
Текст Решение
Пробирка состоит из полусферы и цилиндра одинакового радиуса. Объем воды, необходимый для заполнения всей трубы, равен 5159 г.6 см3 и 42356 см3 воды требуется, чтобы заполнить пробирку до уровня, который находится на 4 см ниже верха пробирки. Найдите радиус трубы и длину ее цилиндрической части.
643657638
Цилиндрический сосуд наполнен водой до высоты 1 м от дна.
 (2))
(2))TS EAMCET ДОКУМЕНТЫ ЗА ПРЕДЫДУЩИЙ ГОД-TS EAMCET 2018 (7 МАЯ СМЕНА 1)-ФИЗИКА
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари адки ки киаваке видео бина!
Updated On: 27-06-2022
Text Solution
A
80 cm
B
60 cm
C
40 cm
D
20 cm
Answer
The правильный ответ А
Раствор
Высота воды в сосуде =1 м
Пусть отверстие находится на глубине h сверху
Время, необходимое для подъема уровня воды до отверстия,
t=AA0√2xg
где, A0= площадь отверстия и A = базовая площадь.
Дано, AA0=100,t=20s⇒20=100√2×10
√x5=15⇒x=15=0,2 или 20см
Теперь высота отверстия от основания,
h=100−20=см
Ответ
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.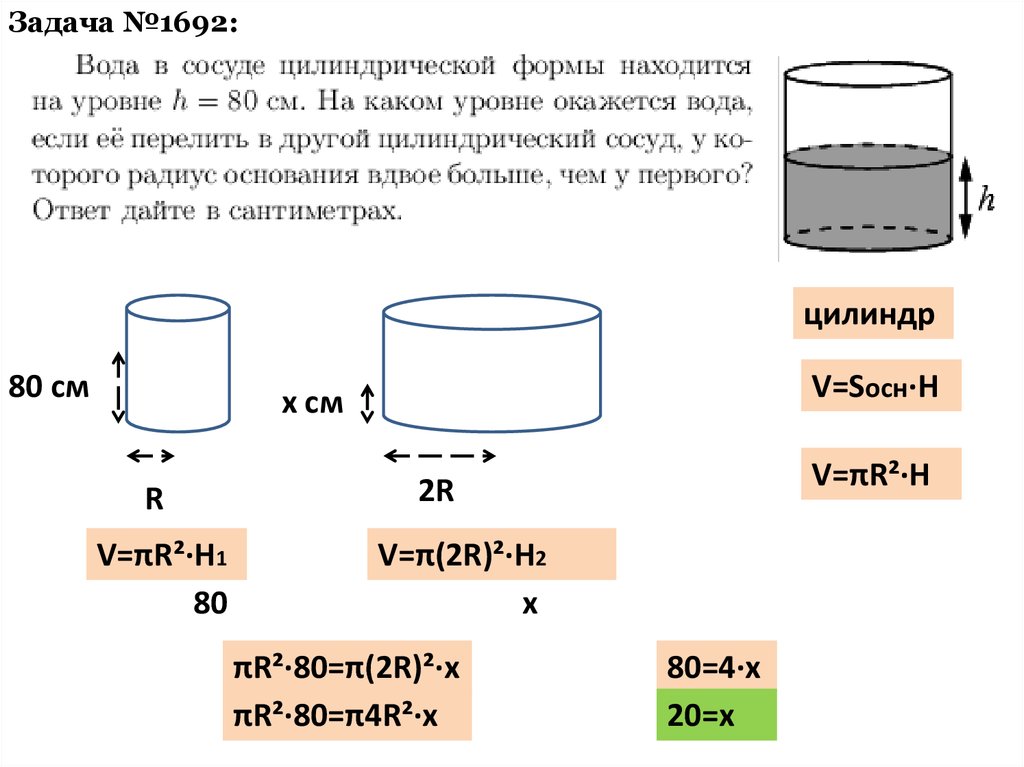 2 . Влиянием поверхностного натяжения пренебречь.]
2 . Влиянием поверхностного натяжения пренебречь.]
10058943
Чем наполнен цилиндрический контейнер на высоту 3м. Отношение площадей поперечного сечения горловины и стакана равно 0,1. Квадрат скорости жидкости, выходящей из отверстия, равен (g=10 м/с2).
11750642
Резервуар высотой H и площадью основания A наполовину заполнен водой, на дне имеется небольшое отверстие и находится тяжелый твердый цилиндр с площадью основания A3, высота цилиндра такая же, как у так. Вода вытекает из отверстия. Здесь цилиндр помещается в бак, чтобы увеличить скорость вытекания воды.
Скорость воды, вытекающей из отверстия после удерживания в нем цилиндра, равна
13077625
Резервуар высотой H и площадью основания A наполовину заполнен водой, на дне есть небольшое отверстие и есть тяжелый сплошной цилиндр, имеющий площадь основания А3 и высоту цилиндра такую же, как у так. Вода вытекает из отверстия. Здесь цилиндр помещается в бак, чтобы увеличить скорость вытекания воды. (2) )
(2) )
614528226
На дне сосуда с водой на высоте 10 м над отверстием делается отверстие площадью 10 кв.мм. Какая сила действует на сосуд
642694055
Текст Решение
Цилиндрический сосуд высотой 500 мм имеет отверстие (маленькое отверстие) на дне. Отверстие первоначально закрыто и в него налита вода до высоты H. Теперь верх полностью закрыт пробкой, а отверстие внизу открыто. Некоторое количество воды выходит из отверстия и уровень воды в сосуде стабилизируется при высоте водяного столба 200 мм. Найдите падение высоты (в мм) уровня воды из-за открытия отверстия. 92. Влиянием поверхностного натяжения пренебречь.]
642749597
Высота жидкости H, глубина отверстия от уровня воды h, высота отверстия от дна h, радиус отверстия r (очень мало по сравнению с крестом -секция контейнера). Тогда скорость истечения
644161560
Текст Решение
Высота жидкости H, глубина отверстия от уровня воды h’, высота отверстия от дна h, радиус отверстия r (очень мало по сравнению с поперечное сечение контейнера). Горизонтальное расстояние, пройденное струей воды, равно
Горизонтальное расстояние, пройденное струей воды, равно
644161581
Текст Решение
В открытом сосуде находится вода высотой до 50 см. Какова скорость истечения через отверстие на высоте 30 см над уровнем дна? [Возьмем g = 10 м/с2]
644357072
Резервуар высотой H и площадью основания A наполовину заполнен водой, на дне есть небольшое отверстие и находится тяжелый твердый цилиндр с площадью основания (A). /(3) и высота цилиндра такая же, как у так. Вода вытекает из отверстия. Здесь цилиндр помещается в бак, чтобы увеличить скорость вытекания воды. Скорость воды, вытекающей из отверстия после удержания в нем цилиндра, равна
644526968
Резервуар высотой H и площадью основания A наполовину заполнен водой, на дне есть небольшое отверстие и имеется тяжелый сплошной цилиндр с площадью основания (A)/(3) и высотой цилиндра такое же, как у так. Вода вытекает из отверстия. Здесь цилиндр помещается в бак, чтобы увеличить скорость вытекания воды.


 поверхности цилиндра.
поверхности цилиндра.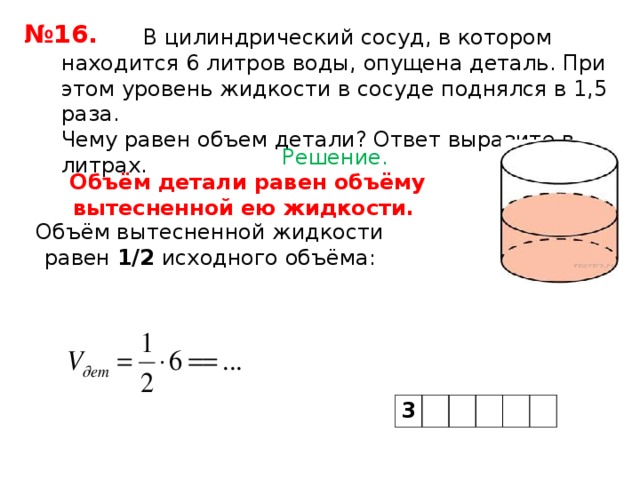
Leave A Comment