Во сколько раз уменьшится сила тяготения между однородным шаром: Во сколько раз уменьшится сила тяготения между однородным шаром и материальной точкой, — Спрашивалка

Закон всемирного тяготения — формула, определение, формулировка

Гравитационное взаимодействие

Земля — это большой магнит. Причем на самом деле магнит, с настоящим магнитным полем. Но сейчас речь пойдет о другом явлении — явлении притяжения тел к Земле, от прыгающего с дерева котика до летящего мимо астероида. Называется это явление гравитацией.

Возьмем два тела — одно с большой массой, другое с маленькой. Натянем гигантское полотно ткани и положим на него тело с большей массой. После чего положим туда тело с массой поменьше. Мы будем наблюдать примерно такую картину:

Маленькое тело начнет притягиваться к тому, что больше, — это и есть гравитация. По сути, Земля — это большой шарик, а все остальные предметы — маленький (даже если это вовсе не шарики).

Гравитационное взаимодействие универсально. Оно справедливо для всех видов материи. Гравитация проявляется только в притяжении — отталкивание тел гравитация не предусматривает.

Из всех фундаментальных взаимодействий гравитационное — самое слабое. Хотя гравитация действует между всеми элементарными частицами, она настолько слаба, что ее принято не учитывать. Все дело в том, что гравитационное взаимодействие зависит от массы объекта, а у частиц она крайне мала. Эту зависимость впервые сформулировал Исаак Ньютон.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Закон всемирного тяготения

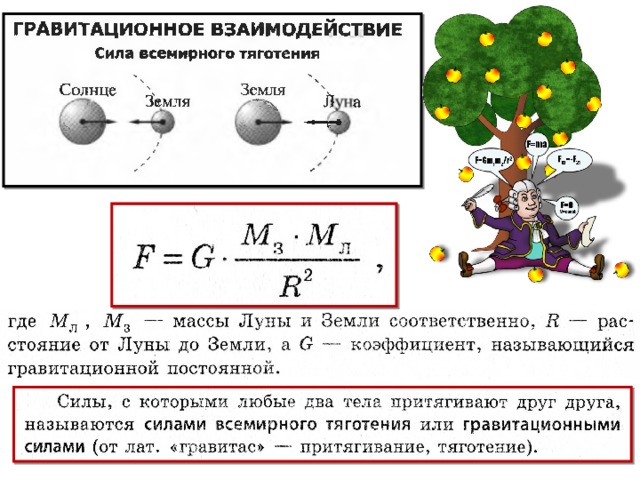
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше примерно в шесть раз.

Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.

Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.

Задачка раз

Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планеты к звезде?

Решение

По закону всемирного тяготения сила притяжения планеты к звезде обратно пропорциональна квадрату радиуса орбиты.

Таким образом, в силу равенства масс отношение сил притяжения к звезде первой и второй планет обратно пропорционально отношению квадратов радиусов орбит:

По условию, у первой планеты радиус орбиты вдвое больше, чем у второй, то есть R₁ = 2R₂.

Это значит, что:

Ответ: отношение сил притяжения первой и второй планет к звезде равно 0,25.

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка два

У поверхности Луны на космонавта действует сила тяготения 144 Н. Какая сила тяготения действует со стороны Луны на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Луны на расстоянии трех лунных радиусов от ее центра?

Решение

По закону всемирного тяготения сила притяжения космонавта со стороны Луны обратно пропорциональна квадрату расстояния между ним и центром Луны. У поверхности Луны это расстояние совпадает с радиусом спутника. На космическом корабле, по условию, оно в три раза больше. Таким образом, сила тяготения со стороны Луны, действующая на космонавта на космическом корабле, в 9 раз меньше, чем у поверхности Луны, то есть:

144 : 9 = 16 Н

Ответ: на расстоянии трех лунных радиусов от центра сила притяжения космонавта будет равна 16 Н.

Важный нюанс!

Правильно говорить не «на тело действует сила тяготения», а «Земля притягивает тело с силой тяготения».

Ускорение свободного падения

Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.

Сила тяжести — сила, с которой Земля притягивает все тела.

Сила тяжести F = mg F — сила тяжести [Н] m — масса тела [кг] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2, но подробнее об этом чуть позже. 😉

На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.

Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.

На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.

Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к ней притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:

Приравниваем правые части:

Делим на массу тела левую и правую части:

Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.

Закон всемирного тяготения g — ускорение свободного падения [м/с2] M — масса планеты [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2

Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.

Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.

Но разве это не зависит еще и от массы предмета?

Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения. Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.

Третий закон Ньютона

Третий закон Ньютона обобщает огромное количество опытов, которые показывают, что силы — результат взаимодействия тел.

Он звучит так: тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Если попроще — сила действия равна силе противодействия.

Если вам вдруг придется объяснять физику во дворе, то можно сказать и так: на каждую силу найдется другая сила. 🙈

Третий закон Ньютона F1 — сила, с которой первое тело действует на второе [Н] F2 — сила, с которой второе тело действует на первое [Н]

Так вот, для силы тяготения третий закон Ньютона тоже справедлив. С какой силой Земля притягивает тело, с той же силой тело притягивает Землю.

Задачка для практики

Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю?

Решение

Согласно третьему закону Ньютона, сила, с которой Земля притягивает мяч, равна силе, с которой мяч притягивает Землю.

Ответ: мяч притягивает Землю с силой 5 Н.

Поначалу это кажется странным, потому что мы ассоциируем силу с перемещением: мол, если сила такая же, то на то же расстояние подвинется Земля. Формально это так, но у мяча масса намного меньше, чем у Земли. И Земля смещается на такое крошечное расстояние, притягиваясь к мячу, что мы его не видим, в отличие от падения мяча.

Если каждый брошенный мяч смещает Землю на какое-то расстояние, пусть даже крошечное, возникает вопрос — как она еще не слетела с орбиты из-за всех этих смещений. Но тут как в перетягивании каната: если его будут тянуть две равные по силе команды, канат никуда не сдвинется. Так же и с нашей планетой.

8. Тесты по динамике: гравитационные взаимодействия

afportal — 14 февраля, 2007 — 11:33

(Если вы просматриваете сайт как турбо-страницу Яндекса, то для решения тестов перейдите на полную (мобильную) версию сайта по кнопке снизу. Турбо-страницы не содержат всех необходимых скриптов)

1. Во сколько раз уменьшится сила тяготения между однородным шаром и материальной точкой, соприкасающейся с шаром, если материальную точку удалить от поверхности шара на расстояние, равное двум диаметрам шара?
4
16
2.5
6.25
25
затрудняюсь ответить

2. На какой высоте (в км) над поверхностью Земли ускорение свободного падения в 16 раз меньше, чем на земной поверхности? Радиус Земли 6400 км.
12800
19200
6400
25600
1600
затрудняюсь ответить

3. Спутник движется по круговой орбите в плоскости экватора на высоте от поверхности планеты, равной ее радиусу. Найдите линейную скорость (в км/с) спутника. Радиус планеты 7200 км. Ускорение свободного падения на поверхности планеты 10 м/с.
7.8
7
6
5.8
нет правильного ответа
затрудняюсь ответить

4. Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше, чем на экваторе. Период вращения планеты вокруг своей оси Т = 2 ч 40 мин.
1000 кг/м³
1500 кг/м³
2000 кг/м³
2500 кг/м³
3000 кг/м³
затрудняюсь ответить

5. Имеется шар массой M и радиусом R и материальная точка массой m. Во сколько раз уменьшится сила тяготения между ними, если в шаре сделать сферическую полость радиусом 5R/6? Материальная точка лежит на прямой, проведенной через центры шара и полости, на расстоянии R от центра шара и на расстоянии 5R/6 от центра полости.
6
5
1.2
30
нет правильного ответа
затрудняюсь ответить

6. Телу, находящемуся на поверхности Земли, сообщена вертикальная скорость 15 км/с. Какую скорость будет иметь тело, когда удалится в бесконечность?
10 км/с
12 км/с
8 км/с
6 км/с
нет правильного ответа
затрудняюсь ответить

7. Спутник поднимают на высоту h = 6370 км и запускают его по круговой орбите на той же высоте. Определить отношение работ на поднятие и на запуск спутника.
1
2
4
1/2
1/4
затрудняюсь ответить

8. Космический корабль, имеющий скорость v = 10 км/с, попадает в неподвижное облако микрометеоров. В объеме V_o = 1 m³ пространства находится n = 1 микрометеор. Масса каждого микрометеора m_o = 2?10^-5 кг. На сколько должна возрасти сила тяги двигателя, чтобы скорость корабля при прохождении через облако не изменилась? Лобовое сечение корабля S = 49 м² . Удар микрометеоров об обшивку корабля считать неупругим.
25 кН
50 кН
75 кН
100 кН
нет правильного ответа
затрудняюсь ответить

9. На какой высоте ускорение свободного падения составляет 25% его значения на поверхности Земли?
R/2
2R
R
R/5
5R
затрудняюсь ответить

10. В безграничной среде плотностью r_o = 1000 кг/м³ находятся на расстоянии 20 см от центров друг друга два шара объемами V₁ = 30 см³ и V₂ = 40 см³ , плотностью r = 2000 кг/м³ . Определить силу взаимодействия между шарами.
6 нН
6 мкН
6 кН
6 пН
6 мН
затрудняюсь ответить

Следующий тест: Динамика: Импульс. Закон сохранения импульса

5.5: Закон всемирного тяготения Ньютона

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14463

• Boundless (теперь LumenLearning)
• Boundless

Закон всемирного тяготения

Объекты с массой ощущают силу притяжения, которая пропорциональна их массам и обратно пропорциональна квадрату расстояния.

цели обучения

• Выразить закон всемирного тяготения в математической форме

Хотя яблоко, возможно, и не попало в голову сэру Исааку Ньютону, как предполагает миф, падение одного из них вдохновило Ньютона на одно из величайших открытий в механике: Закон всемирного тяготения . Размышляя о том, почему яблоко никогда не падает ни вбок, ни вверх, ни в каком-либо другом направлении, кроме перпендикулярного к земле, Ньютон понял, что сама Земля должна быть ответственна за движение яблока вниз.

Теоретизируя, что эта сила должна быть пропорциональна массам двух вовлеченных объектов, и используя предыдущую интуицию об обратной квадратичной зависимости силы между Землей и Луной, Ньютон смог сформулировать общий физический закон по индукции.

Закон всемирного тяготения гласит, что каждая точечная масса притягивает любую другую точечную массу во Вселенной силой, направленной по прямой линии между центрами масс обеих точек, и эта сила пропорциональна массам объектов. и обратно пропорциональна их расстоянию. Эта сила притяжения всегда направлена ​​внутрь, от одной точки к другой. Закон применим ко всем объектам с массой, большой или малой. Два больших объекта можно рассматривать как точечные массы, если расстояние между ними очень велико по сравнению с их размерами или если они сферически симметричны. В этих случаях массу каждого объекта можно представить в виде точечной массы, расположенной в его центре масс. 92}\). Из-за величины \(\mathrm{G}\) гравитационная сила очень мала, если только не задействованы большие массы.

Силы, действующие на две массы : Все массы притягиваются друг к другу. Сила пропорциональна массам и обратно пропорциональна квадрату расстояния.

Гравитационное притяжение сферических тел: однородная сфера

Теорема оболочки утверждает, что сферически симметричный объект влияет на другие объекты, как если бы вся его масса была сосредоточена в его центре. 92}}\]

Однако большинство объектов не являются точечными частицами.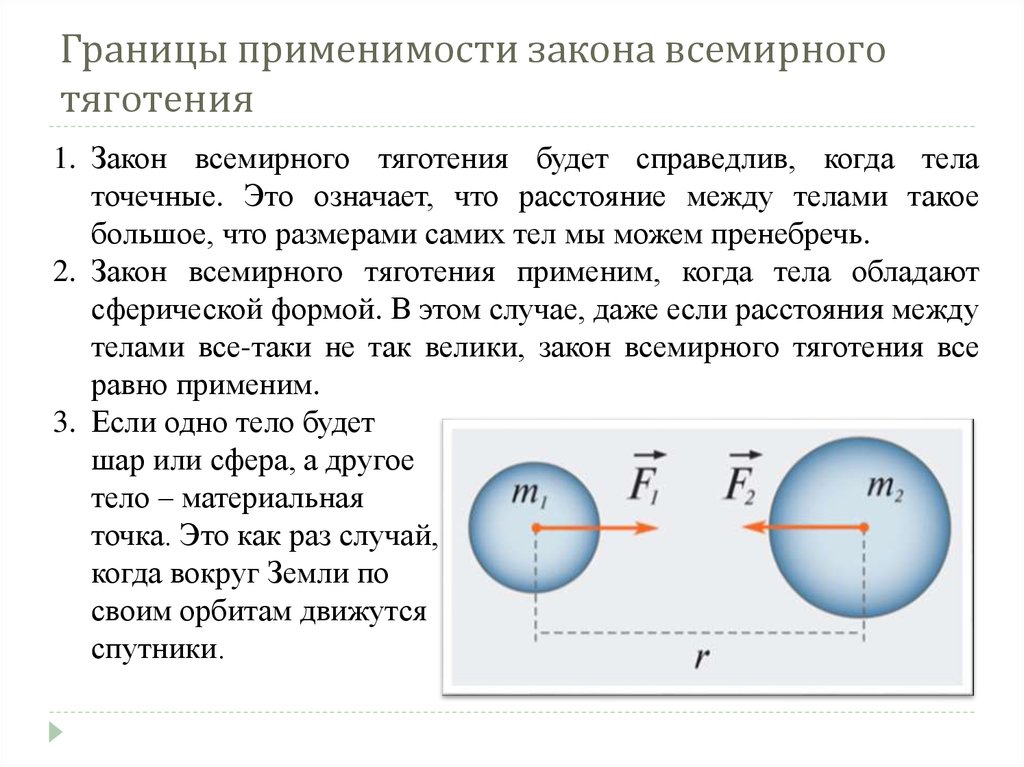 Чтобы найти гравитационную силу между трехмерными объектами, нужно рассматривать их как точки в пространстве. Для высокосимметричных форм, таких как сферы или сферические оболочки, найти эту точку несложно.

Теорема Оболочки

Исаак Ньютон доказал Теорему Оболочки, которая утверждает, что:

1. Сферически симметричный объект гравитационно воздействует на другие объекты, как если бы вся его масса была сосредоточена в его центре,
2. Если объект представляет собой сферически-симметричную оболочку (т.е. полый шар), то результирующая гравитационная сила на тело внутри его равна нулю.

Поскольку сила является векторной величиной, сумма векторов всех частей оболочки/сферы дает результирующую силу, и эта результирующая сила эквивалентна одному измерению силы, взятому из середины сферы или центра масс (ЦМ) . Таким образом, при нахождении силы тяжести, действующей на мяч массой 10 кг, расстояние, измеренное от мяча, берется от центра масс мяча до центра масс Земли.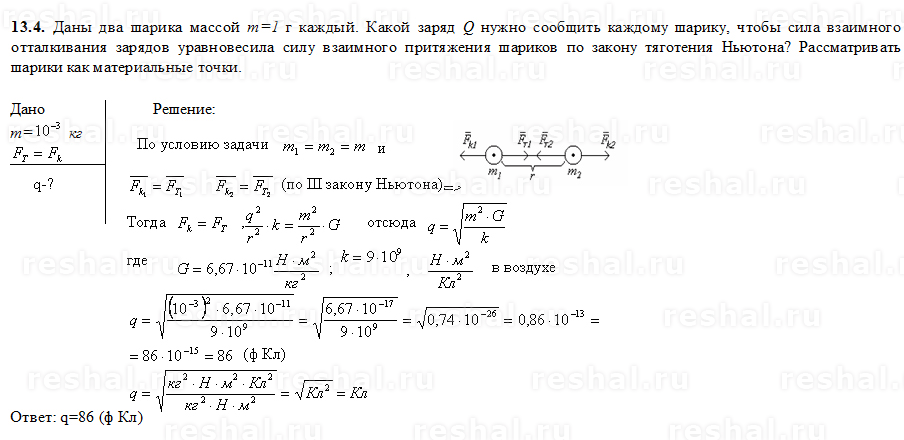

Учитывая, что сферу можно рассматривать как набор бесконечно тонких, концентрических, сферических оболочек (подобных слоям луковицы), можно показать, что следствием теоремы об оболочке является то, что сила, приложенная к объекту внутри сплошной сферы зависит только от массы сферы внутри радиуса, на котором находится объект. Это связано с тем, что оболочки с большим радиусом, чем тот, на котором находится объект, вносят , а не силы в объект внутри них (Утверждение 2 теоремы).

При рассмотрении гравитационной силы, действующей на объект в точке внутри или вне однородного сферически-симметричного объекта радиуса RR, необходимо рассмотреть две простые и различные ситуации: случай полой сферической оболочки, и твердая сфера с равномерно распределенной массой.

Случай 1: полая сферическая оболочка

Гравитационная сила, действующая сферически-симметричной оболочкой на точечную массу внутри it, представляет собой векторную сумму сил гравитации, действующих на каждую часть оболочки, и эта векторная сумма равна нулю. То есть масса мм внутри сферически-симметричной оболочки массой \(\mathrm{M}\) не будет ощущать результирующей силы (утверждение 2 теоремы оболочки).

Чистая гравитационная сила, которую сферическая оболочка массы \(\mathrm{M}\) оказывает на тело вне ее , представляет собой векторную сумму гравитационных сил, действующих каждой частью оболочки на внешний объект , которые в сумме составляют результирующую силу, действующую так, как будто масса \(\mathrm{M}\) сосредоточена в точке в центре сферы (утверждение 1 теоремы Оболочки).

Диаграмма, используемая в доказательстве теоремы о Шелле : Эта диаграмма описывает геометрию, рассматриваемую при доказательстве теоремы о Шелле. В частности, в этом случае сферическая оболочка массы \(\mathrm{M}\) (левая часть рисунка) действует с силой на массу \(\mathrm{m}\) (правая часть рисунка) вне ее . Площадь поверхности тонкого среза сферы показана цветом. (Примечание: доказательство теоремы здесь не представлено. Заинтересованные читатели могут продолжить изучение, используя источники, перечисленные в конце этой статьи.)

Случай 2: сплошная однородная сфера

Вторая ситуация, которую мы рассмотрим, относится к сплошной однородной сфере массы \(\mathrm{M}\) и радиуса \(\mathrm{R}\), оказывающей сила, действующая на тело массой \(\mathrm{m}\) с радиусом \(\mathrm{d}\) внутри его (то есть, \(\mathrm{d

(\(\mathrm{ρ}\) — массовая плотность шара, и мы предполагаем, что она не зависит от радиуса. То есть масса шара распределена равномерно.)

Следовательно , объединяя два приведенных выше уравнения, мы получаем:

\[\mathrm{F=\dfrac{4}{3}πGmρd}\]

что показывает, что масса mm испытывает силу, которая линейно пропорциональна ее расстоянию, dd, от центра масс шара.

Как и в случае полых сферических оболочек, результирующая гравитационная сила, с которой твердая сфера с равномерно распределенной массой \(\mathrm{M}\) действует на тело вне его, является векторной суммой гравитационных сил, действующих каждой оболочкой сферы на внешний объект. Результирующая чистая гравитационная сила действует так, как будто масса \(\mathrm{M}\) сосредоточена в точке в центре сферы, которая является центром масс или COM (утверждение 1 теоремы Шелла). В более общем смысле этот результат верен, даже если масса \(\mathrm{M}\) равна , а не равномерно распределена, но ее плотность изменяется радиально (как в случае с планетами).

Масса Земли

Когда тела имеют пространственную протяженность, гравитационная сила рассчитывается путем суммирования составляющих их точечных масс.

цели обучения

• Описать, как рассчитывается гравитационная сила для тел с пространственной протяженностью

Закон всемирного тяготения Ньютона гласит, что каждая точечная масса во Вселенной притягивает любую другую точечную массу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. 92}}\]

где \(\mathrm{F}\) — сила между массами, \(\mathrm{G}\) — гравитационная постоянная, \(\mathrm{m_1}\) — первая масса, \(\mathrm{m_2}\) — вторая масса и \(\mathrm{r}\) — расстояние между центрами масс.

Если рассматриваемые тела имеют пространственную протяженность (а не являются теоретическими точечными массами), то гравитационная сила между ними рассчитывается путем суммирования вкладов условных точечных масс, составляющих тела. В пределе, когда точечные массы компонентов становятся «бесконечно малыми», это влечет за собой интегрирование силы (в векторной форме, см. Ниже) по протяженности двух тел.

Таким образом можно показать, что объект со сферически-симметричным распределением массы оказывает такое же гравитационное притяжение на внешние тела, как если бы вся масса объекта была сосредоточена в точке в его центре.

Для точек внутри сферически-симметричного распределения материи можно использовать теорему Ньютона о Шелле, чтобы найти гравитационную силу. Теорема говорит нам, как различные части распределения масс влияют на гравитационную силу, измеренную в точке, расположенной на расстоянии \(\mathrm{r_0}\) от центра распределения масс:

1. Часть массы, расположенная на радиусах \(\mathrm{r
2. Часть массы, расположенная на радиусах \(\mathrm{r>r_0}\), не оказывает результирующей гравитационной силы на расстоянии \(\mathrm{r_0}\) от центра. То есть отдельные гравитационные силы, действующие на элементы сферы в точке \(\mathrm{r_0}\) , компенсируют друг друга.

Как следствие, например, внутри оболочки одинаковой толщины и плотности нигде в пределах полой сферы нет результирующего гравитационного ускорения. Кроме того, внутри однородной сферы гравитация линейно увеличивается с расстоянием от центра; увеличение за счет дополнительной массы в 1,5 раза меньше уменьшения за счет большего расстояния от центра. Таким образом, если сферически-симметричное тело имеет однородное ядро ​​и однородную мантию с плотностью, меньшей \(\mathrm{\frac{2}{3}}\) плотности ядра, то гравитация первоначально убывает наружу за границей, и если сфера достаточно велика, дальше наружу гравитация снова увеличивается, и в конечном итоге она превышает гравитацию на границе ядра и мантии.

Гравитация Земли может быть максимальной на границе ядра и мантии, как показано на рисунке 1:

Гравитационное поле Земли : Диаграмма напряженности гравитационного поля внутри Земли.

Ключевые моменты

• Закон всемирного тяготения сэра Исаака Ньютона вдохновил падение яблока с дерева.
• Понимание Ньютоном свойства обратных квадратов силы тяготения было основано на интуитивных представлениях о движении Земли и Луны. 92}}\), где \(\mathrm{G}\) — гравитационная постоянная.
• Поскольку сила является векторной величиной, сумма векторов всех частей оболочки дает результирующую силу, и эта результирующая сила эквивалентна одному измерению силы, взятому из середины сферы или центра масс (ЦМ).
• Сила гравитации на объект внутри полой сферической оболочки равна нулю.
• Гравитационная сила, действующая на объект в пределах однородной сферической массы, линейно пропорциональна его расстоянию от центра масс сферы (ЦМ).
• Закон всемирного тяготения Ньютона гласит, что каждая точечная масса во Вселенной притягивает любую другую точечную массу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
• Второй шаг в вычислении массы Земли произошел с разработкой закона всемирного тяготения Ньютона.
• Приравнивая второй закон Ньютона к его закону всемирного тяготения и вводя для ускорения a экспериментально проверенное значение 9{24} кг}\), что позволяет вычислить вес Земли при любом гравитационном поле.
• Гравитация Земли может быть максимальной на границе ядра и мантии

Ключевые термины

• индукция : Используйте индуктивное рассуждение для обобщения и интерпретации результатов применения закона всемирного тяготения Ньютона.
• , обратный : Противоположное по действию, природе или порядку.
• центр масс : Центр масс (ЦМ) — это уникальная точка в центре распределения масс в пространстве, обладающая тем свойством, что взвешенные векторы положения относительно этой точки в сумме равны нулю.
• масса точки : Теоретическая точка с присвоенной ей массой.
• вес : Сила, действующая на объект из-за гравитационного притяжения между ним и Землей (или любым астрономическим объектом, на который он в первую очередь влияет).
• гравитационная сила : Очень дальнодействующая, но относительно слабая фундаментальная сила притяжения, действующая между всеми частицами, имеющими массу; считается опосредованным гравитонами.

ЛИЦЕНЗИИ И АВТОРСТВО

CC ЛИЦЕНЗИОННЫЙ КОНТЕНТ, ПРЕДОСТАВЛЕННЫЙ РАНЕЕ

• Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike

CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ​​СПЕЦИАЛЬНОЕ АВТОРСТВО

• Закон всемирного тяготения Ньютона. Предоставлено : ВИКИПЕДИЯ. Расположен по адресу : en.Wikipedia.org/wiki/Newton’s_law_of_universal_gravitation . Лицензия : CC BY-SA: Attribution-ShareAlike
• Исаак Ньютон. Предоставлено : ВИКИПЕДИЯ. Расположен по адресу : en. Wikipedia.org/wiki/Isaac_Newton%23Apple_incident . Лицензия : CC BY-SA: Attribution-ShareAlike
• индукция. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/induction . Лицензия : CC BY-SA: Attribution-ShareAlike
• инверс. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/inverse . Лицензия : CC BY-SA: Attribution-ShareAlike
• Теорема оболочки. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Shell_theorem . Лицензия : CC BY-SA: Attribution-ShareAlike
• Центр масс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Center_of_mass . Лицензия : CC BY-SA: Attribution-ShareAlike
• Предоставлено : Свет и Материя. Расположен по адресу : http://lightandmatter.com/mef.pdf . Лицензия : CC BY: Attribution
• Закон всемирного тяготения Ньютона. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Newton’s_law_of_universal_gravitation . Лицензия : CC BY-SA: Attribution-ShareAlike
• центр масс. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/center%20of%20mass . Лицензия : CC BY-SA: Attribution-ShareAlike
• Shell-diag-1. Предоставлено : Wikimedia Commons. Расположен по адресу : commons.wikimedia.org/wiki/File:Shell-diag-1.png . Лицензия : CC BY-SA: Attribution-ShareAlike
• Закон всемирного тяготения. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Law_of_universal_gravitation . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42073/latest/?collection=col11406/1.7 . Лицензия : CC BY: Атрибуция
• Гравитационная постоянная. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Gravitational_constant . Лицензия : CC BY-SA: Attribution-ShareAlike
• Закон всемирного тяготения. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Law_of_universal_gravitation . Лицензия : CC BY-SA: Attribution-ShareAlike
• вес. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/weight . Лицензия : CC BY-SA: Attribution-ShareAlike
• точки массы. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/point_mass . Лицензия : CC BY-SA: Attribution-ShareAlike
• гравитационная сила. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/gravitational_force . Лицензия : CC BY-SA: Attribution-ShareAlike
• Shell-diag-1. Предоставлено : Wikimedia Commons. Расположен по адресу : https://commons.wikimedia.org/wiki/File:Shell-diag-1.png . Лицензия : CC BY-SA: Attribution-ShareAlike
• Предоставлено : Wikimedia. Расположен по адресу : http://upload.wikimedia.org/Wikipedia/commons/4/43/Earth-G-force.png . Лицензия : CC BY-SA: Attribution-ShareAlike

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Безграничный

   Показать оглавление

   нет

2. Теги

   1. центр масс
   2. Гравитационная сила
   3. индукционный
   4. обратный
   5. точечная масса
   6. вес

Центр тяжести | Определение и факты

центр тяжести

Посмотреть все СМИ

Ключевые люди:

Альберт Саксонский

Связанные темы:

масса центр масс

См. все связанные материалы →

центр тяжести , в физике воображаемая точка в теле материи, где для удобства некоторых расчетов можно считать, что сосредоточена полная масса тела. Эта концепция иногда полезна при проектировании статических конструкций (например, зданий и мостов) или при прогнозировании поведения движущегося тела под действием силы тяжести.

В однородном гравитационном поле центр тяжести идентичен центру масс, термин, предпочитаемый физиками. Однако они не всегда совпадают. Например, центр масс Луны очень близок к ее геометрическому центру (это не точно, потому что Луна не является идеальной однородной сферой), но ее центр тяжести немного смещен к Земле из-за более сильной гравитационной силы на Луне. ближняя сторона.

Расположение центра тяжести тела может совпадать с геометрическим центром тела, особенно в объекте симметричной формы, состоящем из однородного материала. Однако асимметричный объект, состоящий из множества материалов с разными массами, вероятно, будет иметь центр тяжести, расположенный на некотором расстоянии от его геометрического центра. В некоторых случаях, таких как полые тела или объекты неправильной формы, центр тяжести (или центр масс) может находиться в пространстве в точке, внешней по отношению к физическому материалу, например, в центре теннисного мяча или между ножками тела. кресло.

В опубликованных таблицах и справочниках указаны центры тяжести наиболее распространенных геометрических фигур. Для треугольной металлической пластины, такой как изображенная на рисунке, расчет будет включать суммирование моментов весов всех частиц, составляющих металлическую пластину, относительно точки A. Приравнивая эту сумму к весу пластины W, умноженному по неизвестному расстоянию от центра тяжести G до АС можно определить положение G относительно АС. Суммирование моментов можно легко и точно получить с помощью интегрального исчисления.

Центр тяжести любого тела также можно определить с помощью простой физической процедуры. Например, для пластины на рисунке точка G может быть расположена путем подвешивания пластины на веревке, прикрепленной в точке А, а затем на веревке, прикрепленной в точке С.