Ось симметрии проходит через вершину параболы и параллельна оси \(y\) (ординат). \(x_1\) и \(x_2\) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.
3 параметра позволяющих сопоставить формулу квадратичной функции и график:
|
1. |
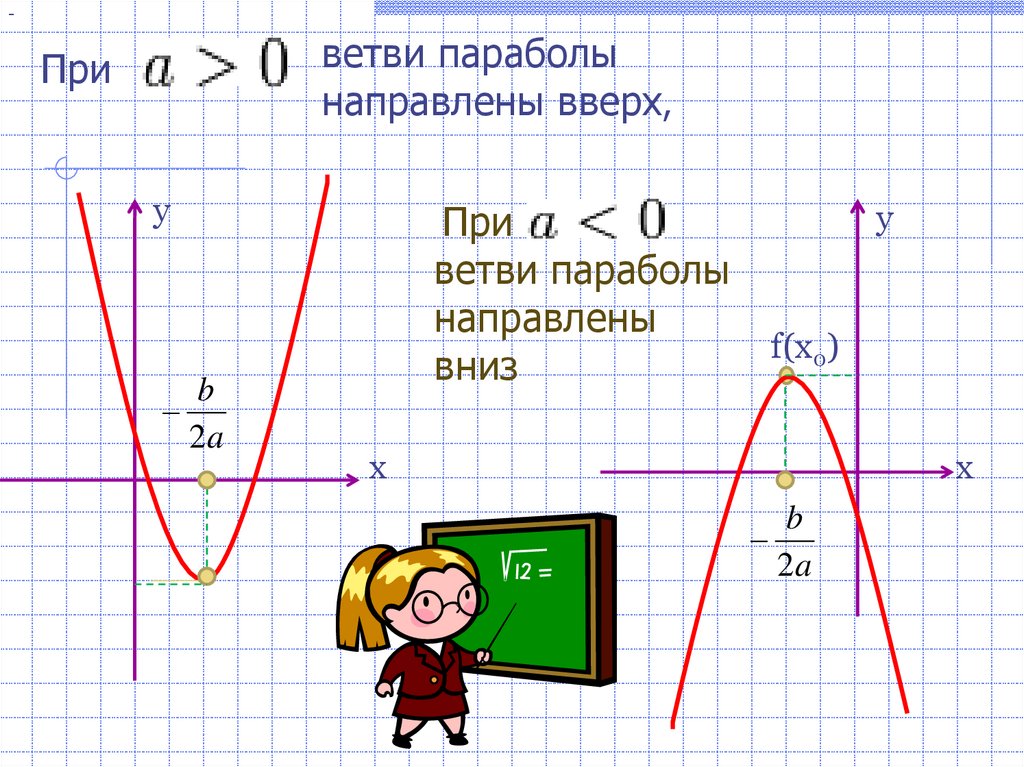
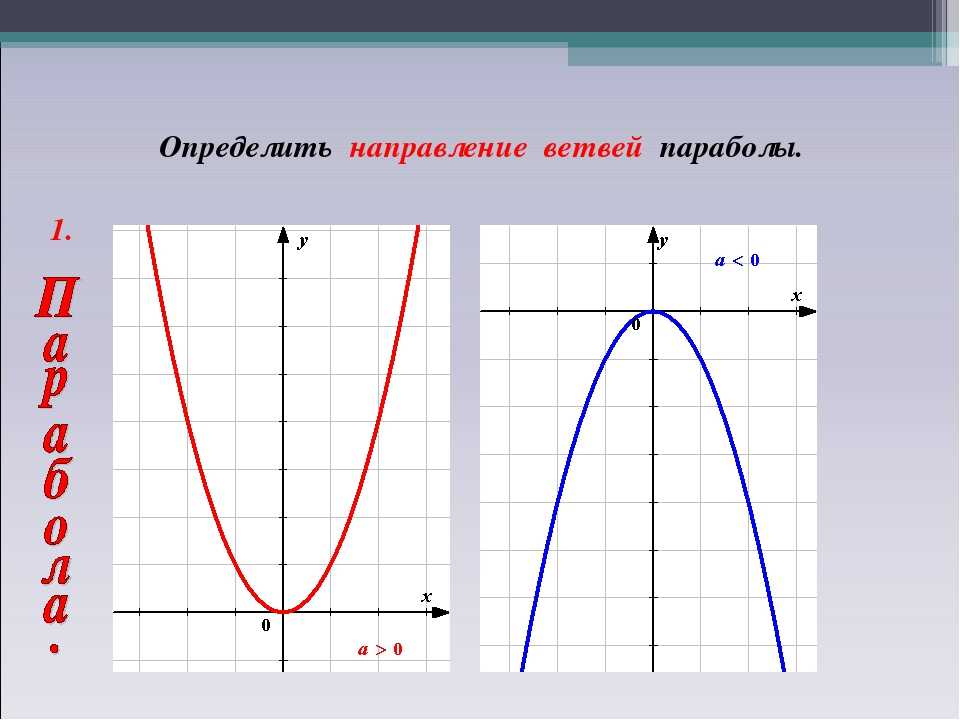
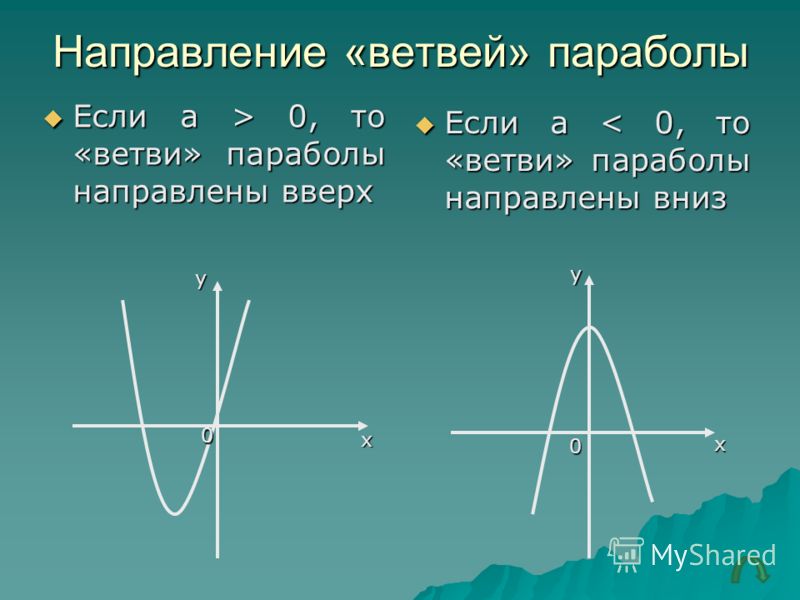
\(a>0\) — ветви параболы направлены вверх |
|
||||
|
\(a<0\) — ветви параболы направлены вниз |
|
|||||
|
2. |
\(c\) равна ординате точки пересечения |
|
||||
|
3. Ответ:
Как построить график квадратичной функции (параболу)?Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь
|
2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\))
Смотрите также:
Линейная функция
Виды графиков функций
Квадратные неравенства
§ Квадратичная функция. Как построить параболу
Квадратичная функция. Как построить параболу Как решать задачи на квадратичную функцию
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.
Запомните!
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a, b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.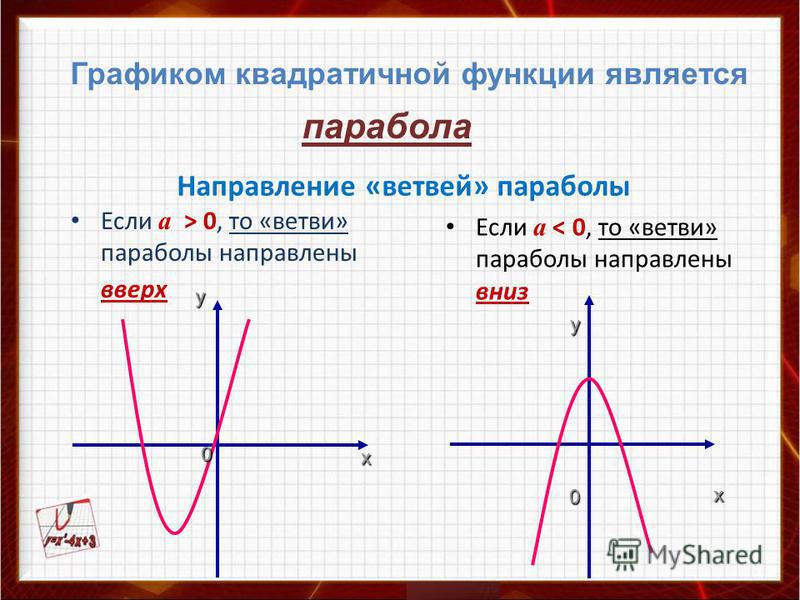
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a», «b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.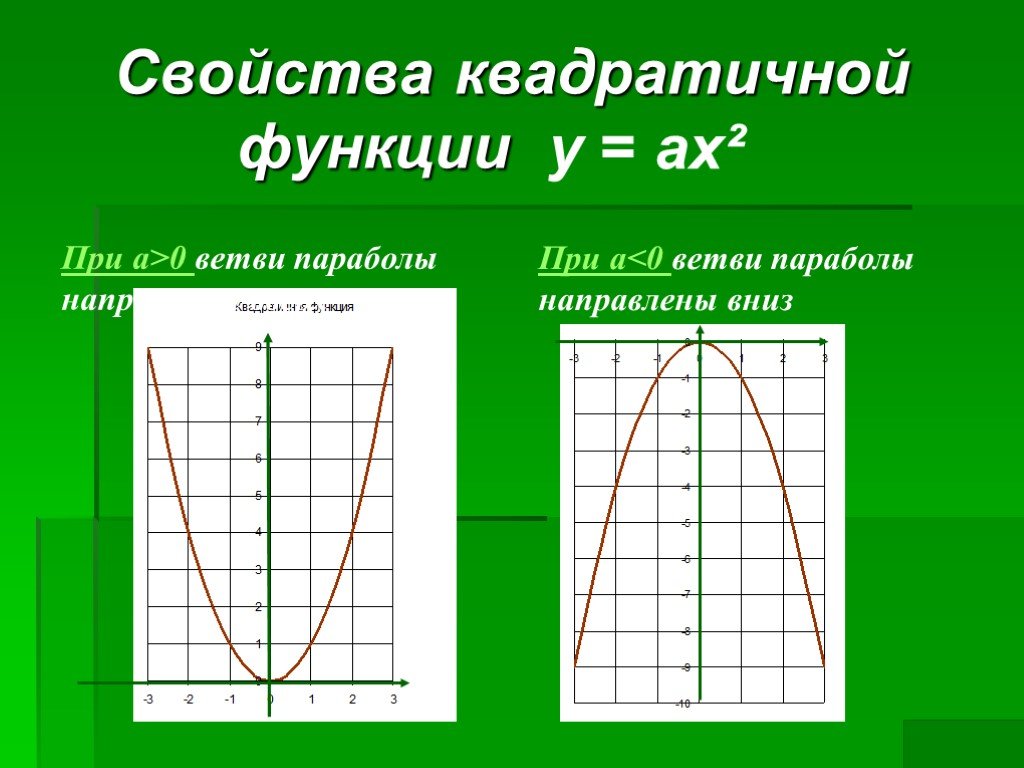
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
- Координаты вершины параболы
Запомните!
Чтобы найти «x0» (координата вершины по оси «Ox») нужно использовать формулу:
x0 =
x0 =
= = 3,5− (−7) 2 · 1 Теперь нам нужно найти «y0» (координату вершины по оси «Oy»). Для этого нужно подставить найденное значение «x0» в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
y0(3,5) = (3,5)
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси «Oy».
- Нули функции
Для начала давайте разберемся, что называют нулями функции.
Нули функции — это точки пересечения графика функции с осью «Ox» (осью абсцисс).
Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси «Oy» равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y = 0».
Подставим в заданную функцию «y = x
0 = x2 −7x + 10
x2 −7x + 10 = 0
x1;2 =7 ± √49 − 4 · 1 · 10 2 · 1
x1;2 =7 ± √9 2
x1;2 =7 ± 3 2 x1 = x2 = 7 − 3 2 x1 = x2 = x1 = 5 x2 = 2 Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x». Целесообразно брать целые числовые значения на оси «Ox», которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.
x 1 3 4 y Для каждого выбранного значения «x» рассчитаем «y».
- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 = 4
- y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 = −2
- y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 = −2
- y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 = 4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Назовем эти точки и выпишем их координаты.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции «y = −3x2 − 6x − 4».
- Направление ветвей параболы «a = −3» — ветви параболы направлены вниз.
- Координаты вершины параболы
x0 =
x0 =
−(−6) 2 · (−3) =
= −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ± √62 − 4 · 3 · 4 2 · 1 x1;2 =
−6 ± √36 − 48 2 x1;2 =
−6 ± √−12 2 Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось «Ox».
- Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».
- y(−3) = −3 · (−3)2 − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
- y(−2) = −3 · (−2)2 − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
- y(0) = −3 · 02 − 6 · 0 − 4 = −4
- y(1) = −3 · 12 − 6 · 1 − 4 = −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13
Отметим вспомогательные точки.
Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Квадратичная функция. Как построить параболу Как решать задачи на квадратичную функцию
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
Основные свойства параболы
В этом разделе мы обсудим наиболее важные свойства параболы, а также покажем, как найти ее вершину, корни и точки пересечения. Эта информация необходима для построения графика, а также позволяет анализировать поведение заданной параболы.
Мы уже показали, как рисовать графики квадратичной функции, а теперь переходим к наиболее важным деталям. Начнем с рассмотрения уравнения параболы. Мы уже знаем, как выглядит парабола. Напомним, что график параболы имеет U-образную форму: 92 мы должны установить a=1, b=c=0.
Парабола — квадратичная функция. Это означает, что наибольшая степень x должна быть равна двум в нашем уравнении. Вы видите коэффициенты a,b,c , которые являются определенными числами, они могут быть как натуральными, так и рациональными, или даже иррациональными. Они определяют форму нашей параболы. Рассмотрим подробнее уравнение и коэффициенты a,b,c и выясним, как от них зависит парабола.
Вот видеоверсия этого урока:
Во-первых, рассмотрим коэффициент a рядом с x в квадрате в уравнении. Знак этого параметра определяет, направлены ветви данной параболы вверх или вниз. Парабола, отмеченная красным на картинке ниже, имеет a=1, а для зеленой — a=-1:9.2+c для нескольких значений коэффициента c:
Итак, грубо говоря, коэффициент c или, другими словами, отрезок y определяет, насколько «высокой» является вершина параболы.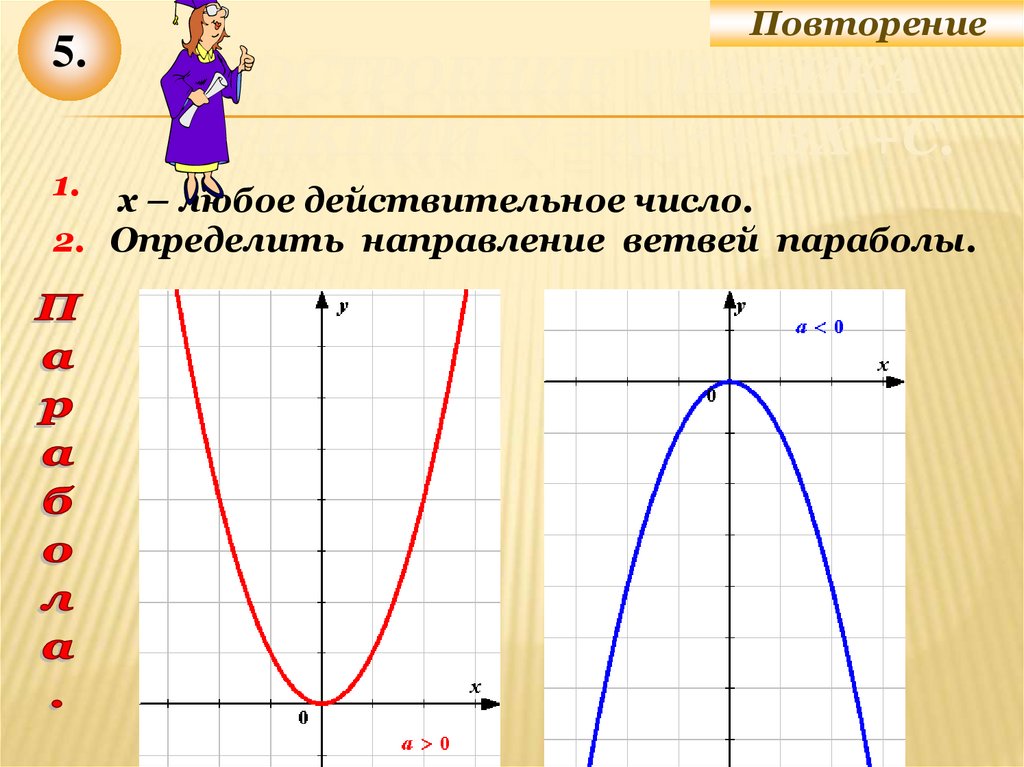
Давайте продолжим и обсудим x-пересечения параболы. Как видно на графике, парабола может пересекать ось x по-разному. По сути, есть три возможности: парабола либо пересекает горизонтальную ось в двух разных точках, либо касается оси x в одной точке с ординатой y=0, либо парабола находится полностью выше (или ниже) оси x. 92-4ac (оставаясь под квадратным корнем в формуле выше) называется дискриминантом квадратного уравнения. Вы можете легко узнать, сколько корней имеет конкретное квадратное уравнение, проанализировав значение дискриминанта.
Если D>0, то есть два разных корня, потому что \sqrt D >0:
x_{1,2}=\frac{-b\pm \sqrt{D}}{2a}
Если $D=0 $ есть только один корень, потому что квадратный корень \sqrt D=0:
x=\frac{-b}{2a}
Если D<0, данное уравнение не имеет действительных корней, потому что квадратный корень из отрицательного числа не существует . 92
В общем случае ось симметрии параболы параллельна оси у.
Также у каждой параболы есть вершина , т.
е. точка, в которой она поворачивается, поэтому она также называется точкой поворота (показана стрелками на рисунке ниже):
x-координата вершины определяется следующим образом:
x_0 =-\frac{b}{2a}
В этой точке парабола достигает минимума, если a>0 (парабола направлена вверх), и максимума, если a<0 (парабола направлена вниз). Это становится понятно после построения графика. Если ваша парабола имеет вид чаши, вершина является точкой минимума, иначе парабола имеет максимум. Поэтому набросок полезен для лучшего понимания. 92-4ac}}{2a}
Подставляя наши коэффициенты, получаем:
x_{1,2}=\frac{-4\pm \sqrt{76}}{2\cdot 3}=\frac{-4 \pm \sqrt{76}}{6}
x_1=\frac{-4+\sqrt{76}}{6}\приблизительно 0,78
x_2=\frac{-4-\sqrt{76}}{ 6}\приблизительно -2.12
Найдите вершину параболы (при раскрытии нашей параболы это будет точка минимума):
x_0=-\frac{b}{2a}=-\frac{4} {6}=-\frac{2}{3}
Чтобы получить y-координату вершины, нам нужно подставить x_0 вместо x в исходное уравнение: 92+4(-\frac{2}{3})-5=\frac{12}{9}-\frac{8}{3}-5=\frac{12-24-45}{9}\ \&=-\frac{57}{9}=-\frac{19}{3} \end{aligned}
Теперь у нас достаточно информации для построения графика:
Подводя итог, мы Мы обсудили общее уравнение параболы и то, как его коэффициенты $a, c$ влияют на график.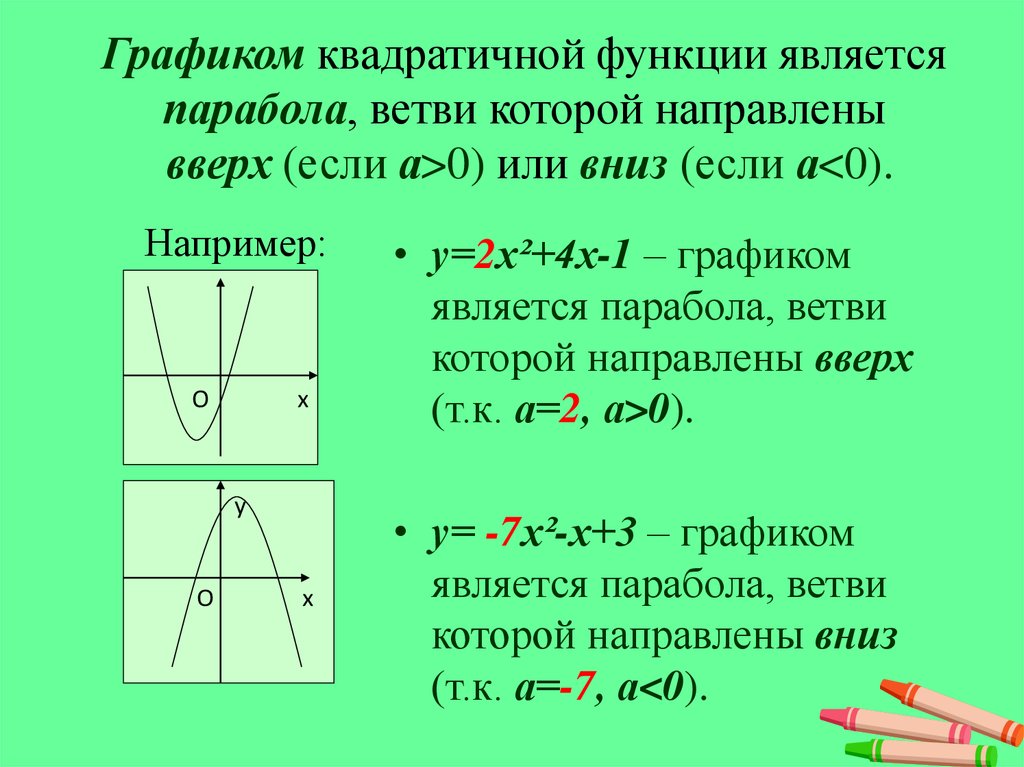
Третий коэффициент b будет рассмотрен в одном из следующих разделов. Также мы поговорили о y- и x-перехватах и о том, как их найти, и мы получили формулу для вершины параболы, которая является точкой максимума (или минимума, в зависимости от коэффициента a). Вся эта информация может быть полезна для домашней работы по алгебре, поэтому полезно запомнить формулы.
9 Акции
- Фейсбук
- Твиттер
- Копировать ссылку
асимптотика — Существует ли парабола, подобная ветви гиперболы?
Задавать вопрос
спросил
Изменено 4 года, 4 месяца назад
Просмотрено 1к раз
$\begingroup$
Парабола и ветвь гиперболы визуально выглядят одинаково.
Единственное отличие, которое я нахожу, состоит в том, что когда x стремится к бесконечности, гипербола приближается к прямой линии (асимптоте). Тогда как, если я нарисую произвольную линию, парабола будет проноситься мимо этой линии и продолжать удаляться от нее.
Но все же, существует ли парабола, которая в точности похожа на ветвь гиперболы?
- асимптотика
- конические сечения
- системы координат
$\endgroup$
1
$\begingroup$
Две параболы различаются только местоположением, ориентацией и коэффициентом масштабирования. Как отмечается в комментарии, все они имеют одинаковую форму.
Гиперболы, однако, бывают разных форм. Некоторые из них асимптотичны паре перпендикулярных прямых. Другие живут внутри гораздо большего или гораздо меньшего угла между их асимптотическими линиями.
Теперь рассмотрим последовательность гипербол, построенную следующим образом. Мы помещаем одну вершину гиперболы в фиксированную точку и отодвигаем другую вершину, позволяя углу между асимптотическими линиями приближаться к нулю, когда другая вершина уходит в бесконечность. Если мы умело сбалансируем скорость, с которой угол становится меньше, а другая вершина уходит дальше, гиперболы будут приближаться к форме параболы.
Так что нет, вы не можете сделать параболу похожей на ответвление типичной гиперболы. Но вы можете сделать ветвь гиперболы почти похожей на параболу.
Совпадение все равно не будет точным. С таким же успехом можно попросить положительное число, равное нулю.
$\endgroup$
$\begingroup$
Ни одна парабола не имеет асимптоты, а каждая ветвь гиперболы имеет две асимптоты. Поэтому никогда не может быть параболы, которая выглядит точно так же, как ветвь гиперболы.
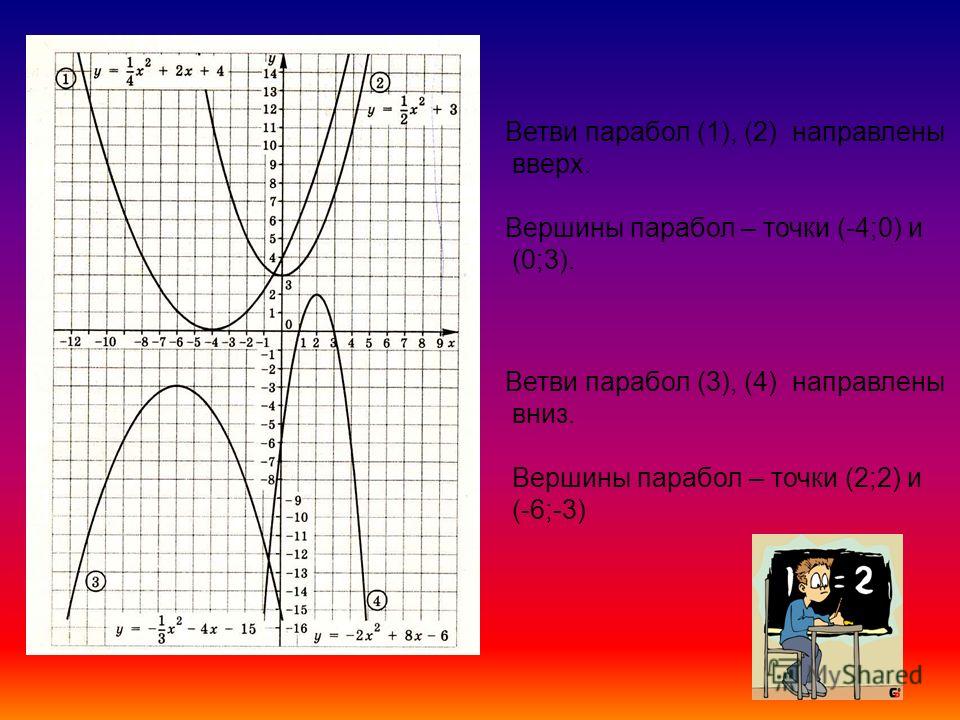
Leave A Comment