Страница не найдена (ошибка 404)
Цветовая схема:
C C C C
Шрифт
Arial Times
Размер шрифта
A A A
Интервал между буквами
Нормальный Увеличенный Большой
Изображения:
муниципальное бюджетное общеобразовательное учреждение города Ростова-на-Дону «Школа № 100 имени Героя Российской Федерации Трошева Г.Н.»
- 344092, г. Ростов-на-Дону, бульвар Комарова 6
- 8(863)235-9-777,8(863)233-5-777
- [email protected]
Для слабовидящих Обычная версия
Cведения об образовательной организации
- Программа воспитания
- Организация питания в образовательной организации
- Дистанционное обучение
- Основные сведения
- Руководство.
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав - Платные образовательные услуги
- Противодействие коррупции
- Образование
- Отчет о результатах самообследования и публичный отчет
- Документы
- Образовательные стандарты
- Платные образовательные услуги
- Материально-техническое обеспечение и оснащенность образовательного процесса
- Структура и органы управления образовательной организацией
- Вакансии
- Вакантные места для приема (перевода)
- Информационная безопасность в школе
- Стипендии и иные виды материальной поддержки
- Доступная среда
- Международное сотрудничество
Информационные ресуры
Федеральная служба по надзору в сфере образования и науки
Министерство общего и профессионального образования Ростовской области
Региональная служба по надзору и контролю в сфере образования Ростовской области
Федеральный институт педагогических измерений
РОЦОИСО
Управление образования города Ростова-на-Дону
Информационная система сопровождения деятельности федеральных инновационных прощадок
Домашняя работа по геометрии за 9 класс к учебнику «Геометрия.
 7-9 класс» А.В.Погорелов§14. Площади фигур
7-9 класс» А.В.Погорелов§14. Площади фигурРешебники и ГДЗ
Начните вводить часть условия (например, могут ли, чему равен или найти):
- № 1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.
- № 2. Стороны двух участков земли квадратной формы равны 100 ми 150 м. Найдите сторону квадратного участка, равновеликого им.
- № 3. Найдите площадь квадрата S по его диагонали а.
- № 4. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в ту же окружность?
- № 5. Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза?
- № 6. Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
- № 7. Чему равны стороны прямоугольника, если они относятся как 4:9, а его площадь 144 м2?
- № 8.
 Чему равны стороны прямоугольника, если его периметр 74 дм, а площадь 3 м2 ?
Чему равны стороны прямоугольника, если его периметр 74 дм, а площадь 3 м2 ? - № 9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.
- № 10. Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? 0бъясните ответ.
- № 11. Найдите площадь ромба, если его высота 10 см, а острый угол 30°.
- № 12. Найдите площадь ромба, если его высота 12 см, а меньшая диагональ 13 см.
- № 13. Докажите, что площадь ромба равна половине произведения диагоналей.
- № 14. Найдите, стороны ромба, зная, что его диагонали относятся как 1:2, а площадь ромба равна 12 см2.
- № 15. Разделите данный треугольник на три равновеликие части прямыми, проходящими через одну вершину.
- № 16*. Решите предыдущую задачу, взяв вместо треугольника параллелограмм.
- № 17. Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м? ΔАВС — равнобедренный, АВ = ВС = 100 м, АС = 120 м.

- № 18. Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а. Рассмотрим ΔАВС, ∠С = 90°, ВС = АС, АВ = а — гипотенуза.
- № 19. У треугольника со сторонами 8 см и 4 см проведены высоты к этим сторонам. Высота, проведенная к стороне 8 см, равна 3 см. Чему равна высота, проведенная к стороне 4 см?
- № 20. Докажите, что стороны треугольника обратно пропорциональны его высотам, т.е.:
- № 21. Найдите площадь равностороннего треугольника со стороной а.
- № 22. Найдите площадь правильного треугольника, вписанного вкруг радиуса 5.
- № 23. Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см.
- № 24. Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2?
- № 25. У треугольника ABС АС = а, ВС = E. При каком угле С площадь треугольника будет наибольшей?
- № 26. Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними равен 70°.

- № 27. Найдите площадь параллелограмма, если его стороны 2 ми 3 м, а один из углов равен 70°.
- № 28*. Найдите площадь треугольника по стороне a и прилежащим к ней углам а и b.
- № 29. Выведите формулу Герона для площади треугольника:
- № 30. Найдите площадь треугольника по трем сторонам:
- № 31. Стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.
- № 32. Боковые стороны треугольника 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равное: 1) 25 см; 2) 11 см.
- № 33. Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную на боковую сторону.
- № 35. Найдите высоту треугольника со сторонами
- № 36. Найдите наименьшую высоту треугольника со сторонами: 1) 5, 5, 6; 2) 17,65, 80 и наибольшую высоту
- № 37. Найдите площадь трапеции, у которой параллельные стороны 60 см и 20 см, а непараллельные — 13 см и 37 см.

- № 38. В равнобокой трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Найдите площадь трапеции.
- № 39. В равнобокой трапеции большее основание равно 44 м, боковая сторона 17 ми диагональ 39 м. Найдите площадь трапеции.
- № 41*. Докажите, что среди всех параллелограммов сданными диагоналями наибольшую площадь имеет ромб.
- № 42. Выведите следующие формулы для радиусов описанной (R) и вписанной (r) окружностей треугольника:
- № 43. Найдите радиусы описанной (5) и вписанной (г) окружностей для треугольника со сторонами: 1) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7. 1) а = 13, b = 14, с = 15. Полупериметр треугольника:
- № 44. Боковая сторона равнобедренного треугольника 6 см, высота, проведенная к основанию, 4 см. Найдите радиус описанной окружности. Пусть АВС — равнобедренный треугольник, АВ = ВС =
- № 45. Найдите радиусы окружностей описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.

- № 46. Найдите радиус г вписанной и радиус 5 описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.
- № 47. Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.
- № 48. Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.
- № 49. Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.
- № 50. Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН.
- № 51. Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна А.
- № 52. Периметры правильных n-угольников относятся как а:b.
 Как относятся их площади?
Как относятся их площади? - № 53. Найдите площадь круга, если длина окружности l.
- № 54. Найдите площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 ми 6,5 м; 3) а и b, а > b.
- № 55. Во сколько раз увеличится площадь круга, если его диаметр увеличить: 1) в 2 раза; 2) в 5 раз; 3) в m раз? Если диаметр увеличить в n раз, то радиус увеличится тоже в n раз, тогда площадь увеличится в n2 раз.
- № 56. Найдите отношение площади круга к площади вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. 1) Пусть ABCD — квадрат, вписанный вкруг.
- № 57. Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.
- № 58. Найдите отношение площади круга, описанного около квадрата, к площади круга,вписанного в него.
- № 59. Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен: 1) 40°; 2) 90°; 3) 150°; 4) 240°; 5) 300°; 6) 330°.

- № 60. Дана окружность радиуса 5. Найдите площадь сектора, соответствующего дуге с длиной, равной: 1) R, 2) l.
- № 61*. Найдите площадь кругового сегмента с основанием a√3 и высотой — a/2.
- № 62. Найдите площадь той части круга, которая расположена вне вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга 5. 1)
Калькулятор площади треугольника
Автор: Hanna Pamuła, PhD
Отредактировано Bogna Szyk и Adena Benn
Последнее обновление: 28 апреля 2023 г.
Содержание:- Формула площади треугольника 0009 Как использовать этот калькулятор площади треугольника?
- Как вычислить площадь равностороннего треугольника?
- Часто задаваемые вопросы
Этот калькулятор площади треугольника может помочь в определении площади треугольника. В базовой формуле площади треугольника должны быть заданы основание и высота, но что, если у нас их нет? Как вычислить площадь треугольника, у которого только 3 стороны? Калькулятор площади треугольника здесь для вас. Попробуй! Если вы все еще не знаете, как найти площадь треугольника, посмотрите описание ниже.
Попробуй! Если вы все еще не знаете, как найти площадь треугольника, посмотрите описание ниже.
Формула площади треугольника
Треугольник — одна из самых основных фигур в геометрии. Самая известная и самая простая формула, которую почти все помнят со школы:
-
площадь = 0,5 * b * h, гдеb— длина основания треугольника, аh— это высота/высота треугольника.
Однако иногда трудно найти высоту треугольника. В этом случае можно использовать многие другие уравнения, в зависимости от того, что вы знаете о треугольнике:
Три стороны (SSS)
Если известны длины всех сторон, используйте формулу Герона:
площадь = 0,25 * √( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
Две стороны и угол между ними (SAS)
Вы можете легко вычислить площадь треугольника с помощью тригонометрии:
площадь = 0,5 * a * b * sin(γ)
Два угла и сторона между ними (ASA)
Существуют различные версии формул площади треугольника — для ее получения можно использовать, например, тригонометрию или закон синусов:
площадь = a² * sin(β) * sin(γ) / (2 * sin(β + γ))
Если вы ищете другие формулы или калькуляторы, связанные с треугольниками, посмотрите этот калькулятор прямоугольного треугольника, калькулятор теоремы Пифагора и калькулятор закона косинусов.
Как использовать этот калькулятор площади треугольника?
Предположим, что мы знаем две стороны и угол между ними:
- Введите длину первой стороны . В нашем примере он может быть равен 9 дюймам .
- Введите вторую сторону треугольника . Давайте выберем 5 дюймов.
- Определить угол между двумя известными сторонами . Например, 30 градусов.
- Посмотрите, как наш калькулятор площади треугольника выполняет все расчеты за вас! Площадь для нашего случая равна 11,25 дюйма².
Как вычислить площадь равностороннего треугольника?
Чтобы вычислить площадь равностороннего треугольника, нужно знать только сторону:
площадь = a² × √3/4
мы можем сформулировать Быстрый рецепт: чтобы аппроксимировать площадь равностороннего треугольника, возведите длину стороны в квадрат, а затем умножьте на 0,433 .
Хотя мы подготовили отдельный калькулятор для площади равностороннего треугольника, вы можете быстро рассчитать ее в этом калькуляторе площади треугольника. Просто используйте подраздел для площади треугольника с 3 сторонами — как вы знаете, каждая сторона имеет одинаковую длину в равностороннем треугольнике. Эту площадь можно рассчитать и в угол-сторона-угол или сторона-угол-сторона версия — вы, наверное, помните, что каждый угол в равностороннем треугольнике равен 60 градусам (π/3 рад).
Просто используйте подраздел для площади треугольника с 3 сторонами — как вы знаете, каждая сторона имеет одинаковую длину в равностороннем треугольнике. Эту площадь можно рассчитать и в угол-сторона-угол или сторона-угол-сторона версия — вы, наверное, помните, что каждый угол в равностороннем треугольнике равен 60 градусам (π/3 рад).
Часто задаваемые вопросы
Как найти площадь треугольника по сторонам?
Если известны длины всех сторон ( a , b и c ) треугольника, можно вычислить его площадь:
- Вычислить половину периметра
½(а + б + в). Обозначим это значение черезс. - Вычислить
s-a,s-bиs-c. - Умножьте на три числа из шага 2.
- Умножить результат на
s. - Возьмите квадратный корень из результата .

- Это площадь вашего треугольника — молодец! Используемый нами метод называется Формула Герона .
Как найти площадь треугольника по углам?
Вы не можете определить площадь треугольника, если знаете только углы. Это потому, что существует бесконечно много треугольников с одинаковыми углами . Вы должны знать хотя бы одну сторону (или высоту) треугольника, чтобы определить его площадь.
Как вычислить площадь прямоугольного треугольника?
Чтобы вычислить площадь прямого угла, вам нужно всего лишь умножить длины катетов вашего треугольника, а затем разделить результат на 2. Например, если катетов 3 дюймов и 4 дюймов, тогда площадь равна 3 × 4/2 = 12/2 = 6 дюймов кв.
Чему равна площадь равностороннего треугольника со стороной 10?
Площадь примерно 43,3 . Точный ответ: 25 × √3 . Чтобы получить этот ответ, вспомните формулу площади равностороннего треугольника со стороной a : площадь = a 2 × √3 / 4 .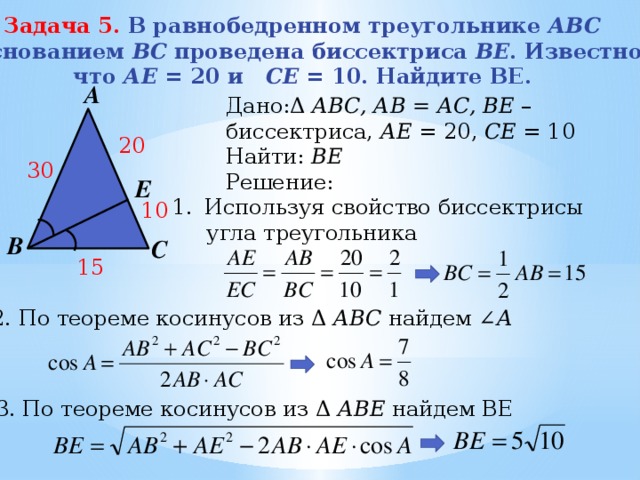 Для треугольника со стороной 10 получаем площадь = 10 2 × √3/4 = 100 × √3/4 = 25 × √3 , что примерно равно 43,3 . — вопрос №1725, задачи построения геометрии
Для треугольника со стороной 10 получаем площадь = 10 2 × √3/4 = 100 × √3/4 = 25 × √3 , что примерно равно 43,3 . — вопрос №1725, задачи построения геометрии
Нарисуйте прямоугольный треугольник ABC, если |AB| = 5 см |ВС| = 3 см, |AC| = 4 см. Нарисуйте окружность Фалеса над гипотенузой треугольника ABC.
Правильный ответ:
r = 2,5 смПошаговое объяснение:
c=5 см a=3 см b=4 см r=c/2=5/2=2,5 см
Сделал вы нашли ошибку или неточность? Не стесняйтесь
написать нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.
Чтобы решить эту математическую задачу со словами, вам необходимо знать следующие знания:
- геометрия
- теорема Фалеса
- планиметрия
- прямоугольный треугольник
- окружность
- треугольник 9 0010
Темы, темы:
- задачи на построение геометрии
Класс словесной задачи:
- практика для 13-летних
- практика для 14-летних
Мы рекомендуем вам посмотреть этот обучающий видеоролик по этой математической задаче: видео1
- Гипотенуза 65744
Постройте прямоугольный треугольник ABC с гипотенузой AB: а) | АБ | = 72 мм, | Британская Колумбия | = 51 мм б) | АБ | = 58 мм, | переменный ток | = 42 мм - Нарисуйте треугольник
Постройте равнобедренный треугольник ABC, если AB = 7см, то угол ABC равен 47°, стороны | переменный ток | = | до нашей эры |. Измерьте размер стороны ВС в мм.
Измерьте размер стороны ВС в мм. - Вычислить 60993
В прямоугольном треугольнике ABC вычислить величину внутренних углов, если / AB / = 13 см; /ВС/ = 12 см и /АС/ = 5 см. - Треугольник 3552
Нарисуйте круг k (S, r = 3см). Постройте треугольник ABC так, чтобы его вершины лежали на окружности k, а длина сторон была (AB) = 2,5 см (AC) = 4 см - Нарисуйте треугольник
Постройте прямоугольный треугольник MNO с гипотенузой o = 5 см и углом MNO = 37° - В 18
В прямоугольном треугольнике ABC, Гипотенуза AB = 15 см, а B = 25 градусов. Какова длина BC с точностью до сантиметра? - Sin cos tan
В треугольнике ABC с прямым углом в B. Стороны /AB/=7см, /BC/=5см, /AC/=8,6см. Найдите два десятичных знака. A. Синус C B. Косинус C C. Тангенс C. - Биссектриса 2
ABC — равнобедренный треугольник. Поскольку AB=AC, AX — биссектриса угла ∢BAC, пересекающего сторону BC в точке X. Докажите, что X — середина BC. - Квадраты над сторонами
Два квадрата построены на двух сторонах треугольника ABC. Площадь квадрата над стороной ВС равна 25 см². Высота vc до стороны AB равна 3 см. Пятка Р высотой vc делит сторону АВ в соотношении 2:1. Сторона AC длиннее стороны BC. Расчет
Площадь квадрата над стороной ВС равна 25 см². Высота vc до стороны AB равна 3 см. Пятка Р высотой vc делит сторону АВ в соотношении 2:1. Сторона AC длиннее стороны BC. Расчет - Координаты 32183
Дан на плоскости треугольник ABC. A (-3,5), B (2,3), C (-1, -2) запишите координаты векторов u, v, w, если u = AB, v = AC и w = BC. Введите координаты центров линий SAB (..), SAC (…), SBC (. ..) - Применяет 14683
Точка B является центром окружности. Линия AC касается окружностей в точке C и применяет AB = 20 см и AC = 16 см. Чему равен радиус окружности ВС? - Треугольник ABC
В треугольнике ABC длина стороны BC 2 см. Точка К является средней точкой АВ. Точки L и M делят сторону АС на три равные линии. КЛМ — равнобедренный треугольник с прямым углом в точке К. Определить длины сторон АВ, АС треугольника А - Рассчитайте 2556
Рассчитайте длину стороны b трапеции ABCD, если a = 12 см, c = 4 см, d (AC) = d (BC) и площадь S (треугольник ABC) = 9 см2.

 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав Чему равны стороны прямоугольника, если его периметр 74 дм, а площадь 3 м2 ?
Чему равны стороны прямоугольника, если его периметр 74 дм, а площадь 3 м2 ?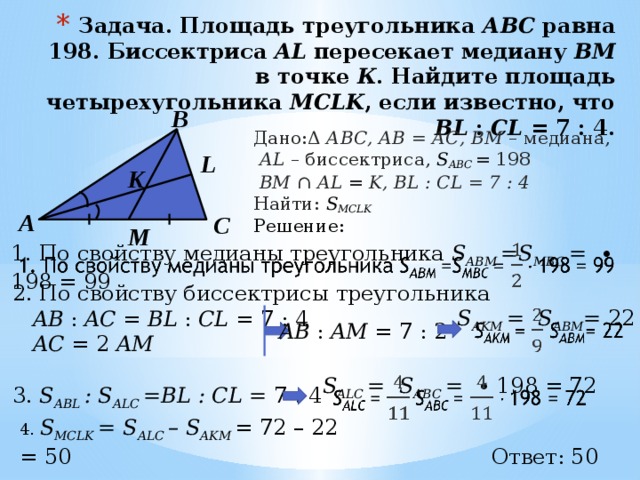

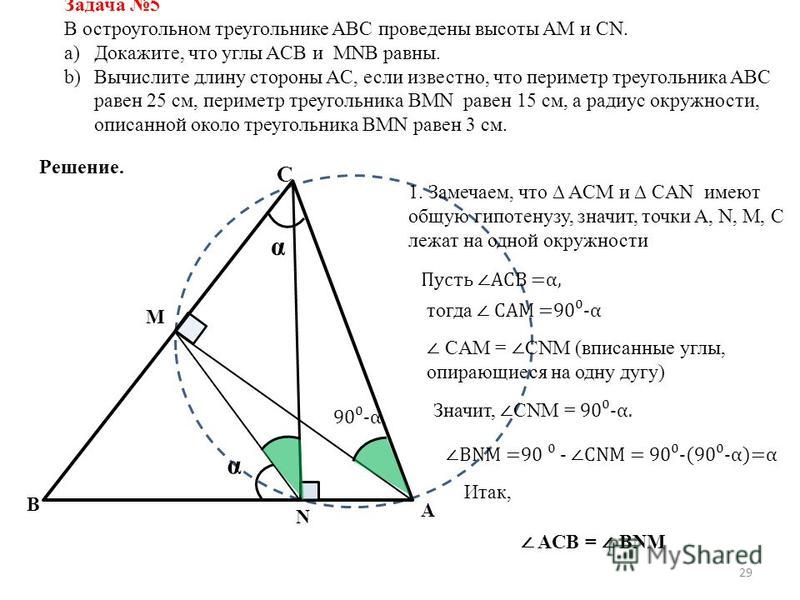
 Как относятся их площади?
Как относятся их площади?
 Измерьте размер стороны ВС в мм.
Измерьте размер стороны ВС в мм. Площадь квадрата над стороной ВС равна 25 см². Высота vc до стороны AB равна 3 см. Пятка Р высотой vc делит сторону АВ в соотношении 2:1. Сторона AC длиннее стороны BC. Расчет
Площадь квадрата над стороной ВС равна 25 см². Высота vc до стороны AB равна 3 см. Пятка Р высотой vc делит сторону АВ в соотношении 2:1. Сторона AC длиннее стороны BC. Расчет
Leave A Comment