В треугольнике ABC угол A равен
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-01-24
Продолжаем рассматривать задачи, в которых требуется вычислить углы в треугольнике. В статье «Сумма углов треугольника. Часть 1!» уже было представлено решение некоторых задач, посмотрите обязательно. Треугольники рассматриваются совершенно различные.
Это целая группа заданий, входящих в ЕГЭ, где требуется знание лишь теоремы о сумме углов треугольника. Правда в некоторых задачах необходимо знание ещё некоторых свойств. Например, при решении одной из рассмотренных в этой статье используется свойство связанное с выпуклым четырёхугольником. Напомню его:
Сумма углов четырёхугольника равна 360 градусам
Следует добавить, что иногда в условии задаётся отношение углов. Что это значит? Вообще, если задано отношение сторон, углов, либо других элементов в любой фигуре, то это по сути говорит нам во сколько раз один элемент больше другого.
Например, стороны параллелограмма относятся как 1:4. Это означает, что одна его сторона больше другой в 4 раза, то есть они могут быть равны 2 и 8, 4 и 16, 10 и 40, 150 и 600, вариантов бесконечное множество. И получаются они умножением на один и тот же (один и тот) коэффициент:
1х и 4х
Этот коэффициент называется коэффициентом пропорциональности. Как правило в задачах, где задаются отношения каких-либо элементов, имеются ещё условия. Например, если в нашем параллелограмме будет дана сумма соседних сторон, то мы всегда сможем найти этот коэффициент пропорциональности и далее вычислить сами длины сторон. Пусть сумма соседних сторон будет равна 40, тогда получим
х + 4х = 40
5х = 40
х = 8
Стороны будут равны 8 и 32.
Рассмотрим задачи:
Один из внешних углов треугольника равен 65о. Углы, не смежные с данным внешним углом, относятся как 6:7. Найдите наибольший из них. Ответ дайте в градусах.
Сумма внутреннего угла треугольника и смежного с ним внешнего угла равна , значит
Введём коэффициент пропорциональности х и обозначим один неизвестный угол как 6х, другой 7х. По теореме о сумме углов треугольника:
По теореме о сумме углов треугольника:
Таким образом, больший угол будет равен 7∙5 = 350
Ответ: 35
*Можно было сразу использовать теорему о внешнем угле треугольника.
Один из углов равнобедренного треугольника равен 920. Найдите один из других его углов. Ответ дайте в градусах.
Рассмотрим данный треугольник AВC. Понятно, что угол 920 это угол при его вершине С. Почему?
Угол такой величины не может лежать в основании, так как в этом случае оба угла при основании в сумме составят 194 градуса, а это невозможно.
Поэтому обозначим угол А как x, тогда
Так как сумма углов треугольника равна 180 градусам, то
*Конечно, условие немного может запутать, не совсем обычно звучит «дан один угол, найти другой». Было бы понятнее, если бы стояло такое условие «угол при вершине равен 92 градуса, вычислить угол при основании». Но зная теорему о сумме углов треугольника вы всегда сможете проанализировать и понять, что в подобном задании имеется ввиду.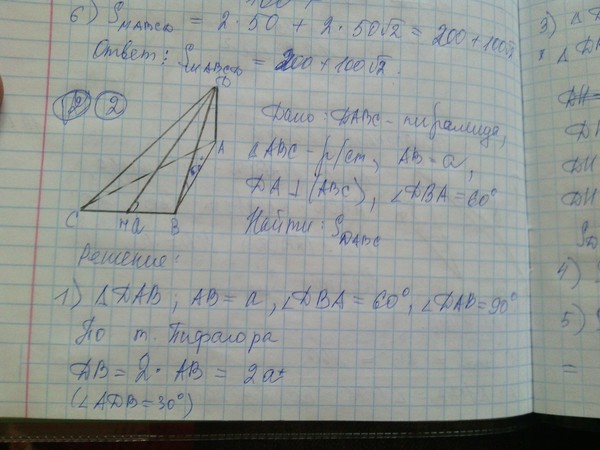
Ответ: 44
Углы треугольника относятся как 3:4:5. Найдите больший из них. Ответ дайте в градусах.
Известно, что о сумма углов треугольника равна 1800. Введём коэффициент пропорциональности x. Тогда меньший из его углов равен 3x, другие два угла равны 4x и 5x соответственно. Получаем уравнение
Таким образом, больший из углов треугольника равен 5∙150 = 750
Ответ: 75
Один угол равнобедренного треугольника на 1410 больше другого. Найдите меньший угол. Ответ дайте в градусах.
Рассмотрим равнобедренный треугольник AВC.
По свойству равнобедренного треугольника углы при его основании равны Сумма всех углов треугольника равна 1800. Понятно, что меньший угол это угол при основании треугольника. Если предположить, что он был бы большим, то в сумма углов при основании была бы больше 1800, а это невозможно.
Обозначим угол А через x, тогда
Получаем уравнение:
Меньший угол равен 13 градусам.
Ответ: 13
В треугольнике ABC угол A равен 300, угол B равен 710, CH — высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.
Рассмотрим прямоугольный треугольник ACH. По свойству прямоугольного треугольника сумма его острых углов равна 900, то есть
Значит
Рассмотрим прямоугольный треугольник BCH. Аналогично:
Значит
Найдём разность
Ответ: 31
В треугольнике ABC угол A равен 630, а углы В и С — острые. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
Рассмотрим четырёхугольник ADOE.
Известно, что сумма всех углов выпуклого четырёхугольника равна 3600, то есть
Так как СЕ и BD высоты, то
Таким образом, в четырёхугольнике известны три угла, можем найти четвёртый:
Ответ: 117
Два угла треугольника равны 750 и 500.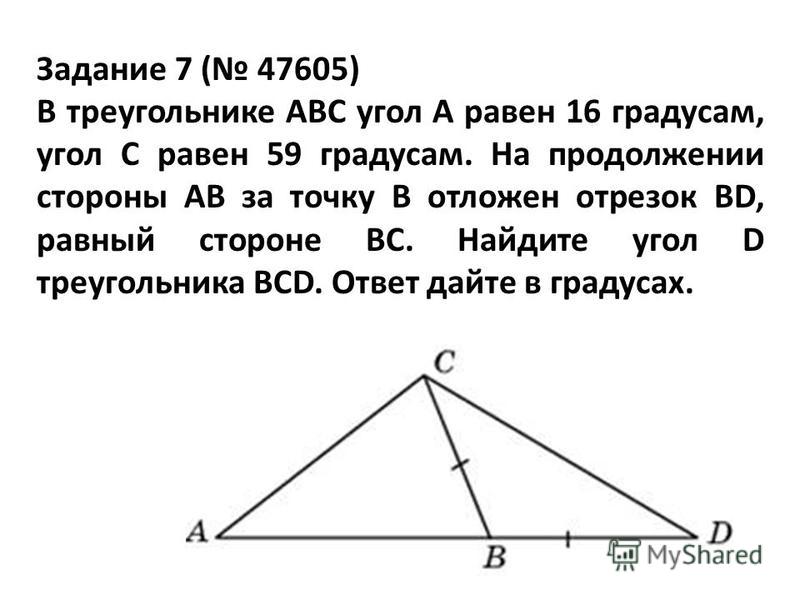 Найдите тупой угол, который образуют высоты треугольника, исходящие из вершин этих углов. Ответ дайте в градусах.
Найдите тупой угол, который образуют высоты треугольника, исходящие из вершин этих углов. Ответ дайте в градусах.
Рассмотрим треугольник ABC. Построим высоты выходящие из этих вершин А и В. Пусть они пересекаются в точке О. Нам известно два угла в треугольнике, найдём третий:
Рассмотрим четырёхугольник CDOE. Сумма всех углов четырёхугольника равна 3600, значит
Таким образом, искомый угол равен 125 градусам.
Ответ: 125
27749. Один из внешних углов треугольника равен 85о. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Посмотреть решение
27750. Один из углов равнобедренного треугольника равен 980. Найдите один из других его углов. Ответ дайте в градусах.
Посмотреть решение
27752. Углы треугольника относятся как 2:3:4. Найдите меньший из них. Ответ дайте в градусах.
Ответ дайте в градусах.
Посмотреть решение
27754. Один угол равнобедренного треугольника на 900 больше другого. Найдите меньший угол. Ответ дайте в градусах.
Посмотреть решение
27756. В треугольнике ABC угол A равен 600, угол B равен 700, CH — высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.
Посмотреть решение
27762. В треугольнике ABC угол A равен 720, а углы В и С — острые. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
Посмотреть решение
27763. Два угла треугольника равны 580 и 720. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Посмотреть решение
На этом всё! В будущем рассмотрим ещё задания, связанные с вычислением углов в треугольнике, не пропустите!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Решение треугольников | ЕГЭ-№1Углы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Особые свойства треугольника с углом 60 градусов — NovaInfo 32
- Баталаев А.В.
Калмыцкий государственный университет
Опубликовано
Раздел: Физико-математические науки
Язык: Русский
Просмотров за месяц: 632
CC BY-NC
Аннотация
Треугольник с углом 60 градусов обладает необычными свойствами. Если этот треугольник не является правильным, то все три угла всегда образуют арифметическую прогрессию. Выполняется и обратное утверждение: Если сумма углов треугольника образует арифметическую прогрессию, то один из углов равен 60 градусам. Кроме того, между треугольниками с углами 45, 60, 75 и 30, 60, 90 градусов существует сложная взаимность.
Если этот треугольник не является правильным, то все три угла всегда образуют арифметическую прогрессию. Выполняется и обратное утверждение: Если сумма углов треугольника образует арифметическую прогрессию, то один из углов равен 60 градусам. Кроме того, между треугольниками с углами 45, 60, 75 и 30, 60, 90 градусов существует сложная взаимность.
Ключевые слова
ГЕОМЕТРИЯ, УГЛЫ, СВОЙСТВО ТРЕУГОЛЬНИКА, АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ, АЛГЕБРЫ, УГОЛ 60 ГРАДУСОВ, ВЗАИМНОСТЬ
Аудиоверсия
Текст научной работы
Докажем свойство треугольника с углом 60 градусов.
Теорема. Если треугольник с углом 60 градусов не является правильным, то его углы составляют арифметическую прогрессию.
Рисунок 1.Доказательство:
Пусть в треугольнике ABC угол B равен 60о, а угол A=α (рис.1). Так как сумма углов треугольника равна 180о, то ÐA+ÐC=120o. Тогда, ÐС=120o−α.
Таким образом, ÐA=α, ÐB=60o=α+(60o−α), ÐC=120o−α=α+2(60o−α) (1)
Из соотношения (1) видно, что углы треугольника составляют арифметическую прогрессию с разностью 60o−α. Теорема доказана.
Теорема доказана.
Справедливо и обратное утверждение.
Теорема. Если углы треугольника составляют арифметическую прогрессию, то один из углов равен 60о.
Рисунок 2.Доказательство:
Пусть ÐA=α, ÐB=α+d, ÐC=α+2d (рис.2). Сумма углов треугольника равна 180о, поэтому α+α+d+α+2d=180o=>3α+3d=180o=>α+d=60o=>d=60o−α.
Отсюда ÐB=α+60o−α=60o. Теорема доказана.
Существуют и другие необычные свойства треугольников с углами 60о.
Для треугольника 45о, 60о, 75о ортоцентрическим является треугольник с углами 30о, 60о, 90о. Если продолжить высоты треугольника до их пересечения с описанной окружностью, то получим треугольник подобный высотному (рис.3).
Рисунок 3. Высотный треугольник и ему подобныйНазовём инцентрическим треугольник, образованный основаниями перпендикуляров опущенных из центра вписанной окружности на стороны. Для треугольника с углами 30о, 60о, 90о инцентрическим будет треугольник с углами 45о, 60о, 75о (рис.4).
Для треугольника с углами 30о, 60о, 90о инцентрическим будет треугольник с углами 45о, 60о, 75о (рис.4).
Читайте также
Список литературы
- Алгебра. 9 класс : учеб. для общеобразоват. организаций [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова] ; под ред. С. А. Теляковского. – 21-е изд. – М.: Просвещение, 2014. – 271 с.: ил.
- Геометрия: учеб. для 7-9 кл. сред. шк. /Л. С. Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1990. – 336 с.
Цитировать
Баталаев, А.В. Особые свойства треугольника с углом 60 градусов / А.В. Баталаев. — Текст : электронный // NovaInfo, 2015. — № 32. — URL: https://novainfo.ru/article/3266 (дата обращения: 21.03.2023).
Поделиться
Q8 Построить треугольник ABC, если AB 54 см A 30 и B 90 Измерить C и сторону BC…
Вопрос 8 Упражнение 26(B)
Q8) Построить треугольник ABC, если:
AB = 5,4 см, ∠A = 30° и ∠B = 90°. Измерьте ∠C и сторону BC.
Измерьте ∠C и сторону BC.
Ответ:
Решение:
- Проведите отрезок AB = 5,4 см
- В точке А постройте угол А = 30
- В точке B постройте угол B = 90
- AD и BE пересекаются друг с другом в точке C.
- ABC искомый треугольник
- При мерке С = 60 сторона ВС = 31 см.
Стенограмма видео
Здравствуйте, добро пожаловать в вести. Меня зовут Нельсон ап Рэй. Я собираюсь увидеть, что мы увидим, что построить треугольник ABC, когда b равно 5 точкам 4 сантиметра, угол равен 30 °, угол B равен синусоидальной жидкости, измеряющей угол C и сторону BC. Давай на машине, чтобы вынуть линейку. Мы должны смазать линию стимула 5,4. Если мы нарисуем линию пять целых четыре пять целых четыре года пять точка B RX. Ага. Это пройдет на 0,4 Пи примерно F и перейдет к следующему.


Связанные вопросы
Q1) Постройте треугольник ABC, если: AB = 6 см, BC = 8 см и AC = 4 см.
Q2) Постройте треугольник ABC, если: AB = 3,5 см, AC = 4,8 см и BC = 5,2 см.
Q3) Постройте треугольник ABC, если: AB = BC = 5 см и AC = 3 см. Измерьте углы A и C.
Q4) Постройте треугольник ABC, если: AB = BC = CA = 4,5 см. Измерьте все углы треугольника. Ар…
Q5) Постройте треугольник ABC, если: AB = 3 см, BC = 7 см и ∠B = 90°.
Q6) Постройте треугольник ABC, если: AC = 4,5 см, BC = 6 см и ∠C = 60°.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Углы треугольника — Бесплатная помощь по математике
Углы можно складывать
Как и обычные числа, углы можно складывать для получения суммы, например, для определения меры неизвестного угла. Иногда мы можем определить недостающий угол, потому что знаем, что сумма должна быть определенной величиной. Помните: сумма градусных мер углов любого треугольника равна 180 градусам. Ниже приведено изображение треугольника ABC, где угол A = 60 градусов, угол B = 50 градусов и
угол С = 70 градусов.
Иногда мы можем определить недостающий угол, потому что знаем, что сумма должна быть определенной величиной. Помните: сумма градусных мер углов любого треугольника равна 180 градусам. Ниже приведено изображение треугольника ABC, где угол A = 60 градусов, угол B = 50 градусов и
угол С = 70 градусов.
Если сложить все три угла любого треугольника, получится 180 градусов. Итак, градусная мера угла А + угол В + угол С = 180 градусов. Это верно для любого треугольника в мире геометрии. Мы можем использовать эту идею, чтобы найти меру углов, где градусная мера отсутствует или не задана.
Нахождение недостающего угла
В треугольнике ABC ниже угол A = 40 градусов, а угол B = 60 градусов. Чему равен угол С?
Мы знаем, что сумма мер любого треугольника равна 180 градусам. Используя тот факт, что угол A + угол B + угол C = 180 градусов, мы можем найти меру угла C.
угол А = 40
угол C = мы не знаем.
Чтобы найти угол C, мы просто подставляем в приведенную выше формулу и находим C.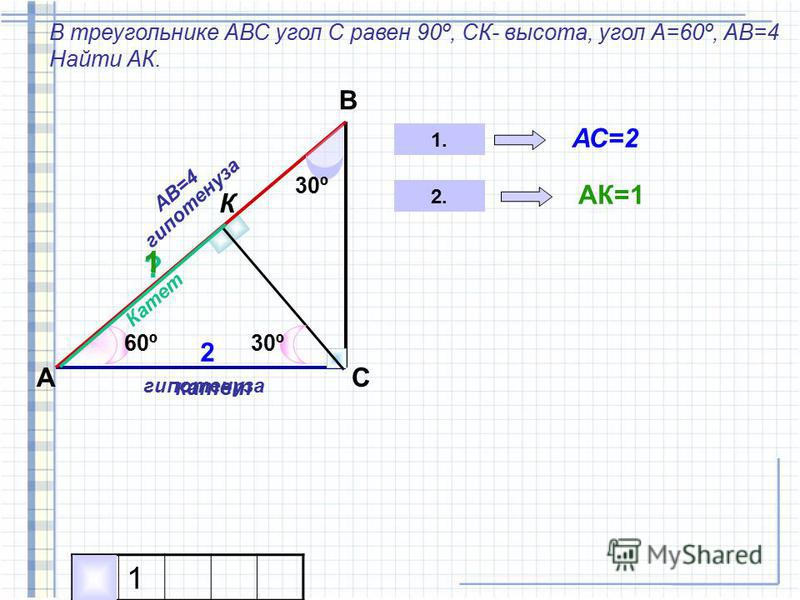
A + B + C = 180
С = 180 — А — В
С = 180 — 40 — 60
C = 80
Чтобы проверить правильность 80 градусов, добавим все три меры угла. Если мы получим 180 градусов, то наш ответ для угла C правильный.
Итак:
40 + 60 + 80 = 180
180 = 180… Проверяет!
Вам не всегда нужно подставлять эти значения в уравнение и решать. Как только вы освоитесь с такой задачей, вы сможете сказать: «Хорошо, 40 + 60 = 100, значит, другой угол должен быть равен 80!» и это намного быстрее.
Равносторонние треугольники
Если треугольник равносторонний, какова градусная мера каждого из его углов?
Помните, все стороны равностороннего треугольника имеют равная мера . Они также, как вы узнаете, имеют равные углы! Пусть x = градусная мера каждого угла. У треугольников три угла, поэтому мы прибавим х ТРИ раза.
У нас есть это:
х + х + х = 180
3x = 180
x = 60
Имеет смысл, верно? Если все углы равны и в сумме дают 180, то должно быть 60 градусов!
A Отношение углов
Градусы углов треугольника находятся в соотношении 4 : 5 : 9.
Какова градусная мера наименьшего угла треугольника?
Обратите внимание, что наименьший угол представлен наименьшим числом в заданном отношении. Наименьшее данное число равно 4, верно? Поскольку это отношение, мы должны умножить все эти значения (4,5,9) на некоторый общий коэффициент, чтобы получить фактические углы. (Например, 60 и 80 находятся в соотношении 3:4 с коэффициентом 20)
Пусть 4x = мера наименьшего угла треугольника. Теперь мы можем сказать, что 5x и 9x = градусные меры остальных углов треугольника. Мы просто складываем 4x + 5x + 9x, приравниваем сумму к 180 градусам и находим x. Найдя x, мы подставляем значение x в 4x и упрощаем, чтобы найти меру наименьшего угла треугольника под рукой.
4х + 5х + 9х = 180
9х + 9х = 180
18х = 180
х = 180/18
x = 10
Мы нашли значение x, но это НЕ означает, что мы закончили.
Чтобы найти величину наименьшего угла треугольника, умножаем 4 на 10.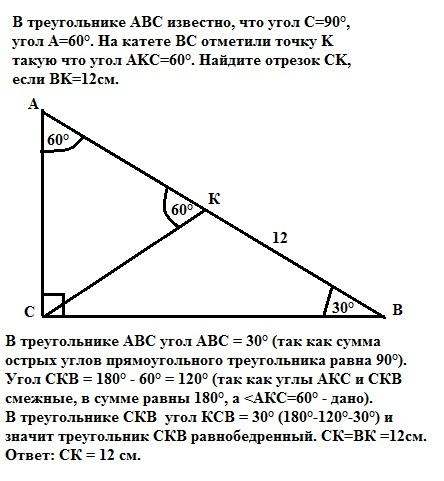

Leave A Comment