Вписанный и описанный треугольник — материалы для подготовки к ЕГЭ по Математике
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Рассмотрим важные теоремы, которые помогут нам при решении задач.
Теорема 1. Вокруг любого треугольника можно описать окружность, причем только одну. Ее центр – это точка пересечения серединных перпендикуляров к сторонам треугольника.
Иногда говорят, что окружность описана около треугольника. Это означает то же самое – все вершины треугольника лежат на окружности.
Доказательство этой теоремы здесь: Свойство серединных перпендикуляров.
Теорема 2. В любой треугольник можно вписать окружность, причем только одну. Ее центром является точка пересечения биссектрис треугольника.
Доказательство теоремы здесь: Свойства биссектрис треугольника.
Теорема 3. Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы, а радиус этой окружности равен половине гипотенузы.
Доказательство:
Медиана, проведенная к гипотенузе, равна ее половине, по свойству медианы прямоугольного треугольника.
Поэтому середина гипотенузы – это точка, равноудаленная от вершины прямого угла и от концов гипотенузы, то есть от всех вершин прямоугольного треугольника.
Теорема 4.
Центр окружности, описанной вокруг остроугольного треугольника, лежит внутри этого треугольника.
Центр окружности, описанной вокруг прямоугольного треугольника, лежит на середине гипотенузы.
Центр окружности, описанной вокруг тупоугольного треугольника, лежит вне этого треугольника.
Теорема 5. Радиус окружности , вписанной в прямоугольный треугольник с катетами и и гипотенузой , вычисляется по формуле:
Доказательство теоремы здесь: Радиус окружности, вписанной в прямоугольный треугольник.
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Напомним определение правильного многоугольника:
Правильным называется многоугольник, все стороны и все углы которого равны. Центры вписанной и описанной окружностей правильного многоугольника находятся в одной точке.
Из этого определения, понятно, что правильный треугольник – равносторонний. Для решения такого треугольника полезно уметь выводить формулы радиусов вписанной и описанной окружностей.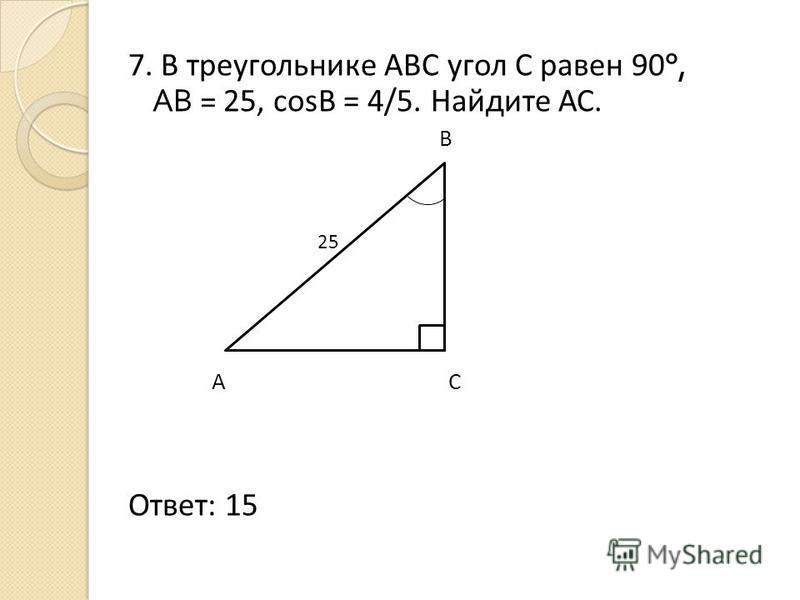
Теорема 6.
Для правильного треугольника со стороной а радиус описанной окружности равен
А радиус окружности, вписанной в правильный треугольник, равен
Докажем эту теорему.
У равностороннего треугольника медианы, биссектрисы, высоты и серединные перпендикуляры совпадают, и точка их пересечения является центром как вписанной, так и описанной окружностей.
Пусть в правильном треугольнике стороны , точка О – центр вписанной и описанной окружностей, — медианы и высоты. По свойству медиан треугольника, отрезки в точке О делятся в отношении 2 : 1, считая от вершин. Тогда
Получаем, что
Из треугольника АВН получаем, что длина стороны
Тогда
Значит, формула радиуса окружности, описанной около правильного треугольника —
Формула радиуса окружности, вписанной в правильный треугольник
Как видим, часто геометрическая задача решается с помощью несложных формул, и помогает в этом алгебра.
Разберем задачи ОГЭ и ЕГЭ по теме: Вписанные и описанные треугольники.
Задача 1, тренировочная. Периметр правильного треугольника АВС равен 15. Найдите радиус вписанной и описанной окружностей.
Решение:
Длина стороны равностороннего треугольника равна
Радиусы – вписанной и – описанной окружностей можно найти по формулам:
где — сторона треугольника.
Значит,
Ответ:
Решая задачи по теме «Вписанные и описанные треугольники», мы часто пользуемся формулами площади треугольника, а также теоремой синусов.
Вот две полезные формулы для площади треугольника.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
,
где — полупериметр,
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Теорема синусов:
R — радиус описанной окружности
Задача 2, ЕГЭ. Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.
Найдите диаметр окружности, вписанной в треугольник со сторонами 13, 14 и 15.
Решение:
Выразим площадь треугольника двумя разными способами:
где – полупериметр треугольника, a – его стороны.
Тогда , а диаметр окружности равен
Ответ: 8.
Задача 3, ЕГЭ. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Решение:
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что .
Тогда .
В ответ запишем .
Ответ: 4.
Задача 4, ЕГЭ. В треугольнике сторона равна , а угол равен . Найдите радиус описанной около этого треугольника окружности.
Решение:
По теореме синусов
Тогда
Ответ: 7.
Задача 5, ЕГЭ. В треугольнике угол А равен , а угол В – . Найдите радиус окружности, описанной около треугольника , если сторона равна 10.
Решение:
Зная, что сумма углов треугольника равна , найдем угол С.
По теореме синусов
Значит,
Ответ: 10.
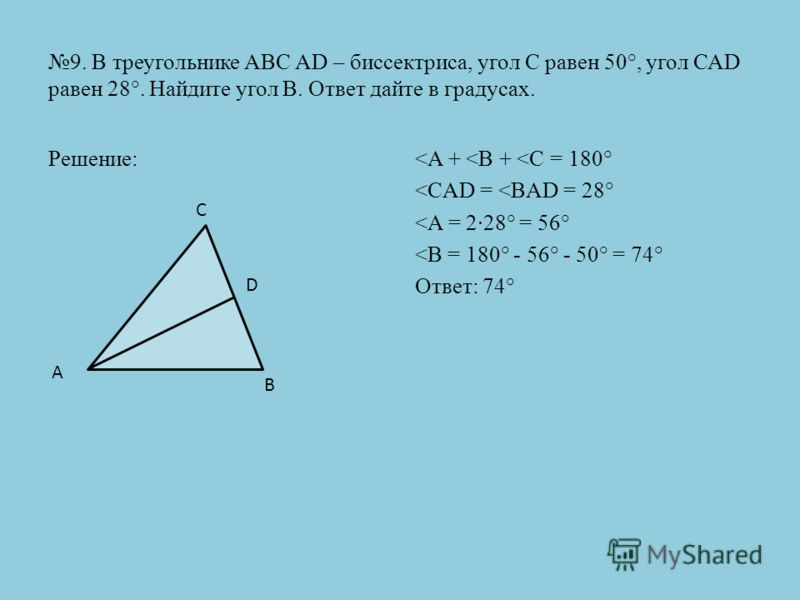
Задача 6, ЕГЭ. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
Получаем, что . Угол — тупой. Значит, он равен .
Ответ: 150.
Задача 7, ЕГЭ. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем .
По теореме Пифагора найдем .
Тогда .
Ответ: 25.
Задача 8, ОГЭ.
Решение:
Высота , проведенная к основанию , является медианой. Значит, .
находится по теореме Пифагора из треугольника :
Периметр треугольника – это сумма длин сторон, т.е.
Площадь треугольника
Радиус вписанной окружности r найдем по формуле
Ответ:
Задача 9, ОГЭ. Стороны и треугольника равны 6 и соответственно, угол . Найдите диаметр окружности, описанной около треугольника .
Решение:
Найдем длину стороны по теореме косинусов, используя длины сторон , и косинус угла В, противолежащего стороне :
Теперь воспользуемся теоремой синусов:
Значит, диаметр окружности, описанной около треугольника , равен 6.
Ответ: 6.
Задача 10. Найдите площадь прямоугольного треугольника, если радиус описанной окружности равен 5, а вписанной 1.
Решение:
Пусть длина радиуса описанной окружности , а длина радиуса вписанной окружности
Мы знаем, что , где – полупериметр, – стороны треугольника.
Значит,
Отсюда
Тогда
Ответ: 11.
Задача 11. Найдите площадь прямоугольного треугольника, если радиус вписанной окружности равен 2, а гипотенуза 10.
Решение:
Пусть радиус вписанной окружности , а гипотенуза
Мы знаем, что в прямоугольном треугольнике
Значит, отсюда
Площадь находится по формуле где – полупериметр, – стороны треугольника.
Ответ: 24.
Рассмотрим также задачу из 2 части ЕГЭ по математике.
Задача 12. Точка О – центр вписанной в треугольник окружности. Прямая вторично пересекает описанную около треугольника окружность в точке Р.
а) Докажите, что
б) Найдите площадь треугольника , если радиус окружности, описанной около треугольника равен 10,
Решение:
а) Пусть О – центр вписанной окружности, значит, и – биссектрисы углов и соответственно, и
как вписанные углы, опирающиеся на одну и ту же дугу
Тогда
– внешний угол треугольника , поэтому он равен сумме двух внутренних углов, не смежных с ним, т.е.
Значит, Что и требовалось доказать.
б) , следовательно, треугольник – равнобедренный, – основание,
Угол равен , значит,
По теореме синусов для треугольника :
Тогда отрезок равен отрезку , т.е. .
Найдем угол С из треугольника :
как вписанные углы, опирающиеся на дугу .
Площадь треугольника находится по формуле:
Ответ:
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Информация на странице «Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 07.02.2023
Центральные и вписанные углы. Как найти?
Поможем понять и полюбить математику
Начать учиться
Угол и окружность: на первый взгляд — ничего общего. Давайте разберемся, что же такого привлекательного в этих углах, что окружность все время позволяет им вписываться.
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
ㄥAOB = ◡ AB
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
187.8K
Факториал
К следующей статье
Прямоугольный параллелепипед. Что это такое?
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
геометрия — В $\треугольнике ABC$ $D$ лежит на $BC$, $\angle ADB=60$, $\angle ACB=45$ и $BD=2CD$.
 Найдите $\угол ABC$
Найдите $\угол ABC$$\begingroup$
Вопрос соответствует заголовку. На следующем рисунке с заданными углами и двумя сторонами цель состоит в том, чтобы найти меру $\angle ABC$. Эта задача основана на задаче, появившейся на местном математическом конкурсе в Турции. Я опубликую свой подход к этому ниже в качестве ответа! Пожалуйста, покажите свои собственные методы решения этой проблемы!
- геометрия
- тригонометрия
- конкурс-математика
- евклидова геометрия
- треугольники
$\endgroup$
$\begingroup$
Вот мой подход. Я опубликую краткое объяснение ниже!
1.) Проведите перпендикуляр из $D$ на отрезок $AD$ так, чтобы он пересекался в точке $E$. Соединить точку $E$ с точкой $C$ через $EC$. Обратите внимание, что $\треугольник BED$ является треугольником $30-60-90$, поэтому $ED=DC=a$ и $\angle EBD=\angle DEC=\angle DCE=30$.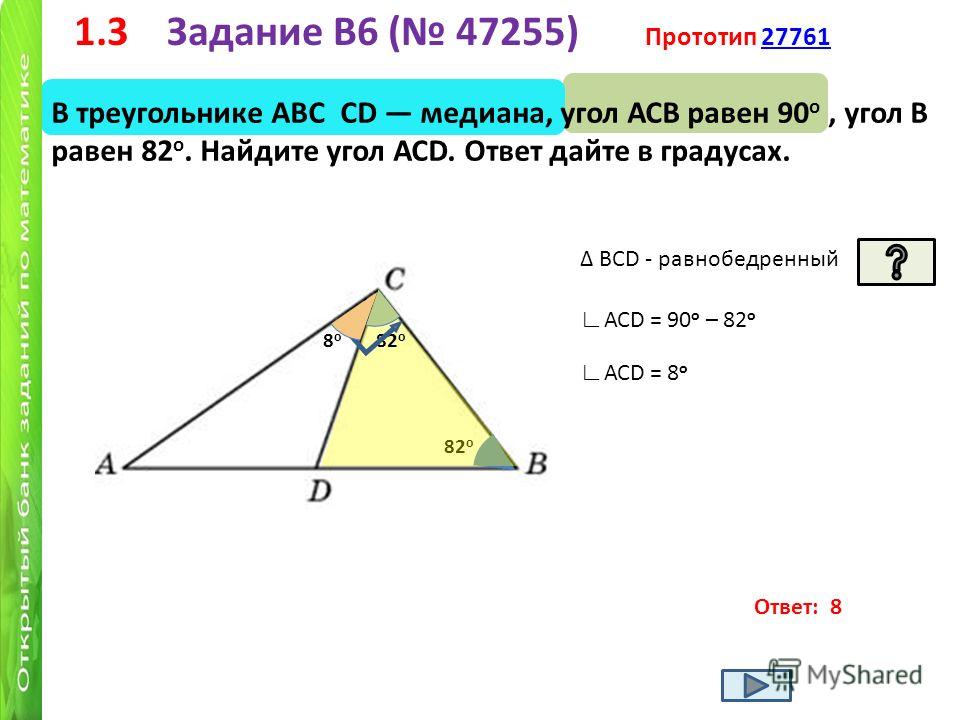 Мы также знаем, что $BE=EC=a\sqrt3$. 9о$
Мы также знаем, что $BE=EC=a\sqrt3$. 9о$
$\endgroup$
$\begingroup$
Альтернативный подход:
По исходному рисунку в исходной проводке построить отрезок перпендикулярной прямой из точки $A$ к отрезку прямой $\overline{BC}$. Предположим, что перпендикулярный отрезок пересекает $\overline{BC}$ в точке $G$.
- Пусть $r$ обозначает длину $\overline{AG}.$
- Пусть $s$ обозначает длину $\overline{BG}.$ 9\circ) = \sqrt{3}.$
- $\displaystyle \frac{r}{s} = \tan(\angle ABC).$
- $(s + t) = 2a.$
Тогда
$$\frac{a+t}{t} = \frac{\frac{r}{t}}{\frac{r}{a + t}} = \sqrt{3} \ подразумевает $$
$$a + t = t\sqrt{3} \ подразумевает a = t\left[~-1 + \sqrt{3}~\right] \ подразумевает $$
$$s = 2a — t = t\left[~-3 + 2\sqrt{3}~\right] \ подразумевает $$
$$\tan\left(\angle ABC\right) = \frac{r}{s} = \ frac{r}{t\left[~-3 + 2\sqrt{3}~\right]}$$
$$= \frac{r}{t} \times \frac{1}{\left[ ~-3 + 2\sqrt{3}~\right]}$$ 9\circ $
$\endgroup$
Геометрия: ключ ответа
Здесь представлены ответы и решения для задания «Вставь меня, тренер!» ящики для упражнений, организованные по секциям.
Снятие бремени с доказательств
- Да
- Теорема 8.3: Если два угла дополняют один и тот же угол, то эти два угла равны.
A и B дополняют друг друга, а C и B дополняют друг друга.
Дано: А и В комплементарны, а С и В комплементарны.
Докажите: A ~= C.
| Заявления | Причины | |
|---|---|---|
| 1. | А и В комплементарны, а С и В комплементарны. | Дано |
| 2. | мА + мВ = 90°, мКл + мБ = 90° | Определение дополнительного |
| 3. | мА = 90 º — мБ, мС = 90° — мБ | Свойство вычитания равенства |
| 4. | мА = мКл | Замена (шаг 3) |
| 5. | А ~= С | Определение ~= |
Доказательство взаимосвязи сегментов и углов
- Если E находится между D и F, то DE = DF EF.
E находится между D и F.
Дано: E находится между D и F
Докажите: DE = DF EF.
| Заявления | Причины | |
|---|---|---|
| 1. | E находится между D и F | Дано |
| 2. | D, E и F являются коллинеарными точками, а E находится на ¯DF | Определение между |
| 3. | DE + EF = DF | Постулат сложения сегментов |
| 4. | DE = DF EF | Свойство вычитания равенства |
2. Если BD делит ABC на два угла, ABD и DBC, то mABC = mABC — mDBC.
BD делит ABC на два угла, ABD и DBC.
Дано: BD делит ABC на два угла, ABD и DBC
Докажите: mABD = mABC — mDBC.
| Заявления | Причины | |
|---|---|---|
| 1. | BD делит ABC на два угла, ABD и DBC | Дано |
| 2. | mABD + mDBC = mABC | Постулат сложения углов |
3. | mABD = mABC — mDBC | Свойство вычитания равенства |
3. Биссектриса угла единственна.
ABC с двумя биссектрисами угла: BD и BE.
Дано: ABC с двумя биссектрисами угла: BD и BE.
Докажите: mDBC = 0.
| Заявления | Причины | |
|---|---|---|
| 1. | BD и BE делят пополам ABC | Дано |
| 2. | ABC ~= DBC и ABE ~= EBC | Определение биссектрисы ангела |
| 3. | mABD = mDBC и mABE ~= mEBC | Определение ~= |
| 4. | mABD + mDBE + mEBC = mABC | Постулат сложения углов |
| 5. | mABD + mDBC = mABC и mABE + mEBC = mABC | Постулат сложения углов |
| 6. | 2mABD = mABC и 2mEBC = mABC | Замена (этапы 3 и 5) |
| 7. | mABD = mABC / 2 и mEBC = mABC / 2 | Алгебра |
8. | mABC / 2 + mDBE + mABC / 2 = mABC | Замена (этапы 4 и 7) |
| 9. | мАВС + мДБЭ = мАВС | Алгебра |
| 10. | мДБЭ = 0 | Свойство вычитания равенства |
4. Дополнение к прямому углу есть прямой угол.
A и B — смежные углы, а A — прямой угол.
Дано: А и В — смежные углы, А — прямой угол.
Докажите: угол B прямой.
| Заявления | Причины | |
|---|---|---|
| 1. | A и B — смежные углы, а A — прямой угол | Дано |
| 2. | мА + мБ = 180º | Определение дополнительных углов |
| 3. | мА = 90º | Определение прямого угла |
| 4. | 90° + mB = 180° | Замена (шаги 2 и 3) |
| 5. | мБ = 90º | Алгебра |
6. | B — прямой угол | Определение прямого угла |
Доказательство связи между строками
- m6 = 105º, m8 = 75º
- Теорема 10.3: Если две параллельные прямые пересечены секущей, то противоположные внешние углы равны.
м.п. срезанный поперечным t.
Дано: l m, разрезанный секущей t.
Докажите: 1 ~= 3.
| Заявления | Причины | |
|---|---|---|
| 1. | л м разрез поперечной т | Дано |
| 2. | 1 и 2 — вертикальные углы | Определение вертикальных углов |
| 3. | 2 и 3 соответствующие углы | Определение соответствующих углов |
| 4. | 2 ~= 3 | Постулат 10.1 |
| 5. | 1 ~= 2 | Теорема 8.1 |
| 6. | 1 ~= 3 | Переходное свойство 3. |
3. Теорема 10.5. Если две параллельные прямые пересечены секущей, то внешние углы по одну сторону от секущей являются дополнительными углами.
Теорема 10.5. Если две параллельные прямые пересечены секущей, то внешние углы по одну сторону от секущей являются дополнительными углами.
м.п., разрезанный поперечным t.
Дано: l m, разрезанный секущей t.
Докажите: 1 и 3 являются дополнительными.
| Заявление | Причины | |
|---|---|---|
| 1. | л м разрез поперечной т | Дано |
| 2. | 1 и 2 — дополнительные углы, а m1 + m2 = 180º | Определение дополнительных углов |
| 3. | 2 и 3 соответствующие углы | Определение соответствующих углов |
| 4. | 2 ~= 3 | Постулат 10.1 |
| 5. | м2 ~= м3 | Определение ~= |
| 6. | м1 + м3 = 180º | Замена (этапы 2 и 5) |
| 7. | 1 и 3 являются дополнительными | Определение дополнительного |
Лучшие 3D-принтеры
Заинтересованы в 3D-печати? Мы изучили основные факторы, которые следует учитывать при покупке 3D-принтера, и выбрали лучшие принтеры 2020 года в соответствии с вашими потребностями.
ПОЛУЧИТЬ ПЕЧАТЬ
4. Теорема 10.9. Если две прямые пересечены секущей так, что внешние углы равны, то эти прямые параллельны.
Прямые l и m пересекаются секущей t.
Дано: Прямые l и m пересекаются секущей t, где 1 ~= 3.
Докажите: l m.
| Заявление | Причины | |
|---|---|---|
| 1. | Прямые l и m пересекаются секущей t с 1 ~= 3 | Дано |
| 2. | 1 и 2 — вертикальные углы | Определение вертикальных углов |
| 3. | 1 ~= 2 | Теорема 8.1 |
| 4. | 2 ~= 3 | Транзитивное свойство ~=. |
| 5. | 2 и 3 соответствующие углы | Определение соответствующих углов |
| 6. | л м | Теорема 10.7 |
5. Теорема 10.11. Если две прямые пересечены секущей так, что внешние углы по одну сторону от этой секущей смежны, то эти прямые параллельны.
Линии l и m пересекаются t секущей t.
Дано: Прямые l и m пересекаются секущей t, углы 1 и 3 — смежные.
Докажите: l m.
| Заявление | Причины | |
|---|---|---|
| 1. | Прямые l и m пересекаются секущей t, а 1 представляет собой 3 дополнительных угла | Дано |
| 2. | 2 и 1 дополнительные уголки | Определение дополнительных углов |
| 3. | 3 ~= 2 | Пример 2 |
| 4. | 3 и 2 соответствующие углы | Определение соответствующих углов |
| 5. | л м | Теорема 10.7 |
Компания двоих. Три треугольника
- Тупоугольный равнобедренный треугольник
- Острые углы прямоугольного треугольника дополняют друг друга.
ABC — прямоугольный треугольник.
Дано: треугольник ABC прямоугольный, угол B прямой.
Докажите: A и C — дополнительные углы.
| Заявление | Причины | |
|---|---|---|
| 1. | ABC — прямоугольный треугольник, а B — прямой угол | Дано |
| 2. | мБ = 90º | Определение прямого угла |
| 3. | мА + мВ + мКл = 180º | Теорема 11.1 |
| 4. | мА + 90° + мКл = 180° | Замена (шаги 2 и 3) |
| 5. | мА + мКл = 90° | Алгебра |
| 6. | A и C являются дополнительными углами | Определение дополнительных углов |
3. Теорема 11.3: Мера внешнего угла треугольника равна сумме мер двух несмежных внутренних углов.
ABC с внешним углом BCD.
| Заявление | Причины | |
|---|---|---|
| 1. | ABC с наружным уголком BCD | Дано |
2. | DCA — прямой угол, mDCA = 180º | Определение прямого угла |
| 3. | мБЦА + мБЦД = мДКА | Постулат сложения углов |
| 4. | mBCA + mBCD = 180º | Замена (шаги 2 и 3) |
| 5. | mBAC + mABC + mBCA = 180º | Теорема 11.1 |
| 6. | мБАК + мАБК + мБЦА = мБЦА + мБЦД | Замена (этапы 4 и 5) |
| 7. | мБАЦ + мАБК = мБЦД | Свойство вычитания равенства |
4. 12 шт. 2
5. 30 единиц 2
6. Нет, треугольник с такими длинами сторон нарушил бы неравенство треугольника.
Конгруэнтные треугольники
1. Рефлексивное свойство: ABC ~= ABC.
Свойство симметрии: если ABC ~= DEF, то DEF ~= ABC.
Переходное свойство: если ABC ~= DEF и DEF ~= RST, то ABC ~= RST.
2. Доказательство: если ¯AC ~= ¯CD и ACB ~= DCB, как показано на рис. 12.5, то ACB ~= DCB.
12.5, то ACB ~= DCB.
| Заявление | Причины | |
|---|---|---|
| 1. | ¯AC ~= ¯CD и ACB ~= DCB | Дано |
| 2. | ¯БК ~= ¯БК | Рефлексивное свойство ~= |
| 3. | ACB ~= DCB | Постулат SAS |
3. Если ¯CB ¯AD и ACB ~= DCB, как показано на рис. 12.8, то ACB ~= DCB.
| Заявление | Причины | |
|---|---|---|
| 1. | ¯CB ¯AD и ACB ~= DCB | Дано |
| 2. | углы ABC и DBC прямые | Определение |
| 3. | mABC = 90° и mDBC = 90° | Определение прямых углов |
| 4. | мАВС = мДВС | Замена (шаг 3) |
| 5. | ABC ~= DBC | Определение ~= |
| 6. | ¯БК ~= ¯БК | Рефлексивное свойство ~= |
7. | ACB ~= DCB | Постулат АСА |
4. Если ¯CB ¯AD и CAB ~= CDB, как показано на рис. 12.10, то ACB~= DCB.
| Заявление | Причины | |
|---|---|---|
| 1. | ¯CB ¯AD и CAB ~= CDB | Дано |
| 2. | углы ABC и DBC прямые | Определение |
| 3. | mABC = 90° и mDBC = 90° | Определение прямых углов |
| 4. | мАВС = мДВС | Замена (шаг 3) |
| 5. | АВС ~= ДБК | Определение ~= |
| 6. | ¯БК ~= ¯БК | Рефлексивное свойство ~= |
| 7. | ACB ~= DCB | Теорема AAS |
5. Если ¯CB ¯AD и ¯AC ~= ¯CD, как показано на рис. 12.12, то ACB ~= DCB.
| Заявление | Причины | |
|---|---|---|
| 1. | ¯CB ¯AD и ¯AC ~= ¯CD | Дано |
2. | треугольники ABC и DBC прямоугольные | Определение прямоугольного треугольника |
| 3. | ¯БК ~= ¯БК | Рефлексивное свойство ~= |
| 4. | ACB ~= DCB | HL Теорема для прямоугольных треугольников |
6. Если P ~= R и M — середина ¯PR, как показано на рис. 12.17, то N ~= Q.
| Заявление | Причины | |
|---|---|---|
| 1. | P ~= R и M — середина ¯PR | Дано |
| 2. | ¯PM ~= ¯MR | Определение средней точки |
| 3. | NMP и RMQ — вертикальные углы | Определение вертикальных углов |
| 4. | NMP ~= RMQ | Теорема 8.1 |
| 5. | PMN ~= RMQ | Постулат АСА |
| 6. | Н ~= Q | КПОКТАК |
Похожие треугольники
- х = 11
- х = 12
- 40° и 140°
- Если A ~= D, как показано на рис.
 13.6, то BC / AB = CE / DE .
13.6, то BC / AB = CE / DE .
| Заявление | Причины | |
|---|---|---|
| 1. | А ~= Д | Дано |
| 2. | BCA и DCE — вертикальные уголки | Определение вертикальных углов |
| 3. | БКА ~= ДСЕ | Теорема 8.1 |
| 4. | ACB ~ DCE | AA Теорема подобия |
| 5. | BC / AB = CE / DE | КССТАП |
5. 150 футов.
Открытие дверей с помощью подобных треугольников
- Если прямая параллельна одной стороне треугольника и проходит через середину второй стороны, то она проходит через середину третьей стороны.
¯DE ¯AC, а D — середина ¯AB.
Дано: ¯DE ¯AC и D – середина ¯AB.
Докажите: E — середина ¯BC.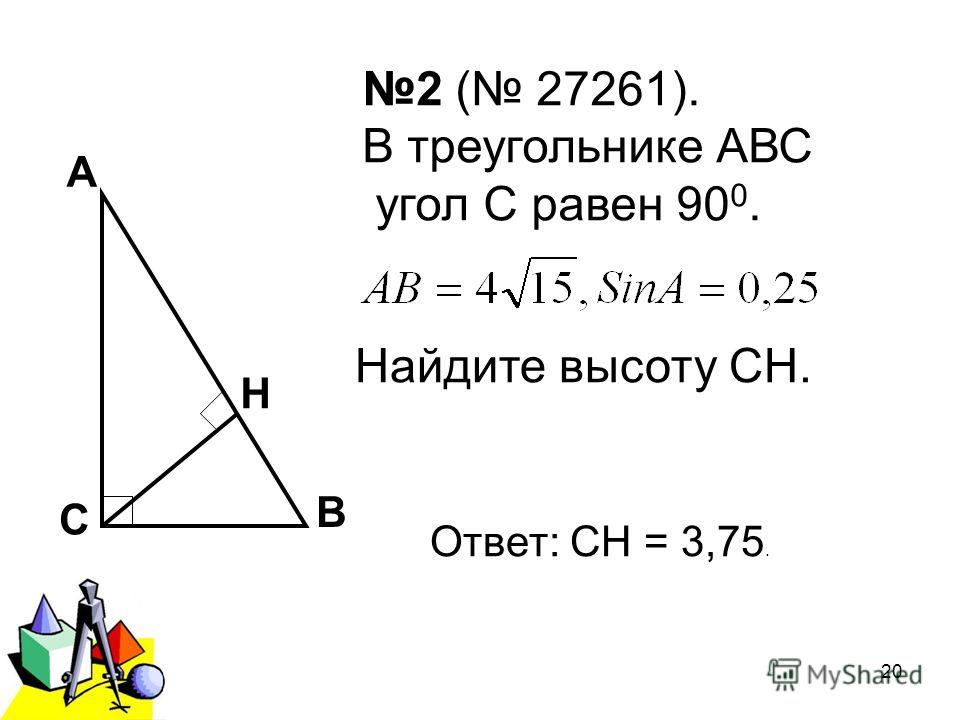
| Заявление | Причины | |
|---|---|---|
| 1. | ¯DE ¯AC, а D – середина ¯AB. | Дано |
| 2. | ¯DE ¯AC и пересекается поперечной AB | Определение поперечной |
| 3. | BDE и BAC соответствующие углы | Определение соответствующих углов |
| 4. | БДЭ ~= БАК | Постулат 10.1 |
| 5. | Б ~= Б | Рефлексивное свойство ~= |
| 6. | ABC ~ DBE | AA Теорема подобия |
| 7. | ДБ / АВ = БЭ / БК | КССТАП |
| 8. | ДБ = АВ / 2 | Теорема 9.1 |
| 9. | ДБ / АВ = 1 / 2 | Алгебра |
| 10. | 1 / 2 = БЭ / БЭ | Замена (этапы 7 и 9) |
11. | г. до н.э. = 2BE | Алгебра |
| 12. | БЭ + ЕС = БК | Постулат сложения сегментов |
| 13. | БЭ + ЕС = 2БЭ | Замена (шаги 11 и 12) |
| 14. | ЕС = ВЕ | Алгебра |
| 15. | E — середина ¯BC | Определение средней точки |
2. AC = 43, AB = 8, RS = 16, RT = 83
3. AC = 42, BC = 42
Четырехугольники на первый план
- АД = 63, ВС = 27, РС = 45
- ¯AX, ¯CZ и ¯DY
Трапеция ABCD с показанными четырьмя высотами XB CY.
3. Теорема 15.5. В воздушном змее одна пара противоположных углов конгруэнтна.
Воздушный змей ABCD.
Дано: Воздушный змей ABCD.
Докажите: B ~= D.
| Заявление | Причины | |
|---|---|---|
| 1. | ABCD — воздушный змей | Дано |
2. | ¯AB ~= ¯AD и ¯BC ~= ¯DC | Определение воздушного змея |
| 3. | ¯AC ~= ¯AC | Рефлексивное свойство ~= |
| 4. | АВС ~= АЦП | Постулат ССС |
| 5. | Б ~= Д | КПОКТАК |
4. Теорема 15.6: Диагонали воздушного змея перпендикулярны, а диагональ, противоположная конгруэнтным углам, делит другую диагональ пополам.
Воздушный змей ABCD.
Дано: Воздушный змей ABCD.
Докажите: ¯BD ¯AC и ¯BM ~= ¯MD.
| Заявление | Причины | |
|---|---|---|
| 1. | ABCD — воздушный змей | Дано |
| 2. | ¯AB ~= ¯AD и ¯BC ~= ¯DC | Определение воздушного змея |
| 3. | ¯AC ~= ¯AC | Рефлексивное свойство ~= |
| 4. | АВС ~= АЦП | Постулат ССС |
| 5. | БАК ~= ЦАП | КПОКТАК |
6. | ¯AM ~= ¯AM | Рефлексивное свойство ~= |
| 7. | ПРО ~= АДМ | Постулат SAS |
| 8. | ¯BM ~= ¯MD | КПОКТАК |
| 9. | БМА ~= прямой доступ к памяти | КПОКТАК |
| 10. | мБМА = мДМА | Определение ~= |
| 11. | MBD — прямой угол, mBMD = 180º | Определение прямого угла |
| 12. | мБМА + мДМА = мБМД | Постулат сложения углов |
| 13. | mBMA + mDMA = 180º | Замена (шаги 9 и 10) |
| 14. | 2mBMA = 180º | Замена (шаги 9 и 12) |
| 15. | mBMA = 90º | Алгебра |
| 16. | BMA прямоугольный | Определение прямого угла |
| 17. | ¯BD ¯AC | Определение |
5. Теорема 15.9: Противолежащие углы параллелограмма равны.
Параллелограмм ABCD.
Дано: Параллелограмм ABCD.
Докажите: ABC ~= ADC.
| Заявление | Причины | |
|---|---|---|
| 1. | Параллелограмм ABCD имеет диагональ ¯AC. | Дано |
| 2. | ABC ~= CDA | Теорема 15.7 |
| 3. | АВС ~= АЦП | КПОКТАК |
6. 144 шт. 2
7. 180 шт. 2
8. Кайт ABCD имеет площадь 48 шт. 2 .
Параллелограмм ABCD имеет площадь 150 единиц 2 .
Прямоугольник ABCD имеет площадь 104 единицы 2 .
Ромб ABCD имеет площадь 35 / 2 единиц 2 .
Анатомия круга
- Окружность: 20 футов, длина ˆRST = 155 / 18 футов
- 9 футов 2
- 15 футов 2
- 28º
Единичный круг и тригонометрия
- 3 / 34 = 334 / 34
- 1 / 3 = 3 / 3
- коэффициент тангенса = 40 / 3 , коэффициент синуса = 40 / 7
- отношение тангенса = 5 / 56 = 556 / 56 , отношение косинуса = 56 / 9
Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии.


 13.6, то BC / AB = CE / DE .
13.6, то BC / AB = CE / DE .
Leave A Comment