В трапецию сумма длин боковых сторон которой равна 16: В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.

Подготовка к ОГЭ. Окружность — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Подготовка к ОГЭ.

Окружность.

2. Уровень А

3. Хорды АВ и CD окружности пересекаются в точке М. Найдите МА, если МВ = 8 см, МС = 6 см, МD = 4 см.

AМ ∙ МВ = СМ ∙ MD
D
4
А
M
AМ ∙ 8 = 6 ∙ 4
8
В AМ = 3
6
С

4. Окружность с центром О касается сторон угла с вершиной А в точках В и С.

Найдите угол ВАС, если угол ВОС равен 147.А
Сумма углов четырехугольника — 360
Радиусы, проведенные в точку
касания – перпендикулярны
касательной.
С
В
0
ВАС = 360 – 90 – 90 – 147 = 33

5. Точки А и В делят окружность на две дуги, длины которых относятся как 5:7. Найдите величину центрального угла, опирающегося на

меньшую из
дуг.
5х
А
В
0
7х
5х + 7х = 360
х = 30
АОВ = 5 ∙ 30 = 150

6. Радиус окружности равен 15 см. Найдите расстояние от центра окружности до хорды, длина которой равна 18 см.

Т.к. ОС АВ, то АС=ВС=9
по т. Пифагора
0
15
А
ОС = 152 9 2 (15 9)(15 9)
С
18
6 24 6 6 4 6 2 12
В

7. Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через

точку А, если угол АОВ равен 28.
ОА АС (как радиус, проведенный в
точку касания)
АОВ — равнобедренный
0
28
А
(ОА=ОВ – как радиусы одной окружности)
В
С
ОАВ ОВА (180 28) : 2
ВАС 90 ОАВ
90 76 14

8.

Отрезки АВ и ВС являются соответственно диаметром и хордой окружности с центром О. Найдите угол АОС, если угол ОСВ равен 39.ВОС — равнобедренный
В (ОС=ОВ – как радиусы одной окружности)
ВОС 180 39 2 102
0
А
АОС 180 ВОС
180 102 78
39
С
или
АОС 39 39 78
Внешний угол треугольника
равен сумме двух углов, не
смежных с ним.

9. Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр

треугольника АВС, если АР = 4
см, ВМ = 6 см, СК = 3 см.
А
4
Отрезки касательных, проведенных
из одной точки равны.
ВМ = ВК
АМ = АР
СР = СК
4
М
Р
6
3
В
6
К
3
С
АВ = 10
АС = 7
ВС = 9
Р = 10 + 7 + 9 = 26

10. Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а

противолежащий
этому углу катет равен 15 см.
Центр описанной около п/у
треугольника окружности лежит на
середине гипотенузы.
d = AC
А
sinA=3/7
sinA = ВС/АС
3/7 = 15/АС
АС = 35
В
15
С

11. Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120, а расстояние от центра

окружности до вершины
этого угла равно 18 см.
В
120
А
0
С
Т.к. в вписанном треугольнике
тупой угол, то этот треугольник
лежит по одну сторону от центра
окружности.
ОВ = r = 18

12. Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра

окружности до
этой стороны равно 24 см.
Т.к. ОК АС, то АК=КС=10
В
по т. Пифагора
24
А
20
К
ОС = 102 242 26
0
С

13. Уровень В

14. Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 10 см, а расстояния от центра окружности до хорд

АВ и CD
равны соответственно 12 см и 5 см.
C
АХ = 5
Y
D
5
А
X
по т. Пифагора
52 122 13
0
ОА =
12
ОА = ОС = 13
10
В
по т. Пифагора
СY =
132 52 12
CD = 24

15. Отрезки АВ и BC являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен 42.

В
А
42
0
С
АСВ – вписанный угол,
АОВ – соответствующий ему
центральный
АОВ = 180 – 42∙2=96
АОВ= 96 : 2 = 48

16. В окружность вписан четырехугольник АВСD. Найдите угол АСD, если углы BAD и ADB равны соответственно 73 и 37.

А
37
D
73
В
С
ABD: ABD = 180 – (73 + 37) = 70
АВD = ACD – как вписанные углы,
опирающиеся на одну дугу
AСD = 70

17. Окружность с центром О касается сторон угла с вершиной А, величина которого равна 40, в точках В и С. Найдите углы треугольника

ВОС.
А
АОВ – п/у (радиус, проведенный в точку касания,
перпендикулярен касательной)
АОВ = АОС по катету и гипотенузе (АО –
общая, ОВ = ОС = r)
С
В
0
ОАВ = 20
ВОА= 70
ВОС = 140
ОВС = ОСВ = (180 – 140) : 2 = 20

18.

Отрезки АВ и АС являются хордами окружности с центром О. Найдите угол ВАС, если известно, что он является острым и что углы АВОи АСО равны
соответственно 23 и 32.
В
23
А
0
32
С
Угол ВАС – острый, значит его стороны
лежат по разные стороны от центра
окружности.
АОВ — равнобедренный
ОАВ = 23
АОС — равнобедренный
ОАС = 32
ВАС = 23 + 32 = 55

19. Радиус окружности, описанной около равнобедренного треугольника равен 5 см, а высота, проведенная к основанию, равна 8 см.

Найдите площадь треугольника.
В
Т.к. треугольник р/б, то центр
описанной окружности лежите на
высоте, проведенной к основанию.
5
ОА = ОВ = R = 5
ОН = 8 – 5 = 3
0
8
по т. Пифагора
А
Н
С
АН =
52 32 4
АС = 8
S = ½ ∙ 8 ∙ 8 = 32

20. Найдите площадь п/у трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать

окружность.
В
10
С
16
Т. к. в трапецию можно вписать
окружность, то суммы
противоположных сторон трапеции
равны.
Т.к. трапеция – п/у, то АВ = h
АВ + CD = ВС + AD = 26
BC AD
S
АВ
2
А
D
S = 130

21. В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5 см.

В
С
Р = 4а
5
А
Т.к. в параллелограмм можно
вписать окружность, он является
ромбом.
Р = 4 ∙ 5 = 20
D

22. В трапецию, сумма длин боковых сторон которой равна 16 см, вписана окружность. Найдите среднюю линию трапеции.

В
К
С
Т.к. в трапецию можно вписать
окружность, то суммы
противоположных сторон трапеции
равны.
L
АВ + CD = ВС + AD = 16
КL
А
D
BC AD
2
КL = 8

English     Русский Правила

РАДИУС ОПИСАННОЙ И ВПИСАННОЙ ОКРУЖНОСТИ (ТРЕУГОЛЬНИК) — Студопедия

Поделись с друзьями: 

ЗАДАНИЕ ЧАСТИ 2

Около трапеции, один из углов которой равен 44°, описана окружность.

Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 52°, описана окружность. Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции

Около трапеции, один из углов которой равен 37°, описана окружность. Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 53°, описана окружность. Найдите остальные углы трапеции.

В трапецию, сумма длин боковых сторон которой равна 16, вписана окружность. Найдите длину средней линии трапеции.

В трапецию, сумма длин боковых сторон которой равна 14, вписана окружность. Найдите длину средней линии трапеции.

В трапецию, сумма длин боковых сторон которой равна 12, вписана окружность. Найдите длину средней линии трапеции.

В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.

В трапецию, сумма длин боковых сторон которой равна 20, вписана окружность. Найдите длину средней линии трапеции.

Около трапеции, один из углов которой равен 37°, описана окружность. Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 36°, описана окружность. Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 34°, описана окружность. Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 48°, описана окружность. Найдите остальные углы трапеции.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 10.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 8.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 14.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5.

В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

В равнобедренную трапецию, периметр которой равен 200, а площадь равна 1500, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

В равнобедренную трапецию, периметр которой равен 80, а площадь равна 320, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

В равнобедренную трапецию, периметр которой равен 220, а площадь равна 2420, можно вписать окружность.

Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 16, а AB=15.

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой

AB в точке B. Найдите диаметр окружности, если AB =1, AC =5.

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3,6, а AB =8.

Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P.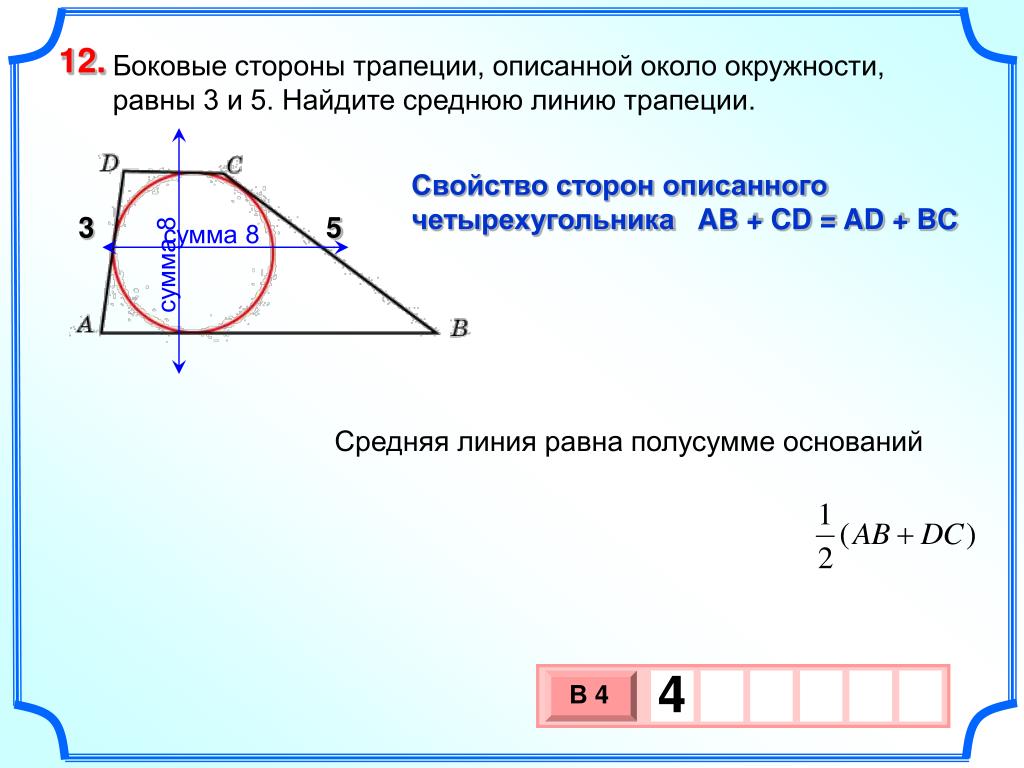 Найдите углы треугольника ABC, если углы треугольника MKP равны 48°, 68° и 64

РАДИУС ОПИСАННОЙ И ВПИСАННОЙ ОКРУЖНОСТИ (ТРЕУГОЛЬНИК)

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания

AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC

Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Основание AC равнобедренного треугольника ABC

равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите этот диаметр, если диаметр описанной окружности треугольника ABC равен 8.

Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



Формула трапеции — GeeksforGeeks

Измерение — это раздел геометрической математики, который измеряет геометрические величины, такие как общая площадь поверхности, площадь боковой поверхности, периметр, длина, ширина и объем. 2D и 3D — это два разных типа измерений.

Двухмерные фигуры состоят из двух или более прямых линий или замкнутых круговых линий. Эти фигуры не имеют ни высоты, ни глубины. Для этих фигур можно определить такие величины, как площадь и периметр. Они известны как фигурки самолетов.

Например, круг, треугольник, квадрат, прямоугольник. Трехмерные фигуры образованы рядом поверхностей или плоскостей. Они имеют длину, ширину и высоту. Это твердые цифры. Для этих фигур можно определить общую площадь поверхности, площадь боковой поверхности и объем. Пример: конус, цилиндр, куб.

Что такое трапеция?

Четырехугольник с одной парой параллельных сторон и набором непараллельных сторон. Параллельные стороны называются основаниями. Две другие непараллельные стороны называются боковыми сторонами. Высота или высота — это кратчайшее расстояние между двумя параллельными сторонами.

Типы трапеций

Существует три типа трапеций. Это

1. Равнобедренная трапеция: длины непараллельных сторон равны.
2. Прямоугольная трапеция: имеет набор прямых углов.
3. Разнонаправленная трапеция: стороны не равны.

Свойства трапеции

• Трапеция имеет только одну пару параллельных сторон.
• Сумма всех углов трапеции равна 360 ^или .
• У равнобедренной трапеции оба угла при основании конгруэнтны, непараллельные стороны конгруэнтны и диагонали конгруэнтны.
• Медиана параллельна обоим основаниям и является средней длиной оснований.
• Сумма смежных углов равна 180 ^o .

Формулы трапеции

Формула трапеции состоит из площади и периметра. Теперь давайте посмотрим, как выводятся формулы.

Площадь трапеции

 

Рассмотрим трапецию  PQRS, SR и PQ — параллельные стороны, а ST — кратчайшее расстояние между ними, которое является перпендикулярным и обозначается через h. Разобьем трапецию на отрезки. Это дает нам два треугольника PTS и UQR и прямоугольник TURS. Теперь, если мы найдем площади всех трех и просуммируем их, мы получим площадь трапеции.

При записи площадь треугольника, PTS = 1/2 (основание × высота)

Площадь треугольника, PTS = 1/2 (PT × ST)

= 1/2 (xh)                     …..(1)

При записи площади прямоугольника TURS = длина × ширина  

Площадь прямоугольника TURS = bh                     …..(2)

3 Площадь треугольника UQR = 1/2 (основание × высота) 

Площадь треугольника UQR = 1/2 ( yh)                     …..(3)

Суммируя три площади, т. е. уравнения (1), (2) и ( 3) получаем площадь трапеции.

При суммировании всех трех уравнений 

Площадь трапеции = 1/2 (xh) + bh + 1/2 (yh)

Взяв 1/2 (h) общего, мы можем записать уравнение как 

Площадь трапеции = (1/ 2) h (x + 2b + y)

Площадь трапеции = (1/2) h ( x + b + b + y)

Из рисунка видно, что суммируя x, b и у дает а. Итак,

Площадь трапеции = (1/2) × h × (a+b)

или

Площадь трапеции = (1/2) × (высота) × (сумма параллельных сторон )

Следовательно, площадь трапеции равна половине произведения высоты на сумму параллельных сторон.

Периметр трапеции

Для нахождения периметра необходимо сложить длины всех сторон.

Периметр трапеции = сумма длин параллельных и непараллельных сторон

или

Периметр трапеции = PQ + RS + QR + PS

или

Периметр трапеции = a + b + c + d

Следовательно, периметр трапеции равен сумме длин параллельных сторон и сумме длин непараллельных сторон.

Примеры вопросов 

Вопрос 1. Найдите площадь трапеции, если основания равны 10 см и 16 см. Кратчайшее расстояние между параллельными сторонами равно 8 см.

Ответ:  

Даны длины оснований, a = 10 см и b = 16 см, высота h = 8 см.

Площадь трапеции = (1/2) h (a+b)

= (1/2) 8 (10+16)

= 140 см ²

Вопрос 2: Если площадь длина трапеции равна 240 см ² , а сумма длин параллельных сторон равна 30 см, найдите высоту трапеции.

Ответ:

Дано, Площадь = 240см ² ,(a+b) = 30см

Площадь трапеции = (1/2) h (a+b) 90 002/1900 2) ч (30)

h = (240 × 2) / 30

= 16 см

Отсюда высота трапеции 16 см .

Вопрос 3: Найдите периметр трапеции, если длины сторон равны 15 см, 6 см, 12 см и 8 см соответственно.

Ответ:

Дано, a = 15 см, b = 6 см, c = 12 см и d = 8 см.

Периметр трапеции = сумма длин параллельных сторон и сумма длин непараллельных сторон.

= a + b + c + d

= 15+6+12+8

= 41 см

Вопрос 4. Если периметр трапеции равен 48 см, а сумма параллельных сторон равна 26 см, а длина третьей стороны 10 см. Найдите длину четвертой стороны.

Ответ: 

Дано, a+b = 26 см, c = 10 см и периметр = 48 см

Периметр трапеции = сумма длин параллельных сторон и сумма длин непараллельных стороны.

Периметр трапеции = a + b + c + d

48 = 26 + 10 + d 

d = 48- 26 – 10

= 12 см

Отсюда длина четвертой стороны равна

3

.

Вопрос 5: Если длина одной стороны больше другой на 6 см, а площадь трапеции равна 240 см ² . Найдите длины параллельных сторон, если кратчайшее расстояние между параллельными сторонами равно 14 см.

Ответ:

Дано, Площадь = 240 см ² , Высота = 14 см.

Пусть параллельная сторона a = x ,

По заданному условию

b = x + 6

Площадь трапеции = (1/2) h (a+b)

240 = (1 /2) (14) (x + x + 6)

(240×2) / 14 = 2x + 6

2x = 34,28 – 6

2x = 28,28

x = 14,1420 a5 см

b = x + 6

b = 14,14 + 6

b = 20,14 см

Отсюда 14,14 см и 20,14 см — длины параллельных сторон.

Площадь трапеций: формула, примеры, вывод

Что такое трапеция? Трапеция или трапеция – это четырехугольник, по крайней мере, с одной парой параллельных сторон. Параллельные стороны называются основаниями. Когда две другие стороны непараллельны, их называют сторонами или боковыми сторонами. В противном случае есть две пары оснований. Примерами из реальной жизни, где вы можете увидеть область трапеций, являются сумки, банки из-под попкорна и цимбалы, похожие на гитару. Площадь трапеции – это полное пространство, ограниченное четырьмя ее сторонами. Существует два подхода к нахождению площади трапеций.

1. Первый метод — это прямой метод, использующий прямую формулу для нахождения площади трапеции с известными размерами (см. пример 1)
2. Для второго метода, во-первых, если нам дана длина всех сторон, мы разбиваем трапецию на меньшие многоугольники, такие как треугольники и прямоугольники. Далее найдем площади треугольников и прямоугольников по отдельности. Наконец, мы добавим площадь многоугольников, чтобы получить общую площадь трапеции. (см. пример 2 для более точного понимания)

Какая формула используется для расчета площади трапеций?

Мы можем вычислить площадь трапеции, если знаем длину ее параллельных сторон и расстояние (высоту) между параллельными сторонами. Формула площади трапеции:   

A = ½ (a + b) h

Здесь (A) – площадь трапеции.

‘a’ и ‘b’ — параллельные стороны трапеции

‘h’ — высота, т. е. перпендикулярное расстояние между параллельными сторонами.

Пример площади трапеции 

Вот пример площади трапеции с использованием прямой формулы и пример площади трапеции с альтернативным методом.

Пример 1: Найдите площадь трапеции, если длины параллельных сторон 22 см и 12 см соответственно. Высота 5 см. Решение: Дано: Основания: а = 22 см; б = 10 см; высота h = 5 см. Площадь трапеции = A = ½ (a + b) h A = ½ (22 + 10) × (5)  A = ½ (32) × (5)  A = ½  × 160 A = 80 cm 2

Example 2 : Найдите площадь трапеции, параллельные стороны которой равны 10 см и 16 см соответственно, а непараллельные стороны равны 5 см каждая. Решение: Поскольку в этом вопросе у нас нет высоты трапеции, мы выполним следующие шаги, чтобы вычислить площадь трапеции. Дано: а =10 см; б =16 см; непараллельные стороны = 5 см каждая Шаг 1: Чтобы найти высоту трапеции, сначала начертим высоту трапеции с обеих сторон. Теперь мы видим, что трапеция состоит из прямоугольника ABQP и двух прямоугольных треугольников APD и BQC. Шаг 2 : Теперь нам нужно найти длину DP и QC. Так как ABQP является прямоугольником, AB = PQ DC = 16 см (Дано) Итак, PQ = AB Мы можем найти общую длину DP + QC следующим образом DC – PQ = 16 – 10 = 6 см Итак, DP + КК = 6 6 ÷ 2 = DP = QC  3 см = DP = QC Шаг 3 : AP = BQ (противоположные и равные стороны прямоугольника)   AD = BC = 5 см (Дано) Итак, мы можем рассчитать высоты AP и BQ по теореме Пифагора. В прямоугольном треугольнике ADP AP = √(AD 2 – DP 2 ) AP = √(5 2 – 3 2 ) AP = √ 1(5 – AP2 = √ 1) = 4 см Так как ABQP прямоугольник, то его противоположные стороны равны. Итак, АР = BQ = 4 см. Шаг 4 : Теперь мы знаем все размеры трапеции. Мы можем вычислить площадь, используя формулу. Площадь трапеции = ½ (a + b) h; где h = 4 см, a = 10 см b = 16 см При подстановке значений получаем: Площадь = ½ (10 + 16) × 4 Площадь = ½ × 26 × 4 Площадь = 52 см 2 Мы можем рассчитать, сложив площадь прямоугольника и двух треугольников Площадь трапеции = площадь ABPQ + площадь ADP + площадь BQC Площадь трапеции = (l × b) + 2(ab/2) Площадь трапеции = (10 × 4) + 2(3 × 4/2) A = 40 + 12 A = 52 см 2

из двух равных трапеций, соединенных четырьмя прямоугольниками. Трапеции расположены сверху и снизу. Таким образом, они образуют основу для призм и имеют многоугольники, образующие их основания. Четыре прямоугольника образуют боковые грани призмы-трапеции. Итак, трапециевидная призма состоит из-

• Шесть граней
• Восемь вершин
• Двенадцать ребер

Площадь поверхности трапециевидной призмы

Площадь трапециевидной призмы равна сумме поверхностей призмы. Эта площадь равна площади всех граней трапециевидной призмы. Поскольку трапециевидная призма имеет две трапециевидные грани и четыре прямоугольные грани, сумма их площадей даст площадь поверхности призмы. Однако существует простая и прямая формула для расчета площади поверхности трапециевидной призмы. Формула:

Площадь поверхности трапециевидной призмы = h (b + d) + l (a + b + c + d) квадратных единиц.

Здесь h = высота

b и d — длины основания

a + b + c + d — периметр

l — площадь боковой поверхности трапециевидной призмы

Вывод площади поверхности a Трапециевидная призма 

Основание трапециевидной призмы имеет форму трапеции. Здесь

b и d — параллельные стороны трапеции

H = расстояние между параллельными сторонами

l = длина трапециевидной призмы

Итак, общая площадь поверхности трапециевидной призмы (TSA) = 2 × площади основания + площадь боковой поверхности ————- (1)

Площадь трапеции = ½ (основание 1 + основание 2) высоты

Итак, площадь основания трапеции = h (b + d)/2 ——————— (2)

Площадь боковой поверхности трапеции трапециевидная призма (ЛПП) = сумма площадей каждой прямоугольной поверхности

Итак, ЛПП = (a × l) + (b × l) + (c × l) + (d × l) ——————- (3)

Подставив значения из уравнения (2) и уравнения (3) в уравнение 1, т. е. формулу TSA, мы получим:

(TSA) = 2 × h (b + d)/2 + (a × l) + (b × l) + (c × l) + (d × l)

TSA = h (b + d) + [(a × l) + (b × l) + (c × l) + (d × l) l)]

Суммарная площадь поверхности трапециевидной призмы = h (b + d) + l (a + b + c + d)

Таким образом, TSA трапециевидной призмы = h (b + d) + l ( a + b + c + d) единичный квадрат

Как найти площадь поверхности трапециевидной призмы?

Вот шаги, как найти площадь поверхности трапециевидной призмы.

Шаг 1 : Найдите четыре стороны трапеции – a, b, c и d. Они представляют собой ширину четырех прямоугольников. Сложение этих 4 значений даст периметр P.

Шаг 2 : Найдите длину h призмы.

Шаг 3 : Найдите боковую площадь трапециевидной призмы.

Шаг 4: Определите b1, b2 и h трапеции. Теперь найдите площадь основания B, используя формулу (b1 + b2) h/2

Шаг 5: Наконец, подставьте значения в формулу = 2B + Площадь боковой поверхности, чтобы вычислить общую площадь поверхности трапециевидной призмы.