В равнобедренный треугольник вписана окружность: Окружность, вписанная в равнобедренный треугольник

Радиус вписанной окружности в равнобедренный треугольник онлайн

С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Содержание

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота

1.

Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона

Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.

Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:

где полупериметр p вычисляется из формулы:

Учитывая, что у равнобедренного треугольника боковые стороны равны (\( \small b=c \)), имеем:

\( \small p=\frac{\large a+b+c}{\large 2} \) \( \small =\frac{\large 2b+a}{\large 2}, \)

(3)

\( \small p-a=\frac{\large 2b+a}{\large 2}-a \) \( \small =\frac{\large 2b-a}{\large 2}, \)

(4)

\( \small p-b=p-c=\frac{\large 2b+a}{\large 2}-b \) \( \small =\frac{\large a}{\large 2}. \)

(5)

Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:

Пример 1. Известны основание a=13 и боковая сторона b

=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения \( \small a,\; b \) в (6):

Ответ:

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании

Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.

Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см.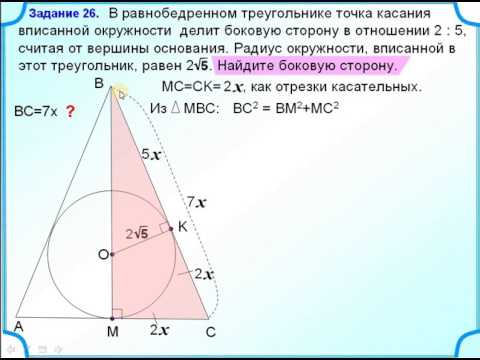

статью Прямоугольный треугольник. Тогда \( \small \angle OCE=\angle OCH=\frac{\large \beta}{\large 2}. \) Для прямоугольного треугольника OCH можно записать:

\( \small \frac{\large OH}{\large HC}=\frac{\large r}{\large \frac{a}{2}}=\mathrm{tg}\frac{\large \beta}{\large 2} .\)

Откуда получим формулу радиуса вписанной в треугольник окружности:

\( \small r=\frac{\large a}{\large 2} \cdot \mathrm{tg}\frac{\large \beta}{\large 2} .\)

(8)

Учитывая формулы половинного угла тригонометрических функций, формулу (8) можно записать так:

\( \small r=\frac{\large a}{\large 2} \cdot \frac{\large \sin \beta}{\large 1+\cos \beta} .\)

(9)

Пример 2. Известны основание \( \small a=15 \) и \( \small \beta=30° \) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения \( \small a=15, \; \beta=30° \) в (8):

Ответ:

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании

Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.

Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:

\( \small \frac{\large CH}{\large AC}=\frac{\large \frac{a}{2}}{\large b}= \cos \beta .\)

Откуда:

\( \small a=2b \cdot \cos \beta .\)

(10)

Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:

\( \small r=\frac{\large a}{\large 2} \cdot \mathrm{tg}\frac{\large \beta}{\large 2}=\frac{\large 2b \cdot \cos \beta}{\large 2} \cdot \mathrm{tg}\frac{\large \beta}{\large 2} \) \( \small =b \cos \beta \cdot \mathrm{tg}\frac{\large \beta}{\large 2} \)

или

\( \small r=b \cdot \cos \beta \cdot \mathrm{tg}\frac{\large \beta}{\large 2} \)

(11)

Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:

\( \small r=b \cdot \frac{\large \sin \beta \ \cdot \ \cos \beta}{\large 1+ \cos \beta} \)

(12)

Пример 3. 2 }}\)(21)

Пример 5. Основание и высота равнобедренного треугольника равны \( \small a=7 ,\) \( \small h=9, \) соответственно. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения \( \small a=7 ,\) \( \small h=9 \) в (21):

Ответ:

Смотрите также:

• Окружность, описанная около треугольника
• Радиус описанной окружности около треугольника онлайн
• Радиус описанной окружности около равнобедренного треугольника онлайн
• Радиус описанной окружности около равностороннего треугольника онлайн
• Радиус описанной окружности около прямоугольного треугольника онлайн
• Радиус вписанной в треугольник окружности онлайн

Окружность вписана в треугольник

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2014-05-08

Окружность вписана в треугольник.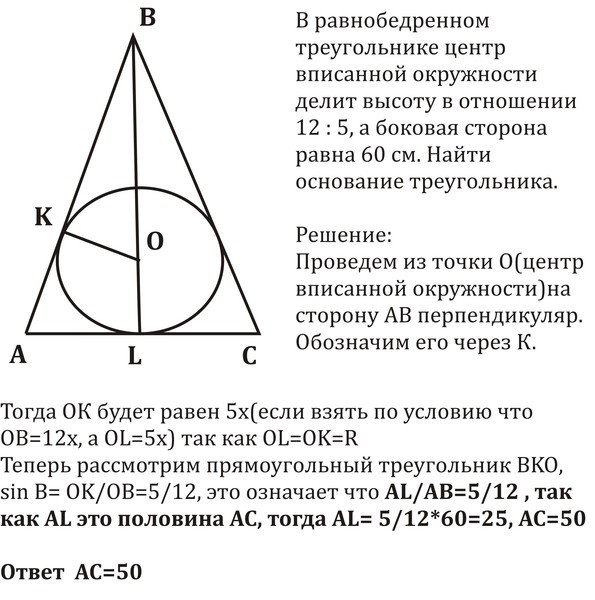 В данной статье собрал для вас задачи, в которых даётся треугольник с вписанной в него или описанной около него окружностью. В условии ставится вопрос о нахождении радиуса окружности или стороны треугольника. 

Данные задания удобно решать используя представленные формулы. Рекомендую их выучить, бывают очень полезны не только при решении этого типа заданий. Одна формула выражает связь радиуса вписанной в треугольник окружности с его сторонами и площадью, другая радиус описанной около треугольника окружности также с его сторонами и площадью:

где a, b, c –  стороны треугольника

S – площадь треугольника

Рассмотрим задачи:

27900. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120⁰. Найдите диаметр описанной окружности этого треугольника.

Здесь окружность описана около треугольника.

Первый способ:

Диаметр мы сможем найти, если будет известен радиус.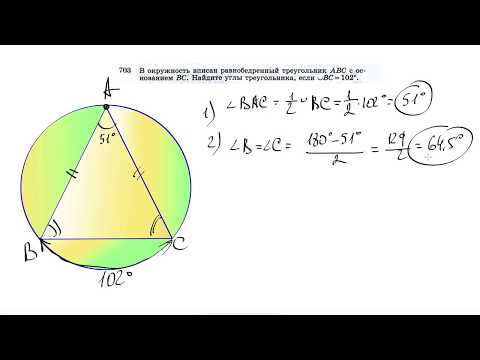 Используем формулу радиуса описанной около треугольника окружности:

где a, b, c – стороны треугольника

S –  площадь треугольника

Две стороны нам известны (боковые стороны равнобедренного треугольника), третью мы можем вычислить используя теорему косинусов:

Теперь вычислим площадь треугольника:

*Использовали формулу (2) из этой статьи.

Вычисляем радиус:

Таким образом диаметр будет равен 2.

Второй способ:

Это устные вычисления. Для тех кто имеет навык решения заданий с вписанным в окружность шестиугольником, тот сразу определит, что стороны треугольника АС и ВС «совпадают» со сторонами вписанного в окружность шестиугольника (угол шестиугольника как раз равен 120⁰, как и в условии задачи). А далее на основании того, что сторона вписанного в окружность шестиугольника равна радиусу этой окружности  не сложно сделать вывод о том, что диаметр будет равен 2АС, то есть двум.

Подробнее о шестиугольнике посмотрите информацию в этой статье (п.5).

Ответ: 2

27931. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите .

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:

А площадь  треугольника будет  равна 0,5х².

Значит

Таким образом, гипотенуза будет равна:

В ответе требуется записать:

Ответ: 4

 

27933. В треугольнике ABC АС = 4, ВС = 3, угол C равен 90⁰. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S –  площадь треугольника

Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.

По теореме Пифагора:

Найдём площадь:

Таким образом:

Ответ: 1

 

27934. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c –  стороны треугольника

S – площадь треугольника

Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:

Тогда

Таким образом:

Ответ: 1,5

27624. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

Посмотреть решение

27625. Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.

Посмотреть решение

27626. Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.

Посмотреть решение

27923. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.

Посмотреть решение

 

27932. Катеты равнобедренного прямоугольного треугольника равны  . Найдите радиус окружности, вписанной в этот треугольник.

Посмотреть решение

Небольшой итог.

Если  в условии дан треугольник и вписанная или описанная окружность, и речь идёт о сторонах, площади, радиусе, то сразу вспомните об указанных формулах и пробуйте использовать их при решении. Если не получается, то тогда уже ищите другие способы решения. 

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Решение треугольников | ЕГЭ-№1

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

В равнобедренный треугольник ABC вписана окружность с AB = AC, касающаяся сторон BC, AC и AB в точках P, Q и R соответственно. Докажите, что точка касания P делит сторону BC пополам.

Вопрос

Вопрос

---

AGRAWAL ПУБЛИКАЦИИ-КРУГИ-ПРИМЕР

20 видео

РЕКЛАМА

Ab Padhai каро бина объявления ке

Khareedo sikorukisavari видео!

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.

---

Похожие видео

Стороны AB, BC и AC треугольника ABC касаются окружности с центром O и радиусом r в точках P Q и R соответственно.

Окружность касается стороны BC △ABC в точке P и касается AB и AC, образующихся в точках Q и R соответственно. Докажите, что AQ=12(периметр △ABC).

32536299

Text Solution

Вписанная окружность равнобедренного треугольника ABC, где AB=AC, касается сторон AB, BC, CA в точках D,E и F соответственно.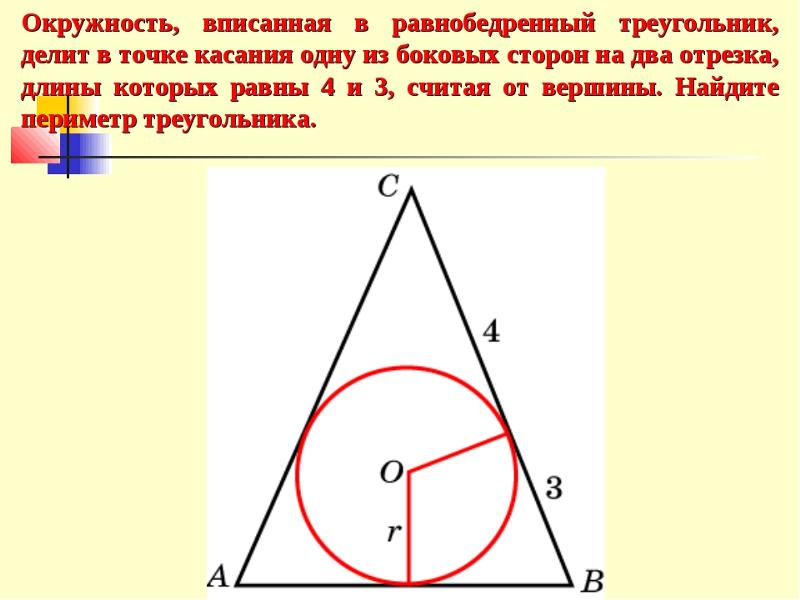 Докажите, что E делит BC пополам.

61733655

Окружность с центром P вписана в ΔABC Стороны AB, стороны BC и стороны A C касаются окружности в точках L, M и N соответственно. Докажите, что
A(ΔABC)=12(AB+BC+AC)×r

111400420

Окружность с центром P вписана в △ ABC. Сторона AB, сторона BC и сторона AC касаются окружности в точках L, M и N соответственно. Радиус окружности равен r. Докажите, что: A(△ABC)=12(AB+BC+AC)×r.

119564930

В прямоугольном треугольнике ABC есть окружность со стороной. AB как диаметр пересекает гипотенузу AC в P. Докажите, что касательная к окружности в точке P делит сторону BC пополам.

515795955

В прямоугольном треугольнике ABC есть окружность со стороной. AB как диаметр пересекает гипотенузу AC в P. Докажите, что касательная к окружности в точке P делит сторону BC пополам.

516945168

В ΔABC пусть P и Q — точки на AB и AC соответственно такие, что PQ∣∣BC.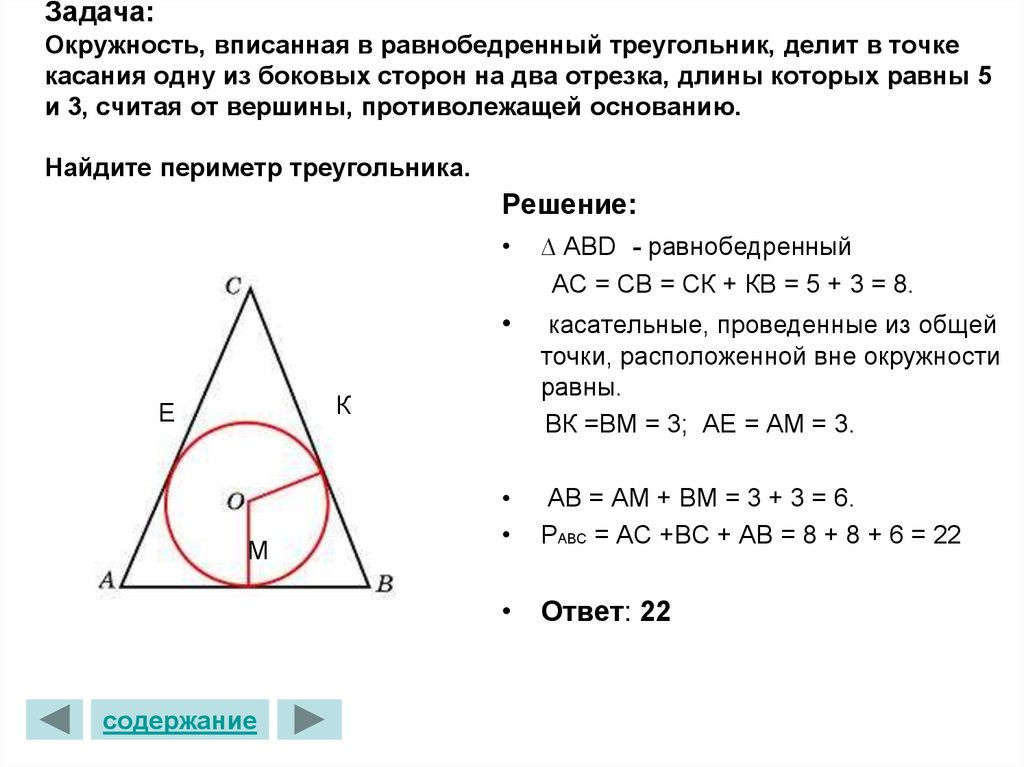 Докажите, что медиана AD делит PQ пополам.

599037469

На этом рисунке равнобедренный треугольник ABC с AB=AC описывает окружность. Докажите, что точка касания P делит основание BC пополам.

608077619

ΔABC — равнобедренный треугольник, AB = AC. Если все стороны АВ. BC и CA ΔABC касаются окружности в точках D, E и F соответственно. Тогда BE равно:

643372727

Окружность касается стороны BC △ABC в точке P и касается AB и AC, образующихся в точках Q и R соответственно. Докажите, что AQ=12(AB+BC+CA)=12(Периметр△ABC).

644267520

Окружность касается стороны BC △ABC в точке P и касается AB и AC, образующихся в точках Q и R соответственно. Докажите, что AQ=12(периметр △ABC).

644856984

O треугольника ABC касается сторон AB, BC и CA центрального концевого треугольника в точках P, Q и R соответственно. Докажите, что радиус окружности равен r. AB + CQ = AC + BQ

645173469

В прямоугольном треугольнике ABC окружность со стороной AB пересекает гипотенузу AC в точке P.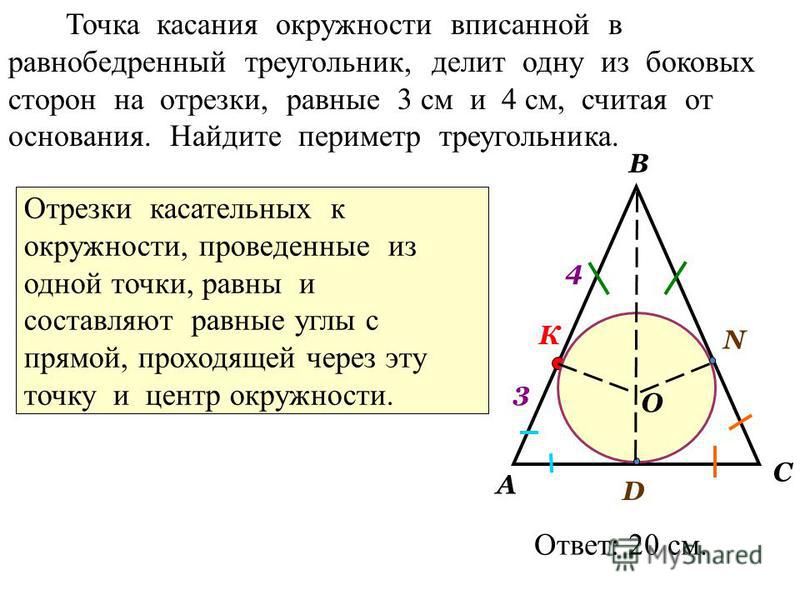 Докажите, что касательная к окружности в точке P делит сторону BC пополам.

645188969

На приведенном здесь рисунке окружность касается стороны BC треугольника ABC в точках P и AB, а AC образуется в точках Q и R соответственно. Чему равен АК?

646302901

Если окружность касается стороны BC в точке P, продолженной стороны AB в точке Q и продолженной стороны AC в точке R. Тогда AQ равен:

646460640

Треугольник, вписанный в окружность

Геометрия

Вопрос задан 22.02.22

Равнобедренный треугольник ABC с вершиной A вписан в окружность. Хорда AD пересекает BC в точке E.

Докажите, что квадрат длины AB минус квадрат длины AE равен произведению длины BE на длину CE.

Подписаться І 1

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Пол М. ответил 23.02.22

Репетитор

5,0 (24)

Бакалавр математики, MD

Об этом репетиторе ›

Об этом репетиторе ›

Mark is correct (as he most often is!

I will not use the vinculum .

F is the midpoint of BC

AB ² = AF ² + BF ²

AE ² = AF ² + EF ²

^{Тогда немного алгебры даст ответ!}

Голосовать за 0 Понизить

Подробнее

Отчет

Барри Д. ответил 23.02.22

Репетитор

5,0 (981)

Репетитор по геометрии

Об этом репетиторе ›

Об этом репетиторе ›

Я рекомендую использовать косвенное доказательство, AE^2 = (BE)(CE). 92

=(AE)(ED + AE) = (AE)(AD)

Я ищу использование формулы/уравнения секущей-тангенса, чтобы остановиться здесь.

Я открыт для критики, исправления, совета!

Голосовать за 0 Понизить

Подробнее

Отчет

Марк М. ответил 22.02.22

Репетитор

5,0 (270)

Учитель математики — высококвалифицированный специалист NCLB

Об этом репетиторе ›

Об этом репетиторе ›

Используйте теорему Пифагора.

Голосовать за 0 Понизить

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.