ОГЭ — 2016. Открытый банк заданий по математике. Модуль «Геометрия»
ОГЭ — 2016
Открытый банк заданий
по математике.
Модуль «Геометрия»
Вашему вниманию представлены тридцать шесть
прототипов задач по модулю «Геометрия»
открытого банка заданий по математике. ОГЭ – 2015.
Прямоугольный треугольник.
Равносторонний треугольник.
Произвольный треугольник.
Прямоугольник.
Ромб.
Параллелограмм.
Трапеция.
Круг. Круговой сектор.
В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив него,
равен 300 . Найдите площадь треугольника.
А
Подсказка (3):
300
S-?
С
10
1
S CB CA
2
1
ВС АВ
2
2
2
2
АВ АС ВС
В
50 3
АВ
АС
В прямоугольном треугольнике один из
катетов равен 10, а острый угол,
прилежащий к нему, равен 300.
Найдите площадь треугольника.
А
Подсказка (3):
10
1
S CB CA
2
BC
0
cos 30
AB
300
S-?
С
АВ АС ВС
2
В
2
2
50 3
2
АВ
ВС
В прямоугольном треугольнике гипотенуза
равна 10, а один из острых углов равен 300.
Найдите площадь треугольника.
А
Подсказка (3):
1
S BС AС
2
0
0
С 90 А 30
300
10
1
ВС АВ
2
АС АВ2 ВС 2
S-?
С
В
25 3
2
В прямоугольном треугольнике один из катетов
равен 10, а угол, лежащий напротив него,
равен 450 . Найдите площадь треугольника.
А
Подсказка (2):
1
S CB CA
2
450
С 90 В 45
0
А В 90
0
S-?
С
10
В
СА СВ
50
0
В прямоугольном треугольнике гипотенуза
равна 10, а один из острых углов равен 450.
Найдите площадь треугольника.
А
Подсказка (3):
1
2
S AС
2
450
10
S-?
С 90
А В 90
АВ 2АС
2
С
В
0
0
2
25
В 45
0
СА СВ
АС2
В прямоугольном треугольнике один
из катетов равен 10, а угол,
лежащий напротив, равен 600.
Найдите площадь треугольника.
А
10
Подсказка (3):
1
S BС AС
2
AC
0
АВ
sin 60
AB
S-?
ВС АВ АС
2
600
С
В
50 3
2
В прямоугольном треугольнике один
из катетов равен 10, а острый угол,
прилежащий к нему, равен 600.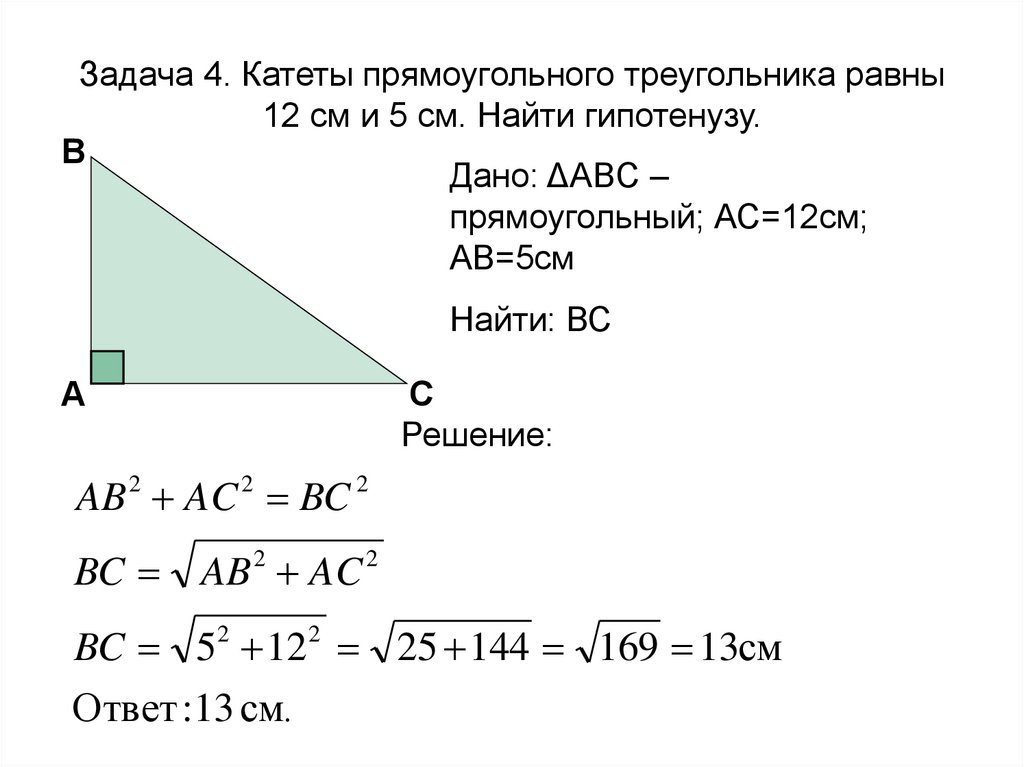
Найдите площадь треугольника.
А
Подсказка (4):
1
S BС AС
2
0
0
А 30
В 60
1
АВ
ВС АВ
S-?
2
АС АВ2 ВС 2
600
С
10
В
50 3
В прямоугольном треугольнике
гипотенуза равна 10,
а один из острых углов равен 600.
Найдите площадь треугольника.
А
Подсказка (3):
1
S BС AС
2
AC
0
sin 60
AB
BC
0
cos 60
AB
10
S-?
600
С
В
25 3
2
АС
ВС
Сторона равностороннего треугольника
равна 10. Найдите его площадь.
А
Подсказка (4):
1
S BC AH
2
10
S-?
В
Н
АВ ВС АС
С
1
ВН ВС
2
2
2
АН АВ ВН
25 3
Периметр равностороннего треугольника
равен 30. Найдите его площадь.
А
Подсказка (3):
1
S BC AH
2
АВ ВС АС
1
ВН ВС
2
S-?
25 3
В
Н
РАВС 30
С
АН АВ 2 ВН 2
25 3
Высота равностороннего треугольника
равна 10.
Найдите его площадь.
А
Подсказка (3):
1
S BC AH
2
АВ ВС АС х
10
S-?
1
ВН х
2
25 3
В
Н
АН 10
С
АВ2 АН 2 ВН 2
20 3
3
В равнобедренном треугольнике боковая
сторона равна 10, а угол, лежащий
напротив основания равен 1200.
Найдите площадь треугольника.
Подсказка (4):
А
1200
10
S-?
В
1
S BC AH
2
АВН : Н 90 , А 60 , В 30
0
0
АВ2 АН 2 ВН 2
25 3
Н
АВ 10
С
25 3
0
Периметр равнобедренного треугольника
равен 16, а боковая сторона — 5.
Найдите площадь треугольника.
Подсказка (4):
А
1
S BC AH
2
Р АВ ВС АС
АВН :
0
5
S-?
В
ВС
Н 90 , АВ 5, ВН 3
25 3
Н
Р 16
С
АВ2 АН 2 ВН 2
12
Периметр равнобедренного треугольника
равен 16, а основание — 6.
Найдите площадь треугольника.
Подсказка (4):
А
S-?
В
1
S BC AH
2
Р АВ ВС АС
АВН :
0
Н 90 , АВ 5, ВН 3
25 3
Н
Р 16
АВ
С
ВС 6
АВ2 АН 2 ВН 2
12
В равнобедренном треугольнике боковая
сторона равна 10, основание — 10 2 2 ,
а угол, лежащий напротив основания,
равен 1350.
Найдите площадь треугольника.
Подсказка (2):
А
1350
10
1
S АB AС sin A
2
0
0
0
S-?
В
ВС 10 2 2
sin 135 sin 180 45 sin 450
С
25 2
Задание 16
(№ 169854)
В треугольнике одна из сторон равна 10,
другая равна10 3 , а угол между
ними равен 600.
Найдите площадь треугольника.
В
С
S-?
10 3
10
?
600
Подсказка:
1
S AB AC sin A
2
А
75
В треугольнике одна из сторон равна 10,
другая равна 12,
а косинус угла между ними равен 2 2 .
3
Найдите площадь треугольника.
Подсказка (2):
В
С
S-?
12
10
?
1
S AB AC sin A
2
sin A cos A 1
2
2
А
20
В треугольнике одна из сторон равна 10,
другая равна 12,
2
а тангенс угла между ними равен
.
4
Найдите площадь треугольника.
В
С
1
S AB AC sin A
2
S-?
12
Подсказка (3):
10
?
А
1 tg A
2
1
cos A
2
2
sin A cos A 1
20
2
В прямоугольнике одна сторона 6,
а диагональ 10.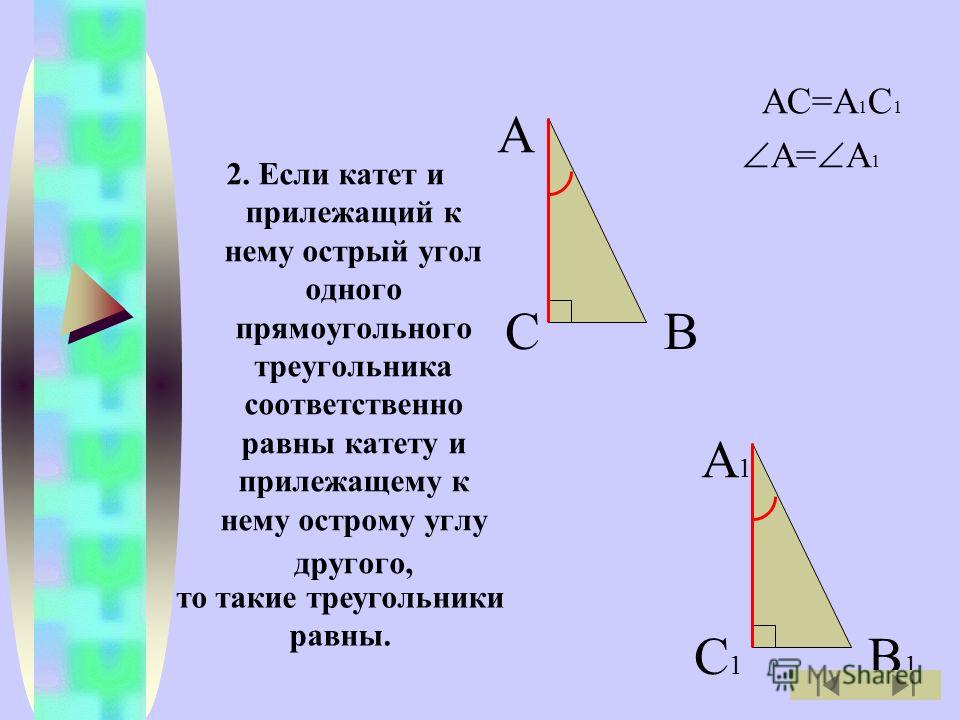
Найдите площадь прямоугольника.
Подсказка (3):
В
S-?
6
А
S AB ВC
С
0
В
90
АВС :
АС АВ ВС
2
10
2
D
48
2
ВC
В прямоугольнике диагональ равна 10,
а угол между ней и одной из сторон 300.
Найдите площадь прямоугольника.
Подсказка (4):
В
S AB0 ВC
С
АВС : В 90 , А 30
300
10
1
ВС АС
2
S-?
D
А
ВАС 30
0
АВ ВС АС
2
2
0
ВC
2
25 3
АВ
В прямоугольнике диагональ равна 10,
угол между ней и одной из сторон равен 300,
длина этой стороны 5 3 .
Найдите площадь прямоугольника.
Подсказка (2):
В
С
S 2S ACD
S-? 10
S ACD
300
А
D
5 3
DAC 30
1
AC AD sin А
2
0
25 3
Сторона ромба равна 5,
а диагональ равна 6.
Найдите площадь ромба.
А
Подсказка (4):
1
S ВD AH
2
0
АDH : Н 90
5
6
D
Н
S-?
В
AH DН AD
2
2
S ромба 2 S
24
С
2
АН
Периметр ромба равен 40,
а один из углов равен 300 .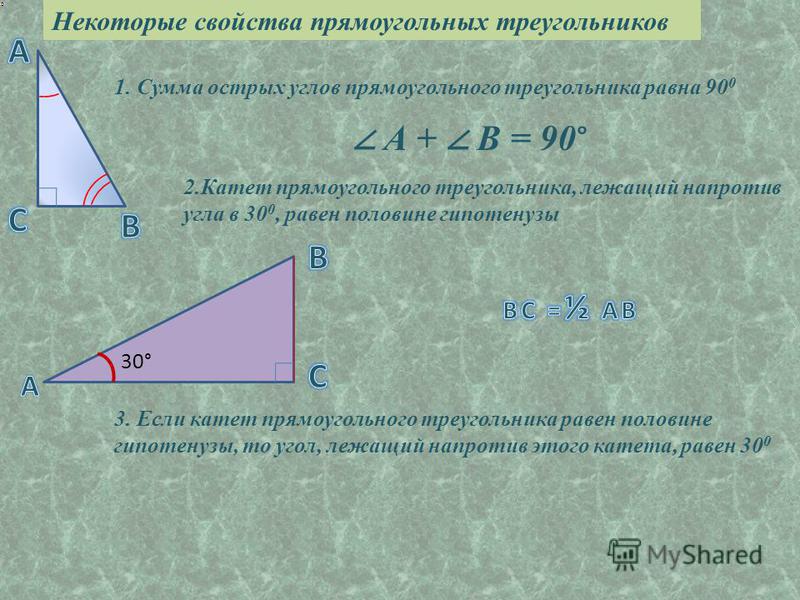
Найдите площадь ромба.
А
Подсказка (4):
S ABD
300
В
D
S-?
С
Р 40
1
AВ AD sin A
2
Р 4 АВ
АВ
S ромба 2 S
50
Периметр ромба равен 24, 2
а тангенс одного из углов равен
.
Найдите площадь ромба. 4
А
Подсказка (4):
S ромба 2 S
S ABD
В
D
S-?
С
Р 24
1
AВ AD sin A
2
1
1 tg A
2
cos A
2
2
sin A cos A 1
12
2
В ромбе сторона равна 10,
одна из диагоналей — 10 2 2 , а угол,
лежащий напротив этой диагонали, равен 450.
Найдите площадь ромба.
А
Подсказка (2):
S 2S ABD
450
10
В
D
S-?
С
S ABD
BD 10 2 2
1
AВ AD sin A
2
50 2
В ромбе сторона равна 10,
одна из диагоналей — 5 6 2 , а угол,
из которого выходит эта диагональ, равен 1500.
Найдите площадь ромба.
А
Подсказка (3):
10
S ромба 2 S
1500
В
D
S-?
С
1
S АD AВ sin A
2
0
АDВ : А 180 2 ADC
BD 5 6 2
50
Задание 16
(№ 169876)
Одна из сторон параллелограмма равна 12,
другая равна 5, а один из углов — 450.
Найдите площадь параллелограмма.
Подсказка (3):
А
5
450
D
Н
12
В
S DC AH
АВС :
Н 90 , D 45 , А 45
АН DH
0
S-?
С
0
AD 2АН
2
2
30 2
0
АН
Одна из сторон параллелограмма равна 12,
1
другая равна 5, синус одного из углов равен .
3
Найдите площадь параллелограмма.
Подсказка:
А
В
5
D
S АD DC sin D
S-?
12
С
20
Одна из сторон параллелограмма равна 12,
другая равна 5, косинус одного из углов 2 2 .
Найдите площадь параллелограмма. 3
Подсказка (2):
А
В
S АD DC sin D
5
D
S-?
12
sin D cos D 1 :
2
2
С
20
Основания трапеции равны 18 и 12,
одна из боковых сторон равна 4 2 , а угол
между ней и одним из оснований равен 1350.
Найдите площадь трапеции.
Подсказка (3):
В
12
С
1
S BС АD) ВН
2
АВН :
1350
4 2
А
S-?
Н
18
Н 90 , В А 45
АН ВН
0
D
0
АВ 2ВН
2
60
2
ВН
Основания трапеции равны 18 и 12,
одна из боковых сторон равна 6, а синус
угла между ней и одним из оснований
1
равен 3 .
Найдите площадь трапеции.
Подсказка (5):
В
12
S-?
6
А
С
Н
18
1
S BС АD) ВН
2
1
S ABD AB AD sin A
2 1
ВН
S ABD АD BH
2
D
30
Основания трапеции равны 18 и 12,
одна из боковых сторон равна 6, а косинус
угла между ней и одним из оснований
равен 2 2 . Найдите площадь трапеции.
Задание 16
(№ 169884)
3
Подсказка (5):
В
12
S-?
6
А
С
Н
18
1
S BС АD) ВН
2
2
2
sin А cos А 1 :
1
S ABD AB AD sin A
2 1
ВН
S ABD АD BH
D
2
30
Радиус круга равен 1.
Найдите его площадь
Подсказка:
1
S-?
О
3,14
S R
2
3,14
Найдите площадь кругового сектора,
если радиус круга равен 3,
а угол сектора равен 1200.
S-?
Подсказка:
1200
3
3,14
О
S
R
2
360
10,42
Найдите площадь кругового сектора,
если длина ограничивающей его дуги
равна 6 , а угол сектора равен 1200
S-?
Подсказка (5):
6π
R
l
1200
О
3,14
180
S
R
R
2
360
9,68
Радиус круга равен 3, а длина
ограничивающей его окружности равна 6π.
Найдите площадь круга.
Подсказка (3):
3
S-?
О
3,14 С 6
S R
2
С 2 R
С 6
28,26
R
При создании презентации были использованы
задачи с сайта
«Открытый банк заданий по математике»
ГИА – 2015.
http://www.mathall.ru/
в прямоугольном треугольнике один из катетов равен 40 а угол лежащий напротив него равен 45. найдите площадь треугольника — Знания.site
Последние вопросы
Математика
1 час назад
Не могу решить задачу помогите пожалуйста важен правильный ответМатематика
1 час назад
Помогите пожалуйста нужно правильно решениеМатематика
1 час назад
Помогите Пожалуйста Срочно!Математика
1 час назад
ПОМОГИ ПОЖАЛУЙСТА ДАЮ 70 БАЛЛОВсрочно надо 1 час назад
Розвяжіть рівняння 12.
8-(х+4.723)=1.05Математика
1 час назад
Знайти розв язок задачі Коші.Математика
1 час назад
25+(-9)=Кто решит дам 13 балов!!Математика
1 час назад
Знайдіть швидкість катера проти течіі річки,якщо швидкість течіі дорівнює 1.8км/год.,а швидкість катера за течією річки-18км/год.Математика
1 час назад
-8-(-7)Кто решит дам 12 балов!!Математика
2 часа назад
Домашнее задание помогите решить пожалуйсиа2 часа назад
На координатній прямій позначте точки, координати яких задовольняють умову |x| <4,2/Запишіть усі цілі числа, для яких виконується вказана умова. допоможіть пжМатематика
2 часа назад
И Какой телефон у этого «умника»?Математика
3 часа назад
Звести подiбнi доданки 9b — 4b -5bМатематика
3 часа назад
Помогите срочно пожалуйста, математика, 5 классМатематика
3 часа назад
Мне крч соль позвоночник вырвала чо делать а еще колени топором перерубила но это так не страшно шутка
так чо делать
8-(х+4.723)=1.05
допоможіть пжВсе предметы
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Как найти длину стороны прямоугольного равнобедренного треугольника 45/45/90
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Справка по основам геометрии » Плоская геометрия » Треугольники » 45/45/90 Прямоугольные равнобедренные треугольники » Как найти длину стороны 45/45/90 прямоугольный равнобедренный треугольник
Периметр треугольника 45-45-90 равен 100 дюймам.
Какова длина каждой ноги с точностью до десятой доли дюйма?
Возможные ответы:
Правильный ответ:
Объяснение:
Позвольте быть длиной ноги; тогда гипотенуза равна , а периметр равен
Следовательно,
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Правильный ответ:
4
4
4 Объяснение:
Сообщить об ошибке
Угол в треугольнике, показанном ниже, равен 45 градусам.
Сторона имеет длину 10. Какова длина стороны?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку мы знаем два из трех углов этого треугольника, мы можем вычислить третий, .
Следовательно, это прямоугольный треугольник 45/45/90. Помните, что прямоугольные треугольники 45/45/90 имеют отношение катет: катет: гипотенуза 1:1:.
Мы знаем гипотенузу, поэтому мы можем быстро вычислить длину одного из катетов, , разделив на :
Чтобы это выглядело как один из вариантов ответа, рационализируйте знаменатель, умножив дробь на:
Сообщить об ошибке
– треугольник.
Какова длина?
Возможные ответы:
Недостаточно информации для ответа на этот вопрос.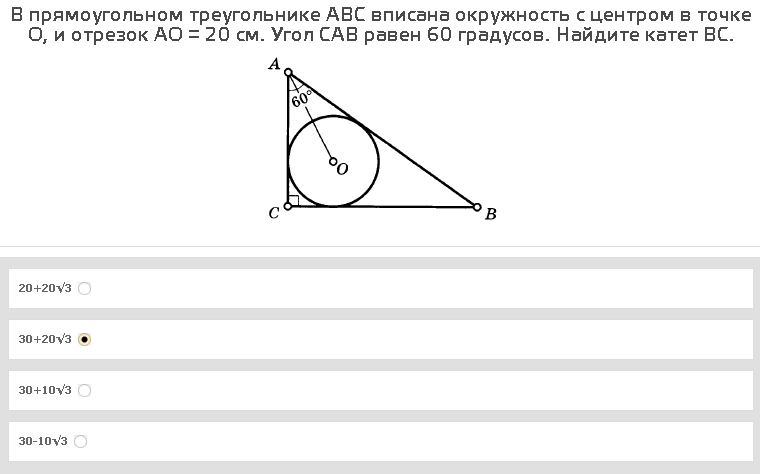
Правильный ответ:
Пояснение:
Мы знаем, что стороны треугольников находятся в отношении , где меньшая сторона лежит против углов, а длинная сторона является гипотенузой и лежит против прямого угла. Нам известно, что гипотенуза равна .
Разделите длину гипотенузы на , чтобы вычислить коэффициент увеличения.
Умножьте длину более коротких сторон на коэффициент увеличения.
Таким образом, длина (и ) равна .
Сообщить об ошибке
Следующее изображение не в масштабе.
Найдите длину одной из сторон прямоугольного треугольника.
Возможные ответы:
Правильный ответ:
Пояснение:
Из-за засечек на обеих сторонах мы можем определить, что этот прямоугольный треугольник является треугольником 45/45/90.
Поскольку длина обоих катетов одинакова, это означает, что угол, противоположный каждому катету, также одинаков.
Треугольники 45/45/90 особенные, как и треугольники 30/60/90. Решение для одной из длин сторон можно легко определить, если вспомнить следующее:
Используя это и 7 футов, мы можем найти «s», что даст нам длину стороны.
хотя это правильный ответ, предлагаемые варианты представлены в виде упрощенных радикалов.
Сообщить об ошибке
Если гипотенуза прямоугольного равнобедренного треугольника равна , какова длина стороны треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Прямоугольный равнобедренный треугольник также является треугольником.
Чтобы найти длину стороны, нам нужно использовать теорему Пифагора:
Поскольку это равнобедренный треугольник,
Теорема Пифагора может быть переписана следующим образом:
Поскольку мы пытаемся найти длину стороны этого треугольника, найдите .
Упрощение.
Умножьте дробь на единицу в виде .
Решить.
Теперь замените длину гипотенузы на , чтобы найти сторону треугольника в вопросе.
Упрощение.
Уменьшить.
Сообщить об ошибке
Если гипотенуза прямоугольного равнобедренного треугольника равна , какова длина стороны треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Прямоугольный равнобедренный треугольник также является треугольником.
Чтобы найти длину стороны, нам нужно будет использовать теорему Пифагора:
Поскольку это равнобедренный треугольник,
Теорема Пифагора может быть переписана следующим образом:
Поскольку мы пытаемся найти длину стороны этого треугольника, найдите .
Упрощение.
Умножьте дробь на единицу в виде .
Решить.
Теперь замените длину гипотенузы на , чтобы найти сторону треугольника в вопросе.
Упрощение.
Уменьшить.
Сообщить об ошибке
Если гипотенуза прямоугольного равнобедренного треугольника равна , какова длина стороны этого треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Прямоугольный равнобедренный треугольник также является треугольником.
Чтобы найти длину стороны, нам нужно использовать теорему Пифагора:
Поскольку это равнобедренный треугольник,
Теорема Пифагора может быть переписана следующим образом:
Поскольку мы пытаемся найти длину стороны этого треугольника, найдите .
Упрощение.
Умножьте дробь на единицу в виде .
Решить.
Теперь замените длину гипотенузы на , чтобы найти сторону треугольника в вопросе.
Упрощение.
Уменьшить.
Сообщить об ошибке
Если гипотенуза прямоугольного равнобедренного треугольника равна , какова длина стороны этого треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Прямоугольный равнобедренный треугольник также является треугольником.
Чтобы найти длину стороны, нам нужно использовать теорему Пифагора:
Поскольку это равнобедренный треугольник,
Теорема Пифагора может быть переписана следующим образом:
Поскольку мы пытаемся найти длину стороны этого треугольника, найдите .
Упрощение.
Умножьте дробь на единицу в виде .
Решить.
Теперь замените длину гипотенузы на , чтобы найти сторону треугольника в вопросе.
Упрощение.
Уменьшить.
Сообщить об ошибке
← Предыдущая 1 2 3 4 Следующая →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Узнайте по концепции
Математические головоломки Ника: решение 77
- головоломки:
- 1-10
- 11-20
- 21-30
- 31-40
- 41-50.5046446464444444444646464446464446464644646464644646464646446464646464646464646тели
- 71-80
- 81-90
- 91-100
- 101-110
- 111-120
- 121-130
- 131-140
- 141-150
- 151-160
- Индекс
- |
- Дом
- О
- Доступность
49464964646464646464646464646464646464646464646464646464646464669н. 70
Кусок деревянной доски в форме равнобедренного прямоугольного треугольника со сторонами 1, 1, , распилить на две части.
Найдите длину и расположение кратчайшего прямого разреза, делящего доску на две равные части.
Рассмотрим два случая:
- Разрез 1 поперек одного из острых углов.
- Вырез 2 под прямым углом.
Разрез 1
Пусть X лежит на AB с AX = x, а Y лежит на AC с AY = y. Тогда XY — прямой разрез длины z.
Площадь ABC = ½ × основание × перпендикулярная высота = ½.
Площадь AXY, считая AX за основу, равна ½ × x × (y/) = xy/(2).
Поскольку площадь AXY = ½ × площадь ABC, мы имеем xy = 1/.
Применение закона косинусов (также известного как cosine rule ) to AXY:
| z 2 | = x 2 + y 2 − 2xy cos A |
| = x 2 + y 2 − 1 , поскольку cos A = 1/ | |
| = (x − y) 2 + (− 1) |
Следовательно, минимальное значение z 2 возникает, когда x = z y, так что z 2 = − 1.
Тогда, поскольку xy = 1/, x = y = 1/.
Интуитивно кажется очевидным, что резка под меньшим углом, как указано выше, даст более короткий минимальный разрез, чем резка под прямым углом. Ниже мы проверим эту интуицию.
Разрез 2
Пусть Y лежит на AB, причем BY = y, а X лежит на BC, причем BX = x. Тогда XY — прямой разрез длины z.
Площадь BXY = ½xy.
Так как площадь BXY = ½ × площадь ABC, мы имеем xy = ½.
Применение теоремы Пифагора к BXY:
| z 2 | = x 2 + y 2 |
| = (x — y) 2 + 1 |
hrue the ginward of zence of zence of zence of zence of zence of zence of zence of zence of zence or zence of zence or as zence of zence a o zence a o so zend a so zend a so zend a so zend a so moin z 2 = 1.
Это больше, чем минимальная длина, установленная для разреза 1 выше.
Минимальный разрез
Следовательно, минимальный прямой разрез имеет длину , причем на первой диаграмме AX = AY = (Конечно, по симметрии существует эквивалентный разрез равной длины от BC до AC.
)
Замечания
Естественно спросить, возможен ли более короткий разрез, если мы не ограничены использованием прямой линии. Ответ: да! Чтобы понять почему, воспользуемся симметрией.
Рассмотрим приведенную ниже диаграмму, полученную путем последовательного отражения треугольника от его сторон. Площадь всего квадрата равна 4; площадь (правильного) восьмиугольника равна 2.
Результат, известный как изопериметрическая теорема, утверждает, что из всех плоских фигур с одинаковой площадью круг имеет самый короткий периметр. Следовательно, круг с той же площадью, что и восьмиугольник, будет иметь минимальный периметр. Отсюда следует, что минимальная дуга, делящая пополам равнобедренный прямоугольный треугольник, , проходящая через один катет и гипотенузу , является дугой такой окружности с центром в 45° вершине треугольника. См. ниже.
(Чтобы доказать, что это кратчайшая дуга, которая делит пополам равнобедренный прямоугольный треугольник, нам нужно показать, что никакая другая дуга, например, проходящая через обе стороны, не короче.
Leave A Comment