В прямоугольном треугольнике катет и гипотенуза равны 12 и 20 соответственно: В прямоугольном треугольнике катет и гипотенуза равны соответственно 12 и 20. найдите другой катет этого…

Прямоугольный треугольник. Теорема Пифагора. | СПАДИЛО

Определение

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Свойства прямоугольного треугольника

• В прямоугольном треугольнике гипотенуза является наибольшей стороной.
• В прямоугольном треугольнике катет, лежащий напротив угла 30⁰, равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30⁰.

Например, пусть угол А=30⁰, а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30⁰. Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30

0.

• Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
• Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
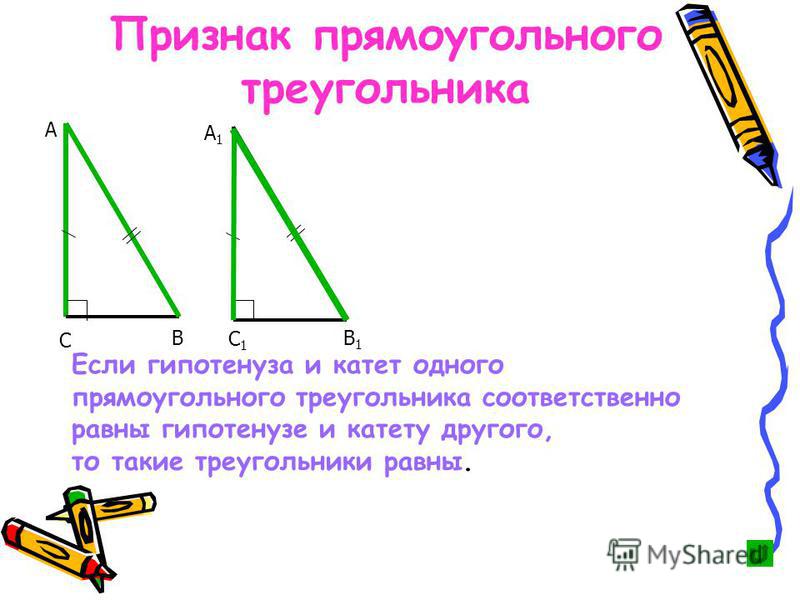
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

1. по катетам;
2. по катету и прилежащему острому углу;
3. по гипотенузе и острому углу;
4. по гипотенузе и катету.

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

Трактовка

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ²=АС²+ВС²

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ²

=9²+12²=81+144=225=15², значит АВ=15 см.

Египетский треугольник

Определение

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Определение

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа.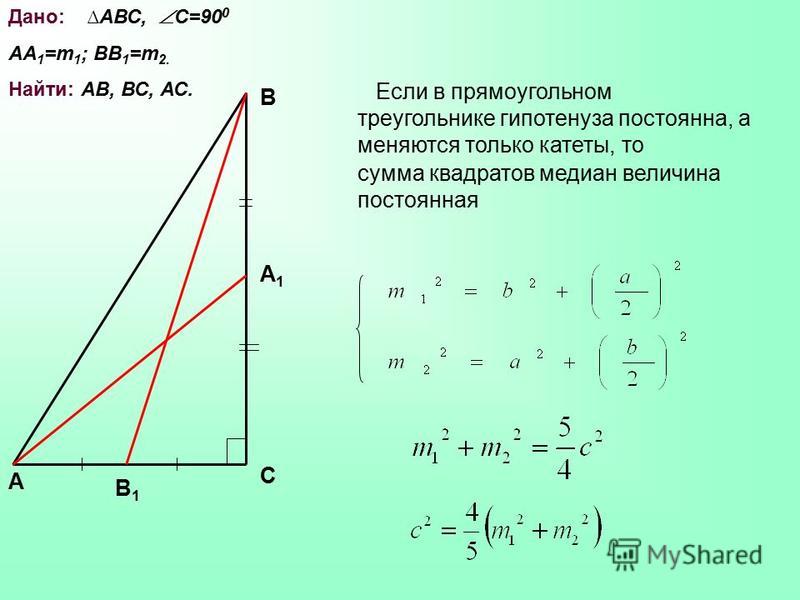 Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16²+12²=20², 256+144=400, 400=400.

Даниил Романович | Просмотров: 7.1k

Катет «A» и угол «α» прямоугольного треугольника

Зная стороныдва угла и сторонудве стороны и уголпрямоугольный треугольникравнобедренный треугольникравносторонний треугольникоснование и высоту

катетыкатет и гипотенузукатет и уголгипотенузу и угол

катет aкатет b

угол αугол β

Катет треугольника a

Угол треугольника α

Зная один из катетов в прямоугольном треугольнике, можно найти второй катет и гипотенузу используя тригонометрические отношения – синус и тангенс известного угла. Так как отношение противолежащего углу катета к гипотенузе равно синусу этого угла, следовательно, чтобы найти гипотенузу нужно катет разделить на синус угла. a/c=sin⁡α c=a/sin⁡α

Второй катет можно найти из тангенса известного угла, как отношение известного катета к тангенсу.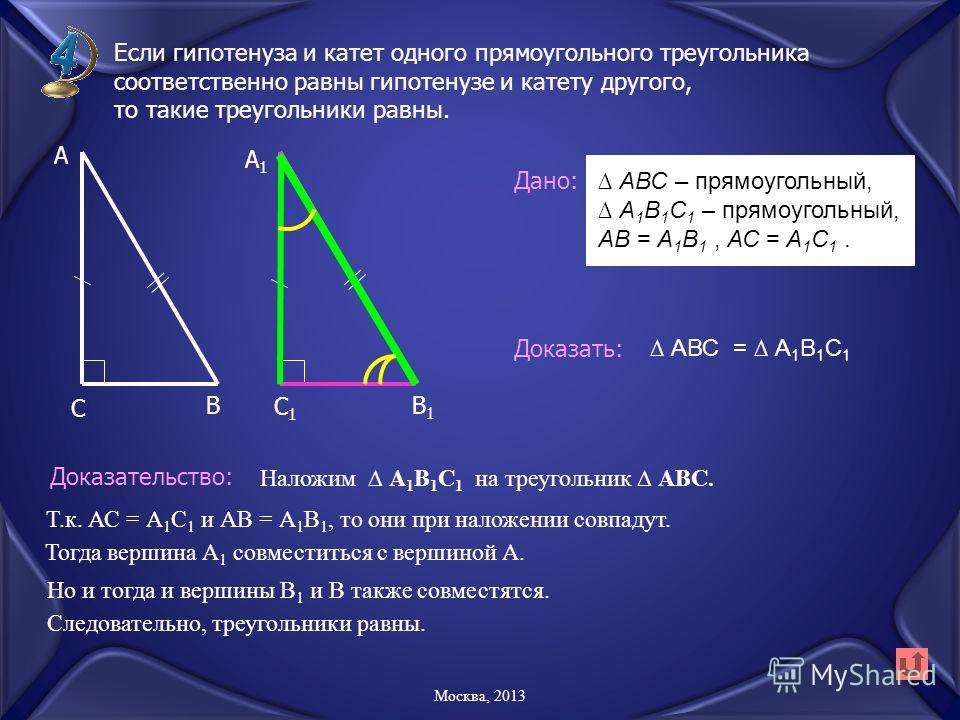

2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(a/tan⁡α √(2c(a/tan⁡α +c) ))/(a/tan⁡α +c)=(a√(2c(a/tan⁡α +c) ))/(a+c tan⁡α ) l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(a√(2c(a+a/sin⁡α ) ))/(a+a/sin⁡α )=(a sin⁡α √(2c(a+a/sin⁡α ) ))/(a sin⁡α+a)

Средняя линия проходит параллельно одной из сторон треугольника, при этом образуя еще один подобный прямоугольный треугольник с такими же по величине углами, в котором все стороны в два раза меньше, чем у изначального. Исходя из этого, средние линии можно найти по следующим формулам, зная только катет и противолежащий ему угол. (рис.79.7) M_a=a/2 M_b=b/2=a/(2 tan⁡α ) M_c=c/2=a/(2 sin⁡α )

Радиус вписанной окружности равен разности катетов и гипотенузы, деленной на два, а чтобы найти радиус описанной окружности, нужно разделить на два гипотенузу. Заменяем второй катет и гипотенузу на отношения катета a к синусу и тангенсу соответственно. (рис. 79.5, 79.6) r=(a+b-c)/2=(a+a/tan⁡α -a/sin⁡α )/2=(a tan⁡α sin⁡α+a sin⁡α-a tan⁡α)/(2 tan⁡α sin⁡α ) R=c/2=a/2sin⁡α

5.

9: Теорема Пифагора — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

24413

Пифагор был греческим математиком и философом, родившимся на острове Самос (ок. 582 г. до н.э.). Он основал ряд школ, одну, в частности, в городке Кротоне на юге Италии, члены которого впоследствии стали известны как пифагорейцы. Внутренний круг школы, математики, жили в школе, избавились от всего личного имущества, были вегетарианцами и соблюдали строгий обет молчания. Они изучали математику, философию и музыку и верили, что числа составляют истинную природу вещей, придавая числам мистические или даже духовные качества.

Сегодня о трудах Пифагора ничего не известно, возможно, из-за секретности и молчания пифагорейского общества.

Однако одна из самых известных теорем во всей математике носит его имя — теорема Пифагора.

Прежде чем раскрыть содержание теоремы Пифагора, мы остановимся, чтобы дать определение прямоугольного треугольника и его составных частей.

Прямоугольный треугольник

Треугольник с одним прямым углом (90 ^◦ ) называется прямоугольный треугольник . На рисунке ниже прямой угол отмечен квадратиком.

Сторона треугольника, лежащая прямо напротив прямого угла, называется гипотенузой . Стороны треугольника, включающие прямой угол, называются

катетами прямоугольного треугольника.

Теперь мы можем сформулировать одну из древнейших теорем математики, теорему Пифагора .

Теорема Пифагора

92\), гипотенуза лежит сама по себе на одной стороне уравнения.

Теорему Пифагора можно только применить к прямоугольным треугольникам.

Давайте рассмотрим простое применение теоремы Пифагора.

Пример 1

Стороны прямоугольного треугольника имеют длину 3 и 4 метра соответственно. Найдите длину гипотенузы.

Решение

Давайте следовать требованиям

для решения задач Word . 92 ~ & \textcolor{red}{ \text{ Добавить: } 16+9=25.} \\ 5 = c~ & \textcolor{red}{ \text{ Извлечь неотрицательный квадратный корень.}} \end{aligned }\nonumber \]

Технически есть два ответа на c ² = 25, то есть c = −5 или c = 5. Однако c представляет собой гипотенузу прямоугольного треугольника. и должен быть неотрицательным. Следовательно, мы должны выбрать c = 5.

4. Ответить на вопрос . Гипотенуза имеет длину 5 метров. 92\16+9=25\25=25\end{aligned}\nonumber\]

Всё хорошо!

Упражнение

Катеты прямоугольного треугольника имеют длину 5 и 12 футов соответственно. Найдите длину гипотенузы.

Ответить

13 футов

Пример 2

Дан прямоугольный треугольник, найдите длину недостающей стороны.

Решение

Обратите внимание, что гипотенуза (против прямого угла) имеет длину 13. Эта величина сама по себе должна лежать на одной стороне уравнения Пифагора. Сумма квадратов катетов переходит на другую сторону. Следовательно, 92 = 144 ~ & \textcolor{red}{ \text{ Упростить обе стороны.}} \\ x= 12 ~ & \textcolor{red}{ \text{ Извлечь неотрицательный квадратный корень из 144.}} \end{aligned }\номер\]

Упражнение

Гипотенуза прямоугольного треугольника равна 25 сантиметрам. Одна сторона прямоугольного треугольника равна 24 сантиметрам. Найдите длину оставшейся ноги.

Ответить

7 сантиметров

Совершенные квадраты хороши, но не обязательны. 92 = 95 ~ & \textcolor{red}{ \text{ Упростить обе стороны.}} \\ x = \sqrt{95} ~ & \textcolor{red}{ \text{ Извлечь неотрицательный квадратный корень из 95.}} \end{aligned}\nonumber \]

Следовательно, точная длина недостающей стороны равна \(\sqrt{95}\).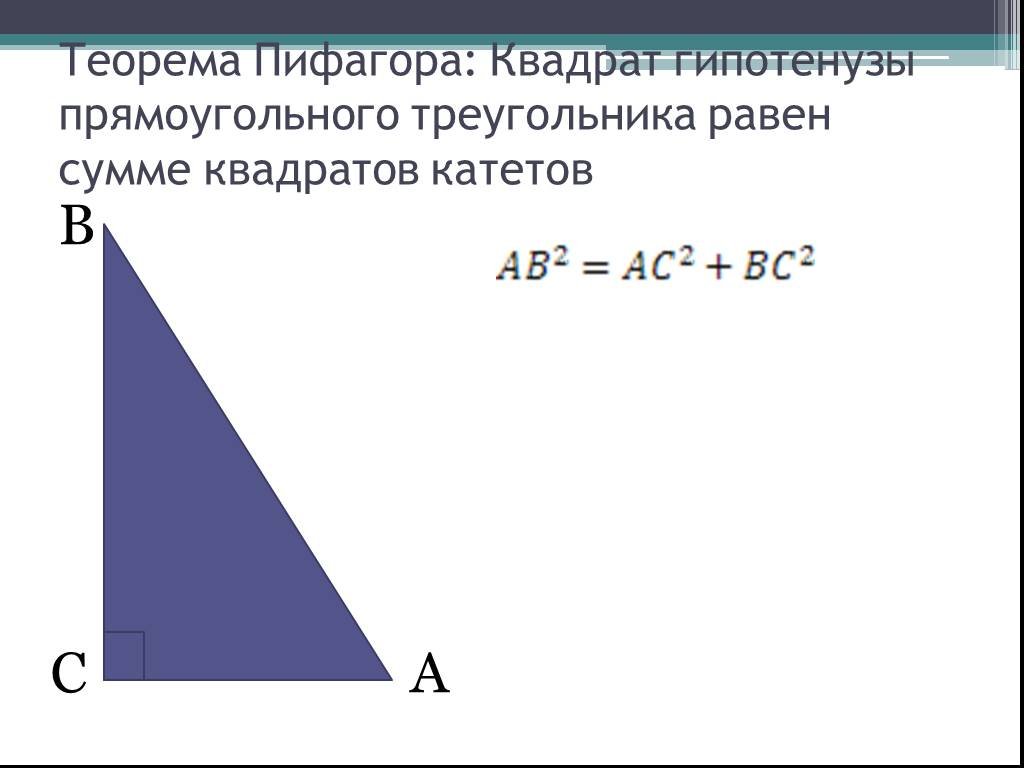

Упражнение

Гипотенуза и катет прямоугольного треугольника соответственно равны 9 и 7 дюймам. Найдите длину оставшейся ноги.

Ответить

Добавьте сюда текст. Не удаляйте этот текст первым.

Важное замечание

Любая попытка использовать ваш калькулятор для приблизительного вычисления 95 в примере 3 будет ошибкой, так как инструкции требуют точного ответа .

Иногда требуется приблизительный ответ, особенно в приложениях.

Пример 4

Джинни хочет создать огород в углу своего двора в форме прямоугольного треугольника. Она отрезает две доски длиной 8 футов, которые образуют ножки ее сада. Найдите длину доски, которую она должна отрезать, чтобы образовать гипотенузу своего сада, с точностью до ближайшей десятой доли фута. 92 = 128 ~ & \textcolor{red}{ \text{ Добавить: } 64 + 64 = 128.} \\ x = \sqrt{128} ~ & \textcolor{red}{ \text{ Извлечь неотрицательный квадратный корень. }} \end{aligned}\nonumber \]

4. Ответ на вопрос . Точная длина гипотенузы составляет \(\sqrt{128}\) футов, но нас просят найти гипотенузу с точностью до десятой доли фута. Используя калькулятор, мы находим приближение для \(\sqrt{128}\).

\[\sqrt{128} \ приблизительно 11.313708499\номер \]

Чтобы округлить до десятых, сначала определите цифры округления и проверки. 92 = 127,69\номер \]

Это почти одно и то же, расхождение связано с тем, что мы округлили, чтобы найти приближение для гипотенузы.

Упражнение

15-футовая лестница прислонена к стене здания. Основание лестницы находится в 5 футах от основания стены. До какой высоты до стены доходит верхняя часть лестницы? Округлите ответ до ближайшей десятой доли фута.

Ответить

14,1 фута

Упражнения

В упражнениях 1–16 ваши решения должны включать четко обозначенный эскиз.

1. Длина одного катета прямоугольного треугольника 15 метров, а длина гипотенузы 25 метров. Найдите точную длину другой ноги.

2. Длина одного катета прямоугольного треугольника 7 метров, а длина гипотенузы 25 метров. Найдите точную длину другой ноги.

3. Длины двух катетов прямоугольного треугольника равны 12 м и 16 м. Найдите точную длину гипотенузы.

4. Длины двух катетов прямоугольного треугольника равны 9 м и 12 м. Найдите точную длину гипотенузы.

5. Длина одного катета прямоугольного треугольника 13 метров, а длина гипотенузы 22 метра. Найдите точную длину другой ноги.

6. Длина одного катета прямоугольного треугольника 6 метров, а длина гипотенузы 15 метров. Найдите точную длину другой ноги.

7. Длины двух катетов прямоугольного треугольника равны 2 метра и 21 метр. Найдите точную длину гипотенузы.

8. Длины двух катетов прямоугольного треугольника равны 7 м и 8 м. Найдите точную длину гипотенузы.

9. Длина одного катета прямоугольного треугольника 12 метров, а длина гипотенузы 19 метров. Найдите точную длину другой ноги.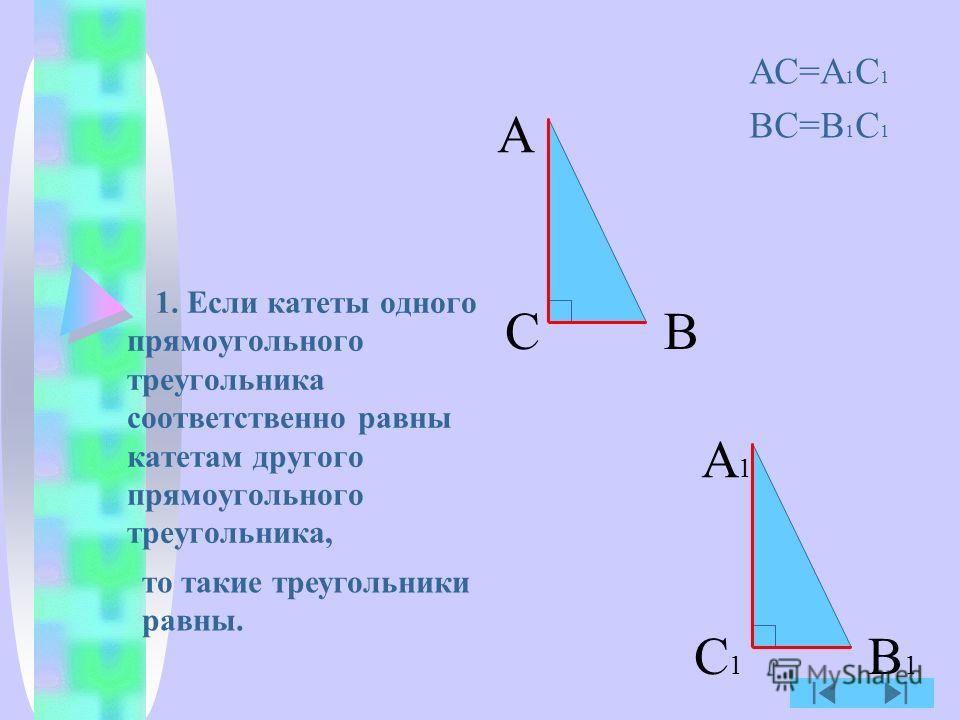

10. Длина одного катета прямоугольного треугольника 5 метров, а длина гипотенузы 10 метров. Найдите точную длину другой ноги.

11. Длины двух катетов прямоугольного треугольника равны 6 м и 8 м. Найдите точную длину гипотенузы.

12. Длины двух катетов прямоугольного треугольника равны 5 м и 12 м. Найдите точную длину гипотенузы.

13. Длина одного катета прямоугольного треугольника 6 метров, а длина гипотенузы 10 метров. Найдите точную длину другой ноги.

14. Длина одного катета прямоугольного треугольника 9 метров, а длина гипотенузы 15 метров. Найдите точную длину другой ноги.

15. Длины двух катетов прямоугольного треугольника равны 6 м и 22 м. Найдите точную длину гипотенузы.

16. Длины двух катетов прямоугольного треугольника равны 9 м и 19 м. Найдите точную длину гипотенузы.

---

В упражнениях 17-24 ваши решения должны включать четко обозначенный эскиз.

17. Длины двух катетов прямоугольного треугольника равны 3 м и 18 м. Найдите длину гипотенузы. Округлите ответ до сотых.

18. Длины двух катетов прямоугольного треугольника 10 футов и 16 футов. Найдите длину гипотенузы. Округлите ответ до десятых.

19. Длина одного катета прямоугольного треугольника 2 метра, а длина гипотенузы 17 метров. Найдите длину другой ноги. Округлите ответ до десятых.

20. Длина одного катета прямоугольного треугольника 4 метра, а длина гипотенузы 12 метров. Найдите длину другой ноги. Округлите ответ до сотых.

21. Длины двух катетов прямоугольного треугольника равны 15 футам и 18 футам. Найдите длину гипотенузы. Округлите ответ до сотых.

22. Длины двух катетов прямоугольного треугольника равны 6 футам и 13 футам. Найдите длину гипотенузы. Округлите ответ до десятых.

23. Длина одного катета прямоугольного треугольника 4 метра, а длина гипотенузы 8 метров. Найдите длину другой ноги. Округлите ответ до сотых.

24. Длина одного катета прямоугольного треугольника 3 метра, а длина гипотенузы 15 метров.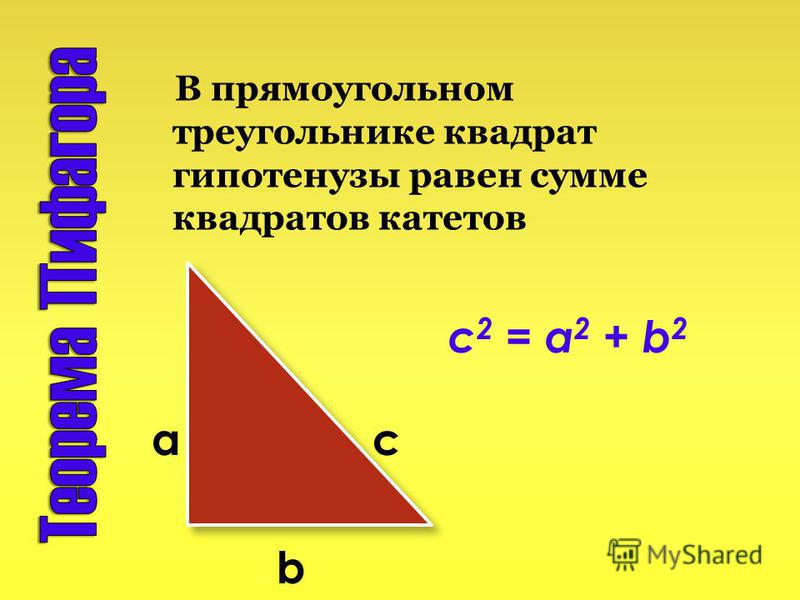 Найдите длину другой ноги. Округлите ответ до десятых.

---

25. Грета и Фриц сажают прямоугольный сад размером 13 на 18 метров и выкладывают его веревкой. Они хотели бы знать длину диагонали, чтобы убедиться, что углы образованы прямыми. Найдите длину диагонали. Округлите ответ до сотых. Ваше решение должно включать хорошо обозначенный эскиз.

26. Маркос и Анджелина сажают прямоугольный сад размером 11 на 19 метров и выкладывают его веревкой. Они хотели бы знать длину диагонали, чтобы убедиться, что углы образованы прямыми. Найдите длину диагонали. Округлите ответ до десятых. Ваше решение должно включать хорошо обозначенный эскиз.

27. Основание оттяжки длиной 24 метра находится в 10 метрах от основания телефонного столба, к которому она крепится. До какой высоты до столба доходит растяжка? Округлите ответ до сотых. Ваше решение должно включать хорошо обозначенный эскиз.

28. Основание 30-футовой растяжки расположено в 9 футах от основания телефонного столба, к которому он крепится. До какой высоты до столба доходит растяжка? Округлите ответ до сотых. Ваше решение должно включать хорошо обозначенный эскиз.

---

29. Походная тропа. Пешеходная тропа проходит на юг 8 километров, затем поворачивает на запад примерно 15 километров, а затем направляется на северо-восток по прямой дороге к начальной точке. Какова длина всей тропы?

30. Звериная тропа. Звериная тропа тянется на восток от водопоя 12 километров, затем идет на север 5 километров. Затем тропа поворачивает на юго-запад по прямой дороге обратно к водопою. Какова длина всей тропы?

31. Верхнее окно. 10-футовая лестница прислонена к стене дома. Насколько близко к стене должно быть основание лестницы, чтобы дотянуться до окна на высоте 8 футов над землей?

32. Как высоко? 10-футовая лестница прислонена к стене дома. Какой высоты будет лестница, если нижняя часть лестницы находится на расстоянии 4 м от стены? Округлите ответ до десятых.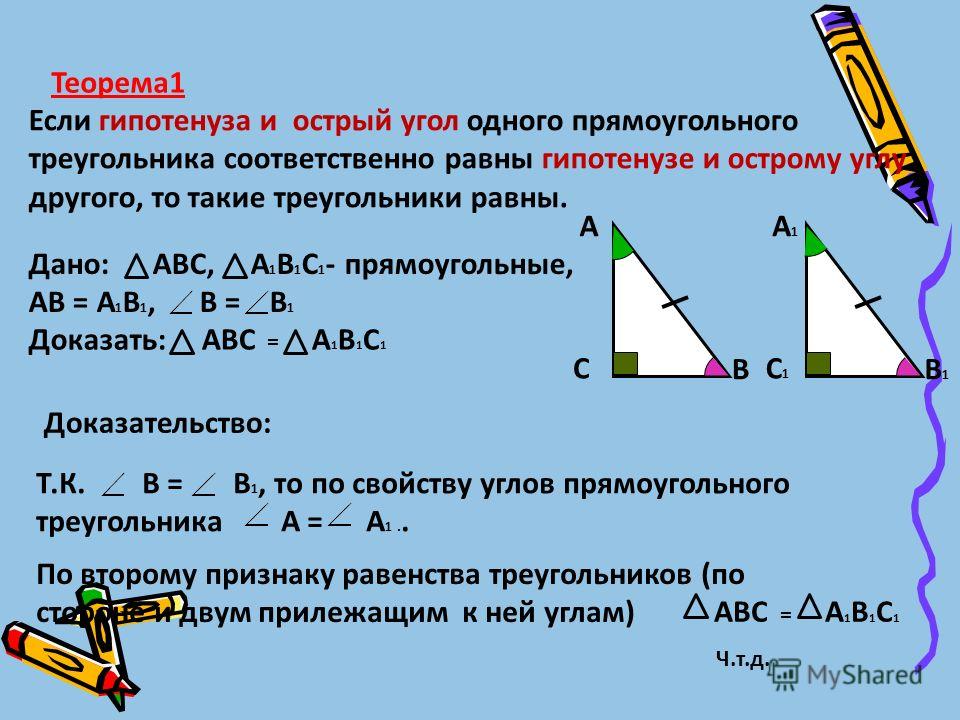

---

Ответы

1. 20 метров

3. 20 метров

5. √315 метров

7. \(\sqrt{445}\) метров

9. \(\sqrt{217}\) метров

11. 10 метров

13. 8 метров

15. \(\sqrt{520 } \) метры

17. 18,25 метра

19. 16,9 метра

21. 23,43 фута

23. 6,93 метра

25. 22,20 метра

27. 21.82 Метры

29.3. 39.3. 39.3. 39.13 29.3123 29.3. 3900 29.2923 29.3. 39.13 29.312 3900 29.3. 29.3. 39.13 29.3. 3900 2900 29.23. 39.312. 29.2923 29.3. 29.312.

29.312.

29.312 3900. 6 футов

---

5.9: Теорема Пифагора распространяется под лицензией CC BY-NC-SA и была создана, изменена и/или курирована LibreTexts.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   нет

2. Теги

   1. гипотенуза
   2. Теорема Пифагора
   3. прямоугольных треугольников
   4. урезать

5 12 13 Треугольник (Углы, стороны и способы решения)

Похожие материалы

сообщите об этом объявлении

сообщите об этом объявлении

Содержание урока

Что такое треугольник 5 12 13?

Треугольник 5 12 13 представляет собой особый прямоугольный треугольник SSS с отношением длин его сторон, равным 5, 12 и 13. Это обычная пифагорейская тройка, которую стоит запомнить, чтобы сэкономить время при работе с прямоугольными треугольниками. Другой распространенный специальный прямоугольный треугольник SSS — это треугольник 3 4 5.

Использование отношения 5 12 13 к нашему преимуществу

Треугольник 5 12 13 считается разносторонним, поскольку все три его стороны имеют разную длину. Если мы встретим прямоугольный треугольник и две из известных сторон входят в соотношение 5 12 13, мы можем сразу определить, что третья сторона будет оставшимся числом в соотношении. Обратите внимание, что сторона «13» всегда будет гипотенузой. Отношение 5 12 13 является масштабируемым и применимо к любому прямоугольному треугольнику со сторонами, которые являются любым общим кратным чисел 5, 12 и 13.

Список треугольников 5 12 13 общие кратные отношения 5 12 13, и все они считаются треугольниками 5 12 13. Заучивать этот список не обязательно, но очень полезно понимать, что 5 12 13 — это соотношение, которое может проявляться меньшими или большими числами, чем само соотношение.

— 2,5 6 6,5
— 5 12 13
— 7,5 18 19,5
— 15 36 39

5 12 13 Треугольные углы

A 5 12 13 ТРИ -Рууурины содержит следующие внутренние раковины в градусах:
22.6. °, 90° .

И в радианах:
0,39, 1,18 и 1,57 .

Не предполагается их запоминание. Мы можем использовать правило Soh Cah Toa и обратные тригонометрические функции для нахождения углов, поскольку мы знаем длины сторон. См. изображение ниже, где показаны эти ракурсы.

Какова площадь треугольника 5 12 13?

Вычисляя площадь треугольника 5 12 13, получаем A = ( ¹ ⁄ ₂ )(5)(12) = 30 . Если треугольник соответствует соотношению 5 12 13, но масштабирован, то есть треугольник 2,5 6 6,5, мы по-прежнему используем две более короткие стороны в качестве основания и высоты. В этом случае площадь будет равна ( ¹ ⁄ ₂ )(2,5)(6) = 7,5.