Разбор задания для подготовки к ЕГЭ по математике: базовый уровень
Базовая математика — обязательный предмет ЕГЭ, который ежегодно сдают все российские школьники. Для того, чтобы получить школьный аттестат, вполне достаточно минимального балла по базовой математике, а вот для поступления в вуз может потребоваться экзамен по профильной математике. Минимальный балл, который необходимо набрать для получения аттестата — 23. Чтобы поступить в вуз, понадобится не менее 27 баллов. Рассмотрим демовариант ЕГЭ по математике 2019 и разберем некоторые из этих заданий.
Задание №1
Это задание основано на проверке простейших математических навыков: сложение, вычитание, деление, умножение, а также действия десятичными дробями и перевод одних единиц измерения в другие.
Пример задачи
В 23.50 минут по московскому времени из Санкт-Петербурга в Москву выехал поезд. В Москву он приехал на следующие сутки в 7 часов 50 минут. Необходимо вычислить, какое количество времени поезд был в пути.
Решение
Зная о том, что в сутках всего 24 часа, и их начало приходится на 00:00, а конец — на 24 часа, вычисляем: в первые сутки поезд находился в пути десять минут, во вторые — 7 часов и 50 минут.
7 ч. 50 мин. + 0 ч. 10 мин. = 7 ч. 60 мин. или 8 часов
Задание №2
Задание проверяет, насколько хорошо выпускники умеют интерпретировать различные таблицы, графики и диаграммы, а также совершать с их помощью простейшие вычисления. Как правило, речь идет об анализе графика функции и поиске наибольших и наименьших значений.
Пример задачи
В задаче представлен график, отображающий среднюю температуру Сочи за каждый месяц 1920 года. Необходимо определить, сколько месяцев в году температура была выше 18 градусов Цельсия.
Решение
Для того, чтобы найти правильное решение, необходимо провести горизонтальную линию от точки с цифрой 18 (указана температура в градусах Цельсия). Таким образом станет очевидно, что такая температура держалась 4 месяца подряд: в июне, июле, августе и сентябре.
Задание №3
Школьники должны продемонстрировать знание основ планиметрии, а именно: уметь вычислять площадь фигур, рассчитывать градусные меры углов, диаметры и находить другие значения. Например, найти площадь треугольника, начерченного на бумаге с размером клеток 1х1. В этом задании важно продемонстрировать знание формул и умение пользоваться различными способами решения задачи.
Задание №4
Задача из курса “Теория вероятностей и статистика”. Выпускникам предлагается высчитать вероятность того или иного события, произошедшего в повседневной ситуации.
Пример задачи
Ученикам предложено выучить 25 билетов по биологии. Лишь два из них содержат вопрос о грибах. Каждому школьнику предстоит ответить лишь на один билет. Вычислите вероятность того, что вопрос о грибах будет содержаться именно в этом билете.
Решение
Вероятность события можно рассчитать по формуле Р(А) = m/n, где m — количество благоприятных исходов, а n — общее их количество.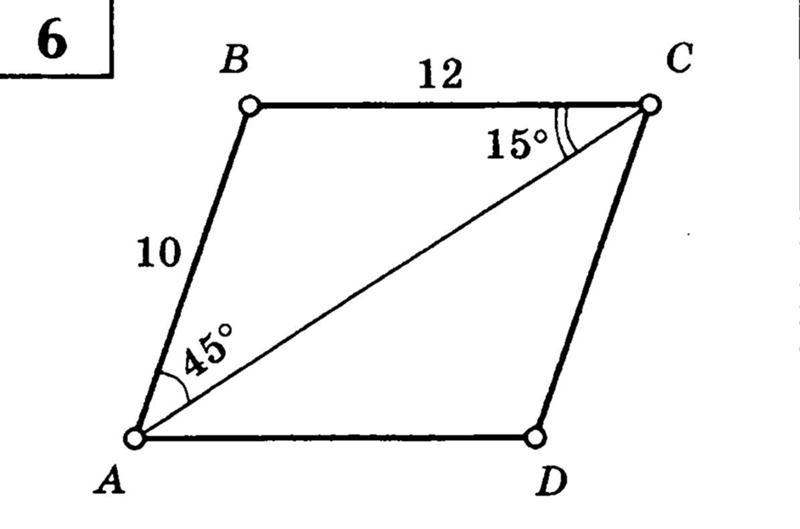 25 билетов означают 25 исходов, 2 из которых — благоприятные. Значит, вероятность равна 2/25, то есть 0,08.
25 билетов означают 25 исходов, 2 из которых — благоприятные. Значит, вероятность равна 2/25, то есть 0,08.
Задача №5
Здесь проверяется умение решать уравнения, находить неизвестные, извлекать корни и т. д.
Пример задачи
Найти корень уравнения 3x-5 = 81
Решение
3х-5 = 34
х-5 = 4
х = 9
Задание №6
Здесь необходимо продемонстрировать умение моделировать различные ситуации при помощи геометрических понятий. Важно знание теорем, умение определять длину, градус угла и другие величины.
Пример задачи
Треугольник с углами А, B и С вписан в окружность с центром О. Угол BAC — 32 градуса. необходимо найти угол BOC.
Решение
COB — центральный угол, равный дуге CB
САВ — вписанный угол, равный ½ дуги СВ
Значит, САВ = ½ СОВ. Так как ½ угла СОВ равна 32 градусам, то угол СОВ равен 64о
Ответ: 64о
Задача №7
Выпускник должен продемонстрировать знание понятия “функция” и умение выполнять с ним различные действия: руководствуясь графиком, описывать свойства и поведение функции; находить наибольшие и наименьшие значения; самостоятельно строить графики.
Пример задачи
На графике дифференцируемой функции y = f(x) на оси абсцисс отмечены девять точек. Необходимо найти все точки, в которых производная функции f(х) отрицательна.
Решение
Необходимо проследить, в каких местах графика убывает функция: именно там ее производная будет отрицательна. Всего на этом графике 4 таких точки.
Задача №8
Задачи на знание основ стереометрии, простейших геометрических понятий и умение использовать при решении стереометрических задач планиметрические методы.
Пример задачи
В условии даны два цилиндрических сосуда. Уровень жидкости в первом достигает 16 сантиметров. Всю жидкость перелили во второй сосуд, диаметр которого дважды превышает диаметр основания первого. Необходимо определить уровень жидкости во втором сосуде.
Решение
Для вычисления объема цилиндра следует воспользоваться этой формулой: V = πR2H, где R — это радиус цилиндра, а Н — его высота. Так как уровень жидкости поднимается до 16 см, значит, высота также равна 16.
V = πR2H = πR216
Зная о том, что диаметр второго сосуда в два раза больше первого, мы можем сделать вывод, что радиус второго сосуда в два раза больше первого (2R). Вычисляем объем жидкости во втором сосуде: V = π(2R)2h или V = 4R2h
При переливании жидкости из одного сосуда в другой ее объем не изменился.
πR216 = π4R2h
4h = 16
Задача №9
В этом разборе задания очень важно уметь выполнять простейшие вычисления и преобразования, поэтому знание формул просто необходимо.
Пример задачи
Необходимо найти sin2α, если учесть, что cosα = 6, а π
Решение
sin2α = 2sinα х cosα
(sinα)2 + (cosα)2 = 1
(sinα)2 + (0,6)2 = 1
(sinα)2 = 1 — 0,36
(sinα)2 = ±0,8
sinα = –0,8
sin2α = 2 х (–0,8) х (0,6)
sin2α = –0,96
Задача №10
Здесь выпускники демонстрируют умение решать прикладные задачи социально-экономической и физической направленности. Необходимо знать и уметь пользоваться формулами, быть точным в расчетах и внимательным при записи ответа.
Пример задачи
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий̆ первым, окажется из России.
Решение
Вероятность определяется, как количество положительных вариантов к количеству всех вариантов. Например, у вас есть 10 монеток и только 2 из них — десятирублёвые, то если вы возьмёте одну монетку, вероятность того, что она будет десятирублёвой, составит
В нашей задаче 35 спортсменов, из которых 7 — из России.
Значит, вероятность того, что первый спортсмен будет из России, составляет:
Ответ: 0.2.
Задача №11
Текстовые задачи с чуть более сложными условиями нужны для того, чтобы экзаменуемый продемонстрировал не только свои знания, но также аналитические способности и умение мыслить логически.
Пример задачи
На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.
По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.
Решение
Из графика видно, что наименьшей цена была 6 марта.
Ответ: 6.
Задача №12
12 задача из демоверсии ЕГЭ по математике базового уровня посвящена теме “экстремум”. Здесь необходимо найти производную функции и ее критические точки.
Пример задачи
Турист подбирает себе экскурсионную программу. Сведения о некоторых музеях и парках, подготовленные туристическим бюро, представлены в таблице.
Пользуясь таблицей, подберите экскурсионную программу так, чтобы турист посетил не ме-нее трёх достопримечательностей за один день.
В ответе для подобранной программы укажите номера экскурсий без пробелов, запятых и других дополнительных символов.
Решение
У туриста всего 10 часов.
При выборе четвертой успевает только на вторую. Таким образом, 4 и 2. При выборе третьей посмотреть три достопримечательности никак не успеет.
Ответ: 1 и 5 или 2 и 4.
Задача №13
Задания из этого раздела демо-варианта ЕГЭ проверяют знание стереометрии. Необходимо знать формулы нахождения площадей разных фигур: прямоугольного параллелепипеда, призмы, пирамиды, куба, цилиндра и т. д.
Пример задачи
В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 4. Найдите длину отрезка OS.
Решение
Отрезок OS высотой треугольной пирамиды SABC, ее объем выражается формулой
Значит,
Ответ: 6.
Задача №14
Для решения этого задания стоит повторить свойства функций. Необходимо знать, что такое область определения и область значений, экстремальные значения, убывание и возрастание.
Необходимо знать, что такое область определения и область значений, экстремальные значения, убывание и возрастание.
Пример задачи
На диаграмме показано количество запросов со словом СНЕГ, сделанных на поисковом сайте Yandex.ru во все месяцы с марта 2008 по октябрь 2009 года. По горизонтали указываются месяцы, по вертикали — количество запросов за данный месяц.
Пользуясь диаграммой, установите связь между промежутками времени и характером изме-нения количества запросов.
ПРОМЕЖУТКИ ВРЕМЕНИ | ХАРАКТЕР ИЗМЕНЕНИЯ КОЛИЧЕСТВА ЗАПРОСОВ |
А) Весна 2008 года | 1) Количество запросов резко снижалось |
Б) Лето 2008 года | 2) Количество запросов заметно увеличивалось |
В) Осень 2008 года | 3) Количество запросов практически не менялось |
Г) Зима 2008-2009 года | 4) Количество запросов плавно снижалось |
Решение
Весной 2008 года количество запросов падало примерно со 120 000 до 100 000.
Летом 2008 года количество запросов изменялось примерно с 82 000 до 80 000.
Осенью 2008 года количество запросов возрастало примерно со 115 000 до 283 000.
Зимой 2008 года количество запросов падало с 500 000 до 280 000.
Таким образом, получаем следующее: A — 4, Б — 3, В — 2, Г — 1.
Ответ: 4321.
Задача №15
Еще одна задача по планиметрии, для решения которой необходимо повторить формулы нахождения площади фигур на плоскости. и основные теоремы.
Пример задачи
В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, AD=8. Найдите синус угла B.
Решение
Ответ: 0,5.
Задача №16
Задача на знание стереометрии. Для ее решения необходимо разбираться в типах пространственных фигур, знать их элементы, а также основные формулы: объем, площадь поверхности и т. д.
Пример задачи
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Ответ дайте в градусах.
Решение
Площадь основания конуса равна Sосн = πr2, а площадь боковой поверхности Sбок = πrl. Из условия имеем:
Значит, в прямоугольном треугольнике, образованном высотой, образующей и ра-диусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Значит, угол между образующей конуса и плоскостью осно-вания равен 60°.
Задача №17
Решение простейших неравенств. В этом задании необходимо составить математическую модель и прописать, что является здесь переменной x, p и переменной z. Даже если само уравнение решить не получится, за правильно составленную задачу вы сможете получить один балл.
Пример задачи
На координатной прямой отмечены точки A, B, C, и D.
Число m равно log54.
Каждой точке соответствует одно из чисел в правом столбце. Установите соответ-ствие между указанными точками и числами.
ТОЧКИ ЧИСЛА
А) A
Б) B
В) C
Г) D
В таблице под каждой буквой укажите соответствующий номер.
Решение
Ответ: 2431.
Задача №18
Выпускникам предлагается решить задачу с параметром, в которой необходимо будет проявить аналитические способности и владение логикой.
Пример задачи
Когда какая-нибудь кошка идёт по забору, пёс Шарик, живущий в будке возле дома, обязательно лает. Выберите утверждения, которые верны при приведённом условии.
1) Если Шарик не лает, значит, по забору идёт кошка.
3) Если по забору идёт чёрная кошка, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение
Согласно условию, если кошка идёт по забору, то Шарик лает. Рассмотрим предложенные утверждения:
- Если Шарик не лает, значит, по забору идёт кошка — неверно, так как, если кошка идёт, то Шарик обязательно лает.
- Если Шарик молчит, значит, кошка по забору не идёт — верно, так как, если молчит — значит, никакая кошка не идет.

- Если по забору идёт чёрная кошка, Шарик не лает — неверно, так как, если любая кошка идет по забору — Шарик лает.
- Если по забору пойдет белая кошка, Шарик будет лаять — верно, согласно условию.
Задача №19
Чтобы решить задание под номером 19 по математике базового уровня, необходимо владеть следующими понятиями: числа и их свойства, числовые последовательности и прогрессии, признаки делимости чисел. В самом задании выпускникам для разбора будет предложена задача.
Пример задачи
Найдите трёхзначное число, сумма цифр которого равна 25, если известно, что его квадрат делится на 16.
Решение
Разложим число 25 на слагаемые: 25 = 9 + 9 + 7 = 9 + 8 + 8.
Квадрат числа делится на 16, значит, само число делится на 4. Это значит, что оно заканчивается на чётную цифру. То есть первый набор отпадает, так как в нём нет четных чисел. Из второго мы можем составить числа 988 и 898. Первое число походит по условия задачи.
Ответ: 988.
Задача №20
Одно из самых интересных заданий заставляет задействовать не только логику, но и смекалку: правильный ответ необходимо найти при помощи рассуждений и внимательного отношения к каждой детали.
Пример задачи
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Решение
Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14 + 4 + 6 = 24 линии, следовательно, кусков будет 25.
Ответ: 25.
Таким образом видим, что разбор заданий для подготовки к ЕГЭ не представляет особых трудностей: при желании к экзамену можно как следует подготовиться и сдать его на максимально высокие баллы.
Как найти площадь параллелограмма? Ответ на webmath.ru
Содержание:
- Формулы
- Примеры вычисления площади параллелограмма
Формулы
Первый способ. Чтобы найти площадь параллелограмма (рис. 1), нужно найти произведение стороны $a$ параллелограмма на высоту $h_a$, проведенную к этой стороне, то есть
$$S=ah_{a}$$
Второй способ. Чтобы найти площадь параллелограмма, надо найти произведение двух его смежных сторон $a$ и $b$, умноженное на синус угла $\alpha$ между ними (рис. 2):
$$\mathrm{S}=a b \sin \alpha$$
Третий способ. Чтобы найти площадь параллелограмма, надо найти полупроизведение его диагоналей $d_1$ и $d_2$ на синус угла $\beta$ между ними (рис. 3):
$$\mathrm{S}=\frac{1}{2} d_{1} d_{2} \sin \beta$$
Примеры вычисления площади параллелограмма
Пример
Задание. Найти площадь параллелограмма, если его сторона равна 2 см, а высота, проведенная к этой стороне — 3 см. {\circ}=28 \cdot \frac{\sqrt{3}}{2}=14 \sqrt{3}$ (см2)
{\circ}=28 \cdot \frac{\sqrt{3}}{2}=14 \sqrt{3}$ (см2)
Ответ. $\mathrm{S}=14 \sqrt{3}$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно доказать утверждение о том, что площадь параллелограмма есть число, получаемое в результате умножения длин двух его сторон, являющихся смежными, и синуса угла, который образуется между ними?
Параллелограмм следует расположить по горизонтали. Обозначим его верхнее основание как АВ, а противоположное ему основание – как CD. Из точек ВЕ и AF проведем перпендикулярные прямые на нижнее основание фигуры. В результате получится прямоугольник ABEF. Площадь образовавшейся прямоугольной фигуры равна площади параллелограмма по той причине, что параллелограмм ABCD и фигура с прямыми углами ABEF являются равносоставленными, о чем свидетельствует равенство треугольников ВEC и DAF.
Площадь (S) прямоугольника представляет собой произведение длин сторон EF и FA, которое, в свою очередь, равно:
CD*AD*sin(CDA)
Именно это и требовалось доказать.
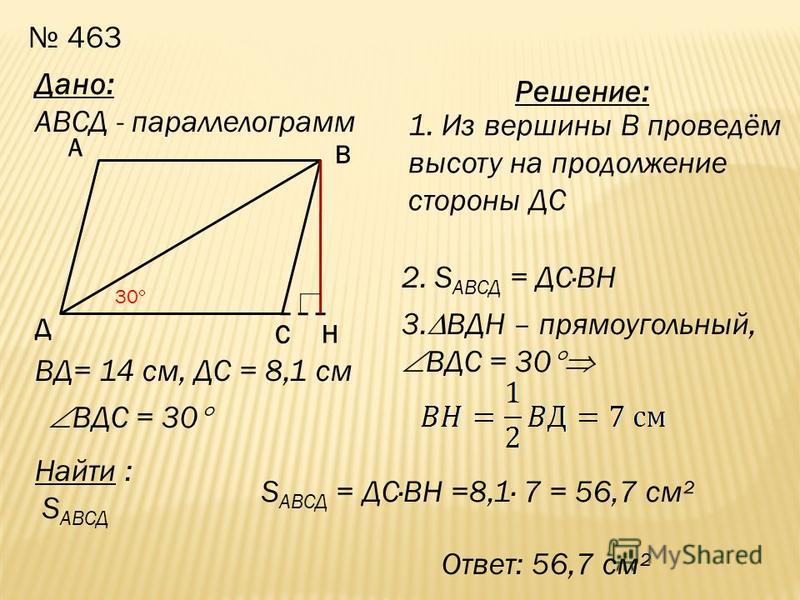
Параллелограмм имеет смежные стороны длиной 26 см и 32 см. Один из углов данной фигуры равен 150 градусам. Каким способом можно вычислить площадь параллелограмма?
Обозначим имеющийся параллелограмм как АВСD. Тогда одна его сторона АВ равна 26 см, а другая АD – 32 см. Угол АВС параллелограмма составляет 150 градусов.
Принимая во внимание тот факт, что сумма внутренних односторонних углов параллелограмма равна 180 градусов, можно говорить о том, что его угол ВАD составляет 30 градусов. Проведем высоту ВК, и в итоге получим треугольник АВК с прямым углом. Длина опущенной высоты как катета, расположенного противоположно углу в 30 градусов, равна 13 см. Площадь (S) параллелограмма есть число, полученное в результате умножения длины высоты на длину стороны. Это значит, что:
S (АВСD) = 13 *32 = 416 см кв.
Ответ: Площадь параллелограмма равна 416 см кв.
Прямая АС проведена через середины двух сторон параллелограмма, которые
являются смежными.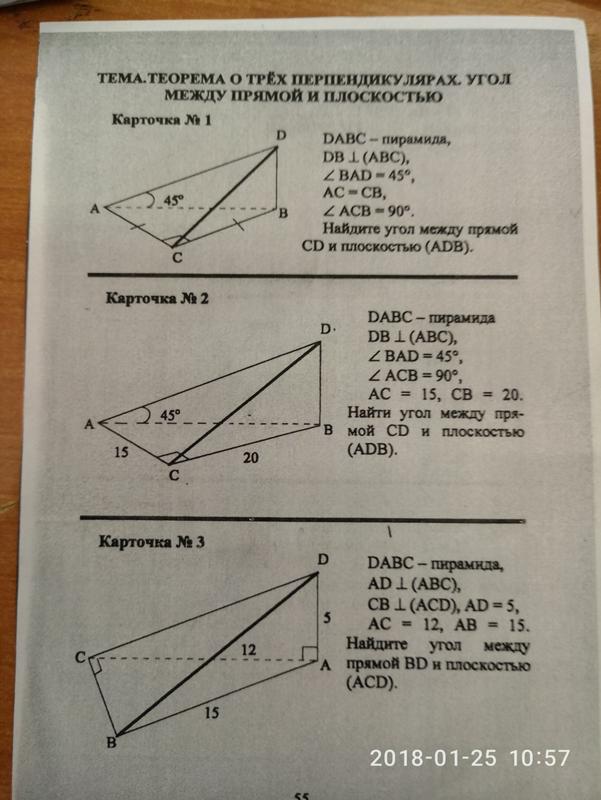 Данная прямая отсекает от параллелограмма два
треугольника – FMD и АDС. Площадь одного из отсеченных треугольников
составляет 32 см кв. Как высчитать площадь параллелограмма?
Данная прямая отсекает от параллелограмма два
треугольника – FMD и АDС. Площадь одного из отсеченных треугольников
составляет 32 см кв. Как высчитать площадь параллелограмма?
Прямая АС представляет собой диагональ биссектрисы. В этом случае образовавшиеся посредством ее проведения треугольники FMD и АDС являются подобными по причине наличия общего угла А и равенства сторон. На основании этого можно говорить о том, что:
SADC=1/2*ab*sin a
SFDM=1/2 *2a*2b sin a
SADC / SFDM= 32/x
1/4=32/x
x=128
Теперь можно рассчитать площадь параллелограмма (S), которая будет равна 2*х:
S = 128*2 = 256 см кв.
Ответ: Площадь параллелограмма равна 256 см кв.
Параллелограмм имеет стороны, длины которых составляют 10 см и 6 см. Данные стороны образуют угол, равный 150 градусам. Как рассчитать площадь параллелограмма в этом случае?
Обозначим угол в 150 градусов буквой В. Зная о том, что внутренние
односторонние углы параллелограмма в сумме дают 180 градусов, можно
вычислить второй угол А. Он будет равен:
Он будет равен:
∠А = 180-150 = 30 градусов.
Теперь следует провести высоту ВВ1, которая образует треугольник АВВ1, являющийся прямоугольным. Длина ВВ1 будет равна половине длины стороны, равной 6 см:
ВВ1 = 6/2 = 3 см.
Тогда площадь (S) параллелограмма можно рассчитать, умножив длину ВВ1 на 10 см (длина смежной стороны):
S = 3*10 = 30 см кв.
Ответ: Площадь параллелограмма равна 30 см кв.
Проведенные диагонали делят параллелограмм на четыре треугольных фигуры. Площадь одной из них равна 7 м кв. Каким образом можно найти площадь параллелограмма?
Обозначим имеющийся параллелограмм как ABCD. Точкой пересечения его
диагоналей является точка О. Образованные диагоналями треугольные фигуры
ABO, BCO, CDO, DAO являются одинаковыми по площади. Об этом
свидетельствует тот факт, что диагонали параллелограмма делятся ровно
пополам в точке их пересечения. Свидетельством того, что все четыре
треугольника имеют одинаковые площади, выступает равенство синусов смежных
углов.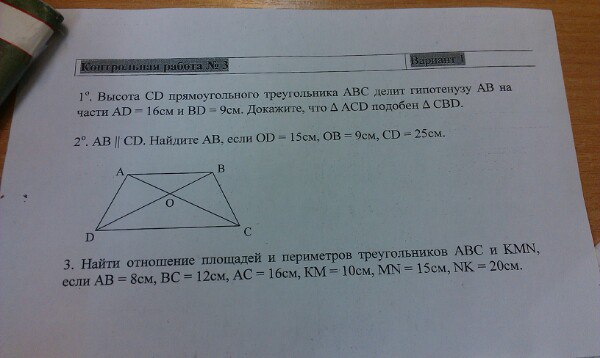 Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Если площади всех четырех треугольных фигур равны, то площадь самого параллелограмма будет в четыре раза превышать площадь любого из них. Это значит, что площадь (S) параллелограмма может быть вычислена следующим образом:
S = 4*7 = 28 м кв.
Ответ: Площадь параллелограмма равна 28 м кв.
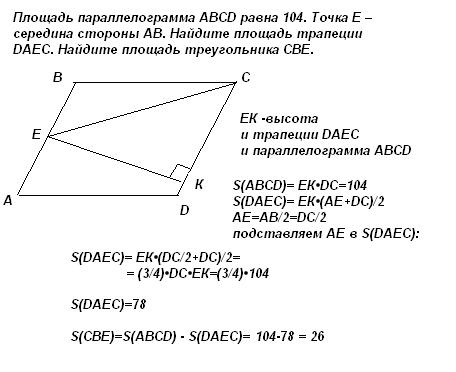
Дан параллелограмм ABCD, на одной из сторон которого АВ поставлена точка М. Известно, что площадь треугольника MCD составляет 38 см кв. Как найти площадь параллелограмма?
Площадь (S) параллелограмма рассчитывается путем умножения длины его основания на длину его высоты.
Прямые МС и МD, проведенные из точки М, делят параллелограмм на треугольники. Площадь первого из них вычисляется как:
S₁ = 1/2 * a * h = 38 см кв.
Формула для расчета площади второго треугольника выглядит так:
S₂ = 1/2 * a₁* h
Площадь третьего треугольника можно найти следующим образом:
S₃ = 1/2 *a₃* h,
где а =а₁ + а₂
Теперь через площади образованных треугольников можно вычислить площадь параллелограмма:
S = S₁ + S₂ + S₃ = 1/2 *(a * h +a₁ * h +a₂ * h) = 1/2 * (a * h + h(a₁ + a₂)) = 1/2 * (a * h + a * h) = 2 * 38 = 76 см. кв.
Ответ: Площадь параллелограмма равна 76 см кв.
Длина основания параллелограмма составляет 5 см, а его высота равна 3 см. Как найти площадь параллелограмма?
Формула расчета площади параллелограмма (S) включает длину его высоты и длину его основания. Данные элементы нужно перемножить, для того чтобы вычислить площадь фигуры:
S = a*h= 5*6=30 см кв.
Ответ: Параллелограмм имеет площадь 30 см кв.
Имеется параллелограмм ABCD. Посередине его стороны АВ поставлена точка Е,
из которой проведена прямая, образующая треугольник CDE площадью 36 см кв.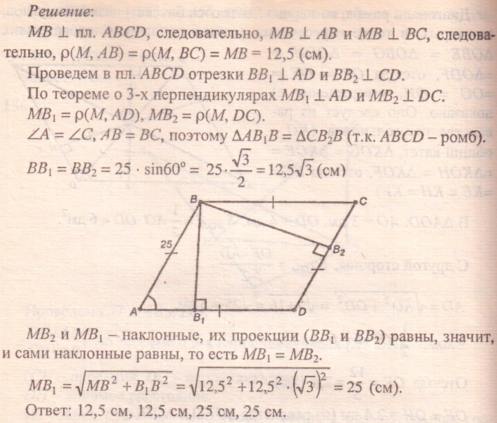 Каким образом можно найти площадь параллелограмма?
Каким образом можно найти площадь параллелограмма?
На продолжение стороны CD опустим перпендикуляр ЕН из точки Е. Он представляет собой высоту для параллелограмма ABCD и треугольника CDE.
Известно, что площадь (S) параллелограмма является произведением длины его стороны и высоты, которая на нее опущена. Площадь треугольника представляет собой ½ от числа, которое получилось в результате умножения длины стороны на высоту, опущенную на нее. На основании этого можно сделать вывод о том, что:
S(ABCD) = EH*CD
S(∆CDE) = ½*EH*CD => 2*S(∆CDE) = EH*CD.
Из этого следует, что:
2*S(∆CDE) = S(ABCD) = 2*36 ед² = 72 ед. кв.
Ответ: Площадь параллелограмма составляет 72 кв. ед.
В каком виде представлена формула, которая предназначена для вычисления площади параллелограмма?
Для получения возможности рассчитать, чему равна площадь (S)
параллелограмма, нужно располагать сведениями о длине его основания (а) и
высоты (h).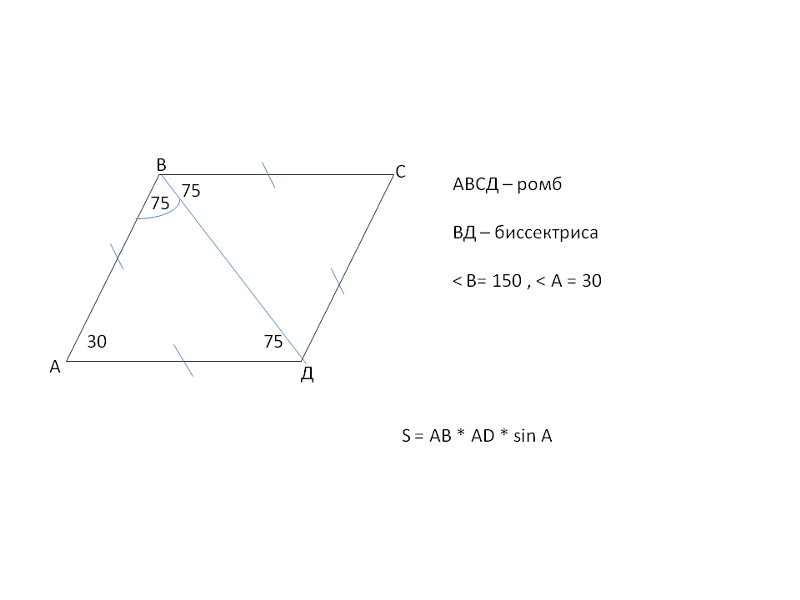 В этом случае площадь можно высчитать при помощи следующей
формулы:
В этом случае площадь можно высчитать при помощи следующей
формулы:
S = а* h.
Как найти площадь параллелограмма через синус, если известно, что длины его сторон равны 8 см и 10 см, а синус одного из его углов составляет 0,05?
Формула, которая предназначена для вычисления площади параллелограмма (S) через синус, выглядит следующим образом:
S = a × b × sin A
В данной формуле буквами a и b обозначены стороны параллелограмма, являющиеся смежными, а А означает угол, который образован между этими сторонами.
Доказано, что синусы смежных углов являются равными. Это значит, что синус тупого угла равен синусу острого угла.
Площадь параллелограмма вычисляем следующим образом:
S = 8 × 10 × 0,05 = 4 см кв.
Ответ: Параллелограмм имеет площадь, равную 4 см кв.
Имеется параллелограмм ABCD, в котором опущена высота на его сторону АВ. Ее
длина равна 12 см. При этом длина AD составляет 24 см. Каким образом можно
высчитать значение синуса угла А?
Каким образом можно
высчитать значение синуса угла А?
Высота, опущенная на сторону АВ параллелограмма, обозначена как СК. Полученный в результате треугольник КВС имеет прямой угол.
Sin B=АВ/ВС.
В этом случае ВС=AD=24 см. Так, синус угла В равен:
sinВ=12/24=1/2, что соответствует углу 30 градусов.
В параллелограмме проведены диагонали, длины которых равны 5 см и 28 см. Между ними образован угол, составляющий 30 градусов. Как можно найти площадь параллелограмма через синус в данном случае?
Площадь любой из четырехугольных фигур может быть вычислена, если известны длины ее диагоналей и синус угла, образованного между ними. Для этого нужно произвести умножение упомянутых величин, а затем разделить полученное число на 2. В случае с параллелограммом, обозначенным как ABCD, площадь рассчитывается по этой же формуле:
S = 1/2 AC*BD*sin∠AOB = ½*28*5*sin30° = 14*5*1/2 = 7*5 = 35 кв. см.
Ответ: Площадь параллелограмма равна 35 см кв.
Представляется ли возможным высчитать площадь параллелограмма при условии, что длины двух его диагоналей и образованный в месте их пересечения угол являются известными величинами?
Площадь параллелограмма (S) представляет собой половину числа, полученного после умножения друг на друга длин проведенных в нем диагоналей, которое умножено на синус образовавшегося в итоге их пересечения угла:
S = ½*d 1*d 2*sin α
Возможно ли рассчитать площадь параллелограмма по диагоналям, длины которых равны 6 см и 4 см? При этом известно, что образованный ими угол является прямым.
Для определения площади параллелограмма через известные длины проведенных в нем диагоналей применяется приведенная ниже формула:
S = ½*d 1*d 2*sin α,
где диагонали фигуры обозначены как d 1 и d 2, а синус образованного в результате их пересечения угла — sin α.
Подставим в указанное равенство величины, приведенные в задании:
S = 1/2 * 4 см * 6 см * sin 90° = 12 см кв.
Ответ: Площадь параллелограмма, вычисленная через диагонали, равна 12 см кв.
На одной из сторон параллелограмма ABCD, обозначенной как ВС, отмечена точка М. Чему будет равна площадь параллелограмма при условии, что площадь треугольника МАD составляет 21 см кв.?
Под площадью параллелограмма (S) понимается величина, полученная в результате умножения длины его стороны (b) на высоту (h), которая опущена к ней. В виде формулы это выглядит следующим образом:
S =b*h
Площадь треугольной фигуры представляет собой ½ числа, полученного произведением длины стороны на высоту, которая к ней проведена:
S=1/2*b*h,
Отсюда получаем, что:
b*h=2Sт=2*21=42 см кв.
Если говорить о треугольнике МАD, то в нем сторона АD представлена в
качестве стороны b, как и в случае с параллелограммом. Высота указанного
треугольника будет также представлять собой высоту параллелограмма. Это
обусловлено тем, что точка М расположена на стороне, которая
противоположна стороне ВС.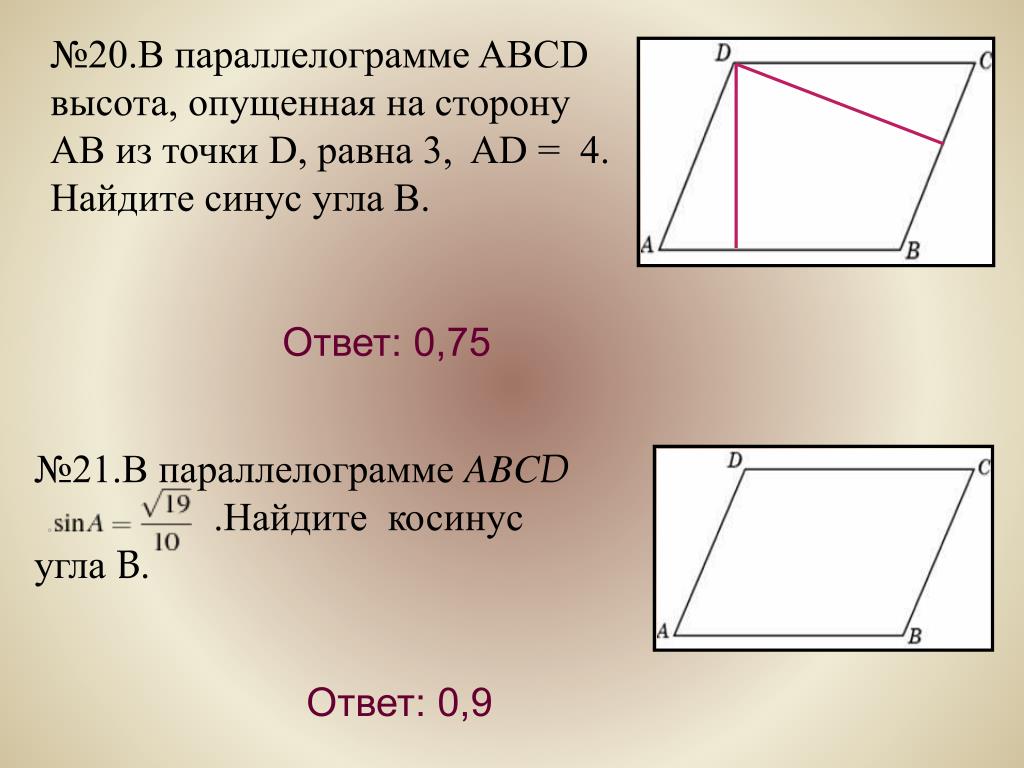 Из этого следует, что площадь параллелограмма
равна 42 см кв.
Из этого следует, что площадь параллелограмма
равна 42 см кв.
Ответ: Площадь параллелограмма равна 42 см кв.
Параллелограмм ABCD имеет стороны длиной 10 см и 14 см, а также острый угол в 60 градусов. Каким образом можно вычислить площадь параллелограмма?
В параллелограмме ABCD нужно провести высоту ВН на сторону AD. После этого получается треугольник АВН с углом в 90 градусов. Можно рассчитать, чему равен еще один угол данного треугольника:
АВН = 90-60 = 30
ВН = АВ*sin60 = 10*корень3/2 = 5*корень3
Таким образом, можно узнать, чему будет равна площадь параллелограмма:
S = AD*ВН = 14*5*√3 = 70*√3 см кв.
Ответ: Площадь параллелограмма составляет 70*√3 см кв.
Дан параллелограмм, через середины пары смежных сторон которого проведена прямая. Она отсекает треугольную фигуру площадью 32 см кв. Чему в данном случае равна площадь параллелограмма?
АС представляет собой диагональ биссектрисы.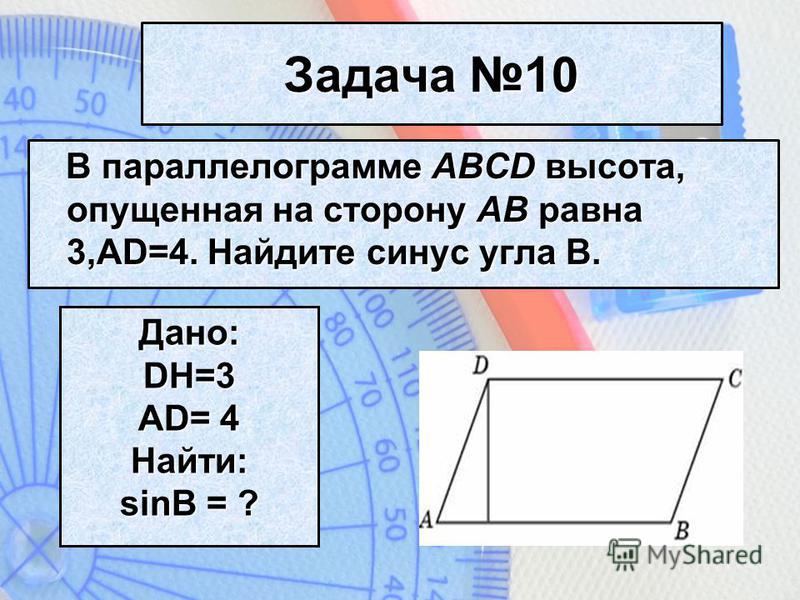 В этом случае оба
треугольника FMD и ADC являются подобными по той причине, что они имеют
общий угол А и их стороны равны. Из этого следует, что:
В этом случае оба
треугольника FMD и ADC являются подобными по той причине, что они имеют
общий угол А и их стороны равны. Из этого следует, что:
S ADC = 1/2*ab*sina
S FDM=1/2 *2a*2bsina
Отношение площадей двух треугольников выглядит как:
S ADC / S FDM= 32/x
1/4=32/x
x=128
Теперь можно высчитать площадь параллелограмма:
S = 128*2 = 256 см кв.
Читать дальше: как найти площадь трапеции.
Математическая задача: Параллелограмм ABCD — вопрос № 48263, алгебра
Имеем параллелограмм ABCD, где AB равно 6,2 см
BC равно 5,4 см
AC равно 4,8 см
вычислить высоту на стороне AB и угол DAB
Правильный ответ:
v = 4,0307 смA = 36,7385 °
Пошаговое объяснение:
a=6,2 см b=5,4 см u=4,8 см s=2a+b+u= 26,2+ 5,4+4,8=541=8,2 см S1=s⋅(s−a)⋅(s−b)⋅(s−u)
=8,2⋅(8,2−6,2)⋅(8,2−5,4)⋅ (8,2−4,8)
≐12,4951 см2 S=2⋅S1=2⋅12,4951≐24,9902см2S=a⋅vv=S/a=24,9902/6,2=4,0307 см
tanA=v: б=4,0307:5,4≐0,7464= 52010:69679 α=arctan(v/b)=arctan(4,0307/5,4)≐0,6412 рад A=α→ °=α⋅ π180 °=0,6412⋅ π180 °=36,739 °=36,7385∘=36°44 ′19 »
Нашли ошибку или неточность? Смело
пишите нам . Спасибо!0034 Для решения этой словесной математической задачи необходимо знать следующие знания:
Спасибо!0034 Для решения этой словесной математической задачи необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- планиметрия
- площадь фигуры
- треугольник
- Формула Герона
- параллелограмм
- четырехугольник
- гониометрия и тригонометрия
- синус
- косинус
- тангенс
Единицы физические количества:
- угол
Уровень задачи:
- практика для 13-летних
- практика для 14-летних
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2
- Параллелограмм 65954
В параллелограмме ABCD AB = 8, BC = 5, BD = 7. Вычислить модуль угла α = ∠DAB (в градусах). - Параллелограмм 72044
Сборочный параллелограмм ABCD: AB = 4,8 см, va = 3 см, BC = 4 см. Рассчитать цепь. Сделайте набросок.
Рассчитать цепь. Сделайте набросок. - Трапециевидная призма
Рассчитайте поверхность четырехугольной призмы ABCDA’B’C’D’ с трапециевидным основанием ABCD. Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см. L - Четырехугольник
Четырехугольник ABCD состоит из двух прямоугольных треугольников, ABD и BCD. Для длины сторон: |AD| = 3см, | Британская Колумбия | = 12см, | БД | = 5см. Сколько квадратных сантиметров (площади) имеет четырехугольник ABCD? Углы DAB и DBC прямые. - Прямоугольная трапеция
Прямоугольная трапеция ABCD: /AB/ = /BC/ = /AC/. Длина медианы 6 см. Вычислите длину окружности и площадь трапеции. - Длина окружности 3088
В параллелограмме ABCD сторона AB в три раза длиннее стороны BC. Длина окружности параллелограмма 20 см. Найдите длины сторон параллелограмма. - ABCD
AC= 40 см, угол DAB=38, угол DCB=58, угол DBC=90, DB перпендикулярен AC, найти BD и AD - Окружность 18443
В параллелограмме ABCD сторона AB в три раза длиннее стороны BC. Длина окружности параллелограмма 20 см. Определить длины сторон параллелограмма.
Длина окружности параллелограмма 20 см. Определить длины сторон параллелограмма. - Трапеция RT
Участок имеет форму прямоугольной трапеции ABCD, где ABIICD с прямым углом при вершине B. Сторона AB имеет длину 36 м. Длины сторон АВ и ВС относятся как 12:7. Длины сторон AB и CD относятся как 3:2. Рассчитать минус - Квадраты над сторонами
Два квадрата построены на двух сторонах треугольника ABC. Площадь квадрата над стороной ВС равна 25 см². Высота vc до стороны AB равна 3 см. Пятка Р высотой vc делит сторону АВ в соотношении 2:1. Сторона AC длиннее стороны BC. Calc - Четырехугольник 3262
Постройте четырехугольник ABCD с размерами AB, BC, AC, BD и углом d = CDA. - Вычислить 2416
В прямоугольнике ABCD длина стороны AB = 16 см, а диагональ AC = 20 см. Вычислите его периметр и площадь. - Биссектриса 2
ABC — равнобедренный треугольник. Поскольку AB=AC, AX — биссектриса угла ∢BAC, пересекающего сторону BC в точке X. Докажите, что X — середина BC.
- Построение ромб
Построение параллелограмм (ромб) ABCD, | АБ | = 4 см альфа = 30° и | БД | = 5 см. - Диагонали трапеций
Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. - Треугольник в квадрате
В квадрате ABCD со стороной a = 6 см точка E — центр стороны AB, а точка F — центр стороны BC. Вычислить величину всех углов треугольника DEF и длины его сторон. - Построить 47633
Построить квадрат, площадь которого равна площади ромба ABCD ak / AB / = 5 см, / AD / = 4 см и углу | ДАБ | = 30 °
Диагональ формулы параллелограмма — GeeksforGeeks
Параллелограмм определяется как четырехугольник, который имеет равные пары противоположных сторон и углов. Одна из пар его противоположных сторон параллельна друг другу. Внутренние углы лежат на добавочных по своей природе, то есть их сумма равна 180 градусам. Диагонали параллелограмма делят друг друга пополам, то есть делят друг друга на две равные части. Сумма всех внутренних углов параллелограмма равна 360 градусов.
Диагонали параллелограмма делят друг друга пополам, то есть делят друг друга на две равные части. Сумма всех внутренних углов параллелограмма равна 360 градусов.
На приведенном выше рисунке изображен параллелограмм ABCD со сторонами AB, BC, CD и AD и диагоналями AC и BD. Здесь длины противоположных сторон AB и CD равны друг другу. Точно так же длины BC и AD одинаковы. Пары противоположных углов, то есть ∠A и ∠C и ∠B и ∠D, равны между собой.
Формула диагонали параллелограммаФормула длины диагонали параллелограмма равна величине равнодействующей любых двух смежных сторон.
x = √(a 2 + b 2 – 2ab cos A) = √(a 2 + b 2 + 2ab cos B) 9 0006
у = √(а 2 + b 2 + 2ab cos A) = √(a 2 + b 2 – 2ab cos B)
где
x и y длины диагоналей, 90 006
а и б длины смежных сторон,
A и B — углы, образованные между сторонами.
Длины диагоналей и сторон параллелограмма связаны друг с другом. Сумма квадратов диагоналей равна удвоенной сумме квадратов двух соседних сторон. 9где 22 x и y — длины диагоналей,
a и b — длины смежных сторон.
Примеры задачЗадача 1. Вычислить длину диагоналей параллелограмма с длинами сторон 5 м и 10 м, если один из внутренних углов равен 60°.
Решение:
У нас есть,
a = 5
b = 10
∠A = 60°
∠B = 120°
Нам нужно найти длины диагоналей x и y.
Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √(5 2 + 10 2 – 2 (5) (10) cos 60°)
= √75
= 8,66 м
y = √(a 2 + b 2 + 2ab cos A)
= √( 5 2 + 10 2 + 2 (5) (10) cos 60°)
= √175
= 13,22 м
Задача 2.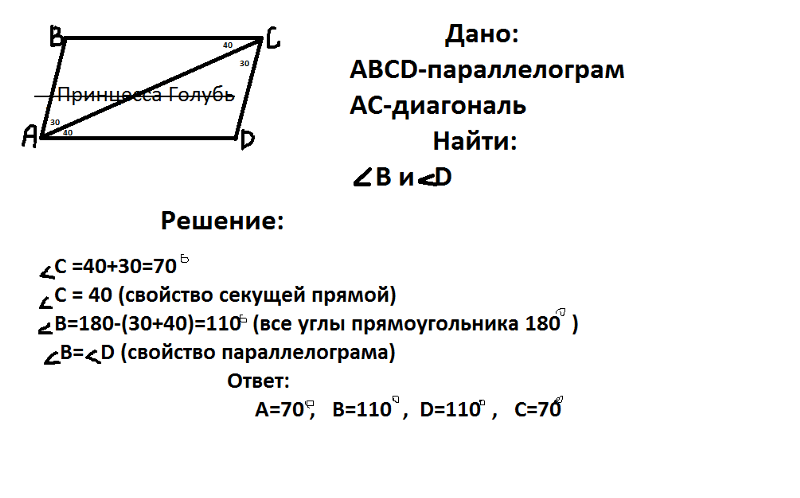 Вычислить длину диагоналей параллелограмма со сторонами 4 м и 7 м, если один из внутренних углов равен 30°.
Вычислить длину диагоналей параллелограмма со сторонами 4 м и 7 м, если один из внутренних углов равен 30°.
Решение:
Имеем,
a = 4
b = 7
∠A = 30°
Мы должны найти длины диагоналей x и y.
Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √(4 2 + 7 2 – 2 (4) (7) cos 30°)
= √16,48
= 4,06 м
y = √(а 2 + б 2 + 2ab cos A)
= √(4 2 + 7 2 + 2 (4) (7) cos 30°)
= √73,63
= 8,5 м 9 0006
Задача 3. Расчет длина одной из диагоналей параллелограмма со сторонами 5 м и 9 м, если один из внутренних углов равен 25°.
Решение:
Имеем,
a = 5
b = 9
∠A = 25°
Нам нужно найти длину диагонали.
Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √(5 2 + 9 2 9 0158 – 2 (5) (9) cos 25°)
= √24,40
= 4,06 м
Задача 4.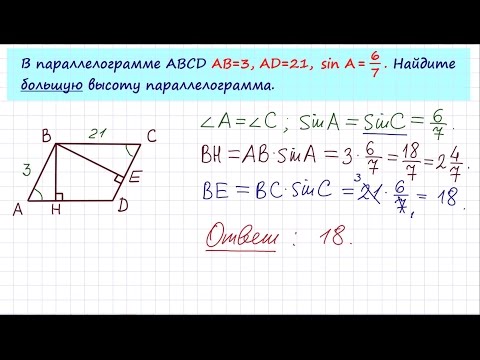 Вычислить длину одной из диагоналей параллелограмма со сторонами 12 м и 16 м, если один из внутренних углов равен 37° .
Вычислить длину одной из диагоналей параллелограмма со сторонами 12 м и 16 м, если один из внутренних углов равен 37° .
Решение:
Имеем,
a = 12
b = 16
∠A = 37°
Имеем найти длину диагонали.
Используя формулу получаем,
x = √(a 2 + b 2 – 2ab cos A)
= √(12 2 + 16 2 – 2 (12) (16) cos 37°)
= √93,315
= 9,66 м
Задача 5. Вычислить длину одной из диагоналей параллелограмма со сторонами 4 м и 6 м, если другая диагональ равна 8 м.
Решение:
Имеем,
a = 4
b = 6
x = 8
Используя формулу получаем, 900 06
х 2 + у 2 = 2( а 2 + b 2 )
=> 8 2 + у 2 = 2 (4 2 + 6 2 ) 900 06
=> 64 + у 2 = 2 (16 + 36)
=> 64 + у 2 = 104
=> у 2 = 40
=> y = 6,32 м
Задача 6.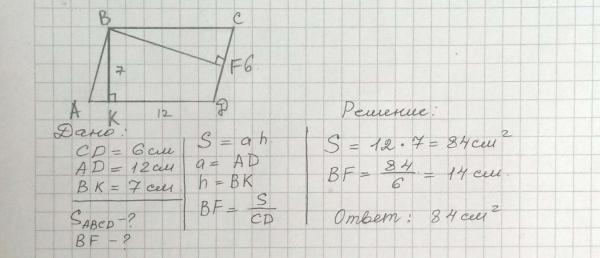


 Рассчитать цепь. Сделайте набросок.
Рассчитать цепь. Сделайте набросок. Длина окружности параллелограмма 20 см. Определить длины сторон параллелограмма.
Длина окружности параллелограмма 20 см. Определить длины сторон параллелограмма.
Leave A Comment