В параллелограмме abcd точка p середина отрезка cd: В параллелограмме ABCD точка P-середина отрезка CD, M- середина стороны BC, отрезки BD и…

Координаты середины отрезка — как найти? Формулы и примеры

Что такое отрезок

Чтобы изучить эту тему досконально, давайте начнем с самого простого: с определения отрезка.

Отрезок — это прямая, у которой есть начало и конец, или же прямая, которая соединяет две произвольные точки, не совпадающие друг с другом.

Отрезок называют заглавными буквами латинского алфавита по названию конечных точек. Причем можно расставлять буквы в любом порядке: АВ и ВА — равноценные варианты. Рассмотрите иллюстрацию, посчитайте и назовите все отрезки.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Что такое середина отрезка

Середина отрезка — это точка, которая находится на равном расстоянии от его концов. Иначе можно сказать так: это точка, которая делит отрезок пополам.

Так, на рисунке ниже D — середина отрезка СК, так как СD = DK. Обратите внимание, как на чертеже обозначаются равные по длине отрезки — мы ставим на них равное количество черточек.

Главный вопрос, который нас сегодня интересует, это координаты середины отрезка.

Координаты — это положение точки в пространстве.

Мы можем рассмотреть отрезок, который лежит на координатной прямой, тогда координата будет одна. В Декартовой системе координат оХУ будет две координаты, причем вначале записывают х, потом у. Например: С (5; 3): К (4; 8). Еще мы можем поместить отрезок в трехмерное пространство, тогда у каждой точки будет три координаты: х, у, z.

Кажется, что чем дальше, тем сложнее, но на самом деле это не совсем так. Хорошая новость: в каждом из случаев мы будем использовать один и тот же принцип, так что вы обязательно во всем разберетесь!

Как найти координаты середины отрезка на координатной прямой

Изобразим горизонтальную координатную прямую оХ и отметим на ней две точки: М и L.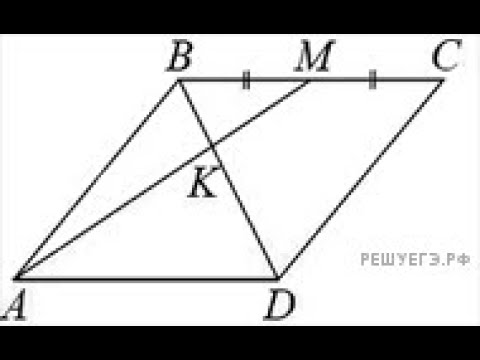 Координату точки М запишем как Хм, точки L — соответственно XL. Поставим лежащую на отрезке точку А — середину ML, MA = LA.

Определим координаты точек: Хм = {2}, XL = {8}. Чтобы найти середину отрезка, воспользуемся формулой X_A=(X_M+X_L)/2 и получим:

Х_А = (2 + 8)/2 = 5.

Проверим, верна ли формула. Для этого определим координаты середины отрезка графическим методом.Действительно: фактическая координата точки А совпадает со значением, которое мы получили.

Подумайте, взяли ли мы эту формулу случайно или же ее можно вывести. Да, конечно, второй вариант верный — в математике не используют ничего непроверенного. Давайте посмотрим, каким образом можно доказать истинность формулы, тем более, что мы возьмем ее за основу при решении более сложных задач.

1. Точка А — это середина отрезка, а значит, MA = LA.

2. Расстояние между точками можно рассчитать через разность модулей их координат: │Х_А – Х_М│=│Х_L – Х_А│.

3. Преобразуем правую часть, вынесем знак минуса: Х_А – Х_М= — (Х_А –Х_L).

4. Перенесем Х_А в левую часть, а все остальное — в правую: 2Х

   А= Х_L+ Х_М.

5. Найдем Х_А: Х_А = (Х_L + Х_М)/2.

Вот мы и вывели формулу координат середины отрезков! Чтобы лучше закрепить материал, сделаем пару заданий.

Задача 1

Определите координаты середины отрезка АВ, если Х_А = –2, Х_B = 10.

Решение

Обозначим точку середины отрезка буквой Т.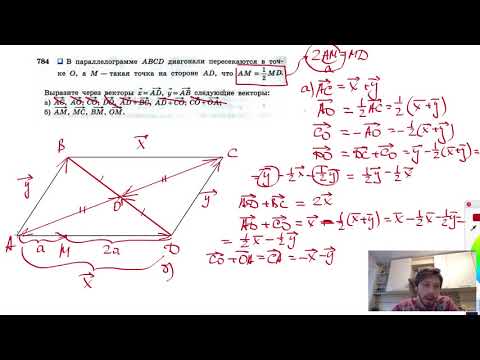 Тогда Хт = (Х_А + Х_B)/2 = (–2 + 10)/2 = 4.

Ответ: Хк = {4}.

Задача 2

Определите координаты начала отрезка КМ с серединой в точке Н, если Х_м = 5, Х_н = 10.

Решение

Вначале запишем формулу для середины отрезка: Х_н = (Х_к + Х_м)/2. Выразим Х_к через нее:

Х_н = (Х_к + Х_м)/2,2Х_н = (Х_к + Х_м),2Х_н – Х_м = Х _к,Х_к = 2Х_н – Х_м = 2 * 5 – 10 = 0.

Ответ: Хк = {0}

Как найти середину отрезка на плоскости

В Декартовой системе координат у каждой точки есть две координаты: по оси оХ и оУ. Изобразим отрезок АВ с координатами А (1; 3), В (3; 6) и точкой С — серединой отрезка.

Чтобы найти координаты точки С, мы воспользуемся уже известной нам формулой, но применим ее к каждой координате в отдельности. Вначале рассчитаем Х

с:

Х_с = (Х_А + Х_B)/2 = (1 + 3)/2 = 2.

Тогда У_C = (У_A + У_B)/2 = (3 + 6)/2 = 4,5. Значит С (2; 4,5).

Не пугайтесь, если отрезок на чертеже параллелен оси оХ или оУ: мы четко идем по нашему алгоритму и ничего не меняем.

Важно заметить: если отрезок параллелен оси оУ, координаты концов и середины отрезка по оХ будут совпадать, Х_А = Х_С = Х_В. Если же отрезок параллелен оси оХ, совпадут координаты по оУ: У_А = У_В = У_С.

И вновь пришло время задачек. Давайте разберем несколько примеров решения.

Задача 3

В системе координат находятся две точки: С (–6; 4) и К (2; 8). Определите координаты середины отрезка.

Решение

Обозначим середину отрезка точкой О. Тогда:

Х_О = (Х_С + Х_К)/2 = (–6 + 2)/2 = –2,У_О = (У_С + У_К)/2 = (4 + 8)/2 = 6.

Ответ: О (-2; 6).

Задача 4

Дан треугольник с вершинами АВС: А (-2; 4), В (4; 6), С (3; -5). Определите координаты точки М — медианы ВМ.

Решение

Медиана — отрезок, который проведен из вершины треугольника и делит противоположную сторону пополам. А значит, медиана ВМ делит на равные части сторону АС, АМ = МС. Тогда:

Х_М = (Х_А + Х_С)/2 = (–2 + 3)/2 = 0,5,У_М = (У_А + У_С)/2 = (4 – 5)/2 = –0,5.

Ответ: М (0,5; –0,5).

Координаты середины отрезка в пространстве

Вспомните, чем пространство отличается от плоскости. Правильно, третьим измерением! В том смысле, что добавляется еще одна координатная ось: оZ. Как это выглядит, можно посмотреть на рисунке ниже.

При этом формула нахождения середины отрезка остается неизменной. Если мы изобразим в трехмерном пространстве отрезок АВ с серединой в точке С, тогда:

Х_С = (Х_А + Х_В)/2,У_С = (У_А + У_В)/2,Z_С = (Z_А + Z_В)/2.

Координаты середины отрезка через радиус-векторы его концов

По сути, этот способ нельзя назвать каким-то новым и уникальным. Он лишь еще раз доказывает истинность формулы координат середины отрезков, только через алгебру.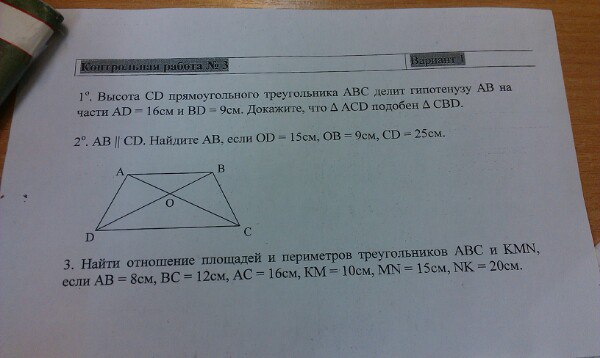 Чтобы разобраться в нем, давайте сначала вспомним определение вектора.

Вектор — это направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.

Векторы — достаточно обширная тема. Чтобы разобраться в ней, не хватит и двух статей. Но сейчас мы с вами будем использовать всего несколько тезисов, которые помогут разобраться в теме.

1. Векторы можно изображать в системах координат оХУ и оХYZ, т. е. в двумерной и трехмерной.

2. Координаты начала и конца векторов записывают так же, как и для отрезков: (x; y) и (x; y; z).

3. Сумму векторов можно найти по методу треугольника или параллелограмма. Картинка ниже поможет вам вспомнить, как ими пользоваться.

Радиус-вектор — вектор, который задает положение точки в пространстве относительно некоторой заранее фиксированной точки — начала координат.

Давайте разберемся, как доказать формулу для нахождения координаты середины отрезка через радиус-векторы его концов. В Декартовой системе координат нарисуем вектор с серединой в точке К. Координаты точки А (Х_А; У_А; Z_А), К (Х_К; У_К; Z_К), С (Х_С; У_С; Z_С).Проведем радиус-векторы , , .

Согласно определению середины отрезка: ОК = ½(ОС + ОА). Координаты векторов ОА, ОК, ОС соответственно равны координатам точек А, К, С, так как координаты точки О (0; 0; 0).

ОА (Х_А – 0, У_А – 0, Z_А – 0) = (Х_А; У_А; Z_А),ОК (Х_К – 0, У_К – 0, Z_К – 0) = (Х_К; У_К; Z_К,),ОС (Х_С– 0, У_С – 0, Z_С – 0) = (Х_С; У_С; Z_С).

Тогда запишем равенство ОК = ½(ОС + ОА) через координаты:

Х_К = 1/2(Х_А + Х_О), У_К = 1/2(У_А + У_О),Z_К = 1/2(Z_А + Z_О).

Напоследок мы сделаем небольшой перерыв, забудем про формулы и числа. Давайте подумаем, как можно найти середину отрезка, если мы не знаем координат его концов.

Например, нарисуем отрезок на песчаном пляже во время каникул. Определить точные координаты в таком случае будет достаточно сложно, правда? Вряд ли вы взяли с собой в отпуск набор линеек, чтобы вычислить длину отрезка. С подобным заданием вы могли столкнуться и на уроках геометрии, где учитель раздавал вам чистые нелинованные листы бумаги и просил найти середину отрезка без использования линейки.

Сейчас мы обучим вас волшебному методу, приготовьтесь! Все что вам понадобится — это циркуль.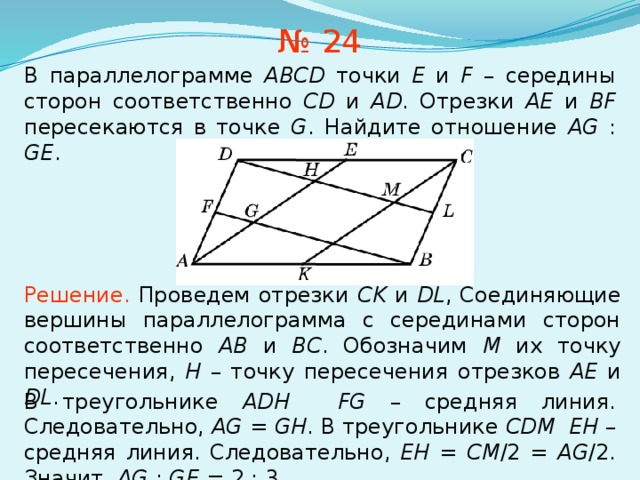 Нарисуем на бумаге отрезок АВ любой длины. Поставим иголку циркуля в точку А и начертим окружность с радиусом, равным АВ. Далее повторим действие — прочертим такую же окружность с центром в точке В.

Мы видим, что окружности пересеклись дважды: снизу и сверху. Если соединить эти две точки, эта прямая пересечет наш исходный отрезок ровно в его середине.

Скептики вспомнят наш пример с пляжем и скажут: «Линейку мы с собой в отпуск не берем, но и циркуль ведь тоже! Что вы скажете на это?» А ответим мы вот что: приходите на курсы по профильной математики в Skysmart! Там вы научитесь не только заменять настоящий циркуль на самодельный, но еще подготовитесь к экзаменам, разовьете логику и узнаете много всего интересного. Ждем вас на занятиях!

Параллелограмм. Задания ЕГЭ по математике (профильный уровень)

Лучшие репетиторы для сдачи ЕГЭ

Математика

Русский язык

История

Открытый банк заданий по теме параллелограмм. Задания B6 из ЕГЭ по математике (профильный уровень)

Тип задания: 6
Тема: Параллелограмм

Условие

В параллелограмме ABCD AB = 6, AD = 9, \sin A = \frac23. Найдите большую высоту параллелограмма.

Показать решение

Решение

Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне, поэтому большая высота проведена к меньшей стороне. Проведём высоту DH к меньшей стороне и рассмотрим треугольник ADH.

\sin A=\frac{DH}{AD}. Получаем: DH=AD\sin A= 9\cdot\frac23= 6.

Ответ

6

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 6
Тема: Параллелограмм

Условие

Площадь параллелограмма равна 60, две его стороны равны 8 и 12. Найдите меньшую высоту этого параллелограмма.

Показать решение

Решение

Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне S = ah_a. Найдём высоты параллелограмма: h_1 = 60 : 8 = 7,5, h_2 = 60 : 12 = 5. Меньшая высота этого параллелограмма равна 5.

Ответ

5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 6
Тема: Параллелограмм

Условие

Площадь параллелограмма ABCD равна 324. Точка P — середина стороны BC. Найдите площадь трапеции APCD.

Показать решение

Решение

Точка P — середина стороны BC, поэтому PC=0,5BC. Обозначим h высоту параллелограмма, проведённую к стороне AD.

Тогда площадь параллелограмма S равна BC\cdot h=324.

Площадь трапеции APCD равна \frac{PC+AD}{2}\cdot h= \frac{0,5BC+BC}{2}\cdot h= \frac{1,5BC}{2}\cdot h= 0,75S=243

Ответ

243

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 6
Тема: Параллелограмм

Условие

Стороны параллелограмма равны 8 и 16. Высота, опущенная на первую из этих сторон, равна 14. Найдите высоту, опущенную на вторую сторону параллелограмма.

Показать решение

Решение

Площадь параллелограмма равна произведению стороны на высоту, проведённую к этой стороне. Для параллелограмма ABCD выполняется S=AB\cdot DH=CB\cdot DE. Получаем 16DH=8\cdot14, DH=7.

Ответ

7

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Тип задания: 6
Тема: Параллелограмм

Условие

Площадь параллелограмма ABCD равна 284. Точка E — середина CD. Найдите площадь треугольника ADE.

Показать решение

Решение

S_{ADE}=\frac{DE\cdot AM}{2},  AM\perp DC

S_{ABCD}=AB\cdot AM,  AB=2DE.

AB\cdot AM=284,  2DE\cdot AM=284.

DE\cdot AM=142,  S_{ADE}=\frac{142}{2}=71.

Ответ

71

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Математика

Русский язык

История

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

© 2016—2023
Все права защищены.

Служба поддержки портала

P — середина стороны CD параллелограмма ABCD. Прямая через C, параллельная PA, пересекает AB в точке Q и DA в точке R. Докажите, что DA = AR и CQ = QR.

NCERT EXEMPLAR-QUADRILATERALS — Четырехугольники

20 видео

РЕКЛАМА

Ab Padhai каро бина объявления ке

Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

Обновлено: 27-06-2022

लिखित उत्तर

Решение

Дано В параллелограмме ABCD точка P является серединой DC.
Чтобы доказать, что DA=AR и CQ=QR
Доказательство ABCD — параллелограмм.

∴ BC=ADandBC∣∣AD
Кроме того, DC=ABandDC∣∣AB
Так как P является серединой DC.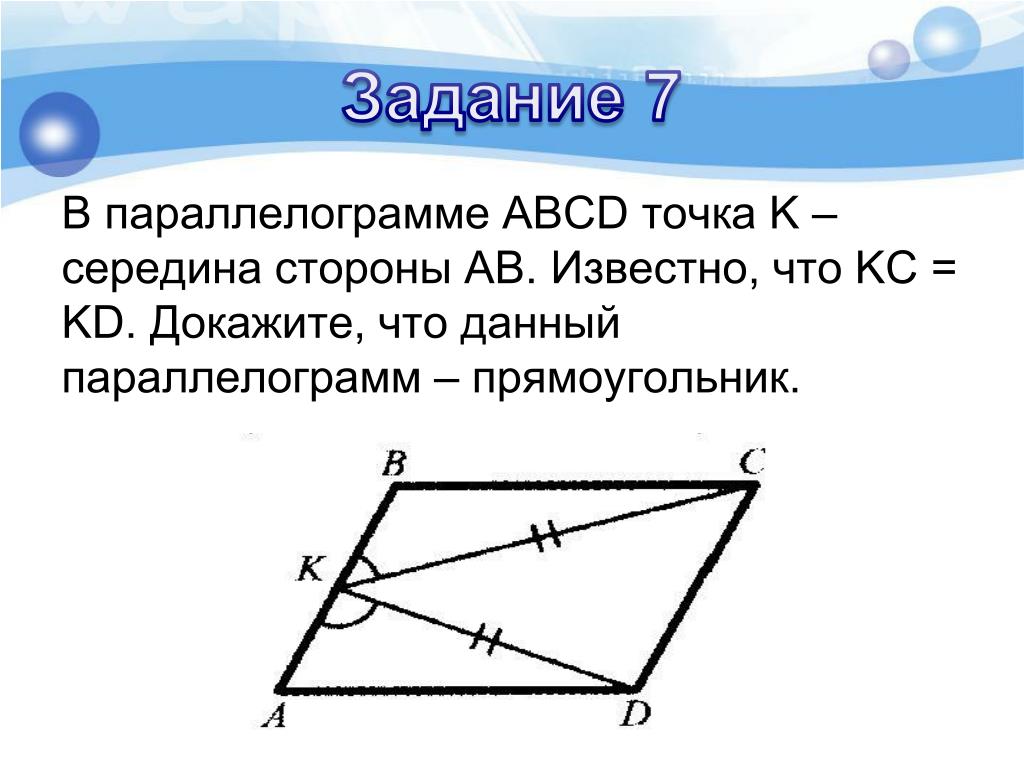
∴ DP=PC=12DC
Теперь QC||APandPC||AQ
Итак, APCQ — параллелограмм.
∴ AQ=PC=12DC
=12AB=BQ [∵DC=AB]…(i)
Теперь в ΔAQR и ΔBQC AQ=BQ [из уравнения (i)]
∠AQR=∠BQC [вертикально противоположные углы]
и ∠ARQ=∠BCQ [альтернативные внутренние углы]
∴ ΔAQR≅ΔBQC [по правилу конгруэнтности AAS] ltBrgt ∴ AR=BC [по правилу CPCT]
Но BC=DA
∴ AR=DA
Кроме того, CQ=QR [по правилу CPCT]
Отсюда доказано.

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

---

संबंधित वीडियो

ABCD — ромб и P,Q,R,S являются серединами AB,BC,CD,DA соответственно. Докажите, что PQRS представляет собой прямоугольник.

П это середина стороны AB параллелограмма ABCD . Линия через B параллельно ПД встречает постоянный ток в Q и н.э. производится в R . Докажите, что (i) AR=2BC (ii) BR=2BQ.

АВСD является четырехугольником; P,Q,RandS точки пересечения сторон AB, BC, CD и DA.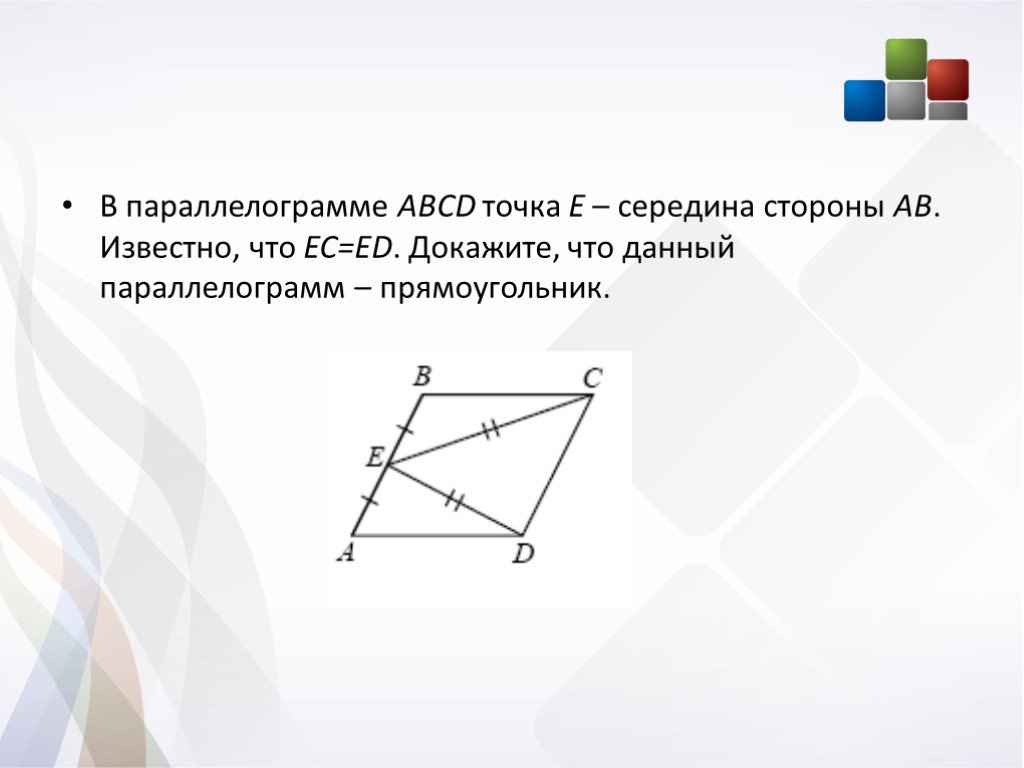 соответственно и примыкают к A и C ; доказать, что PQRS является параллелограммом.

P, Q , R и S — середины сторон AB, BC, CD и DA четырехугольника ABCD, в котором AC = BD. Докажите, что PQRS — ромб.

26522165

P — середина стороны AB параллелограмма ABCD. Прямая, проведенная из B параллельно PD, пересекает CD в точке Q, а AD производит в точке R. Докажите, что:
(i) AR = 2BC (ii) BR = 2BQ

30617439

Стороны четырехугольника ABCD AB ,BC ,CD и DA пересекаются соответственно с точками P ,Q , R и S, смежными с A и C. Докажите, что PQRS является параллелограммом.

127318310

ABCD — четырехугольник, в котором P, Q, R и S — середины сторон AB, BC, CD и DA. АС — диагональ. Покажите, что :
PQRS — параллелограмм.

203476048

P, Q, R и S — середины сторон AB, BC, CD и DA параллелограмма ABCD соответственно. Если площадь ABCD равна 88 кв. см, то площадь PQRS равна

233232278

В четырехугольнике ABCD, если P,Q,R,S являются серединами AB,BC,CD,DA соотв.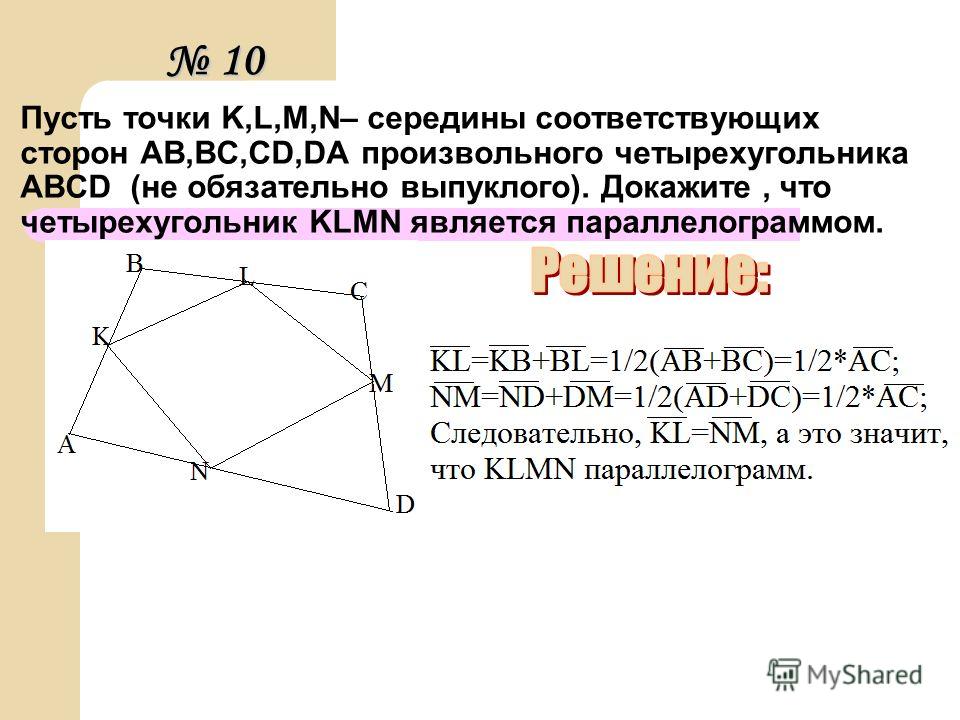 тогда что из следующего верно?

357241889

Текст Решение

В четырехугольнике ABCD, если P,Q,R,S являются серединами AB,BC,CD,DA соотв. тогда SR параллелен

357241891

Text Solution

P, Q , R и S — соответственно середины сторон AB, BC, CD и DA четырехугольника ABCD, в котором AC = BD. Докажите, что PQRS — ромб.

642505458

P — середина стороны CD параллелограмма ABCD. Прямая через C, параллельная PA, пересекает AB в точке Q и DA в точке R. Докажите, что DA = AR и CQ = QR.

642505473

दिए गए चित्र में, यदि भुजाओं ab, bc, cd, तथा da के मध मध मध बिंदु कшить P, q, r तथ तथ हो तो सिद सिद सिद कीजिए कि कि कि कि कि कि कीजिए कीजिए कीजिए कीजिए सिद कीजिए कीजिए कीजिए कीजिए कि कि कि क क क क कि कीजिए कीजिए सिद सिद सिद सिद सिद सिद सिद सिद सिद सिदждения कीजिए कीजिए कीजिए В

643048779

Text Solution

ABCD एक समचतुर्भुज है। AB,BC,CD,DA के मध्य-बिंदु क्रमशः P,Q,R,S हैं। सिद्ध कीजिए कि PQRS एक आयत है।

643113745

P — середина стороны AB параллелограмма ABCD.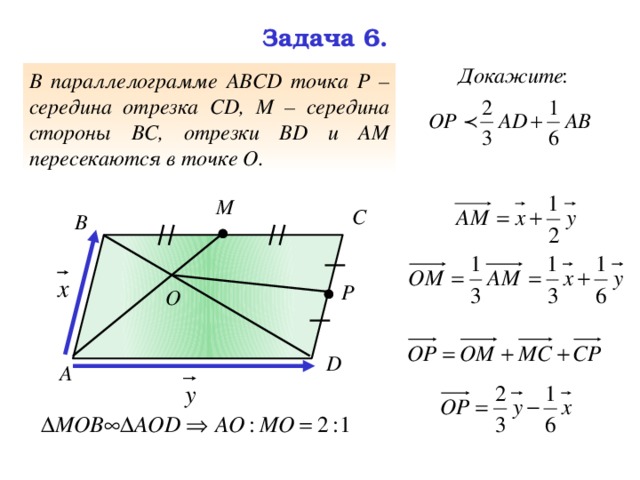 Линия, проходящая через B, параллельная PD, пересекает DC в Q, а AD получается в R. Докажите, что AR=2BC.

647993162

a На приведенном ниже рисунке 1 ABCD — параллелограмм, а X — середина BC. На прямой AX произведено m…

Перейти к

• Прямолинейные фигуры. Упражнение 13.1.
• Прямолинейные фигуры. Упражнение 13.2.

• Рациональные и иррациональные числа
• Сложные проценты
• Расширения
• Факторизация
• Одновременные линейные уравнения
• Задачи на одновременные линейные уравнения
• Квадратные уравнения
• Индексы
• Логарифмы
• Треугольники
• Теорема о средней точке
• Теорема Пифагора
• Прямолинейные фигуры
• Теоремы о площади
• Круг
• Измерение
• Тригонометрические отношения
• Тригонометрические отношения и стандартные углы
• Координатная геометрия
• Статистика

Главная > ML Aggarwal Solutions Класс 9 Математика > Глава 13.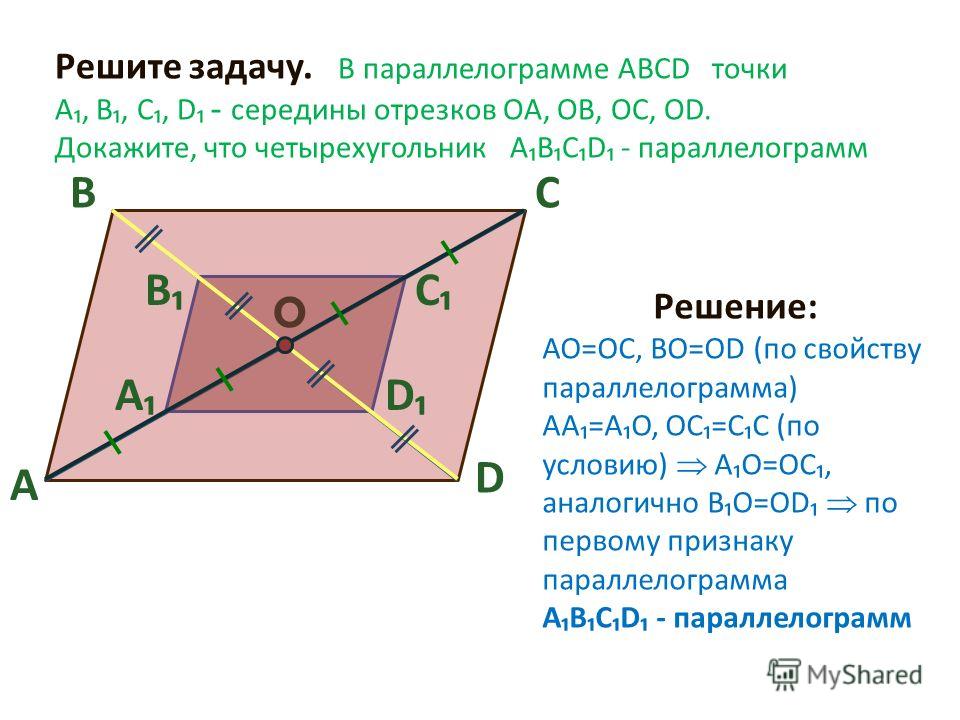 Прямолинейные фигуры > Прямолинейные фигуры. Упражнение 13.1. > Вопрос 9

Вопрос 9 Прямолинейные фигуры Упражнение 13.1

(a) На приведенном ниже рисунке (1) ABCD — параллелограмм, а X — середина BC. Произведенная линия AX

соответствует DC, произведенной в Q. Параллелограмм ABPQ завершен.

Докажите, что:

(i) треугольники ABX и QCX равны;

(ii)DC = CQ = QP

(b) На приведенном ниже рисунке (2) точки P и Q взяты на противоположных сторонах AB и CD

соответственно параллелограмма ABCD, так что AP = CQ. Покажите, что AC и PQ делят каждую девятку пополам.0003

прочее.

Ответ:

(a) Дано: ABCD — параллелограмм, а X — середина BC. Произведенная линия AX соответствует выпуску DC

в Q, а ABPQ представляет собой || гм.

Чтобы доказать: (i) ∆ABX ≅ ∆QCX

(ii) DC = CQ = QP

Доказательство:

В ∆ABX и ∆QCX имеем

BX = XC [X — середина BC]

∠AXB = ∠CXQ [Вертикально противоположные углы]

∠XCQ = ∠XBA [Альтернативный угол, так как AB || CQ]

Итак, ABX ≅ ∆QCX по аксиоме сравнения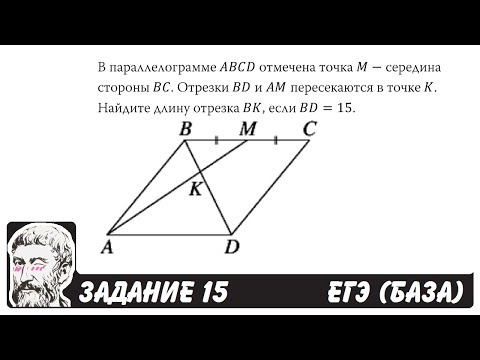 A. S.A

Теперь, по C.P.C.T

CQ = AB

Но,

AB = DC и AB = QP [Поскольку ABCD и ABPQ || gms]

Следовательно,

DC = CQ = QP

(b) In || gm ABCD, P и Q — точки на AB и CD соответственно, PQ и AC пересекаются друг с другом в точке O

и AP = CQ

Чтобы доказать: AC и PQ делят друг друга пополам, т. е. AO = OC и PO = OQ

Доказательство :

В ∆AOP и ∆COQ

AP = CQ [данные]

∠AOP = ∠COQ [вертикально противоположные углы]

∠OAP = ∠OCP [альтернативные углы]

Итак, ∆AOP ≅ ∆COQ по A.A.S.

OP = OQ и OA = OC

Отсюда доказано.

Связанные вопросы

Найдите два угла четырехугольника, равные 40° и 110°, а два других относятся как 3 : 4.

Докажите, что если углы четырехугольника, взятые по порядку, относятся как 1:2:3:4, то…

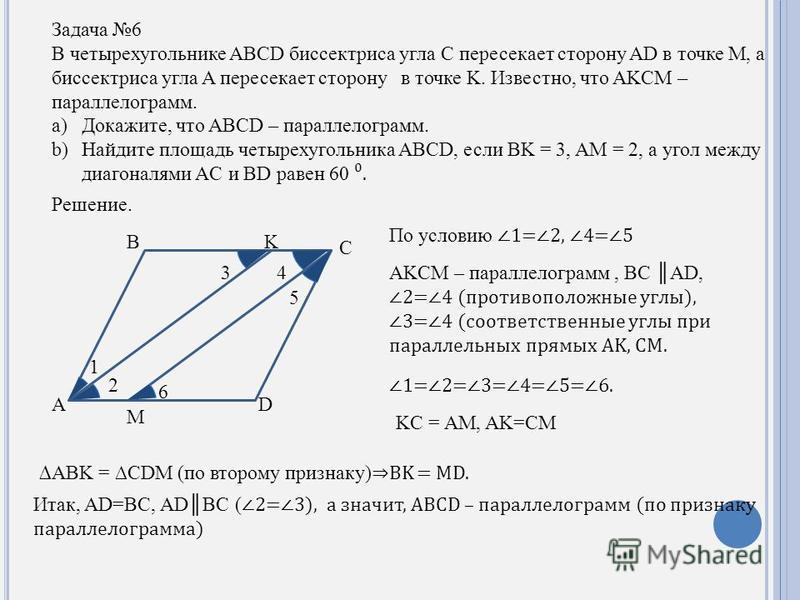
(a) На приведенном ниже рисунке (1) ABCD представляет собой параллелограмм, в котором ∠DAB = 70°, ∠DBC = 80°. Вычислите угол…

Дано, ABCD — прямоугольник. Мы знаем, что диагонали прямоугольника равны и делят друг друга пополам…

(i) Докажите, что каждый угол прямоугольника равен 90°. (ii) Если углы четырехугольника равны, докажите…

(i) Докажите, что биссектрисы любых двух смежных углов параллелограмма прямые. (ii) Доказательство…

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Прямолинейные рисунки Упражнения 13.