Решение №2230 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
Источник: ОГЭ Ященко 2022 (50 вариантов)
Решение:
Параллелограмм АВСD делится диагональю АС на два равных треугольника. ΔАВС = ΔАDС, SABCD = 2·SABC
Площадь треугольника можно найти по двум формулам:
S_{\Delta}=\frac{1}{2}ah=\frac{a+b+c}{2}\cdot r
ОК = 7 – будет являться радиусом окружности и высотой к стороне АС, построим ещё два радиуса ОР и OL, которые будут являться высотами к BC и AB.
Отрезки ОР и ОН будут лежать на одной прямой НР (т.к. BC||AD, OP⊥BC, OH⊥AD), которая является высотой параллелограмма АВСD и высотой треугольника АВС к стороне ВС.
Найдём высоту НР:
НР = ОР + ОН = 7 + 13 = 20
Тогда площадь треугольника АВС по первой формуле равна:
По теореме Пифагора из прямоугольного треугольника найдём АК:
АК2 = АО2 – ОК2
АК2 = 252 – 72 = 576
АК = √576 = 24
Если окружность вписана в треугольник, то расстояния от вершины угла до точек касания окружности со сторонами угла равны:
АК = AL = 24
BL = BP = x
CP = CK = y
Отсюда стороны треугольника АВС равны:
АС = 24 + y
AB = 24 + x
BC = x + y
Площадь треугольника по второй формуле равна:
S_{\Delta}=\frac{a+b+c}{2}\cdot r
Приравняем оба выражения для нахождения площади:
10·ВС = (24 + ВС)·7
10·ВС = 7·24 + 7ВС
10·ВС – 7·ВС = 7·24
3·ВС = 7·24 |:3
ВС = 7·8 = 56
Найдём площадь параллелограмма АВСD:
SABCD = 2·SABC = 2·10·BC = 20·56 = 1120
Ответ: 1120.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 24
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:04.10.2021
- Рубрика записи25. Геометрическая задача повышенной сложности
- Автор записи:Andrei Maniakin
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
05.20Другие ответы
| ||||||||||||
05.20
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
В параллелограмме A B C D диагонали A C и B D пересекаются в точках O и A
Вопрос
Обновлено: 26.
04.2023RD SHARMA-ЧЕТЫРЕХСТОРОННИЕ-Все вопросы
20 видеоРЕКЛАМА 900 03
Текст Решение
Решение
Диагонали параллелограмма делятся пополам. В результате O является средней точкой AC и BD.
Следовательно,
OC=12AC
OC=3,4 см
Теперь
OD=12BD
OD=12×13,6 см
OD=6,8 см
Следовательно, размеры OC и OD равны 3,4 см и 6,8 см соответственно.
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
Если диагонали AC,BD
четырехугольника ABCD,
пересекаются в точке О,
и разделите четырехугольник на четыре треугольника
равных площадей, докажите, что четырехугольник ABCD
является параллелограммом.
ДАННО: Четырехугольник ABCD.
такое, что его диагонали AC
и БД
пересекаются в точке О
и разделить его на четыре части так, чтобы
ar(AOB)=ar(BOC)=ar(COD)=ar(AOD)
ДОКАЗАТЬ: Четырехугольник ABCD
является параллелограммом.
Докажите, что диагонали параллелограмма делят на четыре равновеликих треугольника. ДАННО: Параллелограмм ABCD. . Диагонали АС и БД пересекаются на О. ДЛЯ ДОКАЗАНИЯ: ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
O любая точка на диагонали BD параллелограмма ABCD. Докажите, что ar(OAB)=ar(OBC)
ABCD это трапеция, у которой ABCD . диагонали АС и БД пересекаются в О . Доказывать что (i) AOBCOD (ii) Если ОА=6см , ОС=8см , Находить: Площадь (AOB) Площадь (COD) (b) Площадь (AOD) Площадь (COD)
1410239
АВСD это трапеция такая, что BC∣∣AD и АВ=4см . Если диагонали АС и БД пересекаются в О такой, что AOOC=DOOB=12 , то ВС= 7см (б) 8см (с) 9см (d) 6 см
1410386
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O и AC=6,8 см и BD=5,6 см. . Найдите меры OC и OD
1414617
ABCD это параллелограмм, диагонали которого пересекаются в точке О. Если П любая точка на БО, докажи это: ар (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
1414841
На рисунке ABCD представляет собой прямоугольник, в котором CD=6см, AD=8см Найдите площадь параллелограмма CDEF1414882
В параллелограмме ABCD
диагонали АС
и БД
пересекаются в точке О
и АС=6,8 см
и BD=13,6см.
642565094
Если диагонали AC,BD четырехугольника ABCD, пересекаются в точке О, и разделите четырехугольник на четыре треугольника равных площадей, докажите, что четырехугольник ABCD является параллелограммом. ДАННО: Четырехугольник ABCD. такое, что его диагонали AC и БД пересекаются в точке О и разделить его на четыре части так, чтобы ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) ДОКАЗАТЬ: Четырехугольник ABCD является параллелограммом.
642565179
Диагонали четырехугольника ABCD,AC и БД пересекаются в О. Докажите, что если BO=OD, треугольники АВС и АЦП равны по площади. ДАННО: Четырехугольник ABCD. в котором его диагонали AC и БД пересекаются в точке О такой, что БО = ОД. ДОКАЗАТЬ: ar(ABC)=ar(ADC)
642565181
Покажите, что диагонали параллелограмма делят на четыре равновеликих треугольника. ДАННО: Параллелограмм ABCD. . Диагонали АС и БД пересекаются на О. ДЛЯ ДОКАЗАНИЯ: ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
642565184
АВСD
это
трапеция, у которой АВ параллельна CD
.
диагонали АС
и БД
пересекаются
в О
. Доказывать
что (i) AOB~COD
(ii) Если ОА=6см
, ОС=8см
, Находить:
Площадь (AOB) Площадь (COD)
(b) Площадь (AOD) Площадь (COD)
642569456
диагонали четырехугольника ABCD пересекаются в О . Доказывать что ar(ACB)ar(ACD)=BODO
642569540
ABCD это трапеция такая, что BC∣∣AD и АД=4см . Если диагонали АС и БД пересекаются в О такой, что AOOC=DOOB=12 , то ВС= (а) 7см (б) 8см (с) 9см (d) 6см
642569603
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O и AC=6,8 см и BD=5,6 см. . Найдите меры OC и OD .
642572377
Решения NCERT для математики класса 9, глава 8, четырехугольники
Решения NCERT для математики класса 9, глава 8, четырехугольники Ex 8.1 являются частью решений NCERT для математики класса 9. Здесь мы дали решения NCERT для математики класса 9, глава 8, четырехугольники, пример 8.1.
Решения NCERT для класса 9{ \circ } }{ 30 } \) = 12°
∴ 3x = 3 x 12° = 36°
5x = 5 x 12° = 60°
9x = 9 x 12° = 108°
13a = 13 x 12 ° = 156°
⇒ Искомые углы четырехугольника составляют 36°, 60°, 108° и 156°.
Упражнение 8.1 Математика 9 класса Вопрос 2.
Если диагонали параллелограмма равны, то докажите, что это прямоугольник.
Решение:
Пусть ABCD — параллелограмм такой, что AC = BD.
В ∆ABC и ∆DCB,
AC = DB [Дано]
AB = DC [Противоположные стороны параллелограмма]
BC = CB [Общий]
∴ ∆ABC ≅ ∆DCB [По конгруэнтности SSS]
⇒ ∠ABC = ∠DCB [По C.P.C.T.] …(1)
Теперь, AB || DC и BC являются секущими. [ ∵ ABCD — параллелограмм]
∴ ∠ABC + ∠DCB = 180° … (2) [Со-внутренние углы]
Из (1) и (2) имеем
∠ABC = ∠DCB = 90°
, т.е. , ABCD — параллелограмм, угол которого равен 90°.
∴ ABCD — прямоугольник.
Упражнение 8.1 Математика для 9 класса Вопрос 3.
Покажите, что если диагонали четырехугольника делят друг друга пополам под прямым углом, то это ромб.
Решение:
Пусть ABCD — четырехугольник, такой, что диагонали AC и BD делят друг друга пополам под прямым углом в точке O.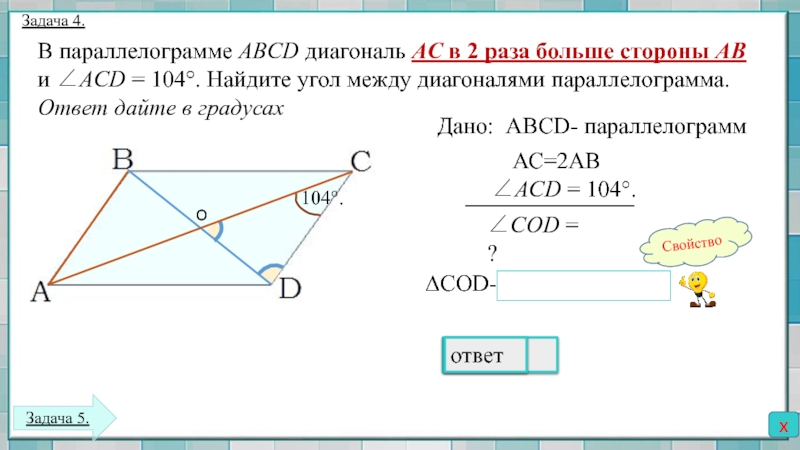
является серединой BD]
∠AOB = ∠AOD [Каждый 90]
∴ ∆AQB ≅ ∆AOD [По конгруэнтности SAS
∴ AB = AD [По C.P.C.T.] ……..(1)
Аналогично, AB = ВС .. .(2)
ВС = CD …..(3)
CD = DA ……(4)
∴ Из (1), (2), (3) и (4) имеем
AB = BC = CD = DA
Таким образом, четырехугольник ABCD является ромбом.
В качестве альтернативы: можно доказать, что ABCD сначала является параллелограммом, а затем, если одна пара смежных сторон равна, получится ромб.
Упражнение 8.1 Математика для 9 класса Вопрос 4.
Докажите, что диагонали квадрата равны и делятся пополам под прямым углом.
Решение:
Пусть ABCD — квадрат, диагонали AC и BD которого пересекаются в точке O.
(i) Чтобы доказать равенство диагоналей, нужно доказать, что AC = BD.
В ∆ABC и ∆BAD имеем
AB = BA [Общий]
BC = AD [стороны квадратного ABCD]
↑ABC = ↑BAD [Каждый угол составляет 90 °]
∴ ∆ABC ≅ ∆BAD [по конгрессу SAS]
AC = BD [C.
P.C.T.]… (1)
(ii) н.э. || BC и AC — секущие. [∵ Квадрат является параллелограммом]
∴ ∠1 = ∠3
[Смежные внутренние углы равны]
Аналогично, ∠2 = ∠4
Теперь, в ∆OAD и ∆OCB, мы имеем
AD = CB [Стороны квадрат ABCD]
∠1 = ∠3 [доказано]
∠2 = ∠4 [доказано]
∴ ∆OAD ≅ ∆OCB [по конгруэнтности ASA]
⇒ OA = OC и OD = OB [по C.P.C.T.]
т. е. диагонали AC и BD делят друг друга пополам в точке O. …….(2)
(iii) В ∆OBA и ∆ODA имеем
OB = OD [Доказано]
BA = DA [Стороны квадрата ABCD]
OA = OA [Common]
∴ ∆Oba ≅ ∆Oda [by SSS Congruency]
⇒ Ϫaob = ♂аод [by C.P.C.T.]… (3)
∵ ♂AOB и ϪAOD образуют линейную пару.
∴∠AOB + ∠AOD = 180°
∴∠AOB = ∠AOD = 90° [By(3)]
⇒ AC ⊥ BD …(4)
Из (1), (2) и (4) получаем получить AC и BD равны и делят друг друга пополам под прямым углом.
Ех 8.1 Класс 9Математика Вопрос 5.
Докажите, что если диагонали четырехугольника равны и делят друг друга пополам под прямым углом, то это квадрат.
Решение:
Пусть четырехугольник ABCD такой, что диагонали AC и BD равны и делят друг друга пополам под прямым углом.
Теперь, в ∆AOD и ∆AOB, мы имеем
ϪAOD = ↑AOB [Каждый 90 °]
AO = AO [Common]
OD = OB [∵ O — средняя точка BD]
∆ ∆AOD ∆ ∆ AOB [согласно SAS]
⇒ AD = AB [согласно C.P.C.T.] …(1)
Аналогично имеем
AB = BC … (2)
BC = CD …(3)
CD = DA …(4)
Из (1), (2), (3) и (4) имеем
AB = BC = CD = DA
∴ У четырехугольника ABCD все стороны равны.
В ∆AOD и ∆COB имеем
AO = CO [Дано]
OD = OB [Дано]
∠AOD = ∠COB [Вертикально противоположные углы]
Итак, ∆AOD ≅ ∆COB [По конгруэнтности SAS]
∴ ∠1 = ∠2 [по C.P.C.T.]
Но они образуют пару чередующихся внутренних углов.
∴ н.э. || BC
Аналогично, AB || DC
∴ ABCD — параллелограмм.
∴ Параллелограмм, у которого все стороны равны, является ромбом.
∴ ABCD — ромб.
Теперь, в ∆ABC и ∆BAD, мы имеем
AC = BD [дано]
BC = AD [доказано]
AB = BA [Common]
∴ ∆ABC ≅ ∆BAD [по конгруэнтностью SSS]
∴ ▲ = ∠BAD [По C.
P.C.T.] ……(5)
С тех пор, AD || BC и AB — секущая.
∴∠ABC + ∠BAD = 180° .. .(6) [Co – внутренние углы]
⇒ ∠ABC = ∠BAD = 90° [By(5) & (6)]
Итак, ромб ABCD имеет один угол равен 90°.
Таким образом, ABCD — квадрат.
Упр. 8.1 Класс 9 Математика Вопрос 6.
Диагональ AC параллелограмма ABCD делит ∠A пополам (см. рисунок). Покажите, что
(i) также делит ∠C пополам,
(ii) ABCD является ромбом.
Решение:
У нас есть параллелограмм ABCD, в котором диагональ AC делит пополам ∠A
⇒ ∠DAC = ∠BAC
(i) Так как ABCD — параллелограмм.
∴ АВ || DC и AC — это трансверсаль.
∴ ∠1 = ∠3 …(1)
[ ∵ Альтернативные внутренние углы равны]
Кроме того, BC || AD и AC — трансверсаль.
∴ ∠2 = ∠4 …(2)
[ v Альтернативные внутренние углы равны]
Кроме того, ∠1 = ∠2 …(3)
[ ∵ AC делит пополам ∠A]
Из (1), (2) и (3), мы имеем
∠3 = ∠4
⇒ AC делит пополам ∠C.
(ii) В ∆ABC имеем
∠1 = ∠4 [Из (2) и (3)]
⇒ BC = AB …(4)
[∵ Стороны, противоположные равным углам ∆, равны]
Аналогично, AD = DC …….
.(5)
Но ABCD — параллелограмм. [Дано]
∴ AB = DC …(6)
Из (4), (5) и (6) имеем
AB = BC = CD = DA
Таким образом, ABCD — ромб.
Упражнение 8.1 Математика 9 класса Вопрос 7.
ABCD — ромб. Покажите, что диагональ AC делит пополам ∠A и ∠C, а диагональ BD делит пополам ∠B и AS ∠D.
Решение:
Так как ABCD — ромб.
⇒ AB = BC = CD = DA
Кроме того, AB || CD и AD || BC
Теперь CD = AD ⇒ ∠1 = ∠2 …….(1)
[ ∵ Углы, противоположные равным сторонам треугольника, равны]
Кроме того, AD || ВС и АС — трансверсаль.
[ ∵ Каждый ромб является параллелограммом]
⇒ ∠1 = ∠3 …(2)
[ ∵ Альтернативные внутренние углы равны]
Из (1) и (2) имеем
∠2 = ∠3 …(3)
Так как AB || DC и AC трансверсальны.
∴ ∠2 = ∠4 …(4)
[ ∵ Альтернативные внутренние углы равны] Из (1) и (4)
имеем ∠1 = ∠4
∴ AC делит пополам ∠C, а также ∠A.
Аналогично можно доказать, что BD делит пополам ∠B и ∠D.
Упр. 8.1 Класс 9 Математика Вопрос 8.
ABCD — прямоугольник, в котором диагональ AC делит пополам ∠A и ∠C. Докажите, что
(i) ABCD является квадратом 9.0015 (ii) диагональ BD делит пополам ∠B и ∠D.
Решение:
У нас есть прямоугольник ABCD такой, что AC делит пополам ∠A и ∠C.
т. е. ∠1 = ∠4 и ∠2 = ∠3 ……..(1)
(i) Так как каждый прямоугольник является параллелограммом.
∴ ABCD — параллелограмм.
⇒ АВ || CD и AC — трансверсаль.
∴∠2 = ∠4 …(2)
[ ∵ Альтернативные внутренние углы равны]
Из (1) и (2) имеем
∠3 = ∠4
В ∆ABC, ∠3 = ∠4
⇒ AB = BC
[ ∵ Стороны, противоположные равным углам A, равны]
Аналогично, CD = DA
Итак, ABCD — прямоугольник, у которого смежные стороны равны.
⇒ ABCD — квадрат.
(ii) Поскольку ABCD — квадрат, а диагонали квадрата делят противоположные углы пополам.
Итак, BD делит пополам ∠B и ∠D.
Упр. 8.1 Класс 9 Математика Вопрос 9.
В параллелограмме ABCD на диагонали BD взяты две точки P и Q так, что DP = BQ (см. рисунок). Покажите, что
Решение:
Имеем параллелограмм ABCD, диагональ BD и точки P и Q таковы, что PD = QB
(i) С, н.э. || BC и BD — трансверсаль.
∴ ∠ADB = ∠CBD [ ∵ Альтернативные внутренние углы равны]
⇒ ∠ADP = ∠CBQ
Теперь в ∆APD и ∆CQB имеем
AD = CB [противоположные стороны параллелограмма ABCD равны]
PD = QB [Дано]
∠ADP = ∠CBQ [Подтверждено]
∴ ∆APD ≅ ∆CQB [согласно SAS]
(ii) Поскольку, ∆APD ≅ ∆CQB [Подтверждено]
⇒ AP = CQ [ C.P.C.T.]
(iii) Так как, AB || CD и BD — трансверсаль.
∴ ∠ABD = ∠CDB
⇒ ∠ABQ = ∠CDP
Теперь в ∆AQB и ∆CPD имеем
QB = PD [Дано]
∠ABQ = ∠CDP [Доказано]
AB = CD [ Y Противоположные стороны параллелограмма ABCD равны]
∴ ∆AQB = ∆CPD [По конгруэнтности SAS]
(iv) Поскольку ∆AQB = ∆CPD [Доказано]
⇒ AQ = CP [По C.P.C.T.]
(v) В четырехугольнике ∆PCQ
Противоположные стороны равны.
[Доказано]
∴ ∆PCQ — параллелограмм.
Упр. 8.1 Класс 9 Математика Вопрос 10.
ABCD — параллелограмм, AP и CQ — перпендикуляры из вершин A и C на диагонали BD (см. рисунок). Покажи, что
Решение:
(i) В ∆APB и ∆CQD мы имеем
ϪAPB = ♂ккд [каждый 90 °]
ab = CD [∵ противоположные стороны параллелограммы ABCD]
ϪBP = ↑CDQ
[ ∵ Альтернативные углы равны AB || CD и BD являются трансверсалью]
∴ ∴ ∆APB = ∆CQD [согласно AAS]
(ii) Поскольку ∆APB ≅ ∆CQD [доказано]
⇒ AP = CQ [согласно C.P.C.T.]
Ex 8.1 Математика для 9 класса Вопрос 11.
В ∆ABC и ∆DEF AB = DE, AB || DE, BC – EF и BC || ЭФ. Вершины A, B и C соединены с вершинами D, E и F соответственно (см. рисунок).
Докажите, что
(i) четырехугольник ABED является параллелограммом
(ii) четырехугольник BEFC является параллелограммом
(iii) AD || CF и AD = CF
(iv) четырехугольник ACFD является параллелограммом
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
Решение:
(i) Имеем AB = DE [Дано]
и AB || DE [Дано]
i.
т. е. ABED — четырехугольник, у которого пара противоположных сторон (AB и DE) параллельны и имеют одинаковую длину.
∴ ABED — параллелограмм.
(ii) BC = EF [Дано]
и БК || EF [Дано]
т.е. BEFC – это четырехугольник, у которого пара противоположных сторон (BC и EF) параллельны и имеют одинаковую длину.
∴ BEFC — параллелограмм.
(iii) ABED — параллелограмм [Доказано]
∴ AD || BE и AD = BE …(1)
[ ∵ Противоположные стороны параллелограмма равны и параллельны] Кроме того, BEFC является параллелограммом. [Доказано]
БЭ || CF и BE = CF …(2)
[ ∵ Противоположные стороны параллелограмма равны и параллельны]
Из (1) и (2) имеем
г. н.э. || CF и AD = CF
(iv) Поскольку AD || CF и AD = CF [Доказано]
т. е. в четырехугольнике ACFD одна пара противоположных сторон (AD и CF) параллельны и имеют одинаковую длину.
∴Четырехугольник ACFD является параллелограммом.
(v) Так как ACFD — параллелограмм. [Доказано]
Итак, AC =DF [∵ Противоположные стороны параллелограмма равны]
(vi) В ∆ABC и ∆DFF имеем
AB = DE [Дано]
BC = EF [Дано]
AC = DE [Доказано в части (v)]
∆ABC ≅ ∆DFF [По конгруэнтности SSS]
Упражнение 8.
1 Математика 9 класса Вопрос 12.
ABCD — трапеция, в которой AB || CD и AD = BC (см. рисунок). Покажите, что
(i)∠A=∠B
(ii)∠C=∠D
(iii) ∆ABC ≅ ∆BAD
(iv) диагональ AC = диагональ BD
[Подсказка: растяните AB и проведите прямую через C параллельно DA, пересекающей AB, полученную в E].
Решение:
Дана трапеция ABCD, в которой AB || CD и AD = ВС.
(i) Произвести AB в E и нарисовать CF || AD.. .(1)
∵ AB || DC
⇒ АЕ || DC Также AD || CF
∴ AECD — параллелограмм.
⇒ AD = CE …(1)
[ ∵ Противоположные стороны параллелограмма равны]
Но AD = BC …(2) [Дано]
По (1) и (2), BC = CF
Теперь в ∆ BCF, имеем BC = CF
⇒ ∠CEB = ∠CBE …(3)
[∵ Углы, противоположные равным сторонам треугольника, равны]
Кроме того, ∠ABC + ∠CBE = 180° … (4)
[Линейное пара]
и ∠A + ∠CEB = 180° …(5)
[Со-внутренние углы параллелограмма ADCE]
Из (4) и (5) получаем
∠ABC + ∠CBE = ∠A + ∠ ЦЕБ
⇒ ∠ABC = ∠A [Из (3)]
⇒ ∠B = ∠A …(6)
(ii) AB || CD и AD — трансверсаль.
∴ ∠A + ∠D = 180° …(7) [Со-внутренние углы]
Аналогично, ∠B + ∠C = 180° … (8)
Из (7) и (8) получаем
∠A + ∠D = ∠B + ∠C
⇒ ∠C = ∠D [Из (6)]
(iii) В ∆ABC и ∆BAD имеем
AB = BA [Общее]
BC = AD [Дано]
∠ABC = ∠BAD [доказано]
∴ ∆ABC = ∆BAD [согласно SAS]
(iv) Поскольку ∆ABC = ∆BAD [доказано]
⇒ AC = BD [согласно C.P.C.T.]
Решения NCERT для класса 9 по математике Глава 8 Четырехугольники (चतुर्भुज) (средний хинди) Ex 8.1
Решения NCERT для математики класса 9 Глава 8 Четырехугольники Пр 8.2
Вопрос 1.
ABCD — четырехугольник, в котором P, Q, R и S — середины сторон AB, BC, CD и DA (см. рисунок). АС — диагональ. Покажите, что
(i) SR || AC и SR = \(\frac { 1 }{ 2 }\) AC
(ii) PQ = SR
(iii) PQRS является параллелограммом.
Решение:
(i) В ∆ACD имеем
∴ S — середина AD, а R — середина CD.
SR = \(\frac { 1 }{ 2 }\)AC и SR || AC …(1)
[По теореме о средней точке]
(ii) В ∆ABC точка P — середина AB, а Q — середина BC.
PQ = \(\frac { 1 }{ 2 }\)AC и PQ || AC …(2)
[По теореме о средней точке]
Из (1) и (2) получаем
PQ = \(\frac { 1 }{ 2 }\)AC = SR и PQ || переменный ток || СР
⇒ PQ = SR и PQ || SR
(iii) В четырехугольнике PQRS
PQ = SR и PQ || SR [Proved]
∴ PQRS — параллелограмм.
Вопрос 2.
ABCD — ромб, а P, Q, R и S — середины сторон AB, BC, CD и DA соответственно. Докажите, что четырехугольник PQRS является прямоугольником.
Решение:
У нас есть ромб ABCD и точки P, Q, R и S являются серединами сторон AB, BC, CD и DA соответственно. Присоединяйтесь к АС.
В ∆ABC P и Q являются серединами AB и BC соответственно.
∴ PQ = \(\frac { 1 }{ 2 }\)AC и PQ || AC …(1)
[По теореме о средней точке]
В ∆ADC R и S являются серединами CD и DA соответственно.
∴ SR = \(\frac { 1 }{ 2 }\)AC и SR || AC …(2)
[По теореме о средней точке]
Из (1) и (2) получаем
PQ = \(\frac { 1 }{ 2 }\)AC = SR и PQ || переменный ток || SR
⇒ PQ = SR и PQ || SR
∴ PQRS — параллелограмм.
…….(3)
Теперь в ∆ERC и ∆EQC
∠1 = ∠2
[ ∵ Диагонали ромба делят противоположные углы пополам]
CR = CQ [ ∵\(\frac { CD }{ 2 }\) = \(\frac { BC }{ 2 }\)]
CE = CE [Common]
∴ ∆ERC ≅ ∆EQC [согласно SAS ]
⇒ ∠3 = ∠4 …(4) [По C.P.C.T.]
Но ∠3 + ∠4 = 180° ……(5) [Линейная пара]
Из (4) и (5) получаем
⇒ ∠ 3 = ∠4 = 90°
Теперь ∠RQP = 180° – ∠b [Y Со-внутренние углы для PQ || AC и EQ поперечно]
Но ∠5 = ∠3
[ ∵ Вертикально противоположные углы равны]
∴ ∠5 = 90°
Итак, ∠RQP = 180° – ∠5 = 90°
∴ Один угол параллелограмма PQRS 90°.
Таким образом, PQRS представляет собой прямоугольник.
Вопрос 3.
ABCD — прямоугольник, а P, Q, R и S — середины сторон AB, BC, CD и DA соответственно. Докажите, что четырехугольник PQRS является ромбом.
Решение:
Имеем,
Теперь в ∆ABC имеем
PQ = \(\frac { 1 }{ 2 }\)AC и PQ || AC …(1)
[По теореме о средней точке]
Аналогично, в ∆ADC имеем
SR = \(\frac { 1 }{ 2 }\)AC и SR || AC …(2)
Из (1) и (2) получаем
PQ = SR и PQ || SR
∴ PQRS — параллелограмм.
Теперь в ∆PAS и ∆PBQ имеем
∠A = ∠B [каждые 90°]
AP = BP [ ∵ P — середина AB]
AS = BQ [∵ \(\frac { 1 }{ 2 }\)AD = \(\frac { 1 }{ 2 }\)BC]
∴ ∆PAS ≅ ∆PBQ [согласно SAS]
⇒ PS = PQ [согласно C.P.C.T.]
Кроме того, PS = QR и PQ = SR [∵противоположные стороны параллелограмма равны]
Итак, PQ = QR = RS = SP, т. е. PQRS — параллелограмм, у которого все стороны равны.
Следовательно, PQRS — ромб.
Вопрос 4.
ABCD — трапеция, в которой AB || DC, BD — диагональ, а E — середина AD. Через Е проведена прямая, параллельная АВ, пересекающая ВС в точке F (см. рисунок). Докажите, что F — середина BC.
Решение:
У нас есть,
В ∆DAB мы знаем, что E является средней точкой
AD и EG || АВ [∵ ЭФ || AB]
Используя обратную теорему о средней точке, мы получаем, что G является средней точкой BD.
Снова в ABDC мы имеем G — середину BD и GF || ОКРУГ КОЛУМБИЯ.
[∵ АВ || DC и EF || AB и GF являются частью EF]
Используя обратную теорему о средней точке, мы получаем, что F является серединой BC.
Вопрос 5.
В параллелограмме ABCD точки E и F являются серединами сторон AB и CD соответственно (см. рисунок). Докажите, что отрезки AF и EC пересекают диагональ BD пополам.
Решение:
Так как противоположные стороны параллелограмма параллельны и равны.
∴ АВ || DC
⇒ AE || FC …(1)
и AB = DC
⇒ \(\frac { 1 }{ 2 }\)AB = \(\frac { 1 }{ 2 }\)DC
⇒ AE = FC …(2)
From (1) и (2), имеем
AE || PC и AE = PC
∴ ∆ECF — параллелограмм.
Теперь в ∆DQC мы имеем F — середину DC и FP || CQ
[∵ AF || CE]
⇒ DP = PQ …(3)
[По обращению теоремы о средней точке] Аналогично, в A BAP E является средней точкой AB, а EQ || АП [∵AF || CE]
⇒ BQ = PQ …(4)
[В силу обращения теоремы о средней точке]
∴ Из (3) и (4) имеем
DP = PQ = BQ
Итак, отрезки AF и EC пересекают диагональ пополам. БД.
Вопрос 6.
Докажите, что отрезки, соединяющие середины противоположных сторон четырехугольника, делят друг друга пополам.
Решение:
Пусть ABCD — четырехугольник, где P, Q, R и S — середины сторон AB, BC, CD и DA соответственно.
Присоединитесь к PQ, QR, RS и SP.
Давайте также присоединимся к PR, SQ и AC.
Теперь в ∆ABC мы имеем P и Q — середины сторон AB и BC соответственно.
∴ ПК || AC и PQ = \(\frac { 1 }{ 2 }\) AC …(1)
[по теореме о средней точке]
Аналогично, RS || AC и RS = \(\frac { 1 }{ 2 }\)AC …(2)
∴ Из (1) и (2) получаем
PQ || RS, PQ = RS
∴ PQRS — параллелограмм.
А диагонали параллелограмма делят друг друга пополам, т. е. PR и SQ делят друг друга пополам. Таким образом, отрезки, соединяющие середины противоположных сторон четырехугольника ABCD, делят друг друга пополам.
Вопрос 7.
ABC — треугольник с прямым углом в точке C. Прямая, проходящая через середину M гипотенузы AB и параллельная BC, пересекает AC в D. Докажите, что
(i) D — середина AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac { 1 }{ 2 }\)AB
Решение:
имеем
(i) В ∆ACB имеем
M – середина -точка АВ.
Leave A Comment