Уравнение движения — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. Уравнение движения
Пояснения к первому слайду:Самое простое движение – это движение тела по
прямой и с постоянной скоростью (V).Скорость
такого движения не изменяется с течением времени,
она постоянная: V = constanta. Движение тела
можно изобразить геометрически. Для этого
используется числовая ось, эта прямая линия, на
которой расставлены координаты, числа.
(Показываю на доске).
 Условие движения нужно
Условие движения нужносекундомер «пошел»), движение прекратилось
(t=0).Теперь надо указать направление движения.
Оно может быть направлено с право на лево, или
обратно слева на право.
Любая числовая ось имеет направление. Любая
координата расположенная справа больше
координаты расположенной левее. Координаты
Продолжение второго слайда
Движение тела с постоянной скоростью (V = constanta) и начало самого движения
(t>0) и обозначение этого процесса мы умеем. Но прежде, чем начать движение
оно должно где-то стоять. Место стоянки любого тела, её начальная координата
так же обозначаются на числовой оси как Х0. Тело в момент времени t = 0 стоит
(показываю эти координаты на доске!!!). Движение слева на право совпадает с
направлением числовой оси – это движение в положительном направление (+), а
если тела движется с права на лево, то тело движется против направления
числовой оси – это движение в отрицательном направлении (-).

Тело может двигаться с различной скоростью и различную величину скорости
можем обозначить величиной отрезков, которые имеют различную длина – длина
отрезков всегда число положительное, оно не может быть отрицательным. Эта
Все величины должны выражаться в системе СИ (пояснить кратко размерность
СИ, СГСЕ и другие системы измерения)
.
Как обозначить движение тела, движущееся по прямой и с постоянной скоростью.
Допустим тело движется слева на право с постоянной скоростью и прямолинейно.
Величина скорости 5 км и начальная координата движения Хо = 3. Тело находится
в начале движение в точке Хо=3, От точки Хо=3 откладываю на право отрезок
равный 5, конец отрезка совпадает с числом 8, конец обозначают стрелой –
указывает на направление движения. Тело двигалось 4 секунды, путь пройденный
просто: X(4) = Xo +V*t =3+20=23 (X – конечная координата тела, конец движения.

Аналогия (подобие): Х = Хо + V*t =3 +5*4 =23, а для любого момента времени t
уравнение движения будет иметь вид: X(t) =Xo + V*t или X(t) = 3 + 5t, где Хо = 3, а
V*t = 5t, где V=5, а Хо=3, движение совпадает с направление числовой оси поэтому
вектор скорости 5 положительный. Напишите это движение с начальной
координатой Хо = 3 и скоростью V= -5. Оно будет выглядеть так: Х(t) = 3-5t.
Рассмотрим уравнения 1, 2 и 3 определим в этих уравнениях параметры Xo и V?
Как построить графики этих уравнений:
1) Х =-2 + 4t
Тело стоит, значит t = 0. В первом и во втором
уравнении координата Х зависит от t, а в третьем Х= -3
2) X = t
-времени t. Это значит, что тело не движется, а ее
начальная координата Хо = -3.
3) X = — 3
Как только тела начинают движение, переменная t
становится больше 0.
Обозначения:
Тела стоят, движения тел не происходит, тогда t = 0;
Тела начали двигаться, тогда t > 0.
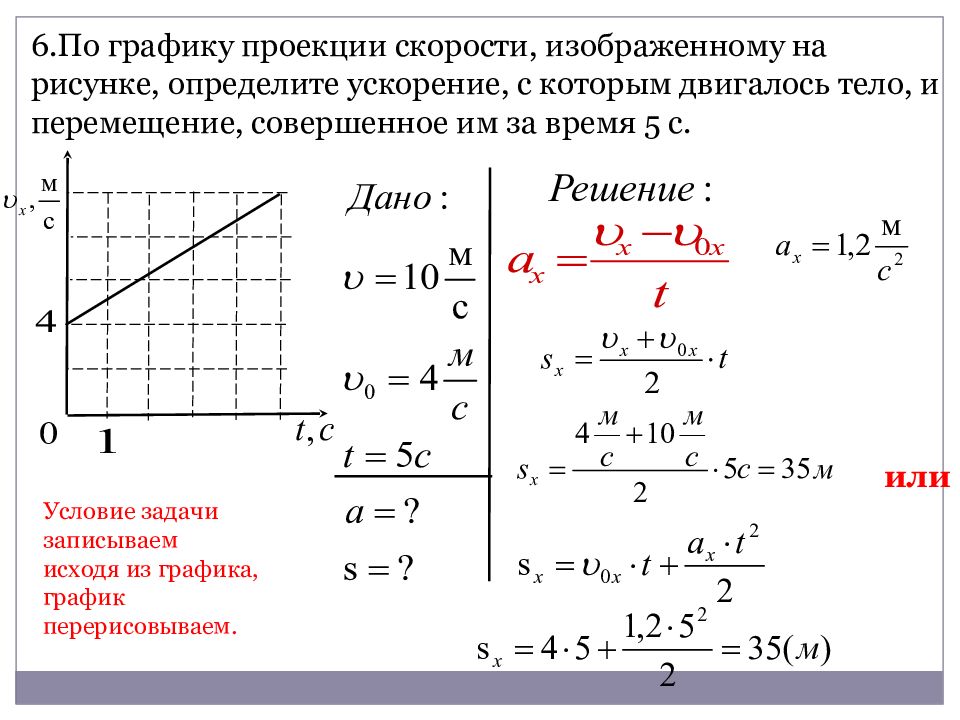
Если тело стоит, то t = 0, тогда уравнение первое Х = -2 + 4*0 = -2, при t = 0, Х
Даны три уравнения движения нужно изобразить
эти УДВ графически
Даны три графика движени – 1, 2 и 3. Нужно для каждой
прямой написать уравнение движения, определить начальное
положение и скорость движения:
Даны три графика (1,2,3.) для каждого
графиков нужно определить Хо и Vx и
написать УДВ
Равноускоренное прямолинейное движение
1. Ускорение равно изменению скорости ΔV, которое произошло за время
Δt, то есть, тело в момент времени t1 имело скорость v1, а в момент
времени t2 –скорость v2, тогда изменение времени Δt = t2 – t1, а
изменение скорости за время Δt будет Δv=V2 – V1. Ускорение равно
2. Ускорение это векторная величина, поэтому на слайде даны их обозначения
даны в трех вариантах (см. слайд 19, т.е. следующий).
Равноускоренное движение.
 Изменение скорости
Изменение скоростипри постоянном ускорении
Даны три прямые надо написать для этих прямых уравнения движения
определить для каждой прямой начальную скорость Vo, ускорение а и
начальную координату Хо.
1. Изменение скорости в зависимости от времени t:
Vx =Vo + ax*t; ax = (Vx – Vo)/t
Vo = 2, t = 4, Vx = 4, ax = 0,5
2. И так далее…..
Зависимость скорости Vx от времени t
Рис.2
Продолжение слайда 23 (рис.1; рис.2)
Сложение и вычитание векторов
Относительная скорость
English Русский Правила
Движение тела, брошенного горизонтально или под углом к горизонту.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Движение тела, брошенного горизонтально или под…
Движение тела, брошенного горизонтально или под углом к горизонту. | ||
| ||
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное. | ||
Движение тела, брошенного горизонтально. | ||
Выразим проекции скорости и координаты через модули векторов.
| ||
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y: | ||
| — между координатами квадратичная зависимость, траектория – парабола! | ||
Движение тела, брошенного под углом к горизонту. | ||
Порядок решения задачи аналогичен предыдущей. Решим задачу для случая х0=0 и y0=0. | ||
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории): . Мы получили квадратичную зависимость между координатами. Значит траектория — парабола. | ||
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0. | Время полета: | |
| Следовательно, для решения этой задачи необходимо решить уравнение | ||
| Оно будет иметь решение при t=0 (начало движения) и | ||
Зная время полета, найдем максимальное расстояние, которое пролетит тело: | Дальность полета:
| |
Из этой формулы следует, что: — максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450; — на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т. | ||
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело. | Время подъема: | |
Тогда: | Максимальная высота:
| |
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна | ||
Угол, под которым направлен вектор скорости в любой момент времени: | ||
Теги:
конспект
Объем распространения — StatPearls
Книжная полка NCBI. Служба Национальной медицинской библиотеки, Национальных институтов здоровья.
StatPearls [Интернет]. Остров сокровищ (Флорида): StatPearls Publishing; 2023 янв.
StatPearls [Интернет].
Показать подробности
Критерий поиска
Асад Мансур; Навид Махабади.
Информация об авторе и организациях
Последнее обновление: 25 июля 2022 г.
Определение/Введение
Объем распределения (Vd) представляет собой фармакокинетический параметр, отражающий склонность отдельного лекарственного средства либо оставаться в плазме, либо перераспределяться в другие отделы тканей. По определению, Vd представляет собой константу пропорциональности , которая связывает общее количество лекарства в организме с его концентрацией в плазме в данный момент времени.[1][2][3] Следующее уравнение может представить Vd:
Объем распределения (л) = Количество лекарства в организме (мг) / Концентрация лекарства в плазме (мг/л)
На основании приведенного выше уравнения:
Лекарство с высокой Vd склонно покидать плазму и попадать во внесосудистые отделы организма, что означает, что более высокая доза лекарственного препарата требуется для достижения заданной концентрации в плазме.
 (Высокий Vd -> Большее распространение в другие ткани)
(Высокий Vd -> Большее распространение в другие ткани)И наоборот, лекарство с низким Vd имеет склонность оставаться в плазме, что означает более низкая доза лекарственного средства требуется для достижения заданной концентрации в плазме. (Низкий Vd -> меньшее распространение в другие ткани)
Вопросы, вызывающие озабоченность
Общие принципы, связанные с распространением лекарств
Фармакокинетика фокусируется на перемещении лекарственных средств по организму человека посредством процессов всасывания , распределения и выведения . После введения лекарство перемещается из места введения и всасывается в системный кровоток, откуда затем распространяется по всему телу. Процесс распределения относится к перемещению лекарственного средства между внутрисосудистыми (кровь/плазма) и внесосудистыми (внутриклеточными и внеклеточными) отделами организма. В каждом отделе организма лекарство находится в равновесии между связанной с белком или свободной формой. Со временем лекарства в кровотоке будут метаболизироваться и выводиться из организма печенью и почками.[1][3]
Со временем лекарства в кровотоке будут метаболизироваться и выводиться из организма печенью и почками.[1][3]
Модели с одним и несколькими отсеками раздачи
Сразу после внутривенного болюсного введения лекарство попадает в «центральное» отделение, , состоящее из плазмы, органов с высокой перфузией (печень, почки и т. д.) и других тканей, в которых лекарство распределяется мгновенно. В конце концов, некоторые лекарства могут начать перемещаться из центрального компартмента в «периферический» компартмент , который состоит из тканей, в которых лекарство распределяется медленнее.[1][2][3][4]
Лекарственные препараты, для которых кинетика распределения в одном компартменте представлена прямолинейным графиком на кривых зависимости плазмы от времени. Поскольку считается, что лекарство распределяется мгновенно, начальную концентрацию лекарства в плазме в момент времени = 0 (Co) трудно измерить, и поэтому она оценивается путем экстраполяции до времени = 0 на кривой зависимости концентрации в плазме от времени. [1] [2] ][3]
[1] [2] ][3]
Многокомпонентная модель: Большинство лекарств имеют более медленную кинетику распределения, которая включает раннюю фазу распределения, за которой следует более поздняя фаза выведения. Препараты, отображающие 9Многокамерные модели 0031 распределения будут перемещены из центрального отделения в периферийные перед устранением.[1][2][3][4][5] Фазы, связанные с многокомпонентными моделями распределения, включают:
Фаза распространения: после введения концентрация препарата в плазме сначала снижается, в то время как общее количество препарата в организме остается прежним. Это явление приведет к тому, что одно лекарство будет иметь кратных значения Vd, каждое из которых зависит от времени.
Конечная фаза выведения : После фазы распределения лекарство выводится из центрального компартмента (почками/печенью), вызывая изменения как количества лекарства в организме, так и концентрации лекарства в плазме.
 Следовательно, дополнительные значения Vd можно рассчитать во время терминала фаза элиминации (Vбета), которая представляет собой значение Vd, зависящее от клиренса препарата .
Следовательно, дополнительные значения Vd можно рассчитать во время терминала фаза элиминации (Vбета), которая представляет собой значение Vd, зависящее от клиренса препарата . Стабильное состояние: Между фазами распределения и элиминации существует переходная точка, известная как «устойчивое состояние». Стабильное состояние представляет собой период «динамического равновесия» лекарственного средства по всему телу, в течение которого лекарство полностью распределяется между центральным и периферическим отделами. В стационарном состоянии суммарный поток лекарства между центральным и периферическим отделами равен 0. Во время стационарного состояния можно рассчитать другое значение Vd ( ВСС ). Это значение, как правило, является наиболее клинически значимым, поскольку оно используется для определения нагрузочной дозы лекарственного средства.
Лекарственные препараты, демонстрирующие кинетику распределения в нескольких компартментах, имеют графики, представляющие собой двухфазные линии на кривых зависимости плазмы от времени.
Период полувыведения и объем распределения
Период полувыведения (t1/2) означает время, необходимое для снижения концентрации препарата в плазме на 50%. t1/2 зависит от константы скорости (k), которая связана с Vd и клиренсом (CL).[1][2][3] Период полураспада можно выразить с помощью следующих уравнений:
Только лекарство, находящееся в центральном отделе, может быть выведено из организма, поскольку процесс выведения в основном осуществляется печенью и почками. В препаратах с высоким Vd большая часть препарата остается за пределами центрального отсека. Между тем, часть лекарственного средства в плазме будет элиминирована, что приведет к смещению равновесия, в результате чего лекарство, находящееся в периферическом отделе, сместится в центральное отделение. Этот сдвиг приведет к тому, что концентрация в плазме останется постоянной, несмотря на удаление лекарства из организма. Это явление вызывает более медленное снижение концентрации в плазме во время фазы элиминации в условиях высокого Vd. [1][3]
[1][3]
Следовательно, при постоянной скорости клиренса лекарство с высоким Vd будет более длительным элиминированием период полувыведения , чем у препарата с более низким Vd.
Подобно различным значениям Vd, которые существуют в зависимости от фармакокинетической фазы, также важно знать два значения периода полувыведения:
Период полувыведения распределения (t1/2a), который представляет собой количество времени, необходимое для снижения концентрации в плазме на 50% во время фазы распределения.
Период полувыведения (t1/2b), который представляет собой количество времени, необходимое для снижения концентрации в плазме на 50% в течение фазы выведения.
Особенности лекарственных средств, влияющие на объем распределения
Кислотно-основные характеристики
Как обсуждалось ранее, лекарства могут иметь склонность связывать белки по всему телу, где они достигают точки равновесия между связанной и несвязанной фазами.
 В зависимости от заряда лекарственного средства при физиологическом рН лекарство может иметь тенденцию связывать макромолекулы внутри или вне плазмы.[2]
В зависимости от заряда лекарственного средства при физиологическом рН лекарство может иметь тенденцию связывать макромолекулы внутри или вне плазмы.[2]Основные (щелочные) молекулы сильно взаимодействуют с отрицательно заряженными головными группами фосфолипидов, расположенными на фосфолипидных мембранах. Степень этого связывания также зависит от общей липофильности препарата. Как правило, основные молекулы покидают системный кровоток, что приводит к выше Vd по сравнению с кислотными молекулами.
Кислые молекулы имеют более высокое сродство к молекулам альбумина при более низкой липофильности, чем нейтральные или основные молекулы. Следовательно, кислые препараты с большей вероятностью связывают альбумин и остаются в плазме, что приводит к снижению Vd по сравнению с более основными молекулами.
Липофильность
Помимо взаимодействий, связанных с ионами/зарядом, между лекарственным средством и макромолекулами аналогичную роль играют и гидрофобные взаимодействия.
 Препараты с более высокой липофильностью обладают более высокой проницаемостью липидной мембраны и, следовательно, более высокой вероятностью выхода из плазмы и взаимодействия с другими гидрофильными остатками в периферических тканях (например, в жировой ткани). Однако белки плазмы, такие как альбумин, обладают высоким сродством к липофильным препаратам, и в этом случае определяющим фактором степени связывания с белками плазмы двух одинаково липофильных препаратов являются кислотно-основные характеристики, как описано выше.[2] Но в целом действуют следующие принципы:
Препараты с более высокой липофильностью обладают более высокой проницаемостью липидной мембраны и, следовательно, более высокой вероятностью выхода из плазмы и взаимодействия с другими гидрофильными остатками в периферических тканях (например, в жировой ткани). Однако белки плазмы, такие как альбумин, обладают высоким сродством к липофильным препаратам, и в этом случае определяющим фактором степени связывания с белками плазмы двух одинаково липофильных препаратов являются кислотно-основные характеристики, как описано выше.[2] Но в целом действуют следующие принципы:Липофильные молекулы с большей вероятностью проходят через липидные бислои и, следовательно, с большей вероятностью покидают кровоток и распределяются в области с высокой плотностью липидов (жировая ткань) и, следовательно, имеют более высокое значение Вд.
Гидрофильные молекулы с меньшей вероятностью проходят через липидные бислои и, следовательно, с большей вероятностью остаются в кровотоке и, следовательно, имеют более низкий Вд.

Клиническая значимость
Как обсуждалось ранее, множественные значения Vd могут быть рассчитаны в зависимости от внутренней кинетики лекарственного средства (модели с одним или несколькими компартментами), а также фазы кинетики лекарственного средства после введения лекарственного средства ( фаза распределения по сравнению с устойчивым состоянием по сравнению с терминальной фазой элиминации). Однако, с клинической точки зрения, одиночное наиболее важное применение Vd — это расчет нагрузочной дозы лекарства .[1][3]
Нагрузочную дозу лучше всего рассчитывать с использованием Vd в равновесном состоянии (Vss), поскольку он наиболее точно отражает фармакокинетические свойства конкретных препаратов при желаемой равновесной концентрации в плазме. Таким образом, нагрузочную дозу можно рассчитать по следующей формуле:
После введения нагрузочной дозы можно вводить дополнительные поддерживающие дозы для поддержания желаемой концентрации препарата в плазме. В отличие от нагрузочной дозы, которая зависит от Vd препарата, поддерживающая доза зависит от клиренса (Cl) [3]. Поддерживающую дозировку можно рассчитать по следующему уравнению:
В отличие от нагрузочной дозы, которая зависит от Vd препарата, поддерживающая доза зависит от клиренса (Cl) [3]. Поддерживающую дозировку можно рассчитать по следующему уравнению:
Ключевые различия между нагрузочными дозами и поддерживающими дозами включают:
Нагрузочная доза зависит от объема распределения , в то время как поддерживающая доза зависит от плазменного клиренса. [3]
Нагрузочная доза требуется только для некоторых препаратов в определенных ситуациях , в то время как поддерживающая доза требуется для большинства препаратов для поддержания равновесной концентрации в плазме.[3]
Ударная доза редко необходимо изменить в то время как поддерживающие дозы необходимо изменить 9002 2 в зависимости от различных характеристик пациента.
 [3]
[3]
Несмотря на то, что лекарства обладают неотъемлемыми свойствами, которые определяют Vd, пациенты также представляют собой переменные, которые могут изменить кажущийся Vd. Поэтому кажущийся Vd некоторых лекарств может значительно различаться между пациентами в зависимости от индивидуальной физиологии каждого пациента и/или патофизиологии . Например:
Дозировка для детей и взрослых — Состав тела меняется с возрастом, и, следовательно, это влияет на распределение лекарств, что означает, что нагрузочные дозы будут различаться для детей и взрослых.[6]
Ожирение в сравнении с нормальным ИМТ — Нагрузочные дозы таких препаратов, как анестетики, могут быть рассчитаны на основе различных скалярных значений веса, таких как общая масса тела в сравнении с идеальной массой тела, в зависимости от фармакокинетики конкретных препаратов, чтобы предотвратить передозировку или недостаточную дозировку.
 [7] [8]
[7] [8]Состояния, влияющие на концентрацию белков плазмы – Избыток или недостаток белков плазмы (например, альбумина) может влиять на количество препарата, остающегося в плазме, и, следовательно, на кажущийся Vd.[1][5][9]
Понимание объема распределения важно как для врачей, так и для фармакологов, которые назначают и дозируют лекарства. Дифференциация фармакологических агентов с высоким и низким объемом распределения имеет важное значение для правильного дозирования лекарств для пациентов. В то время как врачи обычно дозируют лекарства в случаях низкой сложности, пациентам в отделении интенсивной терапии может потребоваться дозировка лекарств фармацевтом. Понимание и расчет различных моделей распределения, факторов, которые могут повлиять на объем распределения, нагрузочную дозу и поддерживающую дозу, могут означать разницу между жизнью и смертью. При дозировании лекарств крайне важно своевременно проконсультироваться с межпрофессиональной группой специалистов.
Контрольные вопросы
Доступ к бесплатным вопросам с несколькими вариантами ответов по этой теме.
Комментарий к этой статье.
Ссылки
- 1.
Oie S. Распространение и связывание лекарств. Дж. Клин Фармакол. 1986 ноябрь-декабрь; 26 (8): 583-6. [PubMed: 3793947]
- 2.
Смит Д.А., Бомонт К., Маурер Т.С., Ди Л. Объем распределения при разработке лекарств. J Med Chem. 2015 13 августа; 58 (15): 5691-8. [В паблике: 25799158]
- 3.
Toutain PL, Bousquet-Mélou A. Объемы распределения. J Vet Pharmacol Ther. 2004 декабрь; 27 (6): 441-53. [PubMed: 15601439]
- 4.
Fan J, de Lannoy IA. Фармакокинетика. Биохим Фармакол. 2014 01 января; 87 (1): 93-120. [PubMed: 24055064]
- 5.
Faed EM. Связывание лекарств с белками в плазме, интерстициальной жидкости и тканях: влияние на фармакокинетику. Eur J Clin Pharmacol.
 1981;21(1):77-81. [В паблике: 7333350]
1981;21(1):77-81. [В паблике: 7333350]- 6.
Mahmood I. Дозирование у детей: критический обзор фармакокинетического аллометрического масштабирования и подходов к моделированию при разработке педиатрических препаратов и клинических условиях. Клин Фармакокинет. 2014 апрель; 53(4):327-46. [PubMed: 24515100]
- 7.
Casati A, Putzu M. Анестезия у пациентов с ожирением: фармакокинетические соображения. Джей Клин Анест. 2005 март; 17(2):134-45. [PubMed: 15809132]
- 8.
Цукерман М., Греллер Х.А., Бабу К.М. Обзор токсикологических последствий ожирения. J Med Toxicol. 2015 сен; 11 (3): 342-54. [Бесплатная статья PMC: PMC4547963] [PubMed: 26108709]
- 9.
Czock D, Keller F, Rasche FM, Häussler U. Фармакокинетика и фармакодинамика системно вводимых глюкокортикоидов. Клин Фармакокинет. 2005;44(1):61-98. [PubMed: 15634032]
Copyright © 2023, StatPearls Publishing LLC.


 (Высокий Vd -> Большее распространение в другие ткани)
(Высокий Vd -> Большее распространение в другие ткани) Следовательно, дополнительные значения Vd можно рассчитать во время терминала фаза элиминации (Vбета), которая представляет собой значение Vd, зависящее от клиренса препарата .
Следовательно, дополнительные значения Vd можно рассчитать во время терминала фаза элиминации (Vбета), которая представляет собой значение Vd, зависящее от клиренса препарата .  В зависимости от заряда лекарственного средства при физиологическом рН лекарство может иметь тенденцию связывать макромолекулы внутри или вне плазмы.[2]
В зависимости от заряда лекарственного средства при физиологическом рН лекарство может иметь тенденцию связывать макромолекулы внутри или вне плазмы.[2]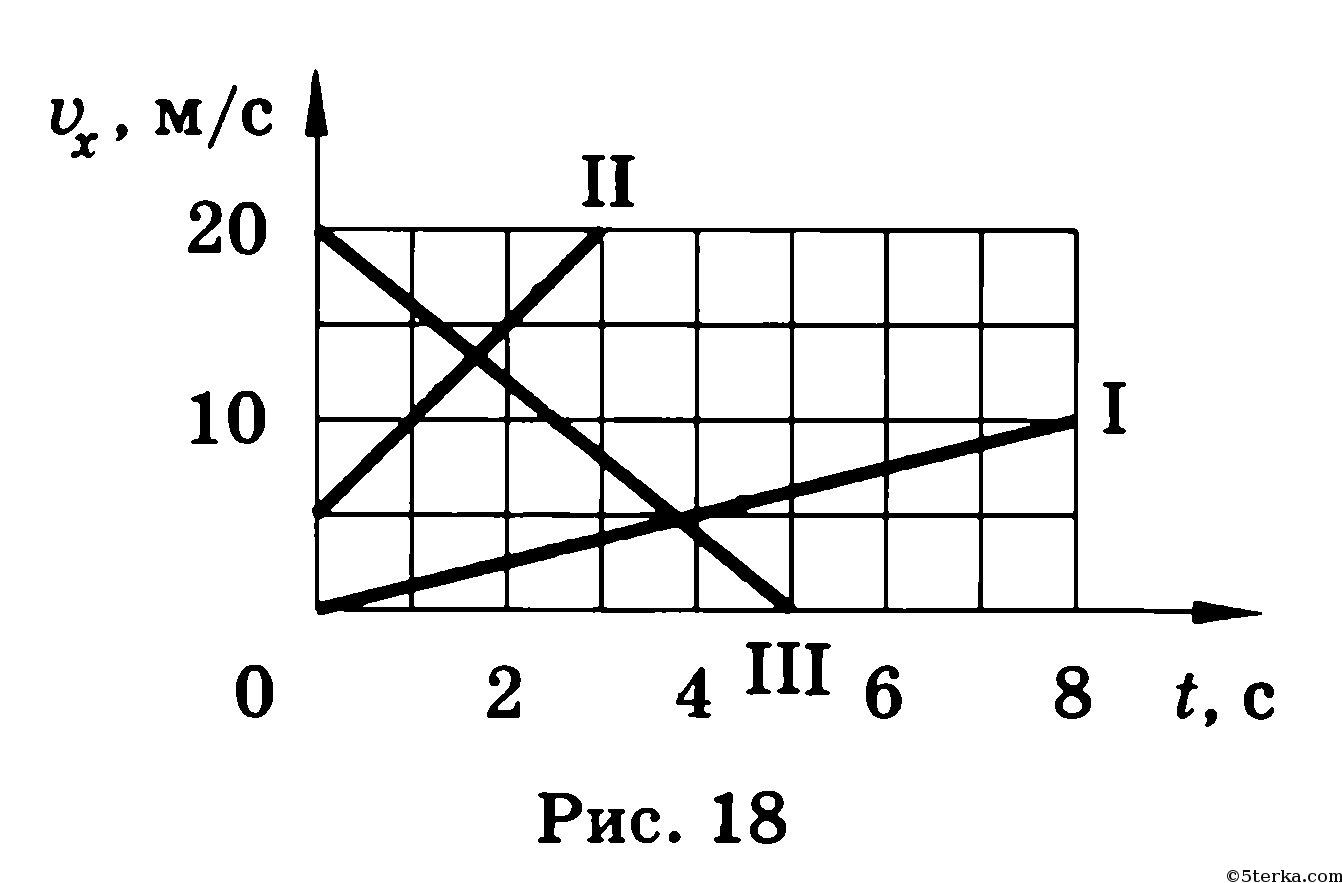 Препараты с более высокой липофильностью обладают более высокой проницаемостью липидной мембраны и, следовательно, более высокой вероятностью выхода из плазмы и взаимодействия с другими гидрофильными остатками в периферических тканях (например, в жировой ткани). Однако белки плазмы, такие как альбумин, обладают высоким сродством к липофильным препаратам, и в этом случае определяющим фактором степени связывания с белками плазмы двух одинаково липофильных препаратов являются кислотно-основные характеристики, как описано выше.[2] Но в целом действуют следующие принципы:
Препараты с более высокой липофильностью обладают более высокой проницаемостью липидной мембраны и, следовательно, более высокой вероятностью выхода из плазмы и взаимодействия с другими гидрофильными остатками в периферических тканях (например, в жировой ткани). Однако белки плазмы, такие как альбумин, обладают высоким сродством к липофильным препаратам, и в этом случае определяющим фактором степени связывания с белками плазмы двух одинаково липофильных препаратов являются кислотно-основные характеристики, как описано выше.[2] Но в целом действуют следующие принципы:
 [3]
[3]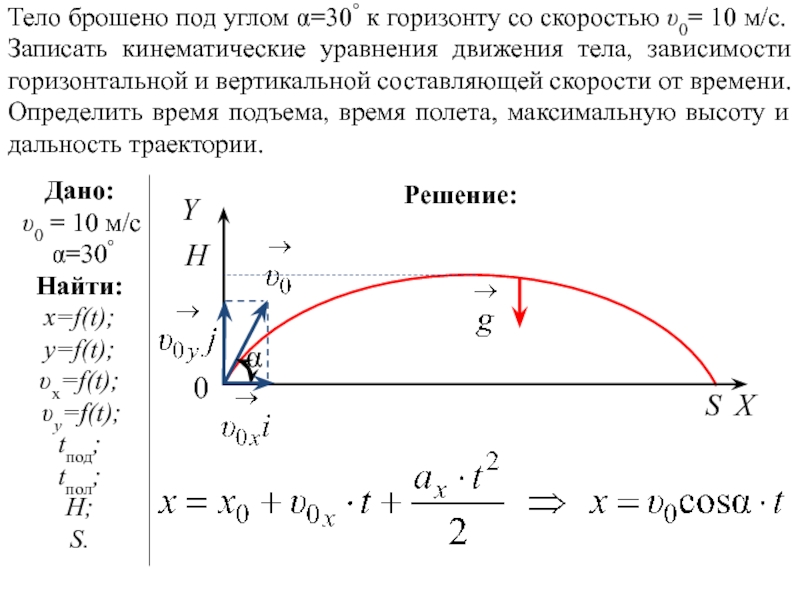 [7] [8]
[7] [8] 1981;21(1):77-81. [В паблике: 7333350]
1981;21(1):77-81. [В паблике: 7333350]
Leave A Comment