Решу егэ математика 500997 — Математика и Английский
Решу егэ математика 500997
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 2 № 500997
В классе 21 учащийся, среди них две подруги — Аня и Нина. Учащихся случайным образом разбивают на 7 равных групп. Найдите вероятность того, что Аня и Нина окажутся в одной группе.
Пусть Аня оказалась в некоторой группе. Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности. Вероятность этого события равна 2 : 20 = 0,1.
Изложим решение иначе.
Пусть Аня оказалась в некоторой группе. Нина может занять любое из оставшихся 20 мест в любой из оставшихся групп. Ровно два места будут в группе с Аней. Поэтому искомая вероятность равна 2 : 20 = 0,1.
Приведем комбинаторное решение.
Всего способов выбрать 3 учащихся из 21 учащегося класса равно Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
Добавить в эту группу еще одного из оставшихся 19 учащихся можно способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна Если Аня уже находится в первой группе, то вероятность того, что Нина окажется в этой же группе равна Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна
Задание 2 № 500997
—>
В классе 21 учащийся, среди них две подруги Аня и Нина.
Ege. sdamgia. ru
25.05.2020 4:52:44
2020-05-25 04:52:44
Источники:
Https://ege. sdamgia. ru/problem? id=500997
Решу ЕГЭ математика профиль 2022 » /> » /> .keyword { color: red; }
Решу егэ математика 500997Решу ЕГЭ математика профиль 2022 поможет подготовиться к единому государственному экзамену по математике, который поводится в качестве обязательного для всех выпускников средних учебных заведений, то есть школ, лицеев и гимназий.
Математика
Что представляет собой ЕГЭ математика? Данный экзамен разделён на два уровня: базовый и профильный. Первый предназначен для тех выпускников, которые не планируют продолжать обучение в вузах вовсе, а также для тех, кто поступает в вузы, где в качестве вступительных испытаний отсутствует предмет «Математика».
Профильный уровень предназначен для выпускников, планирующих продолжать обучение в высших учебных заведениях, при поступлении в которые необходимо сдавать математику.
Отыскать тренировочные варианты как базового, так и профильного уровней можно на ресурсе Решу ЕГЭ. Обновление таких вариантов происходит каждый месяц. При этом варианты составляются из новых заданий, а также тех заданий, которые оказались наиболее сложными по результатам предшествующего месяца. При желании можно обратиться не только к вариантам текущего, но и прошлых месяцев. Сделать это можно по ссылке «Прошлые месяцы». В результате откроется архив вариантов, где среди прочих представлен и 2022 год.
Решу ЕГЭ
После того как работа оказывается выполненной, система осуществляет проверку представленных ответов, показывает правильные решения, а также выставляет оценку.
Помимо тренировочных доступным является персональный вариант. Его формирование осуществляется искусственным интеллектом. Включает такой вариант 10 заданий, которые зависят от накопленной статистики. При этом учитывается текущий уровень, ранее решённые, нерешённые, а также вызвавшие затруднение задания. Для возможности выполнять задания персонального варианта требуется авторизоваться на портале Решу ЕГЭ, то есть осуществить вход в профиль. Перед этим в свою очередь необходимо выполнить регистрацию.
Для регистрации следует перейти по одноимённой ссылке, представленной в правой части веб-страницы Решу ЕГЭ. После этого будет предложено ввести свои данные. Это адрес электронной почты, который в дальнейшем будет использоваться в качестве логина. Также необходимо указать имя и фамилию. Далее следует дважды ввести пароль.
Регистрация
Зарегистрироваться на сайте может ученик, учитель и родитель. Пользователю необходимо выбрать подходящую ему роль. После регистрации родитель может сообщить своему ребёнку логин и попросить предоставить доступ к статистике. Это позволит получать уведомления, касающиеся домашних заданий и выставленных отметок. В том случае если дать разрешение на получение уведомлений с сайта в настройках браузера, то возможным станет получение уведомлений на своё устройство без необходимости заходить на сайт.
После того как все необходимые для регистрации данные указаны, нужно принять правила пользования сайтом и дать согласие на обработку персональных данных. Далее следует нажать на кнопку «Зарегистрироваться». В результате появится профиль на веб-ресурсе Решу ЕГЭ, вход в который можно осуществить в любое удобное для себя время.
Для того чтобы выполнить вход, потребуется указать электронную почту и пароль в специально предназначенных для этого полях в левой части сайта.
Вход в профиль
Помимо тренировочных и персонального вариантов доступным является и вариант учителя. Для того чтобы обратиться к нему, необходимо знать его номер. Такой номер следует указать в специально предназначенное для этого поле, после чего нажать на кнопку «Открыть».
Помимо прочего сайт Решу ЕГЭ позволяет осуществлять поиск в каталоге. Здесь можно искать задания демоверсий, банков пробных работ, прошедших экзаменов с решениями. Для поиска необходимо знать номер или текст задания, которые потребуется ввести в специально предназначенное для этого поле, а затем нажать на кнопку «Открыть».
Ещё одна возможность — конструктор варианта по типам и по темам, позволяющий целенаправленно тренироваться по конкретным темам. Конструктор позволяет составить вариант из нужного количества заданий, представленных в тех или иных разделах задачного каталога.
Что представляет собой базовый уровень математика 2022? Это 21 задание тестовой части, касающиеся вычислений, простейших текстовых задач, размеров и единиц измерений, чтения графиков и диаграмм, задач на квадратной решётке. Для успешной сдачи базового уровня экзамена также понадобятся знания и умения, связанные с вычислениями и преобразованиями, преобразованием выражений, простейших уравнений прикладной геометрии, начал теории вероятностей.
Базовый уровень
Среди тем представлены и выбор оптимального варианта, стереометрия, анализ графиков и диаграмм, планиметрия, неравенства, анализ утверждений, числа и свойства. Также предлагаются текстовые задачи и задачи на смекалку.
Что представляет собой ЕГЭ математика профильного уровня в 2022 году? Это 11 заданий тестовой части и 7 заданий развёрнутой. Какие именно темы охватывают задания, которые потребуется выполнить во время сдачи единого государственного экзамена?
Какие именно темы охватывают задания, которые потребуется выполнить во время сдачи единого государственного экзамена?
Задания тестовой части касаются простейших уравнений, начал теории вероятностей, планиметрии, вычислений и преобразований, стереометрии, производной и первообразной, задач с прикладным содержанием, текстовых задач, графиков функций, вероятностей сложных событий, наибольшего и наименьшего значения функций.
Профильный уровень
Развёрнутая часть профильного уровня ЕГЭ математика 2022 включает уравнения, стереомерическую задачу, неравенства, финансовую математику, планиметрическую задачу, задачу с параметром, задание на числа и их свойства.
Для того чтобы подготовиться к экзамену и успешно его сдать, среди прочего сайт Решу ЕГЭ предлагает выполнять задания, представленные в вариантах Александра Ларина. Такие задания подойдут для тех, кто ищет более сложные варианты, чем обычно предлагают на ЕГЭ. На веб-ресурсе можно отыскать задания с развёрнутым ответом. Новые условия размещаются по субботам, а решения появляются по пятницам.
Новые условия размещаются по субботам, а решения появляются по пятницам.
Таким образом, сайт Решу ЕГЭ позволяет подготовиться к экзамену по математике, выполняя задания различных вариантов. Здесь представлены как задания для тех, кто планирует сдавать базовый уровень данного предмета, так и для тех, кому необходимо сдавать профильный уровень математики для поступления в вузы.
Базовый уровень
Математика
Ещё одна возможность конструктор варианта по типам и по темам, позволяющий целенаправленно тренироваться по конкретным темам.
Reshu-ege. su
23.01.2019 18:18:45
2019-01-23 18:18:45
Источники:
Https://reshu-ege. su/matematika-profil-2022/
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; }
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 11 № 500997
В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
Пусть Аня оказалась в некоторой группе. Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности. Вероятность этого события равна 2 : 20 = 0,1.
Всего способов выбрать 3 учащихся из 21 учащегося класса равно Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна
Приведем еще одно решение.
Пусть Аня оказалась в некоторой группе, наберем к ней группу еще 2 человек. Вероятность того, что среди них не окажется Нины, равна Следовательно, вероятность противоположного события, состоящего в том, что девочки окажутся в одной группе, равна 1 − 0,9 = 0,1.
Задание 11 № 500997
—>
Среди них две подруги Аня и Нина.
Mathb-ege. sdamgia. ru
27.01.2018 1:44:37
2018-01-27 01:44:37
Источники:
Https://mathb-ege. sdamgia. ru/test? pid=500997
Решу егэ математика 500997 — Справочник — ЕГЭ 2022
Решу егэ математика 500997
Задание 4 № 500997
В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
Пусть Аня оказалась в некоторой группе. Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности. Вероятность этого события равна 2 : 20 = 0,1.
Приведем комбинаторное решение.
Всего способов выбрать 3 учащихся из 21 учащегося класса равно Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна
Приведем еще одно решение.
Пусть Аня оказалась в некоторой группе, наберем к ней группу еще 2 человек. Вероятность того, что среди них не окажется Нины, равна Следовательно, вероятность противоположного события, состоящего в том, что девочки окажутся в одной группе, равна 1 − 0,9 = 0,1.
Задание 4 № 500997
Вероятность этого события равна 2 20 0,1.
Math21-gve. sdamgia. ru
25.10.2018 21:16:07
2018-10-25 21:16:07
Источники:
Https://math21-gve. sdamgia. ru/problem? id=500997
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; }
Решу егэ математика 500997Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 2 № 320192
В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников. Вероятность того, что второй друг окажется среди этих 12 человек, равна 12 : 25 = 0,48.
Изложим решение иначе.
Пусть Андрей оказался в некоторой группе. Сергей может занять любое из оставшихся 25 мест. Из них 12 мест будут в группе с Андреем. Поэтому искомая вероятность равна 12 : 25 = 0,48.
Из них 12 мест будут в группе с Андреем. Поэтому искомая вероятность равна 12 : 25 = 0,48.
Приведем комбинаторное решение.
Всего способов выбрать 13 учащихся из 26 учащихся класса равно Выбрать пару «Андрей и Сергей» и поместить их в одну из двух групп можно способами. Добавить в эту группу еще одиннадцать из оставшихся 24 учащихся можно способами. Поэтому вероятность того, что мальчики окажутся в одной группе, равна
Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Андрей окажется в ней, равна Если Андрей уже находится в первой группе, то вероятность того, что Сергей окажется в этой же группе, равна Поскольку обе группы равноправны, вероятность того, что друзья окажутся в одной группе, равна
Приведем еще одно решение.
Пусть Андрей оказался в некоторой группе, наберем к нему в группу еще 12 человек из оставшихся 25. Вероятность того, что среди них не окажется Сергея, равна Следовательно, вероятность противоположного события, состоящего в том, что мальчики окажутся в одной группе, равна 1 − 0,52 = 0,48.
—>
Задание 2 № 320192
Приведем комбинаторное решение.
Ege. sdamgia. ru
03.08.2019 8:13:19
2019-08-03 08:13:19
Источники:
Https://ege. sdamgia. ru/problem? id=320192
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; }
Решу егэ математика 500997Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 11 № 500997
В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
Пусть Аня оказалась в некоторой группе. Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности. Вероятность этого события равна 2 : 20 = 0,1.
Приведем комбинаторное решение.
Всего способов выбрать 3 учащихся из 21 учащегося класса равно Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
Добавить в эту группу еще одного из оставшихся 19 учащихся можно способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна
Приведем еще одно решение.
Пусть Аня оказалась в некоторой группе, наберем к ней группу еще 2 человек. Вероятность того, что среди них не окажется Нины, равна Следовательно, вероятность противоположного события, состоящего в том, что девочки окажутся в одной группе, равна 1 − 0,9 = 0,1.
—>
Задание 11 № 500997
Всего способов выбрать 3 учащихся из 21 учащегося класса равно Выбрать пару Аня и Нина и поместить их в одну из семи групп можно способами.
Mathb-ege. sdamgia. ru
10.05.2020 19:10:32
2020-05-10 19:10:32
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=500997
sdamgia. ru/problem? id=500997
Второй финалист конкурса Intel по школьной истории
- Новости
- Витрина
Даниэла Лапидоус
31 января 2010 г. Финалист конкурса Intel Science Talent Search. Марк Петтингер вернулся с еще одним чеком, чтобы вознаградить ее исследовательские усилия в области астрофизики.
Накануне вечером родители Намраты сказали ей, что нет, они не получали никаких сообщений по электронной почте, сообщающих о чем-то важном. Извини. На следующий день она обнаружила, что идет к передней части спортзала, чтобы ее поздравили. На самом деле ее мама и папа знали о ее достижении за день до этого. «Нам было трудно держать это в себе, но мы не хотели портить сюрприз Намраты», — сказала Нина Ананд.
Намрата успешно оглушен. «Я был очень взволнован. Должна быть честной, я совсем этого не ожидала… Я чувствую себя такой польщенной», — сказала она. Она получила престижное звание и 7500 долларов за свою работу по химическому составу звезд в галактике Андромеды.
Ее исследование проводилось прошлым летом в «большой астрофизической лаборатории» Калифорнийского университета в Санта-Круз под руководством ее наставника, доктора Раджи Тхакурты. Два других полуфиналиста Intel также находились под его астрономической опекой: старшеклассники Эндрю Чжоу и Кевин Чжан. Вишеш Джайн изучал усовершенствования для диагностики сердечных заболеваний.
«Мой наставник был просто феноменален… он действительно дал нам троим необходимое руководство и предоставил нам доступ к этой огромной базе данных», — сказал Намрата. «В любом астрофизическом проекте вы полагаетесь в основном на данные, чтобы делать выводы, потому что сложно выйти в поле и поэкспериментировать».
В марте она примет участие в финальном этапе конкурса в Вашингтоне, округ Колумбия, чтобы побороться за главный приз в размере 100 000 долларов против 39 других. «Если они на самом деле говорят правду о президенте Обаме, я был бы в восторге от встречи с ним!» она сказала.
С самого детства Намрата знала, что хочет стать «каким-то ученым». Ее родители знали, что она подает заявку на участие в конкурсе Intel, но не оказывали на нее давления для достижения каких-либо конкретных целей.
Ее родители знали, что она подает заявку на участие в конкурсе Intel, но не оказывали на нее давления для достижения каких-либо конкретных целей.
«Мы считаем, что учиться, открывать и применять себя гораздо важнее», — сказала ее мать.
Намрата не считает, что это достижение является результатом интенсивного сосредоточения на науках.
«Летом у меня была отличная возможность пройти стажировку; это был отличный шанс вырасти не только как ученый, но и как человек… так уж вышло».
Доктор Кейт Шафер, преподаватель естествознания и исследований в старшей школе, очень гордилась успехом Намраты.
«Я так доволен и горжусь Намратой и всей тяжелой работой, которую она вложила в свой проект и приложение. Это действительно выдающееся достижение. Астрофизика — сложная область, потому что вы не можете напрямую взаимодействовать с изучаемой средой. Нашим студентам очень повезло, что у них была возможность работать с доктором Пурагрой Гухатакуртой в Калифорнийском университете в Санта-Круз, выдающимся наставником, обладающим ресурсами, которые позволили нашим студентам проводить исследования, недоступные большинству старшеклассников. Я просто хотела бы поздравить всех студентов, учителей и наставников, которые потратили столько долгих часов на исследования, написание и исправление всего, чтобы углубить наши знания о мире и вселенной вокруг нас», — сказала она.
Я просто хотела бы поздравить всех студентов, учителей и наставников, которые потратили столько долгих часов на исследования, написание и исправление всего, чтобы углубить наши знания о мире и вселенной вокруг нас», — сказала она.
В марте история будет дополнена новостями о ее результатах в столице.
7.9 Возрастные задачи — Алгебра среднего уровня
Глава 7: Факторинг
Одним из приложений линейных уравнений является так называемая проблема возраста. При решении возрастных задач, как правило, сравнивают возраст двух разных людей (или объектов) как в настоящем, так и в будущем (или прошлом). Целью этих задач обычно является определение текущего возраста каждого субъекта. Поскольку в этих задачах может быть много информации, для организации и решения можно использовать диаграмму. Пример такой таблицы ниже.
| Человек или объект | Текущий возраст | Изменение возраста |
|---|---|---|
Джои на 20 лет моложе Бекки.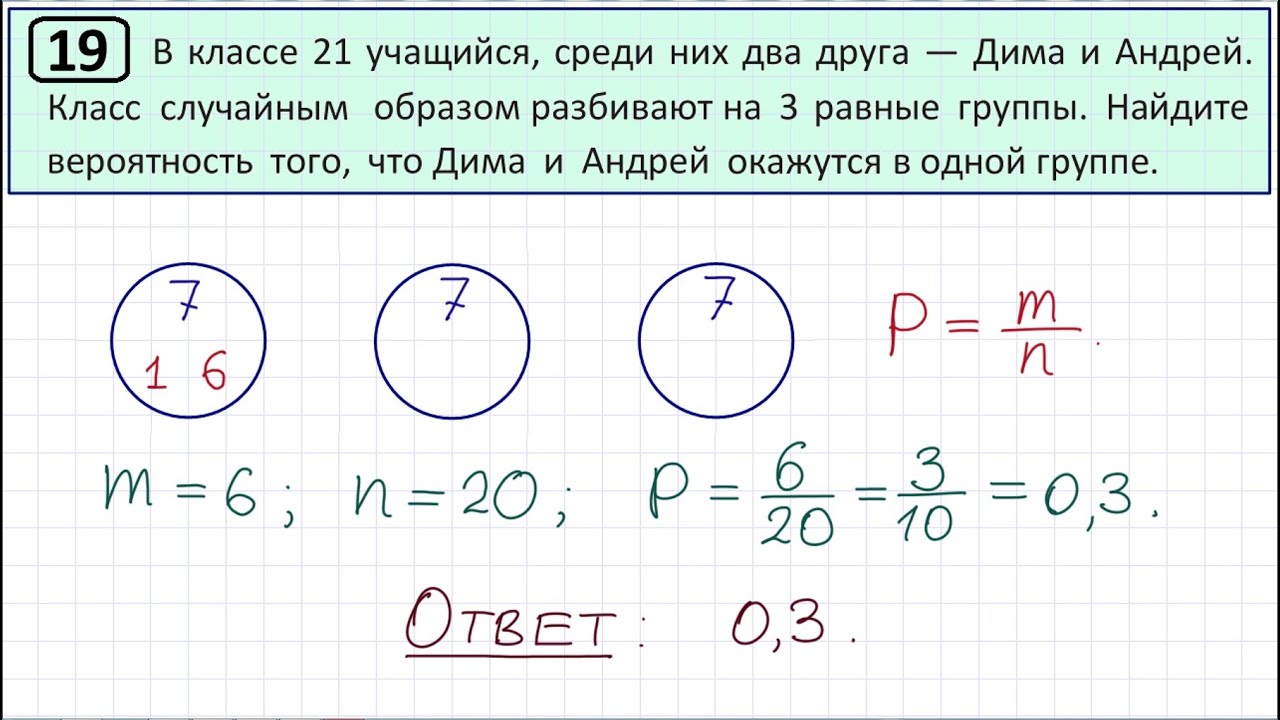 Через два года Бекки будет вдвое старше Джоуи. Заполните таблицу возрастных проблем, но не решайте.
Через два года Бекки будет вдвое старше Джоуи. Заполните таблицу возрастных проблем, но не решайте.
- Первое предложение говорит нам, что Джоуи на 20 лет моложе Бекки (это текущий возраст)
- Второе предложение говорит нам о двух вещах:
- Изменение возраста Джоуи и Бекки составляет плюс два года
- Через два года Бекки будет в два раза старше Джои через два года
| Человек или объект | Текущий возраст | Изменение возраста (+2) |
|---|---|---|
| Джоуи (Дж) | Б − 20 | Б – 20 + 2 Б – 18 |
| Бекки (Б) | Б | Б = 2 |
Использование этого последнего утверждения дает нам решение уравнения:
В + 2 = 2 (В — 18)
Кармен старше Дэвида на 12 лет. Пять лет назад сумма их возрастов равнялась 28. Сколько им сейчас?
- Первое предложение говорит нам, что Кармен старше Дэвида на 12 лет (это текущий возраст)
- Второе предложение говорит нам, что возраст Кармен и Дэвида изменился пять лет назад (−5)
Заполнение таблицы дает нам:
| Человек или объект | Текущий возраст | Изменение возраста (−5) |
|---|---|---|
| Кармен (К) | Д + 12 | Д + 12 − 5 Д + 7 |
| Дэвид (Д) | Д | Д — 5 |
Последнее утверждение дает нам уравнение для решения:
Пять лет назад сумма их возрастов была 28
[латекс]\begin{array}{rrrrrrrrl} (D&+&7)&+&(D& -&5)&=&28 \\ &&&&2D&+&2&=&28 \\ &&&&&-&2&&-2 \\ \hline &&&&&&&2D&=&26 \\ \\ &&&&&&&D&=&\dfrac{26}{2} = 13 \\ \end{array }[/латекс]
Следовательно, Кармен — это возраст Дэвида (13) + 12 лет = 25 лет.
Сумма возрастов Николь и Кристин равна 32 годам. Через два года Николь будет в три раза старше Кристин. Сколько им сейчас лет?
- Первое предложение говорит нам, что сумма возрастов Николь (N) и Кристин (K) равна 32. Таким образом, N + K = 32, что означает, что N = 32 − K или
K = 32 − N ( мы будем использовать эти уравнения, чтобы исключить одну переменную в нашем окончательном уравнении) - Второе предложение говорит нам, что изменение возраста Николь и Кристен произойдет через два года (+2)
Заполнение таблицы дает нам:
| Человек или объект | Текущий возраст | Изменение возраста (+2) |
|---|---|---|
| Николь (Н) | Н | Н + 2 |
| Кристин (К) | 32 − N | (32 – С) + 2 34 – С |
Последнее утверждение дает нам уравнение, которое нужно решить:
Через два года Николь будет в три раза старше Кристин
[латекс]\begin{array}{rrrrrrr} N&+&2&=&3(34&- &N) \\ N&+&2&=&102&-&3N \\ +3N&-&2&&-2&+&3N \\ \hline &&4N&=&100&& \\ \\ &&N&=&\dfrac{100}{4}&=&25 \\ \end {массив}[/латекс]
Если Николь 25 лет, то Кристин 32 − 25 = 7 лет.
Луизе 26 лет. Ее дочери Кармен 4 года. Через сколько лет Луиза будет вдвое старше дочери?
- Первое предложение говорит нам, что Луизе 26 лет, а ее дочери 4 года
- Вторая строка сообщает нам, что изменение возраста Кармен и Луизы должно быть рассчитано ([latex]x[/latex])
Заполнение таблицы дает нам:
| Человек или объект | Текущий возраст | Изменение возраста |
|---|---|---|
| Луиза (L) | [латекс]26[/латекс] | [латекс]26 = х[/латекс] |
| Дочь (Д) | [латекс]4[/латекс] | [латекс]D = х[/латекс] |
Последнее утверждение дает нам уравнение, которое нужно решить:
Через сколько лет Луиза будет вдвое старше своей дочери?
[латекс]\begin{array}{rrrrrrr} 26&+&x&=&2(4&+&x) \\ 26&+&x&=&8&+&2x \\ -26&-&2x&&-26&-&2x \\ \hline &&-x&= &-18&& \\ &&x&=&18&& \end{массив}[/latex]
Через 18 лет Луиза будет вдвое старше своей дочери.
Для вопросов с 1 по 8 напишите уравнения, определяющие отношения.
- Рик на 10 лет старше своего брата Джеффа. Через 4 года Рик будет вдвое старше Джеффа.
- Отец в 4 раза старше сына. Через 20 лет отец будет вдвое старше сына.
- Пэт на 20 лет старше своего сына Джеймса. Через два года Пэт будет вдвое старше Джеймса.
- Диана на 23 года старше своей дочери Эми. Через 6 лет Дайан будет вдвое старше Эми.
- Фред на 4 года старше Барни. Пять лет назад сумма их возрастов равнялась 48.
- Джон в четыре раза старше Марты. Пять лет назад сумма их возрастов равнялась 50.
- Тим на 5 лет старше Джоанн. Через шесть лет сумма их возрастов будет равна 79.
- Джек вдвое старше Лейси. Через три года сумма их возрастов будет 54.
Решите вопросы с 9 по 20.
- Сумма возрастов Джона и Марии равна 32 годам. Четыре года назад Джон был вдвое старше Марии.
- Сумма возрастов отца и сына равна 56.



Leave A Comment