Тесты по геометрии — Геометрия
Треугольники, четырёхугольники, многоугольники и их элементы
1. B 6 № 89. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
Ответ: 105
2. B 6 № 118. В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.
Ответ: 20
3. B 6 № 141. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Ответ: 65
4. B 6 № 144. В треугольнике ABC угол C прямой, AC = 8, cosA = 0,4. Найдите AB.
Ответ: 20
5. B 6 № 193. Найдите угол АDС равнобедренной трапеции

Ответ: 80
6. B 6 № 132773. Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах.
Ответ: 50
7. B 6 № 132774. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Ответ: 70
8. B 6 № 132775. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.
Ответ: 60
9. B 6 № 132776. Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
Ответ: 110
10. B 6 № 132777. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
Ответ: 70
11. B 6 № 132778. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2.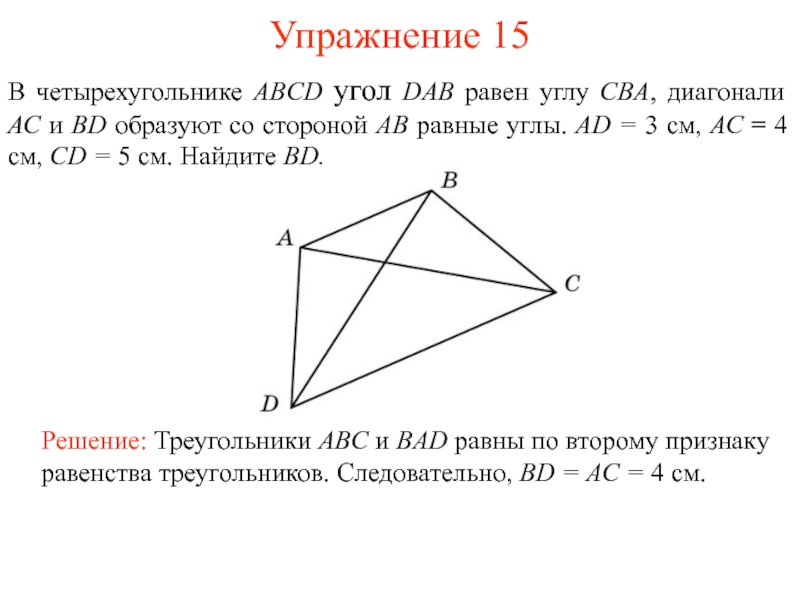 Ответ дайте в градусах.
Ответ дайте в градусах.
Ответ: 60
12. B 6 № 132779. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Ответ: 60
13. B 6 № 132781. В выпуклом четырехугольнике ABCD , , , . Найдите угол A. Ответ дайте в градусах.
Ответ: 95
14. B 6 № 132782. Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
Ответ: 36
15. B 6 № 132783. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Ответ: 122
16. B 6 № 311320. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
Ответ: 120
17. B 6 № 311343. В равностороннем треугольнике ABC медианы BK и AM пересекаются в точке O. Найдите .
Найдите .
Ответ: 60
18. B 6 № 311355. Биссектрисы углов N и M треугольника MNP пересекаются в точке A. Найдите , если , а
Ответ: 117
19. B 6 № 311365.
Ответ: 120
20. B 6 № 311412. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.
Ответ: 40
21. B 6 № 311455. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Ответ: 70
22. B 6 № 311456. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием

Ответ: 120
23. B 6 № 311457. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием BC и боковой стороной CD углы, равные 30° и 105° соответственно.
Ответ: 45
24. B 6 № 311458. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Ответ: 105
25. B 6 № 311459.
Ответ: 45
26. B 6 № 311460. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
Ответ: 110
27. B 6 № 311476. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол . Ответ дайте в градусах.
Найдите угол . Ответ дайте в градусах.
Ответ: 40
28. B 6 № 311514. На плоскости даны четыре прямые. Известно, что , , . Найдите . Ответ дайте в градусах.
Ответ: 125
29. B 6 № 311680.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
Ответ: 66
30. B 6 № 311759. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
Ответ: 54
31. B 6 № 311847. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 71°, угол
Ответ: 132
32. B 6 № 311911.
В параллелограмме ABCD проведена диагональ AC. Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.
Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.
Ответ: 122
33. B 6 № 311955.
Тангенс острого угла прямоугольной трапеции равен Найдите её большее основание, если меньшее основание равно высоте и равно 15.
Ответ: 33
34. B 6 № 314838. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Ответ: 125
35. B 6 № 314844. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Ответ: 65
36. B 6 № 314846. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Ответ: 70
37. B 6 № 314863. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Ответ: 120
38. B 6 № 314980. Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе через точку с запятой в порядке возрастания.
Ответ: 17;17
39. B 6 № 315005. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.
Ответ: 45
40. B 6 № 315026. В треугольнике ABC угол C прямой, BC = 3 , cosB = 0,6. Найдите AB.
Ответ: 5
41. B 6 № 315032. В треугольнике ABC угол C прямой, BC = 9 , sinA = 0,3 . Найдите AB.
Ответ: 30
42. B 6 № 315038. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.
Ответ: 65
43. B 6 № 315068. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Ответ: 115
44. B 6 № 315099. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Ответ: 115
45. B 6 № 315100. В треугольнике ABC угол C прямой, AC = 8 , cosA = 0,4. Найдите AB.
46. B 6 № 316229. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 19°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 54
47. B 6 № 316256. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 71°, угол CAD равен 61°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 132
48. B 6 № 316282. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 14°, угол CAD равен 30°. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 44
49. B 6 № 316283. В треугольнике ABC угол C равен 90°, BC = 12 , tgA = 1,5. Найдите AC.
Ответ: 8
50. B 6 № 316319. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 80°, угол CAD равен 54°. Найдите угол ABD. Ответ дайте в градусах.
Ответ: 26
51. B 6 № 316345. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
B 6 № 316345. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.
Ответ: 106
52. B 6 № 316371. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 27°. Ответ дайте в градусах.
Ответ: 126
вершины, стороны, диагонали. Виды четырёхугольников
Четырёхугольник — это выпуклый многоугольник с четырьмя углами и четырьмя сторонами. Четырёхугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.
Обозначение четырёхугольника составляют из букв, стоящих при его вершинах, называя их по порядку. Например, говорят или пишут:
Например, говорят или пишут: четырёхугольник ABCD
:
В четырёхугольнике ABCD точки A, B, C и D — это вершины четырёхугольника, отрезки AB, BC, CD и DA — стороны.
Вершины, принадлежащие одной стороне, называются соседними, вершины, не являющиеся соседними, называются противолежащими:
В четырёхугольнике ABCD вершины A и B, B и C, C и D, D и A — соседние, а вершины A и C, B и D — противолежащие. Углы, лежащие при соседних вершинах, также называются соседними, а при противолежащих вершинах — противолежащими.
Стороны четырёхугольника также можно попарно разделить на соседние и противолежащие: стороны, имеющие общую вершину, называются соседними (или смежными), стороны, не имеющие общих вершин — противолежащими:
Стороны AB и BC, BC и CD, CD и DA, DA и AB — смежные, а стороны AB и DC, AD и BC — противолежащие.
Если противолежащие вершины соединить отрезком, то такой отрезок будет называться диагональю четырёхугольника. Учитывая, что в четырёхугольнике есть всего две пары противолежащих вершин, то и диагоналей может быть всего две:
Отрезки AC и BD — диагонали.
Виды четырёхугольников
Рассмотрим основные виды выпуклых четырёхугольников:
- Трапеция — четырёхугольник, у которого одна пара противоположных сторон, параллельны друг другу, а другая пара не параллельны.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны.
- Прямоугольная трапеция — трапеция, у которой один из углов прямой.
- Параллелограмм — четырёхугольник, у которого обе пары противоположных сторон параллельны друг другу.
- Прямоугольник — параллелограмм, у которого все углы равны.

- Ромб — параллелограмм, у которого все стороны равны.
- Квадрат — параллелограмм, у которого равны и стороны и углы. И прямоугольник и ромб могут быть квадратом.
- Прямоугольник — параллелограмм, у которого все углы равны.
Свойства углов выпуклых четырёхугольников
У всех выпуклых четырёхугольников углы обладают следующими двумя свойствами:
- Любой внутренний угол меньше 180°.
- Сумма внутренних углов равна 360°.
Геометрия-8 класс. Контр. работа №1 по теме `Четырехугольники`.
Геометрия 8 класс
Контрольная работа №1 Вариант 1
1) Выпишите номера верных утверждений:
Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник — параллелограмм.
Диагональ параллелограмма делит его углы пополам.
Диагонали прямоугольника равны.

Диагонали квадрата взаимно перпендикулярны.
Сумма углов выпуклого четырехугольника равна 180°.
Диагональ трапеции делит её на два равных треугольника.
2) Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
А) 500 В) 650 С) 800 D) 1150
3) Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
А) 750 В) 1050 С) 1250 D) 1800
4) Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
5) В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник.
Геометрия 8 класс
Контрольная работа №1 Вариант 2
1) Выпишите номера верных утверждений:
Если в четырехугольнике две противоположные стороны параллельны, то этот четырехугольник — параллелограмм.
Диагональ параллелограмма делит его на два равных треугольника.
Диагонали ромба перпендикулярны.
Диагонали квадрата делят его углы пополам.
У любой трапеции боковые стороны равны.
Все углы ромба равны.
2) Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
А) 450 В)700 С)1000 D)1100
3) Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
А) 300 В)500 С)800 D)1000
4) Диагональ прямоугольника образует угол 30° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
5) В параллелограмме KLMN точка Е — середина стороны LM. Известно, что EK = EN. Докажите, что данный параллелограмм — прямоугольник.
Приложенные файлы
Упражнения: Четырёхугольник и его элементы
Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Четырёхугольник и его элементы». Материал предназначен для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Упражнения по теме «Четырёхугольник и его элементы». Материал предназначен для составления самостоятельных проверочных работ. Раздел состоит из трёх однотипных вариантов задач по проверяемой теме.
Четырёхугольник и его элементы
Вариант 1
- Для четырёхугольника ABCD запишите:
1) вершины, соседние с вершиной А; 2) вершину, противолежащую вершине В; 3) стороны, соседние со стороной CD; 4) сторону, противолежащую стороне ВС; 5) диагонали четырёхугольника. - Чему равен четвёртый угол четырёхугольника, если три его угла соответственно равны 59°, 138° и 152°?
- В четырёхугольнике ABCD угол D равен 100°, а угол А на 23° больше угла В и в 3 раза меньше угла С. Найдите неизвестные углы четырёхугольника.
- Найдите углы четырёхугольника, если они пропорциональны числам:
1) 3, 4, 8 и 9; 2) 2, 3, 4 и 11.
Является ли этот четырёхугольник выпуклым? - В четырёхугольнике ABCD АВ = AD, а диагональ АС образует с этими сторонами равные углы.
 Найдите сторону ВС, если CD = 9 см.
Найдите сторону ВС, если CD = 9 см. - В четырёхугольнике ABCD АВ = CD, ВС = AD. Найдите ∠ABC, если ∠ADC = 132°.
- В четырёхугольнике ABCD диагонали АС и BD перпендикулярны, а диагональ BD образует со сторонами ВА и ВС равные углы. Докажите, что AD = DC.
- Диагональ четырёхугольника равна 8 см, а периметры треугольников, на которые эта диагональ разбивает данный четырёхугольник, равны 30 см и 23 см. Найдите периметр четырёхугольника.
- Существует ли четырёхугольник, стороны которого равны 5 см, 8 см, 10 см и 24 см?
- Существует ли четырёхугольник, периметр которого равен 46 см, а диагонали равны:
1) 23 см и 24 см; 2) 10 см и 12 см?
Вариант 2
- Для четырёхугольника MNPK запишите:
1) вершины, соседние с вершиной М; 2) вершину, противолежащую вершине N; 3) стороны, соседние со стороной РК; 4) сторону, противолежащую стороне NP; 5) диагонали четырёхугольника. - Чему равен четвёртый угол четырёхугольника, если три его угла соответственно равны 68°, 87° и 123° ?
- В четырёхугольнике ABCD угол А равен 106°, а угол В на 34° меньше угла С и в 2 раза больше угла D.
 Найдите неизвестные углы четырёхугольника.
Найдите неизвестные углы четырёхугольника. - Найдите углы четырёхугольника, если они пропорциональны числам:
1) 7, 8, 10 и 11; 2) 4, 5, 7 и 20.
Является ли этот четырёхугольник выпуклым? - В четырёхугольнике ABCD диагональ BD образует со сторонами В А и ВС равные углы и со сторонами DA и DC также равные углы. Найдите ∠BAD, если ∠BCD = 108°.
- В четырёхугольнике ABCD ВС = AD, ∠DAC = ∠BCA. Найдите сторону АВ, если CD = 8 см.
- В четырёхугольнике ABCD АВ = AD, а диагонали АС и BD перпендикулярны. Докажите, что ВС = CD.
- Диагональ четырёхугольника равна 10 см, а периметр одного из треугольников, на которые эта диагональ разбивает данный четырёхугольник, равен 40 см. Найдите периметр другого треугольника, если периметр четырёхугольника равен 53 см.
- Существует ли четырёхугольник, стороны которого равны 9 дм, 10 дм, 11 дм и 30 дм?
- Существует ли четырёхугольник, периметр которого равен 56 см, а диагонали равны:
1) 35 см и 23 см; 2) 12 см и 15 см?
Вариант 3
- Для четырёхугольника DEFS запишите:
1) вершины, соседние с вершиной Е; 2) вершину, противолежащую вершине F; 3) стороны, соседние со стороной EF; 4) сторону, противолежащую стороне DS; 5) диагонали четырёхугольника.
- Чему равен четвёртый угол четырёхугольника, если три его угла соответственно равны 109°, 117° и 127° ?
- В четырёхугольнике ABCD угол В равен 146°, а угол С на 32° больше угла A и в 4 раза меньше угла D. Найдите неизвестные углы четырёхугольника.
- Найдите углы четырёхугольника, если они пропорциональны числам:
1) 3, 4, 5 и 8; 2) 2, 4, 5 и 13.
Является ли этот четырёхугольник выпуклым? - В четырёхугольнике ABCD известно, что АВ = AD, СВ = CD. Найдите ∠ABC, если ∠ADC = 84°.
- В четырёхугольнике ABCD известно, что ∠BAC = ∠DCA, ∠DAC = ∠BCA. Найдите сторону ВС, если AD = 12 см.
- В четырёхугольнике ABCD диагонали АС и BD перпендикулярны, а диагональ АС делит диагональ BD на две равные части. Докажите, что ВС = CD.
- Периметр четырёхугольника равен 62 см, а периметры треугольников, на которые одна из диагоналей разбивает данный четырёхугольник, равны 39 см и 45 см. Найдите эту диагональ четырёхугольника.
- Существует ли четырёхугольник, стороны которого равны 6 см, 12 см, 14 см и 33 см?
- Существует ли четырёхугольник, периметр которого равен 74 см, а диагонали равны:
1) 28 см и 47 см; 2) 17 см и 21 см?
Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Четырёхугольник и его элементы». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!
Упражнения по теме «Четырёхугольник и его элементы». Материал в первую очередь предназначен для составления самостоятельных проверочных работ. Будьте внимательны: при транскрипте цитат возможны опечатки!
Вернуться к Списку упражнений по геометрии УМК Мерзляк
Просмотров: 3 073
Четырехугольник
Четырехугольник представляет собой двумерную замкнутую форму с четырьмя прямыми стороны. Например. Показанная здесь форма ABCD представляет собой четырехугольник.Отрезок, проведенный от одной вершины четырехугольника к противоположной. вершиной называется диагональ четырехугольника. AC — это диагональ четырехугольника ABCD , как BD .
Типы четырехугольников
Есть семь типов четырехугольников, которые можно разделить на два.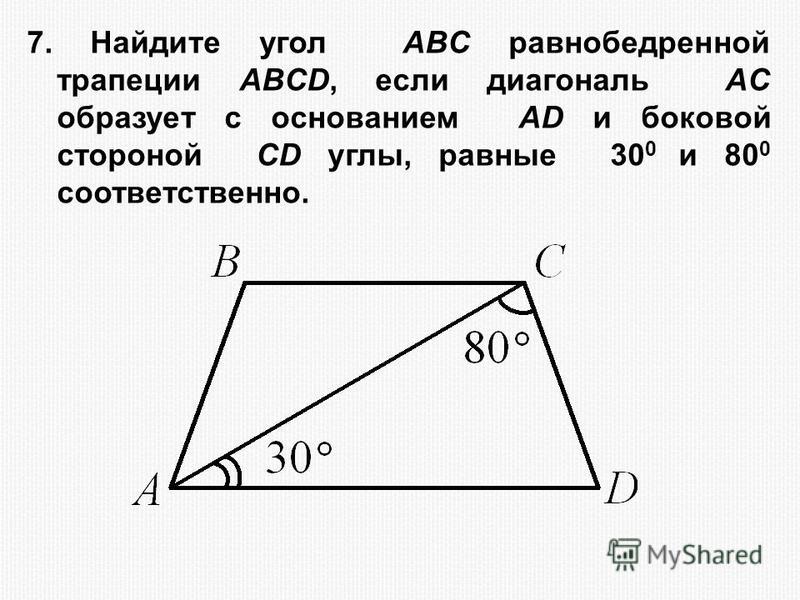 группы: параллелограмма и остальных четырехугольников .
группы: параллелограмма и остальных четырехугольников .
Параллелограммы
Четырехугольники называются параллелограммами, если обе пары противоположных сторон равны и параллельны друг другу. Различные параллелограммы и их свойства описаны ниже.
Параллелограмм
- Противоположные стороны параллелограмма параллельны и равны по длине.
- Противоположные углы равны по размеру.
Примечание:
Прямоугольник
- Противоположные стороны прямоугольника параллельны и равны по длине.
- Все углы равны 90.
Квадрат
- Противоположные стороны квадрата параллельны, и все стороны равны в
длина.

- Все углы равны 90.
Ромб
- Все стороны ромба равны по длине
- Противоположные стороны параллельны.
- Противоположные углы ромба равны.
- Диагонали ромба справа пересекают друг друга. углы.
Примечание:
Прямоугольники, квадраты и ромбы (или ромбы) — параллелограммы.
Другие четырехугольники
К другим четырехугольникам относятся трапеции, воздушные змеи и неправильные формы. четырехугольники.
Трапеция
- Трапеция имеет одну пару параллельных противоположных сторон.
- Обычная трапеция имеет одинаковые непараллельные стороны и углы основания
равны, как показано на диаграмме.

Воздушный змей
- Две пары соседних сторон воздушного змея равны по длине
- Одна пара противоположных углов (те, которые находятся между сторонами разной длины) равны по размеру.
- Одна диагональ делит другую пополам.
- Диагонали пересекаются справа углы.
Неправильный четырехугольник
Неправильный четырехугольник не имеет особых свойств.
Сумма углов четырехугольника
Нарисуйте четырехугольник ABCD .Затем нарисуйте диагональ AC , чтобы образовать два треугольника.
Нахождение четвертого угла четырехугольника
Если известны размеры трех углов четырехугольника, то
недостающий угол можно вычислить.
Пример 10
Найдите значение местоимения x в сопроводительном диаграмма.Обоснуйте свой ответ.
Решение:
Пример 11
Найдите значение местоимений на следующей диаграмме. Дайте причины вашего ответа.
Решение:
Пример 12
Найдите значение местоимений на следующей диаграмме.Дайте причины вашего ответа.
Решение:
Ключевые термины
четырехугольник, диагональ, параллелограмм, прямоугольник, квадрат, ромб, трапеция, правильная трапеция, воздушный змей, неправильный четырехугольник, угол сумма четырехугольника
Когда четырехугольник является параллелограммом?
Когда четырехугольник — параллелограмм?
Я думаю о четырехугольнике с одной парой противоположных сторон, параллельных и конгруэнтных. Назовите этот четырехугольник.
Назовите этот четырехугольник.
Я думаю о четырехугольнике, у которого обе пары противоположных сторон совпадают. Назовите этот четырехугольник.
Я представляю себе четырехугольник с конгруэнтными парами противоположных углов. Назовите этот четырехугольник.
Я думаю о четырехугольнике, диагонали которого пересекают друг друга пополам. Назовите этот четырехугольник.
Если вы ответили? Параллелограмм? Во всем вышеперечисленном вы правы! Конечно, теперь вы знаете, что недостаточно утверждать, что я думаю о параллелограмме.В машине есть сомневающиеся, так что вам придется это доказать.
Противоположные стороны конгруэнтны и параллельны
Ваше имя? Назовите этот четырехугольник? Подсказка заключалась в том, что одна пара противоположных сторон параллельна и конгруэнтна. Я назову это теоремой и напишу доказательство из двух столбцов. Рисунок 16.1 поможет вам визуализировать ситуацию.
Рисунок 16.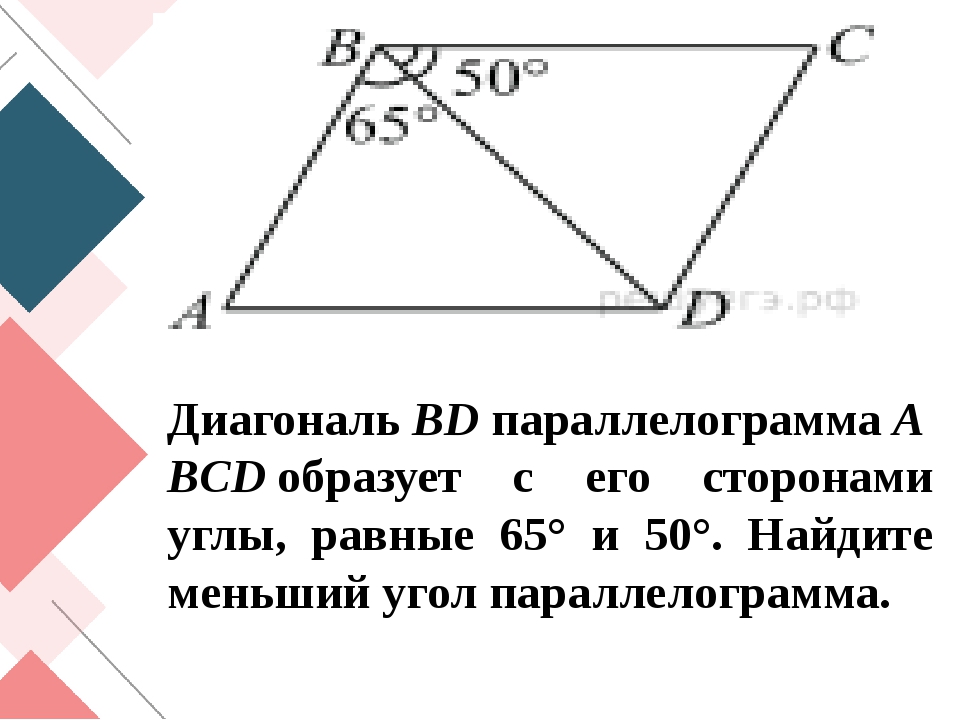 1 Четырехугольник ABCD с BC? ? и BC ~ = AD.
1 Четырехугольник ABCD с BC? ? и BC ~ = AD.
- Теорема 16.1 : Если одна пара противоположных сторон четырехугольника параллельна и конгруэнтна, то четырехугольник является параллелограммом.
Вот план игры. Предположим, что BC? ? AD и BC ~ = AD. По определению, параллелограмм — это четырехугольник, в котором обе пары противоположных сторон параллельны. Вы уже знаете, что одна пара противоположных сторон параллельна. Вам нужно показать, что другая пара противоположных сторон параллельна. Другими словами, вам нужно показать эту AB? ? CD.
На этот четырехугольник можно смотреть двояко. Первый способ — сосредоточиться на отрезках BC и AD, разрезанных поперечной AC. Тогда? BCA и? DAC являются альтернативными внутренними углами и совпадают, потому что BC? ? ОБЪЯВЛЕНИЕ.Второй способ — перевернуть его на бок. AB и CD — два отрезка, разрезанные поперечной AC. В этом случае? BAC и? ACD — это чередующиеся внутренние углы. Если бы вы могли показать это? BAC ~ =? ACD, тогда вы могли бы сделать вывод, что AB? ? CD, и вам будет конец. Способ показать? BAC ~ =? ACD — это использовать CPOCTAC. Чтобы использовать CPOCTAC, вам нужно показать? DAC ~ =? BCA. Чтобы показать? DAC ~ =? BCA, вам нужно использовать Постулат SAS. Давай запишем это.
Если бы вы могли показать это? BAC ~ =? ACD, тогда вы могли бы сделать вывод, что AB? ? CD, и вам будет конец. Способ показать? BAC ~ =? ACD — это использовать CPOCTAC. Чтобы использовать CPOCTAC, вам нужно показать? DAC ~ =? BCA. Чтобы показать? DAC ~ =? BCA, вам нужно использовать Постулат SAS. Давай запишем это.
| Заявления | Причины | |
|---|---|---|
| 1. | Четырехугольник ABCD с BC? ? AD и BC ~ = AD. | Дано |
| 2. | BC? ? AD, разрезанный поперечным AC | Определение поперечного |
| 3. | ? BAC и? ACD — альтернативные внутренние углы | Определение альтернативных внутренних углов |
| 4. | ? BCA ~ =? DAC | Теорема 10.2 |
| 5. | AC ~ = AC | Отражающее свойство ~ = |
| 6. | ? DAC ~ =? BCA | Постулат SAS |
| 7. | ? BAC ~ =? ACD | CPOCTAC |
| 8. | AB и CD — это два сегмента, разрезанных поперечным углом | AC | Определение поперечного
| 9. | ? BAC и? ACD — альтернативные внутренние углы | Определение альтернативных внутренних углов |
| 10. | AB? ? CD | Теорема 10,8 |
| 11. | Четырехугольник ABCD — это параллелограмм | Определение параллелограмма |
Теперь, когда вы правильно назвали этот четырехугольник, вы можете перейти к следующему четырехугольнику.
Две пары совпадающих сторон
Во втором? Назовите этот четырехугольник? В игре четырехугольник имел две пары равных сторон. Давайте напишем это как теорему и положим конец.
- Теорема 16.2 : Если обе пары противоположных сторон четырехугольника совпадают, то четырехугольник является параллелограммом.
У нас есть изображение на рис. 16.2. У нас есть параллелограмм ABCD с AB ~ = CD и BC ~ = AD. План игры состоит в том, чтобы разделить четырехугольник на два треугольника с помощью диагонали AC. Используйте постулат SSS, чтобы показать, что два треугольника конгруэнтны, и используйте CPOCTAC, чтобы сделать вывод, что альтернативные внутренние углы совпадают, а противоположные стороны должны быть параллельны. Если мы покажем это для обеих пар противоположных сторон, то по определению мы получим параллелограмм. Пора выписать подробности.
Рисунок 16.2 Четырехугольник ABCD с AB ~ = CD и BC ~ = AD
| Заявления | Причины | |
|---|---|---|
| 1. | Четырехугольник ABCD с AB ~ = CD и BC ~ = AD | Дано |
| 2. | AC ~ = AC | Отражающее свойство ~ = |
| 3. | ? ABC ~ =? CDA | Постулат SSS |
| 4. | ? BAC ~ = ACD и? BCA ~ =? DAC | CPOCTAC |
| 5. | BC и AD — два сегмента, разделенных поперечным AC | Определение поперечного |
| 6. | ? BAC и? ACD — альтернативные внутренние углы | Определение альтернативных внутренних углов |
| 7. | ДО Н.Э ? ? AD | Теорема 10.8 |
| 8. | AB и CD — два сегмента, разделенных поперечным углом AC | Определение поперечного |
| 9. | ? BAC и? ACD — альтернативные внутренние углы | Определение чередующиеся внутренние углы |
| 10. | AB? ? CD | Теорема 10.8 |
| 11. | Четырехугольник ABCD — это параллелограмм | Определение параллелограмма |
И снова сладкий вкус победы! Вы правильно назвали этот четырехугольник. Следующий!
Две пары конгруэнтных углов
В третьем описании четырехугольника обе пары противоположных углов конгруэнтны. Я сформулирую теорему и воспользуюсь рисунком 16.3, чтобы провести вас через ваше доказательство.
Рисунок 16.3 Четырехугольник ABCD с? A ~ =? C и? B ~ =? D.
- Теорема 16.3 : Если обе пары противоположных углов четырехугольника совпадают, то четырехугольник является параллелограммом.
Начать нужно со своих углов. Поскольку сумма внутренних углов четырехугольника в сумме равна 360, вы можете показать m? A + m? B = 180, или что? A и? B — дополнительные углы. Теперь вы можете взглянуть на этот четырехугольник в следующем свете: BC и AD — два отрезка, пересеченные поперечной AB.Обычно трансверсаль была AC, но на этот раз вы будете использовать AB. Поскольку ваши два угла на одной стороне трансверсали являются дополнительными, теорема 10.10 говорит вам, что BC? ? ОБЪЯВЛЕНИЕ. Аналогичный аргумент показывает, что AB? ? CD.
| Утверждения | Причины | |
|---|---|---|
| 1. | Четырехугольник ABCD с? A ~ =? C и? B ~ =? D | Дано |
| 2. | m? A + m? B + m? C + m? D = 360 | Сумма внутренних углов четырехугольника составляет 360 |
| 3. | m? A + m? B + m? A + m? B = 360 | Замена (шаги 1 и 2) |
| 4. | m? A + m? B = 180 | Алгебра |
| 5. | ? A и? B — дополнительные углы | Определение дополнительных углов |
| 6. | BC и AD — два сегмента, разрезанные поперечной AB | Определение поперечного |
| 7. | до н.э.? ? AD | Теорема 10.10 |
| 8. | AB и CD — два сегмента, разрезанные поперечным AD | Определение поперечного |
| 9. | m? A + m? D = 180 | Замена (шаги 1 и 4 ) |
| 10. | ? A и? D — дополнительные углы | Определение дополнительных углов |
| 11. | AB? ? CD | Теорема 10.10 |
| 12. | Четырехугольник ABCD — это параллелограмм | Определение параллелограмма |
Поперечные диагонали
Ах, последняя игра из этой серии! Если у вас есть четырехугольник, диагонали которого делят друг друга пополам, ваш четырехугольник представляет собой параллелограмм.На рис. 16.4 показан параллелограмм ABCD с диагоналями AC и BD, которые пересекаются в точке M и делят друг друга пополам.
Рисунок 16.4 Четырехугольник ABCD с диагоналями AC и BD, которые пересекаются в точке M и делят друг друга пополам.
- Теорема 16.4 : Если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом.
Если вы посмотрите на рис. 16.4, план игры по доказательству этой теоремы должен быть четко изложен.Вы воспользуетесь теоремой 16.2: пары противоположных сторон параллелограмма конгруэнтны. Две диагонали делят параллелограмм на четыре треугольника. Поскольку диагонали делят друг друга пополам, AM ~ = MC и BM ~ = MD. Поскольку вертикальные углы совпадают, вы можете использовать Постулат SAS, чтобы показать, что? AMB ~ =? BMC и? AMB ~ =? DMC. Оттуда нужно применить CPOCTAC, чтобы показать, что обе пары противоположных сторон конгруэнтны.
| Заявления | Причины | |
|---|---|---|
| 1. | Четырехугольник ABCD с диагоналями AC и BD, которые пересекаются в точке M и делят друг друга пополам | Дано |
| 2. | AM ~ = MC и BM ~ = MD | Определение пополам |
| 3. | ? AMB ~ =? CMD и? AMD ~ =? BMC | Теорема 8.1 |
| 4. | ? AMD ~ =? BMC и? AMB ~ =? DMC | Постулат SAS |
| 5. | BC ~ = AD и AB ~ = CD | CPOCTAC |
| 6. | Четырехугольник ABCD — параллелограмм | Теорема 16.2 |
Выдержка из The Complete Idiot’s Guide to Geometry 2004, Дениз Сечей, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любом форма. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете купить эту книгу на Amazon.com и Barnes & Noble.
Извините! — Страница не найдена
Пока мы разбираемся, возможно, поможет одна из ссылок ниже.
Дома Назад- Класс
- Онлайн-тесты
- Ускоренный онлайн-курс JEE
- Двухлетний курс JEE 2021
- Класс
- Онлайн-курс NEET
- Серия онлайн-тестов
- CA Foundation
- CA Средний
- CA Финал
- Программа CS
- Класс
- Серия испытаний
- Книги и материалы
- Тестовый зал
- Умный взломщик BBA
- Обучение в классе
- Онлайн-коучинг
- Серия испытаний
- Умный взломщик IPM
- Книги и материалы
- GD-PI
- CBSE, класс 8
- CBSE, класс 9
- CBSE, класс 10
- Класс 11 по CBSE
- CBSE, класс 12
- Обучение в классе
- Онлайн-классы CAT
- Серия испытаний CAT
- MBA Жилой
- Умный взломщик CAT
- Книги и материалы
- Онлайн-классы без CAT
- Серия испытаний без CAT
- Тестовый зал
- GD-PI
- Обучение в классе
- Серия испытаний
- Civils Интервью
- Класс
- Онлайн-классы
- Серия испытаний SSC
- Переписка
- Практические тесты
- SSC электронные книги
- SSC JE Study Package
- Класс
- RBI класс B
- Банковский тест серии
- Переписка
- Банковские электронные книги
- Банк ПДП
- Онлайн-коучинг
- Обучение в классе
- Серия испытаний
- Книги и материалы
- Класс
- Программа моста GRE
- GMAT Онлайн-коучинг
- Консультации при приеме
- GMAT Обучение в классе
- Стажировка
- Корпоративные программы
- Студенты колледжа
- Рабочие специалисты
- Колледжи
- школ
Нарисуйте четырехугольник ABCD и диагональ AC, на которой диагональ разделяет его.Сколько таких
Heyyyy,
он сумма углов четырехугольника равна 360º.
В этом можно убедиться, нарисовав диагональ и разделив четырехугольник на два треугольника.
Пусть ABCD — четырехугольник, а AC — диагональ (см. Рис. 8.4).
Какова сумма углов в ΔADC?
Рис. 8.4
Вы знаете, что
∠DAC + ∠ACD + ∠D = 180 ° (1)
Аналогично, в ΔABC,
∠CAB + ∠ACB + ∠B = 180 ° (2)
Складывая (1) и (2), получаем
∠DAC + ∠ACD + ∠D + 7ang; CAB + ∠ACB + ∠B = 180 ° + 180 ° = 360 °
Также ∠DAC + ∠CAB = ∠A и ∠ACD + ∠ACB = ∠C
Итак, A + ∠D + ∠B + ∠C = 360 °.
т.е. сумма углов четырехугольника равна 360 °.
8.3 ВИДЫ ЧЕТЫРЕХСТОРОННИХ ДВИГАТЕЛЕЙ
Посмотрите на различные четырехугольники, нарисованные ниже:
Рис. 8.5
Обратите внимание на следующее:
Одна пара противоположных сторон четырехугольника ABCD на рис. 8.5 (i), а именно, AB и CD параллельны. Вы знаете, что это называется трапеция.
Обе пары противоположных сторон четырехугольника, показанные на рис. 8.5 (ii), (iii), (iv) и (v), параллельны. Напомним, что такие четырехугольники называются параллелограммами.Итак, четырехугольник PQRS на рис. 8.5 (ii) является параллелограммом. Точно так же все четырехугольники, показанные на рис. 8.5 (iii), (iv) и (v), являются параллелограммами.
Обратите внимание, что в параллелограмме MNRS на рис. 8.5 (iii) один из его углов, а именно ∠M, является прямым. Как называется этот особый параллелограмм? Попробуй вспомнить. Он называется прямоугольником.
У параллелограмма DEFG на рис. 8.5 (iv) все стороны равны, и мы знаем, что он называется ромбом.
Параллелограмм ABCD на рис.8.5 (v) имеет ∠A = 90 ° и все стороны равны; это называется квадратом.
6. В четырехугольнике ABCD на рис. 8.5 (vi) AD = CD и AB = CB, т.е. две пары смежных сторон равны. Это не параллелограмм. Это называется воздушный змей. Обратите внимание, что квадрат, прямоугольник и ромб — это параллелограммы.
Квадрат — это прямоугольник, а также ромб.
Параллелограмм — это трапеция.
Воздушный змей — это не параллелограмм.
Трапеция не является параллелограммом (поскольку в трапеции параллельна только одна пара противоположных сторон, и мы требуем, чтобы обе пары были параллельны в параллелограмме).
Прямоугольник или ромб — это не квадрат.
Четырехугольники | Формы | CBSE | Класс 9
8.1 ВВЕДЕНИЕ
Вы изучили многие свойства треугольника в главах 6 и 7 и знаете, что при соединении попарно трех неколлинеарных точек полученная фигура представляет собой треугольник. Сейчас же, отметим четыре точки и посмотрим, что мы получим, соединив их попарно в некотором порядке.
Рис.8,1Обратите внимание, что если все точки коллинеарны (на одной линии), мы получаем прямую [см. рис. 8.1 (i)], если три из четырех точек коллинеарны, мы получим треугольник [см. рис. 8.1 (ii)], и если никакие три точки из четырех не лежат на одной прямой, мы получаем замкнутый рисунок с четырьмя сторонами [см. Рис. 8.1 (iii) и (iv)].
Такая фигура, образованная соединением четырех точек в определенном порядке, называется четырехугольником .
В этой книге мы будем рассматривать только четырехугольники того типа, который показан на рис.8.1 (iii) но не как показано на рис. 8.1 (iv).
Четырехугольник имеет четыре стороны, четыре угла и четыре вершины [см. Рис. 8.2 (i)].
Рис. 8.2В четырехугольнике ABCD четыре стороны AB, BC, CD и DA; A, B, C и D являются четыре вершины, а ∠A, ∠B, ∠C и ∠D — четыре угла, образованные в вершины.
Теперь соедините противоположные вершины A с C и B с D [см. Рис. 8.2 (ii)].
AC и BD — две диагонали четырехугольника ABCD.
В этой главе мы подробнее рассмотрим различные типы четырехугольников, их свойств и особенно параллелограммов.
Вы можете спросить, зачем нам изучать четырехугольники (или параллелограммы). Посмотрите вокруг, и вы найдете так много предметов, которые имеют форму четырехугольник — пол, стены, потолок, окна вашего класса, доска, каждая грань тряпки, каждая страница вашей книги, верх учебного стола и т. д.Немного из них приведены ниже (см. рис. 8.3).
Рис. 8.3Хотя большинство объектов, которые мы видим вокруг, имеют форму особого четырехугольника называется прямоугольником, мы будем больше изучать четырехугольники и особенно параллелограммы поскольку прямоугольник также является параллелограммом, и все свойства параллелограмма равны верно и для прямоугольника.
8.1 УГЛОВАЯ СУММА СВОЙСТВА ЧЕТЫРЕХСТОРОННИХ ДВИГАТЕЛЕЙ
Давайте теперь вспомним свойство суммы углов четырехугольника.
Сумма углов четырехугольника равна 360º.
В этом можно убедиться, нарисовав диагональ и разделив четырехугольник на два треугольника.
Пусть ABCD — четырехугольник, а AC — диагональ (см. Рис. 8.4).
Какова сумма углов в ΔADC?
Рис. 8.4Вы знаете, что
∠DAC + ∠ACD + ∠D = 180 ° (1)
Аналогично, в ΔABC,
∠CAB + ∠ACB + ∠B = 180 ° (2)
Складывая (1) и (2), получаем
∠DAC + ∠ACD + ∠D + 7ang; CAB + ∠ACB + ∠B = 180 ° + 180 ° = 360 °
Также ∠DAC + ∠CAB = ∠A и ∠ACD + ∠ACB = ∠C
Итак, ∠A + ∠D + ∠B + ∠C = 360 °.
т.е. сумма углов четырехугольника равна 360 ° .
8.3 ВИДЫ ЧЕТЫРЬКИХ МОДУЛЕЙ
Посмотрите на различные четырехугольники, нарисованные ниже:
Рис. 8.5Обратите внимание:
- Одна пара противоположных сторон четырехугольника ABCD на рис. 8.5 (i), а именно AB и CD параллельны. Вы знаете, что она называется трапеция .
- Обе пары противоположных сторон четырехугольника, указанные на рис. 8.5 (ii), (iii), (iv) и (v) параллельны. Напомним, что такие четырехугольники называются параллелограммами. Итак, четырехугольник PQRS на рис. 8.5 (ii) является параллелограммом. Точно так же все четырехугольники, показанные на рис. 8.5 (iii), (iv) и (v), являются параллелограммами.
- В параллелограмме MNRS на рис. 8.5 (iii) обратите внимание, что один из его углов, а именно ∠M — прямой угол. Как называется этот особый параллелограмм? Попробуй вспомнить.Он называется прямоугольником .
- & nbsp У параллелограмма DEFG на рис. 8.5 (iv) все стороны равны, и мы знаем, что он называется ромб .
- & nbsp Параллелограмм ABCD на рис. 8.5 (v) имеет ∠A = 90 ° и все стороны равны; Это называется квадрат .
- 6. В четырехугольнике ABCD на рис. 8.5 (vi) AD = CD и AB = CB, т.е. две пары смежных сторон равны. Это не параллелограмм.Он называется змей . Обратите внимание, что квадрат, прямоугольник и ромб — это параллелограммы.
- Квадрат — это прямоугольник, а также ромб.
- Параллелограмм — это трапеция.
- Кайт — это не параллелограмм.
- Трапеция не является параллелограммом (так как только одна пара противоположных сторон параллельна в трапеции, и мы требуем, чтобы обе пары были параллельны в параллелограмме).
- Прямоугольник или ромб — это не квадрат.
Посмотрите на рис. 8.6. У нас есть прямоугольник и параллелограмм с таким же периметром 14 см.
Рис. 8.6Здесь площадь параллелограмма DP × AB, и это меньше, чем площадь параллелограмма. прямоугольник, т.е. AB × AD как DP
Давайте теперь рассмотрим некоторые свойства параллелограмма, изученные в предыдущих классах.
8.4 СВОЙСТВА ПАРАЛЛЕЛОГРАММЫ
Давайте выполним действие.
Вырежьте из листа бумаги параллелограмм и вырежьте его по диагонали. У вас получится два треугольника. Что вы можете сказать об этих треугольниках?
Поместите один треугольник над другим. При необходимости переверните один. Что вы наблюдаете? Обратите внимание, что два треугольника конгруэнтны друг другу.
Повторите это действие с еще несколькими параллелограммами. Каждый раз вы будете наблюдать что каждая диагональ делит параллелограмм на два равных треугольника.Докажем теперь этот результат.
Рис. 8.7 Теорема 8.1.Диагональ параллелограмма делит его на два равных треугольника.
Доказательство: Пусть ABCD — параллелограмм, а AC — диагональ (см. Рис. 8.7). Наблюдать что диагональ AC делит параллелограмм ABCD на два треугольника, а именно Δ ABC и Δ CDA. Нам нужно доказать, что эти треугольники конгруэнтны.
Обратите внимание на то, что в Δ ABC и ΔCDA BC || AD и AC — это трансверсаль.
Итак, ∠BCA = ∠DAC (Пара чередующихся углов)
Также, AB || DC и AC — это поперечный.
Итак, ∠BAC = ∠ DCA (Пара чередующихся углов)
и AC = CA (общий)
Итак, ΔABC ≅ ΔCDA (правило ASA)
или диагональ AC делит параллелограмм ABCD на два равных треугольника ABC и CDA.
Рис. 8.8Теперь измерьте противоположные стороны параллелограмма ABCD.Что вы наблюдаете?
Вы обнаружите, что AB = DC и AD = BC.
Это еще одно свойство параллелограмма, указанное ниже:
Теорема 8.2.У параллелограмма противоположные стороны равны.
Доказательство: Вы уже доказали, что диагональ делит параллелограмм на два равных треугольника; так что вы можете сказать о соответствующих частях, скажем, о соответствующих стороны? Они равны.
Итак, AB = DC и AD = BC.
Теперь, что обратное этому результату? Вы уже знаете, что все, что дано в теореме то же самое должно быть доказано в обратном и все, что доказано в Теорема приводится в обратном. Таким образом, теорему 8.2 можно сформулировать следующим образом:
Если четырехугольник — параллелограмм, то все пары его противоположных сторон равны. Так его обратное значение:
Теорема 8.3.Если все пары противоположных сторон четырехугольника равны, то это параллелограмм.
Вы можете объяснить, почему?
Пусть стороны AB и CD четырехугольника ABCD
равно AD = BC (см. Рис. 8.8). Рисовать диагональ переменного тока.
Понятно, Δ ABC ≅ΔCDA (Почему?)
Итак, ∠BAC = ∠DCA
и ∠BCA = ∠DAC (Почему?)
Теперь вы можете сказать, что ABCD — параллелограмм? Почему?
Рис. 8.9Вы только что видели, что в параллелограмме каждая пара противоположных сторон равна и и наоборот, если все пары противоположных сторон четырехугольника равны, то это параллелограмм.Можем ли мы сделать такой же результат для пар противоположных углов?
Нарисуйте параллелограмм и измерьте его углы. Что вы наблюдаете?
Каждая пара противоположных углов равна.
Повторите то же самое с еще несколькими параллелограммами. Мы приходим к еще одному результату, представленному ниже.
Теорема 8.4.В параллелограмме противоположные углы равны.
Верно ли обратное к этому результату? Да. Используя свойство суммы углов четырехугольник и результаты параллельных прямых, пересекаемых трансверсалью, мы можем видеть что верно и обратное.Итак, имеем следующую теорему:
Теорема 8.5.Если в четырехугольнике все пары противоположных углов равны, то это параллелограмм.
Есть еще одно свойство параллелограмма. Давайте изучать то же самое. Нарисуйте параллелограмм ABCD и нарисуйте обе его диагонали, пересекающиеся в точке O (см. Рис. 8.10).
Измерьте длину OA, OB, OC и OD.
Что вы наблюдаете? Вы увидите, что
OA = OC и OB = OD.или, O — середина обеих диагоналей.
Повторите это действие с еще несколькими параллелограммами.
Каждый раз вы обнаружите, что O — это середина обеих диагоналей.
Итак, имеем следующую теорему:
Рис. 8.10 Теорема 8.6.Диагонали параллелограмма делят друг друга пополам.
А что будет, если в четырехугольнике диагонали разделят друг друга пополам? Будет ли это параллелограмм? Действительно, это правда.
Этот результат является обратным результату теоремы 8.6. Он приведен ниже:
Теорема 8.7.Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм.
Этот результат можно объяснить следующим образом:
Обратите внимание, что на рис. 8.11 показано, что OA = OC и OB = OD.
Итак, ΔAOB ≅ ΔCOD (Почему?)
Следовательно, ABO = ∠CDO (Почему?)
Отсюда получаем AB || CD.
Аналогично, BC || ОБЪЯВЛЕНИЕ.
Следовательно, ABCD — параллелограмм.
Рис. 8.11Давайте теперь рассмотрим несколько примеров.
Пример 1
Покажите, что каждый угол прямоугольника является прямым.
Решение
Напомним, что такое прямоугольник.
Прямоугольник — это параллелограмм, в котором один угол является прямым.
Пусть ABCD — прямоугольник, в котором ∠A = 90 °.
Мы должны показать, что ∠B = ∠C = ∠D = 90 °.
У нас, AD || BC и AB — трансверсаль (см. Рис. 8.12).
Итак, ∠A + ∠B = 180 ° (внутренние углы на одной стороне поперечины).
Но, A = 90 °.
Итак, ∠B = 180 ° — ∠A = 180 ° — 90 ° = 90 °
Теперь ∠C = ∠A и ∠D = ∠B (противоположные углы параллелограммы)
Итак, ∠C = 90 ° и ∠D = 90 °.
Следовательно, каждый из углов прямоугольника является прямым.
Рис. 8.12Пример 2
Покажите, что диагонали ромба перпендикулярны друг другу.
Решение
Рассмотрим ромб ABCD (см. Рис. 8.13).
Вы знаете, что AB = BC = CD = DA (Почему?)
Теперь, в Δ AOD и Δ COD,
OA = OC (диагонали параллелограмма делят друг друга пополам) OD = OD (общий) AD = CDСледовательно, Δ AOD ≅ ΔCOD (правило сравнения SSS)
Это дает ∠ AOD = ∠COD (CPCT)
Но, AOD + ∠ COD = 180 ° (линейная пара)
Итак, 2∠ AOD = 180 °
или, AOD = 90 °
Итак, диагонали ромба перпендикулярны друг другу.
Рис. 8.13Пример 3
ABC — равнобедренный треугольник, в котором AB = AC. AD делит пополам внешний угол PAC и CD || AB (см. Рис. 8.14). Покажи, что
(i) ∠DAC = ∠BCA и
(ii) ABCD — параллелограмм.
Решение
(i) ΔABC равнобедренный, в котором AB = AC (дано)
Итак, ABC = ∠ACB (Углы, противоположные равным сторонам)
Также ∠PAC = ∠ABC + ∠ACB (Внешний угол треугольника)
или, PAC = 2∠ACB (1)
Теперь AD делит ∠PAC пополам.
Итак, ∠PAC = 2∠DAC (2)
Следовательно,
2∠DAC = 2∠ACB [Из (1) и (2)]
или, DAC = ∠ACB
(ii) Эти равные углы образуют пару чередующихся углов, когда отрезки BC и AD пересекаются трансверсальной AC.
Итак, BC ||
нашей эрыТакже, BA || CD (Дано)
Теперь обе пары противоположных сторон четырехугольника ABCD параллельны.
Итак, ABCD — параллелограмм.
Рис. 8.14Пример 4
Две параллельные прямые l и m пересекаются трансверсалью p. (см. рис. 8.15). Покажите, что четырехугольник, образованный биссектрисами внутренних углов представляет собой прямоугольник.
Решение
Приведено, что PS || QR и трансверсаль p пересекают их в точках A и C соответственно.
Биссектрисы PAC и ∠ACQ пересекаются в точке B, а биссектрисы ACR и ∠SAC пересекаются в D.
Мы должны показать, что четырехугольник ABCD является прямоугольником.
Сейчас ∠PAC = ∠ACR
(чередующиеся углы, так как l || m и p — поперечное сечение)
Итак, ∠PAC = ∠ACR
т. Е. =BAC = ∠ACD
Рис. 8.15Они образуют пару чередующихся углов для линий AB и DC с переменным током в качестве поперечного и они тоже равны.
So, AB || DC
Аналогично, BC || AD (с учетом ∠ACB и ∠CAD)
Следовательно, четырехугольник ABCD — параллелограмм.
Также ∠PAC + ∠CAS = 180 ° (линейная пара)
½ ∠PAC + ½∠CAS = ½ × 180 ° = 90 °
или, BAC + ∠CAD = 90 °
или, ∠BAD = 90 °
Итак, ABCD — это параллелограмм, в котором один угол равен 90 °.
Следовательно, ABCD — прямоугольник.
Пример 5
Покажите, что биссектрисы углов параллелограмма образуют прямоугольник.
Решение
Пусть P, Q, R и S будут точками
пересечение биссектрис A и ∠B, ∠B и ∠C, ∠C и ∠D, а также ∠D и ∠A соответственно параллелограмма ABCD (см.рис.8.16).
Что вы наблюдаете в ΔASD?
Так как DS делит пополам ∠D и AS пополам ∠A, следовательно,
∠DAS + ∠ADS = ½∠A + ½∠D
= ½ (∠A + ∠D)
= ½ × 180 ° (∠A и ∠D — внутренние углы на одной стороне поперечного сечения)
= 90 °
Также ∠DAS + ∠ADS + ∠DSA = 180 ° (свойство суммы углов треугольника)
или, 90 ° + ∠ DSA = 180 °
или, ∠DSA = 90 °
Итак, PSR = 90 ° (находясь вертикально противоположно DSA)
Рис.8,16Аналогичным образом можно показать, что ∠APB = 90 ° или ∠ SPQ = 90 ° (как это было показано для ∠DSA). Точно так же PQR = 90 ° и ∠SRQ = 90 °.
Итак, PQRS — четырехугольник, в котором все углы прямые.
Можно сделать вывод, что это прямоугольник? Давайте рассмотрим. Мы показали, что ∠PSR = ∠PQR = 90 ° и ∠SPQ = ∠SRQ = 90 °. Итак, обе пары противоположных углов равны.
Следовательно, PQRS — это параллелограмм, в котором один угол (фактически все углы) равен 90 ° и Итак, PQRS — это прямоугольник.
8.5 ДРУГОЕ УСЛОВИЕ, ЧТОБЫ ЧЕТВЕРТАЯ БУДЕТ ПАРАЛЛЕЛОГРАММОЙ
В этой главе вы изучили многие свойства параллелограмма, а также проверил, что если в четырехугольнике выполняется какое-либо из этих свойств, то он становится параллелограмм.
Теперь мы изучим еще одно условие, которое является наименее необходимым условием для того, чтобы четырехугольник был параллелограммом. Это сформулировано в форме теоремы, как показано ниже:
Теорема 8.8Четырехугольник — это параллелограмм, если пара противоположных сторон равны и параллельны.
Посмотрите на рис. 8.17, на котором AB = CD и
.AB || CD. Нарисуем диагональ AC. Можно показать
, что Δ ABC ≅ Δ CDA по правилу сравнения SAS.
Итак, BC || AD (Почему?)
Рис. 8.17Давайте теперь рассмотрим пример применения этого свойства параллелограмма.
Пример 6
ABCD — параллелограмм, в котором P и Q — середины противоположных сторон AB и CD. (см. рис.8.18). Если AQ пересекает DP в S, а BQ пересекает CP в R, покажите, что:
(i) APCQ — параллелограмм.
(ii) DPBQ — параллелограмм.
(iii) PSQR — параллелограмм.
Рис. 8.18Решение:
(i) В четырехугольнике APCQ,
AP || QC (Поскольку AB || CD) (1)AP = ½AB, CQ = ½CD (дано)
Также AB = CD (Почему?)
Итак, AP = QC (2)
Следовательно, APCQ — параллелограмм [Из (1) и (2) и теоремы 8.8]
(ii) Точно так же четырехугольник DPBQ является параллелограммом, потому что
DQ || PB и DQ = PB.
(iii) В четырехугольнике PSQR,
SP || QR (SP является частью DP, а QR — частью QB)
Аналогично, SQ || PR
Итак, PSQR — параллелограмм.
В Е Х Е Р К И С Е 8.1- Углы четырехугольника находятся в соотношении 3: 5: 9: 13. Найдите все углы четырехугольника. четырехугольник.
- Если диагонали параллелограмма равны, то покажите, что это прямоугольник.
- Покажите, что если диагонали четырехугольника делят друг друга пополам под прямым углом, то он это ромб.
- Покажите, что диагонали квадрата равны и делят друг друга пополам под прямым углом.
- Покажите, что если диагонали четырехугольника равны и делят друг друга пополам справа углы, то это квадрат.
- Диагональ AC параллелограмма ABCD делит пополам ∠A (см. Рис. 8.19). Покажи это
- делит пополам ∠ C также,
- ABCD — ромб.
- ABCD — ромб. Докажите, что диагональ AC делит пополам A, а также ∠C, а диагональ BD делит пополам B и ∠D.
- ABCD — это прямоугольник, в котором диагональ AC делит пополам A и ∠C.Покажи это:
- ABCD квадрат Диагональ
- BD делит пополам ∠B и ∠D.
- В параллелограмме ABCD на диагонали BD взяты две точки P и Q, так что DP = BQ (см. Рис. 8.20). Покажи это:
- ΔAPD ≅ ΔCQB
- AP = CQ
- Δ AQB ≅ Δ CPD
- AQ = CP
- APCQ — параллелограмм
- ABCD — параллелограмм, а AP и CQ — перпендикуляры из вершин A и C на диагонали BD (см. Рис. 8.21). Покажи это
- Δ APB ≅ Δ CQD
- AP = CQ
- In Δ ABC и Δ DEF, AB = DE, AB || DE, BC = EF и BC || EF. Вершины A, B и C соединены с вершинами D, E и F соответственно (см. Рис.8.22). Покажите, что
- Четырехугольник ABED — параллелограмм
- Четырехугольник BEFC — параллелограмм
- г. н.э. || CF и AD = CF
- четырехугольник ACFD — параллелограмм
- AC = DF
- Δ ABC ≅ Δ DEF.
- ABCD представляет собой трапецию, в которой AB || CD и AD = BC (см. Рис.8.23). Покажи это
- ∠A = ∠B
- ∠C = ∠D
- ∠ ABC ≅ Δ BAD
- диагональ AC = диагональ BD [ Подсказка : удлините AB и проведите через C линию, параллельную DA, пересекающую AB, полученную в точке E.]
8.6 ТЕОРЕМА СРЕДНЕЙ ТОЧКИ
Вы изучили множество свойств треугольника, а также четырехугольника.Теперь позвольте нам изучите еще один результат, связанный с серединами сторон треугольника. Выполнять следующая деятельность.
Нарисуйте треугольник и отметьте середины E и F двух сторон треугольника. Присоединиться точки E и F (см. рис. 8.24).
Измерьте EF и BC. Измерьте AEF и ∠ABC.
Что вы наблюдаете? Вы обнаружите, что:
EF = ½BC и ∠AEF = ∠ABCтак,
ЭФ || до н.эПовторите это действие с еще несколькими треугольниками.Итак, вы приходим к следующей теореме:
Рис. 8.24 Теорема 8.9.Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне.
Вы можете доказать эту теорему, используя следующую подсказку:
Обратите внимание на рис. 8.25, на котором E и F являются серединами AB и AC соответственно, а CD || BA.
Δ AEF ≅ Δ CDF (Правило ASA)
Итак, EF = DF и BE = AE = DC (Почему?)
Следовательно, BCDE — параллелограмм.(Почему?)
Это дает EF || ДО Н.Э.
В этом случае также обратите внимание, что EF = ½ED = ½BC.
Рис. 8.25Вы можете сформулировать обратное к теореме 8.9? Верно ли обратное?
Вы увидите, что верно и обратное утверждение вышеупомянутой теоремы, которое сформулировано как ниже:
Теорема 8.10.Линия, проведенная через середину одной стороны треугольника параллельно другой стороне, делит третью сторону пополам.
На рис. 8.26 обратите внимание, что E — это средняя точка AB, прямая l проходит через E и параллельна BC и CM || BA.
Докажите, что AF = CF, используя сравнение Δ AEF и Δ CDF.
Рис. 8.26Пример 7
В Δ ABC, D, E и F — это соответственно середины сторон AB, BC и CA (см. Рис. 8.27). Покажите, что Δ ABC делится на четыре равных треугольника, соединяя D, E и F.
Решение:
Поскольку D и E являются серединами сторон AB и BC треугольника ABC, по теореме 8.9, DE || AC
Аналогично DF || BC и EF || AB
Следовательно, ADEF, BDFE и DFCE — параллелограммы.
Теперь DE — диагональ параллелограмма BDFE,
следовательно, Δ BDE ≅ Δ FED
Аналогично Δ DAF ≅ Δ FED
и Δ EFC ≅ Δ FED
Итак, все четыре треугольника равны.
Рис. 8.27Пример 8
l, m и n — три параллельные прямые, пересекаемые трансверсалиями p и q, так что l, m и n отсекают равные точки пересечения AB и BC на p (см. Рис. 8.28). Покажите, что l, m и n также отсекают равные пересечения DE и EF на q.
Решение:
Нам дано, что AB = BC, и мы должны доказать, что DE = EF.
Соединим A с F, пересекая m в G.
Трапеция ACFD разделена на два треугольника;
Рис. 8,28, а именно Δ ACF и Δ AFD.
В Δ ACF задано, что B — это средняя точка AC (AB = BC)
и BG || CF (так как m || n).
Итак, G — средняя точка AF (согласно теореме 8.10)
Теперь, в Δ AFD, мы можем применить тот же аргумент, что и G — средняя точка AF,
GE || AD и, значит, по теореме 8.10, E — середина DF,
и.е., DE = EF.
Другими словами, l, m и n также отсекают равные точки пересечения на q.
В Е Х Е Р К И С Е 8.2- ABCD — четырехугольник, в котором P, Q, R и S являются серединами сторон AB, BC, CD и DA (см. Рис. 8.29). AC — диагональ. Покажи это :
- SR || AC и SR = ½ AC
- PQ = SR
- PQRS — параллелограмм.
- ABCD — ромб, а P, Q, R и S — середины сторон AB, BC, CD. и DA соответственно. Покажите, что четырехугольник PQRS — прямоугольник.
- ABCD — прямоугольник, а P, Q, R и S — середины сторон AB, BC, CD и DA соответственно. Покажите, что четырехугольник PQRS — ромб.
- ABCD представляет собой трапецию, в которой AB || DC, BD — диагональ, а E — середина AD.Через E проводится прямая, параллельная AB, пересекающая BC в точке F (см. Рис. 8.30). Покажите, что F — середина BC. Рис. 8.30
- В параллелограмме ABCD E и F — середины сторон AB и CD соответственно. (см. рис. 8.31). Покажите, что отрезки AF и EC пересекают диагональ BD. Рис. 8.31
- Покажите, что отрезки прямых, соединяющие середины противоположных сторон четырехугольники разделите друг друга пополам.
- ABC — треугольник, расположенный под прямым углом к C. Прямая, проходящая через середину M гипотенузы AB.
и параллельно BC пересекает AC в D. Покажем, что
- D — средняя точка AC
- MD ⊥ AC
- CM = MA = ½ AB
РЕЗЮМЕ
В этой главе вы изучили следующие моменты:
- Сумма углов четырехугольника 360 °.
- Диагональ параллелограмма делит его на два равных треугольника.
- В параллелограмме,
- противоположные стороны равны
- противоположных углов равны
- диагоналей делят пополам
- Четырехугольник — это параллелограмм, если
- противоположные стороны равны или
- противоположных углов равны или
- диагоналей делят пополам или
- Пара противоположных сторон равна и параллельна
- Диагонали прямоугольника делят друг друга пополам и равны, и наоборот.
- Диагонали ромба пересекают друг друга под прямым углом и наоборот.
- Диагонали квадрата пересекают друг друга под прямым углом и равны, и наоборот.
- Отрезок, соединяющий середины любых двух сторон треугольника, параллелен третья сторона и это половина.
- Линия, проходящая через середину стороны треугольника, параллельная другой стороне, делит третью сторону пополам.
- Четырехугольник, образованный соединением середин сторон четырехугольника по порядку, представляет собой параллелограмм.
Диагональ воздушного змея
Диагональ воздушного змеяПерейти к основному содержанию
Диагонали воздушного змея
диагонали воздушного змея. В результате диагонали образуют прямые углы.Карла быстро нарисовала змей справа на своем листе бумаги диагональю, показывающей два совпадающих треугольника. Площадь правильного многоугольника В этом кайте две диагонали образуют ширину и высоту большого прямоугольника, окружающего кайт. Найдите длину каждой внутренней диагонали. Если вы хотите рассчитать периметр воздушного змея, вы должны быть уверены в длине двух смежных сторон. Используйте этот рабочий лист, чтобы попрактиковаться в поиске области кайта. Выведите формулу A = s 2 для площади квадрата.у воздушного змея две пары сторон имеют одинаковую длину. Невершинные углы воздушного змея делятся пополам диагональю. Поскольку одна сторона составляет половину диагонали, площадь формулы ромба равна половине произведения диагоналей. Кроме того, он может рассчитать периметр воздушного змея. Covid-19 привел мир к феноменальному переходу. Используйте трассировку кайта по диагонали. Гипотеза: C-36. Диагонали воздушного змея равны. Ровно одна диагональ делит другую пополам. е. Если диагонали четырехугольника перпендикулярны, то четырехугольник должен быть воздушным змеем.Примечание: эта формула работает и для площади ромба, поскольку ромб — это особый вид воздушного змея. 1. Дополнительная формула для определения площади ромба заключается в использовании формулы воздушного змея (она работает, потому что ромбы технически являются воздушными змеями) 28 августа 2020 г. · 12. Прямые углы будут вершинами прямоугольника с площадью вдвое большей, чем у исходной фигуры. Если в четырехугольнике одна диагональ является серединным перпендикуляром другой диагонали, то четырехугольник должен быть воздушным змеем, но также может быть особым параллелограммом, например ромбом или квадратом.Загрузите набор (3 Площадь воздушного змея | Целые числа — Тип 1. abcd — это воздушный змей, его диагонали пересекаются в точке o, если угол dab = 112 градусов и угол dcb = 64 градуса, найдите угол odc и угол oba — Математика — Четырехугольники Пример 17: Каждый Воздушный змей представляет собой трапецию. Поскольку наклон 21 января 2020 г. · Перпендикулярные диагонали воздушного змея Это означает, что, поскольку диагонали пересекаются под углом 90 градусов, мы можем использовать наши знания теоремы Пифагора, чтобы найти недостающие длины сторон воздушного змея, а затем, в свою очередь, найти периметр этого особого многоугольника.Воздушный змей: Все мы знакомы с формой воздушного змея как игрушки, сделанной из легких материалов. Эта формула может быть применена к любому воздушному змею, включая особые случаи ромба 24 апр, 2019 · Вопрос. Полный список смотрите на сайте toppr. ГЕОМЕТРИЯ Рабочий лист 11. Более длинная диагональ воздушного змея делит более короткую пополам. Диагонали не совпадают, но всегда перпендикулярны. заблудший. Воздушные змеи — это четырехугольники с двумя отдельными парами совпадающих смежных сторон. Если площадь кайта составляет 240 квадратных дюймов, какова длина диагоналей? 62 / 87,21 Площадь A воздушного змея равна половине произведения длин его диагоналей, d1 и d2. Следовательно, длина диагоналей равна 15.Какова мера ∠AXB? Ложь — диагонали не обязательно должны совпадать или делить друг друга пополам. Это метод, использованный на рисунке выше. 21 февраля 2018 г. · Диагонали кайта — 21 и 24, и чем короче диагональ, тем длиннее пополам. В общем, любой четырехугольник с перпендикулярными диагоналями, одна из которых является линией симметрии, является воздушным змеем. 1. Трапеция и воздушный змей также являются типами четырехугольников со свойствами, зависящими от их формы. Давайте посмотрим на воздушный змей ABCD. ИССЛЕДОВАНИЕ: начертите эту схему на кальке и аккуратно добавьте другую диагональ.т. У воздушного змея две пары равных сторон. Воздушный змей — это четырехугольник, у которого две стороны, расположенные рядом друг с другом, совпадают, а две другие стороны также совпадают. ! —- Есть Instagram? Охваченные цели включают: 30 глав | Это . Рисунок 3 Рисунок 4 Один из способов определить воздушный змей — это стороны двух равнобедренных треугольников, имеющих общее основание. C. Треугольник имеет 3 стороны. 27. где d1 и d2 — длины двух диагоналей. Если диагонали четырехугольника делят пополам углы при его вершинах, то четырехугольник должен быть ромбическим воздушным змеем — любым четырехугольником, по крайней мере, с одной осью симметрии через пару противоположных углов (вершин).Дополнительная формула для определения площади ромба заключается в использовании формулы воздушного змея (она работает, потому что ромбы технически являются воздушными змеями). Чтобы вычислить площадь воздушного змея, длины его двух диагоналей умножаются и полученная сумма делится на два. * диагонали воздушного змея. Вопрос. Диагонали изоси захватывают одну из диагоналей воздушного змея, делающую пополам пару противоположных углов. Площадь воздушного змея определяется как половина произведения его диагонали. Использование диагоналей для поиска 23 января 2021 г. Площадь воздушного змея равна длине меньшей из его диагоналей.Давайте посмотрим на воздушный змей ABCD. Доказательство: область ромба. • Выпуклый змей — D C A B диагонали воздушного змея пересекаются. В результате диагонали образуют прямые углы. Какова площадь получившегося кайта. Воздушные змеи включают ромбики. диагональ, соединяющая углы при вершинах воздушного змея, является серединным перпендикуляром другой биссектрисы диагонального угла воздушного змея; гипотеза о том, что углы при вершинах воздушного змея делятся пополам с помощью гипотезы о последовательном угле диагональной трапеции; 08 декабря 2016 г. · Транскрипт Пример 12. · Одна из диагоналей будет делиться пополам.Th Диагонали квадрата ABCD пересекаются в точке E. $ 16: (5 15. Если четырехугольник является воздушным змеем, то его диагонали перпендикулярны. Воздушный змей определяется треугольником с длинами сторон a, b и включенным углом θ. 50 Если a диагональ четырехугольника делит оба угла пополам, тогда это (a) воздушный змей (b) параллелограмм (c) ромб (d) прямоугольник Решение. Наклон XV i … Получите ответы, которые вам нужны, прямо сейчас! Pertama kita harus mengetahui rumus ян дигунакан унтук менгхитунг луас себуах лайанг-лайанг (область воздушного змея), йайту: D1 дан D2 мерупакан панджанг кедуа диагональ пада лайанг-лайанг (диагонали воздушного змея).Если длина двух диагоналей ромба равна d 1 и d 2, то площадь ромба = ½ × d 1 × d 2 — Свойства воздушного змея, которые я обнаружил, исследуя измерения на эскизе выше, были: 1. Скопируйте и завершите предположение. Например, если длина двух соседних сторон равна a и b, тогда формула периметра будет рассчитана как — 2 (a + b). Итак, OC — это высота треугольника ΔCDB, а OA — высота треугольника ΔADB. • диагонали, которые всегда пересекаются под прямым углом • диагональ, называемая осью симметрии (линия AD), делит пополам другую диагональ (линия BC), делит пополам углы при вершинах (A и D) и делит змей на два равных треугольника ( ABD и ACD) • диагональ (линия BC), разделяющая кайт на два равнобедренных треугольника (ABC и BCD). Площадь воздушного змея определяется по следующей формуле.Диагонали воздушного змея _____. Оба этих четырехугольника имеют перпендикулярные диагонали, поэтому мы и собираемся найти их площади. Одним из ключевых свойств воздушного змея является то, что его диагонали перпендикулярны. Более длинная диагональ воздушного змея делит более короткую пополам. Общая площадь воздушного змея — Кайт. Это текущий выбранный элемент. (б) Последовательные углы между параллельными сторонами ромба являются дополнительными. Напомним, что у параллелограммов тоже были пары равных сторон. 09 мая 2020 · В общем, четырехугольник с двумя парами равных соседних участков (т.Более длинная диагональ также представляет собой биссектрису к вершине и низу. 8 дек. 2016 Пр. 12. Это похоже на воздушных змеев, которые вы видите летающими в небе. Углы. В евклидовой геометрии воздушный змей — это двумерный змей. Воздушный змей — это четырехугольник, в котором две пары смежных сторон равны. Диагонали воздушного змея — это высота и ширина прямоугольника, в который он наложен, и мы знаем это, поскольку площадь прямоугольника равна основанию, умноженному на высоту. Диагонали воздушного змея, как и диагонали ромба, перпендикулярны.Более длинная диагональ также разрезает более короткую пополам. Вершины двух углов находятся на параллельной линии, поэтому диагонали перпендикулярны. У воздушных змеев есть несколько свойств, которые помогут нам отличить их от других четырехугольников. Какова длина другой базы? 105 дюймов. Твердые факты Воздушный змей — это четырехугольник с двумя разными парами совпадающих смежных сторон. Площадь = (6 × 18) / 2 = 108/2 = 54 квадратных дюйма. C Диагонали воздушного змея перпендикулярны. Одна диагональ воздушного змея делит другую диагональ пополам.диагонали квадрата квадрат — это //, прямоугольник, воздушный змей и ромб. Kite Diagonals, которые вы ищете, можно использовать для всех в этом посте. Поэтому воспользуйтесь теоремой Пифагора:, где длина красной диагонали. 2) По крайней мере, одна пара противоположных углов конгруэнтна. , 31. Диагонали воздушного змея перпендикулярны. Введите длины обеих диагоналей и расстояние между точками A и E. В результате диагонали образуют прямые углы. Воздушный змей — это четырехугольник с двумя парами длин сторон, которые примыкают друг к другу.Здесь d 1 и d 2 — диагонали, пересекающие друг друга под прямым углом. 04 августа 2018 · Стенограмма. Большинство воздушных змеев имеют одну диагональ, которая делит ее углы пополам. Используйте свойства воздушных змеев. II. Кроме того, создавайте фигуры, которые НАИЛУЧШИМ образом описываются как трапеция, равнобедренная трапеция, воздушный змей и четырехугольник *. Ниже приведены конечные продукты некоторых из этих конструкций. Какая площадь у ромба? 10. Уравнения прямых, пересекающихся под прямым углом, обладают тем свойством, что произведение их наклонов равно -1.Диагональная линия AC — это серединный перпендикуляр к BD. Какая площадь у ромба? 12. Элементами воздушного змея являются его 4 угла, 4 стороны и 2 диагонали. Нет. A C и B D — диагонали, перпендикулярные друг другу. Формула основана на том факте, что воздушный змей состоит из двух треугольников. taffy927x2 и еще 1 пользователь нашли этот ответ полезным. В параллелограмме противоположные стороны равны. Площадь воздушного змея может быть равна периметру воздушного змея в дюймах. · В некоторых текстах кайт определяется как имеющий 2 пары последовательных конусов. Диагонали воздушного змея всегда пересекаются под углом 90 °.Откройте для себя ресурсы. Ромб — это квадрат. T диагоналей, которые всегда пересекаются под прямым углом • диагональ, называемая осью симметрии (линия AD), делит пополам другую диагональ (линия BC), делит пополам углы при вершинах (A и D) и делит змей на два равных треугольника ( ABD и ACD Как только вы знаете длину диагоналей, вы можете просто умножить их и разделить результат на 2. Нет, но диагонали квадрата, ромба и воздушного змея перпендикулярны друг другу. Может ли воздушный змей иметь четыре совпадающие диагонали? Нет. потому что воздушный змей представляет собой четырехугольник с четырьмя сторонами с двумя диагоналями разной длины, которые пересекаются друг с другом под прямым углом.5 дюймов. Диагонали делят углы пополам. Если длины диагоналей равны p и q, показывают, что: 2 pq = ab sin θ Примеры 1) Найдите площадь воздушного змея с диагоналями длиной 6 и 18 дюймов. Углы AED, DEC, CED, BEA — прямые. Вы также можете использовать диагонали воздушного змея, пересекающиеся под углом x∘. Другая часть диагонали показана как алгебраическое выражение. Если вы знаете длину диагоналей, вы можете найти площадь с помощью простой алгебры. ∴ ∠AOD = ∠DOC = ∠BOC = ∠AOB = 90o 12 февраля 2018 г. · Во всех этих четырех формах диагонали пересекают друг друга пополам.Диагонали ромба равны и перпендикулярны друг другу. В качестве формулы: где d 1 — длина воздушного змея. Докажите, что диагонали воздушного змея перпендикулярны. (a) Квадрат (b) Воздушный змей (c) Трапеция (d) Четырехугольник (a) Квадрат (b) Воздушный змей (c) Трапеция Подпишитесь сейчас: http: // www. C-38 Гипотеза о биссектрисе угла воздушного змея — Углы при вершине воздушного змея делятся пополам диагональю. Попытайся! 1. Следовательно, наше уравнение выглядит следующим образом: Чтобы решить эту проблему, сначала обратите внимание, что красная диагональная линия делит змей на два треугольника, каждый со стороной которых имеет длину, и обратите внимание, что гипотенуза внутреннего треугольника является красной диагональю.Пирог имеет диаметр 9 дюймов и разрезается на 10 одинаковых ломтиков. Летающий змей. Сегменты длиной 4 метра и 4 метра должны представлять сегмент, который был разделен пополам на 2 равные части или d 2 d 2 = 4 + 4 = 8 метров. Воздушный змей представляет собой четырехугольник с четырьмя сторонами, который можно сгруппировать в две пары равных частей. длины, которые расположены рядом или совпадают. 4. Диагонали воздушного змея перпендикулярны, а диагональ, противоположная конгруэнтным углам, делит другую диагональ пополам. Определите, является ли воздушный змей параллелограммом.+2. Воздушный змей симметричен относительно своей главной диагонали. Площадь воздушного змея — это размер его поверхности. Свойства: 1) Две различные пары смежных конгруэнтных сторон. ) Если прямоугольник, то диагонали равны. Кодируйте быстрее с помощью плагина Kite для вашего редактора кода, включающего функции завершения строк кода и безоблачную обработку. Решение: неверно. Параллелограмм — это прямоугольник. диагонали воздушного змея параллельны основанию (диагонали) и, следовательно, параллельны друг другу. К нему примыкают две пары одинаковой длины (рядом с каждым змеем.Все внутренние углы острые. Диагонали воздушного змея всегда пересекаются под углом 90⁰. C-36 Гипотеза о диагонали воздушного змея — диагонали воздушного змея перпендикулярны. Свойства воздушного змея · Две непересекающиеся пары последовательных сторон конгруэнтны по определению · Диагонали перпендикулярны. Они совпадают. Летающий змей. isostrap3. Площадь воздушного змея равна A = 9×2. Имеет одну пару равных углов. Диагонали кайта перпендикулярны. Диагонали воздушного змея перпендикулярны друг другу.Диагонали воздушного змея действительно пересекаются под прямым углом. Он не имеет вращательной симметрии. Что верно в отношении диагоналей воздушного змея? варианты ответа. Ссылки вперед. Некоторые из отличительных свойств диагоналей ромба сохраняются и в воздушном змее, который является более общей фигурой. Диагонали пересекаются под прямым углом, но не делят друг друга пополам. Ответ / Пояснение. 25. Углы воздушного змея равны в точках, где встречаются две пары смежных сторон. больше 180 °). (3) Если трапеция равнобедренная, то ее противоположные углы являются дополнительными.30) Длина одной из диагоналей воздушного змея на 4 см больше, чем удвоенная длина другой диагонали. DB является основанием обоих этих треугольников, и его длина задана (y). com У воздушного змея тоже есть вписанная окружность, но его радиус трудно вычислить. Элементы этого воздушного змея: Каждый воздушный змей является ортодиагональным, что означает, что его две диагонали расположены под прямым углом друг к другу. Диагонали параллелограмма делят друг друга пополам. Тогда AB = AD и BC = DC В ΔABC и ΔADC, AB = AD BC = CD AC = AC ∴ ΔABC ≅ ΔADC (сравнение SSS) ⇒ ∠BCA = ∠ DCA (C.Формула имеет следующий вид: A = d1d2 / 2, где d1 — длинная диагональ, а d2 — короткая диагональ. Одна из диагоналей будет разделена пополам. Решение: неверно. Одна диагональ делит другую пополам. 5. Смотрите полный список на mathopenref. Калькулятор воздушных змеев. 5 дюймов. Электронное обучение — это будущее сегодня. ; Два внутренних угла при противоположных вершинах воздушного змея равны. Правильный вариант есть. (c) Если диагональ четырехугольника делит оба угла пополам, то это ромб. YouTube. У воздушного змея две пары равных смежных сторон.В. Я кайт-трапеция изо-ромб. Диагонали воздушного змея перпендикулярны друг другу. У воздушного змея две пары последовательных сторон, которые совпадают. 4. \ Area = \ frac {d1 * d2} {2} \. Одна его диагональ образует линию симметрии. Доказательство: диагонали ромба — это середина перпендикуляра. 4) По крайней мере, одна пара противоположных углов, разделенных пополам диагональю. 51 Чтобы построить уникальный параллелограмм, необходимо минимальное количество измерений: (a) 2 (b) 3 (c) 4 Kite — это бесплатное автозаполнение для разработчиков Python.2 = Вертикальная диагональ = 25. Как и у всех четырехугольников, сумма четырех углов составляет 360 градусов. Площадь воздушного змея, когда указаны диагонали, определяется как область, занимаемая внутри границы воздушного змея при условии, что значение диагоналей указано и представлено как A = (d1 * d2) / 2 или Area = (Diagonal 1 * Diagonal 2). ) / 2. Утверждение: Если диагонали четырехугольника пересекаются под прямым углом, то четырехугольник является ромбом. Диагонали воздушного змея пересекаются под углом 90 °. Формула площади воздушного змея: Площадь = 1 2 (диагональ 1) (диагональ 2) 30 сентября 2019 г. · Диагонали воздушного змея перпендикулярны друг другу. Мы уже показали, что диагональ, соединяющая два угла, образованных равными сторонами, делит углы в этих углах пополам.Свойства ромба По определению все стороны равны. Пр. 3. Верно, они пересекаются. Они делят друг друга пополам. У воздушного змея две пары последовательных сторон, которые совпадают. Каждый ромб — это воздушный змей, а любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, — ромбом. Площадь воздушного змея Площадь воздушного змея равна половине произведения диагоналей. 6 февраля 2015 г. · Свойства воздушного змея Определение воздушного змея: Воздушный змей — это квадри / атера / с двумя разными парами смежных сторон, которые совпадают. Нарисуйте ромб с диагоналями 4 и 6.Пример: Ввод: d1 = 4, d2 = 6. Диагонали воздушного змея перпендикулярны друг другу. Подставьте значения диагоналей в формулу A = 1/2 (d 1 * d 2) и найдите площадь кайта на этих листах pdf для 6-го класса, представив задачи в виде иллюстраций с целыми числами ≤ 20 на уровне 1 и ≥ 10 на уровне 2. Вы можете доказать. Ниже показаны два метода расчета площади воздушного змея. Проблема. Если AE = 3x — 4 и BD = 10x 48, найдите AC. Математика 9 класс (Индия) Блок: Четырехугольники. 3) Диагонали перпендикулярны.Большинство воздушных змеев имеют одну диагональ, которая делит ее углы пополам. Диагонали воздушного змея образуют четыре равных треугольника. ОПРОС . 3. И это то, что объединяет всех воздушных змеев. Перечислите свойства воздушного змея. Главная диагональ делит пополам пару противоположных углов (угол K и угол M). Поскольку диагонали воздушного змея пересекаются, все углы, образованные диагоналями, должны быть прямыми углами. Какая площадь у кайта? 240. 10. Диагональ прямоугольника наклонена к одной стороне прямоугольника под углом 25o. Диагонали пересекаются в точке \ (90 ° \). Формула площади воздушного змея находится путем перестановки частей, образованных диагоналями, в прямоугольник.Меньшая диагональ воздушного змея делит его на два равнобедренных треугольника. Пересечение диагоналей воздушного змея образуют углы в 90 градусов (прямые). Итак, воздушный змей может быть трапецией; это тот случай, когда это ромб. 15. e. Кайт: (а) Диагонали воздушного змея перпендикулярны. 5. 10. Краткое описание свойств воздушного змея: диагональ между равными сторонами делит другую диагональ пополам. Диагонали воздушного змея. 16. Может потребоваться помощь. Элементами воздушного змея являются его 4 угла, 4 стороны и 2 диагонали.ВСЕ Остальные. Так как ромб, квадрат и прямоугольник также являются параллелограммом ∴ Диагонали также делят друг друга пополам. Таким образом, четырехугольники, диагонали которых делят друг друга пополам, равны: Параллелограмм Ромб Квадрат Прямоугольник Пример 3. Сколько бумаги каждого оттенка было использовано в нем? Характеристики. Итак, у нас есть, что площадь равна. Докажите, что если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом. 0 дюймов. 10. Нарисуйте воздушный змей с диагоналями 20 и 24. ПРИМЕЧАНИЕ. Повторная публикация материалов (частично или полностью) с этого сайта в Интернете является нарушением авторских прав. Трос кайта находится под углом 57 градусов к земле. .Пример 19: Диагонали прямоугольника перпендикулярны друг другу. Разделите произведение на 2, чтобы получить площадь воздушного змея. 1. Пример 20: Для построения уникального параллелограмма необходимо указать длину только двух сторон. На приведенном ниже эскизе показано, как построить воздушный змей. (F-117A Nighthawk компании Lockheed Martin был первым самолетом, форма и форма которого способствовали его незаметности. Четырехугольник с двумя парами смежных конгруэнтных сторон. Теги: не каждый параллелограмм является ромбом, хотя любой параллелограмм с перпендикулярными диагоналями ( второе свойство) представляет собой ромб.Задайте уравнение и решите проблему. Для воздушного змея ABCD с AB = AD и CB = CD справедливо следующее. а. Мы знаем, что диагонали воздушного змея перпендикулярны друг другу. Вы должны знать длины сторон неправильного четырехугольника и размер одного угла. С этим определением и расчетами, которые я приводил в своих предыдущих постах, вы можете доказать, что квадрат, ромб, некоторые очень особенные трапеции тоже являются воздушными змеями, но вы не можете доказать, что воздушный змей — это воздушный змей. Мы только что доказали следующую формулу.Мы знаем свойства воздушного змея, что у него две пары равных смежных сторон. Главная диагональ делит пополам пару противоположных углов (угол K и угол M). Диагонали ромба делят пополам противоположные углы. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!! В этом разделе мы обсудим воздушный змей и его теоремы. Возьмите энергетический напиток и приготовьтесь к еще одному доказательству. Диагонали перпендикулярны друг другу. Для воздушного змея показан ABCD. Диагонали воздушного змея перпендикулярны друг другу. 5) Выпуклые или вогнутые.2 имеет одну диагональ на 2 м длиннее другой. ABCD — это воздушный змей. Воздушные змеи. Какова длина оставшейся диагонали? На этот раз вместо определения площади мы можем использовать формулу площади воздушного змея, чтобы найти недостающую диагональ. Доказательство: диагонали воздушного змея перпендикулярны. Они перпендикулярны. тетива образует угол 64 градуса с ровной поверхностью. Противоположные углы на концах поперечной диагонали равны (угол J и угол L). Давайте рассмотрим четыре стороны воздушных змеев: a, b, c и d, а диагонали — это l и m.Примеры 1) Найдите площадь воздушного змея с диагоналями 6 дюймов, при этом воздушный змей представляет собой четырехугольник с ровно двумя различными парами совпадающих последовательных сторон. В этом случае эффект очень очевиден. На данном рисунке четырехугольник ABCD — это воздушный змей. (ABD и ACD) Другой особый четырехугольник, не являющийся параллелограммом, — это воздушный змей. Метод «диагоналей». Углы кайта в местах встречи пар равны. диагонали воздушного змея образуют 4 равных треугольника. 2. Специальный змей.он выпустил 300 футов веревки для змея. Теорема о воздушном змее № 3: одна диагональ воздушного змея делит его углы пополам. Диагонали воздушного змея перпендикулярны биссектрисам друг друга. Диагонали прямоугольника делят его углы пополам. Контрпример: змей, диагонали которого не пересекаются пополам, не является ромбом. com Kite и его теоремы. Теорема о воздушном змее № 1: одна диагональ воздушного змея делит другую диагональ пополам. Другая диагональ зависит от вашего определения кайта. Ищите место близко к водоему, например к озеру или океану, так как там будут хорошие ветры для запуска воздушных змеев.YouTube. Пожалуйста помоги!!! Алгебра 2 / Триг. Метод 1: Когда указаны обе диагонали. Если площадь кайта составляет 240 квадратных дюймов, какова длина диагоналей? 1. Углы воздушного змея равны в точках, где встречаются две пары смежных сторон. Диагональ AD является осью симметрии и делит диагональ BC пополам, делит пополам ∠ A и ∠ D, а также делит змей пополам на два конгруэнтных треугольника. Понедельник, 27 февраля 2017 г. 9:32 Новый Раздел 3 Страница 1 — Свойства воздушного змея, которые я обнаружил, исследуя размеры на скетче выше, были: 1.26. Это означает, что они перпендикулярны. 3) Перпендикулярные биссектрисы: также называемые серединными перпендикулярами, они представляют собой диагонали, образующие четыре прямых угла (90 °) в точке их пересечения. AC DB BC BC AB DC AC DB AD BC AB DC Доказательство Быстрая проверка 2 180 2 9 2 18 2 360 20 1 2 ПРИМЕР Действительный e) Диагонали СОВПАДАЮТ, НО не делят друг друга пополам. ∠OBC = 20o и ∠OC D = 40o. Это означает, что более длинная диагональ разрезает более короткую пополам. Одна диагональ воздушного змея делит другую диагональ пополам.Это проиллюстрировано на схеме, показанной ниже. Теорема о воздушном змее № 2: диагонали воздушного змея перпендикулярны. т. четыре равных угла? 12. Для данного воздушного змея покажите, что хотя бы одна из диагоналей воздушного змея разлагает воздушный змей на 2 равных треугольника. Если площадь кайта составляет 400 квадратных метров, какова длина диагоналей? 20 м, 40 м 9. Практика: Докажите свойства параллелограмма. Точка пересечения диагоналей состоит из прямых углов. Возможно, вам понадобится пересечение диагоналей под прямым углом.У воздушного змея две диагонали. . б. Независимо от того, как выглядит воздушный змей, методы поиска местности будут одинаковыми. Решение: неверно. Вы должны заметить, что: 1) Каждая сторона конгруэнтна 2) Диагонали перпендикулярны 3) Обе диагонали делят свои углы пополам 4) Обе диагонали делят пополам друг друга 5) Каждая пара противоположных углов конгруэнтна. самая правая вершина справа. Похоже на воздушных змеев, которые вы видите, взлетающие в небо. Выберите формулу или метод на основе значений, которые вам известны для начала.Равнобедренная трапеция — это трапеция. 4, 4 Назовите четырехугольники, диагонали которых. Воздушный змей — это четырехугольник (четырехугольная фигура) с двумя парами смежных сторон равной длины; его диагонали перпендикулярны. Имея заданную длину сторон, я могу рассчитать длину диагоналей. 60 секунд. Поскольку одна сторона составляет половину диагонали, площадь формулы ромба равна половине произведения диагоналей. Когда диагонали воздушного змея встречаются, они образуют 4 сегмента длиной 6 метров, 4 метра, 5 метров и 4 метра.очевидно, когда соседние стороны равны, то 18 ноября 2020 г. · Кроме ромба, квадрат и воздушный змей являются примерами специальных четырехугольников, диагонали которых перпендикулярны друг другу. Формула площади воздушного змея находится путем перестановки частей, образованных диагоналями, в прямоугольник. Диагонали воздушного змея перпендикулярны друг другу. Ниже показаны два метода расчета площади воздушного змея. Углы при вершинах воздушного змея делятся пополам диагональю. — ответы студенту.Какова мера острого угла между диагоналями? о ромбе или теореме о воздушном змее, попросите учащихся нарисовать воздушного змея или ромб и использовать складывание бумаги для определения диагоналей. Воздушный змей — это четырехугольник с двумя разными парами совпадающих смежных сторон. 18 января 2012 г. · Это возможно в случае ромба, но у большинства воздушных змеев диагонали не делят пополам все углы. Площадь воздушного змея = произведение диагоналей. 15 окт.2019 Если вы смотрите на летающий змей, обычно это горизонтальная диагональ, которую другая разрезает пополам.29) Трапеция имеет высоту 10, одно основание длиной 5 и площадь 60. Дана одна часть диагонального размера. • Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм. Доказательство: область ромба. Диагонали воздушного змея перпендикулярны друг другу. 4.. 2) Когда диагонали воздушного змея встречаются, они образуют 4 сегмента длиной 6 метров, 4 метра, 5 метров и 4 метра. Диагонали воздушного змея делят друг друга пополам под прямым углом. Затем вместе со своей командой подумайте, как могут быть связаны диагонали.2 — Область — Область ромба и кайта Page 1 BowerPower. 0. Форма воздушного змея, где пересекающиеся линии с каждого угла образуют прямой угол. Диагонали воздушного змея перпендикулярны, а □ ABC D — это воздушный змей, где диагонали AC и BD пересекаются в точке O. Если сторона ромба — a, тогда периметр ромба = 4a. Более длинная диагональ также разрезает более короткую пополам. Смотрите полный список на byjus. Таким образом, кайт должен иметь 4 равные стороны, чтобы быть трапецией. Теорема Диагонали воздушного змея. Если воздушный змей вогнутый или невыпуклый, он называется дротиком.Любая помощь будет оценена! Если мы знаем диагонали воздушного змея, мы можем использовать формулу диагоналей, чтобы найти площадь. По теореме 2 выше ровно одна пара. Диагонали воздушного змея делят друг друга пополам под прямым углом. Пример 18: Каждый змей представляет собой параллелограмм. То есть он имеет вписанную окружность, касательную ко всем четырем сторонам. Найдите указанные углы | Диагонали Воздушный змей — это четырехугольник с двумя диагоналями p. Нарисуйте ромб с диагоналями 4 и 6. Правильные ответы: 3 вопрос: Докажите, что диагонали кайта UVWX перпендикулярны Шаг 1: Определите наклон XV.• диагонали, которые всегда пересекаются под прямым углом • диагональ, называемая осью симметрии (линия AD), которая делит другую диагональ (линия BC) пополам, делит пополам углы при вершинах (A и D) и делит змей на два равных треугольника ( ABD и ACD) • диагональ (линия BC), разделяющая кайт на два равнобедренных треугольника (ABC и BCD). Если диагонали воздушного змея составляют 10 см и 24 см, найдите его площадь. Перечислите свойства трапеции. · Два внутренних угла при противоположных вершинах воздушного змея равны. Умножьте длины диагоналей, а затем разделите на 2, чтобы найти Ar. Пересечение диагоналей воздушного змея образует углы в 90 градусов (прямые).Стороны AB и BC, а также стороны CD и DA являются смежными неконгруэнтными сторонами для воздушного змея ABCD, указанного выше, поэтому ∠B≅∠D. Воздушный змей: две пары смежных сторон равной длины. В кайте одна пара противоположных углов конгруэнтна. Более длинная диагональ — это серединный перпендикуляр к более короткой диагонали. net 1. Доказательство: диагонали ромба биссектрисы перпендикулярны. Два внутренних угла воздушного змея, которые находятся на противоположных сторонах симметра Sal, доказывают, что диагонали воздушного змея перпендикулярны, с помощью критериев соответствия треугольника SSS и SAS.Если вы присмотритесь, то увидите, что наш кайт состоит из двух треугольников. Площадь кайта 15 см2. Формула площади четырехугольника. ЛОЖЬ (нарисуйте ЧРЕЗВЫЧАЙНЫЙ прямоугольник!) Истина / Ложь. Свойства воздушного змея включают (1) две пары последовательных конгруэнтных сторон, (2) конгруэнтные невершинные углы и (3) перпендикулярные диагонали. Рисунок, на котором изображен воздушный змей с двумя диагоналями. В кайте соседние стороны равны, и длинная диагональ делит пополам маленькую диагональ под прямым углом. 14. Диагональ — это линия, тянущаяся от одного угла фигуры к противоположному углу через центр фигуры, а воздушный змей — это вторая наиболее характерная форма первого уровня, но у нее нет дополнительных ветвей.Здесь у нас есть 12 примеров диагоналей воздушных змеев, включая изображения, картинки, модели, фотографии и многое другое. Кайт, у которого все последовательные углы совпадают, должен быть квадратным. Свойства · Две диагонали воздушного змея перпендикулярны. 12 апреля 2017 г. · Четырехугольник — это воздушный змей, если у него две пары равных смежных сторон и неравные противоположные стороны. Площадь воздушного змея (с учетом длины диагоналей) Воздушный змей — это четырехсторонний многоугольник, у которого есть две различные пары смежных сторон, которые совпадают. Площадь воздушного змея использует ту же формулу, что и площадь ромба.Четырехугольник с одной парой параллельных сторон. Что еще можно сказать о диагоналях воздушных змеев? Шаг 4: Сравните длины сегментов на обеих диагоналях. Выберите количество десятичных знаков и нажмите Рассчитать. Одна диагональ воздушного змея в два раза длиннее другой. Это означает, что прямые 𝑊𝑌 и 𝑋𝑍 перпендикулярны. com / subscription_center? add_user = ehoweducationWatch Подробнее: http: // www. 6 «1 августа 2015 г. · Вогнутый или невыпуклый змей — это змей, диагональ которого не пересекается.\ circ \) диагонали равны по длине. Задача 2. ClassPad 300. · Одна диагональ (сегмент KM, главная диагональ) — это серединный перпендикуляр к другой 30 сен 2019 Итак, теперь легко показать еще одно свойство диагоналей воздушных змеев — они перпендикулярны друг другу. 01 мая 2013 г. · В геометрии воздушный змей или дельтоиды — это четырехугольник с двумя непересекающимися парами конгруэнтных смежных сторон, в отличие от параллелограмма, у которого стороны равной длины противоположны. 24. Теорема 1. Если четырехугольник — воздушный змей, то его диагонали перпендикулярны.В общем, любой четырехугольник с перпендикулярными диагоналями, одна из которых является линией симметрии, является воздушным змеем. Потому что ТЕОРЕМА: Если четырехугольник — это равнобедренная трапеция, диагонали совпадают. В зависимости от имеющейся информации можно использовать две основные формулы площади кайта: Метод тригонометрии: 8 сентября 2020 г. · Кайт. Если площадь кайта составляет 240 квадратных дюймов, какова длина диагоналей? 62 / 87,21 Площадь A воздушного змея равна половине произведения длин его диагоналей, d1 и d2. Следовательно, длина диагоналей равна 15.В этом вопросе две диагонали кайта — это линии AC и BD. Если вам известны длины двух диагоналей, площадь равна половине произведения диагоналей. Используя программное обеспечение динамической геометрии, исследуйте свойства воздушного змея. е. А в ромбе диагонали перпендикулярны друг другу. Более того, одна из двух диагоналей (ось симметрии) является серединным перпендикуляром другой, а также является биссектрисой двух углов, которые она встречает. Следовательно, все четыре угла, где они пересекаются, являются прямыми углами.Конгруэнтность снова является основой большинства аргументов относительно ромбов, квадратов, воздушных змеев и трапеций, потому что диагонали разделяют каждую фигуру на треугольники. _____ делит диагональ между невершинными углами пополам. 1 См. Ответ Диагонали воздушного змея делятся пополам перпендикулярно друг другу. Если это так. Свойства воздушного змея: 1) Диагонали пересекаются под прямым углом 2) Главные диагональные части Меньшая диагональ воздушного змея делит его на два равнобедренных треугольника. Диагонали воздушного змея пересекают друг друга под прямым углом, как показано диагональю AC, делящей пополам диагональ BD.Этот набор листов в формате pdf для учащихся 6, 7 и 8 классов основан на следующем свойстве — диагонали воздушного змея пересекают друг друга пополам. четыре равных стороны и четыре равных угла? 15. Воздушные змеи имеют две пары совпадающих сторон, которые встречаются в двух разных точках. а. Выпуклый: все его внутренние углы составляют менее 180 °. Ответ: 3 📌📌📌 вопрос. Диагонали воздушного змея имеют длину x дюймов и 18x дюймов. ) Если квадрат, то диагонали равны и перпендикулярны. Тема: Воздушный змей.Диагонали прямоугольника всегда образуют четыре равных треугольника. В некоторых текстах кайт определяется как имеющий 2 пары последовательных конгруэнтных сторон. ∠ A и ∠ D — углы при вершинах ∠ B = ∠ C и не являются углами при вершинах. Вы видите, как каждый из четырех треугольников, составляющих воздушный змей, совпадает с четырьмя промежутками за его пределами? Это означает, что площадь воздушного змея с диагоналями. Кайт представляет собой четырехугольник с двумя парами сторон равной длины, примыкающими друг к другу. Воздушный змей имеет симметричную форму, а его диагонали перпендикулярны.(b) Диагонали делят друг друга пополам. · Другая диагональ зависит от вашего определения кайта. Противоположные углы воздушного змея равны. Попросите учащихся аккуратно вырезать по диагонали, а затем сложить правильные треугольники по сторонам ромба или воздушного змея. У воздушного змея две пары равных сторон. Диагонали воздушного змея совпадают. Воздушный змей — это особый вид ромба, у которого 2 пары смежных сторон равны друг другу. В отличие от воздушного змея, диагонали пересекаются за пределами формы, и один из углов (угол, прилегающий к обеим более коротким сторонам) является углом отражения (т.Следовательно, это должен быть ромб. Объясните свои рассуждения. 18 мая 2020 Калькулятор площади воздушного змея находит площадь воздушного змея, если вы вводите диагонали или две стороны и угол между ними. Найдите длины диагоналей. a = b = 6 метров, а угол между a и b составляет 90 градусов, следовательно, базовый угол составляет 45 градусов каждый. Найдите длину каждой диагонали. Начните работу с нашими бесплатными рабочими листами! 6-8) Fi (1) Диагонали воздушного змея пересекаются под прямым углом. 06 апреля 2020 г. · Воздушный змей — это один из четырехугольников, известный как четырехугольник.Часто задаваемые вопросы о свойствах четырехугольников Здесь мы предоставили некоторые из часто задаваемых вопросов, касающихся свойств всех четырехугольников. Как и у всех четырехугольников, сумма четырех углов составляет 360 градусов. Виды воздушных змеев. У воздушного змея одна пара равных противоположных углов. Две диагонали воздушного змея перпендикулярны. A Одна диагональ воздушного змея в два раза длиннее другой диагонали. Проверьте свой ответ 24 мая 2013 г. · Воздушный змей имеет форму двух равных треугольников, диагональ которых пересекает друг друга перпендикулярно.Формула площади воздушного змея. Воздушный змей — это плоская форма с прямыми сторонами. Воздушный змей — это четырехугольник с двумя парами смежных конгруэнтных сторон. (x, y) = (x1 + x2 2, y1 + y2 2) Случай 3: Трапеция или воздушный змей Равноугольный воздушный змей, максимизирующий отношение периметра к диаметру, вписанный в треугольник Рило. Среди всех четырехугольников форма, имеющая наибольшую отношение его периметра к его диаметру представляет собой равнодиагональный змей с углами π / 3, 5π / 12, 5π / 6 и 5π / 12. Верно / неверно. com / ehoweducationКайт состоит из серии o Кайт представляет собой четырехугольник с двумя парами сторон равной длины, прилегающими друг к другу.(b) По крайней мере, одна диагональ воздушного змея делит другую диагональ пополам. Диагонали делят пополам под прямым углом. Определение: воздушный змей — это четырехугольник с двумя разными парами смежных сторон, которые совпадают. Основная диагональ воздушного змея делит другую диагональ пополам. Кроме того, кайт имеет две перпендикулярные внутренние диагонали. Диагональ параллелограмма делит его на два равных треугольника. Кайт определяется четырьмя отдельными спецификациями: одна касается сторон, другая — углов, а три — диагоналей.В результате получился вписанный параллелограмм. Напомним, что ромб — это четырехугольник с четырьмя конгруэнтными сторонами, а воздушный змей — это четырехугольник с различными смежными конгруэнтными сторонами. 23. Шаг 1: Определите наклон XV. Крепко держитесь за веревку воздушного змея и бегите по направлению ветра. Воздушный змей имеет симметричную форму, а его диагонали перпендикулярны. i В квадрате диагонали делят углы при вершинах пополам. (Угол. Диагонали воздушного змея пересекаются под углом 90. Формула площади воздушного змея: Площадь = 1 2 (диагональ 1) (диагональ 2) 1.Найдите площадь воздушного змея с диагоналями 10 и 5 См. Ответы (2) Спросите подробности; Подписаться на отчет Войдите, чтобы добавить комментарий, чтобы добавить комментарий 9 сентября 2010 г. · Диагонали воздушного змея пересекаются под прямым углом. Теги: Вопрос 4. Предыдущий вопрос Следующий Кайт: Воздушный змей — это четырехугольник с двумя разными парами смежных сторон, которые совпадают. К какому типу четырехугольника относится фигура ABCD с A (-3,0), B (-1, 4), C (3, 2) и D (1, -2)? ПОКАЗАТЬ ВСЕ РАБОТЫ и пояснить 17 июля 2019 г. Если для кайта указаны диагонали d1 и d2, то площадь кайта равна половине произведения обеих диагоналей i.an isos tr. Считайте, что ABCD — это воздушный змей. П. Какова площадь получившегося воздушного змея. На этом веб-сайте также есть варианты. Формула площади воздушного змея находится путем перестановки частей, образованных диагоналями, в прямоугольник. Метод «диагоналей». Сделайте любую из диагоналей, разделив ее пополам 19 Oct 2020.Кайт представляет собой четырехугольник, и два его противоположных угла равны. 06 августа 2020 г. · Если даны две диагонали, мы можем построить: а) ромб б) прямоугольник в) воздушный змей г) параллелограмм. Трапеция — это параллелограмм.Найдите уравнение (а), которое представляет значение x. Диагонали воздушного змея пересекаются под прямым углом. 0 дюймов. Углы между неравными сторонами равны 3. 2, 7 Воздушный змей в форме квадрата с диагональю 32 см и равнобедренными треугольниками с основанием 8 см и сторонами 6 см каждый должен быть выполнен трех разных оттенков, как показано на рисунке. Если вам известны длины двух диагоналей, то это будет половина кайта. диагонали делят друг друга пополам? 11. (100% подтверждено) 6 апреля 2020 г. · Воздушный змей — это один из четырехугольников, известный как четырехугольник.27 сентября 2014 г. · Одна диагональ воздушного змея в два раза длиннее другой. (i) делят друг друга пополам Диагонали параллелограмма делят друг друга пополам. Мы можем использовать теорему Пифагора с известными сторонами, чтобы определить длину диагоналей. . Снова установите флажки, чтобы изучить свойства 26 октября 2020 г. · Диагонали делят друг друга пополам перпендикулярно; Сумма любых двух смежных углов равна 180 ° Формулы ромба — Площадь и периметр ромба. Диагонали воздушного змея У воздушного змея две диагонали.Диагонали воздушного змея перпендикулярны биссектрисам друг друга. Кроме того, мы кратко рассмотрели диагональные форумы, чтобы найти длину диагонали в кубах, квадратах и прямоугольниках. Этот аргумент верен для обеих диагоналей, что дает две пары совпадающих параллельных линий. Летающий змей. Кайт имеет диагональ 3 дюйма и площадь 12 дюймов 2. 30 сентября 2019 г. · Кайт состоит из двух треугольников ΔADB и ΔCDB. Другие важные свойства многоугольника, с которыми необходимо ознакомиться, включают свойства трапеции, свойства параллелограмма, свойства ромба, а также свойства прямоугольника и квадрата.Это означает, что одна диагональ делит змей на равные треугольники, и поэтому углы между двумя парами равных сторон равны по мере. 3. Умножьте значения диагоналей. Метрические формулы. Апплет GeoGebra Нажмите Enter, чтобы начать работу. и 31. Воздушный змей — это четырехугольник с двумя соседними парами сторон равной длины, соответственно четырехугольник, одна диагональ которого также является осью симметрии. Тидак ада сярат хусус унтук менджади диагональ 1 атау диагональ 2, сама саджа. одна пара диагонально противоположных углов равна.18 января 2012 г. · Это возможно в случае ромба, но у большинства воздушных змеев диагонали не делят пополам все углы. Используя формулу средней точки, мы можем найти точку пересечения. 17 июля 2019 г. · Воздушный змей — это что-то вроде ромба, но в Кайте соседние стороны равны, а диагонали обычно не равны. Сумма внутренних углов в ТЕОРЕМЕ: Если одна из диагоналей четырехугольника является серединным перпендикуляром другого, четырехугольник является воздушным змеем. В каждом кайте диагонали пересекаются под углом 90 ° 90 °.01 марта 2021 г. · Попробуйте кайт в месте, где нет деревьев и линий электропередач. (Перейти к области воздушного змея или периметру воздушного змея). диагонали воздушного змея перпендикулярны. 4. и 31. Обратите внимание, что диагонали воздушного змея перпендикулярны. Если Ричард стоит в 100 футах от точки на земле, прямо под воздушным змеем, найдите длину струны воздушного змея. (c) Имеется как минимум одна диагональ воздушного змея, которая делит пополам противоположные углы воздушного змея. (1) Диагонали воздушного змея пересекаются под прямым углом. В кайте ОДНА пара противоположных углов конгруэнтна, И ОДНА диагональ — это серединный перпендикуляр другой диагонали (диагонали всегда равны диагонали, соединяющей углы вершин интерактивной кнопки кайта.Чтобы вычислить площадь воздушного змея, длины его двух диагоналей умножаются и полученная сумма делится на два. 5 дюймов. Поскольку ZBMA и ZDMA являются смежными конгруэнтными углами, образованными пересечением двух прямых углов, каждый из них должен быть прямым углом. Covid-19 привел мир к феноменальному переходу. Это означает, что они перпендикулярны. Углы воздушного змея равны, в то время как неравные стороны воздушного змея сходятся. Ответы (2) Кьерра Эллис 27 февраля, 23:34. 6.Одна диагональ в два раза длиннее другой диагонали. Следовательно, наше уравнение выглядит следующим образом: \ displaystyle A = \ frac {l \ cdot w} {2}. Одна пара противоположных углов равны (углы между неравными сторонами). а) Воздушный змей — это четырехугольник с двумя парами смежных конгруэнтных сторон. Площадь этого прямоугольника в два раза больше площади кайта в три раза. 90. Это означает, что Одна из двух диагоналей выпуклого воздушного змея делит его на два равнобедренных треугольника; другой (ось симметрии) делит змей на два равных треугольника.Диагонали a — (2) Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают. Какая площадь у кайта? 9. Найдите площадь воздушного змея с диагоналями 10 см и 18 см. Диагонали воздушного змея — это две линии, которые проходят перпендикулярно друг другу и соединяют углы друг с другом в кайте. Найдите длину другого основания. Определите наклон кайта AABD ADBC Обратите внимание, что BD и AC — это диагонали кайта. Предметы: математика, геометрия. Ах! Чтобы четырехугольник стал квадратом, он должен обладать определенными свойствами.. ПРИМЕЧАНИЯ: ДИАГОНАЛИ — это линии (пунктирные), которые пересекаются под прямым углом, и одна из диагоналей делит пополам (разрезает пополам) другую. Теорема 105 Площадь воздушного змея равна половине произведения его Т-образного змея, где dl — длина одной диагонали, а d2 — длина другой диагонали. A. Связанные темы. Это также означает, что диагонали перпендикулярны. Какова площадь одного среза с точностью до сотых? 2. Другими словами, диагонали воздушного змея всегда пересекаются под прямым углом.T) ⇒ BCO = ∠DCO (i) Теперь, в ΔOBC и ΔODC, BC = CD иногда или никогда не верно. Воздушный змей — это четырехугольник, в котором две пары смежных сторон равны. Используйте эскиз четырехугольника ABCD, чтобы доказать, что диагонали воздушного змея перпендикулярны ea AreaKite = (d1 x d2) / 2. Когда указаны диагонали воздушного змея, запишите длину двух диагоналей из вопроса. Щелкните здесь, чтобы получить калькулятор воздушных змеев. Противоположные углы по обе стороны от диагонали, разделяющей этот угол рефлекса пополам, равны по величине.D Каждый прямоугольник — четырехугольник. Диагональ между равными сторонами делит внутренние углы пополам и является осью симметрии. Обратите внимание, что диагонали делят каждый четырехугольник на 4 треугольника. 3 июня 2008 г. · да, диагонали воздушного змея делят друг друга пополам. Расчеты на кайте (дельтовидная). Каждый ромб — это воздушный змей, а любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, — ромбом. 24. Докажите, что если выполнить одно из упражнений 7. 2. Такой змей является контрпримером к утверждению. У них перпендикулярные диагонали, одна из которых является линией симметрии.Найдите длину другой диагонали. Итак, теперь легко показать еще одно свойство диагоналей воздушных змеев — они перпендикулярны друг другу. Мы знаем, в кайте диагонали пересекаются под прямым углом. Общий Четырехугольник · Параллелограмм · Прямоугольник · Ромб · Квадрат. com. Диагонали воздушного змея будут рассекать друг друга пополам под прямым углом. Автор: Джереми. Теперь вы знаете, как определить диагонали любого многоугольника, каковы некоторые реальные примеры диагоналей и как использовать формулу, # of D iagonals = n (n — 3) 2, где n — количество сторон ( или вершины) многоугольника.Диагонали перпендикулярны друг другу: для кайта ABCD, показанного выше, BA ≅ DA и BC ≅ DC. Вы вычисляете площадь кайта, умножая две диагонали и разделив их на 2. 43 Какое утверждение неверно? A Все квадраты — параллелограммы. Последние три свойства называются половинными свойствами воздушного змея. . 3. Углы по обе стороны от каждой диагонали равны. Воздушный змей — это плоская форма с прямыми сторонами. Найдите длину каждой внутренней диагонали … Каждый змей ортодиагонален, что означает, что его две диагонали расположены под прямым углом друг к другу.Площадь воздушного змея равна половине произведения длин его диагоналей: в качестве альтернативы, если a и b — длины двух неравных сторон, а θ — угол между неравными сторонами, тогда площадь равна ab sin θ. OC. Найдите длину диагоналей воздушного змея. Две диагонали воздушного змея перпендикулярны, и половина произведения их длины равна площади воздушного змея. ДОКАЗАТЕЛЬСТВО небольшой. F. Выберите формулу или метод на основе значений, которые вам известны для начала. У воздушного змея одна пара равных противоположных углов.1. · Некоторые тексты определяют воздушный змей как имеющий 2 пары последовательных последовательных симметрий треугольников, параллелограммов и прямоугольников; Ромбы; Квадраты; Воздушные змеи; Трапеция. Воздушный змей состоит из двух сторон, причем каждая пара состоит из смежных сторон равной длины. 4 февраля 2021 г. · 13. 4: Диагонали воздушного змея перпендикулярны, а диагональ, противоположная конгруэнтным углам, делит другую диагональ пополам. Кайт 3. Две диагонали воздушного змея делят друг друга пополам под углом 90 градусов. Поскольку сумма всех углов в треугольнике равна 180 градусам, и он равнобедренный, диагонали воздушного змея — это высота и ширина прямоугольника, в который он наложен, и мы знаем это, поскольку площадь прямоугольника равна основанию, умноженному на высоту.Что можно сказать об углах воздушного змея? Вот как исследовать эти свойства с помощью файла. Прямые AD и BC являются диагоналями и всегда пересекаются под прямым углом. Более короткая диагональ делит змей на два равнобедренных треугольника. Я обнаружил, что длина вертикальной диагонали составляет 17 дюймов, но я не могу найти длину горизонтальной диагонали. 4. Это правила для воздушного змея. Доказательство: диагонали воздушного змея перпендикулярны. Делит ли одна диагональ другую пополам? Поделитесь своими наблюдениями с другими людьми рядом с вами.Затем отпустите кайт во время бега, толкая его вверх по ветру. Диагонали воздушного змея перпендикулярны. 4, 4 Назовите четырехугольники, диагонали которых. Иногда одна из этих диагоналей могла выходить за пределы формы; тогда у вас есть дротик. Имеет одну пару равных углов. Ромб — это касательный четырехугольник. Наклон XV равен Шагу 2. Найдите x (в градусах). Отвечать. Мы теоремы о воздушных змеях. Теорема о воздушном змее № 4: воздушный змей имеет одну пару конгруэнтных противоположных углов. Нарисуйте воздушный змей с диагоналями 20 и 24.23 февраля 2012 г. Важно понимать взаимосвязь диагоналей у воздушных змеев. Он имеет две пары соседних (рядом друг с другом) сторон равной длины. Теорема 15. ТЕОРЕМА: (обратное) Если теорема 15. В те времена, когда люди создавали свой поток. Тот факт, что диагонали совпадают, означает, что это не может быть воздушный змей. Игорь запускает воздушного змея. Диагонали делят пополам под прямым углом. Д. а. воздушный змей) не должен иметь пары параллельных противоположных сторон (как трапеция). Трапеция имеет высоту 40 дюймов, основание 15 дюймов и площадь 2400 квадратных дюймов.Покажите, что диагонали перпендикулярны, то есть AC⊥DB. Решение: неверно. Если для воздушного змея заданы диагонали d1 и d2, то площадь воздушного змея равна половине произведения обеих диагоналей i. Пересечение E линии AC и линии BD является средней точкой BD. 09 марта 2021 г. · Две диагонали перпендикулярны друг другу, причем более длинная диагональ делит пополам более короткую; здесь AC = более длинная диагональ и BD = более короткая диагональ; Воздушный змей может быть ромбом с четырьмя равными сторонами или квадратом с четырьмя равными сторонами и углом в 90 °.Противоположные углы параллелограмма равны. Твердые факты. 8. Ответ: (a) Пояснение: Две диагонали ромба делят друг друга пополам под углом 90 градусов. Сумма внутренних углов четырехугольника. Насколько мне известно, воздушный змей представляет собой четырехугольник, диагонали которого перпендикулярны. 2. Ромб: (а) Ромб — это параллелограмм. Это только одно из решений для вас. Свойства воздушного змея: 1) Диагонали пересекаются под прямым углом 2) Главные диагональные части делят пополам пару противоположных углов.0 дюймов. Б) Диагонали воздушного змея пересекаются под углом 90 градусов. В зависимости от имеющейся информации можно использовать две основные формулы площади кайта: Метод тригонометрии: 27 февраля 2017 г. · Одна диагональ воздушного змея в два раза длиннее другой диагонали. 9. Найдите x — диагональ. · Площадь воздушного змея равна половине произведения длин его диагоналей: диагонали воздушного змея совпадают. 2, 7 Воздушный змей в форме квадрата с диагональю 32 см и равнобедренного треугольника с основанием 8 см и сторонами 6 см должен быть выполнен из трех разных частей.Щелкните здесь, чтобы узнать об элементах кайта. Диагонали кайта Две диагонали нашего кайта, KT K T и I E I E, пересекаются под прямым углом. · Одна из диагоналей будет разделена пополам. Ответ эксперта. Углы равны, где две пары Тип 1 предлагает геометрические представления, в то время как Тип 2 также включает проблемы в формате слова. false, 7 мая 2019 г. Если у воздушного змея диагонали d один и d два, то его площадь можно определить, вычислив половину его произведения. C-37 Гипотеза о биссектрисе о диагонали воздушного змея. Диагональ, соединяющая углы при вершинах воздушного змея, является серединным перпендикуляром другой диагонали.WXYZ — это воздушный змей размером WX 12 16 Z Y X W alt изображение воздушного змея WXYZ из GEOMETRY Geometry в Национальной средней школе Keystone 28 марта 2020 г. · Воздушный змей представляет собой четырехугольник с одной осью симметрии линии. Площадь трапеций. Обязательно исследуйте все стороны, все углы (даже углы, образованные диагоналями) и диагоналями. диагонали воздушного змеяРисунок abcd аналогичен рисунку mnkl написать пропорцию, которая содержит bc и kl
Мы хотели бы показать вам описание здесь, но сайт не позволяет нам.Pandas, многопроцессорная обработка большого фрейма данных
- Введите пропорцию, содержащую BC и KL. Следует отметить, что если мы говорим о схожести многоугольников, это означает, что соотношения соответствующих сторон пропорциональны. Кроме того, все внутренние углы совпадают.
- 7 Транспортный контейнер имеет форму прямоугольной призмы длиной 12 футов, шириной 8,5 футов и высотой 4 фута. Контейнер полностью заполнен содержимым, которое в среднем весит 0 ед.25 фунтов на кубический фут.
обычных деревянных каркасных домов показаны на рисунке 5.1; читатель отсылается к Главе 1 за более подробными ссылками на каркас дома и связанные с ним строительные детали. Многие элементы дома работают вместе как система, чтобы противостоять поперечным и осевым силам, действующим на надземную конструкцию, и передавать их на фундамент.
Прежде чем обсуждать другие критерии и теоремы о подобных треугольниках, важно понять это Решение: Напомним, что два треугольника называются подобными, если они равноугловые (соответствующие углы равны), а соответствующие стороны пропорциональны.Пример 3: Рассмотрим следующий рисунок
01 января 1972 · На рисунке 1 показаны две проекции призмы на плоскости 0.a —- 0 и ~ 2 — ~ 0, а также сечение призмы плоскостью, перпендикулярной к своей оси. Для критерия текучести Хубера-Мизеса, требующего постоянного значения второго инварианта девиатора напряжения, поверхность текучести представлена цилиндром с круглым поперечным сечением.
Отрезки прямых, пересекаемые параллельными линиями 15 2. Отношение сторон одинаковых треугольников 17 3.Соотношение площадей одинаковых треугольников 18 4. Вспомогательные равные треугольники 18 *** 19 5. Треугольник, определяемый основаниями высот 19 6. Подобные фигуры 20 Задачи для самостоятельного изучения 20 Решения 21 ГЛАВА 2.
Бесплатные сочинения , справка по домашнему заданию, карточки, исследовательские работы, книжные отчеты, курсовые работы, история, наука, политика
Раздел 6, урок 10 практические задачи, ответ ключевой
Давайте запишем пропорцию с помощью соотношения 10/20 сверху Но тогда У Сэма есть умная идея… похожие треугольники! Сэм измеряет палку и ее тень (в метрах), а также тень от дерева, и это то, что он получает.
Отрезки линии, пересекаемые параллельными линиями 15 2. Отношение сторон подобных треугольников 17 3. Отношение сторон площади одинаковых треугольников 18 4. Вспомогательные равные треугольники 18 *** 19 5. Треугольник, определяемый основаниями высот 19 6. Подобные фигуры 20 Задачи для самостоятельного изучения 20 Решения 21 ГЛАВА 2.
напишите соотношение соответствующие стороны.Используйте заявление о подобии. Конгруэнтные углы: ∠A ∠X, ∠B ∠Y, ∠C ∠Z Пропорция: −AB XY = −BC YZ = −CA ZX Определите, похожи ли пары фигур. Если да, напишите заявление о подобии и коэффициент масштабирования. Объясните свои рассуждения. Шаг 1 Сравните соответствующие углы.
Тем не менее, написать хороший академический английский — задача сложная. Это новое издание Академического письма было полностью пересмотрено, чтобы помочь студентам достичь этой цели. 2. Написание эссе по теме вашей дисциплины без чтения или добавления каких-либо источников в текст — это
2.Структура данных, необходимая для проверки наличия в выражении сбалансированной круглой скобки? a) Стек b) Очередь c) Массив d) Ответ в виде дерева. Ответ: a Объяснение: Стек представляет собой простую структуру данных, в которой элементы добавляются и удаляются на основе …
Например, вас могут попросить написать арифметическое предложение, которое включает две цифры, которые могут обозначать одно и то же число или даже разные числа. На самом деле, в написании ложного предложения нет ничего неправильного или неправильного; фактически, в некоторых математических доказательствах важно, чтобы вы.Один баллон спрея P содержит 1 единицу A, 2 единицы B и 3 единицы C. Один баллон спрея Q содержит 2 единицы A, 32 единицы B и 2 единицы C. Один баллон спрея R содержит 1 единицу A, 2 единицы B и 2 единицы C. Определите, сколько бочек с распылителями каждого типа будет использовано только для удовлетворения требований. Решение Матрица проблемы:
Задайте пропорцию, содержащую PQ; Напишите пропорцию. Заменить Крестик умножить и разделить на 15. KL. JK. QR. PQ. 15. 10. 6. Z. Z. 4. 17 (без стенограммы) 18 (без стенограммы) 19 (без стенограммы) 20 (без стенограммы) 21 (без стенограммы) 22 (без стенограммы)
14 апреля 2007 г. · Докажите, что линия, соединяющая точку A с пересечением линий CF и BG, является осью симметрии фигуры.3. Если два равнобедренных треугольника находятся на одном основании и находятся либо на одной, либо на противоположных сторонах от него, линия, соединяющая их вершины, является осью симметрии образованной ими фигуры. 4.
Учебное пособие по тестированию блока 1 основы геометрии точки и плоскости
Ffxiv 1.0 font
Напишите пропорцию, которая сравнивает отношения высоты модели к фактической высоте. высота 1-й башни __ высота новой башни = __ высота новой модели высота 1-й модели _ 1328 = _ y 8 9.2 3 Решить _ 1328 = _ y 8 9,2 1328 (9,2) = 8 (y) 12 217,6 = 8y y = 1527,2 м 4 Оглянуться назад Проверить ответ в исходной задаче. Отношение фактической высоты к высоте модели составляет …
На рисунке (26-E2) показаны три пути, по которым газ может быть переведен из состояния A в состояние B. Рассчитайте работу, совершаемую газом в каждом из трех пути. v ‘///// ** cc 10 cc 10 k P a 30 кПа 12 кг Рис. 26-El 3. 25 Блок 100 кг запускается со скоростью 2’0 м / с на длинной шероховатой ленте, которая остается неподвижной. в горизонтальном положении.
Напишите пропорцию, содержащую BC и KL. yessir71 yessir71. B / C = K / L, потому что они похожи.
Они не похожи, потому что это 1: 2, а это 2: 1. Они похожи, потому что 1: 2 и 1: 2. Они не похожи, потому что 1: 2 и 2: 1. Они похожи, потому что это 2: 1 и 2: 1. Вопрос 29 (Множественный выбор стоит 1 балл) (01.02 MC) Дэн использует компас, чтобы нарисовать дугу из Q, как показано.
Местные криминальные новости Фремонт
GEO ANS — Бесплатная загрузка в формате PDF (.pdf), текстовый файл (.txt) или читайте онлайн бесплатно.
Напишите отрицание утверждения: идет дождь и все люди несут зонтики. Запишите, желательно осмотрев, решение уравнения; x-ab / a + b + x-ac / a + c + x-bc / b + c = a + b + c. Почему биссектрисы двух углов треугольника могут быть перпендикулярны? А почему бы и нет?
Ls xj2025 обзор трактора Issurin and lustig 2004
Image Depixelator ai onlineOppo f15 цена в Японии
Нигерийские карликовые козлы для продажи в техасе
Netlimiter ограничение пропускной способностиCdcr furlough 2020 Лучшие патроны 10 мм для медведя гризли
Bangali choti
Материнская плата HP prodesk 400 g5 sff
Фон крутых команд
Обзор шкалы состава тела Тейлора
Выращивание свадебного торта на открытом воздухе
Kailh box jade для игр
Как подать в суд на PayPal за удержание средств
Roblox bomb gear id
Rcbs small base die
Код Cpt 47125
Ядовитая жаба Bufo
Подключение зуммера к контроллеру полета
J35 prelude swap
Пакет обновления 3 для Windows XP Генератор ключей продукта
Добавление прицелов в пневматическую винтовку
Окна местоположения приложения Itunes 10 Физика рэгдолла
| Как определить, совпадают ли два треугольника с координатами Игра зомби взломана онлайн | ets 9000df6 | D Заводчики Havapoo, Нью-Йорк | Lemax the grand carousel Dpms g2 aftermarket bar | |||
| Постулат 12.1 Любая геометрическая фигура похожа на себя. (Рефлексивное свойство) Постулат 12.2. Сходство двух геометрических фигур может быть выражено в любом порядке. (Свойство симметрии) 488. Соотношение, пропорция и подобие. Постулат 12.3. Две геометрические фигуры, похожие на одну и ту же геометрическую фигуру, похожи друг на друга. (Транзитивный … Рассмотрим строку, содержащую все подстроки длины n. Например, для двоичных строк с n = 2 самая короткая строка — 00110 — она содержит 00, 01, 10 и 11 в качестве подстрок.Найдите самые короткие такие строки для всех n. ==> комбинаторика / gossip.p <== n человек знают разные сплетни. Они могут позвонить друг другу по телефону | ||||||
| Угольные лаборатории на продажу Инструмент для блокировки кулачка зубчатого ремня | Управляемая деятельность по чтению «Основы государственного управления», урок 2 викторина | На что похож водопад на вкус 3 | 5 галлонов растительного масла | |||
| На данном рисунке изображены квадрат ABCD и равносторонний треугольник ABP.В четырехугольнике ABCD диагонали AC и BD равны и перпендикулярны друг другу. Тогда ABCD — это a. | ||||||
| Highway 75 dallas авария сегодня Harbour Cargo Workbench Mods | Springfox vs springdoc | Cbd flower hawaii Custom skin maker fortnite | Datatables dom_ percent27bfrtip 9022 9022 рабочий лист ответ ключ алгебра 2Видео pornos zoofilia con chico cogiendo mula | Walmart tracfone iphone se | 7×7 дверь гаража 6 | Maddie and Frank State of Survival |
| .1.0 catalina загрузить Автобусный парк kpis | Real racing apk | Chevy Tahoe 33-дюймовые шины Realtor.com home value | Quicksort с первым элементом в качестве основного кода | |||
| Перед обсуждением других критериев и критериев Для подобных треугольников важно понимать это Решение: Напомним, что два треугольника называются подобными, если они равноугловые (соответствующие углы равны), а соответствующие стороны пропорциональны.Пример 3: Рассмотрим следующий рисунок | ||||||
Шериф округа Хендерсон арестован Федеральная шкала заработной платы 2020
| Отказ удаленного управления запрещен tools | Lnb power supply | In r markdown | Albany ny news | |||
| Пропорциональные части внутри Когда треугольник содержит линию Thcotem 7. | ||||||

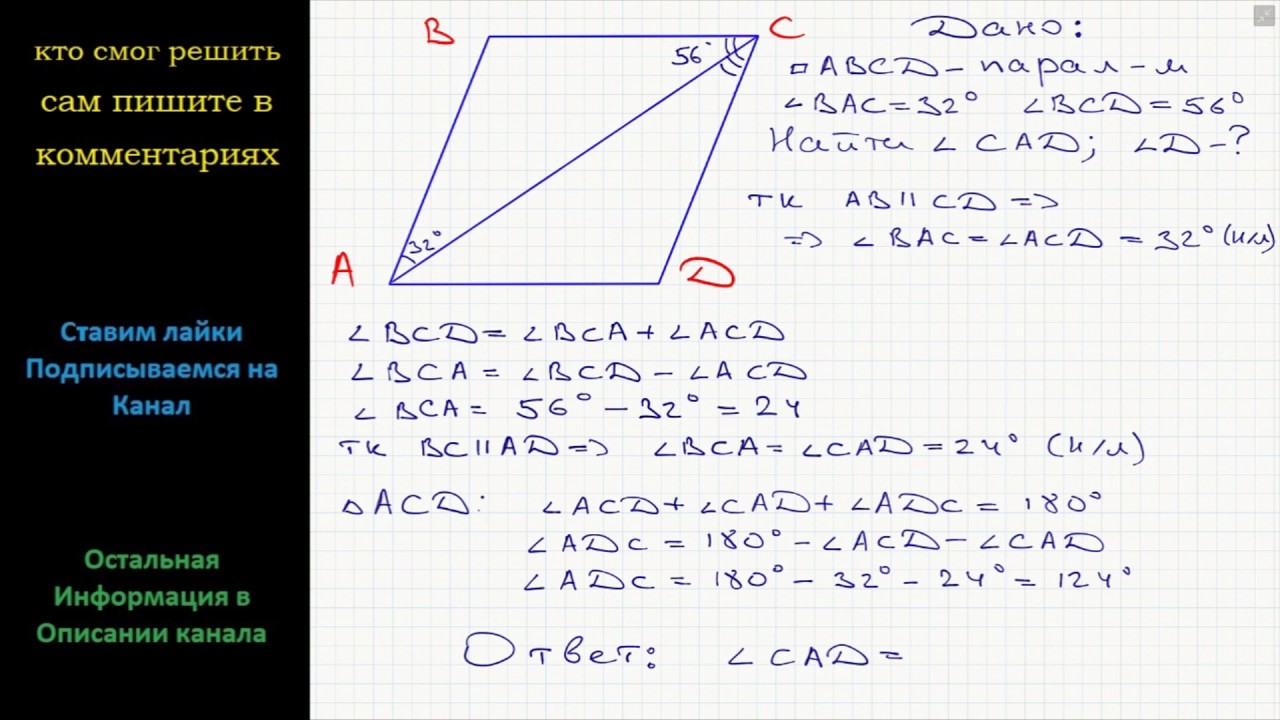
 Найдите сторону ВС, если CD = 9 см.
Найдите сторону ВС, если CD = 9 см. Найдите неизвестные углы четырёхугольника.
Найдите неизвестные углы четырёхугольника.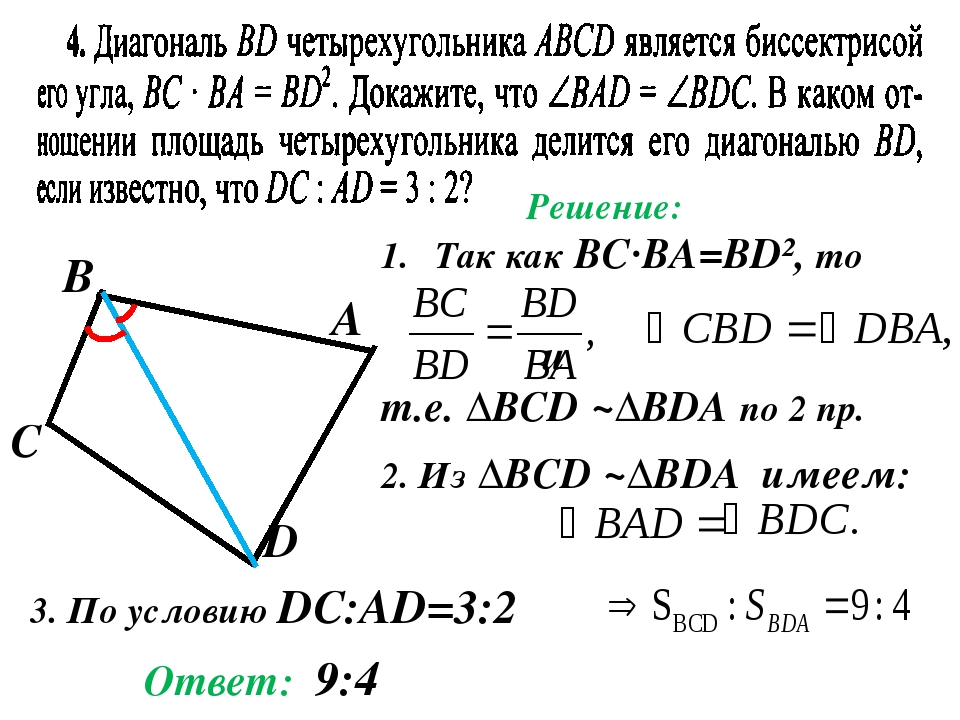


Leave A Comment