Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 H, летит равномерно со скорость 800 км/час. Какую мощность он развивает?Задачи на расчет количества теплоты
Слайд 1
Описание слайда:
Задачи на расчет количества теплоты
Слайд 2
Описание слайда:
Условие
В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С.
Слайд 3
Описание слайда:
Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С. Какая температура установится в калориметре?
Слайд 4
Описание слайда:
Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С. Какая температура установится в калориметре?
Слайд 5
Описание слайда:
Условие
В алюминиевый калориметр массой 45 г,
содержащий 100 г воды при температуре 20°С,
поместили чугунную гирю массой 50 г,
предварительно нагретую до 100°С.
Слайд 6
Описание слайда:
Какие тепловые процессы происходят в задаче? Назовите процессы, которые происходят с каждым из этих тел
Слайд 7
Описание слайда:
Условие В алюминиевый калориметр массой 45 г, содержащий 100 г воды при температуре 20°С, поместили чугунную гирю массой 50 г, предварительно нагретую до 100°С. Какая температура установится в калориметре?
Слайд 8
Описание слайда:
Обсуждение
Слайд 9
Описание слайда:
Решение
Слайд 10
Описание слайда:
Решение
Слайд 11
Описание слайда:
Решение
Слайд 12
Описание слайда:
Решение
Слайд 13
Описание слайда:
Ответ
Джанколи 7-е издание, глава 14, задача 31
Физика Джанколи: принципы с применением, 7-е издание
14
Heat
Глава
14-1: Тепло в качестве передачи энергии
1
1:11 1000 2 14-1: тепло в качестве передачи энергии
1
1:11.
2
0:34
3
2:08
4
1:07
5
2:07
. 8
1:15
14-3 и 14-4: удельная теплоемкость; Калориметрия
9
0:40
10
0:40
11
1:07
12
2:40
13
1:32
14
9000 4.04 1:3214 20003 9000 4.04
9000 3 1:3214 0003 9000 4000 2
1:32
14 0003 9000 40002 13
15
2:36
16
2:32
17
2:34
18
1:34
19
2:07
20
2:33
210002 211121 210003 21000320 0003
2:33
21000 210003
20 0003
2:33
21000 210003
1:15
22
2:23
23
1:45
14-5: скрытая тепло
24
0:42
25
1:00
26
1:18
27 27 27
2:10
28
2:03
29
2:00
30
2:32
31
3:02
32
1:27
33
1:16
34
2:49
35
1:16
от 14-6 до 14-8: проводимость, конвекция, излучение
36
0:50
37
1:02
38
1:57
39
3:46
40
1:18
41
1:06
42
1:19
43
3:04
44
2:49
45
4:33
9000.
Вопрос. Вопрос. , Дуглас С., Физика: принципы с приложениями, 7-е изд., © 2014 г., перепечатано с разрешения Pearson Education Inc., Нью-Йорк. 94 \textrm{ Дж/кг}1,12×104 Дж/кгЧтобы посмотреть это решение, вам необходимо оформить подписку.
Начать бесплатную пробную версию
Посмотреть пример решения
|
Войти
ВИДЕО ТЕХНОЛОГИЯ
Это Джанколи Отвечает с г-ном Дычко. Вода и алюминий в калориметре потеряют часть энергии, а Меркурий получит часть энергии. И Меркурий получит энергию, прежде всего, для того, чтобы изменить свою фазу из твердой в жидкую. Таким образом, это будет масса Меркурия, умноженная на скрытую теплоту плавления, а затем, когда он полностью станет жидким, он повысит свою температуру и поглотит столько энергии в результате повышения своей температуры. Это будет масса Меркурия, умноженная на удельную теплоемкость жидкого Меркурия, умноженная на конечную температуру минус начальная температура Меркурия, которая будет, ну, начинается с точки плавления.
Вот такую температуру мы туда поставили, минус 39.градусов Цельсия. Итак, на стороне калориметра у нас есть энергия, потерянная алюминием, масса алюминия, умноженная на его удельную теплоемкость, умноженная на начальную температуру калориметра минус конечная температура. А затем для воды это масса воды, умноженная на удельную теплоемкость воды, умноженная на ту же начальную температуру калориметра. Вода и алюминий вместе составляют калориметр, и они оба начинают с одной и той же начальной температуры, все три вещества заканчиваются одной и той же конечной температурой. И тогда мы можем решить на LF , удельная теплота плавления Меркурия, принимая… Мы возьмем этот член влево, что составит минус mHg cHg , Tf минус TiHg . И я вынес это TIc для калориметра за вычетом TF из обоих этих двух терминов. Итак, вы видите, что в скобках умножается масса алюминия, удельная теплоемкость алюминия плюс масса воды, умноженная на удельную теплоемкость воды.
И затем разделите обе части на массу Меркурия после того, как вы сделали это, переместив этот термин туда. Затем также поменяйте стороны. Итак, удельная теплота плавления Меркурия — это разница температур здесь, умноженная на это, все эти вещи, я думаю, что я как бы рассмотрел это здесь. А по цифрам начальная температура для калориметра составляет 12,8 градусов по Цельсию минус конечная температура 5,06 градусов по Цельсию. А затем мы умножаем это на 0,62 кг алюминия, умноженное на 9.00 джоулей на килограмм градусов Цельсия, удельная теплоемкость алюминия, плюс 0,4 килограмма воды, умноженные на 4186 джоулей на килограмм градусов Цельсия, а затем минус 1 килограмм ртути, умноженный на его удельную теплоемкость, когда он жидкий, 138 джоулей на килограмм градусов Цельсия, умноженный на конечный результат. температура 5,06 градусов по Цельсию минус минус 39 градусов по Цельсию. В конце концов, это плюс. А затем разделите это на массу Меркурия, 1 килограмм. А это дает примерно 1,5 умножить на 10 до 4 джоулей на килограмм, скрытую теплоту плавления для Меркурия.
Политика конфиденциальностиУсловия обслуживанияСправочный центр
Найдите нас по телефону:
Giancoli Ответы, включая решения и видео, защищены авторским правом © 2009-2023 Shaun Dychko, Ванкувер, Британская Колумбия, Канада. Giancoli Answers не имеет отношения к издателю учебника. Обложки книг, названия и имена авторов приведены только для справки и являются собственностью соответствующих владельцев. Giancoli Answers — ваш лучший источник решений Giancoli для физики 7-го и 6-го изданий.
Конечная температура после помещения теплого металла в более холодную воду: Задачи 1
Конечная температура после помещения теплого металла в более холодную воду: Задачи 1 — 15Когда теплый металл помещают в более холодную воду, какой получается конечная температура?
Проблемы 1 — 15
Перейти к расчету конечной температуры при смешивании металла и воды
Перейти к расчету конечной температуры при смешивании двух проб воды
Назад в меню термохимии
Задача №1: Кусок медной трубки весом 610 г нагревают до 95,3 °C и помещают в изолированный сосуд, содержащий 45,0 г воды при 36,5 °C.
Решение:
1) Эту проблему можно резюмировать следующим образом:
q потеряно медью = q получено водой + q получено калориметром
2) Поэтому:
(610, г) (95,3 °C − x) (0,387 Дж·г¯ 1 K¯ 1 ) = (45,0 г) (x − 36,5 °C) (4,184 Дж·г¯ 1 °C ¯ 1 ) + [(10,0 Дж/К) (х — 36,5 °С)]Комментарий: K и °C взаимно исключаются, потому что °C в этой задаче представляет собой разность температур (а не одно конкретное значение) и «размер» одного K = одному °C.
3) Разве алгебра не забавна?
22497,471 — 236,07х = 198,28х — 7237,22424,35х = 29734,691
х = 70,1 °С
Задача №2: Образец вещества массой 45,0 г при температуре 55,0 °C (s = 1,66 кал/г °C) был помещен в калориметр в виде кофейной чашки (c = 4,20 кал/°C), который содержал 50,0 г этилового спирта при 25,0°С (s = 0,590 кал/г°С).
Какова результирующая температура?
Комментарий перед решением: обратите внимание, что в этой задаче используются калории, а не джоули. На технику решения это не влияет.
Решение:
1) Составьте следующее уравнение:
(масса вещества) (Δt вещества) (C p вещества) = (масса спирта) (Δt спирта) (C p спирта) + (калориметрическая постоянная) (Δt спирта)Существует неявное предположение, что спирт и калориметр начинаются при одной и той же температуре. Это очень надежное предположение.
2) Вставьте соответствующие значения:
(45,0 г) (55,0 − x) (1,66 кал/г °C) = (50,0 г) (x − 25,0) (0,590 кал/г °C) + (4,20 кал/°C) (x − 25,0)
3) Получается алгебра:
4108,5 — 74,7х = 29,5х — 737,5 + 4,2х — 105х = 45,7 °С
Задача №3: Кольцо из чистого золота и кольцо из чистого серебра имеют общую массу 17,0 г.
Два кольца нагревают до 65,4°С и опускают в 12,4 мл воды при 22,3°С. Когда достигается равновесие, температура воды составляет 24,7 °С. Какова масса золотого кольца?
Решение:
1) Составьте следующее уравнение:
(масса золота) (Δt золота) (С р золота) + (масса серебра) (Δt серебра) (С р серебра) = (масса воды) (Δt воды) (С р воды)
2) Вставьте соответствующие значения:
(х) (40,7 °С) (0,129 Дж г¯ 1 °С¯ 1 ) + (17,0 г − х) (40,7 °С) (0,237 Дж г¯ 1 °С¯ 1 ) = (12,4 г) (2,4 °C) (4,184 Дж г¯ 1 °C¯ 1 )
3) Алгебра:
х = 8,98 г
4) Комментарии:
а) Я посмотрел значения удельной теплоемкости золота и серебра в Интернете. Кстати, вы уже должны были запомнить удельную теплотворную способность жидкой воды.
б) Термины для масс золотых и серебряных колец исходят из того, что их сумма равна 17,0 г.Мы присваиваем «x» массе золотого кольца, поэтому масса серебряного кольца равна 17,0 минус x.
Мы присваиваем «x» массе золотого кольца, поэтому масса серебряного кольца равна 17,0 минус x.Задача №4: Образец алюминия массой 5,00 г (удельная теплоемкость = 0,89Дж г¯ 1 °С¯ 1 ) и образец железа массой 10,00 г (удельная теплоемкость = 0,45 Дж г¯ 1 °С¯ 1 ) нагревают до 100,0 °С. Затем смесь горячего железа и алюминия по каплям опускают в 91,9 г воды при 23,7°С. Рассчитайте конечную температуру смеси металла и воды, при условии отсутствия потерь тепла в окружающую среду.
Решение:
1) Настройте это:
q Al + q Fe = q вода(5,00 г) (100 °C − x) (0,89 Дж·г¯ 1 °C¯ 1 ) + (10,00 г) (100 °C − x) (0,45 Дж·г¯ 1 °C¯ 1 ) = (91,9 г) (x − 23,7 °C) (4,184 Дж г¯ 1 °C¯ 1 )
2) Проделаем алгебру (и отбросим все единицы):
(445 — 4,45x) + (450 — 4,5x) = 384,5096x — 9112,87752393,4596х = 10007,87752
х = 25,4 °С
Задача №5: Образец металлического железа массой 50,6 г нагревают и помещают в 104,0 г воды при 190,7 ° C в калориметре.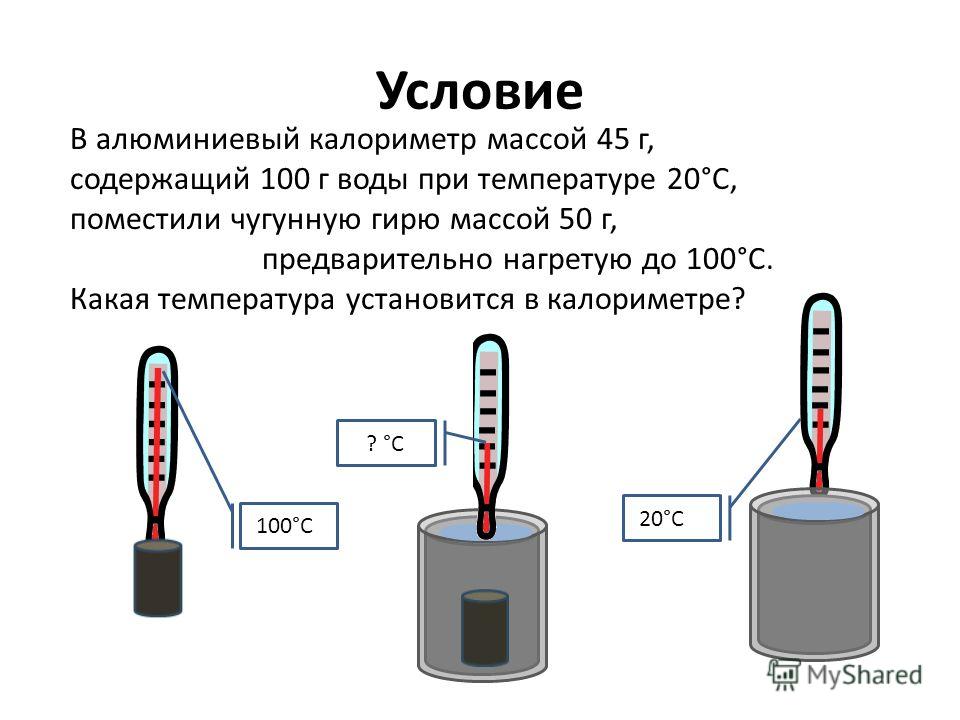
Если конечная температура образца железа и воды равна 24,3 °С, то какой была температура образца железа, когда его поместили в воду?
Решение:
1) тепло, отдаваемое железом = тепло, получаемое водой:
(масса железа) (Δt железа) (C p железа) = (масса воды) (Δt воды) (C p воды)(50,6 г) (x — 24,3 °C) (0,450 Дж/г °C) = (104,0 г) (4,6 °C) (4,184 Дж/г °C)
4,6 получилось из 24,3 минус 19.7.
x − 24,3 °C – это Δt железа. Он перешел от высокой температуры «x» к более низкой температуре 24,3 ° C.
2) Найдите х:
(50,6x — 1229,58) (0,450) = 2001,625622,77х — 553,311 = 2001,6256
22,77х = 2554,9366
х = 112,2 °С
Задача № 6: Кусок медной трубки весом 505,0 г нагревают до 99,9 °C и помещают в изолированный сосуд, содержащий 59,8 г воды при 24,8 °C. Предполагая отсутствие потерь воды и теплоемкость сосуда 10,0 Дж/К, какова конечная температура системы? (С p меди = 0,387 Дж/г К)
Решение:
Решение не предоставлено.
Обратите внимание, что K и °C отменяются в задаче. Это связано с тем, что (а) температуры в фактических расчетах представляют собой разницу между двумя значениями температуры и (б) «размер» 1 К равен «размеру» 1 ° C.
Задача № 7: Какой объем воды температурой 18,5 °С нужно добавить вместе с куском железа массой 1,23 кг (С p = 0,449 Дж/г °С) при температуре 68,5 °С в изолированном сосуде , чтобы конечная температура смеси вода/металл оставалась постоянной и составляла 25,6 °C?
Решение:
тепло, отдаваемое металлом = тепло, получаемое водой(1230 г) (42,9 °С) (0,449 Дж/г °С) = (масса) (4,184 Дж/г °С) (7,1 °С)
масса = 797,562 грамма
округление до 3 цифр кажется разумным
798 мл
Задача №8: A 2,00 x 10 2 г латунного блока при 85,0 °C помещают в чашку из пенопласта, содержащую 2,00 x 10 2 г воды при 50,0 °C. Тепло не передается чашке или окружающей среде.
Найдите конечную температуру смеси.
Решение:
Для решения этой проблемы требуется удельная теплоемкость латуни. Используйте этот сайт, чтобы найти значение.
Решение предоставляется читателю.
Задача №9: Для двух одинаковых блоков T f является средним значением начальных температур, так что T f = 1/2 (T 1 + T 2 ). Покажите для системы из двух блоков, полностью изолированных от окружающей среды, что это верно. (Подсказка: так как блоки сделаны из одного и того же материала, они будут иметь одинаковую C стр .)
Решение:
Я буду использовать T 1 для начальной температуры теплого блока и T 2 для начальной температуры холодного блока.тепла, потерянного теплым блоком = количество тепла, полученного холодным блоком
(масса) (ΔT теплая ) (C p ) = (масса) (ΔT холодная ) (C p )
для одинаковых блоков, масса = масса и C p = C p ; поэтому:
ΔТ warm = ΔT cold
T 1 − T f = T f − T 2
2T f = T 1 + T 2
T f = 1/2 (Т 1 + Т 2 )
Задача №10: 50,0 г меди при 200,0 °C помещают в лед при 0,0 °C.
Сколько граммов льда растает?
Решение:
1) Температура меди понизится до нуля градусов Цельсия, выделив определенное количество тепла:
(50,0 г) (200,0 °С) (0,385 Дж/г °С) = 3850 Дж
2) Все тепло от меди плавит лед:
(334,16 Дж/г) (х) = 3850 Джx = 11,5 г (до трех знаков фиг.)
Задача №11: Предположим, что 0,82 г воды конденсируется на 75,0-граммовом железном блоке, который изначально имеет температуру 24,0 °C.? Если выделяющееся при конденсации тепло идет только на нагрев железного бруска, то какова конечная температура (в °С) железного бруска?
Решение:
(0,82 г / 18,01532 г/моль) (40,7 кДж/моль) = 1,8525673 кДж = 1852,5673 Дж теряется с водойЧтобы продолжить расчет, нужно знать удельную теплоемкость железа. В этом источнике указано 0,444 Дж/г °C.
1852,5673 Дж = (75,0 г) (x) (0,444 Дж/г °C)
x = 55,6 °C изменение
24,0 °С + 55,6 °С = 79,6 °С
Задача № 12: 400,0 г железа нагревают в пламени, а затем бросают в химический стакан, содержащий 1,00 кг воды.
Исходная температура воды составляла 20,0 °С, а конечная температура воды и железа после достижения теплового равновесия составляла 32,8 °С. Какова была первоначальная температура раскаленного железного стержня? (Предположим, что тепло не передается стакану или окружающему воздуху.)
Решение:
q железо = q вода(400,0 г) (x − 32,8 °C) (0,444 Дж/г °C) = (1000 г) (12,8 °C) (4,184 Дж/г °C)
177,6х — 5825,28 = 53555,2
х = 334,35 °С
Инжир до трех знаков, 334 °C
Задача № 13: Металлический образец массой 30,66 г имеет температуру 81,0 °C, когда его помещают в чашку из пенопласта, содержащую 40,0 г воды при 23,0 °C. Температура воды повысилась до 25,0 °С. Теплоемкость чашки 42 Дж/°С.
а) Сколько джоулей потерял металл в воде?
(б) Какова удельная теплоемкость металла?
(c) Какова атомная масса металла?
(d) Что это за металл?
Решение:
q = [(40,0 г) (2,0 °C) (4,184 Дж/г °C)] + [(42 Дж/°C) (2,0 °C)] = 418,72 Дж (ответ на вопрос а)418,72 Дж = (30,66 г) (56,0 °С) (х)
х = 0,244 Дж/г°С) (ответ на б)
Используйте закон Дюлонга-Пти для атомной массы:
(удельная теплоемкость) умножить на (атомную массу) = 3R
(0,244 Дж/г°С) (x) = (3) (8,31447 Дж/К моль)
х = 102,2 г/моль (ответ на в)
Примечание: °C и K взаимно исключаются, потому что «размер» каждой единицы измерения температуры одинаков, 1 °C = 1 K.
родий ближе всего с 102,9 г/моль (ответ на d)
Поиск удельной теплоемкости для Rh, я нашел 0,242 Дж/г С.
Задача №14: Неочищенный образец цинка имеет массу 7,35 г. Образец реагирует со 150,00 г разбавленной соляной кислоты внутри калориметра. Масса калориметра 520,57 г, удельная теплоемкость 0,400 Дж/г°С. При протекании реакции температура внутри калориметра повышается с 14,5°С до 29°С.0,7 °С. Какова процентная чистота образца цинка?
Комментарий: мы предполагаем, что плотность раствора HCl составляет 1,00 г/мл, а удельная теплоемкость раствора HCl такая же, как у чистой воды.
Решение:
1) Суммарная энергия, выделяемая при реакции цинка с HCl:
q = (масса воды) (Δt) (C p вода) + (масса калориметра) (Δt) (C p калориметр)q = (150,0 г) (15,2 °С) (4,184 Дж/г °С) + (370,57 г) (15,2 °С) (0,400 Дж/(г °С))
q = 9539,52 + 2253,0656 = 11792,5856 Дж
Примечание: 370,57 получается из 520,57 минус 150,00
2) Теперь нам нужно посмотреть, сколько цинка выделяет вышеуказанное количество тепла.
Для этого нам понадобится энтальпия этой реакции:
Zn(т) + 2HCl(водн.) —> ZnCl 2 (водн.) + H 2 (г)Поиск в Интернете (см. задачу 5.66) приводит к значению -152,4 кДж на моль Zn.
Этот расчет:
11792,5856 Дж разделить на 152400 Дж/моль = 0,07738 моль Zn
Тогда этот расчет:
0,07738 моль умножить на 65,409 г/моль = 5,06 г
3) Определите процентное содержание цинка в образце:
(5,06 г / 7,35 г) умножить на 100 = 68,8% (до трех цифр)
Задача № 15: Кусок железа весом 25,75 г и кусок золота весом 28,45 г, каждый при температуре 100,0 °C, были брошены в 570,0 мл воды при температуре 17,70 °C. Молярная теплоемкость железа и золота равна 25,19 Дж моль¯ 1 °С¯ 1 и 25,41 Дж моль¯ 1 °С¯ 1 соответственно. Какова конечная температура воды и кусков металла?
Решение:
1) Установка для решения проблемы:
общее количество джоулей, выделяемых железом + общее количество джоулей, выделяемых золотом = общее количество джоулей, поглощаемых водой(25,75 г / 55,845 г/моль) (100,0 − x) (25,19 Дж/моль °C) + (28,45 г / 196,97 г/моль) (100,0 − x) (25,41 Дж/моль °C) = (570,00 г ) (х — 17,70) (4,184 Дж/г°С)
Найдите x, то есть конечную температуру.
2) Вот что означают некоторые термины:
(25,75 г / 55,845 г/моль) —> моль Fe(28,45 г / 196,97 г/моль) —> моль золота
(100,0 − x) —> изменение температуры Fe и Au (каждая из них начинается со 100 °C и снижается до конечной температуры, обозначенной буквой «x»)
(x − 17,70) —> изменение температуры воды
Обратите внимание, что удельная теплоемкость воды измеряется в граммах, а Fe и Au — в молях. Это нормально, поскольку я использую моли Fe и Au (чтобы компенсировать моль в удельной теплоемкости Fe и Au) и использую граммы воды (чтобы компенсировать граммы в удельной теплоемкости воды). Каждая единица будет отменена должным образом.
Задача №16: Рассчитайте количество граммов льда, которое растает, если 1000,0 г железа при температуре 500,0 °C бросить в смесь льда и воды. Теплота плавления воды 334,166 Дж/г. Удельная теплоемкость железа = 0,448 Дж/г°С. Предположим, что льда достаточно, чтобы некоторое его количество осталось после достижения теплового равновесия.
Решение:
Последнее предложение имеет решающее значение, потому что оно гарантирует, что температура не изменится, только лед растает, а вся система останется при нуле по Цельсию.
1) Определить энергию, выделяемую железом:
q = (масса) (изменение температуры) удельная теплоемкость)q = (1000,0 г) (500,0 °C) (0,448 Дж/г °C)
q = 224000 Дж
Тот факт, что некоторое количество льда осталось, позволяет нам точно знать, что температура железа упадет с 500,0 °C до 0 °C.
2) Определите лед, который растает:
224000 Дж разделить на 334,166 Дж/г = 670,3 г
3) Эту проблему можно было бы решить так:
(1000,0 г) (500,0 °C) (0,448 Дж/г °C) = x / 334,166 Дж/гЗдесь предполагается, что 100% энергии, теряемой железом, идет на таяние льда.
Задача № 17: 18,0 мл воды при 28,0 °C добавляют в горячую сковороду.
Вся вода превращается в пар при температуре 100,0 °C. Масса кастрюли 1,25 кг, молярная теплоемкость железа 25,19 Дж/моль °С. Как меняется температура сковороды?
Решение:
1) Определить потребность в энергии для нагрева и кипячения воды:
тепло: q = (18,0 г) (72,0 °C) (4,184 Дж/г °C) = 5422,464 Дж = 5,422464 кДжварить: q = (40,7 кДж/моль) (18,0 г / 18,0 г/моль) = 40,7 кДж
всего: 40,7 кДж + 5,422464 кДж = 46,122464 кДж
Не буду округлять до окончательного ответа.
2) Определить изменение температуры сковороды:
46122,464 Дж = (22,38338 моль) (Δt) (25,19 Дж/моль °C)Δt = 81,8 °С
Обратите внимание, что используются моли железа, а не граммы. Это связано с единицами измерения удельной теплоемкости, предусмотренными в задаче.
Задача №18: Медный шарик имеет массу 125 граммов и находится при температуре 145 °C. Этот шарик помещают в калориметр, содержащий 25,0 граммов льда при температуре -35,0 °C.
Какой будет конечная температура медного шарика? (удельная теплоемкость меди = 0,387 Дж/г °C)
Решение:
Медный шар отдает тепло льду. Весь лед сначала нагреется до 0°С, а затем начнет таять. Когда лед тает, создается система жидкий лед, температура которой остается равной 0 °C. Если медь расплавит весь лёд, то только тогда жидкая вода перейдёт от нуля °С до некоторой конечной, равновесной с медью температуры.
1) Давайте нагреем лед с −35 °C до 0 °C и посмотрим, сколько энергии на это потребуется.
q = (25 г) (35 °C) (2,06 Дж/г °C) q = 1802,5 Дж
2) Посмотрим, что произойдет с температурой меди при удалении 1802,5 Дж.
1802,5 Дж = (125 г) (x) (0,387 Дж/г°C)х = 37,26 °С
145 — 37,26 = 107,74 °С
3) Теперь давайте охладим медный шарик до нуля и посмотрим, сколько энергии при этом высвободится.
q = (125) (107,74) (0,387) = 5211,9225 Дж4) Далее нам нужно выяснить, сколько льда растаяло, используя 5211,9225 Дж энергии.
5211,9225 Дж = (х) (6020 Дж/моль) х = 0,86577 моль0,86577 моль умножить на 18,015 г/моль = 15,6 г
Поскольку изначально у нас было 25 г льда, при таянии 15,6 г льда в системе остается некоторое количество льда. Поскольку весь лед должен растаять, прежде чем мы сможем уйти от 0 °C, мы заключаем, что вся система жидкий лед-медь находится при 0 °C, когда достигается равновесие.
Задача №19: Медный кубик массой 100 граммов нагревают на кипящей водяной бане до 100,0 градусов Цельсия. Куб вынимают из ванны и помещают на очень большой кусок льда, температура которого равна 0,00 по Цельсию. Какова максимальная масса льда, который можно растопить в результате теплообмена, если предположить, что вся тепловая энергия расходуется на таяние льда?
Решение:
1) Определим, сколько энергии выделила медь при плавлении льда:
q = (масса) (Δt) (удельная теплоемкость)q = (100,0 г) (100,0 °C) (0,385 Дж/г °C)
q = 3850 Дж
2) Теперь определяем, сколько льда можно растопить:
q = (масса) (теплота плавления)3850 Дж = (334,166 Дж/г) (х)
х = 17,25 г
до трех знаков инжир, 17,2 г (с использованием правила округления до пяти)
3) Комментарии:
(а) удельную теплоемкость меди можно посмотреть в учебнике или в Интернете.
(b) теплоту плавления можно посмотреть (или рассчитать по молярной теплоте плавления, 6,02 кДж/моль)Задача № 20: Кусок алюминия массой 12,0 г при температуре 22,0 °C помещают в 175,0 мл воды при температуре 85,0 °C и дают ему прийти к тепловому равновесию. Какой будет конечная температура? (Другие факторы, такие как передача тепла воздуху, следует игнорировать.) Удельная теплоемкость алюминия составляет 0,215 кал / г ° C.
Решение:
1) Прежде чем приступить к решению, можете ли вы найти ошибку в этом предложенном решении (и дело не в том, что ни на чем нет единиц)?
(175,0) (4,184) (85,0 — Т) = (12) (0,215) (Т — 22,0)Ошибка в неправильном смешивании юнитов. 4,184 – удельная теплоемкость жидкой воды в Дж г¯ 1 °С¯ 1 и 0,215 – удельная теплоемкость алюминия в кал г¯ 1 °С¯ 1 .
Вы не можете иметь эти две единицы теплоты в одной и той же задаче и быть правы.
Leave A Comment