Главная → Видеоуроки → ОГЭ (ГИА) по математике. Задача 5. Описание видеоурока: Подготовка к ОГЭ (ГИА) 2015 по математике. Модуль Алгебра. Решение пробного варианта ГИА (ОГЭ). Условие задачи 5: Установите соответствие между графиками функций и формулами, которые их задают. Основные требования: Уметь строить и читать графики функций. 00:11:08 Валерий Волков 50 10.01.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Определение функций с помощью графиков | Колледж Алгебра
Результаты обучения
- Проверка функции с помощью теста вертикальной линии
- Проверка взаимно однозначной функции с помощью теста горизонтальной линии
- Определение графиков функций инструментария
Как мы видели в примерах выше, мы можем представить функцию с помощью графика.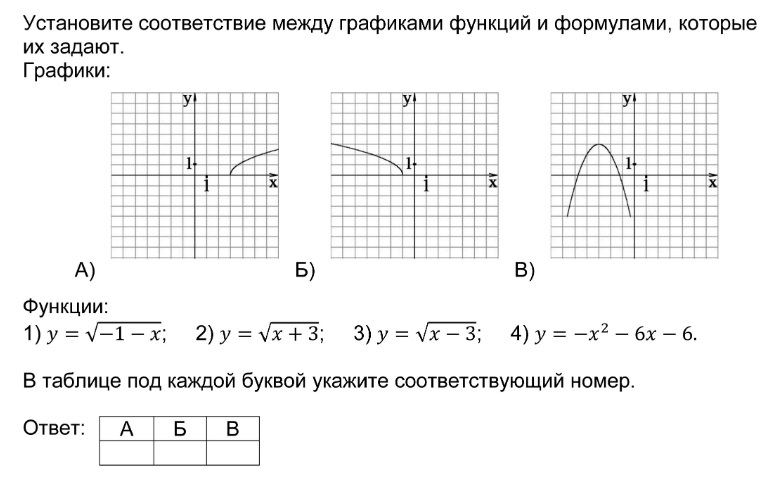 Графики отображают множество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают множество пар вход-выход на небольшом пространстве. Визуальная информация, которую они предоставляют, часто облегчает понимание отношений. Обычно мы строим графики с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение [латекс]x[/латекс] и выходное значение [латекс]у[/латекс], и мы говорим, что [латекс]у[/латекс] является функцией [латекс]х [/latex], или [latex]y=f\left(x\right)[/latex], когда функция называется [latex]f[/latex]. График функции представляет собой множество всех точек [латекс]\влево(х,у\вправо)[/латекс] на плоскости, удовлетворяющих уравнению [латекс]у=f\влево(х\вправо)[/латекс ]. Если функция определена только для нескольких входных значений, то график функции представляет собой всего несколько точек, где x -координата каждой точки является входным значением, а y -координата каждой точки является соответствующим выходным значением.
Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Вертикальная линия включает все точки с определенным значением [latex]x[/latex]. Значение [latex]y[/latex] точки, в которой вертикальная линия пересекает график, представляет собой результат для этого входного значения [latex]x[/latex]. Если мы можем нарисовать 
Как: Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Изучите график, чтобы увидеть, пересекает ли какая-либо вертикальная линия кривую более одного раза.
- Если такая линия есть, то график не представляет функцию.
- Если ни одна вертикальная линия не может пересекать кривую более одного раза, график представляет собой функцию.
Пример: применение теста вертикальной линии
Какой из графиков представляет функцию [latex]y=f\left(x\right)?[/latex]
Показать решение
Попробуйте
Представляет ли график ниже функцию?
Показать раствор
Проверка горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — использовать тест горизонтальной линии . Проведите горизонтальные линии через график. Горизонтальная линия включает все точки с определенным значением [latex]y[/latex]. Значение [latex]x[/latex] точки, в которой вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex]y[/latex]. Если мы можем нарисовать любая горизонтальная линия , которая пересекает график более одного раза, то график , а не представляет собой функцию, потому что это значение [latex]y[/latex] имеет более одного входа.
Проведите горизонтальные линии через график. Горизонтальная линия включает все точки с определенным значением [latex]y[/latex]. Значение [latex]x[/latex] точки, в которой вертикальная линия пересекает функцию, представляет вход для этого выходного значения [latex]y[/latex]. Если мы можем нарисовать любая горизонтальная линия , которая пересекает график более одного раза, то график , а не представляет собой функцию, потому что это значение [latex]y[/latex] имеет более одного входа.
Как: Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно однозначного соответствия.
- Изучите график, чтобы увидеть, пересекает ли какая-либо горизонтальная линия кривую более одного раза.
- Если такая строка есть, то функция не является однозначной.
- Если ни одна горизонтальная линия не может пересекать кривую более одного раза, функция является однозначной.
Пример: применение теста горизонтальной линии
Рассмотрим функции (a) и (b), показанные на графиках ниже.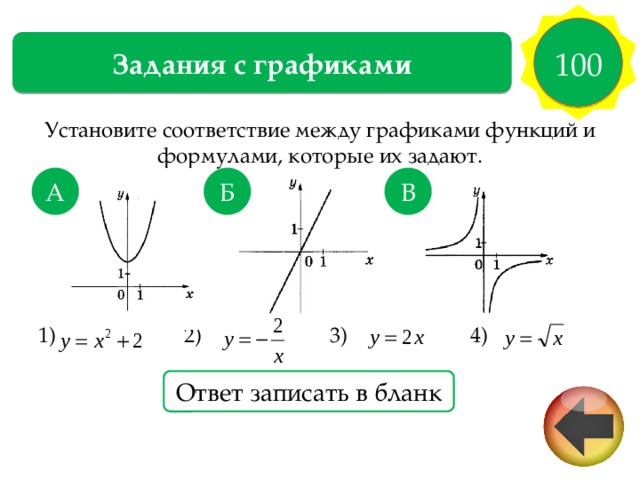
Является ли какая-либо из функций взаимно однозначной?
Показать раствор
Идентификация основных функций набора инструментов
В этом тексте мы исследуем функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения задач с ними. При обучении чтению мы начинаем с алфавита. При обучении арифметике мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор элементов стандартного блока. Мы называем их «инструментальными функциями», которые образуют набор основных именованных функций, для которых мы знаем график, формулу и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать [latex]x[/latex] в качестве входной переменной и [latex]y=f\left(x\right)[/latex] в качестве выходной переменной.
Мы будем часто встречаться с этими инструментальными функциями, комбинациями инструментальных функций, их графиками и преобразованиями в этой книге. Будет очень полезно, если мы сможем быстро распознать эти функции инструментария и их функции по имени, формуле, графику и основным свойствам таблицы. Графики и примерные табличные значения прилагаются к каждой функции, показанной ниже.
| Функции набора инструментов | ||
|---|---|---|
| Имя | Функция | 9{2}}[/латекс]|
| Корень квадратный | [латекс]f\влево(х\вправо)=\sqrt{x}[/латекс] | |
| Кубический корень | [латекс]f\влево(х\вправо)=\sqrt[3]{х}[/латекс] | |
Попробуй
Попробуй
В этом упражнении вы начертите график функций инструментария с помощью интерактивного графического инструмента.
- Нарисуйте график каждой функции инструментария, используя обозначения функций.

- Создайте таблицу значений, которая ссылается на функцию и включает как минимум интервал [-5,5].
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее

 5 класс.
5 класс.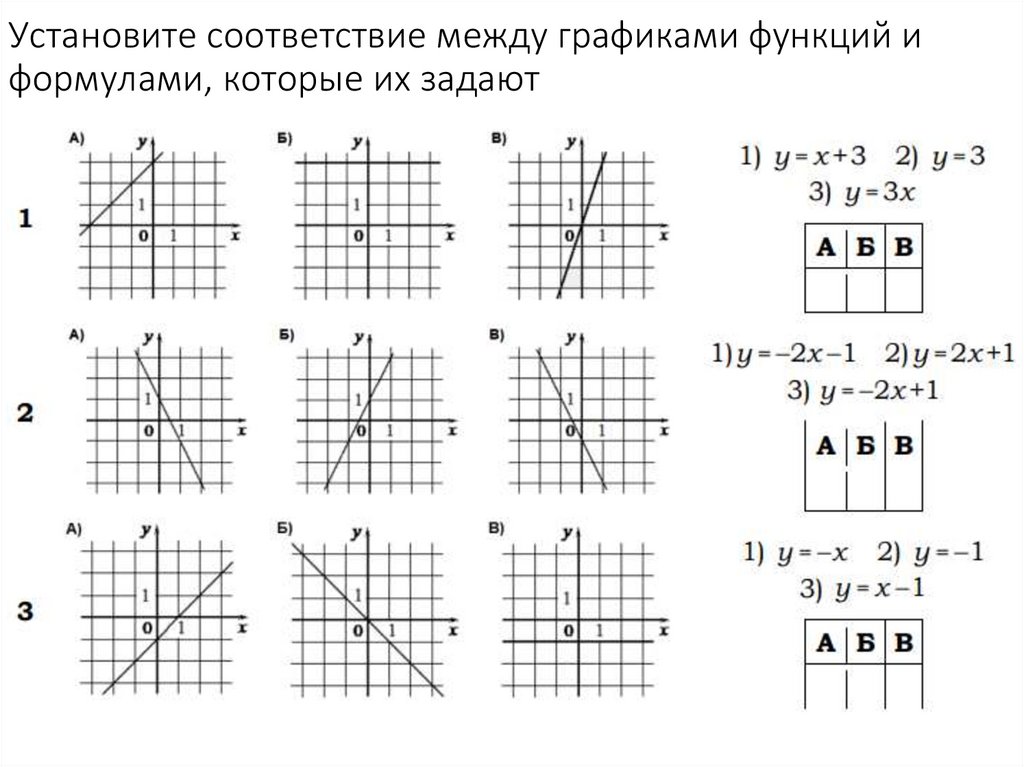 10 — 11 класс.
10 — 11 класс.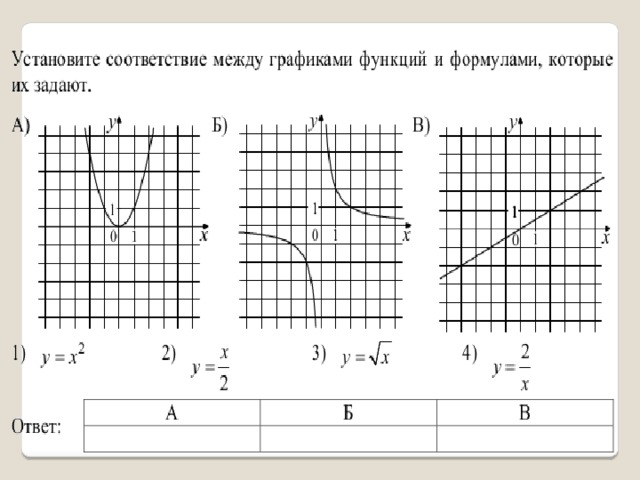
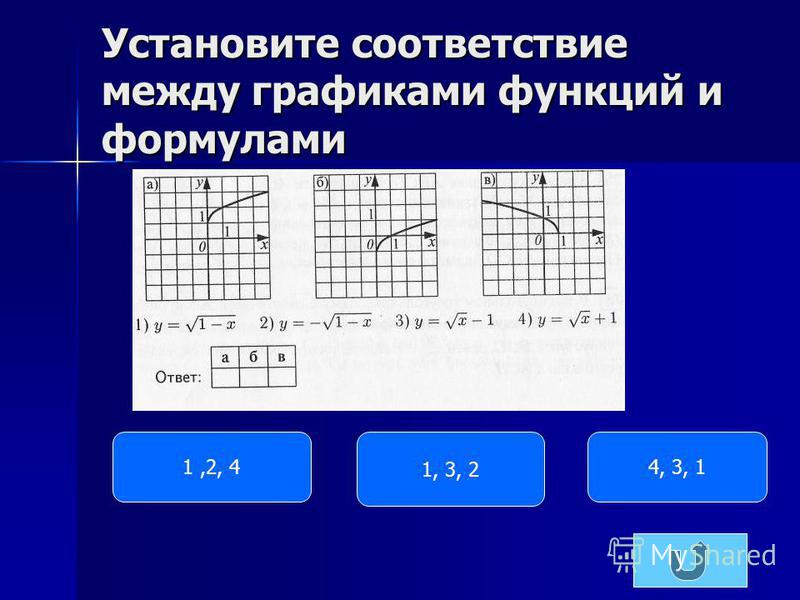
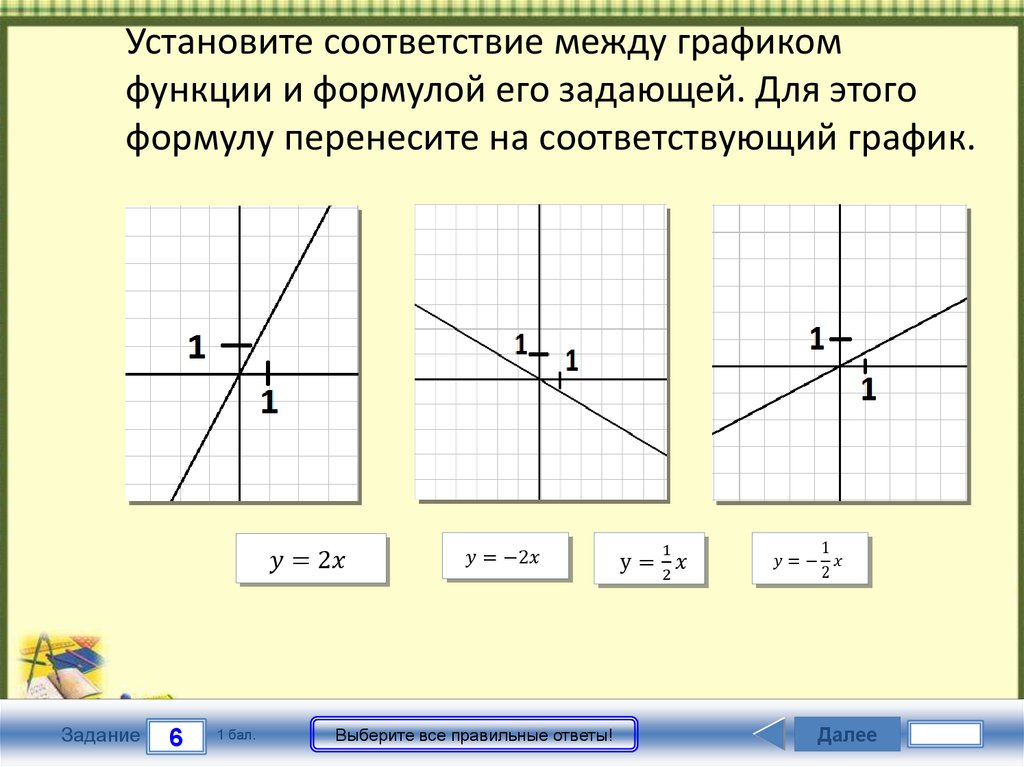 Соотнесите фамилии с функциями. Сопоставьте графики с фамилиями. Внимательно читайте карты, чтобы правильно их сопоставить.
Соотнесите фамилии с функциями. Сопоставьте графики с фамилиями. Внимательно читайте карты, чтобы правильно их сопоставить. 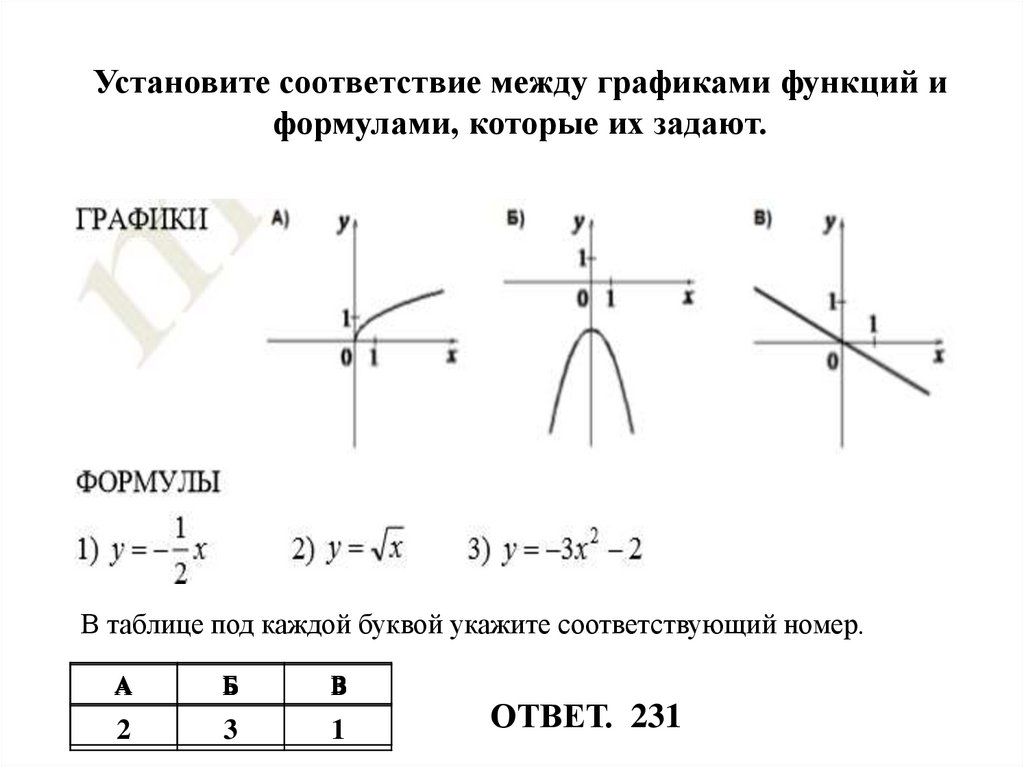
Leave A Comment