Физические основы механики
ЦЕЛЬ РАБОТЫ
Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Основные законы динамики материальных точек — это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:
|
|
(1) |
называют основным уравнением динамики.
Эскиз машины Атвуда показан на рис. 1.
Рис. 1. Эскиз машины Атвуда
Два одинаковых груза с массами
Основное уравнение динамики для груза с перегрузком имеет вид:
|
|
(2) |
а для другого груза (без перегрузка):
|
|
(3) |
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
|
|
(4) |
где SMk — алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I — момент инерции блока относительно оси вращения; e — его угловое ускорение.
Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим
|
|
(4а) |
где: R — радиус блока; Мтр — момент силы трения.
Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
|
|
(5) |
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
|
|
(6) |
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
или
|
|
(7) |
Проецируя уравнения (2) и (3) на ось у, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):
|
|
(8) |
Умножая первое из уравнений (8) на (-1), и складывая все уравнения (8), получим
|
|
(9) |
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
|
|
(10) |
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
|
|
(11) |
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m:
|
|
(12) |
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
|
|
|
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).
Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:
где у1, v1 — начальные параметры.
Исключая из этих уравнений время t, при условии v1=0, получим
|
|
(14) |
Система грузов перемещается на величину sy=L1, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу
получим
|
|
(15) |
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным.
С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:
|
|
(16) |
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
К основанию 1 экспериментальной установки (см. рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
Рис. 2. Схема экспериментальной установки
На верхнем конце стойки находится неподвижный блок 5. Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4 подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см. рис. 1) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером в секундах и показанное в окне «время».
Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ
1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
Таблица 1
|
m=… кг |
L=… м |
L2=… м |
|
|
№ наблюдения |
Время ti, с |
||
|
1 |
|||
|
2 |
|||
|
3 |
|||
|
4 |
|||
|
5 |
|||
2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.
3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L2 от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см. Измерьте установленное расстояние L2 по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
4. Нажмите кнопку «ПУСК».
5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с.
6. Нажмите кнопку «СБРОС».
7. Повторите пункты 3 — 5 ещё четыре раза, не меняя расстояние L2.
8. Вычислите среднее значение времени <t>. Результат занесите в таблицу расчетов 2.
Таблица 2
|
№ наблюдения |
ti |
ti-<t> |
(ti-<t>)2 |
|
1 |
|||
|
2 |
|||
|
3 |
|||
|
4 |
|||
|
5 |
|||
|
Суммы |
Sti=… |
S(ti-<t>)2 |
|
|
<t>=… |
s=… |
||
|
E= |
9. Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
10. Возведите в квадрат каждое отклонение и просуммируйте квадраты отклонений.
11. Рассчитайте среднее квадратичное отклонение s, применив для его расчёта формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей
12. Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени
где tP(n) — коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы n=n-1.
Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 имеем из таблицы коэффициентов Стьюдента t0.9(5-1)=2.13.
13. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.
Тогда результат измерения времени t запишем в виде
14. Произведите расчет относительной погрешности в определении времени Et (в процентах) по формуле:
15. Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L2 имеем приборные погрешности, равные половине цены деления линейки
16. Ускорение грузов а рассчитывается по формуле (16), в которую подставляется среднее значение времени <t> и измеренные линейкой значения расстояний L и L2.
17. Относительная погрешность в определении ускорения найдётся по формуле:
18. Результат измерения ускорения а запишется в виде
Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
19. Определите величину ускорения свободного падения g по формуле
При этом значение массы грузов принять равным M=90 г.
20. Полуширину доверительного интервала Dg найдите с помощью формулы
Значения погрешностей в определении масс в данной работе принять равными приборной погрешности при их взвешивании:
21. Оформите отчёт по работе.
ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ
На рис.3 представлена реальная лабораторная установка, используемая для выполнения данной работы.
Рис.3. Лабораторная установка «Машина Атвуда»
После ознакомления с принципом работы установки необходимо проделать работу на виртуальной лабораторной установке, представленной в правом окне. В процессе выполнения измерений можно свернуть-развернуть окно с описанием лабораторной работы либо свернуть-развернуть окно с лабораторной установкой.
После окончания измерений следует сохранить результаты работы. Для этого необходимо нажать на клавишу или. После этого будет предложено сохранить результаты в файле, имя которого — название лабораторной работы (имя файла изменять не рекомендуется), месторасположение — рабочий стол (можно изменить место сохранения файла). Так как результаты сохраняются в формате html, в дальнейшем вы можете просмотреть результаты, открыв сохраненный файл, а также можете отправить файл на проверку правильности выполнения лабораторной работы преподавателю.
РЕКОМЕНДАЦИИ
по оформлению отчета по лабораторным работам (физика)
1. Отчет оформляют в электронном виде в редакторе Word
2. Объем отчета составляет 2-3 страницы.
3. В отчете необходимо указать:
3.1 Фамилию, имя, отчество студента;
3.2 Номер группы;
3.3 Дисциплину;
3.4 Фамилию, имя, отчество преподавателя;
4. Рекомендуемая структура отчета:
4.1 Название работы;
4.2 Цель работы;
4.3 Таблицы измерений и таблицы расчетов, сохраненные в виде отдельного файла.
4.5 Формулы и законы, используемые для расчетов;
4.6 Результаты расчетов, не вошедшие в таблицу расчётов;
4.7 Выводы, которые можно сделать из работы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется системой отсчета?
2. Дайте определение материальной точки.
3. Сравните понятия пути и перемещения.
4. Дайте определения средней и мгновенной скоростей.
5. Дайте определения среднего и мгновенного ускорений.
6. Укажите формулы, связывающие кинематические величины при равноускоренном прямолинейном движении.
7. Дайте определение силы.
8. Что характеризует масса тела?
9. Сформулируйте основные законы динамики — законы Ньютона.
10. Какая система тел называется изолированной?
11. Сформулируйте законы сохранения импульса и полной механической энергии системы.
12. Какое движение тела называется свободным падением?
13. Как изменится ускорение свободного падения при подъеме с уровня моря на высоту h=10 км? Радиус Земли R3=6 370 км.
14. При каком условии ускорения тел, используемых в машине Атвуда, одинаковы по модулю?
Что такое ускорение? Формулы ускорения при равноускоренном движении по прямой траектории
Содержание статьи:Ускорение в физике — это одна из важных кинематических характеристик, без знания которой невозможно описать ни один вид движения. В данной статье рассмотрим, что это за величина, а также приведем формулы ускорения при движении равноускоренном прямолинейном.
Ускорение и причина его появления
В физике величину, которая характеризует изменение во времени скорости, называют ускорением. Математическая формула для ускорения выглядит так:
a¯ = dv¯/dt.
Чем быстрее изменяется скорость, тем больше будет ускорение тела. Например, значение a = 1 м/с2 говорит о том, что за 1 секунду скорость увеличилась на 1 м/с.
Вам будет интересно:Упразднить — что это значит? Когда используется?
Ускорение у тел возникает за счет действия на них внешних сил любой природы. Этот факт был установлен Ньютоном в XVII веке. В настоящее время он носит название 2-го закона Ньютона:
F¯ = m*a¯.
Обе формулы говорят о том, что вектор ускорения направлен в сторону изменения вектора скорости или в сторону вектора силы (F¯ и dv¯ направлены одинаково). Если направления векторов a¯ и v¯ совпадают, тогда тело будет ускоряться, если они противоположны, то тело будет замедлять свое движение, если же они направлены под некоторым углом, тогда траектория перемещения будет кривой линией.
Равноускоренное прямолинейное движение. Скорость и ускорение
Указанный вид движения предполагает, что траектория тела является прямой линией, а величина ускорения в процессе перемещения тела не изменяется ни по модулю, ни по направлению. Поскольку тело движется по прямой линии, то векторы a¯ и v¯ направлены либо в одну сторону, либо в противоположные.
Предположим, что тело находилось в покое. Затем на него начала действовать постоянная сила, которая придала ему ускорение. В таком случае скорость v в любой момент времени t может быть вычислена так:
v = a*t.
Где a = const. Графиком этого уравнения является возрастающая прямая, которая начинается с точки (v=0; t=0).
Если же тело до начала действия силы уже имело некоторую скорость v0, тогда будут справедливы такие формулы:
v = v0 + a*t;
v = v0 — a*t.
В первом случае речь идет об ускоренном движении, во втором — о замедленном (торможение).
Из последних двух выражений можно получить формулы ускорения при равноускоренном движении тела по прямой линии:
a = (v-v0)/t;
a = (v0-v )/t.
Время t отсчитывается от момента действия силы на тело.
Ускорение и путь
При решении задач на равноускоренное перемещение часто требуется найти ускорение, зная пройденный путь. Покажем, какие формулы для этого следует применять.
Путь рассчитать несложно при равноускоренном движении по прямой. Для этого следует взять интеграл по времени от уравнения v(t). Выполнив это математическое действие, получим три рабочие формулы:
S = a*t2;
S = v0*t + a*t2;
S = v0*t — a*t2.
Первое выражение описывает ускоренное перемещение тела из состояния покоя, второе — ускоренное перемещение с наличием начальной скорости, третье — торможение. Графики всех трех функций S(t) являются параболами.
Как выразить ускорение из формул равноускоренного движения для пути? Для этого необходимо изолировать множитель a*t2 в одной части равенства, а затем все равенство поделить на квадрат времени. Из формул выше получаем:
a = S/t2;
a = (S — v0*t)/t2;
a = (v0*t — S)/t2.
Первое уравнение используется для экспериментального определения ускорения свободного падения g, когда тяжелые тела сбрасывают вниз с некоторой высоты. Подобные эксперименты проводил еще Галилей в конце XVI века. В настоящее время для определения ускорения g в исследуемой местности используют абсолютные гравиметры, принцип работы которых также основан на свободном падении.
Два последних уравнения отличаются друг от друга лишь знаком ускорения. При торможении ускорение считают отрицательным.
Все три выражения приводят к одной и той же единице измерения величины a — м/с2.
Задача на вычисление ускорения
Разобравшись с основными формулами ускорения при равноускоренном движении, решим следующую проблему практического характера: водитель автомобиля, который двигался со скоростью 63 км/ч, увидел, что впереди загорелся красный сигнал светофора. После нажатия на педаль тормоза автомобиль полностью остановился через 100 метров. Зная, что время торможения заняло 14 секунд, необходимо рассчитать соответствующее ускорение.
Для решения задачи можно сразу же воспользоваться одной из записанных выше формул:
a = (v0*t — S)/t2.
Переведем начальную скорость автомобиля из км/ч в м/с, получаем:
v0 = 63*1000/3600 = 17,5 м/с2.
Теперь можно подставить значения из условия задачи и получить ответ: a = 0,74 м/с2. Поскольку речь идет о торможении, то данное ускорение следует взять со знаком минус: a = — 0,74 м/с2.
Источник
Методические указания к лабораторной работе «Машина Атвуда»
Цель работы
Экспериментальная проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение ускорения свободного падения лабораторной установке – машине Атвуда.
Экспериментальная установка
 Машина Атвуда (рис.1) состоит из легкого блока 2, через который переброшена нить с двумя наборными грузами на концах (массы обоих грузов одинаковы и равны m). Грузы могут двигаться вдоль вертикальной рейки со шкалой 1. Если на правый груз положить небольшой перегрузок Dm, грузы начнут двигаться с некоторым ускорением. Для приема падающего груза служит полочка 3.
Машина Атвуда (рис.1) состоит из легкого блока 2, через который переброшена нить с двумя наборными грузами на концах (массы обоих грузов одинаковы и равны m). Грузы могут двигаться вдоль вертикальной рейки со шкалой 1. Если на правый груз положить небольшой перегрузок Dm, грузы начнут двигаться с некоторым ускорением. Для приема падающего груза служит полочка 3.
Время движения грузов измеряется с помощью ручного или стационарного секундомера.
Силы трения в машине Атвуда сведены к минимуму, но не равны нулю. Для возможно полной их компенсации масса одного из грузов (в нашей установке – правого) делается немного больше массы другого. Эта операция производится при помощи кусочков пластилина и выполняется с таким расчетом, чтобы а) грузы могли находиться в статическом положении сколь угодно долго, но б) от легкого толчка вниз правого груза вся система приходила в равномерное движение. Масса используемого пластилина столь мала, что в последующих расчетах в массу грузов не включается. Перегрузки Dm, с помощью которых системе задается движение, укладывают также на правый груз системы.
Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити.
Теоретическая часть
Второй закон Ньютона в проекциях на вертикальную ось для каждого из тел системы (рис.2) в предположении невесомости блока, отсутствия силы трения и нерастяжимости нити дает:
 (1)
(1)
Где g — ускорение свободного падения,
a — ускорение грузов,
T1 и T2 — сила натяжения нити.
Выразим из данной системы ускорение a.
 (2)
(2)
Проверим равноускоренный характер движения грузов, экспериментально получая значения пути данных грузов S (для обоих грузов он одинаков) и время движения t.
Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то

 (3)
(3) 
Третье соотношение часто называют законом перемещений: «Перемещение при равноускоренном движении прямо пропорционально квадрату времени движения».
Соотношение (3) может быть проверено экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение, с которым движется тело, прямо пропорционально равнодействующей действующих на него сил и обратно пропорционально массе этого тела».
Подставляя ai в (2) получаем следующую формулу:
 (4)
(4)
Для получения более точного значения g, необходимо учесть момент инерции блока — Jб, (T1 T2). Рассмотрим получения вышеописанных формул с учётом новой величины. Вычислим g из закона динамики для вращательного движения тела (в данном случае блока).
T2). Рассмотрим получения вышеописанных формул с учётом новой величины. Вычислим g из закона динамики для вращательного движения тела (в данном случае блока).
 (5)
(5)
 — сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции
— сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции
 (6)
(6)
Где r — радиус блока, Jб — момент инерции блока.
Выразим из уравнения (1) разность сил натяжения (T1 – T2 ) и подставив ее в уравнение (6) получим:
 (7)
(7)
Выразим ускорение грузов a:
 (8)
(8)
Учитывая, что значение момента инерции блока
 (9),
(9),
k- коэффициент распределения массы блока относительно оси вращения (k < 1), окончательно получаем выражение для определения ускорения свободного падения:
11)
Экспериментальная часть
Задание 1. Проверка второго закона Ньютона.
Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем раздельного исследования двух зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе системы и 2) зависимости ускорения от массы системы при постоянной действующей силе.
Исследование зависимости ускорения от силы при постоянной массе
Измерения и обработка результатов
1. Тщательно балансируют грузы, выбрав их массы в пределах 150 — 200 г каждый.
2. Затем на правый груз последовательно накладывают перегрузки. В результате в системе появляется движущая сила равная mg, где m — суммарная масса перегрузков. При этом, конечно, общая масса системы незначительно увеличивается, но этим изменением массы по сравнению с массой грузов можно пренебречь, считая массу системы постоянной.
3. Измеряют время равноускоренного движения системы на пути, например, 1 метр. Все данные заносят в таблицу 1.3 отчета.
4. Пользуясь законом путей (1.6), вычисляют ускорение а.
5. Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.
6. Строят график зависимости ускорения движения от действующей силы. Точку (F=0, a=0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение действительно прямо пропорционально силе.
7. По угловому коэффициенту полученной прямой определяют массу системы и сравнивают ее реальной массой.
Исследование зависимости ускорения от массы при постоянной силе
Измерения и обработка результатов
1. Все опыты проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе. Ускорение системы измеряется также как и в предыдущем задании.
2. Для изменения массы системы одновременно на правый и левый груз кладут дополнительные одинаковые грузы. Все данные записывают в таблицу отчета.
3. График обратно пропорциональной зависимости ускорения от массы представляет собой гиперболу, которую невозможно идентифицировать. Для проверки предположения об обратно пропорциональной зависимости между ускорением и массой  необходимо построить график зависимости ускорения от обратного значения массы системы: a = f(М-1). Подтверждением предположения является прямолинейность этого графика.
необходимо построить график зависимости ускорения от обратного значения массы системы: a = f(М-1). Подтверждением предположения является прямолинейность этого графика.
4. По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе
Задание 2. Определение ускорения движения грузов
В полученном уравнении прямой  коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов (a =2k) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.
коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов (a =2k) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.
Задание 3. Определение ускорения свободного падения
(Выполняется по результатам измерений и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и перегрузка, а также ускорение движения системы, из формулы (3) найдите ускорение свободного падения. Результаты занесите в отчет. В выводе сравните полученный результат с табличной величиной.
Для нахождения погрешности измерения величины ускорения свободного падения Δg используем формулу:
12)
где  ;
;  ;
;  ;
;  ;
;
 – частные производные функции
– частные производные функции
Проанализируйте результаты своих наблюдений и сформулируйте вывод.
Какое движение называется поступательным?
Дайте определение инерциальной системы отсчета. Приведите примеры ИСО.
Сформулируйте первый закон Ньютона. Приведите примеры его проявления.
Дайте определение инертной массы тела. Гравитационной? От чего и как зависит масса тела?
Сформулируйте второй закон Ньютона. Приведите варианты его математической формы.
Покажите все силы, действующие на один из грузов в машине Атвуда, и составьте для него уравнение динамики.
Запишите систему уравнений динамики для машины Атвуда с учетом момента инерции блока. Силы трения в блоке?
ЛР № 1
ЦЕЛЬ РАБОТЫ
Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Основные законы динамики материальных точек это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:
| (1) |
называют основным уравнением динамики.
Эскиз машины Атвуда показан на рис. 1.
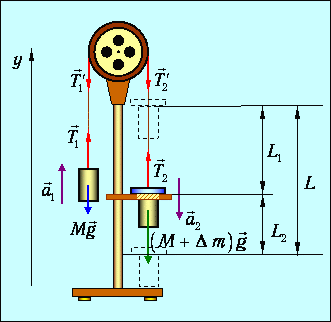
Рис. 1. Эскиз машины Атвуда
Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m (в виде шайбы), то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т1 или Т2, а на блок с силами Т‘1 и Т‘2. Тогда на каждый груз действует сила тяжести и сила натяжения нити.
Основное уравнение динамики для груза с перегрузком имеет вид:
| (2) |
а для другого груза (без перегрузка):
| (3) |
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
| (4) |
где Mk алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I момент инерции блока относительно оси вращения; его угловое ускорение.
Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим
| (4а) |
где: R радиус блока; Мтр момент силы трения.
Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
| (5) |
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
| (6) |
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
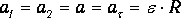
или
| (7) |
Проецируя уравнения (2) и (3) на ось у, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):
| (8) |
Умножая первое из уравнений (8) на (-1), и складывая все уравнения (8), получим
| (9) |
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
| (10) |
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
| (11) |
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m:
| (12) |
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
| (13) |
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).
Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:
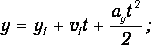
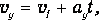
где у1, v1 начальные параметры.
Исключая из этих уравнений время t, при условии v1=0, получим
| (14) |
Система грузов перемещается на величину sy=L1, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу
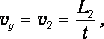
получим
| (15) |
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным.
С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:
| (16) |
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
К основанию 1 экспериментальной установки (см. рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
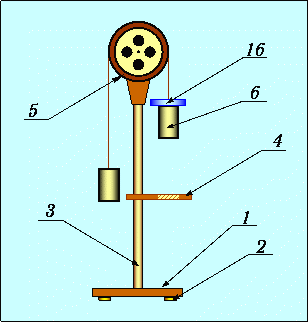
Рис. 2. Схема экспериментальной установки
На верхнем конце стойки находится неподвижный блок 5. Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см. рис. 1) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером в секундах и показанное в окне «время».
Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ
Исходными данными в данной работе являются значения величин m, L, L1 и L2 . Здесь m — масса перегрузка, размещаемого на правом основном грузе массой М. L — полное расстояние , проходимое основным грузом. L1 — длина участка с равноускоренным движением: от верхнего положения перегрузка до подвижного кольца (положение которого определяется красной чертой). L2 — длина участка с равномерным движением: от подвижного кольца (положение определяется красной чертой) до нижней точки траектории вершины груза (определяется границей зелёного фона). Величина L в работе не изменяется и равна L = 33 см. Значения величин m, L1 и L2 устанавливаются студентом в процессе выполнения работы, причём L1 + L2 = L .
1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
Таблица 1
m=… кг | L=… м | L2=… м | |
№ наблюдения | Время ti, с | ||
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.
3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L2 от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см. Измерьте установленное расстояние L2 по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
4. Нажмите кнопку «ПУСК».
5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с.
6. Нажмите кнопку «СБРОС».
7. Повторите пункты 3 5 ещё четыре раза, не меняя расстояние L2.
8. Вычислите среднее значение времени <t>. Результат занесите в таблицу расчетов 2.
Таблица 2
№ наблюдения | ti | ti-<t> | (ti-<t>)2 |
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
Суммы | ti=… | (ti-<t>)2 | |
<t>=… | =… | ||
E= |
9. Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
10. Возведите в квадрат каждое отклонение и просуммируйте квадраты отклонений.
11. Рассчитайте среднее квадратичное отклонение , применив для его расчёта формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей
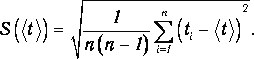
12. Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени
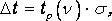
где tP() коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы =n-1.
Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 имеем из таблицы коэффициентов Стьюдента t0.9(5-1)=2.13.
13. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.
Тогда результат измерения времени t запишем в виде
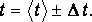
14. Произведите расчет относительной погрешности в определении времени Et (в процентах) по формуле:
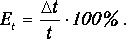
15. Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L2 имеем приборные погрешности, равные половине цены деления линейки
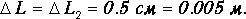
16. Ускорение грузов а рассчитывается по формуле (16), в которую подставляется среднее значение времени <t> и измеренные линейкой значения расстояний L и L2.
17. Относительная
погрешность в определении
ускорения 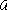 найдётся
по формуле:
найдётся
по формуле:
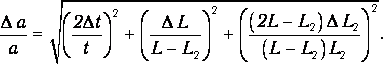
18. Результат измерения ускорения а запишется в виде
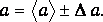
Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
19. Определите значение массы основных грузов М по формуле
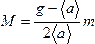
Здесь значение ускорения свободного падения принимается равным g = 9,8 м/с2, <a> — среднее значение ускорения грузов. Погрешность значения М находится из соотношения
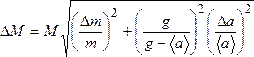 .
.
20. Оформите отчёт по работе. В конце отчёта необходимо привести результаты выполнения лабораторной работы в виде:
Исходные
данные:
m = L1 =
L2 =
Результаты
измерений и расчётов: 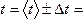
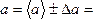
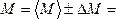
ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ
На рис.3 представлена реальная лабораторная установка, используемая для выполнения данной работы.
 ВИДЕО
ВИДЕО
Рис.3. Лабораторная установка «Машина Атвуда»
После ознакомления с принципом работы установки необходимо проделать работу на виртуальной лабораторной установке:
Внимание! При записи результатов измерений необходимо учесть опечатку на сайте: масса перегрузка m, устанавливаемая в специальном окне, имеет размерность кг, а не г, как это указано на сайте!
РЕКОМЕНДАЦИИ по оформлению отчета по лабораторным работам (физика)
1. Отчет оформляют в электронном виде в редакторе Word
2. Объем отчета составляет 2-3 страницы.
3. В отчете необходимо указать:
3.1 Фамилию, имя, отчество студента;
3.2 Номер группы;
3.3 Дисциплину;
3.4 Фамилию, имя, отчество преподавателя;
4. Рекомендуемая структура отчета:
4.1 Название работы;
4.2 Цель работы;
4.3 Таблицы измерений и таблицы расчетов, сохраненные в виде отдельного файла.
4.5 Формулы и законы, используемые для расчетов;
4.6 Результаты расчетов, не вошедшие в таблицу расчётов;
4.7 Выводы, которые можно сделать из работы.
Определение скоростей и ускорений при вращательном движении
Основные законы и формулы, применяемые при решении задач
Вращательное движение вокруг неподвижной оси
Рассмотри твердое тело, вращающееся вокруг неподвижной оси z. Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t:
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.
Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Скорость точки при вращательном движении тела вокруг неподвижной оси
Рассмотрим точку A, принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .
Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA. При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .
Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA. При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

Ускорение точки при вращательном движении тела вокруг неподвижной оси
Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.
Полное ускорение точки A, или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.
Поступательное прямолинейное движение
Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x. При – противоположно этой оси.
Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x. При – противоположно.
Соприкосновение тел без проскальзывания
Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.
Пример решения задачи

Условие задачи
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r1 = 2 см, R1 = 4 см, у колеса 2 – r2 = 6 см, R2 = 8 см, у колеса 3 – r3 = 12 см, R3 = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s5 = t3 – 6t (см). Положительное направление для s5 – вниз.
Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.
Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.
Дано:
t = 2 с; r1 = 2 см, R1 = 4 см; r2 = 6 см, R2 = 8 см; r3 = 12 см, R3 = 16 см; s5 = t3 – 6t (см).
Решение
Определение скорости и ускорения груза 5
Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t, находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.
Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с2.
Определение угловых скоростей и ускорений колес

Решение задачи
Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t. Дифференцируя по t, находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с–1;
с–2.
Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с–1;
с–2.
Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с–1;
с–2.
Итак, мы нашли:
ω1 = 5.3333 с–1, ω2 = 1.3333 с–1, ω3 = 0.5 с–1, ε1 = 10.6667 с–2, ε2 = 2.6667 с–2, ε3 = 1 с–2.
Определение скоростей точек A и C
Точка A лежит на окружности радиуса R1 с центром в точке O1, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.
Точка C лежит на окружности радиуса R3 с центром O3 на оси вращения. Скорость этой точки:
см/с.
Определение ускорения точки B
Точка B лежит на окружности радиуса R2 с центром O2, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с2.
Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с2.
Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с2.
Определение ускорения рейки 4
Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с:
см/с2.
Ответ
см/с; см/с; с–2; см/с2; см/с2.
Автор: Олег Одинцов. Опубликовано:
Пример решения задачи — Студопедия
Дано:
m1 = 100 г = 0,1 кг
m2 = 700 г = 0,7 кг
m = 300 г = 0,3 кг
d = 30 мм = 30×10-3 м
H = 0,2 м

Найти:
1. Силы реакции шнура F1 и F2 .
2. Линейное ускорение грузов a.
3. Угловое ускорение блока e.
4. Время, в течении которого груз m1 или m2 упадет на поверхностьtп .
5. Количество оборотов, совершенных блоком до падения груза на поверхность N.
6. Построить графики зависимости от времени линейной скорости грузовv(t), угловой скорости блокаω(t), кинетической энергии грузов Eк1(t) и Ек2(t), потенциальной энергии грузов Eп1(t) иEп2(t), момента импульса блока L(t).
Грузы совершают поступательное ускоренное движение, блок – вращательное ускоренное движение. По условию задачи m2 > m1 , поэтому груз m2 опускается, а груз m1 поднимается.
2-й закон Ньютона для 1-го груза:
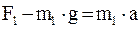 (1)
(1)
где F1 — сила реакции шнура, приложенная к грузу, g = 9,8 м/с2 — ускорение свободного падения, a – линейное ускорение груза, m1g – сила тяжести груза.
2-й закон Ньютона для 2-го груза:
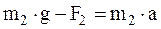 (2)
(2)
Уравнение динамики вращательного движения блока:
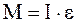 , (3)
, (3)
где M – результирующий момент сил, приложенных к блоку, I – момент инерции блока, ε – угловое ускорение блока.
Так как груз m2 опускается, то  . Результирующий момент сил, приложенных к блоку, равен
. Результирующий момент сил, приложенных к блоку, равен
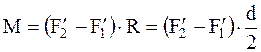 , (4)
, (4)
где 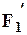 и
и 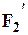 — силы натяжения шнура, приложенные к блоку,
— силы натяжения шнура, приложенные к блоку, 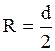 — радиус блока.
— радиус блока.
Момент инерции блока (сплошного цилиндра) равен
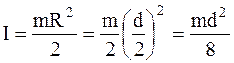 , (5)
, (5)
Считаем, что шнур не проскальзывает по блоку. Тогда:
 (6)
(6)
Согласно третьему закону Ньютона 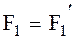 ;
; 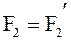 . Поэтому уравнение (4) принимает вид:
. Поэтому уравнение (4) принимает вид:
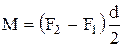 (7)
(7)
Подставив соотношения (7), (5) и (6) в формулу (3), получим:
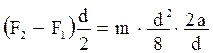
Отсюда следует:
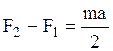 (8)
(8)
Уравнения (1), (2) и (8) — это система трех уравнений с неизвестными величинами: F1 , F2 , а .
Запишем эту систему в канонической форме. Все неизвестные величины переносим в левую часть уравнения, известные – в правую часть уравнения. Если в уравнении отсутствует какая либо неизвестная величина, то ее записываем с множителем «ноль».
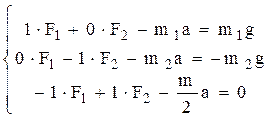
Определитель системы равен:
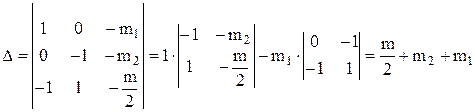 (9)
(9)
Далее по правилам математики находим определители неизвестных величин:
DF1 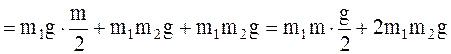
DF2 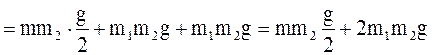
Da 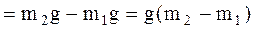
Определяем силы F1 и F2 и ускорение грузов а:
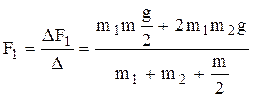 (10)
(10)
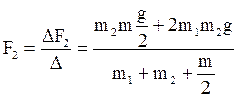 (11)
(11)
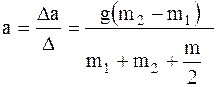 (12)
(12)
Проверка единиц измерений:
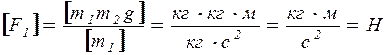
Здесь кг — килограмм, м – метр, с — секунда, Н – ньютон.
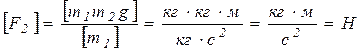
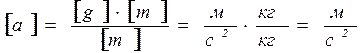
Зависимость скорости грузов Vот времени даётся уравнением:
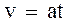 (13)
(13)
Путь S, пройденный телами при падении груза m2 :
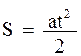 (14)
(14)
Если S = H , то груз m2 упадет на поверхность. Полагая в формуле (14) S = H, находим время падения груза tn :
 (15)
(15)
Угол поворота радиуса блока:
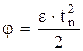
Количество оборотов блока, совершенное до падения груза на поверхность:
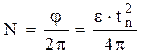 (16)
(16)
Кинетическая энергия 1-го груза:
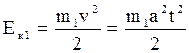 (17)
(17)
Кинетическая энергия 2-го груза:
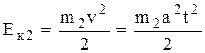 (18)
(18)
Зависимость угловой скорости блока от времени:
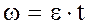 (19)
(19)
Кинетическая энергия блока:
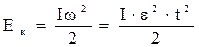 (20)
(20)
Потенциальная энергия первого груза:
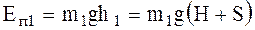 (21)
(21)
Потенциальная энергия второго груза:
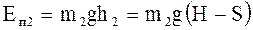 , (22)
, (22)
где ( 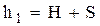 ) и (
) и ( 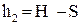 ) — высоты грузов m1 и m2 над поверхностью.
) — высоты грузов m1 и m2 над поверхностью.
Момент импульса блока:
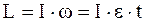 (23)
(23)
Вычисления
1. Определитель системы (формула (9)):
D = 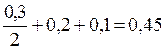 кг
кг
2. Силы реакции шнура (формулы (10),(11)):
F1 = 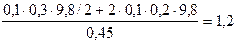 Н
Н
F2 = 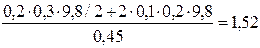 Н
Н
3. Ускорение грузов (формула (12)):
a = 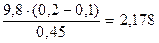 м/с2
м/с2
4. Угловое ускорение блока (формула (6)):
e = 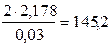 рад./с2
рад./с2
5. Момент инерции блока (формула (5)):
I = 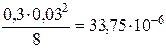 кг×м2
кг×м2
6. Время падения груза (формула (15)):
tп = 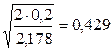 с
с
7. Количество оборотов (формула (16)):
N = 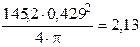
Для построения графиков проводим вычисления по формулам (13), (17) — (23) для различных моментов времени в интервале от 0 до tn . Шаг по времени 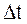 выбираем таким, чтобы на графиках было не менее пяти точек.
выбираем таким, чтобы на графиках было не менее пяти точек.
Результаты вычислений:
F1 = 1,2 H F2 = 1,52 H a = 2,178 м/с2

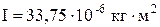
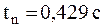
| t c | 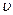 м/с
м/с
| Ω с-1 | Eк1 Дж | Ек2 Дж | Eк Дж | Еп1 Дж | Еп2 Дж | L
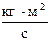
|
| 0,196 | 0,392 | |||||||
| 0,05 | 0,109 | 7,26 | 0,0006 | 0,001 | 0,0009 | 0,199 | 0,387 | 0,00025 |
| 0,1 | 0,218 | 14,52 | 0,002 | 0,005 | 0,004 | 0,207 | 0,371 | 0,00049 |
| 0,15 | 0,327 | 21,78 | 0,005 | 0,011 | 0,008 | 0,220 | 0,344 | 0,00074 |
| 0,2 | 0,436 | 29,04 | 0,01 | 0,019 | 0,014 | 0,239 | 0,307 | 0,00098 |
| 0,25 | 0,545 | 36,3 | 0,015 | 0,03 | 0,022 | 0,263 | 0,259 | 0,00123 |
| 0,3 | 0,653 | 43,56 | 0,021 | 0,043 | 0,032 | 0,292 | 0,2 | 0,00147 |
| 0,35 | 0,762 | 50,82 | 0,029 | 0,058 | 0,044 | 0,327 | 0,131 | 0,00172 |
| 0,4 | 0,871 | 58,08 | 0,038 | 0,076 | 0,057 | 0,367 | 0,05 | 0,00196 |
| 0,429 | 0,934 | 62,29 | 0,044 | 0,087 | 0,065 | 0,392 | 0,00210 |
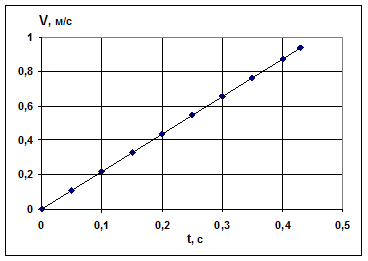
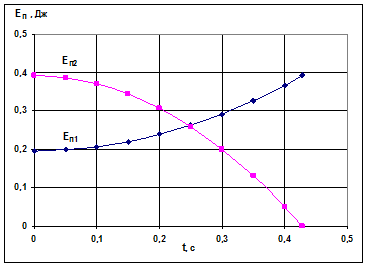
На основании табличных данных построить графики зависимости v, Ω, Eк1, Eк2, Eк, Еп1, Еп2, L от времени t.
Из приведенных в таблице данных следует, что полная механическая энергия системы в отсутствии трения не меняется.
Действительно, при t=0 полная энергия равна:
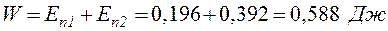 .
.
При падении груза (t=0,429 с) полная энергия равна: 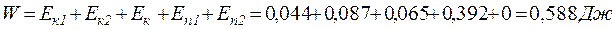
Ниже в качестве примера показаны 3 из требуемых 8 графиков
Постановка задачи.
Для измерения осевого момента инерции, в работе используется крестообразный маховик Обербека.
М
Рис. 3
1
2
3
4
5
аховик Обербека (рис. 3) представляет собой свободно вращающуюся относительно неподвижной горизонтальной оси крестовину, выполненную в виде четырёх взаимно перпендикулярных металлических стержней. Ось крестовины закреплена на вертикальной стойке, установленной на массивном основании. На стержни одеты цилиндрические муфты (2) известной массы, которые закрепляются на заданном расстоянииrот оси вращения с помощью стопорных винтов.Перемещая муфты вдоль стержней на то или иное расстояние r,
можно изменять осевой
момент инерции системы. Используя зависимость (5), считая что масса однородного цилиндра сосредоточена в его геометрическом центре, где размещён стопорный винт, выразим осевой момент инерции муфт по формуле
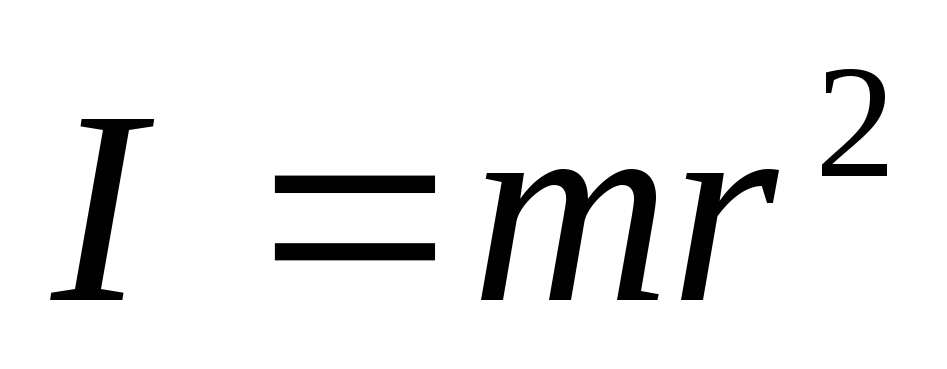 (17).
(17).
На оси маховика жёстко укреплены два соосных шкива различных диаметров d1иd2, на которые в один ряд наматывается нить (нить считаем нерастяжимой и невесомой). Один конец нити прикрепляется к шкиву, к другому концу нити, переброшенной через вспомогательный блок 1, подвешивается груз массойm(4).
Изменением массы
груза m, путём наложения
перегрузков с массойm1,
можно изменять силу натяжения нити Т,
под действием которой маховик совершает
равномерно-ускоренное вращательное
движение с угловым ускорением ,
которое согласно основному закону
динамики вращательного движения (6)
прямо пропорционально моменту силы
натяжения нити
,
которое согласно основному закону
динамики вращательного движения (6)
прямо пропорционально моменту силы
натяжения нити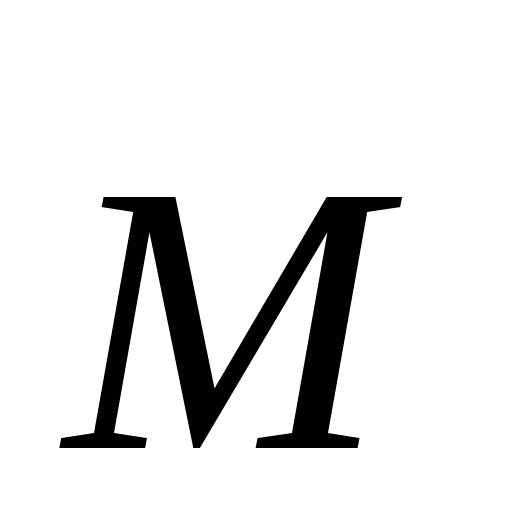 .
Поскольку сила натяжения направлена
вертикально, её плечо в соответствии с
(3) равно
.
Поскольку сила натяжения направлена
вертикально, её плечо в соответствии с
(3) равно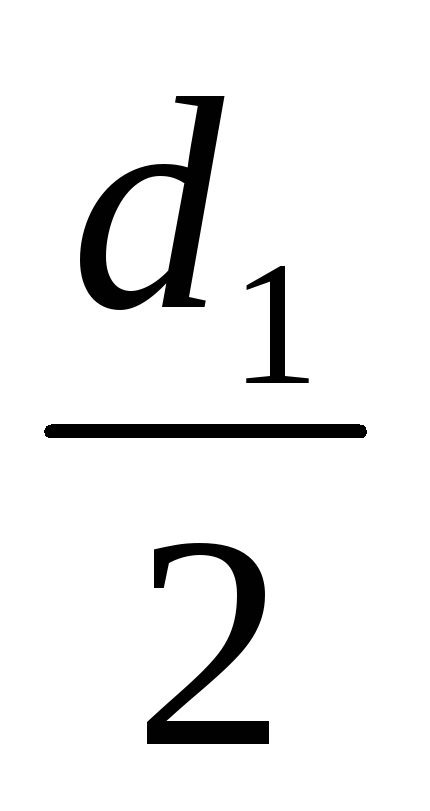 или
или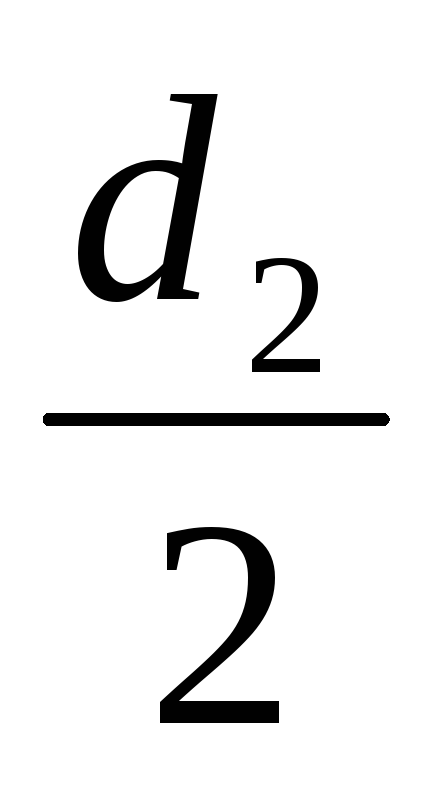 .
.
Одновременно под действием силы тяжести груз mсовершает равноускоренное поступательное движение вниз. При этом считаем, что момент сил трения относительно оси вращения маховика мал по сравнению с моментом силы натяжения нити.
На вертикальной стойке прибора укреплены два кронштейна: нижний (5) – неподвижный, верхний (3) – подвижный. Верхний кронштейн можно перемещать вдоль стойки и фиксировать в любом положении, задавая тем самым длину пути hвертикального перемещения грузаm.
Для измерения длины пути на стойке нанесена миллиметровая шкала.
Прибор снабжён счётчиком времени – миллисекундомером, не ведущим отсчёт времени при нажатых кнопках «сеть» или «сброс».
Измерения времени движения груза mосуществляется с использованием двух фотоэлектрических датчиков, вмонтированных в верхний и нижний кронштейны и подключенных к секундомеру. Расстояние между световыми лучами обоих датчиков равно длине пути вертикального перемещения грузаh. Датчики включаются в работу при нажатии клавиши «сеть».
Нажатие клавиши «пуск» включает секундомер и одновременно выключает электромагнит, удерживающий крестовину, после чего начинается вращение крестовины и движение груза mвниз.
При пересечении
грузом верхнего светового луча секундомер
начинает отсчёт времени. При пересечении
нижнего светового луча секундомер
автоматически выключается. Время
движения груза от одного светового луча
до другого высвечивается на индикаторе
секундомера с абсолютной ошибкой 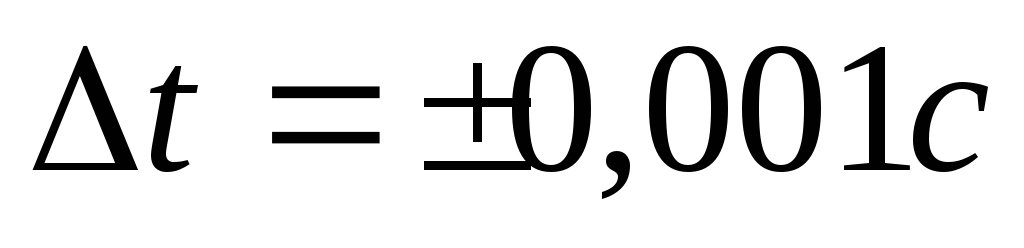 ,
что намного меньше точности измерения
времени человеком-оператором.
,
что намного меньше точности измерения
времени человеком-оператором.
Примечание: при неисправной работе удерживающего электромагнита начало опускания груза 4 можно задавать, удерживая его рукой. При этом одновременно с освобождением груза необходимо нажать кнопку «пуск» на секундомере.
Расстояние 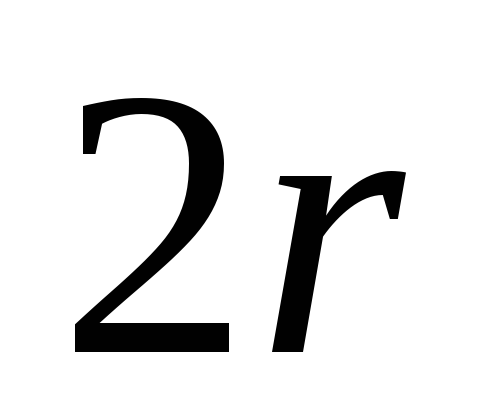 между центрами масс, противоположно
закреплённых грузов, измеряются мерной
линейкой. Диаметры шкивов измеряются
штангенциркулем. Массы грузов 4 заданы
с абсолютной погрешностью
между центрами масс, противоположно
закреплённых грузов, измеряются мерной
линейкой. Диаметры шкивов измеряются
штангенциркулем. Массы грузов 4 заданы
с абсолютной погрешностью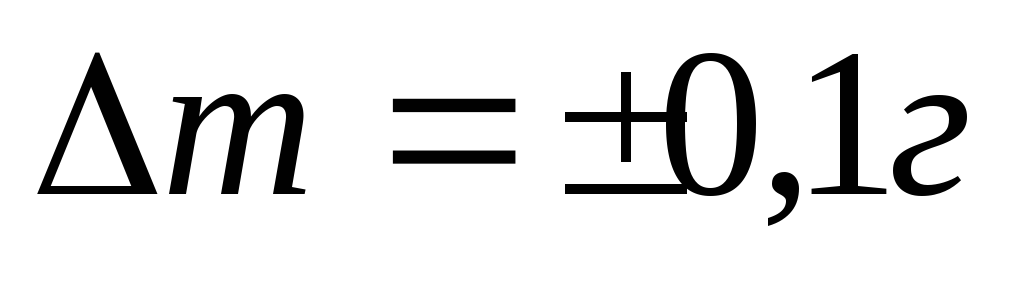 .
.
Перед выполнением опытов на маховике Обербека необходимо добиться симметричного распределения грузов на крестовине. Это делается путём перемещения грузов 2 на противоположных стержнях так, чтобы при ненатянутой нити грузы оставались в состоянии безразличного равновесия.
Для проведения опытов маховик приводят в равноускоренное вращательное движение, опуская груз m1с заданной высоты и измеряя при этом время его движенияtна путиh. Линейное ускорение движения груза можно вычислить по формуле
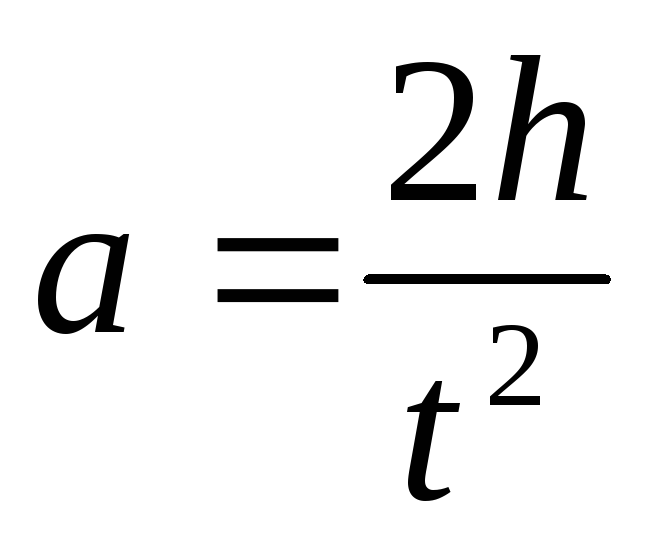 (18).
(18).
Так как при движении
груза нить сматывается со шкива без
проскальзывания, то линейное ускорение
груза  равно касательному ускорению точек,
лежащих на цилиндрической поверхности
шкива. Следовательно, угловое ускорение
маховика
равно касательному ускорению точек,
лежащих на цилиндрической поверхности
шкива. Следовательно, угловое ускорение
маховика
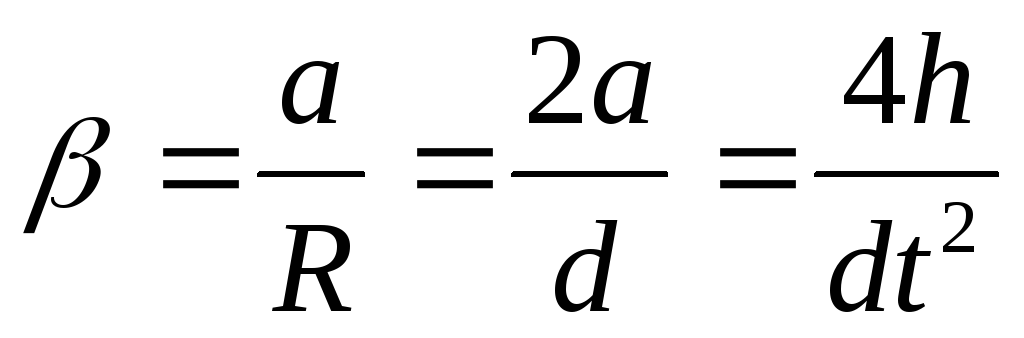 (19)
(19)
(где  — радиус шкива).
— радиус шкива).
С другой стороны
согласно основному закону динамики
вращательного движения (6) угловое
ускорение  пропорционально моменту силы натяжения
нити
пропорционально моменту силы натяжения
нити и обратно пропорционально моменту
инерцииIвсей системы
(блок, крестовина, грузы) —
и обратно пропорционально моменту
инерцииIвсей системы
(блок, крестовина, грузы) —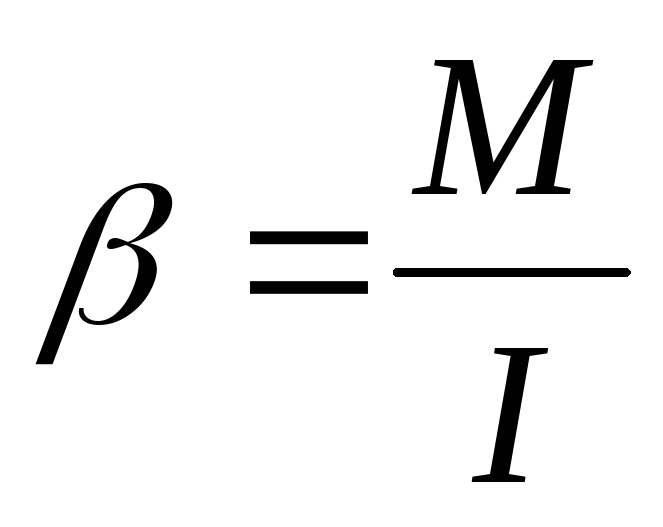 .
Момент силы
.
Момент силы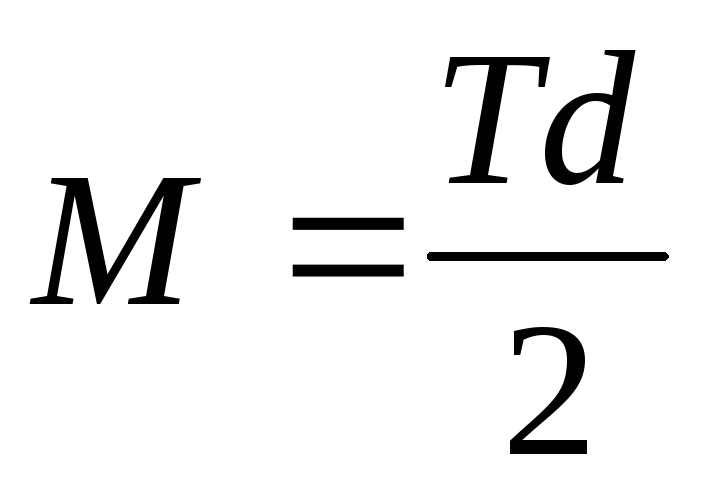
(где Т – сила натяжения нити, d/2 — плечо силы).
Согласно второму закону Ньютона действующая на нить сила
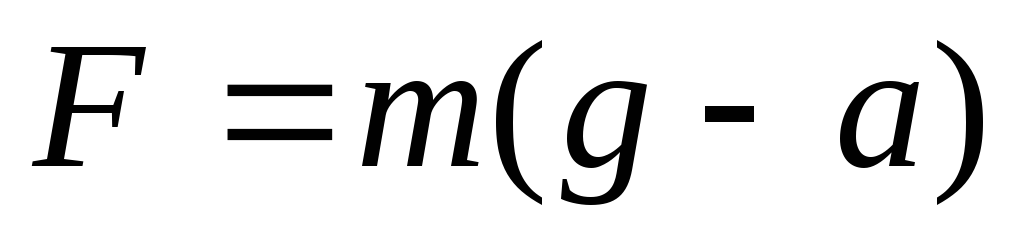 (20),
(20),
(где
g– ускорение свободного
падения, —
линейное ускорение поступательного
движения груза).
—
линейное ускорение поступательного
движения груза).
Поскольку нить не растяжима сила F, уравновешивается силойT. Следовательно, момент силы
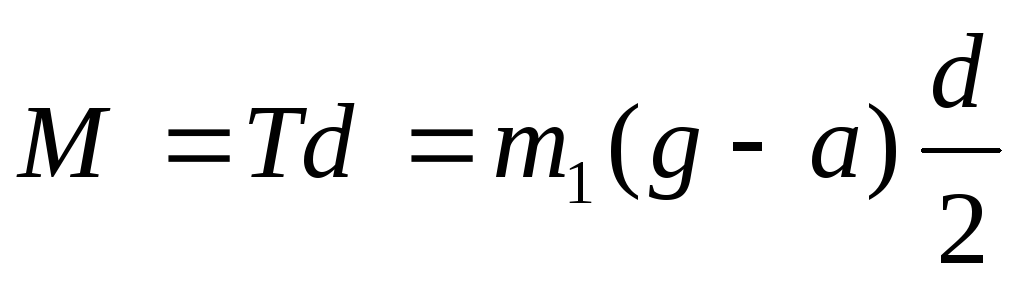 (21).
(21).
Выразив из уравнения
(6) 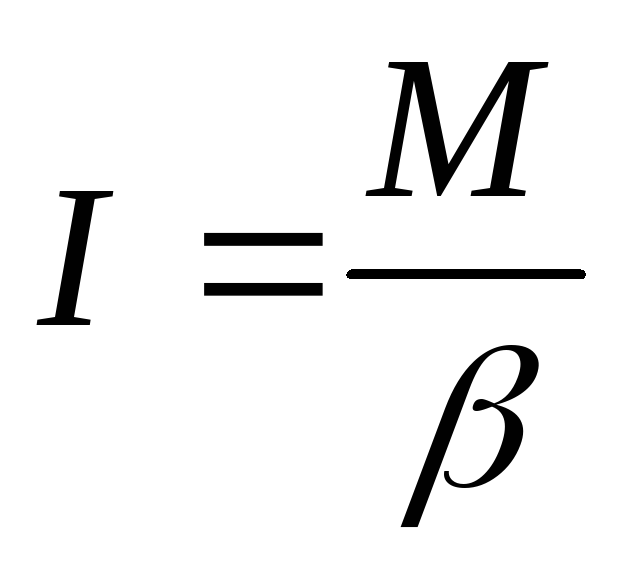 и подставив в эту формулу
и подставив в эту формулу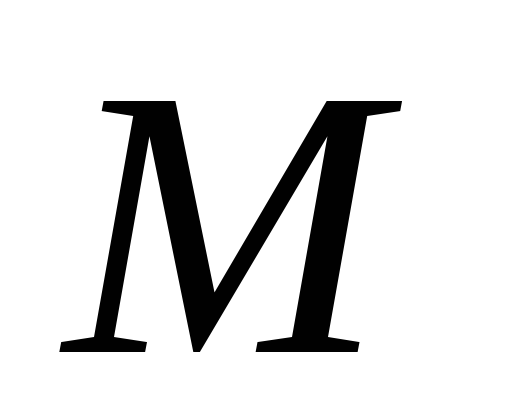 и
и из (18) и (20) получим:
из (18) и (20) получим:
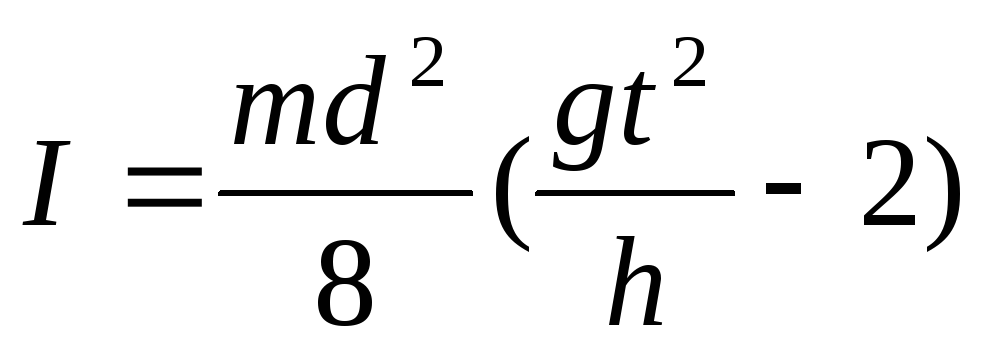 (22).
(22).
Как видно из (22), чтобы косвенно измерить момент инерции, надо прямыми измерениями найти массу груза,
создающего натяжение нити, диаметр блока, по которому движется точка приложения силы, высота с которой опускается груз, и время опускания.
Вычисленное по
формуле (22) значение момента инерции
маховика 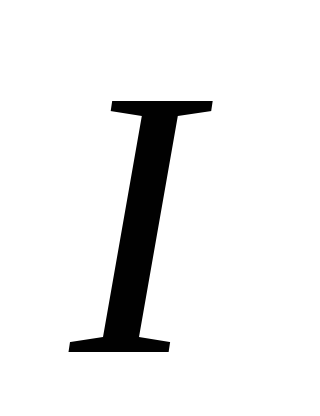 включает в себя момент инерции крестовины
с блоком
включает в себя момент инерции крестовины
с блоком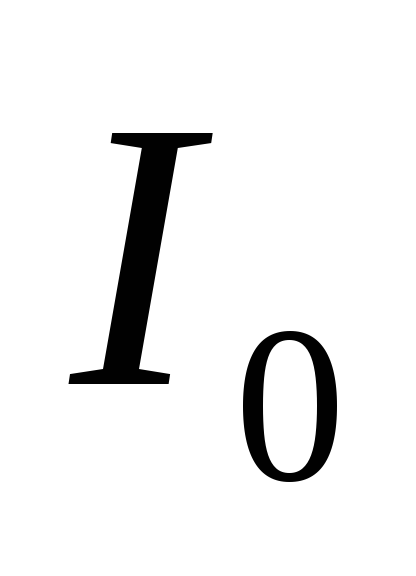 и момент инерции четырёх грузов
и момент инерции четырёх грузов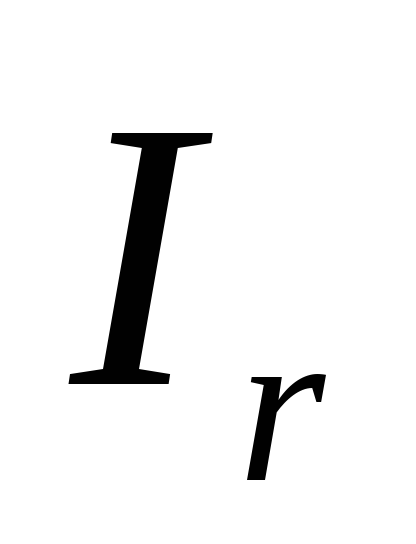 с массойm (2):
с массойm (2):
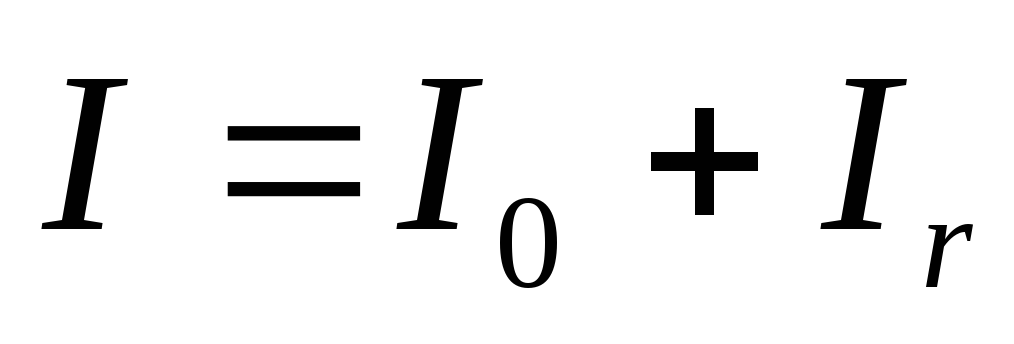 (23).
(23).
Искомый момент инерции грузов
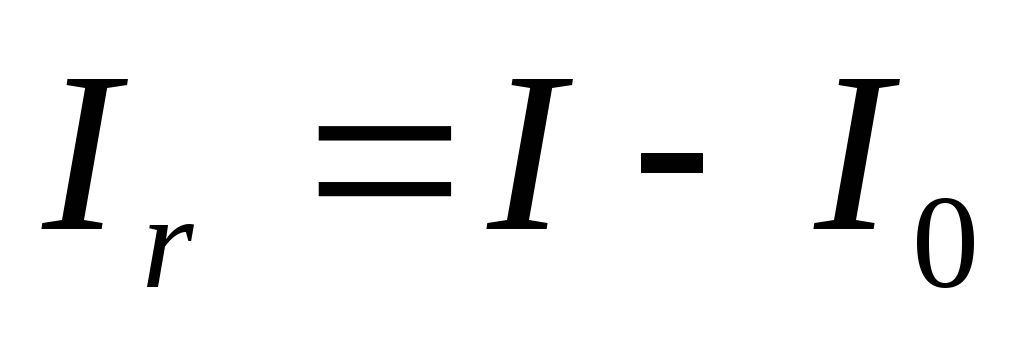 (24),
(24),
где 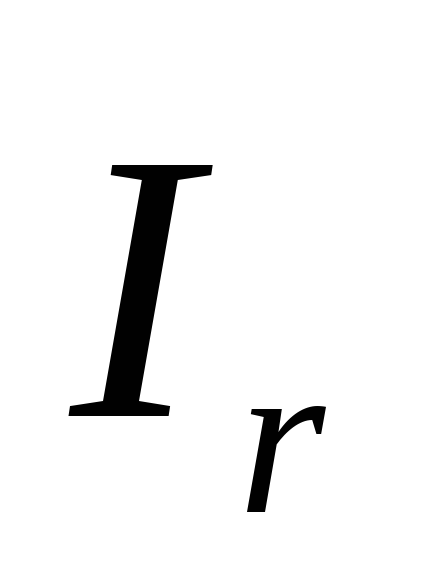 — осевой момент инерции вращающихся
грузов 2;
— осевой момент инерции вращающихся
грузов 2;
 — осевой момент
инерции маховика без грузов;
— осевой момент
инерции маховика без грузов;
 — осевой момент
инерции маховика с грузами.
— осевой момент
инерции маховика с грузами.
Осевой момент
инерции маховика без грузов  измеряется так же, как и момент инерции
измеряется так же, как и момент инерции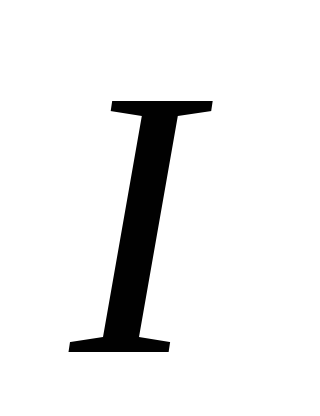 .
В формулу подставляются значения
.
В формулу подставляются значения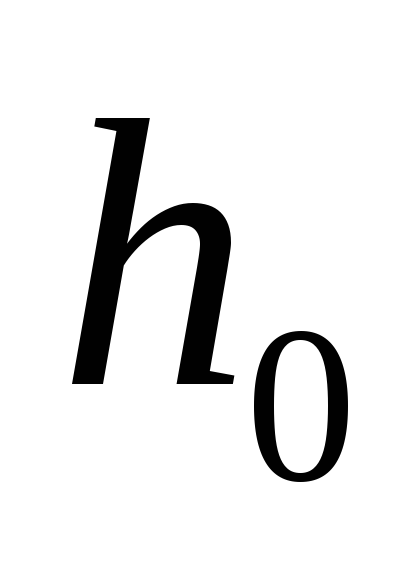 и
и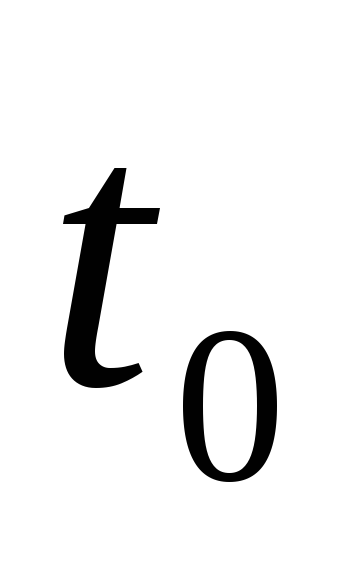 ,
измеренные при вращении крестовины со
снятыми с неё грузами.
,
измеренные при вращении крестовины со
снятыми с неё грузами.
Считая грузы материальными точками, можно рассчитать теоретическое значение осевого момента инерции по формуле (16):
 (25),
(25),
(где m– масса одного вращающегося груза 2,r– расстояние центра масс груза от оси вращения).
Сопоставление значений моментов инерции четырёх вращающихся грузов, рассчитанных по формулам (23) и (24) позволяет судить о качестве проделанной работы.
Проделав косвенные
измерения момента инерции груза 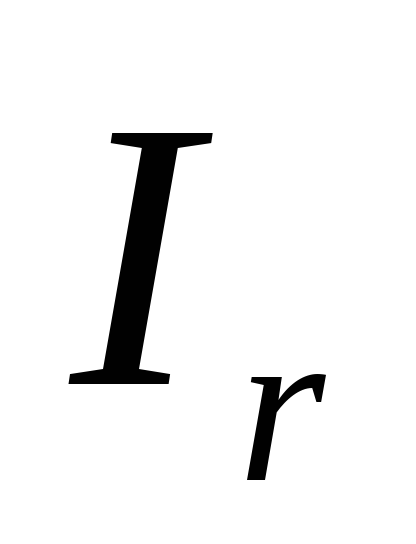 при разных значениях расстояния
при разных значениях расстояния их центров от оси вращения (поочерёдно
размещая грузы 2 на концах стержней, на
их середине и вблизи оси крестовины),
можно опытным путём установить характер
зависимости момента инерции от
распределения массы относительно оси
вращения. По определению момента инерции,
как меры инертности тела при вращательном
движении, эта зависимость является
квадратичной (5). Графиком такой зависимости
является парабола
их центров от оси вращения (поочерёдно
размещая грузы 2 на концах стержней, на
их середине и вблизи оси крестовины),
можно опытным путём установить характер
зависимости момента инерции от
распределения массы относительно оси
вращения. По определению момента инерции,
как меры инертности тела при вращательном
движении, эта зависимость является
квадратичной (5). Графиком такой зависимости
является парабола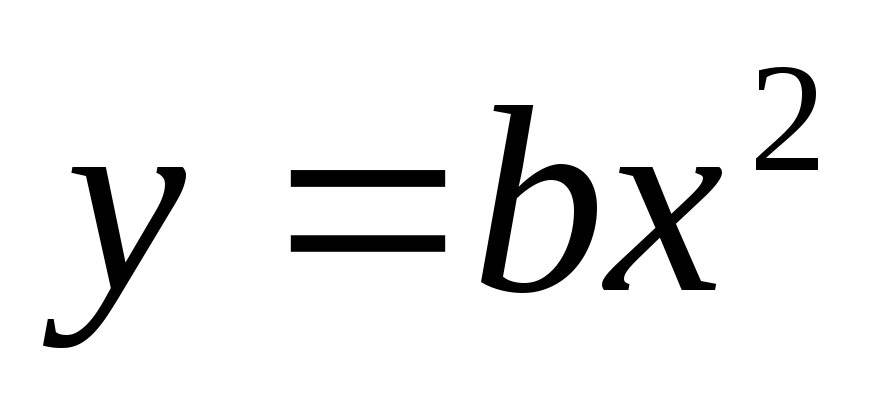 .
Откладывая на оси
.
Откладывая на оси значения моментов инерции, рассчитанных
по формулам (23) и (24), а по оси
значения моментов инерции, рассчитанных
по формулам (23) и (24), а по оси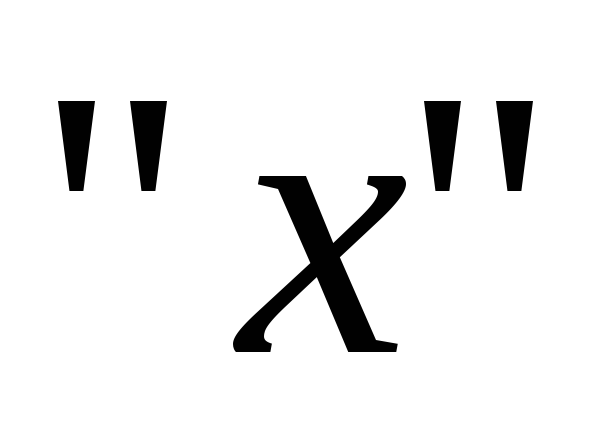 квадрат расстояния
квадрат расстояния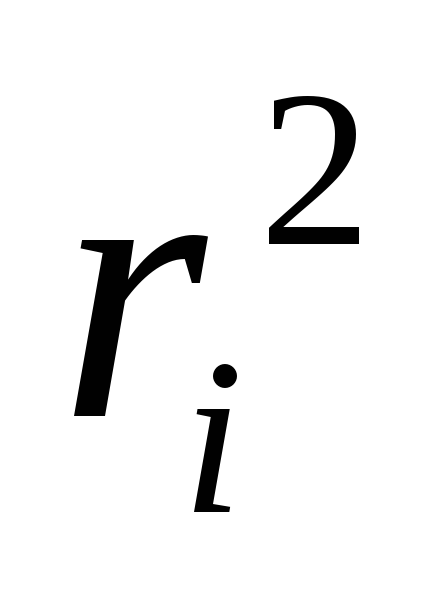 ,
можно построить экспериментальные и
теоретические параболы. При этом
принимать коэффициент
,
можно построить экспериментальные и
теоретические параболы. При этом
принимать коэффициент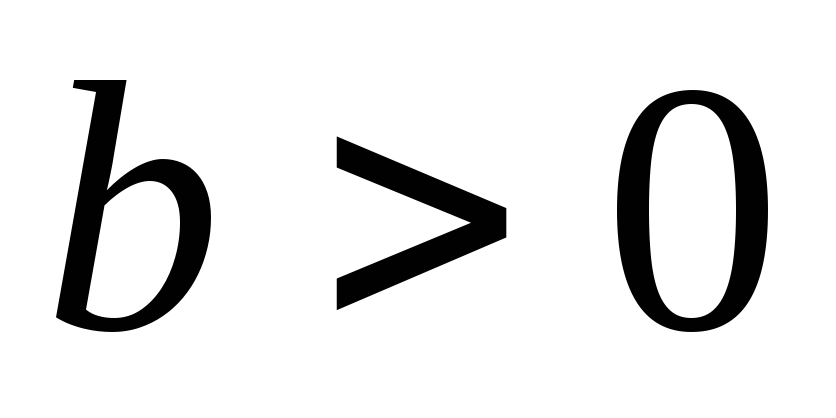 равным массе 4-х грузов (
равным массе 4-х грузов (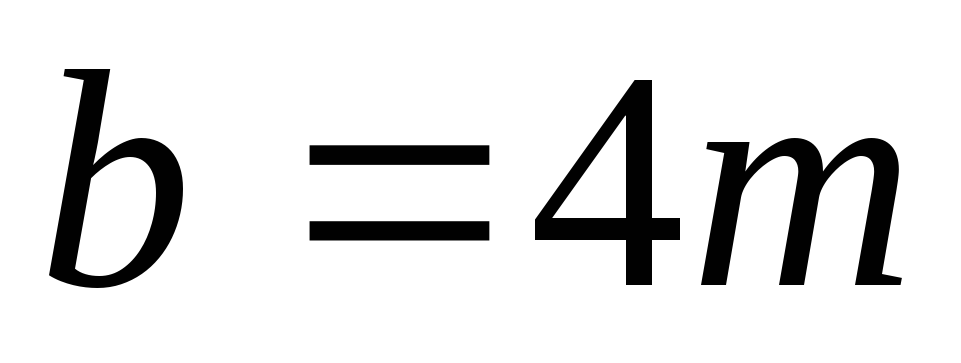 ).
Совмещение точек таких парабол служит
подтверждением качества выполнения
эксперимента и правомерности применения
модели материальных точек к однородным
цилиндрам равной длины.
).
Совмещение точек таких парабол служит
подтверждением качества выполнения
эксперимента и правомерности применения
модели материальных точек к однородным
цилиндрам равной длины.
Формула среднего ускорения с примерами и задачами
Это полное руководство, чтобы узнать, как найти ускорение в физике с помощью формулы ускорения.
Итак, если вы хотите извлечь пользу из этого руководства, вам понравятся полезные советы в этом новом руководстве.
Это руководство включает в себя:
- Определение ускорения
- Формула ускорения
- Примеры из реальной жизни
- Типы
- Подробнее
Давайте приступим непосредственно к делу.
Что такое ускорение?
В физике ускорение определяется как скорость изменения скорости тела во времени.Когда скорость тела изменяется, говорят, что оно ускоряется. Ускорения — это векторные величины. Метр в секунду в квадрате (м / с²) — это единица ускорения. Положительное ускорение и отрицательное ускорение — это два типа ускорения.
Что такое формула ускорения?
Ускорение можно найти по следующей формуле и из второго закона движения Ньютона.

Принимая a как ускорение, начальную скорость как Vi, конечную скорость как Vf, а t — временной интервал, единица измерения ускорения в системе СИ — метр в секунду в секунду мс -2
Ускорение относительно силы
С другой стороны, ньютоновская механика устанавливает для тела постоянной массы (m), рассматриваемого инерционным наблюдателем, соотношение пропорциональности по отношению к силе, приложенной к объекту (F), и полученному ускорению (a), что составляет:
F = m.до
Это соотношение действует в любой инерциальной системе отсчета и позволяет рассчитать ускорение по следующей формуле:
a = F / m
Эта формула подчиняется второму закону Ньютона.
Примеры ускорения
Некоторые примеры ускорения приведены в списке ниже:
1.- Когда вы нажимаете педаль акселератора в автомобиле, автомобиль движется все быстрее и быстрее. Это изменение скорости и есть ускорение.
2.- Если одна и та же сила используется для толкания грузовика и толкания автомобиля, автомобиль будет иметь большее ускорение, чем грузовик, потому что автомобиль имеет меньшую массу.
3.- Пустую тележку для покупок толкать легче, чем полную, потому что полная корзина для покупок имеет большую массу, чем пустая.
4.- Объект двигался на север со скоростью 10 метров в секунду. Объект ускоряется и теперь движется на север со скоростью 15 метров в секунду. Объект был ускорен.
5.- При движении скейтборда нашей ногой происходит изменение ускорения. Давай быстрее.
Что такое среднее ускорение в физике?
Среднее ускорение тела, указанное в приведенном выше уравнении, равно a за время t.Пусть время t разделено на множество более мелких интервалов времени. Если скорость изменения скорости в течение всех этих интервалов остается постоянной, то ускорение также остается постоянным. Говорят, что такое тело обладает равномерным ускорением.
Формула среднего ускорения

Равномерное ускорение в физике
«Тело имеет равномерное ускорение, если оно имеет равные изменения скорости в равные промежутки времени, хотя этот интервал может быть коротким.”
Типы ускорения
Есть два типа ускорения:
- Положительное ускорение
- Отрицательное ускорение
Что такое положительное ускорение?
Ускорение тела положительно, если его скорость увеличивается со временем. Направление этого ускорения такое же, как и тело движется без изменения своего направления.
Примеры положительного ускорения
- Когда поезд покидает станцию, его скорость увеличивается с увеличением времени, это пример положительного ускорения.
- Когда мы заводим автомобиль, его скорость увеличивается со временем, это положительное ускорение.
Что такое отрицательное ускорение?
Ускорение тела отрицательное, если скорость тела уменьшается. Направление отрицательного ускорения противоположно направлению, в котором движется тело. Отрицательное ускорение также называется замедлением или замедлением.
Примеры отрицательного ускорения
- Когда поезд достигает станции, его скорость уменьшается со временем, этот тип ускорения называется отрицательным ускорением.
аналогично:
Например, лифт, движущийся вверх (который мы принимаем за направление положительной скорости), может ускоряться вверх с положительным ускорением и двигаться быстрее или ускоряться вниз с отрицательным ускорением и двигаться медленнее.
Когда он движется вниз с отрицательной скоростью, он может ускоряться вниз с отрицательным ускорением и двигаться медленнее. Когда ускорение и скорость имеют положительные знаки, так что скорость (величина скорости) уменьшается, мы говорим о замедлении.
Как рассчитать ускорение свободного падения?
«Ускорение свободно падающих тел называется ускорением свободного падения». Бросьте объект с некоторой высоты и наблюдайте за его движением. Увеличивается ли его скорость, уменьшается или остается постоянной по мере приближения к земле? Галилей был первым ученым, заметившим, что все свободно падающие объекты имеют одинаковое ускорение независимо от их масс.
Примеры расчета ускорения
- Гоночный автомобиль увеличивает скорость с постоянной скоростью 18.5 м / с при 46,1 м / с за 2,47 секунды. Каким будет его среднее ускорение?
a = dv / dt = (v f — v i ) / (t f — t i ), где v f = 46,1 м / с, v i = 18,5 м / с, t f = 2,47 с, t i = 0 с.
Итак: a = (46,1 — 18,5) / 2,47 = 11,17 м / с 2
- Мотоциклист движется со скоростью 22,4 м / с и понимает, что он ошибся с маршрутом. Включите тормоза, и мотоцикл остановится через 2 секунды.55 с. Каким будет его замедление?
a = dv / dt = (v f — v i ) / (t f — t i ), где v f = 0 м / с, v i = 22,4 м / с, t f = 2,55 с, t i = 0 с.
Итак: a = (0 — 22,4) / 2,55 = -8,78 м / с 2
- Сила величиной 10 ньютонов равномерно действует на массу 2 кг. Каким будет ускорение толкаемого объекта?
a = F / m, где F = 10 Н, m = 2 кг.
Таким образом:
a = 10/2 = 5 м / с 2
- Кто-то тянет в сторону предмет мебели массой 400 кг с чистой силой 150 ньютонов. Другой человек толкает его в том же направлении с силой 200 ньютонов, но есть ветер, дующий в противоположном направлении с силой 10 ньютонов. В каком будет ускорение мебели?
Мы знаем, что a = F / m, где чистая сила будет суммой сил в том же смысле за вычетом той, которая им противодействует: F = 150 Н (человек 1) + 200 Н (человек 2) — 10 Н (ветер), что дает 340 Н.Мы также знаем, что m = 400 кг.
Тогда: a = 340 Н / 400 кг = 0,85 м / с 2
- Самолет с дистанционным управлением массой 10 кг летит с ускорением 2 м / с 2 в северном направлении. , В этот момент дует восточный ветер силой в 100 Н. Какое будет новое ускорение самолета, сохраняющего свой курс?
Поскольку сила ветра перпендикулярна направлению движения самолета, она не оказывает никакого влияния на его движение.Он продолжит ускоряться на север со скоростью 2 м / с 2 .
- Два мальчика, один слабый и один сильный, играют в перетягивание каната, каждый на одном конце веревки. Первая тяга влево делает это с силой 5 Н, а вторая тянет в противоположном направлении с силой 7 Н. Принимая во внимание, что 1 ньютон (Н) равен 1 килограмм-метру / секунда в квадрате. (кг-м / с2), какое ускорение будет достигнуто телом самого слабого ребенка, когда другой тащит его в противоположном направлении?
Из F = ma мы знаем, что a = F / m, но мы должны найти чистую силу, которая будет равна 2 Н (7 Н для сильного ребенка и 5 Н для слабого ребенка).
Затем мы должны найти массу, которая для целей расчета должна быть получена из силы, которой противодействует слабый ребенок, а именно: 1 Н = 1 кг · м / с 2 , то есть это количество силы мобилизовать килограмм массы со скоростью один метр в секунду в квадрате.
Следовательно, 5N = 5кг.м / с 2 . Следовательно, m = 5 кг.
И, наконец, мы знаем, что a = 2N (F) / 5 кг (м) = 0,4 м / с 2
- Пожарная машина увеличивает скорость с 0 до 21 м / с на восток, в 3 раза.5 секунд. Какое у него ускорение?
Мы знаем, что: V i = 0 м / с, V f = 21 м / с, t = 3,5 секунды. Поэтому применяем формулу:
a = dv / dt = (v f — v i ) / (t f — t i ), то есть a = 21 м / с / 3,5 с = 6 м / с 2
- Автомобиль снижает скорость с 21 м / с на восток до 7 м / с на восток за 3,5,0 секунды. Какое у него ускорение?
Зная, что V i = 21 м / с, V f = 7 м / с, t = 3.5 секунд, и что a = dv / dt = (v f — v i ) / (t f — t i ), это просто вычислить:
a = 7 м / с — 21 м / с / 3,5 с = -4 м / с 2 , то есть отрицательное ускорение (замедление).
Связанные темы:
Внешние источники
- http://formulas.tutorvista.com/physics/acceleration-formula
- http://www.physicsclassroom.com/class/1DKin/Lesson-1/Acceleration
| Определение | Формула
Примеры ускорения
Центростремительное ускорение и тангенциальное ускорение
Ускорение — это обычно вектор, поэтому его всегда можно разложить на составляющие. Обычно у нас есть две части, перпендикулярные друг другу: центростремительная и тангенциальная . Центростремительное ускорение изменяет направление скорости и, следовательно, форму следа, но не влияет на значение скорости.С другой стороны, тангенциальное ускорение всегда перпендикулярно траектории движения. Он изменяет только значение скорости , но не ее направление.
В круговом движении (крайний левый рисунок ниже), когда объект движется по окружности круга, присутствует только центростремительный компонент. Объект будет поддерживать постоянную скорость; подумайте о Земле, которая имеет центростремительное ускорение из-за силы тяжести Солнца (на самом деле ее скорость немного меняется в течение года — см. калькулятор орбитальной скорости и калькулятор орбитального периода для получения дополнительной информации).
Когда присутствуют оба компонента, траектория объекта выглядит как на правом рисунке. Что будет, если есть только тангенциальное ускорение? Затем происходит линейное движение. Это похоже на то, когда вы нажимаете педаль газа в автомобиле на прямом участке автострады. А если вы водитель, наш счетчик бензина может вас заинтересовать; оценивает стоимость проезда на автомобиле. Вы указываете экономию топлива, расстояние и цену на бензин, и вы быстро получаете стоимость поездки. Есть даже возможность разделить его с несколькими людьми, ведь вместе путешествовать весело и полезно! Группа разговорчивых друзей в вашей машине будет: e.g., не дать вам заснуть.
Угловое ускорение
Угловое ускорение играет важную роль в описании вращательного движения. Однако не путайте это с ранее упомянутыми центростремительными или тангенциальными ускорениями. Эта физическая величина соответствует скорости изменения угловой скорости. Другими словами, он сообщает вам, насколько быстро ускоряется вращение объекта — объект вращается все быстрее и быстрее (или все медленнее и медленнее, если угловое ускорение меньше нуля).
Знаете ли вы, что мы можем найти аналогию между этим и законом динамики Ньютона во вращательном движении? Согласно его второму закону, если вы можете переключить ускорение с угловым ускорением, силу с крутящим моментом и массу с моментом инерции, вы получите уравнение углового ускорения. Вы могли заметить, что некоторые физические законы, подобные этому, универсальны, что делает их действительно важными для физики.
Ускорение свободного падения
Ранее мы несколько раз упоминали ускорение свободного падения.Он возникает из-за гравитационной силы, которая существует между каждыми двумя объектами, имеющими массу (обратите внимание, что уравнение гравитации не зависит от объема объекта — здесь важна только масса). Сначала это может показаться странным, но согласно третьему закону движения Ньютона вы действуете на Землю с той же силой, что и Земля на вас . Однако масса Земли намного больше, чем масса человека (в ~ 10 ² раз больше), поэтому наше воздействие на Землю практически равно нулю. Это аналогично всем бактериям (в ~ 10¹⁸ раз легче человека), живущим на вашей руке; их даже не заметить! С другой стороны, мы чувствуем влияние нашей планеты, и это ускорение силы тяжести.
Стандартная сила тяжести по определению составляет 31,17405 фут / с² (9,80665 м / с²), поэтому, если человек весит 220 фунтов (около 100 кг), на него действует сила тяжести около 7000 фунтов на квадратный дюйм (1000 Н). Давайте введем это значение в окно № 3 нашего калькулятора вместе с массой Земли (1,317 × 10²⁵ фунтов или 5,972 × 10²⁴ кг в экспоненциальном представлении). Что такое расчетное ускорение? настолько мало , что наш калькулятор считает, что это ноль . Мы ничего не значим по сравнению с планетой!
Ускоритель частиц
После разговора об огромных объектах в космосе, перейдем к микроскопическому миру частиц.Хотя мы не можем видеть их глазами, мы использовали частицы высоких энергий, такие как электроны и протоны, и регулярно используем их в ускорителях частиц; распространены в физике, химии и медицине. Мы используем их для уничтожения раковых клеток, сохраняя при этом окружающие здоровые ткани, или исследуем структуру материалов в атомном масштабе. В последнее время рак — одна из болезней достатка, которая, вероятно, является следствием роста благосостояния в обществе. Даже неправильное питание может увеличить риск рака! С помощью этого ежедневного калькулятора протеина вы можете проверить, сколько протеина вам нужно в день, и, если вы также хотите улучшить свою физическую форму, наш макро-калькулятор здесь, чтобы помочь вам.
Вы, наверное, знаете о Большом адронном коллайдере (ЦЕРН), самом мощном ускорителе элементарных частиц в мире. Это позволяет нам сделать еще один шаг, чтобы понять, как устроена Вселенная, и разработать технологии, которые могут найти множество важных приложений в будущем. Однако, чтобы достичь таких высоких энергий, мы должны разогнать частицы до скоростей, близких к скорости света. Вкратце, мы можем сделать это с помощью магнитных или электрических полей. Чтобы увидеть, насколько быстро частицы ускоряются по сравнению со стандартной силой тяжести, посмотрите наше ускорение в калькуляторе электрического поля, где мы объяснили, как рассчитать ускорение заряженных частиц.
Мир микроскопических частиц управляется статистической физикой, которая уделяет особое внимание концепции вероятности. У нас есть много калькуляторов, связанных с этой темой. Взгляните на калькулятор вероятности, чтобы узнать, как найти вероятность, или попробуйте калькулятор перестановок, чтобы определить количество способов, которыми вы можете упорядочить определенное количество элементов. Физики используют перестановку для предсказания теоретических свойств материала, которые затем можно наблюдать в повседневной жизни. Например, вы можете узнать, какова средняя скорость частиц газа.
,Формулы для постоянного ускорения
(1) x = x_i + v_i * t + (1/2) при 2
(2) v = v_i + при
, где * означает время,
x_i — начальная позиция, x — позиция в момент времени t ,
v_i — начальная скорость, v — скорость в момент времени t ,
и — (постоянное) ускорение.
Я набираю ^ 2 для обозначения «в квадрате».
Из них видно, что:
(3) x — x_i = (1/2) (v_i + v) t и
(4) v 2 = v_i 2 + 2a (x — x_i) .
-Многие учебники называют формулы (1) — (4) «кинематическими уравнениями».
-Эти уравнения можно записать разными способами. Например, во многих книгах v пишется как v_f для «конечной скорости». Некоторые книги пишут x_o и v_o вместо x_i и v_i .2) (5,00 с) = 30,0 м / с
Задача 2) С моста падает камень. Через 1,5 секунды он падает на землю. Как далеко он упал ?.
Решение Это можно сделать с помощью уравнения (1). Мы знаем, что т — это 1,50 с. Если камень «уронили», то можно сказать, что в_и было около 0.
Нам нужно значение ускорения камня. Если мы можем игнорировать трение воздуха, мы можем сказать, что ускорение камня постоянно и равно g , ускорение свободного падения.2 = 11,025 м или около 11,0 м.
Проблема 3) Автомобиль, трогаясь с места, разгоняется с постоянным ускорением и движется со скоростью 35 м / с через 10 секунд. Как далеко он ушел за эти 10 секунд?
Так как автомобиль «стартовал в состоянии покоя», можно сказать, что v_i = 0. Конечная скорость v = 35 м / с. Время t = 10 с.
Первое решение Вероятно, самый быстрый способ решить эту проблему — использовать уравнение (3).Смещение d составляет:
d = x — x_i = (1/2) (v_i + v) t = (1/2) (0 + 35 м / с) (10 с) = 175 м
Второе решение Мы можем использовать уравнение (2), чтобы найти ускорение a , а затем использовать уравнение (1), чтобы найти смещение.
Уравнение (2): v = v_i + at
Таким образом, 35 м / с = 0 + a (10 с)
Решение этого дает a = (35 м / с) / (10 с) = 3.2
или x = +175 м.
Итак, d = x — x_i = 175 м, что, конечно же, является тем же самым ответом, который мы получили ранее. Это пример того, как часто существует несколько способов решения проблемы, связанной с постоянным ускорением.
Задача 4) «Спортивный автомобиль, движущийся со скоростью 30 м / с, должен остановиться на расстоянии 100 м. Если его ускорение при торможении постоянное, какова будет величина этого ускорения?»
Решение Начальная скорость v_i составляет 30 м / с.2
Откуда появился минус? Вначале, когда мы сказали v_i = + 30 м / с, мы приняли положительное направление как направление, в котором двигался спортивный автомобиль. С
.Формула тангенциального ускорения — определение, формула линейного ускорения и решенные примеры
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы бумаги CBSE для класса 7
- Образцы бумаги CBSE для класса 8
- Образцы бумаги CBSE для класса 9
- Образцы бумаги CBSE для класса 10
- Образцы бумаги CBSE для класса 11
- Образцы бумаги CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9 Решения NCERT
- для математики класса 10 Глава 10 Решения
- NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава 13
- NCERT Sol Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10 Глава 1
- Решения NCERT для науки класса 10 Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки 10 класса, глава 8
- Решения NCERT для науки класса 10 Глава 9
- Решения NCERT для науки класса 10 Глава 10
- Решения NCERT для науки класса 10 Глава 11
- Решения NCERT для науки класса 10 Глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки 10 класса Глава 15
- Решения NCERT для науки 10 класса Глава 16
- Class 11 Commerce Syllabus
- ancy Account
- Программа бизнес-исследований 11 класса
- Учебная программа по экономике 11 класса
- Учебная программа по коммерции 12 класса
- Учебная программа по бухгалтерии 12 класса
- Учебная программа по бизнесу 12 класса
- Учебная программа по экономике
- 9000 9000
- Образцы документов по коммерции класса 11
- Образцы документов по коммерции класса 12
- TS Grewal Solutions
- TS Grewal Solutions Class 12 Accountancy
- TS Grewal Solutions Class 11 Accountancy
- Отчет о движении денежных средств
- Что такое Entry eurship
- Защита прав потребителей
- Что такое основной актив
- Что такое баланс
- Формат баланса
- Что такое акции
- Разница между продажами и маркетингом
- ICSE
- Документы
- ICSE
- Вопросы ICSE
- ML Aggarwal Solutions
- ML Aggarwal Solutions Class 10 Maths
- ML Aggarwal Solutions Class 9 Maths
- ML Aggarwal Solutions Class 8 Maths
- ML Aggarwal Solutions Class 7 Maths
- ML 6 Maths
- ML 6 Maths
- Selina Solutions
- Selina Solutions для класса 8
- Selina Solutions для Class 10
- Selina Solutions для Class 9
- Frank Solutions
- Frank Solutions для математики класса 10
- Frank Solutions для математики класса 9
- Класс ICSE 9000 2
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12
- Exam
- IAS
- Civil
- Сервисный экзамен
- Программа UPSC
- Бесплатная подготовка к IAS
- Текущие события
- Список статей IAS
- Пробный тест IAS 2019
- Пробный тест IAS 2019 1
- Пробный тест IAS 2019 2
- Экзамен KPSC KAS
- Экзамен UPPSC PCS
- Экзамен MPSC
- Экзамен RPSC RAS
- TNPSC Group 1
- APPSC Group 1
- Экзамен BPSC
- WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
- Ключ ответов UPSC 2019
- IA S Coaching Бангалор
- IAS Coaching Дели
- IAS Coaching Ченнаи
- IAS Coaching Хайдарабад
- IAS Coaching Mumbai
- BYJU’SEE
- 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
- Вопросник JEE
- Биномиальная теорема
- Статьи JEE
- Квадратичное уравнение
- Программа BYJU NEET
- NEET 2020
- NEET Приемлемость 9000 Критерии 9000 NEET4 9000 NEET 9000 Пример 9000 9000 NEET
- Поддержка
- Разрешение жалоб
- Служба поддержки
- Центр поддержки
- GSEB
- GSEB Syllabus
- GSEB4
- GSEB3 Образец статьи GSEB3
004 - MSBSHSE
- MSBSHSE Syllabus
- MSBSHSE Учебники
- Образцы статей MSBSHSE
- Вопросники MSBSHSE
- AP Board
- APSCERT
- Syll
- AP 9000SC4
- Syll
- AP
- Syll 9000SC4
- Syll
- Syll
- MP Board
- MP Board Syllabus
- MP Board Образцы документов
- Учебники MP Board
- Assam Board
- Assam Board Syllabus
- Assam Board Учебники 9000 9000 Board4 BSEB
- Bihar Board Syllabus
- Bihar Board Учебники
- Bihar Board Question Papers
- Bihar Board Model Papers
- BSE Odisha
- Odisha Board Syllabus
- Odisha Board Syllabus
- Odisha Board Syllabus
- Программа PSEB
- Учебники PSEB
- Вопросы PSEB
- RBSE
- Rajasthan Board Syllabus
- RBSE Учебники
- RBSE Question Papers
- HPBOSE
- HPBOSE
- HPBOSE
- JKBOSE
- Программа обучения JKBOSE
- Образцы документов JKBOSE
- Шаблон экзамена JKBOSE
- TN Board
- TN Board Syllabus
- TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 9000 Paper Papers 9000 TN Board 9000 4 JAC
- Программа JAC
- Учебники JAC
- Вопросники JAC
- Telangana Board
- Telangana Board Syllabus
- Telangana Board Учебники
- Papers Telangana Board Учебники
- Учебный план KSEEB
- Типовой вопросник KSEEB
- KBPE
- Учебный план KBPE
- Учебники KBPE
- Документы по KBPE
- 9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
- Совет по Западной Бенгалии
- Учебный план Совета по Западной Бенгалии
- Учебники для Совета по Западной Бенгалии
- Вопросы для Совета по Западной Бенгалии
- UBSE
- TBSE
- Гоа Совет
- 000
- NBSE0003 Board
- Manipur Board
- Haryana Board
- Государственные экзамены
- Банковские экзамены
- Экзамены SBI
- Экзамены IBPS
- Экзамены RBI
- IBPS
03
- Экзамены SSC 9SC2
- SSC GD
- SSC CPO 900 04
- SSC CHSL
- SSC CGL
- Банковские экзамены
- Экзамены RRB
- RRB JE
- RRB NTPC
- RRB ALP
- O Экзамены на страхование
- LIC4
- LIC4 9000 ADF UPSC CAPF
- Список статей государственных экзаменов
- Класс 1
- Класс 2
- Класс 3
- Вопросы по физике
- Вопросы по химии
- Вопросы по химии
- Вопросы
- Вопросы по науке
- Вопросы для общего доступа
- Домашнее обучение
- BYJU’S CAT Program
- CAT3 9000 Предварительный курс CAT3 Экзамен 9000 9000 CAT3

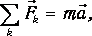
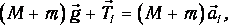
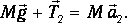
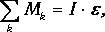
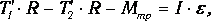

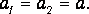
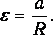
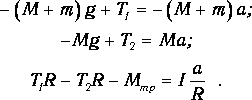
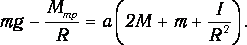
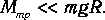
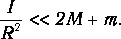
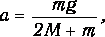
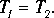
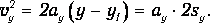
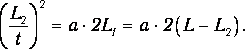
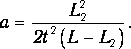
Leave A Comment