упростите выражение abc если известно что a c
Вы искали упростите выражение abc если известно что a c? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и упростите выражение abc если известно что b c, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «упростите выражение abc если известно что a c».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
Где можно решить любую задачу по математике, а так же упростите выражение abc если известно что a c Онлайн?
Решить задачу упростите выражение abc если известно что a c вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Дидактический материал по Геометрии 9 класс.
Вариант 1
1. Начертите неколлинеарные вектора а, b, с . Постройте векторы а + с, с – b.
2. В равнобедренном треугольнике АВС точка В1 – середина основания АС.
а) Упростите выражение ВВ1 – АВ – В1С.
б) Найдите / ВВ1 – АВ – В1С / , если АВ=10см, ВВ1= 8см.
3. Найдите вектор РО – х = РМ
Самостоятельная работа 9кл урок 8
Вариант 2
1. Начертите неколлинеарные вектора p, k, с .
2. В равнобедренном треугольнике АВС , с основанием АВ проведена медиана СС1
а) Упростите выражение ВС1 – АС + АВ,
б) Найдите / ВС1— АС + АВ /, если АС=5см, АВ=6см.
3. Найдите вектор х – МА =РМ
Самостоятельная работа 9кл урок 10 стр 54
Вариант 1.
1. Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,
2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ= 2:1, О- точка пересечения диагоналей. Выразите векторы ОС и СК через векторы а=АВ, и b= АД.
Самостоятельная работа 9кл урок 10 стр 54
Вариант 2.
1. Начертите вектор а , абсолютная величина которого равна 3см. Постройте векторы 2а , -а, 1/3а.
2. В параллелограмме АВСД на стороне ВС взята точка Р так, что ВР:РС=3:1 , О- точка пересечения диагоналей . Выразите векторы АО и РА через векторы х=АВ и у=АД.
Самостоятельная работа 9кл урок 8
Вариант 1
1. Начертите неколлинеарные вектора а, b, с . Постройте векторы а + с, с – b.
2. В равнобедренном треугольнике АВС точка В1 – середина основания АС.
а) Упростите выражение ВВ1 – АВ – В1С.
б) Найдите / ВВ1 – АВ – В1С / , если АВ=10см, ВВ1= 8см.
3. Найдите вектор РО – х = РМ
Самостоятельная работа 9кл урок 8
Вариант 2
1. Начертите неколлинеарные вектора p, k, с . Постройте векторы k+ с, k – p.
2. В равнобедренном треугольнике АВС , с основанием АВ проведена медиана СС1
а) Упростите выражение ВС1 – АС + АВ,
б) Найдите / ВС1— АС + АВ /, если АС=5см, АВ=6см.
3. Найдите вектор х – МА =РМ
Самостоятельная работа 9кл урок 10 стр 54
Вариант 1.
 Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,
Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ= 2:1, О- точка пересечения диагоналей. Выразите векторы ОС и СК через векторы а=АВ, и b= АД.
Самостоятельная работа 9кл урок 10 стр 54
Вариант 2.
1. Начертите вектор а , абсолютная величина которого равна 3см. Постройте векторы 2а , -а, 1/3а.
2. В параллелограмме АВСД на стороне ВС взята точка Р так, что ВР:РС=3:1 , О- точка пересечения диагоналей . Выразите векторы АО и РА через векторы х=АВ и у=АД.
Урок 21 Геометрия 9кл
Самостоятельная работа
1 вариант
1.Окружность задана уравнением (х+5)2+(у-4)2=49.
а) Укажите центр окружности
б) Какие из точек А(2;4), В(1;3), С(-5;-3) лежат на данной окружности.
в) Найдите точку с абциссой -12 , лежащей на данной окружности.
2. Напишите уравнение окружности с центром С и радиусом r: если
а) С(-3;2), r= √ 3 . б) С(0;-6) , r= 4√5.
Найдите sinA, если 1 вариант cosA= -1/3 2 вариант cosA=-1/4
2. Найдите cosA, если 1 вариант sinA= 2/5 2вариант sinA=-2/3
Проверьте, лежат ли на единичной окружности точки:
1 вариант В(7;3),С(0,5;0,5) 2 вариант С(2;3), В(-0,5;0,5)
4. Угол между лучом ОМ, пересекающим единичную полуокружность, и положительной полуосью Ох равен А. Найдите координаты точки М, если
1 вариант ОМ=8, <А=30° 2 вариант ОМ=10, <А=60°
Самостоятельная работа 9кл
По теме : Решение треугольников
1. Дано: △АВС , <А=450 , < С=150 , ВС= 4√6 .
Найти: АВ , АС , < В
2. Дано : △MNK , MN=6см , MK=10см, <M=1200.
Найти : NK , <N , <K.
3. Дано : △ ОРТ , ОР=24 , РТ=30, ОТ=36.
Найти: <О , <Р, <Т.
Самостоятельная работа 9 кл урок 33
Тема Решение треугольников
1 вариант
1. Площадь параллелограмма равна 30V3 см2, а один из углов равен 600. Найдите его периметр, если длина одной из сторон равна 6см.
2. В треугольнике MNK MN=NK , MK=V2 , 0, MA- ,биссектриса. Найдите МА.
3. Стороны треугольника равны 8, 10 и 12см. Найдите угол, лежащий против меньшей стороны.
Самостоятельная работа 9 кл урок 33
Тема Решение треугольников
2 вариант
1. Площадь параллелограмма равна 40V2 см2 , а один из углов равен 450 . Найдите его периметр , если длина одной из сторон равна 10см.
2. В треугольнике СДЕ СМ- биссектриса , <ДСЕ=600 , МЕ= 3V2. Найдите СМ, если < СЕД =45
3. Стороны треугольника равны 6, 9 и 10 см. Найдите угол , лежащий против большей стороны.
Самостоятельная работа 9кл. по геометрии
По теме Правильный многоугольник
1. Найдите углы правильного шестнадцатиугольника .
2. Каждый угол правильного многоугольника равен 1620 . Найдите число его сторон.
3. Чему равен внешний угол правильного восемнадцатиугольника .
4. Внешний угол правильного многоугольника равен 150.Найдите число его сторон.
5. Является ли равнобедренный треугольник с углом при вершине в 600 правильным.
6. Является ли ромб с равными диагоналями правильным четырехугольником .
Самостоятельная работа по геометрии 9кл
По теме Формулы для вычисления площади правильного многоугольника его стороны и радиуса вписанной окружности.
Вариант 1
1. Найдите углы правильного восемнадцатиугольника .
2. Угол правильного n-угольника равен 1080. Вычислите количество его сторон .
3. Сколько сторон имеет правильный вписанный многоугольник , если дуга описанной окружности , которую стягивает его сторона , равна 450.
Урок 44 9класс стр 228
Самостоятельная работа
1 вариант
1. Найдите длину окружности с радиусом 5см. Чему равна длина ее дуги с градусной мерой 360.
2. Длина окружности, описанной около квадрата , равна 12П см. Найдите длину окружности, вписанной в этот квадрат.
Урок 44 9класс стр 228
Самостоятельная работа
2 вариант
1. Найдите длину окружности с радиусом 9см. Чему равна длина ее дуги с градусной мерой 200.
2. Длина окружности , вписанной в правильный треугольник, равна 2√3 П см. Найдите длину окружности, описанной около этого треугольника.
Найдите длину окружности, описанной около этого треугольника.
Самостоятельная работа по геометрии 9кл.
По теме Площадь круга и кругового сектора урок 45
1. Найдите длины дуг , на которые разбивают окружность два радиуса . Угол между радиусами равен 1200, радиус окружности равен 6дм.
2. Найдите длину окружности , в которую вписан квадрат со стороной 5см.
Самостоятельная работа по геометрии 9кл
По теме Длина окружности . Площадь круга.
1 вариант
1. Длина окружности равна 8 П. Вычислите площадь круга , ограниченного данной окружностью.
2. Градусная мера дуги окружности с радиусом 6см. равна 300. Вычислите площадь кругового сектора , соответствующего этой дуге .
Самостоятельная работа по геометрии 9кл
По теме Длина окружности . Площадь круга.
2вариант
1. Длина окружности равна 10П . Вычислите площадь круга , ограниченного данной окружностью.
Длина окружности равна 10П . Вычислите площадь круга , ограниченного данной окружностью.
2. Градусная мера дуги окружности с радиусом 4см равна 450. Вычислите площадь кругового сектора , соответствующего этой дуге.
Самостоятельная работа 9кл урок 53
1 вариант
1.Дан четырехугольник АВСД. Постройте фигуру , симметричную данной:
а) относительно вершины Д б) относительно диагонали АС
2. Докажите , что при движении квадрат отображается в квадрат.
Самостоятельная работа 9кл урок 53
2 вариант
1. Дан четырехугольник АВСД. Постройте фигуру , симметричную данной:
а) относительно вершины А б) относительно диагонали ВД
2.Докажите , что при движении прямоугольник отображается на прямоугольник.
Самостоятельная работа
По геометрии 9кл ур.55
1. В прямоугольном треугольнике АВС ,СК-биссектриса , точки М и Н лежат на СК так , что М лежит между С и Н . Постройте образ треугольника АВС при параллельном переносе на вектор МН .
Постройте образ треугольника АВС при параллельном переносе на вектор МН .
2. Постройте образ треугольника АВС при параллельном переносе на вектор а.
3. Укажите координаты точек А1,В1, если известно , что они являются образами точек А(2;5) , В(-1;-3) при параллельном переносе на вектор а {-3;2}.
Самостоятельная работа
По геометрии 9кл ур.58
1.В результате параллельного переноса точка А(-1;3) переходит в точку А1 (2;4) , а точка В(1;-3) в точку В1.
2. При осевой симметрии относительно координатной оси Оу точка А переходит в точку А1 , а точка В в точку В1 . Найдите координаты точек А1 и В , если А(-2;5) , В1(-3;-8).
3. При центральной симметрии относительно начала координат четырехугольник АВСД
переходит в четырехугольник А1В1С1Д1. Найдите координаты точек А,В,С,Д, если
А1(-6;-1) ,В1(-5;-8), С1(-1;-6) ,Д1(0;0) .
4. В результате поворота вокруг начала координат точка А(4;0) перешла в точку А1(0;4). Найдите точку , в которую перейдет точка А в результате поворота на 300 , 450 ,1200 вокруг того же центра и в том же направления.
5. Какое наименьшее число вершин может иметь многоугольник , у которого есть две оси симметрии , пересекающиеся под углом 300.
Самостоятельная работа
Длина окружности и площадь круга
Вариант 1
1. Вычислите радиус окружности, длина которой равна сумме длины окружности с радиусом 9 см и длины дуги окружности с радиусом 20 см и центральным углом 18°.
Ответ: 10 см.
2. В круг вписан прямоугольный треугольник с катетами, равными 8 см и 15 см. Найдите разность площадей этих фигур.
Ответ:
3. В сектор с центральным углом 90° вписан круг так, что он касается радиусов и дуги.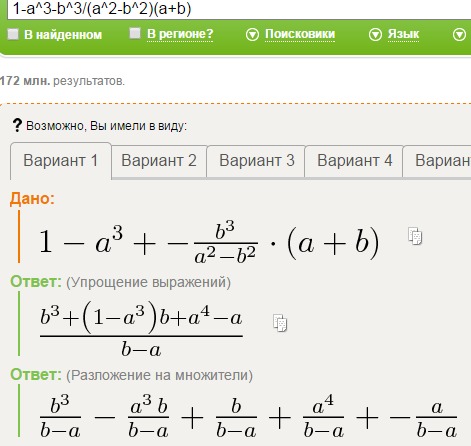 Найдите отношение площади сектора к площади круга.
Найдите отношение площади сектора к площади круга.
Ответ:
Вариант 2
1. Вычислите радиус окружности, длина которой равна разности длины окружности с радиусом 16 см и длины дуги окружности с радиусом 40 см и центральным углом 9°.
Ответ: 15 см.
2. В круг вписан прямоугольный треугольник с катетами, равными 5 см и 12 см. Найдите разность площадей этих фигур.
Ответ:
3. В сектор с центральным углом 120° вписан круг так, что он касается радиусов и дуги. Найдите отношение площади сектора к площади круга.
Ответ:
Решение треугольников
Вариант 1
А1. Найдите площадь равнобедренного △, если его боковая сторона равна 1 м, а угол при вершине равен 45о.
А2. В △ АВС АС = 0,59 дм, А = 40о, С = 35о. Вычислите ВС.
Вычислите ВС.
А3. Две стороны △ равны 1,3 и 42,5, < между ними 100о. Вычислите третью сторону △.
Самостоятельная работа 3.2
Решение треугольников
Вариант 2
А1. Найдите площадь равностороннего △ со стороной, равной 1 м.
А2. В △ АВС АС = 15,2 см, А = 25о, С = 80о. Вычислите ВС.
А3. Две стороны △ равны 27,4 и 16,3, < между ними 70о. Вычислите третью сторону △.
Самостоятельная работа Понятие вектора
Вариант 1
1. В выпуклом четырехугольнике ABCD точки K, L, M, N — середины сторон АВ, ВС, CD, DA соответственно. Установите связь между векторами
Ответ:
2. В прямоугольнике ABCD со сторонами АВ = 12 и AD = 10 точка К принадлежит АВ и АК : КВ = 1 : 2, точка L принадлежит CD и CL : LD = 1 : 3. Найдите величину
Ответ: 5√5.
3. В равностороннем треугольнике АВС со стороной а отрезок AD — медиана. Точка Е — середина отрезка BD. Найдите величину
Ответ:
Вариант 2
1. В выпуклом четырехугольнике ABCD точки K, L, M, N — середины сторон АВ, ВС, CD, DA соответственно. Установите связь между векторами
Ответ:
2. В прямоугольнике ABCD со сторонами АВ = 20 и AD = 12 точка К принадлежит АВ и АК : КВ = 2 : 3, точка L принадлежит CD и CL : LD = 1 : 4. Найдите величину
Ответ: 4√13.
3. В равностороннем треугольнике АВС со стороной а отрезок AD — медиана. Точка Е принадлежит BD и ВЕ : ED = 1 : 2. Найдите величину
Ответ:
Самостоятельная работа по теме векторы 9 класс
Вариант 1
На рисунке от точки А отложите вектор:
а) равный вектору а;
б) сонаправленный вектору b;
в) противоположно направленный вектору с.
с
А . а
b
АВСD – ромб. Равны ли векторы:
а) АВ и СD;
б) ВС и DА;
в) АВ и АD.
Самостоятельная работа
Вариант 2
На рисунке от точки В отложите вектор:
а) равный вектору b;
б) сонаправленный вектору с;
в) противоположно направленный вектору а.
B .
a
b
c
АВСD – квадрат. Равны ли векторы:
а) ВА и DС;
б) ВС и АD;
в) DА и DС.
Самостоятельная работа по теме «Векторы»
Вариант 1
1)Постройте векторы , такие, что векторы неколлинеарны. Постройте: а) б) в)
2)Точки M и N – середины сторон AB и AC △ ABC. Выразите через векторы а) , б) , в) г) , д) , где S – середина BC .
Самостоятельная работа по теме «Векторы»
Вариант 2
1)Постройте векторы , такие, что векторы неколлинеарны. Постройте: а) б) в) .
Постройте: а) б) в) .
2)Точка B1 – середина стороны AC △ ABC. Выразите через векторы а) , б) , в) г) , д) , где K – середина BB1 .
Сложение и вычитание векторов.
Вариант 1.
Постройте четыре попарно неколлинеарных вектора . Постройте а) по правилу треугольника б) по правилу параллелограмма
в) г) двумя способами д) е)
Сложение и вычитание векторов.
Вариант 2.
Постройте четыре попарно неколлинеарных вектора . Постройте а) по правилу треугольника б) по правилу параллелограмма
в) г) двумя способами д) е)
Координаты вектора.
Вариант 1
1.Даны векторы . а) Найдите координаты вектора . б) Запишите разложение вектора по единичным векторам . в) Найдите длину вектора . г) Найдите координаты вектора противоположного вектору .
2. Среди векторов найдите пары коллинеарных. 3. В параллелограмме ABCD . Точки M и N лежат на сторонах BC и СD соответственно так, что BM=MC, CN : ND=3 : 1. Найдите координаты вектора .
3. В параллелограмме ABCD . Точки M и N лежат на сторонах BC и СD соответственно так, что BM=MC, CN : ND=3 : 1. Найдите координаты вектора .
Координаты вектора. Вариант 2
1.Даны векторы . а) Найдите координаты вектора . б) Запишите разложение вектора по единичным векторам . в) Найдите длину вектора . г) Найдите координаты вектора противоположного вектору .
2. Среди векторов найдите пары коллинеарных. 3. В параллелограмме ABCD . Точки K и P лежат на сторонах AB и AD соответственно так, что AP=PD, AK : KB=2 : 1. Найдите координаты вектора .
Самостоятельная работа
Скалярное произведение векторов
Вариант 1
А1. Даны точки А(2; 4), В(5; 8), С(-7; -1), D(5; 8). Найдите скалярное произведение векторов .
А2. Даны векторы . Найдите скалярное произведение векторов.
А3. Вычислите скалярное произведение векторов, если , а угол между ними равен 60о.
Самостоятельная работа
Скалярное произведение векторов
Вариант 2
А1. Даны точки А(2; 4), В(-1; 6), С(-4; -2), D(3; 2). Найдите скалярное произведение векторов и .
А2. Даны векторы . Найдите скалярное произведение векторов.
А3. Вычислите скалярное произведение векторов, если , а угол между ними равен 30о.
Самостоятельная работа Простейшие задачи в координатах
Вариант 1
1. Вершины треугольника АВС имеют координаты А (−4; 2), В (2; −8), С (10; 16). Отрезок AD — медиана треугольника АВС, а АЕ — медиана треугольника ACD. Найдите
Ответ:
2. На осях координат найдите точки, равноудаленные от концов отрезка АВ, если А (−3; 5) и В (6; 4).
Ответ: (1; 0) и (0; −9).
3. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты А (0; 1), В (1; −4), С (5; 2).
Ответ: S = 13.
Вариант 2
1. Вершины треугольника АВС имеют координаты А (−4; 2), В (2; −8), С (10; 16). Отрезок AD — медиана треугольника АВС, а АЕ — медиана треугольника ABD. Найдите
Ответ:
2. На осях координат найдите точки, равноудаленные от концов отрезка АВ, если А (4; −3) и В (8; 1).
Ответ: (5; 0) и (0; 5).
3. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты А (−4; 1), В (−2; 4), С (1; 2).
Ответ: S = 6,5.
Метод координат.
Вариант 1
1. Вершины треугольника ABC имеют координаты A(-5; 13), B(3; 5), C(-3; -1). Найдите: а) медиану, проведенную к стороне AC б) среднюю линию, параллельную стороне BC .
2. Четырехугольник ABCD задан координатами его вершин: A(1; 1), B(3; 5), C(9; -1), D(7; -5). а) Докажите, что ABCD -параллелограмм. б) Найдите координаты середины отрезка CO, где С – точка пересечения диагоналей.
а) Докажите, что ABCD -параллелограмм. б) Найдите координаты середины отрезка CO, где С – точка пересечения диагоналей.
3) △MNK задан координатами своих вершин: M(2;N(0;0), K(3;. Найдите углы и площадь △.
Метод координат.
Вариант 2
1. Вершины треугольника ABC имеют координаты A(13; -5), B(5; 3), C(-1; -3). Найдите: а) медиану, проведенную к стороне AC б) среднюю линию, параллельную стороне BC
2. Четырехугольник ABCD задан координатами его вершин: A(-6; 1), B(2; 5), C(4; -1), D(-4; -5). а) Докажите, что ABCD -параллелограмм. б) Найдите координаты середины отрезка CO, где С – точка пересечения диагоналей.
3) Треугольник MNK задан координатами своих вершин: M(4;N(7;3), K(2;. Найдите углы и площадь треугольника.
Самостоятельная работа Уравнение окружности
Вариант1
1. Напишите уравнение окружности, которая проходит через точки А (−7; 8) и В (−3; −4). При этом хорда АВ является диаметром окружности.
При этом хорда АВ является диаметром окружности.
Ответ: (х + 5)2 + (у − 2)2 = 40.
2. Даны окружность, заданная уравнением х2 + у2 − 4х − 5 = 0, и точка А (5; 4). Напишите уравнение окружности, имеющей центр в данной точке и касающейся данной окружности внешним образом.
Ответ: (х − 5)2 + (у − 4)2 = 4.
3. В квадрат площадью S вписана окружность. Докажите, что сумма квадратов расстояний от любой точки окружности до вершин квадрата есть величина постоянная, и найдите эту величину.
Ответ: 3S.
Вариант 2
1. Напишите уравнение окружности, которая проходит через точки А (−5; 6) и В (−1; 4). При этом хорда АВ является диаметром окружности.
Ответ: (х + 3)2 + (у − 5)2 = 5.
2. Даны окружность, заданная уравнением х2 + у2 − 2у − 8 = 0, и точка А (4; 4). Напишите уравнение окружности, имеющей центр в данной точке и касающейся данной окружности внешним образом.
Напишите уравнение окружности, имеющей центр в данной точке и касающейся данной окружности внешним образом.
Ответ: (х − 4)2 + (у − 4)2 = 4.
3. Около квадрата площадью S описана окружность. Докажите, что сумма квадратов расстояний от любой точки окружности до вершин квадрата есть величина постоянная, и найдите эту величину.
Ответ: 4S.
Самостоятельная работа Уравнение прямой
Вариант1
1. Координаты вершин треугольника А (2; −6), В (4; 2) и С (0; −4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
Ответ: х + у − 1 = 0.
2. Найдите площадь треугольника, ограниченного прямыми, заданными уравнениями у − х = 0, у + х = 0 и у − 2х + 4 = 0.
Ответ: S = 16/3.
3. Прямая 2у + х − 4 = 0 пересекает окружность х2 + у2 = 5. Найдите длину хорды, которая отсекается этой окружностью на прямой.
Найдите длину хорды, которая отсекается этой окружностью на прямой.
Ответ: 6√5/5.
Вариант2
1. Координаты вершин треугольника А (4; −8), В (−2; 6) и С (2; 4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
Ответ: 6х + у − 5 = 0.
2. Найдите площадь треугольника, ограниченного прямыми, заданными уравнениями у + х = 0, у − х = 0 и 2у − х + 6 = 0.
Ответ: S = 12.
3. Прямая у − 3х + 1 = 0 пересекает окружность х2 + у2 = 5. Найдите длину хорды, которая отсекается этой окружностью на прямой.
Ответ: 7√10/5.
Уравнение прямой. Уравнение окружности.
Вариант 1
1. а) Составьте уравнение прямой, проходящей через точки А(4;-1) и В(2;3). б) Лежат ли на этой прямой точки М(1;5) и N(-1;5). в) Найдите точки пересечения этой прямой с осями координат. г) Найдите точку пересечения этой прямой и прямой . д) Докажите, что данная прямая параллельна прямой .
в) Найдите точки пересечения этой прямой с осями координат. г) Найдите точку пересечения этой прямой и прямой . д) Докажите, что данная прямая параллельна прямой .
2. Окружность задана уравнением . а) Найдите координаты центра окружности и ее радиус. б) Докажите, что отрезок АВ, где А(-1;-1), В(5;17), является хордой окружности. в) Выясните взаимное расположение окружности и прямой . г) Найдите расстояние от центра окружности до этой прямой.
Уравнение прямой. Уравнение окружности.
Вариант 2
1. а) Составьте уравнение прямой, проходящей через точки А(-1;3) и В(3;-5). б) Лежат ли на этой прямой точки М(4;9) и N(4;-7). в) Найдите точки пересечения этой прямой с осями координат. г) Найдите точку пересечения этой прямой и прямой . д) Докажите, что данная прямая параллельна прямой .
2. Окружность задана уравнением . а) Найдите координаты центра окружности и ее радиус. б) Докажите, что отрезок АВ, где А(3;-0), В(6;-1), является хордой окружности. в) Выясните взаимное расположение окружности и прямой . г) Найдите расстояние от центра окружности до этой прямой.
в) Выясните взаимное расположение окружности и прямой . г) Найдите расстояние от центра окружности до этой прямой.
Самостоятельная работа
Уравнение окружности. Уравнение прямой
Вариант 1
А1. Начертите окружность, заданную уравнением .
А2. Запишите уравнение окружности с центром в точке С(3;-5), касающейся оси ординат.
А3. Прямая задана уравнением .
а) Начертите эту прямую.
б) Запишите координаты пересечения прямой с осями координат.
в) Найдите площадь треугольника, образованного осями координат и этой прямой.
________________
В1. Окружность задана уравнением . Напишите уравнения касательных к окружности, которые параллельны оси ординат.
_______________
Самостоятельная работа
Уравнение окружности. Уравнение прямой
Вариант 2
А1. Начертите окружность, заданную уравнением .
Начертите окружность, заданную уравнением .
А2. Запишите уравнение окружности с центром в точке С(-2;4), касающейся оси ординат.
А3. Прямая задана уравнением .
а) Начертите эту прямую.
б) Запишите координаты пересечения прямой с осями координат.
в) Найдите площадь треугольника, образованного осями координат и этой прямой.
________________
В1. Окружность задана уравнением . Напишите уравнения касательных к окружности, которые параллельны оси абсцисс.
Самостоятельная работа
Синус, косинус, тангенс угла
Вариант 1
А1. Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найдите косинус меньшего острого угла этого треугольника.
А2. Найдите .
А3. Найдите .
А4. Постройте угол
Самостоятельная работа
Синус, косинус, тангенс угла
Вариант 2
А1. Стороны прямоугольного треугольника равны 5 см, 12 см и 13 см. Найдите тангенс большего острого угла этого треугольника.
Стороны прямоугольного треугольника равны 5 см, 12 см и 13 см. Найдите тангенс большего острого угла этого треугольника.
А2. Найдите .
А3. Найдите .
А4. Постройте угол
Самостоятельная работа синус, косинус и тангенс угла
Вариант 1
1. Известно, что tg α = − 5/12 и 90° < α < 180°. Найдите значение cos α.
Ответ: − 12/13.
2. Найдите значение выражения
Ответ: 4.
3. Упростите выражение
Ответ: 2.
Вариант 2
1. Известно, что tg α = − 15/8 и 90° < α < 180°. Найдите значение cos α.
Ответ: − 8/17.
2. Найдите значение выражения
Ответ: 6.
3. Упростите выражениеОтвет: −2.
Вписанная окружность — самостоятельная работа
1 вариант
1. Четырёхугольник АВСД описан около окружности. Найдите стороны ВС и АД, если АВ=7см, СД=11см, ВС в 2 раза меньше АД.
Четырёхугольник АВСД описан около окружности. Найдите стороны ВС и АД, если АВ=7см, СД=11см, ВС в 2 раза меньше АД.
2. В равносторонний △ со стороной 8см вписана окружность. Найдите радиус окружности.
Вписанная окружность — самостоятельная работа
2 вариант
1. Четырёхугольник АВСД описан около окружности. Найдите стороны АВ и СД, если ВС=6см, АД=9см, АВ в 2 раза больше СД.
2. В равносторонний △ вписана окружность радиусом 4см. Найдите сторону ∆.
Самостоятельная работа. Вписанная и описанная окружность
Вариант 1
1. Вокруг правильного шестиугольника описана окружность. В этот же шестиугольник вписана окружность. Найдите отношение радиусов этих окружностей.
Ответ: 2√3/3.
2. Вокруг одной и той же окружности описаны правильные треугольник и четырехугольник. Найдите отношение площадей этих фигур.
Найдите отношение площадей этих фигур.
Ответ: 3√3/4.
3. Сторона описанного правильного четырехугольника на 3 больше стороны правильного треугольника, вписанного в ту же окружность. Найдите сторону треугольника.
Ответ: 9 + 6√3.
Вариант 2
1. Вокруг правильного треугольника описана окружность. В этот же треугольник вписана окружность. Найдите отношение радиусов этих окружностей.
Ответ: 2.
2. Вокруг одной и той же окружности описаны правильные четырехугольник и шестиугольник. Найдите отношение площадей этих фигур.
Ответ: 2√3/3.
3. Сторона описанного правильного треугольника на 5 больше стороны правильного четырехугольника, вписанного в ту же окружность. Найдите сторону треугольника.
Ответ: 6 + √6.
Самостоятельная работа. Движение
Движение
Вариант1
1. Треугольник А1В1С1 симметричен треугольнику АВС с вершинами А (−1; 3), В (2; −4), С (4; 1) относительно точки D (7; −1). Найдите координаты вершин А1, В1, С1.
Ответ: А1 (15; −5), В1 (12; 2), С1 (10; −3).
2. Окружность задана уравнением (х + 3)2 + (у − 2)2 = 16. Она повернута на угол 90° против часовой стрелки относительно точки А (−2; 1). Напишите уравнение полученной окружности.
Ответ: (х + 3)2 + у2 = 16.
3. Найдите координаты точки, симметричной точке А (1; 7) относительно прямой, заданной уравнением у = х + 2.
Ответ: (5; 3).
Вариант2
1. Треугольник А1В1С1 симметричен треугольнику АВС с вершинами А (−4; 1), В (1; 3), С (3; −5) относительно точки D (5; −1). Найдите координаты вершин А1, В1, С1.
Найдите координаты вершин А1, В1, С1.
Ответ: А1 (14; −3), В1 (9; −5), С1 (7; 3).
2. Окружность задана уравнением (х + 2)2 + (у − 3)2 = 16. Она повернута на угол 90° по часовой стрелке относительно точки А (−1; 2). Напишите уравнение полученной окружности.
Ответ: х2 + (у − 3)2 = 16.
3. Найдите координаты точки, симметричной точке А (7; 2) относительно прямой, заданной уравнением у = −х + 3.
Ответ: (1; −4).
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
1 вариант
Мальчик прошел от дома по направлению на восток 800м. Затем завернул на север и прошел 600м. Под каким углом к направлению на запад он должен идти, чтобы вернуться домой? В ответе укажите целое число градусов.
 (Используйте таблицу тригонометрических функций)
(Используйте таблицу тригонометрических функций)
Горная железная дорога поднимается на 1 м на каждые 30м пути. Используя таблицу тригонометрических функций, найдите угол подъема в градусах. В ответе укажите приближенное значение, выраженное целым числом.
Лестница имеет ступеньки, ширина которых30 см, а высота – 18 см. Используя таблицу тригонометрических функций, найдите угол подъема лестницы. В ответе укажите приближенное значение, выраженное целым числом.
С самолета радируют капитану рыболовецкого судна, что самолет находится над косяком рыбы на высоте 1000 м. С судна определяют, что угол, под которым виден самолет над горизонтом, равен 260. Используя таблицу тригонометрических функций, найдите расстояние от судна до косяка рыбы. В ответе укажите приближенное значение, выраженное целым числом.
Использую данные, приведенные на рисунке, найдите ширину АВ реки.

Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Девочка прошла от дома на запад 500 м. Затем повернула на север и прошла 300м. После этого она повернула на восток и прошла еще 100 м. Под каким углом к направлению на восток она должна идти, чтобы вернуться домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций)
Человек, пройдя вверх по склону холма на 1000 м, поднялся на 90 м над плоскостью основания холма. Используйте таблицу тригонометрических функций, найдите (в среднем) угол наклона холма в градусах. В ответе укажите приближенное значение, выраженное целым числом.
Угол подъема лестница дачного домика равен 580. Используйте таблицу тригонометрических функций, найдите высоту ступенек лестницы, если ширина ступенек равна 20 см.

Самолет приближается к аэропорту А на высоте 8000м. Пилот имеет предписание производить снижение для посадки под постоянным углом 60. Используйте таблицу тригонометрических функций, найдите расстояние АВ от посадочной полосы до того места, над которым самолет должен начать снижение. В ответе укажите приближенное значение, выраженное целым числом метров.
Из окна, расположенного на высоте 15 м над поверхностью земли, нижний край дома, стоящего прямо на другой стороне улицы, виден под углом понижения 320. Найдите ширину улицы.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Грибник, войдя в лес, в течение двух часов шел в направлении на север, а затем с той же скоростью в течение полутора часов – на восток.
 Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов.
Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов.
Угол подъема дороги равен 70. Используя таблицу тригонометрических функций, найдите высоту, на которую поднимается пешеход, пройдя 200 м.
Ширина дачного домика равна 6 м, ширина одного ската его двускатной крыши равна 5 м. Используя таблицу тригонометрических функций, найдите угол между стропилами крыши и потолком.
Расстояние от наблюдателя до башни главного здания МГУ имени М.В.Ломаносова равно 150 м, а угол, под которым видно здание, равен 580. Используя таблицу тригонометрических функций, найдите высоту башни. В ответе укажите приближенное значение, выраженное целым числом метров.
Найдите расстояние между населенными пунктами А и В, расположенными на разных берегах реки, если расстояние между пунктами А и С, расположенными на одном берегу этой реки, равно 2 км, угол САВ равен 800, угол АСВ равен 700.
 В ответе укажите целое число метров
В ответе укажите целое число метров
.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Маятник в виде груза, подвешенного на нитке, отклонили от положения равновесия на угол 600. Длина АС маятника 20 см. На сколько изменилась высота груза по сравнению с положением равновесия?
Пожарная лестница выдвинута на 50 м при предельном угле подъема 720. Используя таблицу тригонометрических функций, найдите высоту, которой достиг верхний конец лестницы, если ее нижний конец отстоит от поверхности земли на 1 м.
Длина балки, на которую опираются стропила крыши, равно 20 м. Используя таблицу тригонометрических функций, найдите высоту крыши, зная, что стропила с этой балкой образуют угол 240.

Расстояние от наблюдателя до башни главного здания МГУ имени М.В.Ломаносова равно 240 м, под каким углом видна эта башня с расстояния 200 м? В ответе укажите приближенное значение, выраженное целым числом градусов.
.
Использую данные, приведенные на рисунке, найдите ширину АВ озера. В ответе укажите целое число метров.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Маятник в виде груза, подвешенного на нитке, отклонили от положения равновесия на угол 600. Длина АВ маятника 20 см. Используя таблицу тригонометрических функций, найдите расстояние СD от груза С до прямой АВ, проходящей через начальное положение маятника.
Используя таблицу тригонометрических функций, найдите приближенное значение угла, под которым виден столб высотой 3 м, находящийся от наблюдателя на расстоянии 100 м.
 В ответе укажите целое число градусов.
В ответе укажите целое число градусов.
Из некоторой точки вершина горы видна под углом 300. При приближении к горе на 1000 м вершина стала видна под углом 450. Найдите приближенную высоту горы. В ответе укажите целое число метров.
Вершина радиомачты видна с расстояния 300 м от ее основания под углом 100. Используя таблицу тригонометрических функций, найдите высоту радиомачты.
Использую данные, приведенные на рисунке, найдите расстояние между населенными пунктами А и В, расположенными на разных берегах озера. В ответе укажите целое число метров.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Маятник АВ длиной 50 см отклонили от положения равновесия на расстояние СD, равное 12 см.
 Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.
Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.
Телеграфный столб высотой 10 м находится на берегу реки. Верхний конец столба виден с другого под углом 200 к горизонту. Используя таблицу тригонометрических функций, найдите ширину реки.
Используя данные, указанные на рисунке, найдите расстояние от корабля К до берега АВ. В ответе укажите целое число метров.
Высота Останкинской телевизионной башни – 540 м. Используя таблицу тригонометрических функций, найдите угол в градусах, под которым видна башня с расстояния 2000 м.
Подводная лодка, находясь впереди корабля, погрузилась в воду и пошла в направлении, перпендикулярном направлению на корабль со скоростью 30 км/ч. Под каким углом к направлению хода подводной лодки должен идти корабль со скоростью 60 км/ч, чтобы в некоторой точке пройти над подводной лодкой? Ответ укажите в градусах.

ОТВЕТЫ
Самостоятельная работа по теме
«Практическое применение подобия»
1 вариант
Используя данные, приведенные на рисунке, найдите расстояние АВ от лодки А до берега В
Для нахождения высоты египетской пирамиды недалеко от нее был установлен шест длиной 1,5 м. Его тень составила 1м. В тот же момент тень пирамиды была равна 96м. Чему равна высота пирамиды?
Какой должна быть ширина (Х) прямоугольной рамки для фотографии, указанной на рисунке, чтобы прямоугольники рамки и фотографии были подобны?
Самостоятельная работа по теме
«Практическое применение подобия»
2 вариант
Используя данные на рисунке , найдите высоту мачты АВ.

Чтобы изменить высоту дерева, ученик держит линейку в вертикальном положении на расстоянии вытянутой руки. Расстояние от глаз ученика дот линейки равно 60см. Часть линейки, закрывающая дерево, составляет 20 см. Расстояние от ученика до дерева равно 18 м. Чему равна высота дерева?
Строительный кирпич весит 4 кг. Сколько граммов весит игрушечный кирпич из того же материала, все размеры которого в 4 раза меньше?
Самостоятельная работа по теме
«Практическое применение подобия»
3 вариант
Используя данные, приведенные на рисунке, найдите ширину реки АВ.
Изображение дерева на фотопленке имеет высоту 15мм. Найдите высоту дерева, если расстояния от
объектива фотоаппарата до изображения и до дерева равны соответственно 50мм и 60мм.
3. Апельсин в два раза больше мандарина. Мандарин весит 40г. Считая их форму шарообразной и удельный вес одинаковым, найдите вес апельсина
ОТВЕТЫ
Недельные домашние задания для подготовки к ОГЭ по математике для 9 класса | Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему:
Вариант №1
1. Сторона квадрата равна 10. Найдите его площадь.
2. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
3. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
4. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на .
5. B 8 № 323396. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
- B 8 № 39. Найдите площадь трапеции, изображённой на рисунке.
7. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
- B 8 № 314882. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
9.Найдите площадь параллелограмма, изображённого на рисунке.
10. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
11. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
12. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен . Найдите площадь ромба.
Вариант №2
1. Периметр квадрата равен 40. Найдите площадь квадрата.
2. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на .
3. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
Найдите площадь треугольника, делённую на .
4. Периметр равностороннего треугольника равен 30. Найдите его площадь,делённую на .
5. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
6. B 8 № 117. Найдите площадь трапеции, изображённой на рисунке.
7.Найдите площадь трапеции, изображённой на рисунке.
- Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
9. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
10. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
11.Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
12. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен . Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
Вариант №3
1 . Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
2. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на
3. Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на
4. В равнобедренном треугольнике . Найдите , если высота .
5. Найдите площадь трапеции, изображённой на рисунке.
6. Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
7. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.
8. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен . Найдите площадь параллелограмма.
9. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
Найдите площадь ромба.
10. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
11. B 8 № 323957. Найдите площадь ромба, если его диагонали равны 14 и 6.
12. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
Вариант №4
1. Периметр квадрата равен 160. Найдите площадь квадрата.
2. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
3. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
4. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
5. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
6. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.
Найдите площадь трапеции.
7. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
- B 8 № 311682. Найдите площадь трапеции, изображённой на рисунке.
9. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.
10.Найдите площадь параллелограмма, изображённого на рисунке.
11. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
12. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Вариант №5
1. Найдите площадь квадрата, если его диагональ равна 1.
2. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
3. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
4. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
Найдите площадь треугольника.
5. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
6. Основания трапеции равны 1 и 13, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
- B 8 № 340197. В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
- В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
- Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
- Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
- Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
12. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Вариант №6
1. Сторона квадрата равна 10. Найдите его площадь.
2. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
3. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
4. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на .
5. B 8 № 323396. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
- B 8 № 39. Найдите площадь трапеции, изображённой на рисунке.
7. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
- B 8 № 314882. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°.
 Найдите площадь трапеции.
Найдите площадь трапеции.
9.Найдите площадь параллелограмма, изображённого на рисунке.
10. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
11. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
12. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен . Найдите площадь ромба.
Вариант №7
1. Периметр квадрата равен 40. Найдите площадь квадрата.
2. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на .
3. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
4. Периметр равностороннего треугольника равен 30. Найдите его площадь,делённую на .
5. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
6.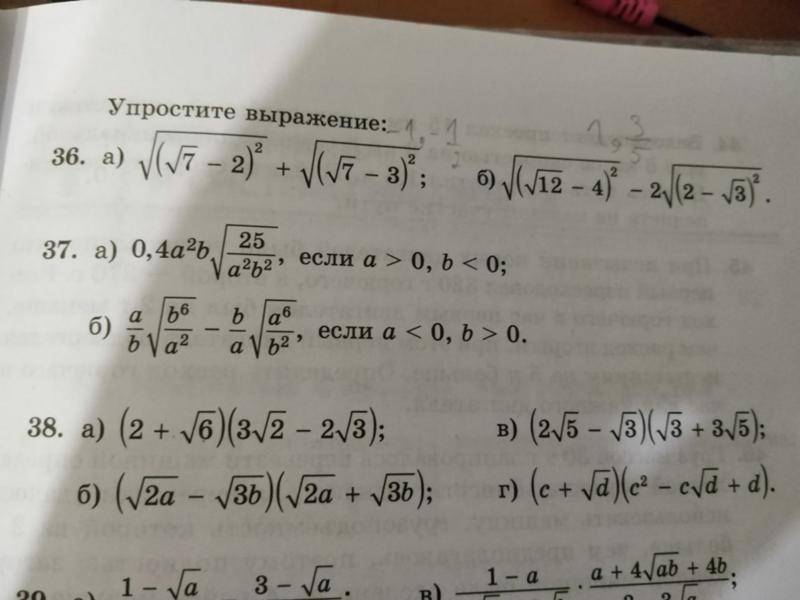 B 8 № 117. Найдите площадь трапеции, изображённой на рисунке.
B 8 № 117. Найдите площадь трапеции, изображённой на рисунке.
7.Найдите площадь трапеции, изображённой на рисунке.
- Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
9. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
10. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
11.Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
12. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен . Найдите площадь параллелограмма.
Вариант №8
1 . Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
2. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на
Найдите площадь прямоугольника, деленную на
3. Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на
4. В равнобедренном треугольнике . Найдите , если высота .
5. Найдите площадь трапеции, изображённой на рисунке.
6. Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
7. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.
8. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен . Найдите площадь параллелограмма.
9. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
10. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
11. B 8 № 323957. Найдите площадь ромба, если его диагонали равны 14 и 6.
12. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
Вариант №9
1. Периметр квадрата равен 160. Найдите площадь квадрата.
2. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
3. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
4. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
5. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
6. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.
7. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
- B 8 № 311682. Найдите площадь трапеции, изображённой на рисунке.

9. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.
10.Найдите площадь параллелограмма, изображённого на рисунке.
11. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
12. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Вариант №10
1. Найдите площадь квадрата, если его диагональ равна 1.
2. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
3. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
4. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
5. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
6. Основания трапеции равны 1 и 13, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Найдите площадь трапеции.
- B 8 № 340197. В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
- В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
- Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
- Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
- Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
12. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Вариант №11
1. Сторона квадрата равна 10. Найдите его площадь.
2. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
3. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
4. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на .
5. B 8 № 323396. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
- B 8 № 39. Найдите площадь трапеции, изображённой на рисунке.
7. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
- B 8 № 314882. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
9.Найдите площадь параллелограмма, изображённого на рисунке.
10. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
11. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
12. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен . Найдите площадь ромба.
Вариант №12
1. Периметр квадрата равен 40. Найдите площадь квадрата.
2. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на .
3. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
4. Периметр равностороннего треугольника равен 30. Найдите его площадь,делённую на .
5. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
6. B 8 № 117. Найдите площадь трапеции, изображённой на рисунке.
7.Найдите площадь трапеции, изображённой на рисунке.
- Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
9. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
10. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
11.Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
12. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен . Найдите площадь параллелограмма.
Вариант №13
1 . Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
2. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на
3. Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на
4. В равнобедренном треугольнике . Найдите , если высота .
5. Найдите площадь трапеции, изображённой на рисунке.
6. Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
7. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.
8. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен . Найдите площадь параллелограмма.
9. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
10. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
11. B 8 № 323957. Найдите площадь ромба, если его диагонали равны 14 и 6.
12. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
Вариант №14
1. Периметр квадрата равен 160. Найдите площадь квадрата.
2. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
3. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
4. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
5. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
6. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.
7. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
- B 8 № 311682. Найдите площадь трапеции, изображённой на рисунке.
9. Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.
10.Найдите площадь параллелограмма, изображённого на рисунке.
11. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
12. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Вариант №15
1. Найдите площадь квадрата, если его диагональ равна 1.
2. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
3. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
4. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
5. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
6. Основания трапеции равны 1 и 13, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
- B 8 № 340197. В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.

- В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
- Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
- Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
- Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
12. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Вариант №16
1. Сторона квадрата равна 10. Найдите его площадь.
2. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
3. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
4. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на .
Найдите его площадь,делённую на .
5. B 8 № 323396. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
- B 8 № 39. Найдите площадь трапеции, изображённой на рисунке.
7. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
- B 8 № 314882. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
9.Найдите площадь параллелограмма, изображённого на рисунке.
10. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
11. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
12. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен . Найдите площадь ромба.
Оценка
: Вычисление выражений и многочленов
Purplemath
«Оценка» в основном означает «упрощение выражения до одного числового значения». Иногда вам будет предложено числовое выражение, и все, что вам нужно сделать, это упростить; это скорее вопрос порядка действий. В этом уроке я сконцентрируюсь на аспекте оценки «включил и нажал»: вставлял значения для переменных и «пробирался» к упрощенному ответу.
Иногда вам будет предложено числовое выражение, и все, что вам нужно сделать, это упростить; это скорее вопрос порядка действий. В этом уроке я сконцентрируюсь на аспекте оценки «включил и нажал»: вставлял значения для переменных и «пробирался» к упрощенному ответу.
(Кстати, да, «plug-n-chug» — довольно стандартная терминология. Это не «технический» термин, поэтому вы, вероятно, не увидите его в своем учебнике, но наверняка услышите его от других студентов, а также, возможно, вашего инструктора.)
MathHelp.com
Обычно единственной сложной задачей при оценке является отслеживание знаков «минус». Я настоятельно рекомендую вам обильно использовать круглые скобки, особенно когда вы только начинаете.
Я настоятельно рекомендую вам обильно использовать круглые скобки, особенно когда вы только начинаете.
Вычислить
a 2 b для a = –2, b = 3, c = –4 и d = 4.
Чтобы найти ответ, я просто вставляю заданные значения, стараясь использовать скобки, особенно вокруг знаков «минус».Особенно, когда я только начинаю, сначала могут быть полезны скобки:
а 2 б
() 2 ()
(–2) 2 (3)
(4) (3)
12
Обратите внимание, как использование круглых скобок помогло мне отследить знак «минус» на значении и . Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2, получив в итоге –4, что было бы неправильно.
Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2, получив в итоге –4, что было бы неправильно.
Кстати, оказалось, что нам не нужны значения переменных c и d . Когда вам дается большой набор выражений для оценки, вы должны ожидать, что часто будут те или иные переменные, которые не будут включены в какое-либо конкретное упражнение из набора.
Вычислить
a — cd для a = –2, b = 3, c = –4 и d = 4.
В этом упражнении они дали мне дополнительную информацию. В выражении, которое они хотят, чтобы я оценил, нет b , поэтому я могу игнорировать это значение в своей работе:
(–2) — (–4) (4)
–2 — (–16)
–2 + 16
16–2
14
Вычислить (
b + d ) 2 для a = –2, b = 3, c = –4 и d = 4.
Я должен позаботиться о том, чтобы не пытаться «распределить» показатель степени через круглые скобки. Экспоненты НЕ распределяются сверх сложения! Я никогда не должен пытаться сказать, что ( b + d ) 2 то же самое, что b 2 + d 2 . Это НЕ одно и то же! Я должен оценить выражение в его нынешнем виде:
Вычислить
b 2 + d 2 для a = –2, b = 3, c = –4 и d = 4.
В этом выражении возведение в квадрат выполняется отдельно для каждой из переменных.
Обратите внимание, что этот последний ответ выше не совпадает с ответом на предыдущую оценку. Это прямо демонстрирует тот факт, что показатели не распределяются по сложению, как это происходит при умножении.
Это прямо демонстрирует тот факт, что показатели не распределяются по сложению, как это происходит при умножении.
Вы должны ожидать хотя бы упражнения, аналогичные двум предыдущим, на следующем тесте, а также на заключительном экзамене.Эта тенденция пытаться распределить показатель степени (а не умножение) над сложением — распространенная ошибка студентов, и ваш преподаватель почти наверняка захочет напоминать вам — часто! — разницы между возведением суммы в квадрат и суммированием двух квадратов. Не путайте их!
Вычислить
bc 3 — ad для a = –2, b = 3, c = –4 и d = 4.
В этом упражнении мне нужно использовать значения всех четырех переменных. Но мне нужно быть осторожным при размещении, потому что это выражение не использует переменные в алфавитном порядке.
(3) (- 4) 3 — (–2) (4)
(3) (- 64) — (–8)
–192 + 8
–184
Партнер
Наиболее распространенным типом «выражения», который вам, вероятно, потребуется вычислить, будут полиномы.Чтобы вычислить многочлен, вы берете этот многочлен и подставляете в переменную (обычно x ) любое число, которое они вам дали.
Вычислить
x 4 + 3 x 3 — x 2 + 6 для x = –3.
Это мой первый многочлен для вычисления, поэтому я начну снова с пустых скобок, показывая мне, где нужно поместить значение переменной.
x 4 + 3 x 3 — x 2 + 6
() 4 + 3 () 3 — () 2 + 6
(–3) 4 + 3 (–3) 3 — (–3) 2 + 6
81 + 3 (–27) — (9) + 6
81 — 81 — 9 + 6
–3
Вычислить 3
x 2 — 12 x + 4 для x = –2.
Я рад, что потренировался использовать круглые скобки, чтобы мои замены были понятны. В этом случае эти скобки помогут мне отслеживать знаки «минус».
3 (–2) 2 — 12 (–2) + 4
3 (4) + 24 + 4
12 + 24 + 4
40
Вычислить
y = 4 x — 3 при x = –1.
Это другое. Они дали мне уравнение с двумя переменными, но дали мне значение только для одной из переменных. Думаю, они хотят, чтобы я подключил x и вычислил полученное значение для y .
Тогда мой ответ — уравнение:
Примечание. В этом последнем упражнении выше мы подставляли значение одной из переменных и упрощали поиск значения другой переменной.Кроме того, для той части, к которой мы подключались, было присвоено имя y . Из-за этого мы не просто оценивали выражение; на самом деле мы вычисляли полиномиальную функцию. Результат нашего plug-n-chug означает, что точка ( x , y ) = (–1, –7) находится на линии y = 4 x — 3; то есть эта точка находится на графике полиномиальной функции.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении выражений для заданных значений переменных. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или перейдите к следующей странице этого урока.)
Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или перейдите к следующей странице этого урока.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/evaluate.htm
Безопасность | Стеклянная дверь
Мы получаем подозрительную активность от вас или от кого-то, кто использует вашу интернет-сеть.Подождите, пока мы убедимся, что вы настоящий человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, напишите нам чтобы сообщить нам, что у вас проблемы.
Nous aider à garder Glassdoor sécurisée
Nous avons reçu des activités suspectes venant de quelqu’un utilisant votre réseau internet. Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание
apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un
электронная почта à
pour nous informer du désagrément.
Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание
apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un
электронная почта à
pour nous informer du désagrément.
Unterstützen Sie uns beim Schutz von Glassdoor
Wir haben einige verdächtige Aktivitäten von Ihnen oder von jemandem, der in ihrem Интернет-Netzwerk angemeldet ist, festgestellt. Bitte warten Sie, während wir überprüfen, ob Sie ein Mensch und kein Bot sind. Ihr Inhalt wird в Kürze angezeigt. Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте: .
We hebben verdachte activiteiten waargenomen op Glassdoor van iemand of iemand die uw internet netwerk deelt.Een momentje geduld totdat, мы исследовали, что u daadwerkelijk een persoon bent. Uw bijdrage zal spoedig te zien zijn. Als u deze melding blijft zien, электронная почта: om ons te laten weten dat uw проблема zich nog steeds voordoet.
Hemos estado detectando actividad sospechosa tuya o de alguien con quien compare tu red de Internet. Эспера
mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo
este mensaje, envía un correo electrónico
a para informarnos de
que tienes problemas.
Эспера
mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo
este mensaje, envía un correo electrónico
a para informarnos de
que tienes problemas.
Hemos estado percibiendo actividad sospechosa de ti o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para hacernos saber que estás teniendo problemas.
Temos Recebido algumas atividades suspeitas de voiceê ou de alguém que esteja usando a mesma rede. Aguarde enquanto confirmamos que Você é Uma Pessoa de Verdade.Сеу контексто апаресера эм бреве. Caso продолжить Recebendo esta mensagem, envie um email para пункт нет informar sobre o проблема.
Abbiamo notato alcune attività sospette da parte tua o di una persona che condivide la tua rete Internet.
Attendi mentre verifichiamo Che sei una persona reale. Il tuo contenuto verrà visualizzato a breve. Secontini
Visualizzare questo messaggio, invia un’e-mail all’indirizzo
per informarci del
проблема.
Secontini
Visualizzare questo messaggio, invia un’e-mail all’indirizzo
per informarci del
проблема.
Пожалуйста, включите куки и перезагрузите страницу.
Это автоматический процесс. Ваш браузер в ближайшее время перенаправит вас на запрошенный контент.
Подождите до 5 секунд…
Перенаправление…
Заводское обозначение: CF-102 / 622d57e47a8fdab0.
примеров упрощения схем | Булева алгебра
Начнем с схемы полупроводникового затвора, нуждающейся в упрощении.
Предполагается, что входные сигналы «A», «B» и «C» поступают от переключателей, датчиков или, возможно, других схем затвора.
Не имеет значения, откуда берутся эти сигналы в задаче уменьшения стробирования.
Как написать логическое выражение для упрощения схем
Нашим первым шагом в упрощении должно быть написание логического выражения для этой схемы.
Эта задача легко выполняется шаг за шагом, если мы начнем с написания подвыражений на выходе каждого элемента, соответствующих соответствующим входным сигналам для каждого элемента.
Помните, что логические элементы ИЛИ эквивалентны логическому сложению, а логические элементы И эквивалентны логическому умножению.
Например, я напишу подвыражения на выходах первых трех ворот:
. . . затем еще одно подвыражение для следующих ворот:
Наконец, результат («Q») равен выражению AB + BC (B + C):
Теперь, когда у нас есть логическое выражение, с которым можно работать, нам нужно применить правила булевой алгебры, чтобы привести выражение к его простейшей форме (простейшая определяется как требующая реализации наименьшего числа вентилей):
Заключительное выражение B (A + C) намного проще исходного, но выполняет ту же функцию.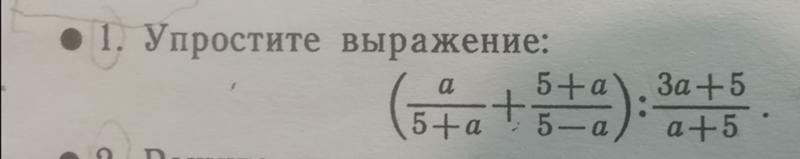
Если вы хотите проверить это, вы можете сгенерировать таблицу истинности для обоих выражений и определить статус Q (выход схемы) для всех восьми комбинаций логических состояний A, B и C для обеих схем. Две таблицы истинности должны быть идентичными.
Создание схематических диаграмм из логических выражений
Теперь мы должны сгенерировать схематическую диаграмму из этого логического выражения.
Для этого оцените выражение, следуя правильному математическому порядку операций (умножение перед сложением, операции в круглых скобках перед любыми другими), и нарисуйте ворота для каждого шага.
Еще раз вспомните, что вентили ИЛИ эквивалентны логическому сложению, а вентили И эквивалентны логическому умножению.
В этом случае мы бы начали с подвыражения «A + C», которое является логическим элементом ИЛИ:
Следующим шагом в оценке выражения «B (A + C)» является умножение (логический элемент И) сигнала B на выходной сигнал предыдущего элемента (A + C):
Очевидно, что эта схема намного проще оригинальной, имея только два логических элемента вместо пяти.
Такое уменьшение компонентов приводит к более высокой скорости работы (меньшее время задержки от перехода входного сигнала к переходу выходного сигнала), меньшему потреблению энергии, меньшей стоимости и большей надежности.
Как использовать логическое упрощение для схем электромеханических реле
Электромеханические релейные схемы, обычно более медленные, потребляющие больше электроэнергии для работы, более дорогие и имеющие меньший средний срок службы, чем их полупроводниковые аналоги, значительно выигрывают от логического упрощения.Рассмотрим пример схемы:
Как и раньше, нашим первым шагом в приведении этой схемы к ее простейшей форме должно быть создание логического выражения из схемы.
Самый простой способ, который я нашел, — это выполнить те же шаги, которые я обычно выполняю, чтобы уменьшить последовательно-параллельную резисторную сеть до одного общего сопротивления.
Например, рассмотрите следующую схему резисторов с резисторами, расположенными по той же схеме подключения, что и контакты реле в предыдущей цепи, и соответствующей формулой общего сопротивления:
На приведенном выше рисунке длинный штрих (-) используется для обозначения последовательного соединения резисторов.
Помните, что параллельные контакты эквивалентны логическому сложению, а последовательные контакты эквивалентны логическому умножению.
Напишите логическое выражение для этой контактной цепи реле в том же порядке приоритета, что и при уменьшении последовательно-параллельной цепи резисторов до полного сопротивления.
Может быть полезно написать логическое подвыражение слева от каждой «ступеньки» лестницы, чтобы упорядочить написание выражений:
Теперь, когда у нас есть логическое выражение, с которым можно работать, нам нужно применить правила булевой алгебры, чтобы привести выражение к его простейшей форме (простейшая определяется как требующая реализации наименьшего числа релейных контактов):
Более склонные к математике должны быть в состоянии увидеть, что два шага, использующие правило «A + AB = A», могут быть объединены в один шаг, причем правило может быть расширено до: «A + AB + AC + AD +. . . = A ”
. . = A ”
Как видите, сокращенная схема намного проще исходной, но выполняет ту же логическую функцию:
ОБЗОР:
- Чтобы преобразовать схему затвора в логическое выражение, пометьте каждый выход затвора логическим подвыражением, соответствующим входным сигналам затвора, пока не будет достигнуто окончательное выражение на последнем затворе.
- Чтобы преобразовать логическое выражение в схему затвора, оцените выражение, используя стандартный порядок операций: умножение перед сложением и операции в круглых скобках перед любыми другими.
- Чтобы преобразовать схему релейной логики в логическое выражение, пометьте каждую ступень логическим подвыражением, соответствующим входным сигналам контактов, до тех пор, пока не будет достигнуто окончательное выражение на последней катушке или индикаторе. Чтобы определить правильный порядок оценки, относитесь к контактам так, как если бы они были резисторами, и как если бы вы определяли общее сопротивление последовательно-параллельной цепи, образованной ими.
 Другими словами, сначала ищите контакты, которые либо непосредственно, последовательно, либо непосредственно параллельно друг другу, а затем «свертывают» их в эквивалентные логические подвыражения, прежде чем переходить к другим контактам.
Другими словами, сначала ищите контакты, которые либо непосредственно, последовательно, либо непосредственно параллельно друг другу, а затем «свертывают» их в эквивалентные логические подвыражения, прежде чем переходить к другим контактам. - Чтобы преобразовать логическое выражение в схему релейной логики, оцените выражение, используя стандартный порядок операций: умножение перед сложением и операции в круглых скобках перед любыми другими.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
вопросов по математике. . . Математические ответы. . .
Включите как можно больше деталей.
Если у вас есть уравнения или информация, включающая математические символы или диаграммы, просто отсканируйте рукописную работу и загрузите ее как картинку.
Нажмите ниже, чтобы увидеть вклад других посетителей этой страницы …
Круги
Али разрабатывает полукруглый…
Математика 126
пожалуйста, помогите мне проблема…
Фракции
как сравнить дроби…
Неравенство
70 + 30
Дополнительные наборы
Перечислите все подмножества {…
Факторинг
Упростите следующее выражение:…
Геометрия
Приведите пример следующего…
Алгбра
8/7 + 2i — комплексное число. …
…
какой отрезок для…
Коэффициент
СООТНОШЕНИЯ используются для представления…
Профсоюзы
что такое союз C и…
ABCD — Математическая головоломка
Четыре числа
Элементы
пытаясь понять эти…
PEMDAS
Ваш друг заплатил десять долларов…
MAT 126
после завершения…
Сб. Подготовка
Подготовка
если среднее двух чисел…
Последовательность
Дана последовательность: -2, -1,…
мат 126
По Проекту №1 выполнить…
Объем
Стив находит старый баскетбольный мяч…
РАСЧЕТ
привет, хотелось бы увидеть / узнать…
Функция
Часть 1
Своими словами…
простое
какой из следующих…
Понимание эквивалентных уравнений в алгебре
Эквивалентные уравнения — это системы уравнений, которые имеют одинаковые решения. Выявление и решение эквивалентных уравнений — ценный навык не только на уроках алгебры, но и в повседневной жизни. Взгляните на примеры эквивалентных уравнений, как решить их для одной или нескольких переменных и как вы можете использовать этот навык за пределами классной комнаты.
Выявление и решение эквивалентных уравнений — ценный навык не только на уроках алгебры, но и в повседневной жизни. Взгляните на примеры эквивалентных уравнений, как решить их для одной или нескольких переменных и как вы можете использовать этот навык за пределами классной комнаты.
Ключевые выводы
- Эквивалентные уравнения — это алгебраические уравнения, которые имеют одинаковые решения или корни.
- Добавление или вычитание одного и того же числа или выражения к обеим сторонам уравнения дает эквивалентное уравнение.
- Умножение или деление обеих частей уравнения на одно и то же ненулевое число дает эквивалентное уравнение.
Линейные уравнения с одной переменной
В простейших примерах эквивалентных уравнений нет переменных. Например, эти три уравнения эквивалентны друг другу:
- 3 + 2 = 5
- 4 + 1 = 5
- 5 + 0 = 5
Признать, что эти уравнения эквивалентны, — это здорово, но не особенно полезно. Обычно задача эквивалентного уравнения просит вас решить для переменной, чтобы увидеть, совпадает ли она (тот же корень с ) с переменной в другом уравнении.
Обычно задача эквивалентного уравнения просит вас решить для переменной, чтобы увидеть, совпадает ли она (тот же корень с ) с переменной в другом уравнении.
Например, следующие уравнения эквивалентны:
В обоих случаях x = 5. Откуда мы это знаем? Как решить это уравнение «-2x = -10»? Первый шаг — узнать правила эквивалентных уравнений:
- Добавление или вычитание одного и того же числа или выражения к обеим сторонам уравнения дает эквивалентное уравнение.
- Умножение или деление обеих частей уравнения на одно и то же ненулевое число дает эквивалентное уравнение.
- Возведение обеих частей уравнения в одну и ту же нечетную степень или извлечение одного и того же нечетного корня даст эквивалентное уравнение.
- Если обе части уравнения неотрицательны, возведение обеих сторон уравнения в одну четную степень или получение одного и того же четного корня даст эквивалентное уравнение.
Пример
Применяя эти правила на практике, определите, эквивалентны ли эти два уравнения:
Чтобы решить эту проблему, вам нужно найти «x» для каждого уравнения. Если «x» одинаково для обоих уравнений, то они эквивалентны. Если «x» отличается (т.е. уравнения имеют разные корни), то уравнения не эквивалентны. Для первого уравнения:
Если «x» одинаково для обоих уравнений, то они эквивалентны. Если «x» отличается (т.е. уравнения имеют разные корни), то уравнения не эквивалентны. Для первого уравнения:
- x + 2 = 7
- x + 2-2 = 7-2 (вычитая обе стороны на одно и то же число)
- x = 5
Для второго уравнения:
- 2x + 1 = 11
- 2x + 1 — 1 = 11 — 1 (вычитая обе части на одно и то же число)
- 2x = 10
- 2x / 2 = 10/2 (разделив обе части уравнения на то же число)
- x = 5
Итак, да, два уравнения эквивалентны, потому что x = 5 в каждом случае.
Практические эквивалентные уравнения
Вы можете использовать эквивалентные уравнения в повседневной жизни. Это особенно полезно при покупках. Например, вам нравится определенная рубашка. Одна компания предлагает рубашку за 6 долларов с доставкой за 12 долларов, в то время как другая компания предлагает рубашку за 7,50 долларов с доставкой за 9 долларов. Какая рубашка имеет лучшую цену? Сколько рубашек (может быть, вы хотите подарить друзьям) вам придется купить, чтобы цена была одинаковой для обеих компаний?
Какая рубашка имеет лучшую цену? Сколько рубашек (может быть, вы хотите подарить друзьям) вам придется купить, чтобы цена была одинаковой для обеих компаний?
Чтобы решить эту проблему, пусть x будет числом рубашек.Для начала установите x = 1 для покупки одной рубашки. Для компании №1:
- Цена = 6x + 12 = (6) (1) + 12 = 6 + 12 = 18 $
Для компании №2:
- Цена = 7,5x + 9 = (1) (7,5) + 9 = 7,5 + 9 = 16,50 $
Итак, если вы покупаете одну рубашку, вторая компания предлагает более выгодную сделку.
Чтобы найти точку, в которой цены равны, оставьте «x» числом рубашек, но приравняйте два уравнения друг к другу. Чтобы узнать, сколько рубашек вам нужно купить, решите для «x»:
- 6x + 12 = 7.5x + 9
- 6x — 7,5x = 9-12 (вычитание одинаковых чисел или выражений с каждой стороны)
- -1,5x = -3
- 1,5x = 3 (деление обеих сторон на одинаковое число, -1)
- x = 3 / 1,5 (деление обеих сторон на 1,5)
- x = 2
Если вы покупаете две рубашки, цена будет одинаковой, независимо от того, где вы ее купите. Вы можете использовать ту же математику, чтобы определить, какая компания предлагает вам более выгодную сделку с более крупными заказами, а также рассчитать, сколько вы сэкономите, используя одну компанию по сравнению с другой.Видите ли, алгебра полезна!
Вы можете использовать ту же математику, чтобы определить, какая компания предлагает вам более выгодную сделку с более крупными заказами, а также рассчитать, сколько вы сэкономите, используя одну компанию по сравнению с другой.Видите ли, алгебра полезна!
Эквивалентные уравнения с двумя переменными
Если у вас есть два уравнения и две неизвестные (x и y), вы можете определить, эквивалентны ли два набора линейных уравнений.
Например, если вам даны уравнения:
- -3x + 12y = 15
- 7x — 10y = -2
Вы можете определить, эквивалентна ли следующая система:
Чтобы решить эту проблему, найдите «x» и «y» для каждой системы уравнений.Если значения совпадают, то системы уравнений эквивалентны.
Начнем с первого подхода. Чтобы решить два уравнения с двумя переменными, выделите одну переменную и подставьте ее решение в другое уравнение. Чтобы изолировать переменную «y»:
- -3x + 12y = 15
- -3x = 15 — 12y
- x = — (15 — 12y) / 3 = -5 + 4y (вставьте «x» во втором уравнении)
- 7x — 10y = -2
- 7 (-5 + 4y) — 10y = -2
- -35 + 28y — 10y = -2
- 18y = 33
- y = 33/18 = 11/6
Теперь вставьте «y» обратно в любое уравнение, чтобы найти «x»:
- 7x — 10y = -2
- 7x = -2 + 10 (11/6)
Проработав это, вы в конечном итоге получите x = 7/3.
Чтобы ответить на вопрос, вы, , могли бы применить те же принципы ко второму набору уравнений, чтобы решить для «x» и «y», чтобы найти, что да, они действительно эквивалентны. В алгебре легко увязнуть, поэтому неплохо проверить свою работу с помощью онлайн-программы для решения уравнений.
Однако умный студент заметит, что две системы уравнений эквивалентны , без каких-либо сложных вычислений. Единственная разница между первым уравнением в каждом наборе состоит в том, что первое в три раза больше второго (эквивалент).Второе уравнение точно такое же.
Логическая алгебра — курс цифровой электроники
Булева алгебра, логическая алгебра, позволяет применять правила, используемые в алгебре чисел, к логике.
Он формализует правила логики. Булева алгебра используется для упрощения логических выражений
которые представляют собой комбинационные логические схемы.
Он сокращает исходное выражение до эквивалентного выражения с меньшим количеством терминов, что означает, что для реализации требуется меньше логических элементов. комбинационная логическая схема.
комбинационная логическая схема.
Калькулятор логических выражений
Используйте калькулятор, чтобы найти сокращенное логическое выражение или проверить свои собственные ответы.
Ваш ответ
- Примечания:
- Используйте ~ * + для обозначения НЕ И ИЛИ соответственно. Не пропускайте оператор * для операции И.
- (~ AB) + (B ~ C) + (AB) вернет ошибку
- (~ A * B) + (B * ~ C) + (A * B) в порядке
- Логические операции следуют порядку приоритета НЕ И ИЛИ. Выражения внутри квадратных скобок () всегда оцениваются первыми, имея приоритет над порядком приоритета.
- Пожалуйста, вводите только переменные, константы типа 0,1 не допускаются.
- Переменные E, I, N, O, Q, S не допускаются
Упрощение логических выражений
Ниже показан пример использования алгебраических методов для упрощения логического выражения
| ~ (A * B) * (~ A + B) * (~ B + B) | |
| ~ (A * B) * (~ A + B) * 1 | 6 — Закон дополнения |
| ~ (A * B) * (~ A + B) | 5 — Закон идентичности |
| (~ A + ~ B) * (~ A + B) | 8 — Закон Деморгана |
| ~ A + ~ B * B | 4 — Закон распределения |
| ~ A + 0 | 6 — Закон дополнения |
| ~ A | 5 — Закон идентичности |
Каждая строка дает новое выражение и правило или правила, использованные для его вывода из предыдущего. Обычно есть несколько способов достичь результата.
Обычно есть несколько способов достичь результата.
Законы булевой алгебры
Законы логической алгебры используются для упрощения логических выражений.
- Идемпотентный закон
- Ассоциативный закон
- (A * B) * C = A * (B * C)
- (А + В) + С = А + (В + С)
- Коммутативный закон
- А * В = В * А
- А + В = В + А
- Распределительное право
- А * (В + С) = А * В + А * С
- А + (В * С) = (А + В) * (А + С)
- Закон о личности
- А * 0 = 0 А * 1 = А
- А + 1 = 1 А + 0 = А
- Закон о дополнении
- Закон об инволюции
- Закон ДеМоргана
- ~ (А * В) = ~ А + ~ В
- ~ (А + В) = ~ А * ~ В
Законы о резервировании
- Поглощение
- А + (А * В) = А
- А * (А + В) = А
- (А * В) + (А * ~ В) = А
- (А + В) * (А + ~ В) = А
- А + (~ А * В) = А + В
- А * (~ А + В) = А * В
Основные логические законы
Каждый закон описывается двумя частями, которые двойственны друг другу. Принцип двойственности
Принцип двойственности
- Перестановка операций + (ИЛИ) и * (И) в выражении.
- Замена элементов выражения 0 и 1 местами.
- Не меняет вид переменных.
Применение булевой алгебры
Разработка комбинационной логической схемывключает следующие шаги
- Из проектной спецификации найдите таблицу истинности
- Из таблицы истинности выведите логическое выражение «Сумма произведений».
- Используйте логическую алгебру, чтобы упростить логическое выражение. Чем проще логическое выражение, тем меньше логических элементов будет использоваться.
- Используйте логические вентили для реализации упрощенного логического выражения.
Поскольку доходы от рекламы падают, несмотря на рост числа посетителей, нам нужна ваша помощь в поддержании и улучшении этого сайта, что требует времени, денег и тяжелого труда. Благодаря щедрости наших посетителей, которые давали раньше, вы можете использовать этот сайт бесплатно.{2}
Благодаря щедрости наших посетителей, которые давали раньше, вы можете использовать этот сайт бесплатно.{2}
Самая низкая или самая высокая точка параболы называется вершиной. Вершина имеет координату x
$$ x = — \ frac {b} {2a} $$
Координата Y вершины — это максимальное или минимальное значение функции.
a> 0 парабола открывает минимальное значение
<0 парабола раскрывается до максимального значения
Практическое правило напоминает нам, что когда у нас есть положительный символ перед x 2 , мы получаем счастливое выражение на графике, а отрицательный символ отображает печальное выражение.
Вертикальная линия, проходящая через вершину и разделяющая параболу пополам, называется осью симметрии. Ось симметрии имеет уравнение
$$ x = — \ frac {b} {2a} $$
Отсечка по оси Y уравнения равна c.
Если вы хотите построить график квадратичной функции, вы начинаете с создания таблицы значений для некоторых значений вашей функции, а затем наносите эти значения на координатную плоскость и проводите плавную кривую через точки. {2} + 2x + 1 $$
{2} + 2x + 1 $$
Составьте таблицу значений для некоторых значений x.Используйте как положительные, так и отрицательные значения!
| x | y = x 2 + 2x + 1 |
| -3 | 4 |
| -2 | 1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 4 |
| 2 | 9 |
| 3 | 16 |
Постройте точки, проведите плавную линию через точки и продолжите ее в обоих направлениях
Обратите внимание, что у нас есть точка минимума, на которую указывает положительное значение a (a = 1).Вершина имеет координаты (-1, 0), которые вы получите, если воспользуетесь формулой для координаты x вершины
.$$ x = — \ frac {b} {2a} = — \ frac {2} {2 \ cdot 1} = — 1 $$
и что линия имеет точку пересечения по оси y (0, 1), которая могла быть определена из значения c, равного 1.

 (Используйте таблицу тригонометрических функций)
(Используйте таблицу тригонометрических функций)
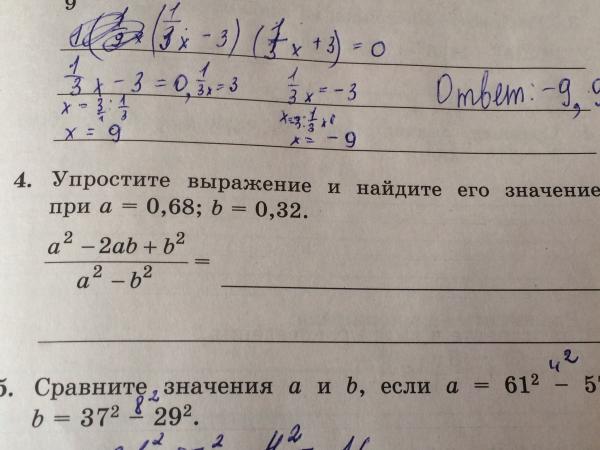
 Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов.
Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов. В ответе укажите целое число метров
В ответе укажите целое число метров
 В ответе укажите целое число градусов.
В ответе укажите целое число градусов.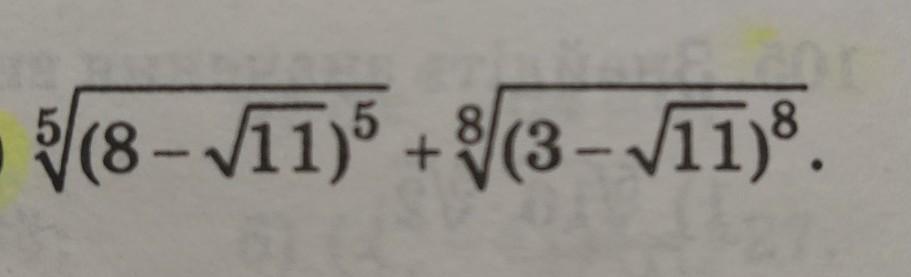 Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.
Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.

 Найдите площадь трапеции.
Найдите площадь трапеции.
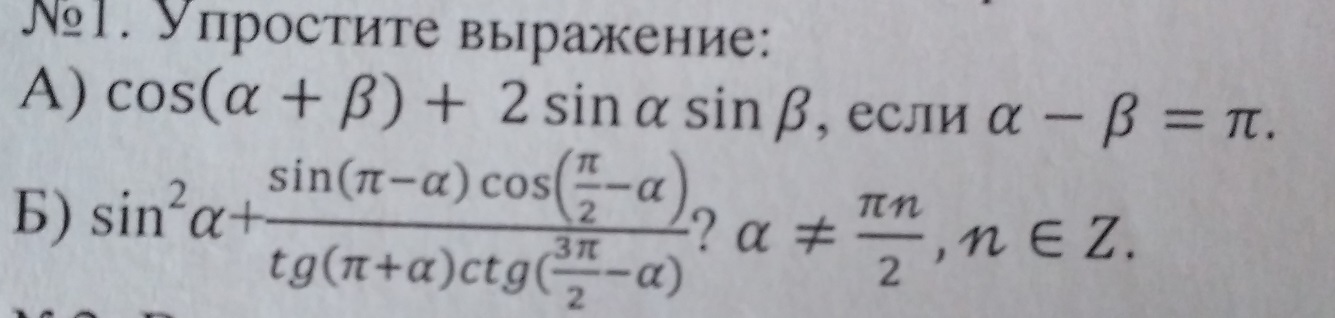

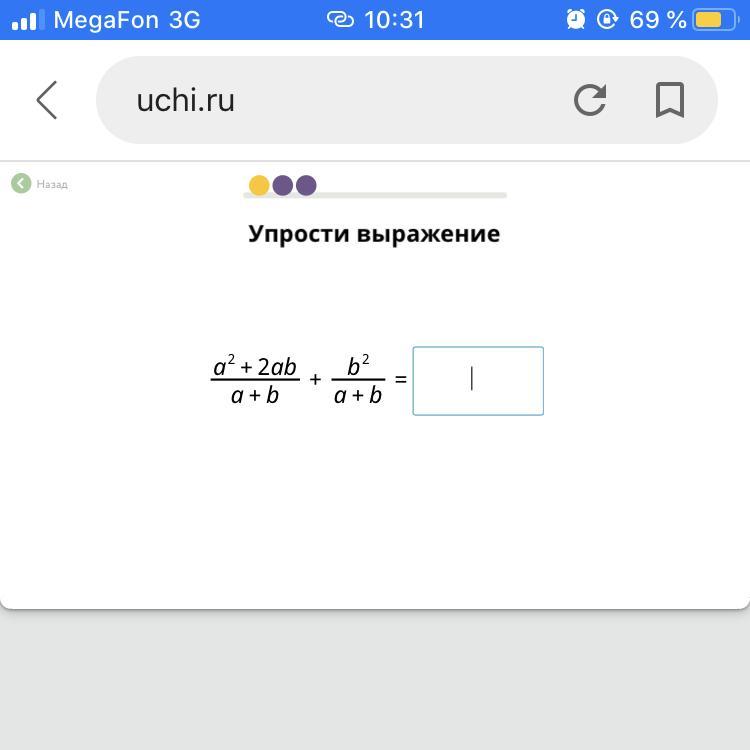
 Другими словами, сначала ищите контакты, которые либо непосредственно, последовательно, либо непосредственно параллельно друг другу, а затем «свертывают» их в эквивалентные логические подвыражения, прежде чем переходить к другим контактам.
Другими словами, сначала ищите контакты, которые либо непосредственно, последовательно, либо непосредственно параллельно друг другу, а затем «свертывают» их в эквивалентные логические подвыражения, прежде чем переходить к другим контактам.
Leave A Comment