2. Упростите выражение Ответ: Ответ:
4. Найдите значение выражения
Государственное бюджетное общеобразовательное учреждение города Москвы «Государственная столичная гимназия» Демонстрационный вариант годовой контрольной работы за курс алгебры 8 класса (база) Инструкция
ПодробнееЧасть 1. Модуль «Алгебра» Желаем успеха!
Диагностическая работа по математике за курс 8 класса. Вариант 1. ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮРАБОТЫ На выполнение всей работы отводится 180 минут. Характеристика работы. Всего в работе 22 задания, из которых
ПодробнееСТРУКТУРА ДИАГНОСТИЧЕСКОЙ РАБОТЫ
Пояснения к демонстрационному варианту контрольных измерительных материалов внутришкольного мониторинга в МОУ «СОШ 55» по математике за курс 5 класса Предмет: Математика Класс: 8 СТРУКТУРА ДИАГНОСТИЧЕСКОЙ
Подробнееучащихся 6 класса учебный год.

Демонстрационный вариант теста для проведения итоговой промежуточной аттестации по математике учащихся 6 класса 2015-2016 учебный год. Составитель: Лебакина В.В. 2016 Пояснительная записка. Предлагаемая
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Работа состоит из двух модулей: «Алгебра», «Геометрия». В модули «Алгебра» и «Геометрия» входят две части, соответствующие проверке на базовом и повышенном уровнях. При проверке базовой
ПодробнееПояснительная записка
Промежуточная аттестация по математике за 2017/2018 учебный год 8 класс Пояснительная записка Промежуточная аттестация по математике проводится в форме письменной работы. Работа дана в двух эквивалентных
Работа по алгебре для 8 класса.
Работа по алгебре для 8 класса. 1.Вид работы: итоговая работа по алгебре в 8 классе Цель работы: оценка уровня достижения учащимися 8 класса планируемых результатов обучения алгебре 2.Перечень проверяемых
1.Вид работы: итоговая работа по алгебре в 8 классе Цель работы: оценка уровня достижения учащимися 8 класса планируемых результатов обучения алгебре 2.Перечень проверяемых
Демонстрационный вариант
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа 1 г. Катав Ивановска» Катав -Ивановского муниципального района Демонстрационный вариант контрольно-измерительных материалов
Инструкция по выполнению работы
Инструкция по выполнению работы Общее время работы 90 минут. Характеристика работы. Всего в работе 18 заданий, из которых 14 заданий базового уровня (часть 1), задания повышенного уровня (часть ). Работа
ПодробнееИнструкция по выполнению работы
Проект Экзаменационная работа для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 009 года (в новой форме) по АЛГЕБРЕ Демонстрационный вариант 009 года
Мониторинговые исследования
МАТЕМАТИКА 8 КЛАСС (Вариант 0 /6) Мониторинговые исследования по МАТЕМАТИКЕ 8 класс Вариант 0 Работа по математике состоит из двух частей, включающих в себя задания. На выполнение работы по математике
На выполнение работы по математике
ДЕМО ВАРИАНТ ХАРАКТЕРИСТИКА РАБОТЫ
Муниципальное общеобразовательное учреждение «Средняя школа 32 имени В.В. Терешковой» Промежуточная аттестационная работа по алгебре и геометрии 8 класса ДЕМО ВАРИАНТ ХАРАКТЕРИСТИКА РАБОТЫ Всего в работе
ЭКЗАМЕНАЦИОННАЯ РАБОТА
Проект ЭКЗАМЕНАЦИОННАЯ РАБОТА для проведения государственной (итоговой) аттестации выпускников IX классов общеобразовательных учреждений в 00 году (в новой форме) по МАТЕМАТИКЕ (АЛГЕБРЕ) Демонстрационный
ПодробнееМониторинговые исследования
МАТЕМАТИКА 8 КЛАСС (Вариант 0 /6) Мониторинговые исследования по МАТЕМАТИКЕ 8 класс Вариант 0 Работа по математике состоит из двух частей, включающих в себя задания На выполнение работы по математике отводится,5
Тест по тригонометрии с ответами
Тест по тригонометрии с ответами — Gee Test наверх Страница 1 из 3Страница 2 из 3Страница 3 из 3- 1.
 cos2а
cos2а - 2. sin-2а
- 3. sin2а
- 4. cos-2а
- 1. -2/3
- 2. 1/4
- 3. π/4
- 4. -1/4
- 1. I или II
- 2. I или III
- 3. I или IV
- 4. II или IV
- 1. 1/2
- 2. 1/3
- 3. -1/2
- 4. 2/3
- 1. sin2a
- 2. sina
- 3. cosa
- 4. cos2a
- 1. ctg2a
- 2. tg2a
- 3. -tg2a
- 4. 1/tga
- 1. tga
- 2. cos2a
- 3. 1/cosa
- 4. ctg2a
- 1. -1/sin2a
- 2. -1/cos2a
- 3. 1/cos2a
- 4. 1/sin2a
- 1. -ctga
- 2. -tga
- 3. tga
- 4. -2cosa
- 2.
 1/2 tg2a
1/2 tg2a - 3. tg4a
- 4. tg2a
- 1. ctga/2
- 2. ctga
- 3. tga/2
- 4. tga
- 1. 2
- 2. 1/cos2а
- 3. 2tg2а
- 4. 2ctg2а
- 1. 3/4
- 2. 1/4
- 3. 1/16
- 4. 3/8
- 1. -1/sin2x
- 2. -1/cos2x
- 3. 1/sin2x
- 4. 1/cos2x
- 2. tga
- 3. 1
- 4. ctgа
- 1. (-1)k·(π/3) + 2πk, k Є Z
- 2. (-1)k·(π/6) + πk, k Є Z
- 3. (-1)k·(π/4) + 2πk, k Є Z
- 4. (-1)k+1·(π/3) + πk, k Є Z
- 1. π + 2πk, k Є Z
- 2. Ø
- 3. 2πk, k Є Z
- 4. π/4 + πk/2, k Є Z
- 1. 15°
- 2. 45°
- 3. 30°
- 4.
 0°
0°
- 1. ±π/3 + 2πk, k Є Z
- 2. π/2 + 2πk, k Є Z
- 3. (-1)k+1·(π/6) + πk; -π/2 + 2πk, k Є Z
- 4. π/2 + 2πk; (-1)k·(π/6) + πk, k Є Z
- 1. ±π/6 + πk, k Є Z
- 2. ±π/4 + πk, k Є Z
- 3. ±π/3 + πk, k Є Z
- 4. ±π/4 + 2πk, k Є Z
- 1. 3πk, k Є Z
- 2. π/2 + (π/3)k, k Є Z
- 3. π/4 + (π/2)k, k Є Z
- 4. (π/3)k, k Є Z
- 1. 45°
- 2. 90°
- 3. 30°
- 4. 60°
- 1. 2πk, k Є Z
- 2. (-1)k (π/6) + πk, k Є Z
- 3. π/2 + 2πk, k Є Z
- 4. π + 2πk, k Є Z
- 1. π/2 + 2πk, k Є Z
- 2. -π/2 + 2πk, k Є Z
- 3. πk, k Є Z
- 4. π + πk, k Є Z
- 1. π/6 + 2πk/3, k Є Z
- 2. ±π/3 + 2πk, k Є Z
- 3. π/4 + πk, k Є Z
- 4. -π/6 + 2πk/3, k Є Z
- 1. πk/2, k Є Z
- 2. πk, k Є Z
- 3. π/2 + πk, k Є Z
- 1. (π/12 + πk; 5π/12 + πk), k Є Z
- 2.
 (π/3 + 2πk; 2π/3 + 2πk), k Є Z
(π/3 + 2πk; 2π/3 + 2πk), k Є Z - 3. (π/6 + 2πk; 5π/6 + 2πk), k Є Z
- 4. (-7π/12 + πk; π/12 + πk), k Є Z
- 1. πk, k Є Z
- 2. π + 2πk, k Є Z
- 3. 2πk, k Є Z
- 4. π/2 + πk, k Є Z
- 1. 135°
- 2. 120°
- 3. 150°
- 4. 180°
- 1. πk, k Є Z
- 2. πk/5, k Є Z
- 3. πk/2, k Є Z
- 4. πk/4, k Є Z
- 1. Ø
- 2. π/2 + 2πk, k Є Z
- 3. π/2 + πk, k Є Z
- 4. x Є R
- 1. π/6 + 2πk, k Є Z
- 2. ±π/3 + 2πk, k Є Z
- 3. (πk)/2, k Є Z
- 4. ±2π/3 + 2πk, k Є Z
- 1. ±π/6 + πk, k Є Z
- 2. (-1)k+1·(π/6) + πk, k Є Z
- 3. (-1)k·(π/6) + πk/2, k Є Z
- 4. ±π/3 + πk, k Є Z
- 1. 2πk, k Є Z
- 2. πk/2, k Є Z
- 3. π/2 + πk, k Є Z
- 4. Ø
- 1. (-1)k·(π/30) + πk/5, k Є Z
- 2. (-1)k·(π/20) + πk/5, k Є Z
- 3. πk/30, k Є Z
- 4.
 πk/4, k Є Z
πk/4, k Є Z
- 1. -4π/3 + 2πk ≤ x ≤ π/3 + 2πk, k Є Z
- 2. π/4 + 2πk ≤ x
- 3. π/4 + 2πk ≤ x ≤ 3π/4 + 2πk, k Є Z
- 4. π/3 + 2πk ≤ x ≤ 2π/3 + 2πk, k Є Z
- 1. π/2 + πk, k Є Z
- 2. πk, k Є Z
- 3. Ø
- 4. πk/2, k Є Z
- 1. π/4; 7π/4
- 2. 3π/4; 5π/4
- 3. 3π/4; 7π/4
- 4. π/6; 11π/6
- 1. π/4 + πk/2, k Є Z
- 2. π/6 + πk, k Є Z
- 3. ±π/6 + 2πk, k Є Z
- 4. ±π/6 + πk/2, k Є Z
| 1. |
Проверь равенство
Сложность: лёгкое |
1 |
2.
|
Коэффициент произведения
Сложность: среднее |
1 |
| 3. |
Записать выражение без скобок
Сложность: среднее |
1 |
4.
|
Упростить выражение, раскрыв скобки
Сложность: среднее |
2 |
| 5. |
Записать сумму или разность двух выражений и упростить её
Сложность: среднее |
2 |
6.
|
Привести подобные слагаемые (коэффициенты — десятичные дроби)
Сложность: среднее |
1 |
| 7. |
Сложи подобные слагаемые (с обыкновенными дробями)
Сложность: среднее |
2 |
8.
|
Найти значение выражения
Сложность: сложное |
3 |
| 9. |
Упростить выражение
Сложность: сложное |
3 |
10.
|
Вычислить
Сложность: среднее |
4 |
| 11. |
Какая сумма денег была у девочек?
Сложность: сложное |
1 |
Тема 6. Тригонометрия1. Определение тригонометрических функций для угла прямоугольного треугольникаВ прямоугольном треугольнике один из острых углов обозначим через α. Катет, противолежащий этому углу, назовем а; прилежащий катет – b, а гипотенузу – с.Существует шесть отношений сторон прямоугольного треугольника относительно фиксированного угла α, каждое из которых, соответственно, назвали: . Рассмотрим «тригонометрический ряд»: . Нетрудно заметить, что произведения тригонометрических функций равноотстоящих от концов «тригонометрического ряда», равны 1: . Из теоремы Пифагора следует: – основное тригонометрическое тождество или, как ещё его называют, «тригонометрическая единица».  Если тождество почленно разделить на или на , то получим ещё два тождества: . Полученные шесть наиболее важных тригонометрических тождеств позволяют отыскать любую из тригонометрических функций при условии, что одна из шести будет известна. 2. Значения тригонометрических функций 30, 45 и 60 градусовРассмотрим равносторонний треугольник со стороной, равной 1. Высота этого треугольника равна и делит сторону пополам.Из левого прямоугольного треугольника найдём: Из прямоугольного равнобедренного треугольника с гипотенузой, равной 1 и острыми углами по 450 найдём: . Сведём все полученные результаты в таблицу: 3. Определение тригонометрических функций на единичной окружностиВеличина угла α для прямоугольного треугольника находится в пределах от 00 до 900 градусов. Необходимо определить тригонометрические функции для других углов. Для этого рассмотрим окружность с радиусом, равным 1, и центром в начале декартовой системы координат. Зададим подвижный радиус OP, первоначальное, «нулевое» положение которого совпадает с положительным направлением оси OX, и вращение против часовой стрелки увеличивает величину угла, а вращение по часовой стрелке величину угла уменьшает. Если точка P лежит в первой четверти, то, рассматривая прямоугольный треугольник с гипотенузой 1 (т.к. радиус окружности равен 1) и острым углом α, получим: , где х, у – координаты точки Р – конца подвижного радиуса. Этими же соотношениями определяются тригонометрические функции углов меньше 00 и больше 900. Необходимо определить тригонометрические функции для других углов. Для этого рассмотрим окружность с радиусом, равным 1, и центром в начале декартовой системы координат. Зададим подвижный радиус OP, первоначальное, «нулевое» положение которого совпадает с положительным направлением оси OX, и вращение против часовой стрелки увеличивает величину угла, а вращение по часовой стрелке величину угла уменьшает. Если точка P лежит в первой четверти, то, рассматривая прямоугольный треугольник с гипотенузой 1 (т.к. радиус окружности равен 1) и острым углом α, получим: , где х, у – координаты точки Р – конца подвижного радиуса. Этими же соотношениями определяются тригонометрические функции углов меньше 00 и больше 900. Из определения тригонометрических функций вытекают важные их свойства: Важное значение при вычислении значений тригонометрических функций имеют формулы приведения, позволяющие свести аргумент тригонометрической функции к углу от 00 до 900. Из рисунка видно, что относительно горизонтального диаметра наименование тригонометрической функции не меняется, а относительно вертикального меняется на кофункцию (синус на косинус, тангенс на котангенс и обратно). Для лучшего запоминания формул приведения можно воспользоваться мнемоническим правилом.  Пусть и α- угловые величины дуг единичной окружности, причём . Для того чтобы привести тригонометрическую функцию числа к тригонометрической функции числа α, необходимо: Пусть и α- угловые величины дуг единичной окружности, причём . Для того чтобы привести тригонометрическую функцию числа к тригонометрической функции числа α, необходимо:1) величину представить в одном из следующих видов: 2) сохранить наименование функции, если дуга величиной α откладывается от горизонтального диаметра изменить наименование функции на кофункцию (синус на косинус, тангенс на котангенс и обратно), если дуга величиной откладывается от вертикального диаметра (см. «Правило носа» ). 3) установить, в какой четверти расположен конец дуги величиной , и определить знак приводимой тригонометрической функции; этот же знак поставить перед значением приведённой функции. «Правило носа». Задайте вопрос: «Функция меняет имя?» и носом водите вдоль той оси координат, от которой откладывается острый угол α.
1.Формулы сложения . 2.Формулы двойного аргумента . 3.Формулы половинного аргумента . 4.Формулы понижения степени 5.Формулы преобразования суммы в произведения 6.Формулы преобразования произведений в суммы . 7. Определения обратных тригонометрических функций . 8. Тригонометрические уравнения . Базовый уровеньПример 1. Вычислить .Решение: Ответ: 1. Пример 2. Найти значение sinα , если .Решение: Так как синус в IV четверти имеет отрицательное значение, то .Ответ: – 0,6. Пример 3. Найти значение , если .Решение: Из формулы найдём . Так как α лежит в I четверти, то cosα положителен и . Из формулы найдём . . Ответ: 7,2. Пример 4. Решите уравнение .Решение: . Умножим левую и правую части равенства на 5 и, учитывая, что , получаем . Ответ: .Пример 5. Вычислить .Решение: Согласно формулам сложения, имеем .Ответ: 1. Пример 6. Приведите значение аргумента к I четверти: .Решение: По алгоритму формул приведения: . Ответ: .Повышенный уровеньПример 7. Упростить .Решение: Ответ: .Пример 8. Вычислить .Решение: Воспользуемся формулами преобразования произведений в сумму и формулами приведения, получим: .Ответ: 1. Задания для самостоятельного решенияОтветы1) 2; 2); 3) – 1; 4) 0,5cosx ; 5) 0; 6) – 0,5; 7) 1; 8) ; 9) 1; 10) 1; 11) 2; 12) – 1,5; 13) ; 14) 0; 15) 0,5; 16) 2,25; 17) ; 18) ; 19) – 3; 20) ; 21) ; 22) а) 0, б) 1; 23) 1; 24) 1; 25) 0,4; 26) 2; 27) 2/7; 28) 0,2; 29) 2250; 30) 300+1800•k1, 1800•k2,; 31) ; 2π; 32); 33) ; |
Алгебра 10 Никольский Контрольная 8 .
 Задания и ответы
Задания и ответыКонтрольная работа № 8 по алгебре в 10 классе с ответами в форме итогового теста. Используется при работе по УМК Никольский. Цитаты из пособия «Алгебра и начала математического анализа. Дидактические материалы. 10 класс : базовый и углубленный уровни / Потапов, Шевкин» использованы в учебных целях. Ответы адресованы родителям. Алгебра 10 Никольский Контрольная 8 + ответы.
Алгебра 10 класс (Никольский)
Итоговый тест. Вариант 1
Смотреть задания Варианта 1
К-8. Вариант 1 (транскрипт)
ЧАСТЬ I. К каждому из заданий А1–А13 дано 4 ответа, из которых только один верный. Для каждого задания запишите номер выбранного вами правильного ответа.
- А1. Упростите выражение 4√a : а–1/2.
- А2. Упростите выражение (b2/5 – 25) / (b1/5 + 5) – b1/5.
- А3. Упростите выражение log3 18 – log3 2 + 5log5 2.

- А4. Решите неравенство (1/2)x–2 > 1/8.
- А5. Укажите промежуток возрастания функции у = f(x), заданной графиком (рис. 42).
- А6. Упростите выражение 2 cos2 a/2 – cos а – 1.
- А7. Решите уравнение log2 x = 1/2.
- А8. Укажите промежуток, которому принадлежит корень уравнения log2(x – 2) = 3.
- А9. Найдите область определения функции у = √((x – 1)/(x + 1)).
- А10. Решите неравенство 9x ≤ 1/3.
- А11. Решите неравенство 2x+2 + 2x > 20.
- А12. Найдите произведение корней уравнения lg2 х – 3 lg х – 10 = 0.
- А13. Решите уравнение 2 cos2 x – 3 sin x = 0.
ЧАСТЬ II. К каждому из заданий В1–В7 укажите полученный вами ответ (только число).
- В1. Найдите сумму корней уравнения 1/(6 • 2x – 11) = 1/(4x – 3).
- В2. Найдите наибольшее целое решение неравенства (log0,3 (x + 1)) / (log0,3 100 – log0,3 9) < 1.

- ВЗ. Вычислите (6√7 – 6√2)(6√7 + 6√2)((3√7 + 3√2)2 – 3√14).
- В4. Сколько корней уравнения sin х + cos х = √2 принадлежит отрезку [–π; 2π]?
- В5. На соревнованиях по кольцевой трассе первый лыжник проходил круг на 2 мин быстрее второго и через час обогнал его на целый круг. За сколько минут первый лыжник проходил один круг?
- В6. Вычислите sin (π/6 + a), если sin а = √3/2 и 0 < а < π/2.
- В7. Найдите значение выражения (1 + cos 2а – sin 2а) / (cos а + cos (π/2 + a)), если cos a = –1/2.
Алгебра 10 класс (Никольский)
Итоговый тест. Вариант 2
Смотреть задания Варианта 2
К-8. Вариант 2 (транскрипт)
ЧАСТЬ I. К каждому из заданий А1–А13 дано 4 ответа, из которых только один верный. Для каждого задания запишите номер выбранного вами правильного ответа.
- А1. Упростите выражение 3√b : b–1/6.

- A2. Упростите выражение (a2/3 – 4)/(a1/3 – 2) – a1/3.
- АЗ. Упростите выражение log4 48 – log4 3 + 6log6 5.
- A4. Решите неравенство (1/3)x–3 < 1/9.
- А5. Укажите промежуток возрастания функции у = f(x), заданной графиком (рис. 43).
- А6. Упростите выражение 2 sin2 a/2 + cos а – 1.
- А7. Решите уравнение log5 х = –1.
- А8. Укажите промежуток, которому принадлежит корень уравнения log3(x + 1) = 2.
- А9. Найдите область определения функции у = √((x + 1)/(x – 1)).
- А10. Решите неравенство 4х ≥ 8.
- А11. Решите неравенство 3х+2 – 3х < 24.
- А12. Найдите произведение корней уравнения lg2 x + lg x – 12 = 0.
- А13. Решите уравнение 2 sin2 x – 3 cos x = 0.
ЧАСТЬ II. К каждому из заданий В1–В7 укажите полученный вами ответ (только число).
- В1.
 Найдите сумму корней уравнения 1/(5 • 2x – 9) = 1/(4x – 5).
Найдите сумму корней уравнения 1/(5 • 2x – 9) = 1/(4x – 5). - В2. Найдите наибольшее целое решение неравенства (log0,2(x + 1,5)) / (log0,2 100 – log0,2 4) < 1.
- ВЗ. Вычислите ((3√5 – 3√2)2 + 43√10)((3√5 – 3√2)2 + 3√10).
- В4. Сколько корней уравнения sin х – cos х = –√2 принадлежит отрезку [–2π; 2π]?
- В5. На соревнованиях по кольцевой трассе первый велосипедист проходил круг на 5 мин медленнее второго и через час отстал от него на целый круг. За сколько минут второй велосипедист проходил один круг?
- В6. Вычислите cos (π/3 + a), если sin a = 1/2 и 0 < a < π/2.
- В7. Найдите значение выражения (1 – cos 2a + sin 2a) / (cos a – sin (2π – a), если sin a = –1/2.
Ответы на итоговый тест
Вернуться к Списку контрольных работ по алгебре в 10 классе (Никольский)
Вы смотрели: Алгебра и начала математического анализа. 10 класс. Контрольная работа в форме итогового теста с ответами. Используется при работе по УМК Никольский. Цитаты из пособия Потапова и Шевкина использованы в учебных целях. Ответы адресованы родителям.
10 класс. Контрольная работа в форме итогового теста с ответами. Используется при работе по УМК Никольский. Цитаты из пособия Потапова и Шевкина использованы в учебных целях. Ответы адресованы родителям.
Алгебра 10 Никольский Контрольная 8 + ответы.
1. Упростить выражение 2. Решить простое уравнение, содержащее одно действие. 3. Выполнить проверку. ( 120 + 180) : х 3 300:х3 х300:3 х100 (120+180): 1003 33.
Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере.
Текстовое содержимое слайдов презентации:
Решение сложных уравнений 18 ∙ х = 90 720 : с = 4 в : 5 = 1400-500у+100 = 450098 – в =63 х:30= 9 350 : х = 5 ∙10 (45 + 18) +х = 103 с – 72 = 65 у-30=1000+200 1 группа –простые уравнения 18 ∙ х = 90 720 : с = 4 98 – в =63 х:30= 9 у+100 = 4500 с – 72 = 65 2 группа- составные уравнения в : 5 = 1400-500 у– 30 = 1000 +200 350 :х =5 ∙10 (45 + 18) +х= 103 в : 5 = 1400-500 у– 30 = 1000 +200 350 : х =5 ∙10 (45 + 18) +х= 103 РАБОТА В ГРУППАХ в:5 =1400-500 в:5=900 в=900 ∙5 в=4500 4500:5=1400-500 900=900у-30=1000+200 у-30=1200 у=1200+30 у=1230 1230-30=1000+200 1200=1200350:х=5∙10 350:х=50 х=350:50 х=7 350 :7=5 ∙10 50=50 Тема урока: «Решение сложных уравнений»Учебная задача: научиться решатьсложные уравнения (45 + 18) +х= 103 63 +х=103 х=103-63 х=40 (45+18)+40=103 103=103 Алгоритм1.
 Упростить выражение 2. Решить простое уравнение, содержащее одно действие3. Выполнить проверку ( 120 + 180) : х = 3 300:х=3 х=300:3 х=100 (120+180): 100=3 3=3 А) 140 :7 +у = 84Б) 180 : с = 150:50В) 784 · 600 + 2 907 · 30 Г) 110 ∙2 — с = 180:60 А) 140 :7 +у = 84Б) 180 : с = 150:50В) 784 · 600 + 2 907 · 30 Г) 110 ∙2 — с = 180:60 А 140 :7 +у = 84 20+у=84 у=84-20 у=64 140:7+64=84 84=84Б 180 : с = 150:50 180:с=3 с =180:3 с=60 180:60 =150:50 3=3 Г 110 ∙2 — с =180:60 220 –с=3 с=220-3 с=217 1102-217=180:60 3=3 Домашнее задание:Стр.
Упростить выражение 2. Решить простое уравнение, содержащее одно действие3. Выполнить проверку ( 120 + 180) : х = 3 300:х=3 х=300:3 х=100 (120+180): 100=3 3=3 А) 140 :7 +у = 84Б) 180 : с = 150:50В) 784 · 600 + 2 907 · 30 Г) 110 ∙2 — с = 180:60 А) 140 :7 +у = 84Б) 180 : с = 150:50В) 784 · 600 + 2 907 · 30 Г) 110 ∙2 — с = 180:60 А 140 :7 +у = 84 20+у=84 у=84-20 у=64 140:7+64=84 84=84Б 180 : с = 150:50 180:с=3 с =180:3 с=60 180:60 =150:50 3=3 Г 110 ∙2 — с =180:60 220 –с=3 с=220-3 с=217 1102-217=180:60 3=3 Домашнее задание:Стр. для всехСтр. – для тех, кто не боится трудностей
для всехСтр. – для тех, кто не боится трудностейПриложенные файлы
- 82864724
Размер файла: 239 kB Загрузок: 0
Математики воскресили 13-ю проблему Гильберта / Хабр
Вопрос Давида Гильберта о многочленах седьмой степени, долгое время считавшийся решённым, открыл исследователям новую сеть математических связей
Успех в математике достигается редко. Спросите хотя бы Бенсона Фарба.
«Проблема математики в том, что в 90% случаев вас ждёт неудача, и вам нужно быть человеком, умеющим это принимать», — сказал однажды Фарб за ужином с друзьями. Когда один из гостей, также математик, удивился тому, что Фарбу удаётся достигать успеха в целых 10% случаев, Фарб признал: «Нет, нет, я сильно преувеличил процент своих успехов».
Фарб, тополог из Чикагского университета, с радостью встретил последнюю свою неудачу – хотя, честно говоря, это не только его заслуга. Вопрос связан с задачей, парадоксальным образом одновременно решённой и нерешённой, открытой и закрытой.
Задача – это 13-я из 23 математических проблем, которые не были решены в начале XX века. Тогда немецкий математик Давид Гильберт составил этот список, который, по его мнению, определял будущее математики. Задача связана с решением полиномиальных уравнений седьмой степени. Полином – это последовательность членом уравнения, каждый из которых состоит из числового коэффициента и переменных, возведённых в степень; между собой члены связываются сложением и вычитанием. Седьмая степень означает самую большую экспоненту у всех переменных.
Математики уже научились ловко и быстро решать уравнения второго, третьего и в некоторых случаях, четвёртого порядка. В эти формулы – в том числе и в знакомую квадратичную формулу для второй степени – входят алгебраические операции, то есть арифметические действия и извлечение корней. Но чем больше экспонента, тем запутаннее уравнение, и решать его становится всё сложнее. 13-я проблема Гильберта – это вопрос, можно ли выразить решение уравнения седьмого порядка через набор сложений, вычитаний, умножений, делений и алгебраических функций от максимум двух переменных.
В 1900 году Дэвид Гильберт составил список из 23 важнейших открытых проблем.
Ответ: вероятно, нет. Однако для Фарба это не просто вопрос решения сложного алгебраического уравнения. Он сказал, что 13-я проблема – одна из самых фундаментальных проблем математики, поскольку она поднимает глубокие вопросы: насколько сложны полиномы, и как это измерить? «Целый слой современной математики был изобретён для того, чтобы лучше понимать корни полиномов», — сказал Фарб.
Эта проблема затянула его и математика Джесси Вольфсона из Калифорнийского университета в Ирвине в математическую кроличью нору, ходы которой они изучают до сих пор. Она также привлекла к их раскопкам Марка Кисина, специалиста по теории чисел из Гарварда и старого друга Фарба.
Фарб признал, что они пока не решили 13-ю проблему Гильберта, и даже не приблизились к решению. Однако они раскопали почти исчезнувшие математические стратегии, и изучили связи проблемы с различными областями знаний, включая комплексный анализ, топологию, теорию чисел, теорию представлений и алгебраическую геометрию. Они применили собственные подходы, в частности, объединив полиномы с геометрией и сузив диапазон возможных ответов на вопрос Гильберта. Также их работа предлагает способ классификации полиномов по метрикам сложности – аналог классов сложности, имеющих отношение к нерешённой задаче равенства классов P и NP.
Они применили собственные подходы, в частности, объединив полиномы с геометрией и сузив диапазон возможных ответов на вопрос Гильберта. Также их работа предлагает способ классификации полиномов по метрикам сложности – аналог классов сложности, имеющих отношение к нерешённой задаче равенства классов P и NP.
«Они на самом деле смогли извлечь из интереса более интересную его версию» по сравнению с теми, что изучались ранее, сказал Дэниел Литт, математик из университета Джорджии. «Они показывают математическому сообществу множество естественных и интересных вопросов».
Открыли, закрыли и снова открыли
Многие математики уже считали проблему решённой. В конце 1950-х гениальный советский учёный Владимир Игоревич Арнольд и его наставник Андрей Николаевич Колмогоров опубликовали свои доказательства. Для большинства математиков работа Арнольда-Колмогорова закрыла этот вопрос. Даже в Википедии – не истине в последней инстанции, но довольно разумном посреднике в поисках знаний – до последнего времени задача была отмечена как решённая.

Владимир Арнольд и его наставник Андрей Колмогоров в 1950-х доказали один из вариантов 13-й проблемы Гильберта – но, возможно, Гильберта интересовал другой её вариант.
Однако пять лет назад Фарб наткнулся на несколько интригующих строчек в эссе за авторством Арнольда, где знаменитый математик размышляет над своей работой и карьерой. Фарб с удивлением узнал, что Арнольд описывает 13-ю проблему как открытую, и сорок лет пытался решить задачу, которую он вроде бы уже решил.
«Существуют научные работы, где просто повторяется тезис о решённости проблемы. Они явно не понимают самой проблемы», — сказал Фарб. В то время он работал вместе с Вольфсоном, бывшим тогда постдоком, над проектом в области топологии. Когда он поделился найденными в работе Арнольда сведениями, Вольфсон подключился к проекту. В 2017 году во время семинара, посвящённого 50-летию Фарба, Кисин услышал доклад Вольсфона и с удивлением понял, что их идеи, касающиеся полиномов, связаны с вопросами его работы по теории чисел. Он присоединился к их команде.
Он присоединился к их команде.
Причина путаницы с этой проблемой вскоре стала ясна: Колмогоров и Арнольд решили только один из её вариантов. В их решении фигурировали непрерывные функции – такие, у которых нет резких разрывов, или точек перегиба. Среди таких функций – знакомые операции вроде синуса, косинуса, экспоненты, а также более экзотические.
Однако не все исследователи согласны с тем, что Гильберта интересовали именно они. «Многие математики считают, что Гильберт имел в виду алгебраические, а не непрерывные функции», — сказал Зиновий Рейхштейн, математик из университета Британской Колумбии. Фарб и Вольфсон работают над проблемой, которую, как они считают, и хотел изучить Гильберт.
Фарб сказал, что 13-я проблема – это калейдоскоп. «Раскрываешь эту штуку – и чем больше изучаешь, тем больше направлений и идей она открывает, — сказал он. – Она приоткрывает дверь к целому массиву задач, показывает всю прекрасную паутину математики».
Корни проблемы
Математики игрались с полиномами с момента изобретения самой математики.
 На каменных табличках 3000-летней давности видно, как вавилонские математики использовали формулу для решения полиномов второго порядка. Это был клинописный предшественник той самой квадратичной формулы, которую сегодня учат на уроках математики. Формула показывает, как найти корни полинома – то есть, значения x, при которых выражение ax2+bx+c, полином второй степени, становится равным нулю.
На каменных табличках 3000-летней давности видно, как вавилонские математики использовали формулу для решения полиномов второго порядка. Это был клинописный предшественник той самой квадратичной формулы, которую сегодня учат на уроках математики. Формула показывает, как найти корни полинома – то есть, значения x, при которых выражение ax2+bx+c, полином второй степени, становится равным нулю.Со временем математики, естественно, заинтересовались вопросом о том, существуют ли такие чёткие и ясные формулы для полиномов высших порядков. «Многотысячелетняя история этой проблемы заключается в том, чтобы прийти к чему-то такому же мощному, простому и эффективному», — сказал Вольфсон.
Чем выше степень полинома, тем более громоздкими они становятся. В книге 1545 года «Ars Magna» [«Великое искусство»] итальянский эрудит Джероламо Кардано опубликовал формулы для поиска корней полиномов третьей и четвёртой степеней.
Корни кубического полинома ax3+bx2+cx+d=0 можно найти по следующей формуле:
Формула для полинома четвёртой степени выглядит ещё хуже.
«С ростом степени растёт и сложность, вырисовывается гора сложностей», сказал Курт Макмаллен из Гарварда. «Как нам покорить эту гору?».
Итальянский математик Паоло Руффини в 1799 году утверждал, что полиномы 5-й и больших степеней нельзя решить при помощи арифметических операций и извлечения корней. В 1824 году это доказал норвежский математик Нильс Хенрик Абель. Иначе говоря, подобной формулы для полинома пятой степени не существует. К счастью, появились другие идеи, предлагавшие способы изучать полиномы высших степеней, которые можно упростить через подстановку. К примеру, в 1786 году шведский юрист Эрланд Бринг показал, что любое уравнение вида ax5+bx4+cx3+dx2+ex+f=0 можно переписать в виде px5+qx+1=0, где p и q – комплексные числа, величину которых определяют a, b, c, d, e и f. Этот факт открыл новые подходы к скрытым свойствам полиномов.
В XIX веке Уильям Роуэн Гамильтон продолжил работы Бринга и других. В числе прочего он показал, что для поиска корней полинома шестой степени понадобятся лишь обычные арифметические операции, квадратные и кубические корни и алгебраическая формула, зависящая только от двух переменных.
В 1975 году американский алгебраист Ричарт Брауэр из Гарварда ввёл идею «степени резольвенты», описывающую минимальное количество членов, необходимых для описания полинома некоторой степени. Менее чем через год после этого Арнольд и японский специалист по теории чисел Горо Шимура в другой работе ввели почти такое же определение.
В модели Брауэра, первой попытке систематизации правил таких подстановок, 13-я проблема Гильберта – это вопрос о том, возможно ли, чтобы у полиномов седьмой степени степень резольвенты была меньше 3. Позднее он выдвинул сходные гипотезы по поводу полиномов шестой и восьмой степеней.
Однако в основе всех этих вопросов лежит более общий: каково наименьшее количество параметров, необходимое для поиска корней любого полинома? До какого нижнего предела можно дойти?
Визуальное мышление
Естественный подход к этому вопросу – представить себе, как выглядят полиномы. Полином можно записать как функцию – к примеру, f(x)=x2−3x+1, — и построить её график.
 Тогда поиски корней сводятся к тому, что функция становится равной нулю там, где её кривая пересекает ось х.
Тогда поиски корней сводятся к тому, что функция становится равной нулю там, где её кривая пересекает ось х.Чем выше степень полинома, тем сложнее его график. Функции третьего порядка с тремя переменными выдают гладкие но перекрученные поверхности в трёх измерениях. Зная, в какие места этих поверхностей смотреть, математики могут многое узнать о лежащей в их основе полиномиальной структуре.
В результате в попытках понять полиномы задействуется множество методов из алгебраической геометрии и топологии – разделов математики, фокусирующихся на том, что происходит с фигурами, когда они деформируются, сжимаются, растягиваются или ещё как-то изменяются без разрывов. «Анри Пуанкаре, по сути, изобрёл топологию, и чётко сказал, что сделал это, чтобы понять алгебраические функции, — сказал Фарб. – В то время люди с трудом изучали эти фундаментальные связи».
Сам Гильберт раскрыл особенно интересную связь, применив геометрию к этой проблеме. К тому времени, как он составил свой список проблем в 1900-м году, у математиков уже был большой набор трюков, позволявших понижать степени полиномов, но они всё равно не могли продвинуться дальше. Однако в 1927 году Гильберт описал новый трюк. Начал он с определения всех возможных способов упростить полиномы девятой степени, и нашёл среди них семейство особых кубических поверхностей.
Однако в 1927 году Гильберт описал новый трюк. Начал он с определения всех возможных способов упростить полиномы девятой степени, и нашёл среди них семейство особых кубических поверхностей.
Гильберт уже знал, что на каждой гладкой кубической поверхности – замысловатой фигуре, описываемой полиномом третьей степени – содержится ровно 27 прямых, вне зависимости от того, насколько перекрученной она выглядит. Эти прямые сдвигаются с изменением коэффициентов полиномов. Он понял, что зная положение одной из них, можно упростить полином девятой степени и найти его корни. Формуле требовалось всего четыре параметра – в современных терминах это значило, что степень резольвенты не превышает 4.
«Потрясающее озарение Гильберта состояло в том, что это чудо геометрии, происходящее из совершенно другого мира, можно было использовать, чтобы уменьшить степень резольвенты до 4», — сказал Фарб.
Движение к паутине связей
Когда Кисин помогал Фарбу и Вольфсону разбираться в задаче, они поняли, что общепринятое мнение о решённости 13-й проблемы Гильберта убило весь интерес в геометрическом подходе к степени резольвенты.
 В январе 2020 года Вольфсон опубликовал работу, оживившую этот подход. Она расширила геометрическое обращение Гильберта с полиномами девятой степени до более общей теории.
В январе 2020 года Вольфсон опубликовал работу, оживившую этот подход. Она расширила геометрическое обращение Гильберта с полиномами девятой степени до более общей теории.Гильберт сконцентрировался на кубических поверхностях для поисков решения полиномов девятой степени, содержавшего всего одну переменную. Но что насчёт полиномов более высоких степеней? Чтобы решить эту задачу сходным образом, подумал Вольфсон, можно заменить кубическую поверхность некоей «гиперповерхностью» высшего порядка, сформированной этими полиномами высших степеней со множеством переменных. Геометрия подобных поверхностей изучена не так хорошо, но за последние несколько десятилетий математики доказали, что в некоторых случаях на них всегда можно найти прямые.
На любой гладкой кубической поверхности, неважно, насколько она перекручена или свёрнута, можно найти ровно 27 прямых линий. Гильберт использовал этот геометрический факт для создания формулы корней полинома девятой степени. Джесси Вольфсон развил эту идею далее, используя прямые на «гиперповерхностях» высших степеней для создания формул для более сложных полиномов.
Идею Гильберта использовать прямые на кубической поверхности можно развить до прямых, находящихся на этих «гиперповерхностях» высших степеней. Вольфсон использовал этот метод для нахождения новых, более простых формул для полиномов определённых степеней. Получается, что даже если представить себе полином 100-й степени у вас не получится, вы можете найти его корни, «просто» найдя плоскость на многомерной кубической гиперповерхности (в данном случае она будет иметь 47 измерений).
При помощи этого нового метода Вольфсон подтвердил найденную Гильбертом величину степени резольвенты для полиномов девятой степени. А для полиномов некоторых других степеней – в особенности, степеней выше 9 – его метод сужает диапазон возможных значений степени резольвенты.
Так что это не прямая атака на 13-ю проблему Гильберта, а подход к полиномам в целом. «Они нашли некие смежные вопросы и смогли достичь прогресса в них, надеясь, что это прольёт свет на оригинальный вопрос», сказал Макмаллен. И их работа указывает новые пути работы с этими математическими конструкциями.
И их работа указывает новые пути работы с этими математическими конструкциями.
Общая теория степени резольвенты также показывает, что гипотезы Гильберта касательно уравнений шестого, седьмого и восьмого порядка эквивалентны другим задачам, известным в, казалось бы, не связанных с полиномами областях математики. Степень резольвенты, по словам Фарба, предлагает способ выстроить эти проблемы по алгебраической сложности, а не группировать их по классам сложности.
И хотя теорию породила 13-я проблема Гильберта, математики не уверены, что она способна решить открытый вопрос по поводу полиномов седьмой степени. Она касается гигантских неизученных математических масштабов в невообразимых измерениях, но при меньших значениях степеней сталкивается с непреодолимыми препятствиями, и не в состоянии определить для них степени резольвенты.
Для Макмаллена отсутствие продвижения – несмотря на намёки на прогресс – интересно само по себе. Из этого следует, что в задаче таятся секреты, которые современная математика просто неспособна объять. «Мы не смогли подступиться к этой фундаментальной проблеме – это означает, что мы не заходили в какие-то тёмные области», — сказал он.
«Мы не смогли подступиться к этой фундаментальной проблеме – это означает, что мы не заходили в какие-то тёмные области», — сказал он.
«Для её решения потребуются совершенно новые идеи», — сказал Рейхштейн, разработавший собственную идею по упрощению полиномов, концепцию, которую он называет «основным измерением». «Предугадать, откуда они появятся, невозможно».
Но троица не отступается. «Я не собираюсь сдаваться, — сказал Фарб. – Эта задача определённо стала моим белым китом. Она заставляет меня не останавливаться в этой паутине связей, и окружающей её математике».
Упрощение выражений с помощью порядка операций
Результаты обучения
- Используйте порядок операций для упрощения математических выражений
- Упростите математические выражения, включая сложение, вычитание, умножение, деление и экспоненты
Упростите выражения, используя порядок операций
Мы ввели большинство символов и обозначений, используемых в алгебре, но теперь нам нужно уточнить порядок операций. В противном случае выражения могут иметь разное значение и приводить к разным значениям.
В противном случае выражения могут иметь разное значение и приводить к разным значениям.
Например, рассмотрим выражение:
[латекс] 4 + 3 \ cdot 7 [/ латекс]
[latex] \ begin {array} {cccc} \ hfill \ text {Некоторые студенты говорят, что это упрощается до 49.} \ Hfill & & & \ hfill \ text {Некоторые студенты говорят, что это упрощается до 25.} \ hfill \\ \ begin {array} {ccc} & & \ hfill 4 + 3 \ cdot 7 \ hfill \\ \ text {Так как} 4 + 3 \ text {дает 7.} \ hfill & & \ hfill 7 \ cdot 7 \ hfill \\ \ text {And} 7 \ cdot 7 \ text {равно 49.} \ hfill & & \ hfill 49 \ hfill \ end {array} & & & \ begin {array} {ccc} & & \ hfill 4 + 3 \ cdot 7 \ hfill \\ \ text {Since} 3 \ cdot 7 \ text {равно 21.} \ hfill & & \ hfill 4 + 21 \ hfill \\ \ text {And} 21 + 4 \ text {составляет 25.} \ hfill & & \ hfill 25 \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Представьте себе путаницу, которая могла бы возникнуть, если бы для каждой проблемы было несколько разных правильных ответов.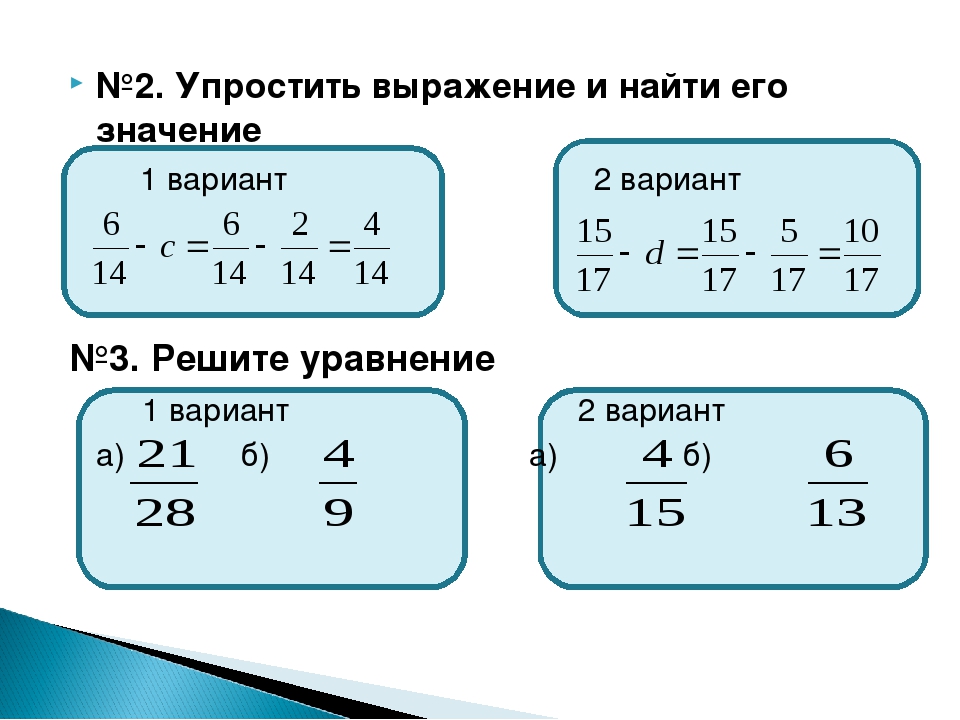 Одно и то же выражение должно дать такой же результат. Поэтому математики установили некоторые правила, называемые порядком операций, которые определяют порядок, в котором части выражения должны быть упрощены.
Одно и то же выражение должно дать такой же результат. Поэтому математики установили некоторые правила, называемые порядком операций, которые определяют порядок, в котором части выражения должны быть упрощены.
Порядок действий
При упрощении математических выражений выполняйте операции в следующем порядке:
1. P аренты и другие символы группировки
- Упростите все выражения внутри скобок или других группирующих символов, работая в первую очередь с самыми внутренними скобками.
2. E xponents
- Упростите все выражения с помощью показателей степени.
3. M ultiplication и D ivision
- Выполните все операции умножения и деления слева направо.Эти операции имеют равный приоритет.
4. A ddition и S ubtraction
- Выполняйте все операции сложения и вычитания слева направо.
 Эти операции имеют равный приоритет.
Эти операции имеют равный приоритет.
Студенты часто спрашивают: «Как мне запомнить порядок?» Вот способ помочь вам запомнить: возьмите первую букву каждого ключевого слова и замените ее глупой фразой. P аренда E xcuse M y D ear A Unt S союзник.
| Порядок работы | |
|---|---|
| P аренда | P аренте |
| E xcuse | E xponents |
| M y D ухо | M ultiplication и D ivision |
| A Unt S союзник | A ddition и S ubtraction |
Хорошо, что « M y D ear» идут вместе, поскольку это напоминает нам, что m ultiplication и d ivision имеют равный приоритет. Мы не всегда выполняем умножение перед делением или всегда делаем деление перед умножением. Делаем их слева направо.
Мы не всегда выполняем умножение перед делением или всегда делаем деление перед умножением. Делаем их слева направо.
Аналогичным образом, « A Unt S союзник» объединяется и таким образом напоминает нам, что a ddition и s ubtraction также имеют равный приоритет, и мы выполняем их в порядке слева направо.
пример
Упростите выражения:
- [латекс] 4 + 3 \ cdot 7 [/ латекс]
- [латекс] \ влево (4 + 3 \ вправо) \ cdot 7 [/ латекс]
Раствор:
пример
Упростить:
- [латекс] \ text {18} \ div \ text {9} \ cdot \ text {2} [/ latex]
- [латекс] \ text {18} \ cdot \ text {9} \ div \ text {2} [/ latex]
Решение:
пример
Упростить: [латекс] 18 \ div 6 + 4 \ left (5 — 2 \ right) [/ latex].
Решение:
| [латекс] 18 \ div 6 + 4 (5-2) [/ латекс] | |
| Круглые скобки? Да, сначала вычтите. | [латекс] 18 \ div 6 + 4 (\ color {red} {3}) [/ латекс] |
| Показатели? № | |
Умножение или деление? Да. | |
| Сначала разделите, потому что мы умножаем и делим слева направо. | [латекс] \ color {красный} {3} +4 (3) [/ латекс] |
| Любое другое умножение или деление? Да. | |
| Умножить. | [латекс] 3+ \ color {красный} {12} [/ латекс] |
| Любое другое умножение или деление? № | |
| Любое сложение или вычитание? Да. | [латекс] 15 [/ латекс] |
В видео ниже мы показываем еще один пример того, как использовать порядок операций для упрощения математического выражения.
Когда имеется несколько символов группировки, мы сначала упрощаем самые внутренние круглые скобки и работаем наружу.{3}} + 3 [0] [/ латекс]

В видео ниже мы показываем еще один пример того, как использовать порядок операций для упрощения выражения, содержащего экспоненты и символы группировки.{2}} [/ латекс]
Упростите полиномиальные и рациональные члены с помощью программы «Пошаговое решение математических задач»
ПОДПИСАННЫЕ НОМЕРА
Цели
В этом разделе вы будете складывать, вычитать, умножать и делить числа со знаком. Также при решении арифметических выражений вы будете использовать порядок операций, включая показатели.
Также при решении арифметических выражений вы будете использовать порядок операций, включая показатели.
Интуитивный подход к сложению и вычитанию:
Пример 1. У меня есть 40 долларов, и я должен вам 75 долларов. Какая у меня чистая стоимость?
Чтобы найти ответ:
Наличие 40 долларов эквивалентно + 40.
Должность 75 долларов эквивалентна — 75.
Моя чистая стоимость будет обозначена как 40 — 75.
или
40 — 75 = -35
Мой собственный капитал равен — 35 долларов.
Поскольку я должен больше, чем имею, ответ должен быть отрицательным.
Правило: Интуитивное правило объединения чисел с в отличие от знаков :
Найдите разность (вычитание) двух чисел и используйте знак большего числа.
Способ использования этого правила — скрыть знаки чисел. Найдите разницу между числами с закрытыми знаками. Используйте знак большего числа.
Пример 2. Я в долгу на 50 долларов, и я должен вам на 60 долларов. Какая у меня чистая стоимость?
Какая у меня чистая стоимость?
Чтобы найти ответ:
Долги на 50 долларов эквивалентны -50.
Должность 60 долларов эквивалентна — 60.
Моя чистая стоимость обозначается как -50 — 60.
или
-50-60 = -110
Моя чистая стоимость составляет — 110 долларов.
Поскольку я в долгу, и я должен вам деньги, мой собственный капитал должен быть отрицательным.
Правило: Интуитивное правило для объединения чисел с подобными знаками : сложите два числа и используйте общий знак.
Учебный совет: Сделайте карточку с правилами сложения и вычитания похожих и непохожих чисел со знаком.Просматривайте карточки с заметками не реже двух раз в неделю в рамках вашего распорядка домашнего задания.
Умножение и деление:
Словарь: Произведение — это ответ на задачу умножения.
Частное — это ответ на проблему деления.
Пример 3. Я буду терять 9 долларов в день каждый из следующих 6 дней. Сколько денег я потеряю?
Сколько денег я потеряю?
Чтобы найти ответ:
Потеря 9 долларов эквивалентна -9.
Поскольку я теряю 9 долларов каждый день в течение следующих 6 дней, у меня будет на 9 * 6 долларов меньше.
или
-9 * 6 = -54
Я потеряю 54 доллара в следующие 6 дней.
Поскольку я теряю деньги, ответ должен быть отрицательным числом.
В приведенном выше примере -54 — это продукт .
Словарь: Факторы — это умножаемые числа. В приведенном выше примере -9 * 6 = -54, -9 и 6 являются множителями.
Правило: Произведение или частное двух чисел с в отличие от знаков всегда отрицательное.
Пример 4. Я потерял 8 долларов в день за предыдущие 7 дней. Сколько еще денег у меня было 7 дней назад?
Поскольку 7 дней назад у меня было больше денег, ответ должен быть положительным.
Чтобы найти ответ:
Потеря 8 долларов эквивалентна -8.
Предыдущие 7 дней эквивалентны -7
Так как я терял 8 долларов каждый день в течение последних 7 дней,
У меня будет на -8 * -7 долларов меньше. или же
-8 * -7 = 56
7 дней назад у меня было еще 56 долларов.
или же
-8 * -7 = 56
7 дней назад у меня было еще 56 долларов.
Правило: Произведение или частное двух чисел с подобными знаками всегда положительно.
Пример 5. Разделить
Поскольку числитель и знаменатель отрицательны, частное должно быть
положительный.
Учебный совет: Сделайте карточки для всех правил и словарного запаса курса.
Задачи умножения можно выразить несколькими способами:
Проблемы с разделением можно выразить несколькими способами:
Задача с нуля в делении
Деление можно проверить с помощью умножения.Например, потому что 18 = 3 * 6
18 разделить на 6 — это то же самое, что спросить, какое число, умноженное на 6, равно 18?
Как ноль в числителе влияет на проблему деления?
Например, это то же самое, что спросить, какое число, умноженное на 31, равно 0? Итак, = 0, потому что 0 * 31 = 0.
Ноль, деленный на любое число, равняется нулю.
Как ноль в знаменателе влияет на проблему деления?
Например, это то же самое, что спросить, какое число, умноженное на 0, равно 17? Не существует числа, которое при умножении на 0 равно 17.Таким образом, ответ на вопрос не определен.
Любое число, деленное на ноль, не определено.
Как ноль в числителе и знаменателе влияет на проблему деления?
Например, это то же самое, что спросить, какое число, умноженное на 0, равно 0? Пять умножить на ноль равно нулю, так что. Кроме того, 3, умноженное на ноль, равно нулю, так что.
Фактически, каждое число, умноженное на ноль, равняется нулю, поэтому равняется любому числу.
Ноль, деленный на ноль, не может быть однозначно определен и называется неопределенным.
Учебный совет: Деление на ноль (ноль в знаменателе) равно undefined . Ноль в числителе и знаменателе называется , неопределенный . Запишите эти концепции на карточку.
Словарь: 3 и -3 являются противоположностями , потому что они оба находятся на одинаковом расстоянии от нуля на числовой прямой, но в противоположных направлениях. Их также называют аддитивными инверсиями , поскольку их сумма равна нулю.
Их также называют аддитивными инверсиями , поскольку их сумма равна нулю.
Противоположность -6 — 6.В математической записи — (-6) = 6. Первый отрицательный знак означает использование противоположного знака; второй знак минус означает, что цифра 6 отрицательна или находится слева от нуля в числовой строке.
В приложении ниже слово «прибыль» используется, даже если число отрицательное, что действительно указывает на убыток.
Пример 6. Приложение: На приведенном ниже графике показаны прибыли и убытки SRH Inc. за период с 2001 по 2006 годы.
а. Какая разница между прибылью 2005 года и убытком 2002 года?
«Разница» означает вычитание.Итак, чтобы ответить на вопрос, вычтите убыток 2002 г. из прибыли 2005 г .:
(прибыль 2005 г.) — (убыток 2002 г.).
7,3 — (-15,8)
Найдите на графике соответствующую прибыль и убыток.
= 7,3 + 15,8
Интерпретируйте — (-15,8) как нахождение противоположности -15,8.
= 23,1
Сложите два числа.
Разница между прибылью 2005 года и убытком 2002 года составила 23,1 миллиона долларов. Ответ положительный, потому что прибыль SRH увеличилась с 2002 по 2005 год.
б .. Какая разница между прибылью 2006 года и прибылью 2005 года? Какое значение имеет отрицательный знак в вашем ответе?
(прибыль 2006 г.) — (прибыль 2005 г.)
5,2-7,3 = -2,1
Разница в прибыли составила -2,1 млн долларов.
Ответ отрицательный, потому что прибыль SRH снизилась с 2005 по 2006 год.
г. Какова средняя (средняя) прибыль за шесть лет?
Чтобы найти среднее значение, сложите прибыли и убытки; затем разделите на количество лет.
Средняя прибыль за шесть лет составила убыток в размере 5,317 миллиона долларов или -5,317 миллиона долларов прибыли.
Использование калькулятора для сложения, вычитания, умножения или деления:
(Для этого курса рекомендуется использовать калькулятор TI-30X II S. См. Страницу электронных ресурсов MAT 011, чтобы узнать, как пользоваться калькулятором.)
См. Страницу электронных ресурсов MAT 011, чтобы узнать, как пользоваться калькулятором.)
Клавиши умножения, сложения и деления стандартные. Обратите внимание, что ключ для умножения на калькуляторе — x, но на экране калькулятора он отображается как *.Для деления клавиша деления — +, но на экране отображается как /.
Пример 7. — 7,4 — 8,6 = -16
— 7,4 указывает, что 7,4 отрицательно. Чтобы ввести отрицательное число в калькулятор, вы должны использовать клавишу, которая отличается от клавиши вычитания
Учебный совет: Перед использованием калькулятора вы должны потратить пару секунд, чтобы мысленно оценить ответ.
Словарь: Показатели: b n означает, что число b используется как множитель n раз.
Пример 8. (-7) 2 = (-7) (- 7) = 49
Порядок операций:
Когда задача числовой алгебры состоит из более чем одной операции, порядок следующий:
Первый: Внутри P скобок, ().
Второй: E xponents
Третий: M ultiplication или D ivision (слева направо)
Четвертый: A ddition или S ubtraction (слева направо)
Учебный совет: P lease E xcuse M y D ear A Unt S ally — мнемоника, используемая для изучения порядка операций.P (круглые скобки), E (показатели), M (умножение), D (деление), A (сложение) и S (вычитание).
Пример 9. -6 (8–13) = -6 (-5) = 30
Сложите числа со знаком в круглых скобках. Произведение чисел с одинаковыми знаками положительное.
Вычислить количество (-3) 2.
Вычислить противоположность +9.
Вычесть по правилам чисел со знаком.
Оценка: важно оценить результат перед использованием калькулятора. Это поможет вам определить, разумен ли ваш ответ.Оценка должна быть быстрой и производиться мысленно. Ключ к оценке — округление.
Резюме:
Числа со знаком — ключевое понятие в Начальной алгебре. Поначалу они могут сбивать с толку, но как только правила выучены и отработаны на практике, эти числа работают очень предсказуемо. Наряду с числами со знаком, порядок действий необходимо освоить в начале семестра. Ответы будут сильно отличаться, если не соблюдать правильный порядок действий.
Поначалу они могут сбивать с толку, но как только правила выучены и отработаны на практике, эти числа работают очень предсказуемо. Наряду с числами со знаком, порядок действий необходимо освоить в начале семестра. Ответы будут сильно отличаться, если не соблюдать правильный порядок действий.
1. Интуитивные правила для сложения и вычитания чисел со знаком:
a. В отличие от знаков: найдите разность (вычитание) двух чисел и используйте знак большего числа.
г. Как знаки: сложите два числа и используйте общий знак.
2. Правила для умножения и деления двух чисел со знаком:
a. В отличие от знаков: результат всегда отрицательный.
г.Знаки вроде: результат всегда положительный.
3. Порядок операций:
Первый: Внутри скобок, ()
Второй: Показатели
Третий: Умножение и деление (слева направо)
Четвертый: Сложение и вычитание (слева направо)
ВВЕДЕНИЕ В ПЕРЕМЕННЫЕ
Целей:
Выполнив аналогичные арифметические действия, вы обнаружите необходимость в переменных.
Пример 1. Вам необходимо арендовать фургон для перевозки грузов. Class Movers взимает базовую ставку в размере 24,95 долларов США плюс 32 цента за милю.
а. Рассчитайте стоимость аренды микроавтобуса, если вы проехали следующие мили:
Словарь: Переменная в алгебре — это буква, которая представляет величину, которая может изменяться. В приведенном выше примере m представляет количество миль, а c — стоимость. И мили, и стоимость могут отличаться или меняться. Переменный член содержит букву и умножающее ее число; 0.32 м — переменный член. Константа — это число, которое никогда не меняет значения; 24,95 — постоянная величина.
г. Какое уравнение связывает стоимость и количество пройденных миль? Последняя строка в приведенной выше таблице содержит ответ c = 0,32m + 24,95
.г. Другая компания по аренде, Zippo Movers, взимает фиксированную ставку в размере 42,95 доллара. Сколько миль вам нужно проехать, чтобы Zippo и Class заряжались одинаково?
Уравнение затрат для Zippo: c = 42,95
Чтобы рассчитать, когда расходы двух компаний одинаковы, приравняйте уравнения затрат друг к другу.
Стоимость Zippo = Стоимость класса
42,95 = 0,32 млн + 24,95
Поскольку мы только начали изучать алгебру, мы будем угадывать решение. Подставьте предположение о количестве миль в уравнение для Class Movers,
c = 0,32 м + 24,95.
Если вы проедете 55 миль, то обе компании будут брать примерно одинаковую плату. Гадать очень утомительно и неточно. Позже в этой главе мы будем использовать алгебру для решения проблемы. Алгебра прямая и точнее, чем догадки.
Пример 2. По оценкам, Минивэн Toyota Sienna 2011 года теряет в стоимости 1800 долларов в год. Первоначально минивэн стоил 42 тысячи долларов.
а. Рассчитайте стоимость минивэна на последующие годы.
г. Какое уравнение связывает стоимость фургона и количество лет, прошедших с 2011 года?
Последняя строка в приведенной выше таблице содержит ответ, v = 42,000 — 1,800t
г. Когда фургон будет стоить 20 400 долларов?
Чтобы ответить на вопрос, вы должны найти значение y, которое составит v = 20 400 или
20 400 = 42 000 — 1800 т.
Поскольку мы еще не знаем, как решить задачу с помощью алгебры, мы будем угадывать решение. Подставляем предположение вместо t, количества лет, прошедших с 2007 года, в уравнение
В = 42,000 — 1,800т.
При повторении этого будет создана следующая таблица.
Минивэн будет стоить 20 400 долларов через двенадцать лет после 2011 года. В 2023 году минивэн будет стоить $ 20 400
.Резюме:
Обучение составлению таблицы — еще один ключевой шаг в изучении алгебры.Убедитесь, что ваша таблица содержит правильное количество столбцов для необходимой информации. Нарисуйте таблицы с помощью линейки, чтобы информация не сбивала с толку.
По каждой проблеме в этом разделе вы должны уметь:
1. Создайте таблицу.
Пояснение: Столбец расчета является самым важным. Он показывает, как вы получаете свое уравнение.
2. Когда вы определили уравнение, вы должны понять, что представляет каждый член уравнения.
Например: с = 0,32 м + 24,95 * c — стоимость аренды фургона. * 0,32 — это сумма, которую взимают Class Movers за милю, m — это количество миль, которое вы проедете на фургоне. * * 24,95 — это базовая ставка или фиксированная стоимость.
Учебный совет: Используйте описательные буквы для переменных в прикладных задачах, c — для стоимости и m — для количества пройденных миль.
УПРОЩЕНИЕ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Цели
В этом разделе начинается процесс решения уравнений.Вы поймете, как объединить одинаковые термины и как использовать распределительное свойство .
Словарь: Термины: частей алгебраического выражения, разделенных знаками сложения или вычитания.
Пример 1. Для 3 + 5 = 8, 3 и 5 являются членами.
Пример 2. Для 3x — 5y, 3x и -5y являются терминами.
Коэффициент: число, умножающее переменную.
Пример 3. Для выражения 7x — 2y + z,
7 — это коэффициент x;
-2 — это коэффициент y, а
1 понимается как коэффициент z.
Как термины: терминов с одинаковой переменной и показателем; и термины, которые являются числами без переменных.
Пример 4. Для выражения 4x + 7y — 3x + 4z, 4x и -3x являются подобными членами.
Правило: Чтобы объединить одинаковые термины , сложите их коэффициенты. 4x + (-3x) = x или 1x.
Пример 5. Объедините похожие термины.
3x — 5 — 6x + 7 = -3x + 2
Обозначьте аналогичные термины, 3x и -6x, -5 и 7.
Добавьте коэффициенты подобных терминов.
Словарь: Распределительное свойство: Определение a (b + c) = a * b + a * c
Пример 6. Эти две арифметические задачи демонстрируют свойство распределенности.
Explanation: Всегда работайте сначала в скобках. Используйте свойство distributive только в том случае, если вы не можете упростить то, что заключено в круглые скобки.
Учебный совет: 1. Вы можете просмотреть порядок операций на стр.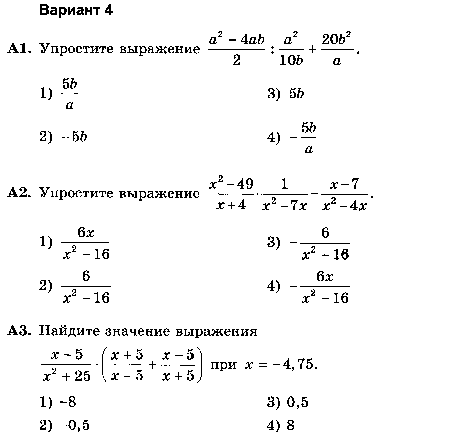 5.2. Напишите эти важные определения и правила на карточках для заметок и используйте их в своей домашней работе.
5.2. Напишите эти важные определения и правила на карточках для заметок и используйте их в своей домашней работе.
Пример 7. Используйте свойство распределения.
3 (6x — 5) = Невозможно объединить термины в круглых скобках, потому что они не похожи на термины.
3 (6x) — 3 (5) = Используя свойство распределения, умножьте 6x и -5 на 3.
8x — 15 Нельзя объединить эти разные термины.
Пример 8. Используйте свойство распределения.
-5 (4x + 2) = Невозможно объединить термины в круглых скобках, потому что они не похожи на термины.
(-5) (4x) + (-5) (2) = Используя свойство распределения, умножьте 4x и 2 на -5.
-20x -10 Невозможно объединить эти непохожие термины.
Упрощение алгебраических выражений:
Пример 10. Упростите выражение.
4- (2x-3) =
Точно так же, как -x означает -1 * x, — (2x-3) означает -1 (2x-3)
4-2x + 3 =
Использование свойства распределения; умножьте 2x и -3 на -1
-2x + 72
Объедините похожие термины.
Пример 11. Упростите выражение.
11x-14x-3 (4x-2) =
Используя свойство распределения, умножьте 4x и -2 на -3.
11x-14-12x + 6 =
Объедините похожие термины, 11x и -12x, а также -14 и 6.
-1x-8 =
-1x означает то же самое, что и -x
-x-8
Нельзя объединить эти непохожие термины.
Резюме:
Упрощение алгебраических выражений
Теперь мы готовы к реальной работе по алгебре. Ключевые определения включают:
1. Распределительное свойство .
a (b + c) = a * b + a * c
Множитель «a» умножает «b» и «c» в скобках.
2. Термины разделяются знаками сложения или вычитания.
3. Подобные термины имеют одинаковую переменную и показатель степени.
4. Коэффициент — это число при умножении переменной.
5. Факторы — это умножаемые элементы.
Важный последний вопрос:
Словарь: Что такое алгебраическое выражение? Алгебраическое выражение состоит из терминов, некоторые из которых содержат переменные.
РЕШЕНИЕ УРАВНЕНИЙ
Целей:
В разделе «Введение в переменные» мы решали уравнения методом предположений.В этом разделе вы узнаете, как решать уравнения с помощью алгебры. Алгебра проще и точнее, чем догадки.
Пример 1. Вам необходимо арендовать фургон. Class Movers взимает базовую ставку в размере 24,95 долларов США плюс 32 цента за милю.
а. Рассчитайте стоимость аренды микроавтобуса, если вы проедете следующие мили.
Уравнение затрат: c = 0,32 млн + 24,95.
г. Используйте уравнение, чтобы рассчитать, сколько миль вы проехали, если стоимость проезда составляет 42 доллара.87.
Логическое решение. Стоимость 42,87 доллара содержит базовую ставку 24,95 доллара. Если вычесть 24,95 доллара из 42,87 доллара, получим 17,92 доллара. Вот какая часть стоимости связана с количеством пройденных миль. Так как он стоит 32 цента за милю, деление 17,92 на 0,32 определяет количество пройденных миль или 56 миль. Та же самая логика — алгебра.
Та же самая логика — алгебра.
Алгебраическое решение: найти m, когда c = 42,87.
42,87 = 0,32 м +24,95
Заменить 42,87 на c.
42,87 — 24,95 = 0,32 м
Вычтите 24.95 из 42,87 из-за стоимости, 42,87 содержит базовую ставку 24,95
17,92 = 0,32 м
Объедините аналогичные термины, 42,87 и 24,95
Стоимость пройденных миль составляет 17,92. Так как это стоит 32 цента за милю, разделите 17,92 на 0,32
56 = m
Ответ.
Вы можете проехать 56 миль за 42,87 доллара.
г. Проверьте свой ответ. Подставляем m = 56 в уравнение c = 0,32m + 24,95; Стоимость должна быть 42,87 $.
Учебный совет: Вы должны ответить на проблему предложением, как в примере 1 выше: (Вы можете проехать 56 миль за 42 доллара.87.), который относится к обеим переменным в проблеме.
Правило: Как решить уравнение:
1. Упростите каждую часть уравнения, используя свойство распределения и , объединяя одинаковые члены .
2. Следующая цель — записать уравнение в форме:
Переменный член = константа
Это делается с помощью свойств сложения или вычитания уравнений.
3. Разделите обе части на коэффициент (число, умножающее переменную) переменной.
Объяснение: член переменной содержит букву, которая может представлять разные значения. Константа — это число, которое никогда не меняет значения.
Пример 2. Решить.
Вычтем 24,95 из обеих частей уравнения.
Объедините одинаковые термины, 42,87 и — 24,95, 24,95 и — 24,95.
Это наша первая цель в решении проблемы.
Разделите на обе стороны на коэффициент m, 0,32
Выполните деление.
Пример 3. Решить.
7x — 4 = 5 (2x + 9) + 3x
Используйте свойство распределения; умножьте 2x и 9 на 5.
7x — 4 = 10x + 45 + 3x
Объедините похожие члены; сложить 10x и 3x
Необходим переменный член, равный постоянному члену. Поскольку в обеих частях уравнения есть постоянный член, добавьте 4 к обеим сторонам уравнения.
7x-4 = 13x + 45
7x — 4 + 4 = 13x + 45 + 4
Объедините похожие члены, -4 и 4, 45 и 4
7x = 13x + 49
Нужен переменный член, равный постоянному члену.Поскольку в обеих частях уравнения есть переменный член, вычтите 13x из обеих частей уравнения.
7x — 13x = 13x — 13x + 49
Объедините похожие термины, 7x и -13x, 13x и -13x.
-6x = 49
Теперь есть переменный член, равный постоянному члену,
, поэтому разделите обе стороны на -6, коэффициент при x.
Разделить.
x = -8,167
Ответ округляется до 3 знаков после запятой.
Пример 4. Решить.
Использовать распределительное свойство; умножьте
6x и -7 на -2.
Объедините одинаковые члены, 4 и 14.
Требуется переменный член, равный постоянному члену. Поскольку в обеих частях уравнения есть переменный член, добавьте 12x к обеим сторонам уравнения.
Объедините похожие термины.
18 никогда не может быть равно 10, поэтому вывод такой: проблема не имеет решения.
Объяснение: Посмотрите на -12×4-18 = -12×4-10 Обратите внимание, что -12x находится с обеих сторон уравнения, но одна сторона имеет 18, а другая 10. Вы понимаете, почему вы не можете найти решение?
Пример 5. Решить.
Воспользуйтесь распределительным свойством. Объедините похожие термины. Требуется переменный член, равный постоянному члену. Поскольку в обеих частях уравнения есть переменный член, вычтите 31 x из обеих частей.
Объедините похожие термины.
-10 всегда равно -10, поэтому вывод состоит в том, что каждое число является решением.
Объяснение: Посмотрите на -31x -10 = -31x- 10 Обратите внимание, что одни и те же алгебраические выражения находятся по обе стороны от знака равенства. Вы понимаете, почему любое число делает уравнение истинным?
Словарь: Условное уравнение имеет конечное число решений.В этом разделе условное уравнение будет иметь одно решение. Примеры 1,2 и 3 являются условными уравнениями.
г. Когда уравнение не имеет решения, оно называется противоречием .
Пример 4 противоречит тому, что, когда все переменные исключены, возникает ложное арифметическое утверждение.
г. Когда все числа являются решениями уравнения, тогда оно называется тождеством .
Пример 5 идентичен, потому что, когда все переменные исключены, получается истинное арифметическое выражение.
Пояснение: Решение уравнений основано на принципе равенства . Принцип равенства гласит: чтобы сохранить равенство, все, что вы делаете с одной стороной уравнения, вы должны делать с другой. В этом примере к обеим сторонам добавлено 5; 2x было вычтено с обеих сторон, и обе стороны были разделены на 4.
Резюме:
Алгебра и арифметика разные. Арифметика включает операции с числами.В алгебре есть переменные, которые могут представлять множество различных чисел. Если вы вспомните раздел «Введение в переменные» в последней строке созданных нами таблиц, мы использовали переменные для представления всей арифметики в предыдущих строках. Алгебра — это обобщение повторяющихся арифметических операций. Уравнения из Введение в переменные содержат две переменные. Если вам известно значение одной из переменных, вы можете использовать процедуры в этом разделе, чтобы найти значение другой.Решение уравнений — основная функция алгебры.
Алгебра — это обобщение повторяющихся арифметических операций. Уравнения из Введение в переменные содержат две переменные. Если вам известно значение одной из переменных, вы можете использовать процедуры в этом разделе, чтобы найти значение другой.Решение уравнений — основная функция алгебры.
Как решать уравнения:
1. Упростите обе части уравнения, используя свойство распределения,
a (b + c) = ab + ac, и комбинируя похожие члены.
2. Первая цель — записать уравнение в форме:
Переменный член = константа
Это делается с помощью принципов сложения и вычитания.
3. Разделите обе части уравнения на коэффициент, полученный при умножении переменной.
4. Решение уравнения этого типа имеет три возможных результата:
a.Одно решение, условное уравнение.
г. Нет решения, противоречие.
г. Все числа — это решения, или проблема имеет бесконечное количество решений, идентичность.
Учебный совет: Вы должны записать шаги на карточке для заметок вместе с примером.
ПРИЛОЖЕНИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ
Цель:
Этот раздел представляет собой обзор курса на сегодняшний день. Вы создадите таблицы для поиска уравнений, а затем решите их с помощью алгебры.
Учебный совет: Если у вас возникли проблемы с этим разделом, просмотрите Раздел «Введение в переменные» и Раздел «Решение уравнений».
Пример 1. Студент покупает новую машину в 2010 году за 36 000 долларов, и автомобиль обесценивается на 3 100 долларов в год.
а. Напишите уравнение, которое связывает стоимость автомобиля с возрастом.
Уравнение v = 36,000 — 3,1 OOt. t — количество лет, прошедших с 2010 года.
г. Когда машина будет стоить 20000 долларов?
Найдите y, когда v = 20,000.
20,000 = 36,000 — 3,100т
Заменено 20,000 вместо v.
-16,000 = — 3,100t
Вычтено 36,000 с обеих сторон.
5,161 = t
Делим с обеих сторон на -3,100.
Автомобиль будет стоить примерно 20 000 долларов через 5 лет, а именно 2015 (2010 + 5).
г. Когда машина станет бесполезной?
Автомобиль бесполезен, если его стоимость равна нулю. Найдите y, когда v = 0.
0 = 36,000 — 3,100t
Заменено 0 вместо v.
3,1 OOt = 36,000
Добавлен 3,1 OOt с обеих сторон,
t = 11,61
Разделим обе стороны на 3,100.
Машина придет в негодность лет через 12, а именно 2022 (2010 + 12).
Учебный совет: В последней задаче мы записали меньше шагов. Вы должны потратить пару минут на то, чтобы детально разобраться в проблеме. Вы должны знать, как был сделан каждый шаг. Используйте свой домашний блокнот. Оставьте достаточно места, чтобы не запутаться.
Пример 2. Компания по аренде грузовиков класса взимает базовый тариф в размере 34,99 доллара плюс 0,20 доллара за милю после первых 15 миль.
а. Напишите уравнение стоимости аренды в Class.
Пояснение: Они берут 20 центов за 15 миль, поэтому, если вы едете 25 миль, с вас взимается только 20 центов за 10 миль, 25-15. Поскольку перед умножением на 0,20 вы вычли 25-15, вам нужны скобки.
Поскольку перед умножением на 0,20 вы вычли 25-15, вам нужны скобки.
Уравнение затрат: c = 0,20 (m — 15) + 34,99.
г. Упростите уравнение.
Б / у в распределительной собственности; умноженное m и -15 на
0,20, 0,20m и 0,20 (-15) = -3
Объединенные одинаковые члены, -3 и 34,99.
г. Сколько миль вы можете пройти, если стоимость билета составляет 85 долларов? Найдите m, когда C = 85.
85 = 0,20m + 31,99
Заменено 85 вместо C.
53,01 = 0,20 м
Вычтено 31.99 с обеих сторон.
265,05 = м
Делим с обеих сторон на 0,20.
Округляя до ближайшей мили, вы можете проехать около 265 миль за 85 долларов.
Резюме:
В этом разделе дается обзор большей части материала, представленного на данный момент в курсе, и поэтому чрезвычайно важен. Вы должны уметь:
1. Прочтите задачу и создайте таблицу, чтобы найти уравнение.
2. Решите алгебраические уравнения, чтобы получить желаемое решение. Мы дошли до уровня сложности, когда «угадывание» — это трудоемкий метод определения алгебраических решений; использовать алгебру.
Мы дошли до уровня сложности, когда «угадывание» — это трудоемкий метод определения алгебраических решений; использовать алгебру.
Советы по обучению: 1. Если какой-либо из вышеперечисленных шагов вам непонятен, задайте вопросы на следующем занятии, обратитесь к своему инструктору в рабочее время, перейдите в учебный центр или воспользуйтесь онлайн-преподавателями.
2. Не продолжайте, пока не освоите этот раздел.
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
Целей:
В этом разделе вы узнаете, как решать уравнения с двумя переменными.Алгебра такая же, как и в предыдущих разделах. Разница в том, что решением будет уравнение, а не число.
Словарь: Литеральное уравнение — это уравнение, которое включает более одной переменной.
Пример 1. Компания сотовой связи взимает базовый тариф в размере 1,25 доллара плюс 0,15 доллара за минуту после первых 10 минут.
а. Заполните таблицу, чтобы узнать стоимость телефонных звонков продолжительностью более десяти минут.
Пояснение: Круглые скобки необходимы, потому что плата составляет 15 центов за минуту только через 10 минут.
г. Какое уравнение связывает стоимость и минуты? Упростите уравнение.
Распределительная собственность: умножить m и -10 на 0,15 Комбинированные одинаковые условия, -1,50 + 1,25
г. Если звонок стоит 2,90 доллара, как долго вы разговаривали по телефону? Найдите m, когда c = 2,90.
Sub 2.90 для c.
2,15 = 0,15 м
Добавил по 0,25 с обеих сторон.
21 = м.
Делится с обеих сторон на 0,15
г. Решите относительно m в уравнении из части b.
(Это единственная новая информация в этом разделе.)
Зачем вам это нужно? Представьте себе ситуацию, когда вы знаете стоимость десяти разных звонков. Вместо того, чтобы решать для C десять раз подряд, вы можете решить для C один раз, а затем использовать арифметику, чтобы найти десять различных значений m.
c = 0,15 м — 0,25
c + 0,25 = 0,15 м
Добавлен по 0,25 с обеих сторон.
Разделены на 0,15 с обеих сторон
Пояснение: Алгебраические шаги такие же, как в Части c. Разница в том, что решение — это не число.Обычный формат для буквальных уравнений — записать результирующую переменную в левой части уравнения.
Резюме:
1. Буквальное уравнение — это уравнение, которое включает более одной переменной.
2. Чтобы решить буквальное уравнение, алгебраические шаги такие же, как задачи из предыдущих двух разделов. Единственная разница в том, что решение — это не число, а алгебраическая формула.
Пример 2. Решите относительно y.
Приведенное выше объяснение не работает для второго уравнения — зачем его включать?
3.8 — Справочник — Упрощение выражений
3.8 — Справочник — Упрощение выражений3.8 — Справочная информация — Упрощение выражений
До вы начинаете работать над выражением (скажем, разложите его на множители, распределите, или комбинируя его с другим выражением) это выражение должно быть в самая простая возможная форма . В противном случае вы сделаете свою жизнь тяжелее, чем она должна быть.
Точно так же после вы закончили работу над выражением, которое вы
всегда следует оставлять его в простейшем виде.Тот, кто должен посмотреть на ваши результаты, это оценит!
В противном случае вы сделаете свою жизнь тяжелее, чем она должна быть.
Точно так же после вы закончили работу над выражением, которое вы
всегда следует оставлять его в простейшем виде.Тот, кто должен посмотреть на ваши результаты, это оценит!В этом разделе мы сначала объясним два возможных типа упрощений которые могут быть применены к выражению: точных упрощений и с плавающей запятой упрощения .
Затем мы даем исчерпывающий список возможных упрощений , начиная от самых базовый, который вы будете постоянно применять к самому сложному, что вы никогда не сможете сталкиваться.
Как и вы, программа Algebra Coach всегда возвращает свои результаты в простейшей форме.Вы можете ввести неупрощенное выражение в список тренера по алгебре и получить его можно преобразовать в простейшую форму, нажав кнопку «Упростить».
Сравнение точных упрощений и упрощений с плавающей запятой
Рассмотрим эти числа: дробь 2/3, радикал и специальные номера e и π. Каждое из этих чисел имеет точное значение и
когда они записаны в только что показанной форме, они считаются равными точным .С другой стороны, написать их так: 0,667, 1,73, 2,7 и 3,14 — это просто приближение . Эта форма называется формой чисел с плавающей запятой.
( с плавающей точкой означает, что число записано с десятичной точкой и
перед десятичной точкой и после нее может быть любое количество цифр.)
Каждое из этих чисел имеет точное значение и
когда они записаны в только что показанной форме, они считаются равными точным .С другой стороны, написать их так: 0,667, 1,73, 2,7 и 3,14 — это просто приближение . Эта форма называется формой чисел с плавающей запятой.
( с плавающей точкой означает, что число записано с десятичной точкой и
перед десятичной точкой и после нее может быть любое количество цифр.)Как правило, все целые числа, дроби, радикалы и числа e и π считаются равными быть точными числами и все числа, записанные в форме с плавающей запятой (т.е. с десятичной точкой) Считаются приблизительными числами .
Выражение, содержащее только точные числа, можно упростить двумя способами:
- к результату, также выраженному в точной форме, или
- округлено до результата, выраженного в форме с плавающей запятой.

Таким образом, прежде чем вы начнете упрощать точное выражение , вы должны решить, хотите ли вы получить результат выражается в точной форме или в форме с плавающей запятой. В чистых математических расчетах предпочтительнее точный результат а в инженерной работе предпочтительнее результат с плавающей запятой.
Тренер по алгебре имеет опцию , которую можно настроить чтобы точные выражения оставались точными при упрощении или выразить их с помощью чисел с плавающей запятой. Эта опция не влияет на выражения содержащие числа с плавающей запятой; они всегда упрощаются с использованием чисел с плавающей запятой.
Пример: Рассмотрим выражение. Это сумма двух дробей, которые считаются точными, поэтому все выражение тоже точно. Его можно упростить до точной формы , используя сложение дробей следующим образом: или дроби могут быть преобразованы в форму с плавающей запятой , а затем добавлены следующим образом:
Пример: Рассмотрим выражение.
 Это выражение с плавающей запятой, поскольку оно содержит число с плавающей запятой.
Его можно только упростить до формы с плавающей запятой , например:
Это выражение с плавающей запятой, поскольку оно содержит число с плавающей запятой.
Его можно только упростить до формы с плавающей запятой , например: Вот список различных упрощений, которые можно применить к выражению. Мы сгруппировали их по категориям:
Домашнее хозяйство или упрощения хорошего стиля
Основные упрощения Упрощения с дробями Упрощения с использованием экспонент Упрощения с использованием квадратных корней (радикалов) Упрощения с использованием логарифмов Упрощения, связанные с функциональными композициями Упрощения с использованием тригонометрических выражений Упрощения с использованием комплексных чиселУборка или упрощение хорошего стиля
Упростите, отсортировав члены выражения от высшей степени к наименьшей
Если выражение представляет собой сумму терминов, то обычно отсортируйте термины от высшей степени к низшей. Например, полином слева нужно упростить до полинома справа:
Например, полином слева нужно упростить до полинома справа: Упростите, отсортировав множители термина по алфавиту, первый порядок коэффициентов
Если выражение является продуктом факторов (то есть одночленом или одночленом), то его принято записывать с одним числом впереди (называемым коэффициентом), за которым следует остальная часть выражения с любыми буквами (называемыми литералами) в алфавитном порядке.Например, выражение слева следует упростить до выражения справа: Кроме того, если выражение является алгебраической дробью а числитель и знаменатель являются произведениями факторов, то приведенное выше соглашение о сортировке применяется к числителю и знаменателю. Например, выражение слева следует упростить до выражения справа:Упростите, отбросив нулевые члены, ненужные знаки + и ненужные множители 1
Ноль раз все равно нулю.Таким образом, если срок в выражении коэффициент равен нулю, тогда этот член равен нулю. Поскольку ноль — это
аддитивная идентичность — нулевой член можно и нужно отбросить.
Вот несколько примеров:
Поскольку ноль — это
аддитивная идентичность — нулевой член можно и нужно отбросить.
Вот несколько примеров: Коэффициент 1 в члене записывать не нужно, поскольку 1 — это мультипликативная идентичность. Также знак + перед одним членом или перед первым членом суммы терминов понимается и не требует написания. Таким образом, следует сделать следующие упрощения: Единственное исключение — когда 1 используется в качестве заполнителя, как в этом примере. (иначе числитель будет пустым): так что никакое упрощение невозможно.
Упростите, отбросив ненужные скобки
Акроним BEDMAS ( B ракетки, E xponents, D ivision и M ultiplication, A ddition и S ubtraction) относится к порядок действий внутри выражения. Скобки вверху списка и их цель — переместить часть выражения наверх списка. Теперь, если часть выражения уже находится наверху списка, тогда добавление
скобки вокруг него не нужны, и эти скобки следует опустить. Вот несколько примеров:
Вот несколько примеров:
Примечание:
- Имейте в виду, что в последнем примере c находится в числителе, а не в знаменателе. Так как это может сбить с толку многих людей, было бы неплохо оставить скобки, или даже лучше записать дробь как .
- В некоторых случаях скобки не появляются в наборной форме, но они необходимо при вводе выражения. Считается, что они находятся в определенных местах, таких как экспонента и числитель вверху и знаменатель под горизонтальной линией деления.Например: Щелкните здесь, чтобы получить дополнительную информацию о невидимых скобках.
Основные упрощения
Упростить, поставив знаки + и —
Распределительный закон гласит, что:a ( b + c ) = a · b + a · cКоличество a может быть знаком + или -, и в этом случае вы распространяете 1 или -1.
 Быть в курсе, что: Вот некоторые примеры:
Быть в курсе, что: Вот некоторые примеры:
до упрощения после упрощения a + b + ( c + d ) а + б + в + г a + (- b ) a — b ( a — b ) + (- c + d ) а — б — в + г a — (- b + c ) а + б — в — (- б + с ) б — в
Упростите, добавив похожие термины
Добавляйте похожие термины, добавляя их коэффициенты.Вот некоторые примеры: Нажмите здесь, чтобы узнать подробнее о добавлении похожих терминов и еще примеры.Примечание:
- Во втором примере похожие члены встречаются в числителе дроби.

- В третьем примере мы вычитаем вместо , добавляем подобных терминов и мы запишем результат как x вместо 1 x .
- В последнем примере коэффициенты являются дробными и . Нажмите здесь, чтобы узнать, как складывать обычные дроби.
Упростите, объединив несколько знаков факторов в один знак
Если термин в выражении имеет несколько отрицательных факторов (в числителе или знаменателе) затем посчитайте, сколько их. Если есть нечетное число, то член отрицательный, и мы должны заменить все знаки — одним знаком. Если есть четное число, то термин положительный.Для получения дополнительной информации нажмите здесь. Вот некоторые примеры:Упростите, объединив несколько числовых коэффициентов в один коэффициент
Если продукт или частное содержит несколько числовых факторов затем их следует объединить в одно число, называемое коэффициентом. Коэффициент может быть любым числом, включая дробь. Вот некоторые примеры: Примечание:
Коэффициент может быть любым числом, включая дробь. Вот некоторые примеры: Примечание: - И первый, и второй примеры содержат число с плавающей запятой 7.2, так что все числа объединяются в одно число с плавающей запятой, 5.76.
- Второй пример дает алгебраическую дробь. Коэффициент 5,76 ставится в числитель (или, возможно, перед дробью).
- В третьем примере числа 7, 4 и 5 считаются точными, поэтому результирующий коэффициент остается точным и записывается как дробь 28/5.
Упростите, комбинируя экспоненциальные множители с одной и той же базой, используя свойства экспонент
Если в выражении есть несколько экспоненциальных множителей с одинаковым основанием (в числителе или знаменателе), то их следует объединить, используя свойства показателей.Вот некоторые примеры:Упростить, вычислив экспоненты
Если основание и показатель экспоненты являются числами тогда мы должны упростить, оценив экспоненту. В этом примере вычисляется экспонента 2 4 : Вычисление экспоненты часто рассматривается как функция, называемая
степенная функция.
В этом примере вычисляется экспонента 2 4 : Вычисление экспоненты часто рассматривается как функция, называемая
степенная функция.Упростите, оценив функции
Если аргумент функции является приблизительным или число с плавающей запятой, тогда значение функции также является числом с плавающей запятой и мы должны упростить, оценив функцию.Если аргумент функции является точным числом, тогда значение функции также является точным числом. Однако только несколько точных аргументов имеют известных простых значений точных функций. Значения этих функций называются специальными значениями . (Например, нажмите здесь, чтобы увидеть специальные значения для функций sin, cos и tan.) Для всех других точных аргументов точные значения функции не известны или настолько сложны, что бесполезны. Таким образом, мы можем либо оставить их без оценки, либо округлить. и дайте приблизительные значения.Эти три случая резюмированы на этой картинке:
Вот пример каждого из этих случаев: Щелкните для получения дополнительной информации о функциях в целом и одиннадцать встроенных функций Algebra Coach.
Помните об альтернативных обозначениях, используемых для квадратных корней, экспоненциальных функций и обратных чисел
Имейте в виду, что квадратный корень x можно записать двумя способами: используя радикальную запись и используя экспоненциальная запись.Радикальные обозначения являются стандартными: Вот пример упрощения, в котором полезно использовать экспоненциальное представление квадратного корня: Экспоненциальную функцию можно записать двумя способами: используя экспоненциальную запись и используя обозначение функций. Экспоненциальная запись является стандартной: Взаимные числа могут быть записаны двумя способами: с использованием дробной записи и с использованием экспоненциальная запись.Дробное представление является стандартом: Среди прочего, экспоненциальная запись для обратных чисел полезна для видя связь между факторингом и поиск общих знаменателей.
Упрощения с дробями
Упростите дробь, умноженную или разделенную на не дробь
Дробь, умноженная на не дробь, должна быть заменена одной дробью, например: На словах, не дробь становится фактором в новом числителе.Это просто частный случай умножение двух дробей. Вот почему: Точно так же дробь, разделенная на не дробь, должна быть заменена одной дробью, например: На словах, не дробь становится фактором в новом знаменателе. Это просто частный случай деления двух дробей. Вот почему:Упростите, заменив произведение двух дробей на одну дробь
Произведение двух фракций можно упростить, заменив его одной дробью, например: Проще говоря, две дроби a / c и b / d умножаются, чтобы получить новая дробь, числитель которой равен ab , а знаменатель — кд . Щелкните для получения дополнительной информации о
умножение обыкновенных дробей и
умножение алгебраических дробей.
Вот пример: Это упрощение действительно является примером
ассоциативный закон умножения, который гласит, что
не имеет значения, в каком порядке мы умножаем и делим множители.
Это упрощение имеет самые разные последствия:
Щелкните для получения дополнительной информации о
умножение обыкновенных дробей и
умножение алгебраических дробей.
Вот пример: Это упрощение действительно является примером
ассоциативный закон умножения, который гласит, что
не имеет значения, в каком порядке мы умножаем и делим множители.
Это упрощение имеет самые разные последствия:- Это показывает, что все следующие формы эквивалентны. Обратите внимание, что во всех случаях a и c находятся в числителе. и b находится в знаменателе.Тренер по алгебре упрощает все другие формы к последней форме:
- Это показывает, что умножение на обратную величину b то же самое как деление на b :
- Путем факторизации числителя и знаменателя с последующим обращением этого упрощения мы можем уменьшить дробь до ее простейшей эквивалентной дроби. Вот пример:
Упростите, заменив частное двух дробей на одну дробь
Частное двух дробей можно упростить, заменив его одной дробью, например: Словом, деление дроби c / d на дробь b / a заменяется на умножение дроби c / d на , обратное a / b . Затем это умножение двух дробей осуществляется, как описано выше.
Щелкните для получения дополнительной информации о
деление обыкновенных дробей и
деление алгебраических дробей.
Вот пример: Вот еще один пример:
Затем это умножение двух дробей осуществляется, как описано выше.
Щелкните для получения дополнительной информации о
деление обыкновенных дробей и
деление алгебраических дробей.
Вот пример: Вот еще один пример: Это очень полезный результат: результат деления двух дробей на равные знаменатели — это дробь, состоящая всего из двух числителей.
Вот еще один полезный пример: не дробь, разделенная на дробь.Обратите внимание, как дробь (потому что она происходит от знаменателя) перевернута:
Упростите, уменьшив обыкновенные дроби, дробные коэффициенты и алгебраические дроби до наименьших членов
Любая дробь должна быть сводится к наименьшим значениям или к простейшей эквивалентной дроби. Это делается путем факторизации числителя и знаменателя дроби. полностью и ищем отмены. Есть три места для поиска отмены.Упрощения с использованием экспонент
Упростите экспоненты с основаниями или показателями 0 или 1
Любая экспонента с основанием или показателем, равным 0 или 1, должна быть упрощена, как показано в этом списке:- Все, что возведено в степень 0, равно 1.
 Для получения дополнительной информации нажмите здесь.
Для получения дополнительной информации нажмите здесь.b 0 = 1
- Любая «вещь» в степени 1 просто равна «вещи»:
b 1 = b
- 1 в любой степени равняется 1.
1 x = 1
- 0 в степени может равняться 0, 1 или быть неопределенным. Для получения дополнительной информации нажмите здесь.
Упростить экспоненты с отрицательными показателями
Одно из свойств экспонент: Другими словами, любая величина в степени −1 просто величина, обратная этому количеству. Форма дроби, 1/ b , в правой части этого свойства обычно рассматривается быть более простой формой, но экспоненциальная форма, b −1 , слева полезна для просмотра, например, связи между факторинг и нахождение общих знаменателей.Вышеупомянутая формула может быть обобщена на любой отрицательный показатель степени:
Вот некоторые примеры: Щелкните здесь для получения дополнительной информации и примеров.
Упростить экспоненты, основания которых являются экспонентами
Свойство экспоненциального возведения в степень гласит, что: Это свойство используется для замены сложной экспоненты в левой части более простой экспоненциальной. на правой стороне.Вот некоторые примеры: Примечание: Последний пример показывает, что возведение величины в степень 1/3 — то же самое, что и взятие кубический корень из этого количества.Упростите экспоненты, в основе которых лежат произведения или частные
Если продукт или коэффициент повышается до некоторой степени, тогда каждый фактор продукта или частного можно отдельно возвести в эту степень. Вот несколько примеров:Обратите внимание, что это упрощение относится только к продуктам или частным лицам.Это НЕ распространяется на суммы или разницы! Щелкните здесь для получения дополнительной информации и примеров.

Упростить экспоненты, экспоненты которых являются дробными
Используя свойство экспоненты экспоненты мы можем написать b m / n двумя способами: Словом, b m / n можно рассматривать как n th корень m th мощность b или как m th power of n th корень б .Вот пример, в котором используется это упрощение:
Для получения дополнительной информации нажмите здесь.Упрощения с квадратными корнями (радикалами)
Упростите, используя тот факт, что
Признавая, что радикалы могут быть выражены экспоненциальной формы, а затем с помощью свойства экспонент, позволяет нам делать различные упрощения с использованием радикалов, такие как:Упростить квадратный корень из полного квадрата
Если подкоренное выражение (величина под квадратным корнем) представляет собой полный квадрат, запишите его в факторизованной форме и отменить квадрат и квадратный корень. Вот два примера:
Вот два примера:Упрощения с использованием квадратных корней из целых чисел
- Если подкоренное выражение (величина под квадратным корнем) содержит коэффициент полного квадрата , то удалить множитель из подкоренного выражения. Вот пример:
- Иногда заменяя произведение квадратных корней из целых чисел квадратным корнем из произведения даст точный квадратный множитель, который затем может удаляются, как описано в первом пункте.Для получения дополнительной информации нажмите здесь. Вот пример:
Упрощение квадратных корней с использованием дробей
Выражение считается более простым, если в знаменателе нет радикалов. Процесс их устранения называется рационализацией знаменателя. Этого можно добиться тремя способами.- Предположим, что знаменатель дроби содержит квадратный корень .
 Затем умножьте числитель и знаменатель дроби на
этот квадратный корень и упростить. Это позволит исключить радикал из знаменателя.
Вот пример:
Затем умножьте числитель и знаменатель дроби на
этот квадратный корень и упростить. Это позволит исключить радикал из знаменателя.
Вот пример: - Предположим, что квадратный корень содержит дробь.
Затем умножьте числитель и знаменатель дроби на знаменатель дроби.
дробь и упростить. Это позволит исключить радикал из знаменателя.
Вот пример:
- Предположим, что знаменатель дроби является биномом, a + b , и что один или оба термина являются радикальными.Затем умножая числитель и знаменатель дроби по биномиальному конъюгату , a — b , знаменателя и распределения исключит все радикалы из знаменателя. Для получения дополнительной информации нажмите здесь. Вот пример:
Упрощения с использованием логарифмов
Упростить логарифм экспоненты
Логарифм экспоненциального свойства логарифмов утверждает, что: Вы можете использовать это свойство, чтобы упростить и заменить выражение слева на выражение справа. Правая часть считается более простой, чем левая, потому что возведение в степень в левой части
заменяется умножением в правой части.
Вот два примера: (Во втором примере сначала использовался логарифм свойства продукта .)
Правая часть считается более простой, чем левая, потому что возведение в степень в левой части
заменяется умножением в правой части.
Вот два примера: (Во втором примере сначала использовался логарифм свойства продукта .)Упростить логарифм обратной
Логарифм обратного свойства логарифмов утверждает, что: Вы можете использовать это свойство, чтобы упростить и заменить выражение слева на выражение справа.Правая сторона считается более простой, чем левая, потому что левая сторона имеет обратную величину. заменяется негативом с правой стороны. Вот пример:Упростим соотношение двух логарифмов чисел
Иногда соотношение логарифмов двух чисел, , можно упростить. Это происходит, когда два числа имеют одинаковое основание, скажем, n , возведены в две разные степени, скажем, a и b .Тогда соотношение упрощается так:Пример: Экспоненциальное уравнение 4 x = 128 может быть решено для x , взяв логарифм обеих сторон, затем используя логарифм экспоненциального свойства слева, а затем решение для x .
 В результате получается соотношение двух логарифмов чисел: Это можно упростить еще больше, если мы узнаем, что 128 и 4 — это 2 в разной степени:
В результате получается соотношение двух логарифмов чисел: Это можно упростить еще больше, если мы узнаем, что 128 и 4 — это 2 в разной степени: Упрощения с функциональными композициями
Упростить, отменив функцию, составленную с ее обратной функцией
Некоторые функции инвертируют друг друга и отменяются, когда составлен.Для любых x следующие композиции можно упростить. (Щелкните любую запись в таблице для получения дополнительной информации):Эти композиции обратных функций часто возникают, когда мы решаем уравнение, проделывая одно и то же с обоими стороны уравнения. Например, уравнение:
10 x = 33можно решить для x , взяв (основание 10) логарифм обеих сторон, например:
журнал (10 x ) = журнал (33)В соответствии с четвертой строкой в приведенной выше таблице левая часть уравнения упрощается следующим образом:
x = журнал (33)и затем можно оценить правую сторону.

Упростить некоторые композиции тригонометрических функций
Определенные композиции тригонометрических функций не отменяют, но они отменяют. упростите , например: Чтобы получить упрощения, обратитесь к треугольникам. Например, первый треугольник настроен так, что θ = арктангенс ( x ). Тогда теорема Пифагора дает длину третьей стороны. Первые два упрощения являются результатом получения значения sin (θ) и cos (θ) для этого треугольника.Остальные упрощения выводятся таким же образом. Эти функциональные композиции часто возникают, когда мы решаем уравнение, выполняя одно и то же с обоими
стороны уравнения. Например, предположим, что в треугольнике, показанном справа, мы хотим найти касательную угла
θ без фактического нахождения θ.
Это можно сделать, заметив, чтоθ = arcsin (0,4)и взяв касательную к обеим частям этого уравнения. 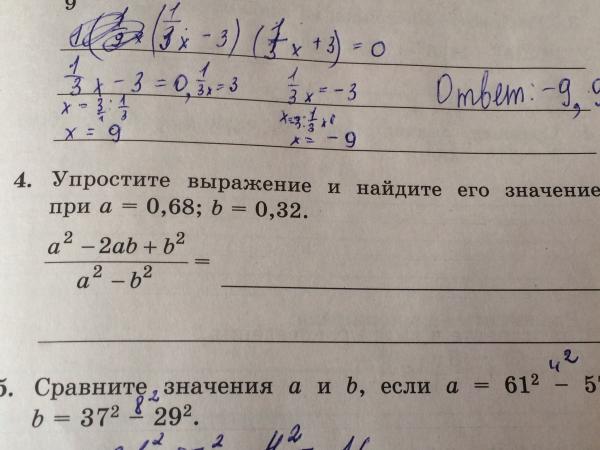 Это дает: Это дает:тангенс (θ) = загар (арксин (0,4)) |
Следующие композиции триггерных функций также упрощают:
arccos (грех (θ)),Все они упрощаются до π / 2 радиан — θ (или до 90 ° — θ в градусном режиме).Чтобы доказать это, обратите внимание, что эти 4 утверждения применимы к показанному треугольнику: Теперь просто примените операции, указанные стрелками:
arcsin (cos (θ)),
арктан (1 / тангенс (θ)).
Упрощения с использованием тригонометрических выражений
Упростить, исключив csc, sec и cot в пользу sin, cos и tan
Взаимные идентичности могут использоваться для устранения cot, sec и csc вместо функций sin, cos и tan. Вот тождества:
Вот тождества:Упростите, исключив отрицательные аргументы sin, cos и tan
Отрицательный угол внутри функции sin, cos или tan можно исключить в пользу положительного угол с использованием тождеств отрицательного угла:sin (- α ) = −sin ( α )cos (- α ) = cos ( α )
tan (- α ) = −tan ( α )
Упростите sin, cos и tan, удалив фазовый сдвиг π / 2 или 90 °
Идентификаторы «сдвиг влево на 90 °»:- sin ( x + π / 2) = cos ( x ) или sin ( x + 90 °) = cos ( x )
- cos ( x + π / 2) = −sin ( x ) или cos ( x + 90 °) = −sin ( x ))
- tan ( x + π / 2) = −1 / tan ( x ) или tan ( x + 90 °) = −1 / tan ( x )
 Например
Напримерsin ( x + 270 °) = cos ( x + 180 °) = −sin ( x + 90 °) = −cos ( x ).Эти идентичности являются важной частью алгоритмов, используемых тренером по алгебре и калькуляторами и компьютерами для оценки грех cos и функции загара.
Упростить с помощью теоремы Пифагора
Теорема Пифагора утверждает, что sin 2 ( α ) + cos 2 ( α ) = 1.В каждом из следующих выражений левую часть можно заменить на правая часть, которая считается более простой, так как содержит только один член:sin 2 ( α ) + cos 2 ( α ) = 11 — sin 2 ( α ) = cos 2 ( α )
1 — cos 2 ( α ) = sin 2 ( α )
Упрощения с использованием комплексных чисел
Выражение квадратных корней отрицательных чисел как мнимых чисел
Мнимое число — это квадратный корень отрицательного числа. Мнимая единица i определяется как: Квадратный корень из любого отрицательного числа можно упростить, выразив его
как кратное мнимой единице i . Вот два примера: В технических областях, где символ i уже представляет электрическую
тока символ j часто используется для обозначения мнимой единицы.
Мнимая единица i определяется как: Квадратный корень из любого отрицательного числа можно упростить, выразив его
как кратное мнимой единице i . Вот два примера: В технических областях, где символ i уже представляет электрическую
тока символ j часто используется для обозначения мнимой единицы.Вычислить сумму, разность, произведение или частное двух комплексных чисел
Щелкните здесь, чтобы увидеть примеры арифметики с комплексными числами.Используйте формулу Эйлера для преобразования комплексных чисел между полярными и прямоугольными координатами
Комплексные числа часто приходится преобразовывать между полярными, прямоугольными и экспоненциальные формы. Формула Эйлера используется для преобразования. В нем говорится, что Для получения дополнительной информации нажмите здесь.Важным частным случаем является личность Эйлера,
e i π = −1.Для получения дополнительной информации нажмите здесь.
Оценить функции, вход или выход которых являются комплексными числами
Нажмите здесь, чтобы узнать, как работают встроенные функции оценивается по комплексным числам.Если вы нашли эту страницу в поиске в Интернете, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
— обширная математическая библиотека для JavaScript и Node.js
Упростите дерево выражений.
Список правил, применяемых к выражению, повторяется по списку до тех пор, пока никаких дальнейших изменений не вносится. Можно передать в функцию собственный набор правил в качестве второго аргумент. Правило может быть указано как объект, строка или функция:
const rules = [
{l: 'n1 * n3 + n2 * n3', r: '(n1 + n2) * n3'},
'п1 * п3 + п2 * п3 -> (п1 + п2) * п3',
function (node) {
// . .. вернуть новый узел или вернуть узел без изменений
узел возврата
}
]
.. вернуть новый узел или вернуть узел без изменений
узел возврата
}
]
Правила для строк и объектов состоят из левого и правого шаблона.Слева используется для сопоставления с выражением, а право определяет, какие совпадения заменяются на. Основное отличие выкройки от обычной выражение состоит в том, что переменные, начинающиеся со следующих символов, являются интерпретируется как подстановочные знаки:
- ‘n’ — соответствует любому узлу
- ‘c’ — соответствует любому ConstantNode
- ‘v’ — соответствует любому узлу, не являющемуся ConstantNode
Список правил по умолчанию отображается в функции как упрощать.правила и может использоваться в качестве основы для создания набора настраиваемых правил.
Подробнее о теории см .:
Необязательный аргумент options может быть передан в качестве последнего аргумента simple .
В настоящее время доступен один вариант:
-
точных фракций: логическое значение, которое по умолчанию равноистинному.
-
fractionsLimit: еслиExactFractionsистинно, будет возвращена дробь только если числитель и знаменатель меньшедробей Предел.Значение по умолчанию — 10000.
Синтаксис #
упростить (выражение)
упрощать (выражение, правила)
упрощать (выражение, правила)
упрощать (выражение, правила, область действия)
упрощать (выражение, правила, область действия, параметры)
упрощать (выражение, объем)
Упростить (выражение, объем, параметры)
Параметры #
| Параметр | Тип | Описание |
|---|---|---|
выраж. | Узел | строка | Выражение для упрощения |
правила | Массив <{l: строка, r: строка} | строка | функция> | Необязательный список с настраиваемыми правилами |
Возврат #
| Тип | Описание |
|---|---|
| Узел | Возвращает упрощенную форму expr | .
Примеры #
математ.(2 - 1) ')
math.simplify (f) // Узел "2 * x"
math.simplify ('0.4 * x', {}, {ightFractions: true}) // Узел "x * 2/5"
math.simplify ('0,4 * x', {}, {ExactFractions: false}) // Узел «0,4 * x»
См. Также #
производная, разобрать оценивать, рационализировать
экспонентов и упрощающих выражений
экспонентов и упрощающих выражений Экспоненты и упрощающие выражения
Что бы вы выбрали?
Вы можете получить оплату либо
- в течение тридцати дней получать один цент в первый день и каждый последующий день в два раза больше, чем в предыдущий день.
Сколько вы получили бы в 30 -й день?
Удвоение суммы — это то же самое, что умножение суммы на два. Итак, ежедневные суммы в центах за каждый день будут:
День 1 1 ¢
День 2 2
День 3 2 × 2 = 4 ¢
День 4 2 × 2 × 2 = 8 ¢
День 5 2 × 2 × 2 × 2 = 16 ¢
День 6 2 × 2 × 2 × 2 × 2 = 32 ¢
День 7 2 × 2 × 2 × 2 × 2 × 2 = 64 ¢
Становится много умножений, которые нужно написать. Мы используем экспоненты, чтобы записывать задачу на каждый день в более короткой форме. Поскольку в день 7 шесть раз используется два в качестве множителя, мы можем записать задачу как
Мы используем экспоненты, чтобы записывать задачу на каждый день в более короткой форме. Поскольку в день 7 шесть раз используется два в качестве множителя, мы можем записать задачу как
День 7 2 6 = 2 × 2 × 2 × 2 × 2 × 2 = 64 ¢
Тогда День 8 будет использовать другой коэффициент 2 для
День 8 2 7 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 ¢
День 9 2 8 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256 ¢
День 10 2 9 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512 ¢
Отметим, что число двойки, используемое в качестве множителя, на единицу меньше числа дня, поэтому
День 30 2 29 .
Здесь говорится, что нам нужно будет 29 умножить на два, чтобы найти сумму денег в центах для тридцатого дня. Определите эту сумму, а затем решите, какой вариант будет лучшим.
Решение
Вышеупомянутая проблема является причиной того, почему экспоненты используются в качестве ярлыка для проблем установки. Приведем больше примеров с экспонентами.
Приведем больше примеров с экспонентами.
Определение экспоненты: Выражение, которое представляет собой n множителей b , используемое для n — 1 умножения , , можно записать как b n . b называется основанием , а n называется показателем .
Примеры:
- Монета подбрасывается трижды. Сколько результатов возможно?
Чтобы решить указанную выше проблему на занятии 9 (старое занятие 9), мы составили древовидную диаграмму (как показано ниже), чтобы решить проблему, чтобы мотивировать фундаментальный принцип подсчета.
Обратите внимание, что мы также можем выразить проблему в экспоненциальной форме как
2 3 = 2 × 2 × 2 = 8.
У нас есть восемь возможных исходов, когда монета подбрасывается три раза. - Что, если бы мы подбросили монету четыре раза? Сколько результатов возможно?
Построив задачу с использованием показателей степени, мы получим 2 4 = 2 × 2 × 2 × 2 = 16. Если монету подбросить четыре раза, будет шестнадцать возможных исходов.
Если монету подбросить четыре раза, будет шестнадцать возможных исходов. - Если мы подбросим монету тринадцать раз, то 2 13 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 8192.У нас было бы 8192 различных возможных исхода, если бы монету подбросили тринадцать раз.
Обратите внимание, что по мере того, как количество раз, которое мы должны повторить умножение, становится больше, запись использования только умножения становится громоздкой. Итак, мы используем сокращенные обозначения с показателями для представления этого типа повторного умножения.
Пример: в 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2, 2 повторяется 13 раз.
Другие примеры:
- 3 2 = 3 × 3 = 9
- Используйте повторное умножение, чтобы найти 5 3 , 10 5 и 9 3 .
5 3 = 5 × 5 × 5 = 25 × 5 = 125
10 5 = 10 × 10 × 10 × 10 × 10 = 100000
9 3 = 9 × 9 × 9 = 9 × 81 = 729 - Дино ест в своем любимом итальянском ресторане.
 В меню три вина, три салата, три основных блюда и три десерта. В его кошельке также лежат три кредитные карты. Сколькими способами он может выбрать еду, выбирая ровно по одному продукту каждого типа, и оплатить его кредитной картой?
В меню три вина, три салата, три основных блюда и три десерта. В его кошельке также лежат три кредитные карты. Сколькими способами он может выбрать еду, выбирая ровно по одному продукту каждого типа, и оплатить его кредитной картой?
Мы применяем фундаментальный принцип счета и используем экспоненты для получения
3 5 = 3 × 3 × 3 × 3 × 3 = 243.
У Дино есть 243 варианта еды и оплаты.
Проблема самопроверки
Стандартный кубик бросается пять раз. Сколько результатов возможно? Запишите задачу в экспоненциальной форме и решите ее.
Решение
Поскольку показатели степени представляют собой повторное умножение, показатели степени также могут использоваться для представления декартовых произведений наборов (набора упорядоченных пар). См. Сессию 9 (Старая Сессия 9). Например, мы можем записать A × A как A 2 .
Примеры:
- Монета подбрасывается дважды. Каковы возможные результаты?
Мы можем решить эту проблему как вопрос о декартовом произведении, задав набору все возможные упорядоченные пары. Пусть C = {H, T}. Тогда
Пусть C = {H, T}. Тогда
C 2 = C × C = {(H, H), (H, T), (T, H), (T, T)}. - Если установить A = {1, 2}, то A 2 = A × A = {(1, 1), (1, 2), (2, 1)}.
- Пусть B = {0, 1, 2}. Определите количество элементов в B 2 , проверьте решение, найдя B 2 , а затем нанесите B 2 на координатную плоскость.
Количество элементов: (n ( B )) 2 = 3 2 = 9. Напоминание: n ( B ) — это кардинальное число для B . У нас
B 2 = B × B = {(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)}.
4. Пусть D будет набором возможных результатов при броске одной 6-гранной кости. Напишите D , используя запись реестра. Выпишите D 2 , используя запись реестра. Что означает D 2 ? Сколько элементов в D 2 ?
Что означает D 2 ? Сколько элементов в D 2 ?
Решения: D = {1, 2, 3, 4, 5, 6}
D 2 = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1) , (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), ( 3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2) , (6, 3), (6, 4), (6, 5), (6, 6)}
D 2 представляет возможные результаты броска кубика дважды или двух кубиков.
Всего 6 2 = 36 элементов в D 2 .
Проблема самопроверки
Напишите декартово произведение для возможных результатов, когда человек дважды выбирает одно число от 1 до 3 включительно.
Решение
Проблема мотивации
Масса земной массы составляет приблизительно 6 000 000 000 000 000 000 000 000 килограммов. Ученые запишут это значение в научном представлении, используя степень десяти или экспоненциальную форму.Ученый написал бы массу Земли как 6 × 10 24 килограмм.
Ученые запишут это значение в научном представлении, используя степень десяти или экспоненциальную форму.Ученый написал бы массу Земли как 6 × 10 24 килограмм.
Научная запись полезна для записи очень больших или очень маленьких чисел. А пока мы сосредоточимся на использовании научных обозначений для записи очень больших чисел. Рассмотрим стоимость трех миллионов. Обычно мы записываем это число как 3 000 000, но мы также можем записать его в научном представлении :
3 000 000 = 3 × 1 000 000 = 3 × 10 6 .
Обратите внимание, что показатель степени равен количеству нулей после 3.Три миллиона — это словесное выражение, 3 000 000 — десятичное выражение, а 3 × 10 6 — научное представление.
Когда мы рассматривали размеченное значение, каждый столбец диаграммы разряда имел разовое значение в 10 раз больше, чем столбец справа от него. Мы можем использовать научную нотацию , чтобы упростить запись значений в диаграмму разряда.
Теперь мы знаем три способа выразить этот тип числа: в виде стандартного числа, в устной форме и в научном представлении.У каждой формы есть свои преимущества.
Примеры:
Стандартная цифра | Устная форма | Научная нотация |
5 000 000 000 | пять миллиардов | 5 × 10 9 |
60 000 000 | шестьдесят миллионов | 6 × 10 7 |
70 000 | семьдесят тысяч | 7 × 10 4 |
120 000 000 | сто двадцать миллионов | 12 × 10 7 |
17 000 000 000 | семнадцать миллиардов | 17 × 10 9 |
Поскольку мы работаем только с целыми числами, мы не записываем научное представление с десятичной точкой. Позже, после того как мы поработаем с десятичными знаками, мы вернемся к научному представлению и будем использовать нормализованную форму для научного обозначения.
Позже, после того как мы поработаем с десятичными знаками, мы вернемся к научному представлению и будем использовать нормализованную форму для научного обозначения.
Проблема самопроверки
Масса Солнца составляет приблизительно 2 000 000 000 000 000 000 000 000 000 000 килограммов. Напишите массу солнца в научных обозначениях и словесной форме.
Решение
Ранее мы научились добавлять выражения переменных с помощью , добавляя похожие термины .Теперь, когда у нас есть показатели, мы также можем умножать выражения переменных. Сначала отметим, что x · x = x 2 , поскольку переменная x использовалась как множитель дважды. Это просто применение определения экспоненты. Аналогично, у нас есть a · a · a · a · a · a = a 6 .
Теперь рассмотрим 3 x (2 x ). Поскольку все в этом выражении умножается, мы используем коммутативные и ассоциативные свойства умножения с определением экспоненты, чтобы найти произведение:
Пример: Умножение (4 x ) (2 x ) ( x ).
Пример: Умножение (3 x ) ( y ) ( x 2 ) (5 y ).
Обратите внимание, что коэффициенты группируются вместе, а затем каждая переменная группируется вместе.
Отметим, что мы только добавляем одинаковые термины и получаем похожие термины . Но когда мы умножаем выражение с переменными, мы делаем , а не , получаем , как термы , вместо этого мы получаем выражения с показателями.Важно научиться делать это различие при упрощении выражений переменных.
Сравните каждое из следующего при сложении или умножении одинаковых членов.
Дополнение | Умножение |
2 x + 3 x = (2 + 3) x | 2 x · 3 x = (2 · 3) x |
4y + y + 2y = (4 + 1 + 2) y | 4y · y · 2y = (4 · 1 · 2) ( y · y · y ) |
a + 2 b + a + b = a + a + 2 b + b | a · 2 b · a · b = 2 · a · a · b · b |
Проблемы самопроверки
Оцените каждое выражение:
4 м + 5 n + м + 7 n + 2 м и 4 м · 5 n · м · 7 n · 2 м
Решения
Проблема мотивации
Найдите значение 5 + 6 (4).
Если у нас нет особых правил нахождения вышеуказанного значения, разные люди могут получить разные ответы. Некоторые могут сначала умножить, а затем добавить, чтобы получить 29, а другой может сначала сложить, а затем кратно, чтобы получить 44. Эта ситуация неприемлема . Итак, люди пришли к соглашению об определенных стандартных правилах определения значений выражений, включающих различные операции. Наиболее общие правила и те, которые мы собираемся использовать, называются алгебраическим порядком операций.Порядок действий — Википедия, бесплатная энциклопедия
Мы изучили операции с показателями, делением, умножением, вычитанием и сложением. Чтобы правильно выполнять сложные вычисления с этими операциями, нам необходимо выполнять эти операции в определенном порядке. Стандартные правила для алгебраического порядка операций:
Сначала мы выполняем операции, которые сгруппированы, например, с помощью скобок.
Во-вторых, мы вычисляем экспоненты.
В-третьих, мы выполняем умножение и деление слева направо.
Наконец, мы выполняем сложение и вычитание слева направо.
Акроним для запоминания порядка операций — PEMDAS, что означает круглые скобки, экспоненты, умножение, деление, сложение и вычитание. Мнемоническое устройство для запоминания этого акронима: P lease E xcuse M y D ear A Unt87.
Пример: Дебютная задача 5 + 6 (4) будет решаться следующим образом.
5 + 6 (4) = 5 + 24, поскольку умножение предшествует сложению
= 29
Распространенная ошибка, связанная с этим аббревиатурой, состоит в том, чтобы забыть, что PEMDAS неправильно отражает слева направо часть правил в первом абзаце. Умножение и деление имеют одинаковый приоритет и выполняются слева направо. Сложение и вычитание имеют одинаковый приоритет и выполняются слева направо.Более точным мнемоническим символом может быть PE MD AS , чтобы напомнить себе, что подчеркнутые пары выполняются вместе, перемещаясь слева направо.
То есть умножение и деление выполняется на том же этапе , а выполняется слева направо .
Пример: В 100 ÷ 4 × 5 умножение и деление должны выполняться слева направо, что означает, что в этом случае деление фактически выполняется на перед умножением на .
100 ÷ 4 × 5 = 25 × 5 = 125
Таким же образом сложение и вычитание выполняются на том же этапе , и они также выполняются слева направо .
Пример: в 20-2 + 8 сложение и вычитание должны выполняться слева направо, что означает, что в этом случае вычитание фактически выполняется перед сложением:
20-2 + 8 = 18 + 8 = 26
Примеры: В каждом из следующих шагов подчеркнутый шаг.
Проблемы самопроверки
Вычислить каждое выражение
92 — 7 · 9 Раствор
7 2 + 4 (3 3 + 2) — 19 Решение
Рассмотрим (2 x ) 4 . В данном случае мы берем весь продукт в скобках в степени 4 th .
В данном случае мы берем весь продукт в скобках в степени 4 th .
(2 x ) 4 = (2 x ) ((2 x ) (2 x ) (2 x ) | Определение степени 4 |
= (2 · 2 · 2 · 2) ( x · x · x · x ) | Коммутативные и ассоциативные свойства |
= 2 4 x 4 | Определение экспонент |
Вот еще один пример: ( ab 2 ) 3 .
( ab 2 ) 3 = ( ab 2 ) · ( ab 2 ) · ( ab 2 ) | Определение степени 3 |
= ( a · a · a ) · ( b 2 · b 2 · b 2 ) | Коммутативные и ассоциативные свойства |
= ( a · a · a ) · ( b · b ) · ( b · b ) · ( b · b ) | Определение степени 2 |
= ( a · a · a ) · ( b · b · b · b · b · b ) | Ассоциативное свойство |
= a 3 b 6 | Определение экспонент |
Другой пример: ( x 4 y 3 ) 2 .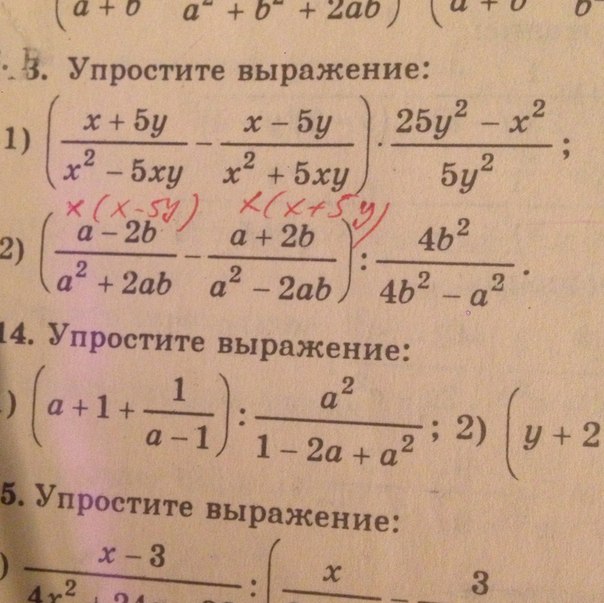
( x 4 y 3 ) 2 = ( x 4 y 3 ) · ( x 4 y 10 | Определение степени 2 |
= (x · x · x · x) · (y · y · y ) · (x · x · x · x) · (y · y · y ) | Определение степеней 4 и 3 |
= (x · x · x · x) · (x · x · x · x) · (y · y · y ) · (y · y · y ) | Коммутативное свойство умножения |
= (x · x · x · x · x · x · x · x) · (y · y · y · y · y · y ) | Ассоциативное свойство умножения |
= x 8 y 6 | Определение экспонент |
Обратите внимание, что эти проблемы мотивируют свойства экспонентов, которые представляют собой методы для более эффективного решения этих проблем. Некоторые свойства экспонент будут рассмотрены позже на занятии 29.
Некоторые свойства экспонент будут рассмотрены позже на занятии 29.
Проблема самопроверки
Вычислить ( м 2 n 3 ) 4 .
Решение
Шутка или цитата
Учитель: «Сколько 7 умножить на 6?»
Студент: «Сейчас 42!»
Учитель: «Очень хорошо! — А сколько 6 умножить на 7?»
Тот же ученик: «24 года!»
Бесплатные рабочие листы для упрощения выражений (предалгебра и алгебра 1)
Вы здесь: Домашняя страница → Рабочие листы → Упростить выраженияС помощью этого генератора рабочих листов вы можете создавать рабочие листы для печати для упрощения выражений переменных для курсов предварительной алгебры и алгебры 1.Рабочие листы могут быть созданы в виде файлов PDF или html (последние можно редактировать в текстовом редакторе).
Выражения включают те, в которых вам нужно объединить одинаковые термины (например, 2 t — 9 — 6 t + 2), использовать свойство распределения (например, 9-2 ( x + 7)) и для умножения и деления одночленов, например, 2 x 2 · (−5 x 3 ) и −4 x 2 · y 2 /3 x 5 .
Основные инструкции для рабочих листов
Каждый рабочий лист генерируется случайным образом и поэтому уникален. Ключ ответа создается автоматически и помещается на вторую страницу файла.
Вы можете создавать рабочие листы либо в формате html, либо в формате PDF. — и то, и другое легко распечатать. Чтобы получить рабочий лист PDF, просто нажмите кнопку с названием « Создать PDF » или « Создать рабочий лист PDF ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Просмотреть в браузере » или « Сделать рабочий лист html ».Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе.
Иногда созданный рабочий лист не совсем то, что вам нужно. Просто попробуйте еще раз! Чтобы получить другой лист с теми же параметрами:
- Формат PDF: вернитесь на эту страницу и снова нажмите кнопку.

- Формат Html: просто обновите страницу рабочего листа в окне браузера.
Рабочие листы готовые
Используйте эти быстрые ссылки, чтобы создать несколько распространенных типов рабочих листов для упрощения выражений.Ниже, с фактическим генератором, вы можете создавать рабочие листы в соответствии с вашими точными спецификациями.
См. Также
Рабочие листы для вычисления выражений с переменными
Рабочие листы для написания выражений с переменными из словесных выражений
Рабочие листы для линейных уравнений
Рабочие листы для линейных неравенств
Генератор
Используйте генератор, чтобы настроить листы по своему усмотрению. Вы можете сделать их как файлы PDF или HTML.Файлы html доступны для редактирования: просто сохраните лист в браузере, а затем откройте его в своем любимом текстовом редакторе.
Чтобы настроить рабочие листы, вы можете контролировать количество задач, уровень сложности, диапазон чисел, используемых в качестве коэффициентов и констант, использование десятичных знаков, количество рабочего пространства, границу вокруг проблем и дополнительные инструкции.
В задачах уровня 1 можно дополнительно исключить использование отрицательных целых чисел (оставить все неотрицательным).
Ключ к учебным пособиям по алгебре
Key to Algebra предлагает уникальный, проверенный способ познакомить студентов с алгеброй. Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Студенты развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа.Книги 5-7 вводят рациональные числа и выражения. Книги 8-10 расширяют охват системы действительных чисел.
=> Узнать больше
Подробная информация о стандартах— SAS
Предметная область — CC.2:
Математика
- Стандартная область — CC.
 2.2: Алгебраические понятия
2.2: Алгебраические понятия - Уровень оценки — CC.2.2.HS: GRADE High School
Расширьте знания об арифметических операциях и примените к многочленам.
- Якорь оценки — A1.1.1
Операции с действительными числами и выражениями
Дескриптор привязки — A1.1.1.1 Представлять и / или использовать числа в эквивалентных формах (например, целые числа, дроби, десятичные дроби, проценты, квадратные корни и показатели степени).

Дескриптор привязки — A1.1.1.2 Примените концепции теории чисел, чтобы показать отношения между действительными числами в настройках решения проблем.
Дескриптор привязки — A1.1.1.3 Используйте экспоненты, корни и / или абсолютные значения для решения проблем.
Допустимый контент — A1.1.1.3.
 1
Упростите / оцените выражения, включающие свойства / законы экспонент, корней и / или абсолютного значения для решения проблем (показатели должны быть целыми числами от -10 до 10).
1
Упростите / оцените выражения, включающие свойства / законы экспонент, корней и / или абсолютного значения для решения проблем (показатели должны быть целыми числами от -10 до 10).
Дескриптор привязки — A1.1.1.4 Используйте стратегии оценки в ситуациях решения проблем.
Дескриптор привязки — A1.1.1.5 Упростите выражения, содержащие многочлены.
Допустимый контент — A1.
 1.1.5.1
Складывать, вычитать и / или умножать полиномиальные выражения (выражать ответы в простейшей форме — не больше, чем двучлен, умноженный на трехчлен).
1.1.5.1
Складывать, вычитать и / или умножать полиномиальные выражения (выражать ответы в простейшей форме — не больше, чем двучлен, умноженный на трехчлен).- Допустимый контент — A1.1.1.5.2
Факторные алгебраические выражения, включая разность квадратов и трехчленов (трехчлены ограничены формой ax 2 + bx + c, где a равно 1 после вычитания всех мономиальных множителей).
Допустимый контент — A1.1.1.5.3 Упростите / сократите рациональное алгебраическое выражение.

- Якорь оценки — A2.1.2
Нелинейные выражения
Дескриптор привязки — A2.1.2.1 Используйте экспоненты, корни и / или абсолютные значения для представления эквивалентных форм или для решения проблем.
Допустимый контент — A2.1.2.1.1 Используйте экспоненциальные выражения для представления рациональных чисел.

Допустимый контент — A2.1.2.1.2 Упростите / оцените выражения, включающие положительные и отрицательные показатели и / или корни (могут содержать все типы действительных чисел — показатели не должны превышать степени 10).
- Допустимый контент — A2.1.2.1.3
Упростите / оцените выражения, включающие умножение на показатели (например, x 6 * x 7 = x 13 ), степеней степеней (например, (x 6 ) 7 = x 42 ) и степеней продуктов (2x 2 ) 3 = 8x 6 (предел рациональных показателей).

- Допустимый контент — A2.1.2.1.4
Упростите или оцените выражения, содержащие логарифмы и показатели степени (например, log 2 8 = 3 или log 4 2 = ½).
Дескриптор привязки — A2.1.2.2 Упростите выражения, содержащие многочлены.


 cos2а
cos2а 1/2 tg2a
1/2 tg2a 0°
0° (π/3 + 2πk; 2π/3 + 2πk), k Є Z
(π/3 + 2πk; 2π/3 + 2πk), k Є Z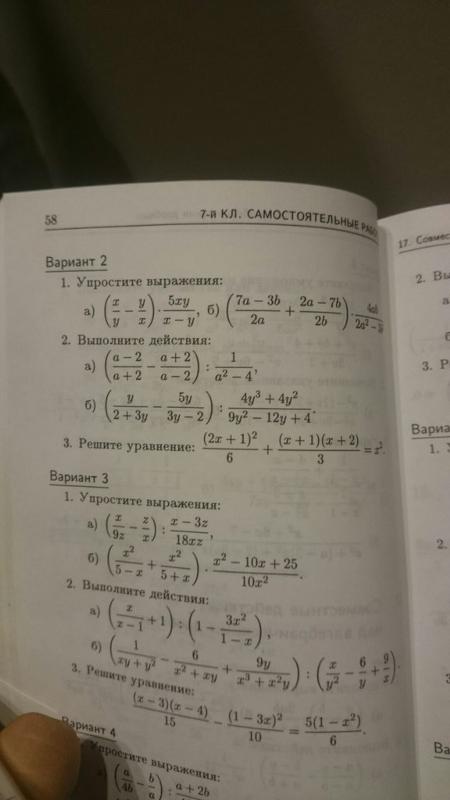 πk/4, k Є Z
πk/4, k Є Z Тригонометрия — Материалы для подготовки к вступительным экзаменам в СГГА
Тригонометрия — Материалы для подготовки к вступительным экзаменам в СГГА




 Найдите сумму корней уравнения 1/(5 • 2x – 9) = 1/(4x – 5).
Найдите сумму корней уравнения 1/(5 • 2x – 9) = 1/(4x – 5). Эти операции имеют равный приоритет.
Эти операции имеют равный приоритет.
 Для получения дополнительной информации нажмите здесь.
Для получения дополнительной информации нажмите здесь. Затем умножьте числитель и знаменатель дроби на
этот квадратный корень и упростить. Это позволит исключить радикал из знаменателя.
Вот пример:
Затем умножьте числитель и знаменатель дроби на
этот квадратный корень и упростить. Это позволит исключить радикал из знаменателя.
Вот пример: 
 .. вернуть новый узел или вернуть узел без изменений
узел возврата
}
]
.. вернуть новый узел или вернуть узел без изменений
узел возврата
}
]


 Если монету подбросить четыре раза, будет шестнадцать возможных исходов.
Если монету подбросить четыре раза, будет шестнадцать возможных исходов.  В меню три вина, три салата, три основных блюда и три десерта. В его кошельке также лежат три кредитные карты. Сколькими способами он может выбрать еду, выбирая ровно по одному продукту каждого типа, и оплатить его кредитной картой?
В меню три вина, три салата, три основных блюда и три десерта. В его кошельке также лежат три кредитные карты. Сколькими способами он может выбрать еду, выбирая ровно по одному продукту каждого типа, и оплатить его кредитной картой?  Пусть C = {H, T}. Тогда
Пусть C = {H, T}. Тогда 
 2.2: Алгебраические понятия
2.2: Алгебраические понятия
 1
Упростите / оцените выражения, включающие свойства / законы экспонент, корней и / или абсолютного значения для решения проблем (показатели должны быть целыми числами от -10 до 10).
1
Упростите / оцените выражения, включающие свойства / законы экспонент, корней и / или абсолютного значения для решения проблем (показатели должны быть целыми числами от -10 до 10). 1.1.5.1
Складывать, вычитать и / или умножать полиномиальные выражения (выражать ответы в простейшей форме — не больше, чем двучлен, умноженный на трехчлен).
1.1.5.1
Складывать, вычитать и / или умножать полиномиальные выражения (выражать ответы в простейшей форме — не больше, чем двучлен, умноженный на трехчлен).
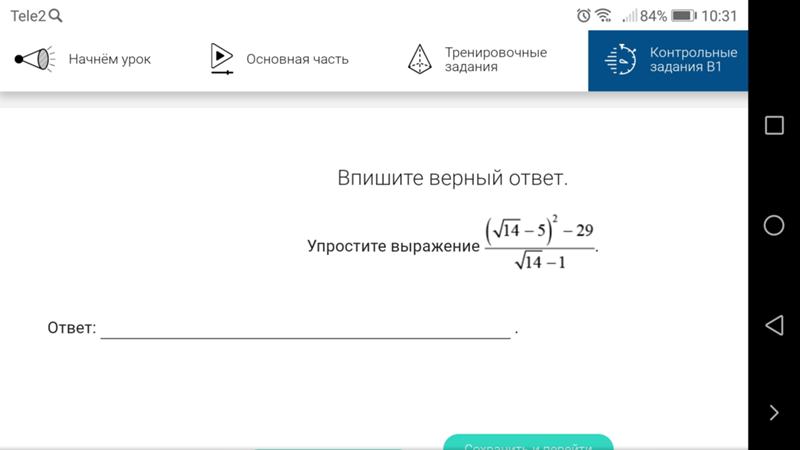

Leave A Comment