Решение задач по системе счисления. Часть 2
Решение задач по системе счисления. Часть 2.
Учитель информатики Батракова Л.В.
11.
Решите уравнение
.
Ответ
запишите в четверичной системе счисления.
Основание системы счисления указывать
не нужно.
Решение: Надо перевести все числа в десятичную систему, решить уравнение и результат перевести в четверичную систему:
1)
из уравнения получаем

переводим 22 в четверичную систему счисления:
Ответ: 112
12. Запись натурального числа в системах счисления с основанием 4 и 6 заканчивается на 0. Найдите минимальное натуральное число, удовлетворяющее этим условиям.
Решение: если запись числа в системе счисления с основанием N заканчивается на 0, то это число делится на N нацело, поэтому в данной задаче требуется найти наименьшее натуральное число, которое делится одновременно на 4 и на 6, то есть это число12.
Ответ: 12
13. Укажите, сколько всего раз встречается цифра 3 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 4.
Решение (вариант 1):
При решении задачи надо помнить, что в 4-ой системе счисления самая старшая цифра – 3.
Запишем первое и последнее число в заданном диапазоне в системе счисления с основанием 4:
13
= 314,
23 = 113
Оба они содержат цифру 3, так что, 2 цифры мы уже нашли.
Между 314 и 1134 есть еще числа:
324, 334, 1004, 1014, 1024, 1034, 1104, 1114, 1124.
В них 4 цифры 3, поэтому всего цифра 3 встречается 6 раз.
Ответ: 6
Решение (вариант 2):
Можно перевести все указанные числа в систему счисления с основанием 4 и подсчитать количество 3:
13
=314 , 14 =324 , 15 =33
Получается 6 штук.
Ответ: 6
14. Укажите наименьшее основание системы счисления, в которой запись числа 50 двузначна.
Решение: Так как число по условию двухзначное, то достаточно найти первое целое число, квадрат которого больше 50; это — 8, так как:
Так как , следовательно, в системе счисления с основанием 7 запись числа 50 будет трехзначна, а в 8-ой системе счисления – двузначной.
Ответ: 8
15. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 6 начинается на 4?
Решение: Поскольку 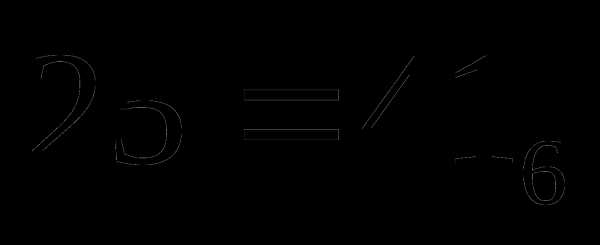 ,
в интересующих нас числах может быть
не более 2 цифр. Есть всего одно однозначное
число, начинающееся на 4, это 4. Выпишем
все числа в шестеричной системе счисления,
которые являются двузначными, начинаются
с 4 и не превосходят 25 в десятичной
системе. Это числа: 40
,
в интересующих нас числах может быть
не более 2 цифр. Есть всего одно однозначное
число, начинающееся на 4, это 4. Выпишем
все числа в шестеричной системе счисления,
которые являются двузначными, начинаются
с 4 и не превосходят 25 в десятичной
системе. Это числа: 40
16. Запись числа 658 в некоторой системе счисления выглядит так: 311N. Найдите основание системы счисления N.
Решение: Из условия задачи следует, что 658 = 311N. Переведем 658 в десятичную систему счисления:
,
Второе число разложим по основанию счисления N:
Так как что 658 = 311N , то можно записать: .
Решаем это уравнение и получаем, что N = 4.
Ответ: 4
17. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 5 единиц. Если таких чисел несколько, укажите наибольшее из них.
1) 3110 * 810 + 110 2) F016 + 110 3) 3518 4) 111000112
Решение: Нужно перевести все заданные числа в двоичную систему, подсчитать число единиц и выбрать наибольшее из чисел, в которых ровно 5 единиц.
Для первого варианта переведем оба сомножителя в двоичную систему:
3110 = 111112 810 = 10002
В первом числе ровно 5 единиц, умножение на второе добавляет в конец три нуля:
3110 * 810 = 111112 * 10002 = 111110002
то есть в этом числе 5 единиц, но надо добавить еще одну единицу в конец, получим число 11111001, в котором 6 единиц. Так как нам нужны числа с 5-ю единицами, то это число не рассматриваем.
Для второго варианта воспользуемся двоичным представлением 16-ричных чисел: каждую цифру шестнадцатеричного числа можно переводить отдельно в тетраду (4 двоичных цифры):
F016 = 111100002
после
добавления единицы F0
Для третьего варианта используем связь между восьмеричной и двоичной системами: каждую цифру восьмеричного числа переводим отдельно в триаду (группу из трёх) двоичных цифр:
3518 = 111010012
это число тоже содержит 5 единиц, но меньше, чем число во втором варианте ответа.
Последнее число 111000112 уже записано в двоичной системе, оно тоже содержит ровно 5 единиц, но меньше второго и третьего числа.
Таким образом, только 3 числа, указанные в вариантах ответов, содержат ровно 5 единиц, но наибольшее из них – второе.
Ответ: 2
18.
Даны 4 целых числа, записанные в двоичной
системе:
10001011, 10111000, 10011011, 10110100.
Сколько
среди них чисел, больших, чем А416 +208?
1) 1 2) 2 3) 3 4) 4
Решение: Надо перевести А416 +208 в двоичную систему счисления, разложив их по тетрадам для 16-х чисел и по триадам для 8-х чисел: А416 — 101001002 и 208 — 100002 и поразрядно сложить: 101001002 + 100002 = 101101002.
Сравнив с заданными числами, видим, что только одно число больше полученного, это: 10111000.
Ответ: 1
19. К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.
Решение: Так как приписали 2 нуля, то для решения задачи достаточно вычислить 82 =64.
Ответ: 64
20. Десятичное число 109 в некоторой системе счисления записывается как «214». Определите основание системы счисления.
Решение: Обозначим искомое основание системы счисления через x, тогда можно записать выражение:
109 = 2x2+x+4 или 2x2+x-105 = 0. Решив это уравнение, получим x=7.
Ответ: 7
Дополнительно (для самых умных):
Запись числа N в системе счисления c основанием 6 содержит две цифры, запись этого числа в системе счисления c основанием 5 содержит три цифры, а запись в системе счисления c основанием 11 заканчивается на 1. Чему равно N? Запишите ответ в десятичной системе счисления.
Решение: Из первых двух условий задачи следует, что 52 = 25 ≤ N 2 = 36, следовательно, значение N надо искать из следующего набора чисел: 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35.
Из третьего условия находим число, которое при делении на 11 дает остаток 1, это число 34.
Проверка: 34 = 546=5· 61 + 4 · 60 , 34 = 1145 = 1· 52 + 1 · 51 + 4 · 50 , 34 = 3111 = 3 · 111 + 1 · 110 .
Ответ: 34
Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.
Решение: Так как старшая цифра в выражении 4, то надо рассматривать системы счисления, начиная с 5-ной.
Пятеричная система не подходит, т.к. 4 + 4 в пятеричной системе даст нам последнюю цифру в ответе 3. Шестеричная система так же не подходит – последняя цифра в ответе будет 2. А вот семеричная система подойдет для всех цифр ответа.
Ответ: 7
Дополнительно (для самых-самых умных):
1. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.
Общий подход:
неизвестно основание системы счисления, мы обозначим его через
пока будем считать, что запись числа 31 в системе с основанием состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через ) нужно найти:
2 1 0 ← разряды
31 = k 1 1N = k·N2 + N1 + N0 = k·N2 + N + 1
можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить как при некотором целом ; например, для числа с пятью разрядами получаем:
4 3 2 1 0 ← разряды
31 = k4 k3 k2 1 1N = k4·N4 + k3·N3 + k2·N2 + N1 + N0
= k·N2 + N + 1
для (из первых трех слагаемых вынесли общий
множитель 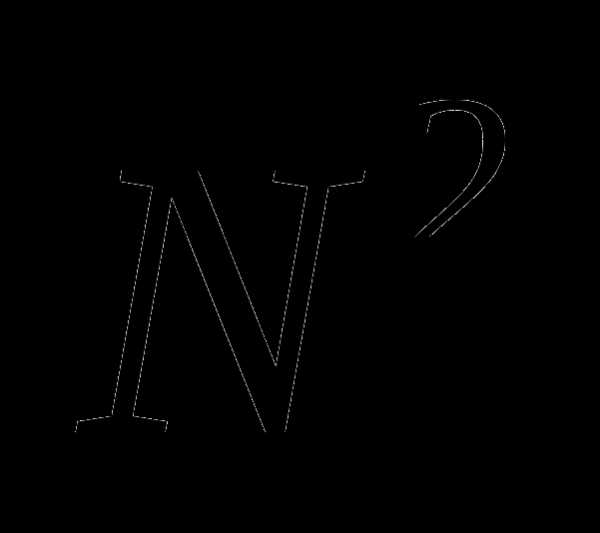 )
)
Решение: Нужно найти все целые числа  ,
такие что
,
такие что
(**)
где – целое неотрицательное число (0, 1, 2, …).
Сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа.
Из формулы (**) получаем , так что задача сводится к тому, чтобы найти все делители числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом , то есть, – целое число.
Выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30.
Из всех этих делителей только для 2, 3, 5 и 30 значение – целое число (оно равно соответственно 7, 3, 1 и 0)
Ответ: 2, 3, 5, 30.
Замечание: Можно, конечно, решить задачу и методом подбора.
31 = 25 – 1 = 111112
31 = 10113
31 = 1115
31 = 1130
2. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 94 начинается на 23.
Решение: Из условия задачи видно, что искомое основание не меньше 4 (в записи есть цифра 3).
Если запись числа 94 в некоторой системе счисления с основанием двузначна (94 = 23x), то справедливо равенство .
Нас интересуют натуральные решения этого уравнения, такие что , но таких решений нет.
Предположим, что число четырехзначное.
Минимальное допустимое четырехзначное
число – 2300x, где
.
При минимальном основании ( )
оно равно.
)
оно равно.
Следовательно, запись нужного нам числа имеет три знака.
Можно записать: , где – целое неотрицательное число, такое что .
Максимальное можно определить как решение уравнения (при 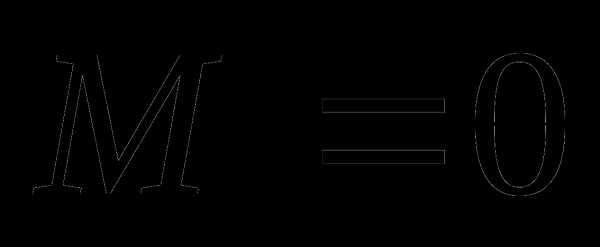 ).
).
Получаем одно из решений – 6,15. Отсюда:
4≤ .
.
определится как: .
Подставим поочередно в эту формулу , пытаясь получить .
Минимальное
=
4 будет при 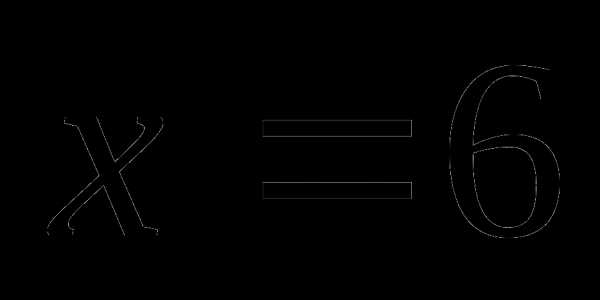 ,
т.е условиевыполняется,
а при
,
т.е условиевыполняется,
а при  получается
получается 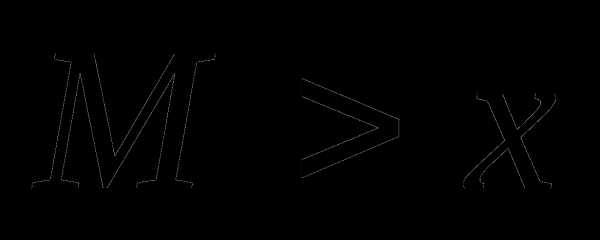 .
.
Ответ: 6
gigabaza.ru
Задачи для тренировки1:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
В системе счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
В системе счисления с некоторым основанием число десятичное 25 записывается как 100. Найдите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на 3.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в четверичной системе счисления оканчивается на 31?
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?
Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.
Укажите, сколько всего раз встречается цифра 1 в записи чисел 12, 13, 14, …, 31 в системе счисления с основанием 5.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 1.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 63 оканчивается на 23.
Десятичное число, переведенное в восьмеричную и в девятеричную систему, в обоих случаях заканчивается на цифру 0. Какое минимальное натуральное число удовлетворяет этому условию?
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.
Укажите наименьшее основание системы счисления, в которой запись числа 50 двузначна.
Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 7?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 6 начинается на 4?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 20, запись которых в системе счисления с основанием 3 начинается на 2?
Какое десятичное число при записи в системе счисления с основанием 5 представляется как 12345?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101?
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 30 оканчивается на 8.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.
В системе счисления с некоторым основанием десятичное число 83 записывается в виде 123. Укажите это основание.
В системе счисления с некоторым основанием десятичное число 144 записывается в виде 264. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 32 оканчивается на 4.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 27, запись которых в двоичной системе счисления оканчивается на 110?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в троичной системе счисления оканчивается на 21?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 45, запись которых в двоичной системе счисления оканчивается на 1010?
Десятичное число кратно 16. Какое минимальное количество нулей будет в конце этого числа после перевода его в двоичную систему счисления?
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
Укажите, сколько всего раз встречается цифра 3 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 4.
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
В саду 100 фруктовых деревьев – 14 яблонь и 42 груши. Найдите основание системы счисления, в которой указаны эти числа.
Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.
Найдите основание системы счисления, в которой выполнено умножение: 3·213 = 1043.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 20, запись которых в системе счисления с основанием 5 оканчивается на 3?
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 100, запись которых в системе счисления с основанием 5 оканчивается на 11?
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 84 оканчивается на 14.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 61 оканчивается на 15.
Найдите десятичное число x, такое что 20 < x < 30, запись которого в системе счисления с основанием 3 заканчивается на 11.
Запись числа 658в некоторой системе счисления выглядит так: 311q. Найдите основание системы счисления q.
Запись числа 30 в некоторой системе счисления выглядит так: 110q. Найдите основание системы счисления q.
Запись числа 2B16в некоторой системе счисления выглядит так: 111q. Найдите основание системы счисления q.
Запись числа 23 в некоторой системе счисления выглядит так: 212q. Найдите основание системы счисления q.
Запись числа 2105в некоторой системе счисления выглядит так: 313q. Найдите основание системы счисления q.
Укажите наименьшее основание системы счисления, в которой запись числа 50 трехзначна.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 348оканчивается на 20.
Запись числа 344 в некоторой системе счисления выглядит так: 1A8q. Найдите основание системы счисления q.
К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.
Запись числа 281 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно максимально возможное основание системы счисления?
Запись числа 381 в системе счисления с основанием N содержит 3 цифры и оканчивается на 3. Чему равно максимально возможное основание системы счисления?
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Запись числа 256 в системе счисления с основанием N содержит 3 цифры и оканчивается на 4. Чему равно минимально возможное основание системы счисления?
Запись числа 325 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно минимально возможное основание системы счисления?
Запись числа 180 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления.
Запись числа 280 в системе счисления с основанием N содержит 3 цифры и оканчивается на 0. Перечислите в порядке возрастания все возможные основания системы счисления.
studfiles.net
Сколько цифр «2» содержится в этой записи
Значение арифметического выражения: 918 + 354 – 9 – записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Демонстрационный вариант Единый государственный экзамен ЕГЭ 2017 г. – задание №16
Решение:918 + 354 – 9 = 32×18 + 354 – 32 = 354 + 336 – 32
Число 3n записывается в троичной системе, как единица и n нулей.
Ответ: 34
Значение арифметического выражения: 98 + 35 – 9 – записали в систем счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Демонстрационный вариант Единый государственный экзамен ЕГЭ 2016 г. – задание №16
Решение:98 + 35 – 9 = 32×8 + 35 – 32 = 316 + 35 – 32
Число 3n записывается в троичной системе, как единица и n нулей.
Ответ: 3
В системе счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.
Решение:N3 + 4 = 129
N3 = 125
N = 5
Ответ: 5
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на 3.
Решение:27 = …3N
27-3 = 24
24 делится на N и N больше чем 3.
4,6,8,12,24
Ответ: 4,6,8,12,24
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?
Решение:
Ответ: 4,8,9,13,17
Укажите, сколько всего раз встречается цифра 1 в записи чисел 12, 13, 14, …, 31 в системе счисления с основанием 5.
Решение:12 = 225
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 30 | 31 | 32 | 33 | 34 | 40 | 41 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| 42 | 43 | 44 | 100 | 101 | 102 | 103 | 104 | 110 | 111 |
Ответ: 13
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 63 оканчивается на 23.
Решение:2 разряда
63 = 23N
2N+3 = 63
N=30
3 разряда
63=X23N
XN2+2N+3 = 63
N(XN+2) = 60
5(2.5+2) = 60
N=5
Ответ: 5,30
Десятичное число, переведенное в восьмеричную и в девятеричную систему, в обоих случаях заканчивается на цифру 0. Какое минимальное натуральное число удовлетворяет этому условию?
Решение:Число делится на 8 и 9/
8.9 = 72
Ответ: 72
Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.
Решение:XN2+YN+Z = 70
Если N=4, X,Y,Z<4;
3.42+3.4+3 = 53 < 70
4 недостаточно, что это следующее число = 5
Ответ: 5
Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 7?
Решение:357 / 7 = 51, остаток 0
51 / 7 = 7, остаток 2
7 / 7 = 1, остаток 0
357 = 10207
Ответ: 4
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 6 начинается на 4?
Решение:25 > 46 = 4
25 > 406 = 24
25 > 416 = 25
Ответ: 2,24,25
Какое десятичное число при записи в системе счисления с основанием 5 представляется как 12345?
Решение:12345 = 1.53 + 2.52 + 3.5 + 4 = 125 + 50 + 15 + 4 = 194
Ответ: 194
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101?
Решение:25 > 1012 = 5
25 > 11012 = 13
25 > 101012 = 21
Ответ: 5,13,21
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.
Решение:31 = …4N
31-4 = 27
27 делится на N и N больше чем 4.
9, 27
Ответ: 9, 27
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в троичной системе счисления оканчивается на 21?
Решение:25 > 213 = 7
25 > 1213 = 16
25 > 2212 = 25
Ответ: 7,16,25
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
Решение:13=1113
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 111 | 112 | 120 | 121 | 122 | 200 | 201 | 202 | 210 | 211 | 212 |
Ответ: 13
Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.
Решение:4 + 4 = 1
8 – 7 = 1
Ответ: 7
Найдите десятичное число x, такое что 20 < x < 30, запись которого в системе счисления с основанием 3 заканчивается на 11.
Решение:a113 = 4+a.32
20 < 4+9.a < 30
Если a=1, 4+9=13; 13 < 20
Если a=2, 4+9.2=22;
20 < 22 < 30
Ответ: 22
Запись числа 2B16 в некоторой системе счисления выглядит так: 111N. Найдите основание системы счисления N
Решение:2B16 = 111N
2B16 = 2.16 + B = 32 + 11 = 43
43 = 111N
N2 + N + 1 = 43
N2 + N – 42 = 0
N=6, N=-7
Ответ: 6
Запись числа 2105 в некоторой системе счисления выглядит так: 313N. Найдите основание системы счисления N.
Решение:2105 = 313N
2105 = 2.52 + 1.5 = 50 + 5 = 55
55 = 313N
3N2 + N + 3 = 55
N = 4
Ответ: 4
Укажите наименьшее основание системы счисления, в которой запись числа 50 трехзначна
Решение:50 = 3024
Ответ: 4
К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.
Решение:XY8 = X.8 + Y
XY008 = X.83 + Y.82 = 82.(X.8+Y)
Ответ: 64
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Решение:338 = XY2N
XN2+YN+2 = 338
XN2+YN = 336
N.(XN+Y) = 336
16.(1.16+5)=16.21 = 336
Ответ: 16
Запись числа 256 в системе счисления с основанием N содержит 3 цифры и оканчивается на 4. Чему равно минимально возможное основание системы счисления?
Решение:256 = XY4N
XN2 + YN + 4 = 256
N.(XN+Y) = 252
Если N=6, 6(5.6+5)=210<252
N=7
Ответ: 7
Решите уравнение 425+x=11223.
Ответ запишите в четверичной системе счисления. Основание системы счисления указывать не нужно.
425 + x = 11223
(20+2) + x = 27+9+6+2
x = 22
22 = ?4
22 / 4 = 5, остаток 2
5 / 4 = 1, остаток 1
Ответ: 112
В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.
Решение:68 – 3 = 65
94 – 3 = 91
91 = 7.13
65 = 5.13
Ответ: 13
Запись числа N в системе счисления c основанием 6 содержит две цифры, запись этого числа в системе счисления c основанием 5 содержит три цифры, а запись в системе счисления c основанием 11 заканчивается на 1. Чему равно N? Запишите ответ в десятичной системе счисления.
Решение:N = XY6 = X.6 + Y = > N ≤ 35
N = ABC5 = A.25 + B.5 + C = > N ≥ 30
N = …111 => N-1 делится на 11
11.3 = 33
Ответ: 33
Сколько единиц в двоичной записи числа 42014 + 22015 – 9?
Решение:24028 + 22015 – 9
Ответ: 2015
Сколько единиц в двоичной записи числа 8125 – 4156 + 2632 – 7?
Решение:2632 + 2375 – 2312 – 7
Ответ: 373
Сколько значащих нулей в двоичной записи числа 4350 + 8340 – 2320 – 12?
Решение:21020 + 2700 – 2320 – 12
Ответ: 324
Значение арифметического выражения: 920 + 360 – 15 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Решение:920 + 360 – 15
360 + 340 – 15
Ответ:
Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8, 4, 2. Часть символов при записи утеряна. Позиции утерянных символов обозначены знаком *:
X= E*16 = *5*8 = ***14 = *****1**2
Определите число X.
Решение(Э. Аян, Казань):X= Ea16 = 14.16+a = 224+a, где 0<a<16
Исходя из равенства X=***14 можем сделать вывод, что число Х делится на 4 с остатком 1. Следовательно, переменная а принимает одно из следующий значений: 5, 9, 13.
При а=5, Х=229
При а=9, Х=233
При а=13, Х=237
Х=*****1**2, следовательно число 233 нам не подходит, так как при переведении его в двоичную систему третий справа бит равен 0, в то время как 229 и 237 подходят.
Х=*5*8, следовательно при переведении Х в восьмеричную систему навторой бит должен принять значение 5.
Х=22910=3458
Х=23710=3558
Ответ: 237
vuz-24.ru


Leave A Comment