Угол между прямой и плоскостью — что это такое? Как найти?
Поможем понять и полюбить математику
Начать учиться
Представьте: на уроке физкультуры вам нужно кинуть мяч точно в нарисованную на стене мишень. «Целься под углом 45°», — советует физрук. Или вы читаете задачу по физике, где солнечные лучи падают на поверхность под углом α. А может быть, вам надо помочь маме в саду и подпереть дверь старой лопатой. Что общего у этих ситуаций?
Правильный ответ такой: все эти случаи можно озаглавить геометрическим понятием «пересечение плоскости прямой под некоторым углом». Об этом мы сегодня и поговорим, а именно:
рассмотрим главные определения и примеры;
изучим свойства и теоремы по теме;
научимся находить угол между прямой и плоскостью.

Определение угла между прямой и плоскостью
Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.
Мы уже знакомы с понятиями «угол», «прямая» и «плоскость» (если подзабыли, то можете повторить по нашим материалам). А сейчас давайте вспомним, что такое проекция.
Проекция — это геометрическое изображение на плоскости, полученное проведением перпендикуляров из всех точек данного тела на плоскость.
То есть под углом между прямой и плоскостью в пространстве мы подразумеваем угол между прямой и её отображением на плоскость.
Важное уточнение
Если прямая перпендикулярна плоскости, то можно считать, что угол между ними равен 90°, что следует из определения перпендикулярности прямой и плоскости. Этот случай — самый простой, его мы рассматривать не будем.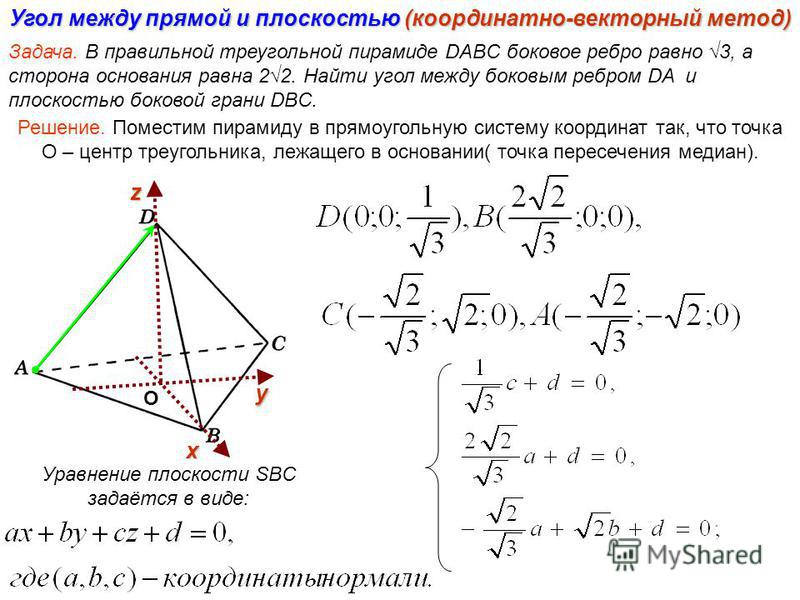
Также стоит заметить, что если прямая параллельна плоскости, то у них нет ни одной общей прямой, а значит, угол между ними не определяется.
Как вы думаете, какой тип имеет угол между прямой и плоскостью? Верно, он может быть только острым. Попробуйте доказать это самостоятельно 😊
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Свойства и теоремы
Свойство угла между прямой и плоскостью
Углом между прямой и плоскостью называется наименьший из углов между прямой и произвольной прямой в плоскости.
Попробуем привести доказательство. Для этого нарисуем плоскость и проведём к ней прямую АВ, являющуюся наклонной. Тогда АВ1 — проекция прямой на плоскость, АН — произвольная прямая, принадлежащая плоскости, а
 Чтобы лучше представить себе этот объёмный чертеж, можно сделать небольшой макет из сложенного листа бумаги, прислонив его к поверхности стола или тетради.
Чтобы лучше представить себе этот объёмный чертеж, можно сделать небольшой макет из сложенного листа бумаги, прислонив его к поверхности стола или тетради.Чтобы проверить истинность свойства, нам необходимо доказать, что угол ∠ВАВ1 намного меньше, чем угол ∠ВАН
Обозначим проблему: значения этих углов, как и других исходных, нам неизвестны. А значит, на помощь может прийти тригонометрия, ведь сравнить углы можно и через их синусы.
Синус — это отношение противолежащего угла к гипотенузе. В таком случае, .
Оба перпендикуляра ВВ1 и ВН проведены из точки В, но только один из них является кратчайшим расстоянием от точки по плоскости, и это перпендикуляр ВВ1. Так как значения синусов представляют собой дроби с одинаковыми знаменателями, большей будет та, у которой больше знаменатель.
Следовательно, sin ∠BAB1 < sin ∠BAH, ∠BAB1 < ∠BAH.
Теорема
Из двух наклонных, проведённых из одной точки к плоскости, меньшая образует с плоскостью больший угол, и наоборот: угол, образованный большей наклонной, будет меньшим из двух.
Существует множество разных доказательств этой теоремы, но мы сосредоточимся на одном из них.
Для этого изобразим плоскость и точку . Из точки А проведём две наклонные прямые, причем АВ < АС, а также перпендикуляр к плоскости АО. Докажем, что
Стороны ОВ и ОС являются проекциями АВ и АС соответственно. Меньшая прямая имеет меньшую проекцию, а значит, ОВ < ОС.
Отложим на стороне ОС отрезок ОЕ, равный ОВ. Можно ли доказать равенство треугольников АОВ и АОЕ?
В данных треугольниках:
ОВ = ОЕ (по построению),
АО — общий катет.
Следовательно, треугольники АОВ и АОЕ равны по двум катетам (или по первому признаку: две стороны и угол между ними). В таком случае равны и соответственные углы: ∠АВО = ∠АЕО.
Угол АЕО является внешним для треугольника АЕС, и по свойству внешнего угла
 Не трудно догадаться: раз угол АЕО равен сумме двух других углов треугольника, не смежных с ним, то он больше любого из этих двух углов.
Не трудно догадаться: раз угол АЕО равен сумме двух других углов треугольника, не смежных с ним, то он больше любого из этих двух углов.∠АЕО > ∠АСЕ, и так как ∠АЕО = ∠АВО, то ∠АВО > ∠АСЕ.
Что и требовалось доказать. 😎
Как найти угол между прямой и плоскостью
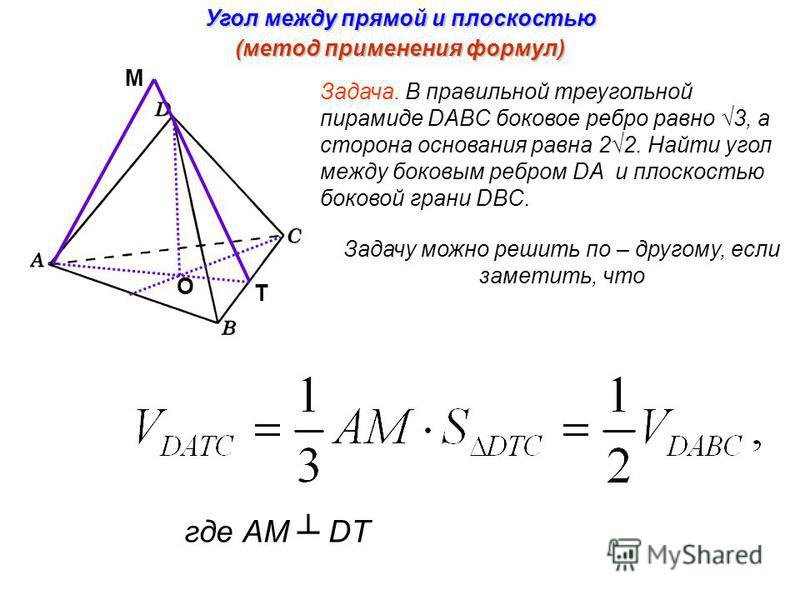
От теории переходим к практике: а как же можно вычислить угол между прямой и плоскостью? Вопрос лёгкий и сложный одновременно. Дело в том, что задач на нахождение угла очень много, и в каждой из них применяется свой алгоритм решения. Большую роль играет предмет и раздел, в котором эта задача приведена: это может быть стереометрия, векторная алгебра и даже физика. Но все эти алгоритмы сводятся к двум методам: геометрическому и алгебраическому или координатному методу. Давайте подробно рассмотрим каждый из них.
Геометрический метод
Чтобы применить геометрический метод, необходимо опустить перпендикуляр на плоскость из точки, принадлежащей исходной прямой. Выясним, чем в этом задании является перпендикуляр, наклонная и проекция, и решим планиметрическую задачку (чаще всего в таких задачах нам будет необходимо найти один из углов прямоугольного треугольника).
Выясним, чем в этом задании является перпендикуляр, наклонная и проекция, и решим планиметрическую задачку (чаще всего в таких задачах нам будет необходимо найти один из углов прямоугольного треугольника).
Задача 1
Из точки А на плоскость проведены две наклонные АВ и АС и перпендикуляр АО, причём О, В и С — точки пересечения с плоскостью .
Определите, чему равен АО, если СО = 10, ВО = 26, а угол АСО в два раза больше угла АВО.
Отметим на стороне ОВ отрезок, равный ОС. Тогда ОС = ОЕ = 10, а ЕВ = 26 – 10 = 16.
Тогда ОС = ОЕ = 10, а ЕВ = 26 – 10 = 16.
Рассмотрим треугольники АСО и АЕО:
СО = ОЕ (по построению),
АО — общий катет.
Следовательно, треугольники равны по двум катетам. А значит, угол
Угол АЕО является внешним для треугольника АЕВ, а значит, ∠АЕО = ∠АВЕ + ∠ВАЕ. Так как ∠ АВЕ = , значит, ∠ ВАЕ = 2-=, и треугольник АЕВ — равнобедренный.
Тогда найдём АО через прямоугольный треугольник АОЕ по теореме Пифагора:
.
Ответ: .
Алгебраический метод
Алгебраический метод или метод координат для нахождения угла между прямой и плоскостью основывается на особой формуле. Чтобы использовать его, необходимо определить координаты двух точек, принадлежащих прямой, описать уравнение плоскости и применить формулу. По сути в этом методе мы находим угол между вектором и плоскостью.
,
где (x1, y1, z1) — это координаты первой точки,
(x2, y2, z2) — координаты второй точки,
А, В и С — это координаты в уравнении плоскости Ax + By + Cz + D = 0.
Иначе эти числа называют координатами вектора нормали плоскости.
Тут может возникнуть вопрос: а что, если в задаче даны не координаты точек, а координаты вектора?
В этом случае вспомним, что координаты вектора находятся через разность координат начала и конца.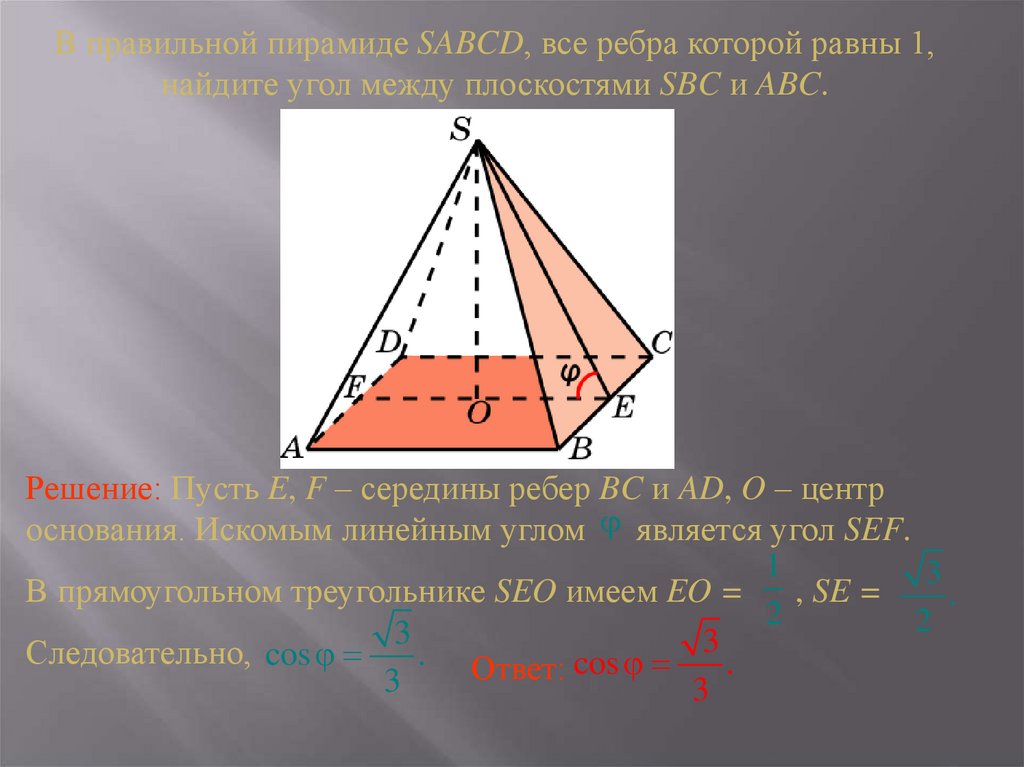 А значит, мы со спокойно душой подставляем эти координаты в формулу вместо (х2 – х1), (y2 – y1) и (z2 – z1).
А значит, мы со спокойно душой подставляем эти координаты в формулу вместо (х2 – х1), (y2 – y1) и (z2 – z1).
В некоторых задачах для нахождения угла между прямой и плоскостью вводят понятие направляющего вектора прямой. Направляющий вектор прямой — это любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Координаты этого вектора можно получить из канонического уравнения прямой:
, где направляющий вектор а имеет координаты (ax, ay).
Тогда угол между прямой и плоскостью можно вычислить по формуле:
.
Задача 2
Найдите угол между прямой и плоскостью 3x – y – z + 1 = 0.
Решение:
Определим координаты направляющего вектора для прямой: (2; –1; 3).

Определим координаты вектора нормали плоскости: (3; –1; –1).
Подставим координаты в формулу для расчёта синуса угла между плоскостью и прямой:
.
Задача 3
Найдите угол между плоскостью, заданной уравнением x + 2y + 2z – 4 = 0, и прямой, которой принадлежат точки А (0, 2, –1) и В (–2, 4, –1).
Решение:
Определим координаты вектора нормали плоскости: (1; 2; 2).
Подставим координаты вектора нормали и координаты точек прямой в формулу:
.
За короткий промежуток времени мы изучили понятие угла между прямой и плоскостью, доказали теоремы, разобрали способы нахождения угла и решили практические задания. Мы — молодцы! 💪
Думаем, вы понимаете, что эта тема очень важна — с её помощью решаются сложные стереометрические задачи, которые встречаются на ОГЭ и ЕГЭ. Подготовиться к таким серьёзным заданиям помогут курсы профильной математики в онлайн-школе Skysmart. На уроках мы сможем более подробно разобрать задачи с пирамидами и параллелепипедами, а ещё научимся составлять уравнения для любой плоскости. Узнать свои сильные и слабые стороны, составить план обучения и познакомиться с онлайн-платформой можно на вводном уроке — это бесплатно.
Подготовиться к таким серьёзным заданиям помогут курсы профильной математики в онлайн-школе Skysmart. На уроках мы сможем более подробно разобрать задачи с пирамидами и параллелепипедами, а ещё научимся составлять уравнения для любой плоскости. Узнать свои сильные и слабые стороны, составить план обучения и познакомиться с онлайн-платформой можно на вводном уроке — это бесплатно.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Дарья Вишнякова
К предыдущей статье
Компланарность векторов
К следующей статье
Теоремы, которые точно пригодятся на ЕГЭ
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Угол между прямой и плоскостью
Угол между прямой и плоскостьюНавигация по странице:
- Определение угла между прямой и плоскостью
- Формула для вычисления угла между прямой и плоскостью
- Вывод формулы вычисления угла между прямой и плоскостью
- Примеры задач на вычисление угла между прямой и плоскостью
Онлайн калькулятор. Угол между прямой и плоскостью
Угол между прямой и плоскостью
Определение.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Формула вычисления угла между прямой и плоскостью
Если в пространстве заданы направляющий вектор прямой L
s = {l; m; n}
и уравнение плоскости
Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
Вывод формулы для вычисления угла между прямой и плоскостью
Из уравнения прямой можно найти направляющий вектор прямой
s = {l; m; n}
Из уравнения плоскости вектор нормали плоскости имеет вид
q = {A; B; C}
Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой
| cos ψ = | | q · s | |
| | s | · |q | |
Так как φ = 90° — ψ, то синус угла между прямой и плоскостью sin φ = cos ψ.
Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.
Пример вычисления угла между прямой и плоскостью
Пример 1.
Найти угол между прямой
| x — 4 | = | y + 2 | = — | z — 6 |
| 2 | 6 | 3 |
и плоскостью x — 2y + 3z + 4 = 0.
Решение.
Из уравнения прямой найдем направляющий вектор прямой
s = {2; 6; -3}
Из уравнения плоскости найдем вектор нормали плоскости
q = {1; -2; 3}
Воспользовавшись формулой, найдем угол между прямой и плоскостью
| sin φ = | | 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √22 + 62 + (-3)2 · √12 + (-2)2 + 32 |
=
| 2 — 12 — 9 |√4 + 36 + 9 · √1 + 4 + 9=
|-19|√49 · √14=
197√14Ответ: sin φ = 197√14.
Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты
Угол между линией и плоскостью
В этой статье мы подробно обсудим понятие угла между линией и плоскостью. Прежде чем приступить к обсуждению этой концепции, сначала давайте посмотрим, что такое прямая и плоскость.
Что такое прямая линия?
Прямая линия, также известная как прямая в геометрии, представляет собой двухмерную фигуру, в которой бесконечное число точек простирается в любом направлении. Прямая линия является частью 2D-геометрии и не имеет ширины или высоты. Длина прямой линии бесконечна.
Лучшие репетиторы по математике
Поехали
Что такое самолет?
Плоскость — это плоская поверхность, образованная бесконечным числом точек, простирающихся без ограничений в любом направлении. Это также фигура 2-D , потому что, как и прямая линия, она не имеет толщины, а имеет только длину и ширину. Например, если вы рисуете что-то на плоской бумаге, то это значит, что вы рисуете что-то на плоскости.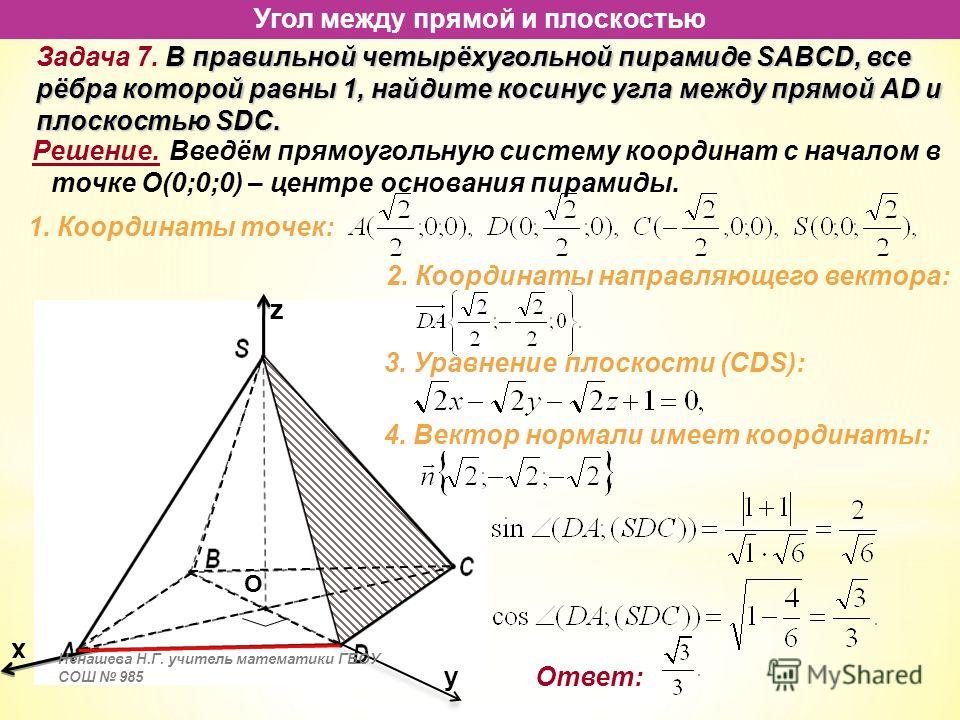
Угол между линией и плоскостью
Угол между линией и плоскостью образуется, когда линия наклонена к плоскости и к плоскости проведена нормаль из точки, где ее касается линия. Этот угол между прямой и плоскостью равен дополнению угла между нормалью и прямой.
Могут быть следующие три сценария, когда прямая и плоскость могут существовать вместе:
- Прямая может быть на плоскости
- Прямая может быть параллельна плоскости
- Линия может быть секущей
Угол, образованный между плоскостью и прямой линией, будет разным в каждом из трех вышеуказанных обстоятельств.
- Если прямая присутствует на плоскости или параллельна ей, то угол, образованный между прямой и плоскостью, будет равен 0 градусов.
- Если линия является секущей плоскости, то угол, образованный между ними, обозначается . Этот угол, который образуется между линией и плоскостью, на самом деле является углом, образованным прямой линией с ее ортогональная проекция на плоскость.

Другими словами, можно сказать, что угол между прямой и плоскостью — это угол, образованный между прямой и ее ортогональной проекцией на плоскость.
Это явление показано на рисунке ниже, поскольку он показывает угол между линией r и плоскостью.
Угол между линией и плоскостью
Если у нас есть информация о следующих элементах, то мы можем определить угол между линией и плоскостью, используя следующую формулу:
- Плоскость
- Прямая
- Определяющий вектор
- Вектор нормали к плоскости
Если линия, r , а плоскость, π , перпендикулярны, вектор направления прямой и вектор нормали к плоскости имеют одинаковое направление и поэтому его компоненты пропорциональны:
Теперь давайте перейдем к следующим примерам, в которых мы будем использовать приведенную выше формулу для определения угла между прямой и плоскостью.
Пример 1
Определить угол между прямой и плоскостью.
Решение
Из уравнений плоскости и прямой линии мы можем найти:
Управляющий вектор прямой =
Вектор нормали к плоскости =
Подставьте эти значения в следующую формулу, чтобы получить угол :
Следовательно, угол между прямой и плоскостью примерно равен 45 градусам.
Пример 2
Определить угол между прямой и плоскостью .
Решение
Из уравнений плоскости и прямой можно найти:
Вектор направления прямой =
Вектор нормали к плоскости =
Подставьте эти значения в следующую формулу, чтобы получить угол:
Следовательно, угол между прямой и плоскостью приблизительно равен 67,09 градуса.
Пример 3
Определить угол между прямой и плоскостью:
Решение
Из уравнений прямой и плоскости в этом примере мы можем найти:
Вектор направления линии:
Вектор нормали плоскости:
Подставьте эти значения в приведенную ниже формулу, чтобы получить угол:
Следовательно, угол между прямой и плоскостью примерно равен 30 градусам. \circ$ (угол в пятиугольнике). Угол $\phi$, который вы ищете, является высотой этого треугольника; это длина дуги, соединяющей вершину треугольника (соответствующую ребру додекаэдра) перпендикулярно противоположному ребру треугольника (соответствующему грани додекаэдра). Сферический закон косинусов, примененный к треугольнику, разрезанному пополам, дает 9{-1}}{\sqrt5}\quad=-\sqrt\frac{5-\sqrt5}{10}.$$
\circ$ (угол в пятиугольнике). Угол $\phi$, который вы ищете, является высотой этого треугольника; это длина дуги, соединяющей вершину треугольника (соответствующую ребру додекаэдра) перпендикулярно противоположному ребру треугольника (соответствующему грани додекаэдра). Сферический закон косинусов, примененный к треугольнику, разрезанному пополам, дает 9{-1}}{\sqrt5}\quad=-\sqrt\frac{5-\sqrt5}{10}.$$
$\endgroup$
$\begingroup$
Сначала определите золотое сечение и его обратную пропорцию
$$ a:=(1+\sqrt{5})/2, \quad b:=1/a=a-1. $$
Из статьи в Википедии правильный додекаэдр, определите
шесть вершин додекаэдра
$$ v_1 = (0,а,б),\; v_2 = (0,а,-б),\; v_3 = (1,1,-1),\\
v_4 = (а,б,0),\; v_5 = (1,1,1),\; v_6 = (a,-b,0)$$
где $\{v_1,v_2,v_3,v_4,v_5\}$
являются вершинами пятиугольной грани и
$v_6-v_4$ — реберный вектор.
Пусть $v_0 := (v_1+v_2)/2 = (0,a,0)$ — середина
ребра грани, противоположной $v_4$. Затем
9\circ-\theta.$
Затем
9\circ-\theta.$
Обратите внимание, что преимущество этого метода заключается в том, что ему требуется только координаты нескольких вершин, используя золотое сечение, скалярное произведение векторов и никакой тригонометрии, кроме самый конец, чтобы получить $\theta$ из его косинуса.
$\endgroup$
0
$\begingroup$
Пользоваться укороченными формулами/построениями из Википедии, может быть, и не очень хорошая привычка, так как настоящий математик должен сам строить свои геометрические или аналитические геометрические фигуры, однако я считаю, что это необходимо, когда у вас мало времени . 92$ с вершинами $(1,1,1),(1,1,-1),(\phi,\frac{1}{\phi},0)$, $(0,\phi,\ frac{1}{\phi}),(0,\phi,-\frac{1}{\phi})$ и с вектором нормали $\vec n=\langle1,\phi,0\rangle$.
Ребро действительно соединяет вершины $P=(1,1,1)$ и $Q=(\frac{1}{\phi},0,\phi)$. {\circ}$$ 9{\circ}$.
{\circ}$$ 9{\circ}$.
$\endgroup$
$\begingroup$
Этот угол может быть получен из двугранного угла $\delta = \arccos (-1/\sqrt{5})$ додекаэдра векторным методом. (Двугранный угол $\delta$ получается при построении додекаэдра — см., например, этот ответ на вопрос «Как это доказательство существования правильного додекаэдра не удается?»).
Рассмотрим группу из трех смежных граней пятиугольника, как показано на рис. 1, в котором пятиугольник $A$ лежит в плоскости страницы, а $B$ и $C$ наклонены вперед и пересекаются с $A$ под двугранным углом. $\дельта$. Каждый пятиугольник образует двугранный угол $\delta$ с двумя другими. Требуемый угол равен $\alpha$ между ребром $e$ и плоскостью пятиугольника $A$. Если $\beta$ — это угол между единичной нормалью $\underline{\mathbf{u}}_A = \underline{\mathbf{k}}$ к $A$ и единичным вектором $\underline{\mathbf{e }}$ вдоль $e$, тогда $\alpha = \beta + 90$.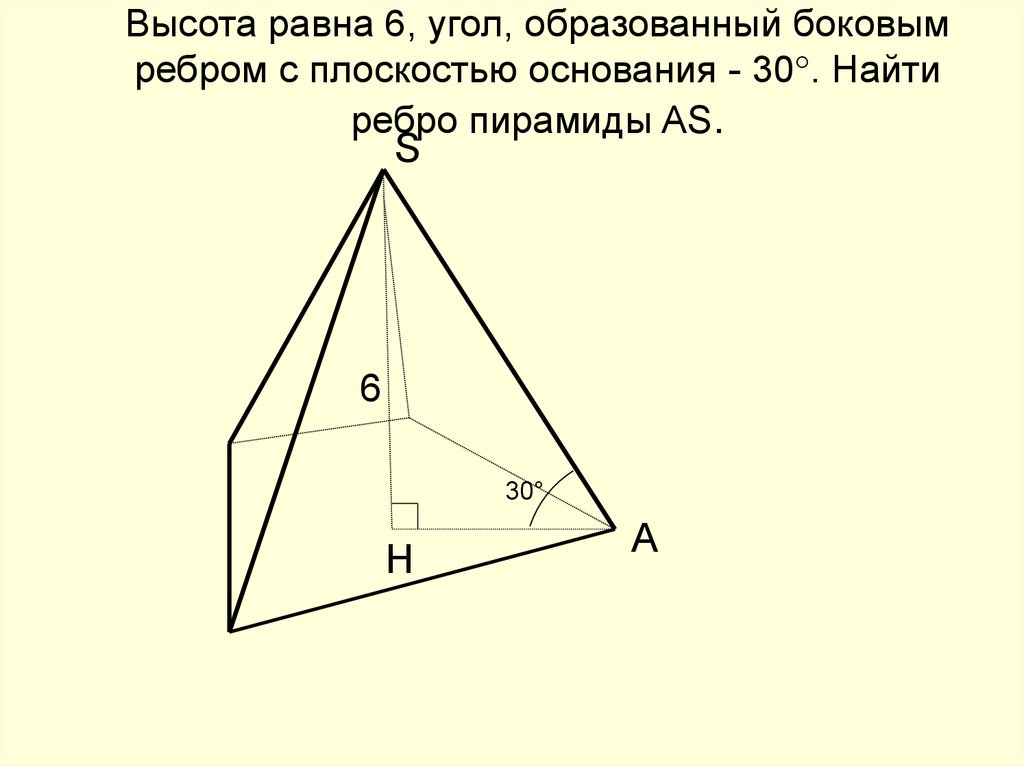


Leave A Comment