Углы в и с треугольника авс равны соответственно 72 и 78: Углы B и C треугольника ABC равны соответственно 72° и 78°... - Матемаматика ОГЭ: решения задач

Интерактивная видеолекция по теме «Геометрические задачи на вычисление»

Сценарий видеолекции

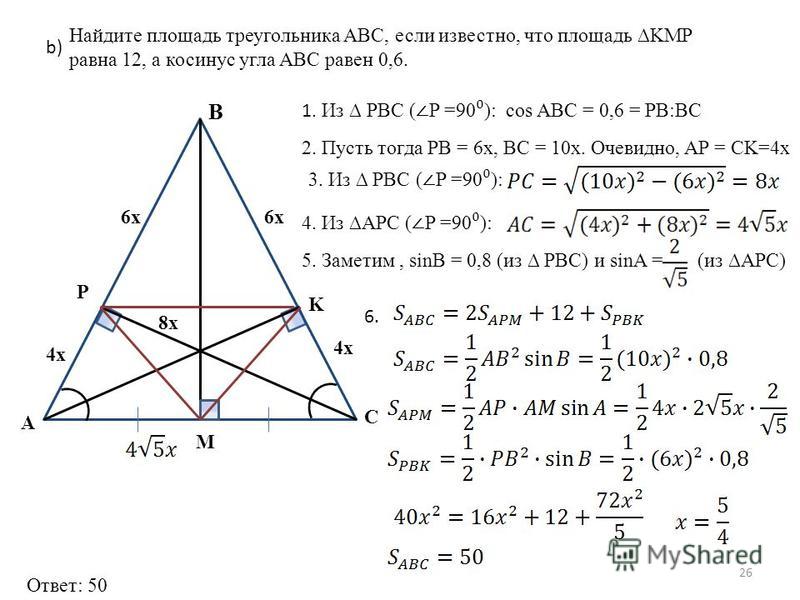
Задание №24 ОГЭ по математике

Тема: Геометрическая задача на вычисление (Геометрическая задача, предполагающая действия с геометрическими фигурами, координатами, векторами.)

Цель: научить ребенка правильному построению графиков, пониманию задачи и логической правильности рассуждений.

Описание задания: задача на нахождение какой-либо длины или значения угла в геометрической системе.

Теория

Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности.

Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника.

Следовательно, около любого треугольника можно описать окружность, так как серединные перпендикуляры к сторонам пересекаются в одной точке.

Для остроугольного треугольника центр окружности находится в треугольнике.

Другая ситуация с прямоугольным и тупоугольным треугольниками.

Формулы:

Радиус описанной окружности

R=23h, поэтому R=a3–√3.

Радиус вписанной окружности

r=13h, где h — высота треугольника.

Если дана сторона треугольника a, то h=a3–√2.

Поэтому r=a3–√6.

Прямоугольный треугольник

Радиус описанной окружности

R=12c, где c — гипотенуза.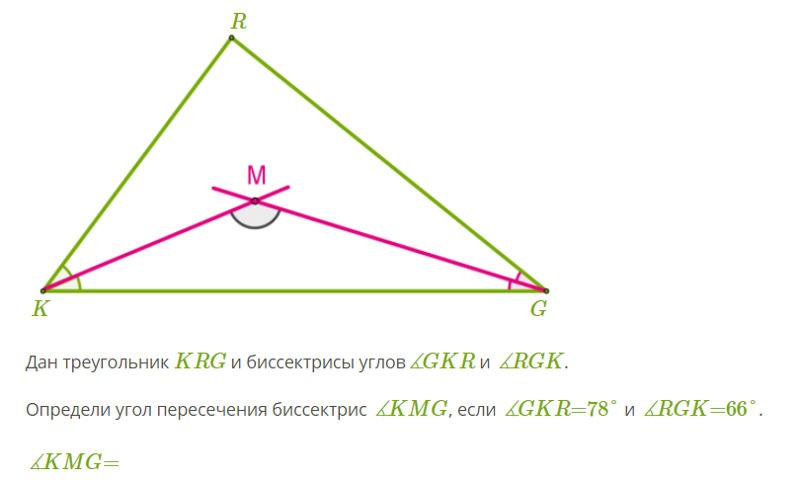

Радиус вписанной окружности

r=SΔp, где p — полупериметр.

Произвольный треугольник

Радиус описанной окружности

R=a⋅b⋅c4⋅SΔ;

R=a2sinα, где α — угол, противолежащий стороне a;

Если SΔ=abc4R,тоR=abc4SΔ;еслиSΔ=p⋅r,то r=SΔp.

Радиус вписанной окружности

r=SΔp, где p — полупериметр.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов:

Радиус описанной окружности

№1 Углы B и C треугольника ABC равны соответственно 66° и 84°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 15.

Алгоритм решения:

Делаем чертеж по условию задания.
Определяем угол А.
Используем следствие из теоремы синусов для треугольника АВС.
Определяем ВС.
Записываем ответ.

Решение:

1. Делаем чертеж, соответствующий условию задания. 2. Найдем угол А треугольнике ABC: 3. Радиус R описанной окружности вокруг треугольника связан с длиной BC и синусом угла A выражением, которое является следствием теоремы синусов: Отсюда получаем:

Ответ: 15

№2 Углы В и С треугольника ABC равны соответственно 72° и 78°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 17.

Алгоритм решения:

Делаем чертеж по условию задания.
Находим угол А в треугольнике.
Используем следствие из теоремы синусов для треугольника АВС.
Определяем ВС.
Записываем ответ.

Решение:

1. Делаем чертеж, удовлетворяющий условию задачи. 2. Рассматриваем треугольник ABC. В нем определяем угол A: ∠А=180⁰—∠В —∠С, откуда ∠А=180⁰ —71⁰—79⁰= 30⁰. 3. По теореме синусов и следствию из нее: где R – радиус описанной окружности. Имеем: 4. Определяем ВС из полученного равенства:

Ответ: 17

№3 Углы В и С треугольника ABC равны соответственно 71° и 79°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 8.

Алгоритм решения:

Делаем чертеж по условию задания.
Находим угол А в данном треугольнике.
Используем следствие из теоремы синусов для треугольника АВС
Определяем ВС.
Записываем ответ.

Решение:

1. Делаем чертеж, удовлетворяющий условию задачи. 2. Определим угол А: ∠А=180⁰ —71⁰—79⁰= 30⁰. 3. Пусть R — радиус описанной окружности, тогда по следствию из теоремы синусов получаем: 4. Тогда, при подстановке в равенство полученных данных, получаем: ВС равно произведению сторон АВ и АС на синус угла А, который равен 30⁰. Следовательно, ВС=2∙8∙0,5=8.

Ответ: 8

Приложение 1.

Ссылка на основную лекцию:

Ссылки на задачи:

Задача №1: https://www.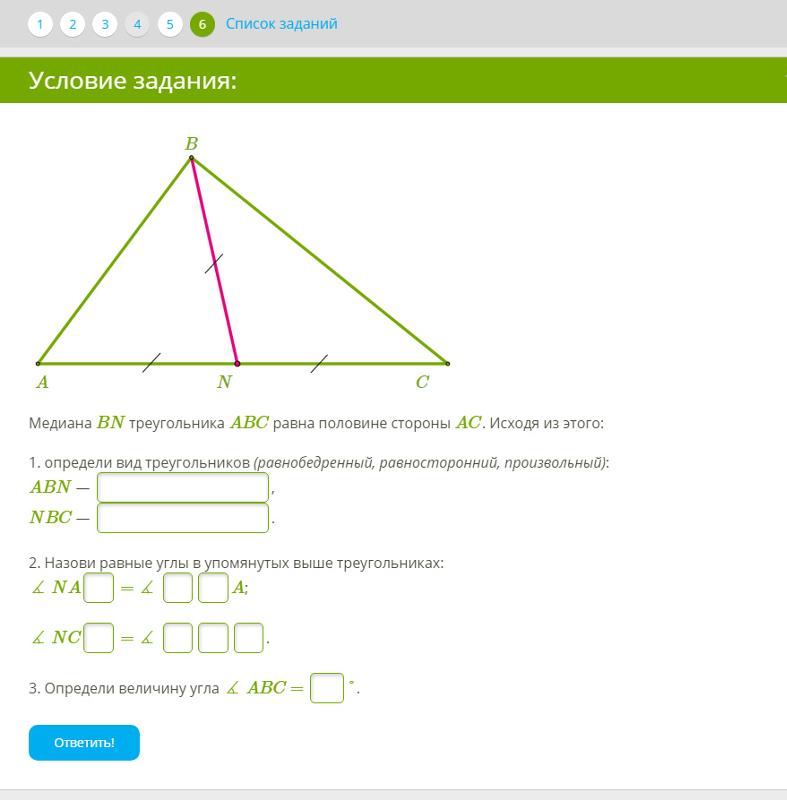 youtube.com/watch?v=8QXkrWEtAw8

Задача №2: https://www.youtube.com/watch?v=lvzmFkBG-ZE

Задача №3: https://www.youtube.com/watch?v=ya_qEKhcZUY&t=16s

Приложение 2.

Ссылки:

Задание №23 ОГЭ по математике
https://math-oge.sdamgia.ru/
ОГЭ 2020. Математика. Сборник заданий. Лаппо Л.Д., Попов М.А. (2020, 160с.)
ОГЭ 2020. Математика. Типовые варианты заданий. 50 вариантов. Под. ред. Ященко И.В. (2020, 280с.)
https://www.yaklass.ru/p/geometria/8-klass/okruzhnost-9230/vpisannaia-i-opisannaia-okruzhnosti-9244/re-44ec2b8e-dc52-456f-a0dc-69a012de326f
https://www.yaklass.ru/p/geometria/9-klass/sootnosheniia-mezhdu-storonami-i-uglami-treugolnika-skaliarnoe-proizvedeni_-9222/sootnosheniia-mezhdu-storonami-i-uglami-treugolnika-9281/re-7ad3359e-27dd-4ae0-9272-8f1ce3e75ec2
https://vk. com/away.php?to=https%3A%2F%2Fvsimse.ru%2Fvn-video-redaktor%2F&cc_key
https://vk.com/away.php?to=https%3A%2F%2Ftrashbox.ru%2Flink%2Ftop-android-qr&cc_key
https://vk.com/away.php?to=https%3A%2F%2Fskysmart.ru%2Farticles%2Fmathematic%2Fteorema-sinusov&cc_key
https://vk.com/away.php?to=https%3A%2F%2Fplay.google.com%2Fstore%2Fapps%2Fdetails%3Fid%3Dcom.mobile.qrcodereader%26hl%3Dru%26gl%3DUS&el=snippet
https://vk.com/away.php?to=https%3A%2F%2Fapps.apple.com%2Fru%2Fapp%2Fqr-code-reader%2Fid1067154451&cc_key

ВПР по Математике(Угл.) 7 класс (2023г) — Задание 13

Образцы вариантов ВПР 2023 года, демоверсии всероссийской проверочной работы для 7 класса по Математике (Углубленный уровень) .

1. В треугольнике ABC проведены медиана BM и высота BH. Известно, что AH  =  54, BC  =  BM. Найдите длину стороны AC.

2. В треугольнике ABC проведена биссектриса CE. Найдите величину угла BCE, если ∠BAC  =  46° и ∠ABC  =  78°.

3. В треугольнике ABC проведена биссектриса AL, угол ALC равен 121°, угол ABC равен 101°. Найдите угол ACB. Ответ дайте в градусах.

4. В треугольнике два угла равны 36° и 73°. Найдите его третий угол. Ответ дайте в градусах.

5. В треугольнике два угла равны 43° и 88°. Найдите его третий угол. Ответ дайте в градусах.

6. В треугольнике ABC проведена биссектриса AL, угол ALC равен 78°, угол ABC равен 52°. Найдите угол ACB. Ответ дайте в градусах.

7. В треугольнике ABC известно, что AD  — биссектриса. Найдите угол BAD. Ответ дайте в градусах.

8. В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ. Найдите медиану АМ, если периметр треугольника АВС равен 40 см, а периметр треугольника АВМ равен 32 см.

9. Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 78 см, а одна из сторон равна 18 см. Найдите две другие стороны треугольника.

10. Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 86 см, а одна из сторон равна 20 см. Найдите две другие стороны треугольника.

11. Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольника АВС, пересекаются в точке М. Найдите углы треугольника, если угол ВМС  =  140°.

12. В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.

13. На сторонах угла BAC и на его биссектрисе отложены равные отрезки AB, AC и AD. Величина угла BDC равна 160°. Определите величину угла BAC.

14. На сторонах угла BAC, равного 20°, и на его биссектрисе отложены равные отрезки AB, AC и AD. Определите величину угла BDC.

15. Отрезки AB и CD  — диаметры окружности с центром O. Найдите периметр треугольника AOD, если известно, что CB  =  13 см, AB  =  16 см.

16. Отрезки AB и CD  — диаметры окружности с центром O. Найдите периметр треугольника AOD, если известно, что CB  =  11 см, AB  =  17 см.

17. В треугольнике ABC стороны AB и BС равны, угол B равен Биссектрисы углов A и C пересекаются в точке M. Найдите величину угла AMC.

18. На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD  =  AC и точка A находится между точками B и D. Найдите величину угла ADC если угол ABC равен

19. На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD  =  AC и точка A находится между точками B и D. Найдите величину угла , ADC если угол ABC равен .

20. На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD  =  AC и точка A находится между точками B и D. Найдите величину угла ADC если угол ABC равен

21. В равнобедренном треугольнике ABC с основанием AC угол B равен 120^°. Высота треугольника, проведённая из вершины A, равна 7. Найдите длину стороны AC.

22. Сторона AB треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что BC=BD. Найдите величину угла, BCD если угол ACB равен 60°, а угол BAC равен 50 .

23. В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 6, а BC =12.

24. В равнобедренном треугольнике АВС с основанием ВС угол А равен 120°. Высота треугольника, проведённая из вершины В, равна 13. Найдите длину стороны ВС.

25. Углы треугольника АВС относятся так: Биссектриса ВМ угла ABC равна 6. Найдите длину отрезка МС.

Запишите решение и ответ.

26. Между сторонами угла АОВ, равного 110°, проведены лучи ОС и ОМ так, что угол АОС на 30° меньше угла ВОС, а ОМ  — биссектриса угла ВОС. Найдите величину угла СОМ. Ответ дайте в градусах.

27. В равнобедренном треугольнике АВС с основанием АВ угол С в 2 раза меньше угла А. Найдите величину внешнего угла при вершине В. Ответ дайте в градусах. Запишите решение и ответ.

28. Внешний угол при вершине В треугольника ABC равен 102°. Биссектрисы углов А и С треугольника пересекаются в точке О. Найдите величину угла АОС. Дайте ответ в градусах. Запишите решение и ответ.

29. Диаметры АВ и CD окружности пересекаются в точке О. Найдите величину угла ADO, если ∠BOD  =  150°. Ответ дайте в градусах. Запишите решение и ответ.

30. Биссектриса внешнего угла при вершине В треугольника ABC параллельна стороне АС. Найдите величину угла САВ, если ∠ABC  =  36°. Ответ дайте в градусах. Запишите решение и ответ.

31. Сторона BC треугольника ABC продолжена за точку B. На продолжении отмечена точка D так, что AB  =  DB. Найдите величину угла BAD, если угол ACB равен 70°, а угол BAC равен 34°. Ответ дайте в градусах. Запишите решение и ответ.

32. На продолжении стороны BC равнобедренного треугольника ABC с основанием AC отметили точку D так, что CD  =  AC и точка C находится между точками B и D. Найдите величину угла ADC если угол ABC равен 36°. Ответ дайте в градусах. Запишите решение и ответ.

33. В треугольнике АВС угол АСВ равен 48°, угол CAD равен 22°, AD  — биссектриса. Найдите величину угла АВС. Ответ дайте в градусах. Запишите решение и ответ.

34. На продолжении стороны AC равнобедренного треугольника ABC с основанием BC отметили точку D так, что CD  =  BC и точка C находится между точками A и D. Найдите величину угла CDB если угол BAC равен 72°. Ответ дайте в градусах. Запишите решение и ответ.

35. В прямоугольном треугольнике АВС угол B прямой, Биссектрисы углов АВС и АСВ пересекаются в точке О. Найдите величину угла ВОС. Ответ дайте в градусах. Запишите решение и ответ.

NCERT Solutions for Class 7 Math Chapter 5

Решения НЦЭРТ
Класс 7
Математика
линии и углы

Математика NCERT 7 класс, глава 5: прямые и углы все о разных прямых , отрезках прямых и углах .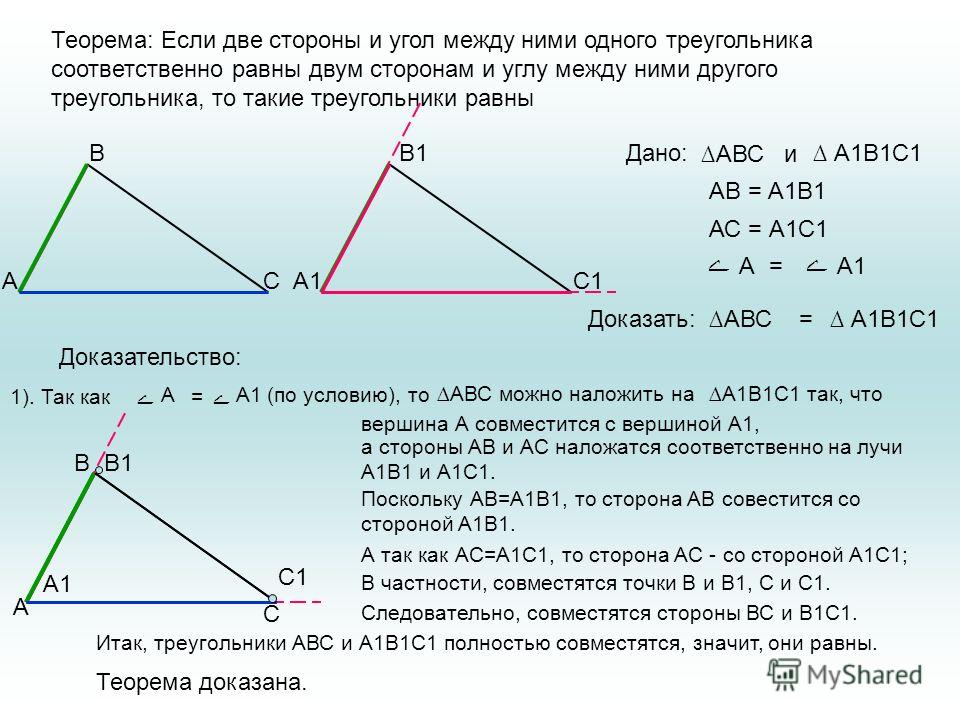

Отрезок прямой имеет две конечные точки.
Луч имеет только одну конечную точку (свою вершину).
Линия не имеет концов ни с одной стороны.

Эта глава проливает свет на такие темы, как связанных углов , пара строк . В главе рассматриваются различные типы углов и линий . В этой главе рассматриваются следующие типы углов:

Пары уголков	Состояние
Два дополнительных уголка	Сумма мер до 90°
Два дополнительных уголка	Сумма мер до 180°
Два смежных угла	Имеют общую вершину и общее плечо, но не имеют общего внутреннего пространства
Линейная пара	Смежный и дополнительный

Линейная пара — это пара смежных углов, необщие стороны которых являются противоположными лучами.

Все типы подробно обсуждаются и дополняются примерами и краткими вопросами.
В теме пара строк обсуждаются различные подразделы, а именно:

Пересекающиеся линии
Поперечный
Уголки, образованные секущей
При пересечении двух прямых (выглядящих как буква X) мы имеем две пар противоположных углов . Их называют вертикально противоположными углами . Они равны в меру.
секущая — это прямая , которая пересекает две или более прямых в различных точках.

В этом разделе обсуждаются шесть углов:
1. Внутренние углы
2. Внешние углы
3. Пары соответствующих углов
4. Пары чередующихся внутренних углов
5.

Пары чередующихся внешних углов
6. Пары внутренних углов на на той же стороне поперечной

Поперечной параллельных прямых

Впоследствии тема- Проверка параллельных линий также обсуждается в главе- Линии и углы .

Когда секущая пересекает две прямые, так что пар соответствующих углов равны , тогда прямые должны быть параллельными .
Когда секущая пересекает две линии, так что пар чередующихся внутренних углов равны , линии должны быть параллельными .
Когда поперечная разрезает две линии, так что пар внутренних углов на одной стороне поперечной являются дополнительными, линии должны быть параллельными .

Там, где это необходимо, в главе также присутствует несколько диаграмм.
Глава состоит из набора вопросов для проверки основного понимания главы, за которыми следует резюме обсуждения для быстрого запоминания.

Страница № 101:

Вопрос 1:

Найти дополнение каждого из следующих углов:

Ответ:

Сумма мера дополнительных углов равна 90º.

(и) 20°

Дополнение = 90° − 20°

= 70°

(ii) 63°

Дополнение = 90° − 63°

= 27°

(iii) 57°

Дополнение = 90° − 57°

= 33°

Страница № 102:

Вопрос 2:

Найдите дополнение каждого из следующих углов:

Ответ:

Сумма дополнительных углов равна 180º.

(i) 105°

Дополнение = 180° − 105°

= 75°

(ii) 87°

Дополнение = 180° − 87°

= 93° 154°

Дополнение = 180° − 154°

= 26°

Номер страницы 102:

Вопрос 3:

Идентифицировать какие из следующих пар углов являются дополнительными, а какие являются дополнительными.

(и) 65°, 115° (ii) 63°, 27°

(iii) 112°, 68° (iv) 130°, 50°

(в) 45°, 45° (vi) 80°, 10°