| Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. cos(0°)=cos(360°)=1; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.
|
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций 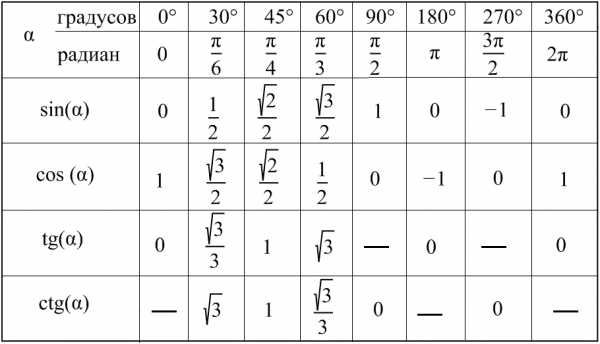 Доп. Инфо:
|
tehtab.ru
Тригонометрические и геометрические преобразования, sin(A + B), sin(A
Коэффициенты для суммы углов
Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B).
Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.
Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.
Нахождение синуса, косинуса или тангенса полного угла (A + B)
Нахождение sin(A + B)
Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке. Большой угол (A + B), состоит из двух маленьких, А и В. Рисунок (1) показывает, что противоположная сторона состоит из двух частей.
Нижняя часть, разделенная линией между углами (2), есть синус А. Линия между двумя углами, разделенная гипотенузой (3), есть косинус B. Умножаем их. Средняя линия и в числителе, и в
знаменателе, поэтому они сокращаются, оставляя нижнюю часть противоположной стороны над гипотенузой (4).
Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).
Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.
Нахождение cos(A + B)
Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.
Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.
Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).
Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
cos(A + B) = cos A cos B — sin A sin B
Нахождение tan(A + B)
Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
tan(A + B) = [sin A cos B + cos A sin B]/[cos A cos B — sin A sin B]
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
tan(A + B) = [tan A + tan B]/[1 — tan A tan B]
Коэффициенты для 75 градусов
Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля.т разницу, некоторые нет!
Коэффициенты углов, больших, чем 90 градусов
До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).
Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют
www.math10.com
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.
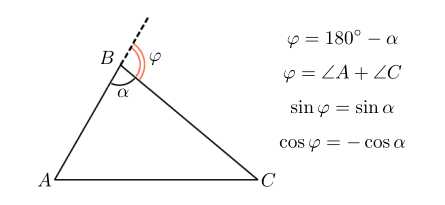
Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .
Пусть — внешний угол при вершине .
Зная , найдем по формуле
Получим:
2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .
Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Таблица косинусов (полная, градусы и значения)
В данной таблице представлены значения косинусов от 0° до 360°. Таблица косинусов нужна, чтобы узнать, чему равен косинус угла. Нужно только найти его в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-kosinusov — uchim.org
Таблица косинусов для 0°-180°
|
|
|
Таблица косинусов для 181°-360°
|
|
|
uchim.org
Тригонометрические тождества и преобразования
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:Простейшие тригонометрические тождества
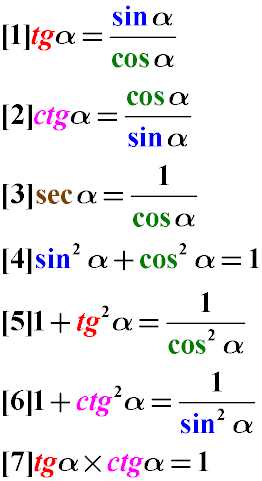
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
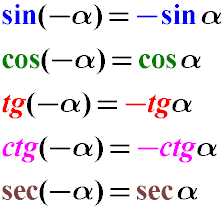
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.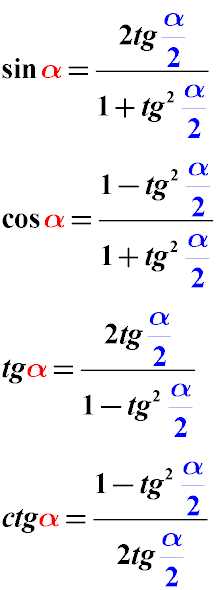
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | -cos α | sin α | sin α | -cos α | -sin α | cos α |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
profmeter.com.ua
Задание 6 — геометрия с элементами тригонометрии
Сегодня рассмотрим задачи B8 c тригонометрией в ее классическом понимании, где изучаются обычные прямоугольные треугольники. Поэтому никаких тригонометрических окружностей и отрицательных углов сегодня не будет — только обычные синусы и косинусы.
Такие задачи составляют примерно 30% от общего числа. Помните: если в задаче B8 хоть раз упоминается угол π, она решается совсем другими способами. Мы обязательно рассмотрим их в ближайшее время. А сейчас — главное определение урока:
Треугольник — фигура на плоскости, состоящая из трех точек и отрезков, которые их соединяют. Фактически, это замкнутая ломаная из трех звеньев. Точки называются вершинами треугольника, а отрезки — сторонами. Важно заметить, что вершины не должны лежать на одной прямой, иначе треугольник вырождается в отрезок.
Довольно часто треугольником называют не только саму ломаную, но и часть плоскости, которая этой ломаной ограничена. Таким образом, можно определить площадь треугольника.
Два треугольника называются равными, если один можно получить из другого путем одного или нескольких движений плоскости: сдвига, поворота или симметрии. Кроме того, существует понятие подобных треугольников: их углы равны, а соответствующие стороны пропорциональны…
Все, что написано выше, можно было не читать. Потому что это не нужно. Вы что, не знаете, что такое треугольник? Вы действительно не знаете, как он выглядит? Хорошо, я сейчас покажу.
Это треугольник ABC. Более того, это прямоугольный треугольник: в нем ∠C = 90°. Именно такие чаще всего и встречаются в задаче B8.
Все, что надо знать для решения задачи B8 — это несколько простых фактов из геометрии и тригонометрии, а также общая схема решения, в которой эти факты используются. Затем останется просто «набить руку».
Начнем с фактов. Они разбиты на три группы:
- Определения и следствия из них;
- Основные тождества;
- Симметрии в треугольнике.
Нельзя сказать, что какая-то из этих групп важнее, сложнее или проще. Но информация, которая в них содержится, позволяет решить любую задачу B8. Поэтому знать надо все. Итак, поехали!
Группа 1: определения и следствия из них
Рассмотрим треугольник ABC, где ∠C — прямой. Для начала — определения:
Синус угла — это отношение противолежащего катета к гипотенузе.
Косинус угла — это отношение прилежащего катета к гипотенузе.
Тангенс угла — это отношение противолежащего катета к прилежащему.
Один угол или отрезок может входить в разные прямоугольные треугольники. Более того, очень часто один и тот же отрезок является катетом в одном треугольнике и гипотенузой — в другом. Но об этом — дальше, а пока будем работать с обычным углом А. Тогда:
- sin A = BC : AB;
- cos A = AC : AB;
- tg A = BC : AC.
Основные следствия из определения:
- sin A = cos B; cos A = sin B — самые часто используемые следствия
- tg A = sin A : cos A — связывает тангенс, синус и косинус одного угла
- Если ∠A + ∠B = 180°, т.е. углы смежные, то: sin A = sin B; cos A = −cos B.
Хотите — верьте, хотите — нет, но этих фактов достаточно, чтобы решить примерно треть всех тригонометрических задач B8.
Группа 2: основные тождества
Первое и самое главное тождество — теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Применительно к треугольнику ABC, рассмотренному выше, эту теорему можно записать так:
AC 2 + BC 2 = AB 2
И сразу — небольшое замечание, которое убережет читателя от множества ошибок. Когда решаете задачу, всегда (слышите, всегда!) записывайте теорему Пифагора именно в таком виде. Не пытайтесь сразу выражать катет, как это обычно требуется. Возможно, вы сэкономите пару строчек вычислений, но именно на этой «экономии» было потеряно больше баллов, чем где-либо еще в геометрии.
Второе тождество — из тригонометрии. Выглядит следующим образом:
sin 2A + cos 2A = 1
Оно так и называется: основное тригонометрическое тождество. С его помощью можно через синус выразить косинус и наоборот.
Группа 3: Симметрии в треугольнике
То, что написано ниже, относится только к равнобедренным треугольникам. Если в задаче таковой не фигурирует, то для решения достаточно фактов из первых двух групп.
Итак, рассмотрим равнобедренный треугольник ABC, где AC = BC. Проведем к основанию высоту CH. Получим следующие факты:
- ∠A = ∠B. Как следствие, sin A = sin B; cos A = cos B; tg A = tg B.
- CH — не только высота, но и биссектриса, т.е. ∠ACH = ∠BCH. Аналогично, равны и тригонометрические функции этих углов.
- Также CH — это медиана, поэтому AH = BH = 0,5 · AB.
Теперь, когда все факты рассмотрены, перейдем непосредственно к методам решения.
Общая схема решения задачи B8
Геометрия отличается от алгебры тем, что в ней нет простых и универсальных алгоритмов. Каждую задачу приходится решать с нуля — и в этом ее сложность. Тем не менее, общие рекомендации дать все-таки можно.
Для начала, следует обозначить неизвестную сторону (если таковая имеется) за X. Затем применяем схему решения, которая состоит из трех пунктов:
- Если в задаче есть равнобедренный треугольник, применить к нему все возможные факты из третьей группы. Найдите равные углы и выразите их тригонометрические функции. Кроме того, равнобедренный треугольник редко бывает прямоугольным. Поэтому ищите в задаче прямоугольные треугольники — они там обязательно есть.
- Применить к прямоугольному треугольнику факты из первой группы. Конечная цель — получить уравнение относительно переменной X. Найдем X — решим задачу.
- Если фактов из первой группы оказалось недостаточно, применяем факты из второй группы. И снова ищем X.
Примеры решения задач
А теперь попробуем с помощью полученных знаний решить наиболее распространенные задачи B8. Не удивляйтесь, что с таким арсеналом текст решения окажется не намного длиннее, чем исходное условие. И это радует 🙂
Задача. В треугольнике ABC угол C равен 90°, AB = 5, BC = 3. Найдите cos A.
По определению (группа 1), cos A = AC : AB. Гипотенуза AB нам известна, а вот катет AC придется искать. Обозначим его AC = x.
Переходим к группе 2. Треугольник ABC — прямоугольный. По теореме Пифагора:
AC 2 + BC 2 = AB 2;
x2 + 32 = 52;
x2 = 25 − 9 = 16;
x = 4.
Теперь можно найти косинус:
cos A = AC : AB = 4 : 5 = 0,8.
Задача. В треугольнике ABC угол B равен 90°, cos A = 4/5, BC = 3. BH — высота. Найдите AH.
Обозначим искомую сторону AH = x и рассмотрим треугольник ABH. Он прямоугольный, причем ∠AHB = 90° по условию. Поэтому cos A = AH : AB = x : AB = 4/5. Это пропорция, ее можно переписать так: 5 · x = 4 · AB. Очевидно, мы найдем x, если будем знать AB.
Рассмотрим треугольник ABC. Он также прямоугольный, причем cos A = AB : AC. Ни AB, ни AC нам не известны, поэтому переходим ко второй группе фактов. Запишем основное тригонометрическое тождество:
sin 2A + cos 2A = 1;
sin 2A = 1 − cos 2A = 1 − (4/5)2 = 1 − 16/25 = 9/25.
Поскольку тригонометрические функции острого угла положительны, получаем sin A = 3/5. С другой стороны, sin A = BC : AC = 3 : AC. Получаем пропорцию:
3 : AC = 3 : 5;
3 · AC = 3 · 5;
AC = 5.
Итак, AC = 5. Тогда AB = AC · cos A = 5 · 4/5 = 4. Наконец, находим AH = x:
5 · x = 4 · 4;
x = 16/5 = 3,2.
Задача. В треугольнике ABC AB = BC, AC = 5, cos C = 0,8. Найдите высоту CH.
Обозначим искомую высоту CH = x. Перед нами равнобедренный треугольник ABC, в котором AB = BC. Следовательно, из третьей группы фактов имеем:
∠A = ∠C ⇒ cos A = cos C = 0,8
Рассмотрим треугольник ACH. Он прямоугольный (∠H = 90°), причем AC = 5 и cos A = 0,8. По определению, cos A = AH : AC = AH : 5. Получаем пропорцию:
AH : 5 = 8 : 10;
10 · AH = 5 · 8;
AH = 40 : 10 = 4.
Осталось воспользоваться второй группой фактов, а именно теоремой Пифагора для треугольника ACH:
AH 2 + CH 2 = AC 2;
42 + x2 = 52;
x2 = 25 − 16 = 9;
x = 3.
Задача. В прямоугольном треугольнике ABC ∠B = 90°, AB = 32, AC = 40. Найдите синус угла CAD.
Поскольку нам известна гипотенуза AC = 40 и катет AB = 32, можно найти косинус угла A: cos A = AB : AC = 32 : 40 = 0,8. Это был факт из первой группы.
Зная косинус, можно найти синус через основное тригонометрическое тождество (факт из второй группы):
sin 2A + cos 2A = 1;
sin 2A = 1 − cos 2A = 1 − 0,82 = 0,36;
sin A = 0,6.
При нахождении синуса вновь был использован тот факт, что тригонометрические функции острого угла положительны. Осталось заметить, что углы BAC и CAD смежные. Из первой группы фактов имеем:
∠BAC + ∠CAD = 180°;
sin CAD = sin BAC = sin A = 0,6.
Задача. В треугольнике ABC AC = BC = 5, AB = 8, CH — высота. Найдите tg A.
Треугольник ABC — равнобедренный, CH — высота, поэтому заметим, что AH = BH = 0,5 · AB = 0,5 · 8 = 4. Это факт из третьей группы.
Теперь рассмотрим треугольник ACH: в нем ∠AHC = 90°. Можно выразить тангенс: tg A = CH : AH. Но AH = 4, поэтому остается найти сторону CH, которую обозначим CH = x. По теореме Пифагора (факт из группы 2) имеем:
AH 2 + CH 2 = AC 2;
42 + x2 = 52;
x2 = 25 − 16 = 9;
x = 3.
Теперь все готово, чтобы найти тангенс: tg A = CH : AH = 3 : 4 = 0,75.
Задача. В треугольнике ABC AC = BC, AB = 6, cos A = 3/5. Найдите высоту AH.
Обозначим искомую высоту AH = x. Снова треугольник ABC — равнобедренный, поэтому заметим, что ∠A = ∠B, следовательно, cos B = cos A = 3/5. Это факт из третьей группы.
Рассмотрим треугольник ABH. По условию, он прямоугольный (∠AHB = 90°), причем известна гипотенуза AB = 6 и cos B = 3/5. Но cos B = BH : AB = BH : 6 = 3/5. Получили пропорцию:
BH : 6 = 3 : 5;
5 · BH = 6 · 3;
BH = 18/5 = 3,6.
Теперь найдем AH = x по теореме Пифагора для треугольника ABH:
AH 2 + BH 2 = AB 2;
x2 + 3,62 = 62;
x2 = 36 − 12,96 = 23,04;
x = 4,8.
Дополнительные соображения
Бывают нестандартные задачи, где рассмотренные выше факты и схемы бесполезны. Увы, в таком случае нужен действительно индивидуальный подход. Подобные задачи любят давать на всевозможных «пробных» и «демонстрационных» экзаменах.
Ниже приведены две реальные задачи, которые предлагались на пробном ЕГЭ в Москве. Справились с ними единицы, что свидетельствует о высокой сложности этих задач.
Задача. В прямоугольном треугольнике ABC из угла C = 90° провели медиану и высоту. Известно, что ∠A = 23°. Найдите ∠MCH.
Заметим, что медиана CM проведена к гипотенузе AB, поэтому M — центр описанной окружности, т.е. AM = BM = CM = R, где R — радиус описанной окружности. Следовательно, треугольник ACM — равнобедренный, и ∠ACM = ∠CAM = 23°.
Теперь рассмотрим треугольники ABC и CBH. По условию, оба треугольника прямоугольные. Кроме того, ∠B — общий. Следовательно, треугольники ABC и CBH подобны по двум углам.
В подобных треугольника соответствующие элементы пропорциональны. В частности:
BCH = BAC = 23°
Наконец, рассмотрим ∠C. Он прямой, и, кроме того, ∠C = ∠ACM + ∠MCH + ∠BCH. В этом равенстве ∠MCH — искомый, а ∠ACM и ∠BCH известны и равны 23°. Имеем:
90° = 23° + MCH + 23°;
MCH = 90° − 23° − 23° = 44°.
Задача. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
Обозначим стороны прямоугольника: AB = x, BC = y. Выразим периметр:
PABCD = 2 · (AB + BC) = 2 · (x + y) = 34;
x + y = 17.
Аналогично выразим площадь: SABCD = AB · BC = x · y = 60.
Теперь рассмотрим треугольник ABC. Он прямоугольный, поэтому запишем теорему Пифагора:
AB 2 + BC 2 = AC2;
AC 2 = x2 + y2.
Заметим, что из формулы квадрата разности следует равенство:
x2 + y2 = (x + y)2 − 2 · x · y = 172 − 2 · 60 = 289 − 120 = 169
Итак, AC 2 = 169, откуда AC = 13.
Смотрите также:
- Задача B8: отрезки и углы в треугольниках
- Центральные и вписанные углы в задании 6
- Дополнительные соображения
- Тест к уроку «Площади многоугольников на координатной сетке» (средний)
- Сложные логарифмические неравенства
- Задача B5: площадь фигуры без клеток
www.berdov.com
Таблица значений тригонометрических функций
Примечание. В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».
См. также полезные материалы:
Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Синус пи, косинус пи, тангенс пи и других углов в радианах
Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.
Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180.
Примеры:
1. Синус пи.
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.
2. Косинус пи.
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.
3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.
Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
0, 15, 30, 45, 60, 90 … 360 градусов
(цифровые значения «как по таблицам Брадиса»)
| значение угла α (градусов) | значение угла α в радианах | sin (синус) | cos (косинус) | tg (тангенс) | ctg (котангенс) |
|---|---|---|---|---|---|
| 0 | 0 |
0 |
1 |
0 |
- |
| 15 |
π/12 |
0,2588 |
0,9659 |
0,2679 |
3,7321 |
| 30 |
π/6 |
0,5000 |
0,8660 |
0,5774 |
1,7321 |
| 45 |
π/4 |
0,7071 |
0,7071 |
1 |
1 |
|
50 |
5π/18 |
0,7660 |
0,6428 |
1.1918 |
0,8391 |
| 60 |
π/3 |
0,8660 |
0,5000 |
1,7321 |
0,5774 |
|
65 |
13π/36 |
0,9063 |
0,4226 |
2,1445 |
0,4663 |
|
70 |
7π/18 |
0,9397 |
0,3420 |
2,7475 |
0,3640 |
| 75 |
5π/12 |
0,9659 |
0,2588 |
3,7321 |
0,2679 |
| 90 |
π/2 |
1 |
0 |
- |
0 |
|
105 |
5π/12 |
0,9659 |
-0,2588 |
-3,7321 |
-0,2679 |
| 120 |
2π/3 |
0,8660 |
-0,5000 |
-1,7321 |
-0,5774 |
| 135 |
3π/4 |
0,7071 |
-0,7071 |
-1 |
-1 |
|
140 |
7π/9 |
0,6428 |
-0,7660 |
-0,8391 |
-1,1918 |
| 150 |
5π/6 |
0,5000 |
-0,8660 |
-0,5774 |
-1,7321 |
| 180 |
π |
0 |
-1 |
0 |
- |
| 270 |
3π/2 |
-1 |
0 |
- |
0 |
| 360 |
2π |
0 |
1 |
0 |
- |
Иногда для быстрых расчетов нужно не точное, а вычисляемое значение (число десятичной дробью), которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Дополнительно в таблицу включены «нестандартные» значения тангенса, косинуса, синуса 140 градусов, синуса 105, 70, косинуса 105 и 50 градусов.
Начать курс обучения
profmeter.com.ua

Leave A Comment