Тригонометрические и геометрические преобразования, sin(A + B), sin(A
Коэффициенты для суммы углов
Как демонстрируют различные примеры, иногда нам нужны значения углов, отличных от 0, 30, 45, 60 и 90 градусов. В этой главе вы должны научиться двум вещам:
1. sin(A + B) не является равным sinA + sinB. В этом случае не срабатывает простое раскрытие скобок, как в алгебре.
2. Формулу, по которой вычисляется sin(A + B).
Во-первых, покажем, что раскрытие скобок не «срабатывает». Пусть A = 30 градусов и B = 45 градусов. Sin30 равен 0.5. Sin45 равен 0.7071. Складывая, получим 1.2071.
Вы знаете, что ни синус, ни косинус не может быть больше 1. Почему? Потому что в дробях, по которым они вычисляются, гипотенуза выступает в качестве знаменателя. Самое большее значение мы получим, если числитель равен знаменателю. Синус или косинус не может быть больше 1, и поэтому значение 1,2071 не верно.
Нахождение синуса, косинуса или тангенса полного угла (A + B)
Нахождение sin(A + B)
Самый простой способ найти sin (A + B) — используя геометрическое построение, показанное на рисунке.
Обратите внимание на маленький прямоугольный треугольник (5). Затененный угол есть A, потому что линия на его верхней части параллельна линии в основании. Подобные прямоугольные треугольники с углом А показывают, что верхний угол, отмеченный А также равен оригинальному углу А. Верхняя часть противоположной (6) над длинной, заштрихованный треугольник является соs А. Противоположный над основной гипотенузой (7) есть синус. Поскольку стороны с пометкой «противоположные» (7) и в числителе и знаменателе, когда cos и sin перемножаются, cosAsinB есть верхняя часть оригинального противоположного — для (A + B) — разделенные основной гипотенузой (8).
Теперь, сложим это все вместе (9). Sin(A + B) есть две части противоположного — все разделенные гипотенузой (9). Записывая это в тригонометрическую форму: sin(A + B) = sin A cos B + cos A sin B.
Нахождение cos(A + B)
Очень похожая конструкция находит формулу для косинуса угла созданного двумя углами, сложенными вместе.
Используя ту же самую конструкцию (1), обратите внимание, что смежная сторона является полной линией основания (для соs A), c частью, которая вычитается справа. Каждая часть должна использовать тот же знаменатель, гипотенузу (A + B) треугольника.
Полная линия основания, разделенная линией между углами A и E есть cosA (2). Эта разделяющая линия, деленная гипотенузой (A + B) треугольника, есть cos B (3). Поэтому, полная линия основания, деленная гипотенузой есть произведение cosAcosB (4).
Теперь, небольшая часть, которая должна быть вычтена. Заштрихованная часть (5) представляет sinA, который умножается заштрихованной частью (6) есть sin E, который есть другой частью и , которая нам нужна (7). Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
Вычитание дает соs (А + В) (8), поэтому формула, которая нам нужна:
cos(A + B) = cos A cos B — sin A sin B
Нахождение tan(A + B)
Полный геометрический вывод формулы для tg (A + B) является сложным. Проще всего вывести его из двух формул, которые мы уже сделали. В любом угле, тангенс равен синус, деленному на косинус. Используя тот факт, tan (A + B) = sin(A + B)/соs(A + B). Это выражение можно расширить к виду:
Разделив верхнюю и нижнюю часть на cos A cos B, что превращает все члены в тангенсы, получаем:
tan(A + B) = [tan A + tan B]/[1 — tan A tan B]
Коэффициенты для 75 градусов
Покажем коэффициенты синуса, косинуса и тангенса, подставляя в формулу суммы, и потом упрощая результат к своей простейшей форме, прежде чем находить суммы. После внесения основных замен в каждом конкретном случае, примерная работа в заштрихованной части, чтобы показать, как результат сводится к простейшей форме для оценки.
Если вы используете ваш карманный калькулятор для оценки, скорей всего, не имеет значения или вы упрщаете выражения сначала или просто пропускаете его! Все зависит от калькулятора: некоторые вычисля.т разницу, некоторые нет!
Коэффициенты углов, больших, чем 90 градусов
До сих пор рассматривалось соотношение острых углов (между 0 и 90 градусами). Другие треугольники с тупым углом (более 90 градусов) и до 180 градусов могут появиться в последующих задачах. Для упрощения классификации углов по размеру, они делятся на сектора (квадранты).
Квадрант есть четвертой частью круга. Так как круг делится на 360 градусов, квадранты имеют по 90 градусов. 0-90 градусов это первый квадрант, 90-180 — второй, 180-270 — третий и 270-360 — четвертый.
Используя линии, обозначающие границы квадранта, 0 или 360 это горизонталь направо, 90 — вертикально вверх, 180 — горизонталь слева и 270 сверху вниз. Теперь, используем этот метод для построения графиков.
Большие углы определяется вектором вращения, начиная с нуля и вращением против часовой стрелки. Горизонтальные элементы х: положительные справа, отрицательные слева. Вертикальные элементы у: положительные вверх, отрицательные вниз. Вращающийся вектор является р. Таким образом, синус угла есть y/r, косинус х/r, и тангенс у/х. Вектор r — всегда положителен. Таким образом, знак отношения может быть вычислен для различных секторов.
Здесь приведены знаки для трех отношений в четырех квадрантах.
Кроме того, как эквивалентный угол в первой четверти «переключается» когда вектор переходит из одного квадранта в другой. В первой четверти, стороны определены в соотношениях для синуса, косинуса и тангенса. При перемещении к большим углам в остальных секторах, противоположная сторона всегда есть вертикальная (у). То, что называется смежное, всегда есть горизонталью (х). Гипотенуза это всегда вращающийся вектор (r). Вы можете видеть картину как изменяются тригонометрические соотношения для углов.
Отношения в четырех квадрантах
Отношения для различных углов
Теперь у вас есть два пути получить формулы для различных углов. Во-первых, используя геометрическую конструкцию, такую, которая, например, была использована для суммы углов, реверсивную так, что (A — B) есть угол B вычитающийся из угла A.
В рассуждениях, аналогичных тем, которые были использованы для суммы углов, здесь представлены несколько сокращенные формулы для синуса и косинуса:
sin(A — B) = sin A cos B — cos A sin B
and
cos(A — B) = cos A cos B + sin A sin B
Формулы суммы и разницы
Второй способ нахождения формулы для разницы углов использует уже полученную формулу суммы, но делает B отрицательным. Из нашего исследования знаков для различных секторов, отрицательные углы с 1-го квадранта будут в 4 квадранте. Проводя эту подстановку, получим тот же результат, который был получен геометрически в предыдущем разделе.
Поиск формулы тангенса проходит тем же методом, или заменой синуса и косинуса в формулах или более непосредственно, превращая tg(-B) = — tg B. В любом случае вы получите:
tan(A — B) = [tan A — tan B]/[1 + tan A tan B]
Отношения с помощью четырех секторов
Вы можете вывести несколько отношений с формулами суммы и разности. Вы уже сделали соотношение для 75 градусов. Теперь можно выполнить то же для 15 градусов. Эти формулы дают соотношения для углов в 15 градусов интервалы через четыре квадранта. Построив их на 360 градусов, вы можете увидеть, как эти три соотношения изменяются, когда вектор проходит через четыре квадранта.
«Волна» синуса и косинуса колеблется вверх и вниз между +1 и -1. Обратите внимание, что «волны» смещены на 90 градусов друг относительно друга. Этот факт станет важным позже.
Кривая тангенса начинается, как синусоида, но вскоре она стремится достичь бесконечности на 90 градусах. Двигаясь » вне видимости» в положительном направлении, она «приходит» с отрицательного направления с другой стороны на 90 градусах.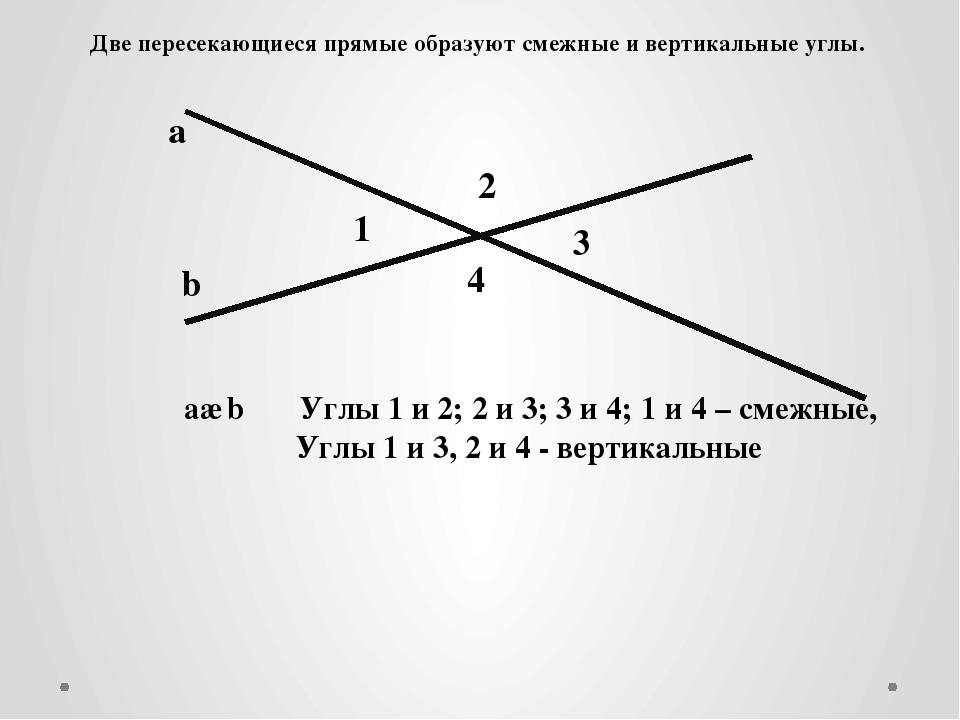
Пифагор в тригонометрии
Формула часто может быть упрощена, так как были найдены выводы формулы тангенса от формул синуса и косинуса, а также изменение ее членов одного отношения к другому отношению, использeущеuj другие члены. При этом, теорема Пифагора, выраженная в тригонометрическом соотношении, очень удобна.
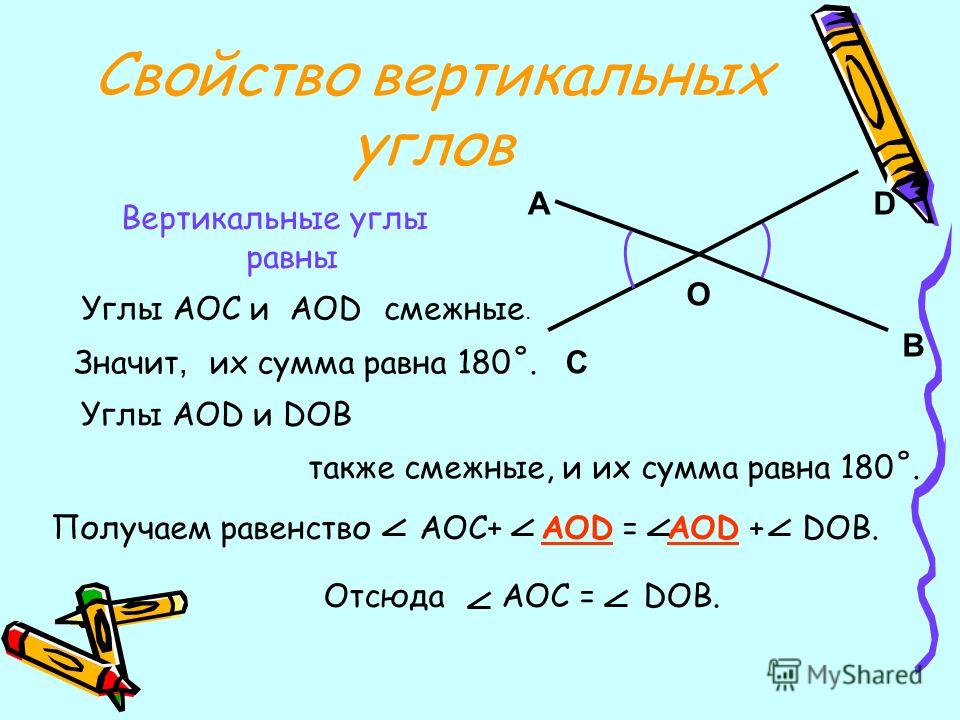 A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол.
A2 было бы то же самое число, возведенное в квадрат. Его значение зависело бы от использованного числового значения, поэтому это не очень хороший член для использования. Это означает квадрат синуса ли косинуса, не сам угол. Формула Пифагора может быть выражена иначе. Например, две другие формы:
cos2 A = 1 — sin2 A, и sin2 = 1 — cos2 A.
Умножение углов
Формулы сумм, вместе с теоремой Пифагора, используются для углов, которые в 2, 3 или больше раз кратны любым оригинальным углам. Здесь приводятся формулы для 2А и 3А.
Формула суммы работает, когда оба угла одинаковые или различны: sin(A + B) или sin(A + A). Однако, sin(A + A) в действительности sin 2A. Поэтому, sin 2A есть sin A cos A + cos A sin A. Оба члена выражения есть одним и тем же произведением, записанным в разном порядке, так что это выражение может быть упрощено до sin 2A = 2 sin A cos A.
Подобным образом, cos 2A = cos A cos A — sin A sin A, что также может быть записано как: cos 2A = cos2 A — sin2 A. Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
Используя теорему Пифагора, изменяем это к виду: cos 2A = 2cos2 A — 1. Наконец, tg 2A = 2 tg A/[1 — tg2 A].
Теперь тройной угол (3А) используется, чтобы показать, как получены следующие кратные углы. В основном, это так же просто, как запись 3A = 2 + A и повторного применения формулы суммы. Но тогда, чтобы получить в результате формулу в работающем виде, необходимо заменить часть 2А, на выражения с простым углом А.
На рисунках внизу вы можете видеть, что с каждым разом вычисления становятся сложнее.
УМНОЖЕНИЕ УГЛОВ Производные от формул суммы
УМНОЖЕНИЕ УГЛОВ Соотношения для 3A
Свойства равнобедренного треугольника
Вы уже видели, что прямоугольный треугольник является полезным строительным блоком для других фигур. Равнобедренный треугольник имеет несколько различных видов использования. Дело в том, что его использование основывается на том, что равнобедренный треугольник имеет две равные стороны и два равные углы между основанием и боковыми равными сторонами.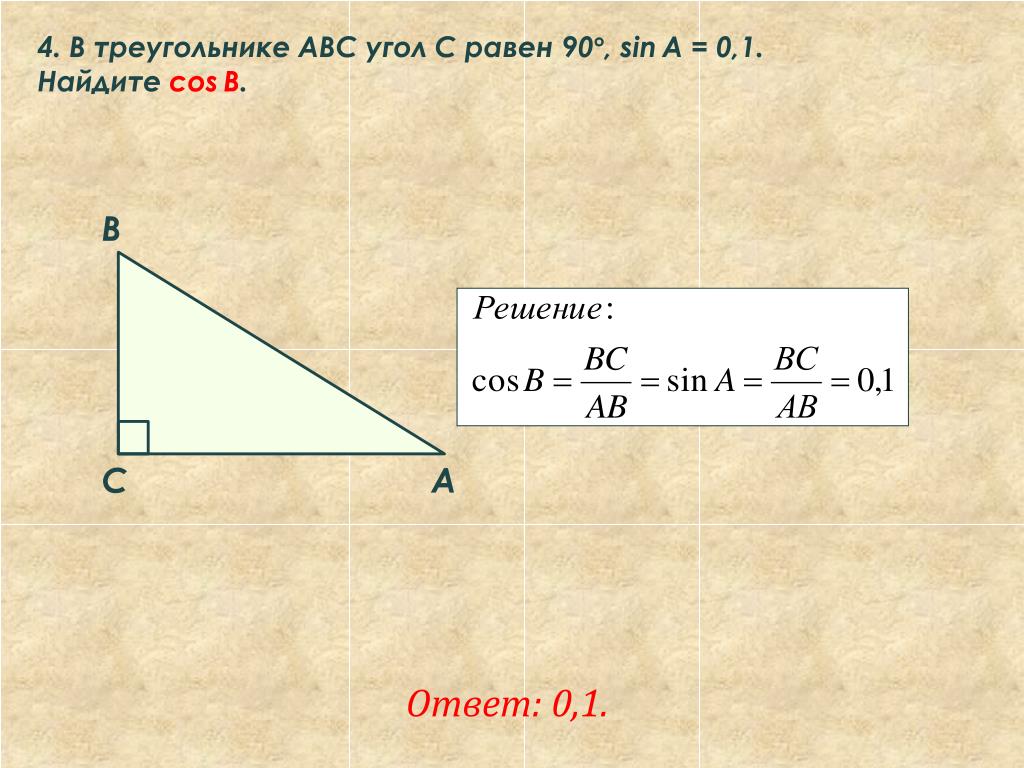 Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.
Перпендикуляр из третьего угла на третью сторону делит ее пополам. Таким образом весь треугольник делится на два равных прямоугольных треугольника.
Любой треугольник, за исключением прямоугольного треугольника, можно разделить на три прилегающих равнобедренных треугольника, разделив каждую сторону на две равные части и построить перпендикуляры из точек разделения. Там, где любые два из этих перпендикуляров встречаются, если линии тянутся к углам исходного треугольника, три линии должны быть равны, потому что две из них образуют стороны равностороннего треугольника. Таким образом, перпендикуляр с третьей стороны исходного треугольника должен также встретиться в одной точке.
Это утверждение справедливо, как мы покажем здесь, независимо от того, является ли исходный треугольник острым или тупым. Разница с тупым прямоугольным треугольником в том, что место встречи перпендикуляров лежит снаружи исходного треугольника, а не внутри.
Что происходит в прямоугольном треугольнике? Перпендикуляры от средней точки гипотенузы другой стороны будут делить пополам эти две стороны — вы получаете два из трех! Место встречи находится гипотенузе.
Углы в окружности
Основное свойство окружности это то, что ее центр находится на одинаковом расстоянии от любой точки окружности. Это расстояние есть радиусом окружности.
Если вы нарисуете любой треугольник внутри круга, перпендикуляры из средней точки его сторон встретятся в центре окружности а радиусы из углов треугольника делят его на три равнобедренных треугольника
Теперь, если вы назовете равные пары углов в каждом равнобедренном треугольнике A, A, B, B, C, C, вы обнаружите, что исходный треугольник имеет один угол A+B, один угол B+C, и один угол A+ C. Три угла в сумме дают 2A + 2B + 2С, а это как известно равно 180 градусов.
В любом равнобедренном треугольнике угол при вершине равен 180 градусов минус удвоенный угол при основании. Поэтому, согласно предыдущего пункта, 180 — 2A должен быть такой же, как и 2B + 2С, например.
Рассмотрим угол правый нижний угол, опирающийся на окружность. Угол в центре равен 2B + 2С. Углом, опирающийся на окружность равен B + C. Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
Вы видите, что для любого сегмента круга, угол в центре всегда в два раза больше угла, опирающегося на окружность.
Утверждение выше приводит к интересным фактам об углах в окружностях. Вместо определения углов со стороной треугольника, используют дугу (часть окружности) круга. Часть окружности, которая определяется углом в центре называется хордой окружности.
Угол в центре в два раза больше чем угол на окружности
Любой угол, касающийся окружности, используя хорду как ограничение угла, равен половине угла в центре. Таким образом, все углы в круге, с основанием на той же хорде, должны быть равны. Предположим, что хорда имеет угол 120 градусов. Угол на окружности будет равен 60 градусам.
Особый случай представляет собой полукруг (точный полукруг). Угол в центре представляет собой прямую линию (180 градусов). Каждый угол в полукруге равен 90 градусам (прямой угол). Любой треугольник в полукруге является прямоугольным треугольником.
Определения
Выше мы часто использовали углы, которые дополняют углы до прямого угла (90 градусов) или до двух прямых углов (180 градусов). Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Когда два угла образовывают угол 180 градусов (два прямых угла), они называются дополнительными. Если два угла добавить до 90 градусов (один прямой угол), их называют комплементарными
Вопросы и задачи
1. Синус угла А равен 0,8 и синус угла B равен 0.6. Из различных зависимостей, полученных до сих пор, найдите следующее: тангенс А, тангенс B, синус (A + B), косинус (A + B), синус (A — B), косинус (A — B), тангенс (А + B) и тангенс (A — B) без использования таблиц или тригонометрических клавиш калькулятора.
2.На экваторе Земля имеет радиус 4000 км. Углы вокруг экватора измеряется в меридианах долготы, с линией с севера на юг проходящей через Гринвич (Англия), в качестве нулевого отсчета. Два места используются для наблюдения за луной: первое это Кения, на экваторе 37,5 к востоку от Гринвича, а другой является Суматра, на экваторе к востоку 100,5. Как далеко друг от друга эти два места, если расстояние измерять мнимой прямой, проходящей через Землю?
3. Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?
Если бы наблюдения были сделаны горизонтально от точки наблюдения в вопросе 2 (к востоку от первой, к западу от второй), под каким углом была бы линия пересечения наблюдений?
4.В определенное время, точно синхронизированное в обоих местах, наблюдается спутник. В Кении, высота линии визирования с центром на спутнике составляет 58 градусов выше горизонтали на восток. На Суматре, высота составляет 58 градусов выше горизонтали на запад. Как далеко находится спутник? Используйте расстояние между точками рассчитанное в вопросе 2.
5. Косинус определенного угла в два раза больше синуса того же угла. Чему равен тангенс этого угла? Не используйте таблицы или калькулятор для ответа на этот вопрос.
6. Синус определенного угла равен именно 0.28. Найдите косинус и тангенс этого угла. Не используйте таблицы или калькулятор для ответа на этот вопрос.
7. Синус определенного угла равен 0.6. Найдите синус углов, больших чем заданный в два и три раза.
8. Найдите синус и косинус угла, большего ровно в два раза чем угол из вопроса 7.
9. Используя 15 градусов, как единичный угол, и формулы для отношения 2А и 3А найдите значения синусов 30 и 45 градусов.
10. Используя 30 градусов, как единичный угол, найти значения синусов 60 и 90 градусов.
11. Используя 45 градусов, как единичный угол, найдите значения тангенсов 60 и 90 градусов.
12. Используя 60 градусов, как единичный угол, найдите значения косинусов 120 и 180 градусов.
13. Используя 90 градусов, как единичный угол, найдите значения косинусов 180 и 270 градусов.
14. Используя формулы тангенса для умножения углов и таблицы, найдите тангенсы утроенных углов в 29, 31, 59 и 61 градусов. Посчитайте изменения знака между утроенным углом 29 и 31 градусов и между 59 и 61 градусов.
15. Синус угла составляет 0,96. Найдите синус и косинус удвоенного угла.
16. Задача сводится к алгебраической выражению вида 8cos2 A + cos A = 3. Решите для косинуса А, и укажите, в каком квадранте будет угол, представляющий каждое решение придет. Приведите приближенные значения из таблицы или используя калькулятор.
Приведите приближенные значения из таблицы или используя калькулятор.
Геометрия 7 Атанасян К-1 Уровень 3 Контрольная работа № 1
Контрольная работа № 1 по геометрии в 7 классе «Основные свойства простейших геометрических фигур. Смежные и вертикальные углы» с ответами УМК Атанасян Просвещение (сложный уровень). Урок 10 поурочного планирования по геометрии. Геометрия 7 Атанасян К-1 Уровень 3 (варианты 5, 6). Цитаты использованы в учебных целях.
Смотреть Список всех контрольных по геометрии в 7 классе по УМК Атанасян.
Другие варианты контрольной работы № 1 в 7 классе:
К-1 Уровень 1 + Ответы К-1 Уровень 2 + Решения
Контрольная работа № 1
Уровень 3 (сложный). Геометрия 7 класс
Вариант 1 (транскрипт)
- На прямой отмечены точки В, С и D. Какую длину может иметь отрезок BD, если ВС = 4,2 см, CD = 5,1 см.

- Найдите все углы, образовавшиеся при пересечении двух прямых, если сумма двух из них в три раза меньше суммы двух других.
- Из вершины угла, равного а, проведен луч, равный биссектрисе данного угла. Какие углы образует этот луч со сторонами данного угла? (см.Примечание)
- * Дано: ∠COD – ∠KOD = 61°, ∠COD – ∠КОС= 53° (рис. 1.137). Найти: ∠COD.
Примечание: в задании № 3 автором пособия допущена опечатка: вместо слова «перпендикулярный» напечатано слово «равный»! Правильное задание должно быть таким: 3. Из вершины угла, равного а, проведен луч, перпендикулярный биссектрисе данного угла. Какие углы образует этот луч со сторонами данного угла?
Вариант 2 (транскрипт)
- На прямой отмечены точки В, С и D. Какую длину может иметь отрезок BD, если CD = 2,6 см, ВС =3,7 см?
- Сумма всех углов, образовавшихся при пересечении двух прямых, в пять раз меньше суммы двух других.
 Найдите все образовавшиеся углы.
Найдите все образовавшиеся углы. - Из вершины угла проведен луч, перпендикулярный его биссектрисе и образующий со стороной данного угла угол, равный β. Найдите величину данного угла.
- * Дано: ∠АОВ – ∠АОС= 27°, ∠АОВ – ∠ВОС = 42° (рис. 1.138). Найти: ∠АОВ.
Решения и ответы на контрольную работу:
Информация для учителя:
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

Другие варианты контрольной работы № 1 в 7 классе:
К-1 Уровень 1 + Ответы К-1 Уровень 2 + Решения
Вы смотрели: Контрольная работа № 1 по геометрии в 7 классе с ответами УМК Атанасян Просвещение (сложный уровень). Урок 10 поурочного планирования по геометрии. Геометрия 7 Атанасян К-1 Уровень 3 (варианты 5-6).
Смотреть Список всех контрольных по геометрии в 7 классе по УМК Атанасян.
В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
длина суммы векторов и теорема косинусов
Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются)
даёт возможность узнать, как расположен относительно начала координат вектор, являющийся
суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и
операции над векторами».
Подробно эти две операции разбирались на уроке «Векторы и
операции над векторами».
Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.
Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:
.
Перейдём к примерам.
Проверить решение можно на Калькуляторе
онлайн.
Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Пример 3. Даны длины векторов и длина их суммы . Найти длину их разности .
Решение.
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:
Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:
Проверить решение можно на Калькуляторе онлайн.
Пример 4. Даны длины векторов и длина их разности . Найти длину их суммы .
Решение.
Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:
Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между и :
Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:
Проверить решение можно на Калькуляторе онлайн.
Пример 6. Какому условию должны удовлетворять векторы и , чтобы имели место слелующие соотношения:
1) длина суммы векторов равна длине разности векторов, т. е. ,
2) длина суммы векторов больше длины разности векторов, т. е. ,
3) длина суммы векторов меньше длины разности векторов, т. е. ?
Решение.
Находим условие для первого соотношения. Для этого решаем следующее уравнение:
То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.
Находим условие для второго соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).
Находим условие для третьего соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами больше косинуса
смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов,
необходимо, чтобы углы образовали тупой угол.
Проверить решение можно на Калькуляторе онлайн.
Поделиться с друзьями
Начало темы «Векторы»
Продолжение темы «Векторы»
Математическая сцена — синус, косинус и тангенс тригонометрии
Математическая сцена — синус, косинус и тангенс тригонометрии — Урок 1 2008 Rasmus ehf | Синус, косинус и тангенс тригонометрии. | Печать |
Урок 1
ABC — прямоугольный треугольник
Угол А составляет 30 градусов.Мы пишем это как: |
а — это обозначение стороны противоположного угла A
b — это обозначение стороны противоположного угла B
c — это обозначение стороны противоположного угла C
Подобные треугольники треугольники, в которых все углы в одном треугольнике равны углам в другой треугольник
Эти два треугольника
похожи. |
Использование обозначений в треугольниках выше получаем следующее:
Соотношение зависит от по размеру угла.
Касательная
Отношение, называемое тангенсом (тангенс) острого угла в прямоугольном треугольнике определяется как соотношение между стороной, противоположной углу, и стороной, прилегающей к углу. |
Пример 1 Найти угол A
Первая Тан A = 3 / 4 = 0,75 |
Нам нужно
используйте обратную функцию для tan, tan -1 ,
найти угол. Эта функция находится на той же клавише калькулятора, что и загар.
функция (сдвиг загара).
Эта функция находится на той же клавише калькулятора, что и загар.
функция (сдвиг загара).
Мы используем следующая последовательность команд:
сдвиг — загар -1 0,75 = 37
Попробуйте следующее на вашем калькуляторе, чтобы увидеть разницу между загаром и загаром -1 :
угол → соотношение соотношение → угол
загар 37 = 0,75 тангенса -1 0,75 = 37
Пример 2 Найти сторона b
коричневый 37 = 4 / b загар 37 b = 4 0.75 б = 4 b = 5,3 |
Снэ
Синус (грех)
острый угол в прямоугольном треугольнике — это соотношение между
сторона, противоположная углу и гипотенуза треугольника. |
Пример 3 Найдите угол А, дающий ответ с точностью до градуса.
sin A = 3 / 5 = 0,6 дает <А = 37 Сдвиг sin -1 0,6 = 37 |
Пример 4 Найдите сторону а.
грех 37 = a / 5 а = грех 37 5 а = 3 |
Косинус
Косинус (cos) острый угол в прямоугольном треугольнике — это соотношение сторон рядом с углом и гипотенузой треугольника. |
Пример 5 Используйте функцию косинуса, чтобы найти угол A, дающий ответ до ближайшего степень.
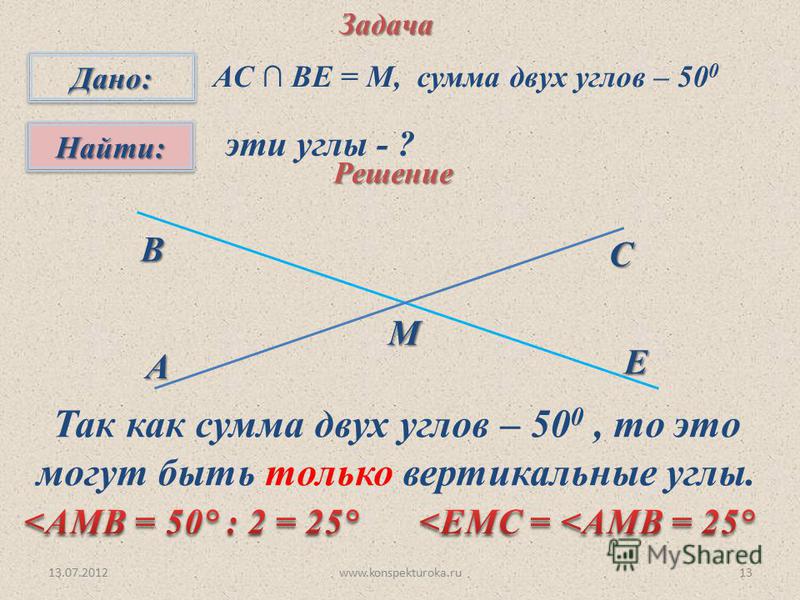
cos A = 4 / 5 = 0,8 дает Сдвиг cos -1 0,8 = 37 |
Пример 6 Найдите сторону b.
cos 37 = b / 5 b = Cos 37 5 b = 4 |
некоторые значения для sin, cos и tan.
| грех 80 = 0,98 | cos 80 = 0,17 | загар 80 = 5,67 |
| грех 60 = 0,87 | cos 60 = 0,5 | загар 60 = 1,73 |
| грех 30 = 0,5 | cos 30 = 0,87 | загар 30 = 0,58 |
грех 10
= 0.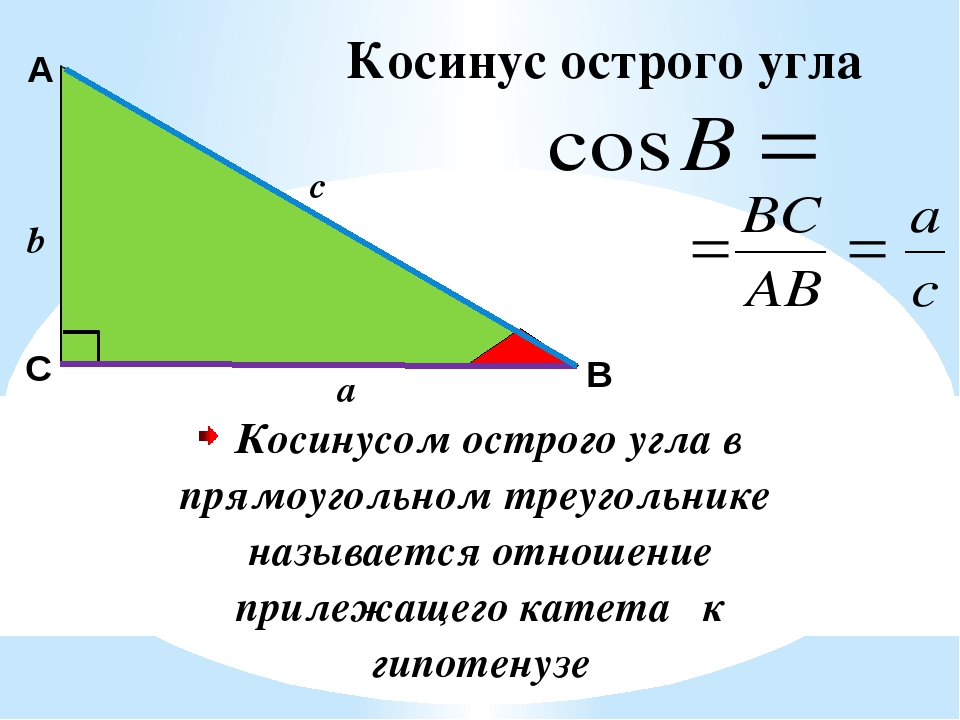 17 17 | cos 10 = 0,98 | загар 10 = 0,18 |
Попрактикуйтесь в этих методах, а затем воспользуйтесь тест по тригонометрии 1 (sin, cos и tan).
Шесть функций (Триггер без слез, часть 2)
Шесть функций (Триггер без слез, часть 2)Триггер без слез Часть 2:
Авторские права 19972020 Стэн Браун, BrownMath.com
Резюме: Каждая из шести триггерных функций просто одна сторона прямоугольного треугольника разделена на другую сторону .Или, если вы нарисуете треугольник в единичной окружности , каждая функция — длина одного отрезка линии. простой способ запомнить все шесть определений: запомнить определения синуса и косинуса а затем запомните остальные четыре как комбинации синуса и косинуса , не как самостоятельные функции.
Два основных: синус и косинус
Картинка стоит тысячи слов (вот почему требуется тысяча слов). раз дольше скачивать).Триггерные функции — это не что иное, как длины различных сторон прямоугольного треугольника в различных соотношениях .
Так как сторон три, то 3 × 2 = 6
разные способы сделать соотношение (дробь) сторон. Это
почему в шесть триггерных функций, не больше и не меньше .
раз дольше скачивать).Триггерные функции — это не что иное, как длины различных сторон прямоугольного треугольника в различных соотношениях .
Так как сторон три, то 3 × 2 = 6
разные способы сделать соотношение (дробь) сторон. Это
почему в шесть триггерных функций, не больше и не меньше .
Из этих шести функций тройка, косинус и касательно львиная доля работы. (Остальные изучаются, потому что их можно использовать для упростите некоторые выражения.) Начнем с синуса и косинуса, потому что они действительно базовые а остальные зависят от них.
Вот один из обычных способов показать
прямоугольный треугольник. Ключевым моментом является то, что строчные буквы а , б , в — стороны, противоположные углам, отмеченным соответствующими
заглавные буквы A , B , C . В большинстве книг используется это соглашение: Строчная буква для стороны, противоположной углу верхнего регистра .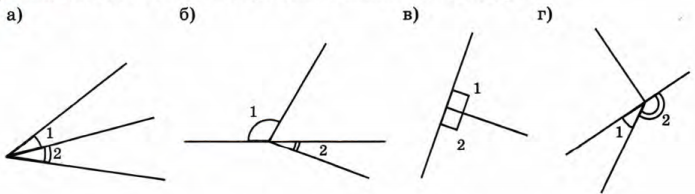
Два основных определения отмечены на схеме. Вы должны сохранить их в памяти .Фактически, они должны стать второй натурой для вы, чтобы вы их узнавали, как бы ни повернулся треугольник вокруг. Всегда, всегда синус угла равен противоположному сторона, деленная на гипотенузу (opp / hyp на схеме). Косинус равен равна смежной стороне, деленной на гипотенузу (adj / hyp).
(1) Запомнить:
синус = (противоположная сторона) / гипотенуза
косинус = (смежная сторона) / гипотенуза
Какой синус у B на диаграмме? Помните opp / hyp: наоборот сторона b , а гипотенуза c , поэтому sin B = b / c .А как насчет косинуса B ? Помните прил / гип: соседняя сторона a , поэтому cos B = a / c .
Вы заметили, что синус одного угла является косинусом другого?
Так как A + B + C = 180 для любого
треугольник, а C равно 90 в этом треугольнике, A + B должен
равно 90.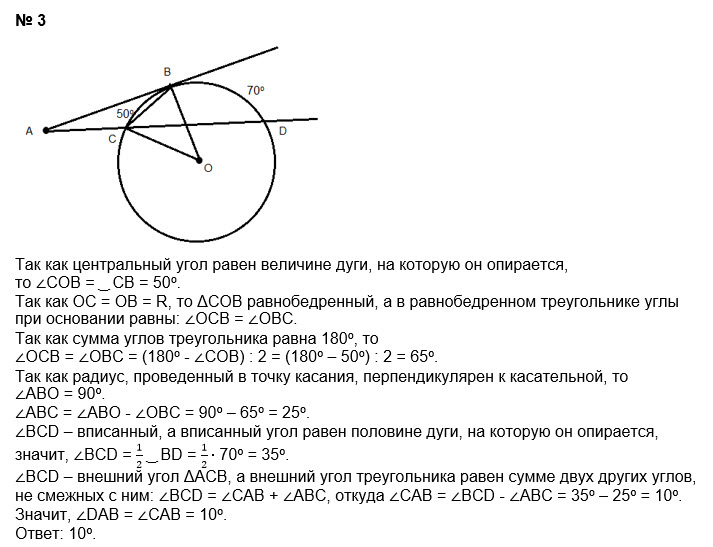 Следовательно A = 90 — B , и B = 90 — A .Когда два угла складываются
90, каждый угол является ° дополнением другого, а синус
каждого угла составляет co синуса другого.
Это идентификаторы совместных функций :
Следовательно A = 90 — B , и B = 90 — A .Когда два угла складываются
90, каждый угол является ° дополнением другого, а синус
каждого угла составляет co синуса другого.
Это идентификаторы совместных функций :
(2) sin A = cos (90 — A ) или cos (π / 2 — A )
cos A = sin (90 — A ) или sin (π / 2 — A )
Выражения для длин сторон
Определения синуса и косинуса можно немного изменить, чтобы
позвольте вам записать длины сторон через
гипотенуза и углы.Например, когда вы знаете
что b / c = cos A , вы
можно умножить на c и получаем b = c × cos A . Вы можете написать еще
выражение для длины b , которое использует синус вместо косинуса?
Помните, что противоположность гипотенузы равна синусу, поэтому b / c = sin B . Умножить
через c и у вас есть b = c × sin B .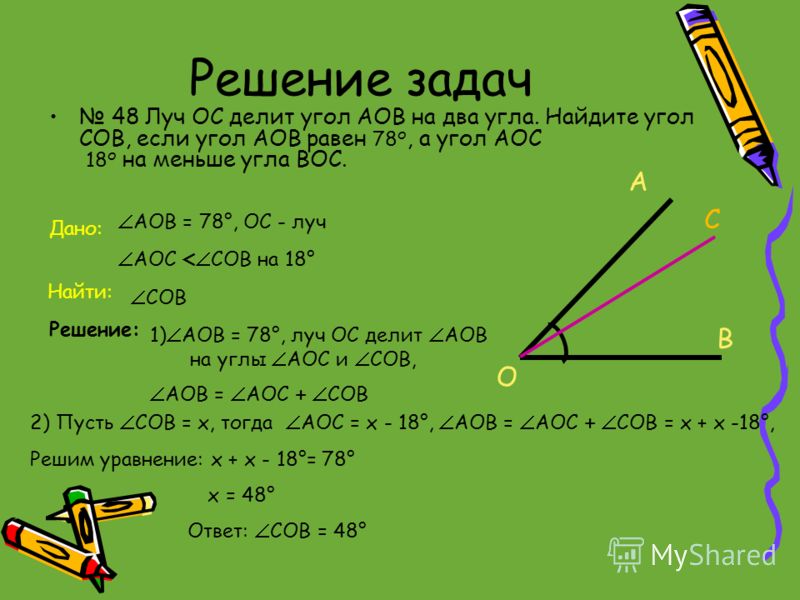
Вы видите, как записать два выражения для длины стороны а ? Работайте с определениями и убедитесь, что a = c × sin A = c × cos B .
Пример: Дан прямоугольный треугольник с углом A = 52 и гипотенуза c = 150 м. Какая длина стороны б ? Подсказка: нарисуйте рисунок и обозначьте A , c , и b .
Решение: Картинки всегда хорошие. Ты не нужно зацикливаться на том, чтобы получить точную картину, но по крайней мере сделать это близко. Это поможет вам понять, когда ваш ответ невозможен, чтобы вы знали, что совершили ошибку. В моем маленьком эскизе я установил наружу сделать угол A чуть больше 45, но на мой взгляд похоже немного меньше. Это нормально.
Вы можете заметить, что я пометил сторону как , хотя мы
не нужно это для проблемы. Я сделал это, поэтому у меня не было
подумать, с какой стороны было б . Всегда помни правило
что сторона с данной буквой противоположна углу с этим
письмо. (И, условно, мы всегда ставим C справа
угол, так что c гипотенуза.)
Всегда помни правило
что сторона с данной буквой противоположна углу с этим
письмо. (И, условно, мы всегда ставим C справа
угол, так что c гипотенуза.)
Когда у вас есть изображение, решить проблему довольно просто простой. Вы хотите что-то, связанное с A , это прилегающая сторона и гипотенуза; это должен быть косинус.
cos A = b / c
б = c × cos A = 150 × cos 52 = около 92.35 м.
Пример: Оттяжка закреплена в земле. и прикреплен к вершине 45-футового флагштока. Если он встречается с землей под углом 63, какова длина растяжки?
Решение: Предположительно флагшток вертикальный, поэтому это прямоугольный треугольник с A = 63, a = 45 футов, и гипотенуза c неизвестный. Какая функция задействует противоположную сторону и гипотенузу? Это должен быть синус. Ты знаешь что
sin A = a / c
Следовательно,
c = a / sin A = 45 / sin 63 =
около 50.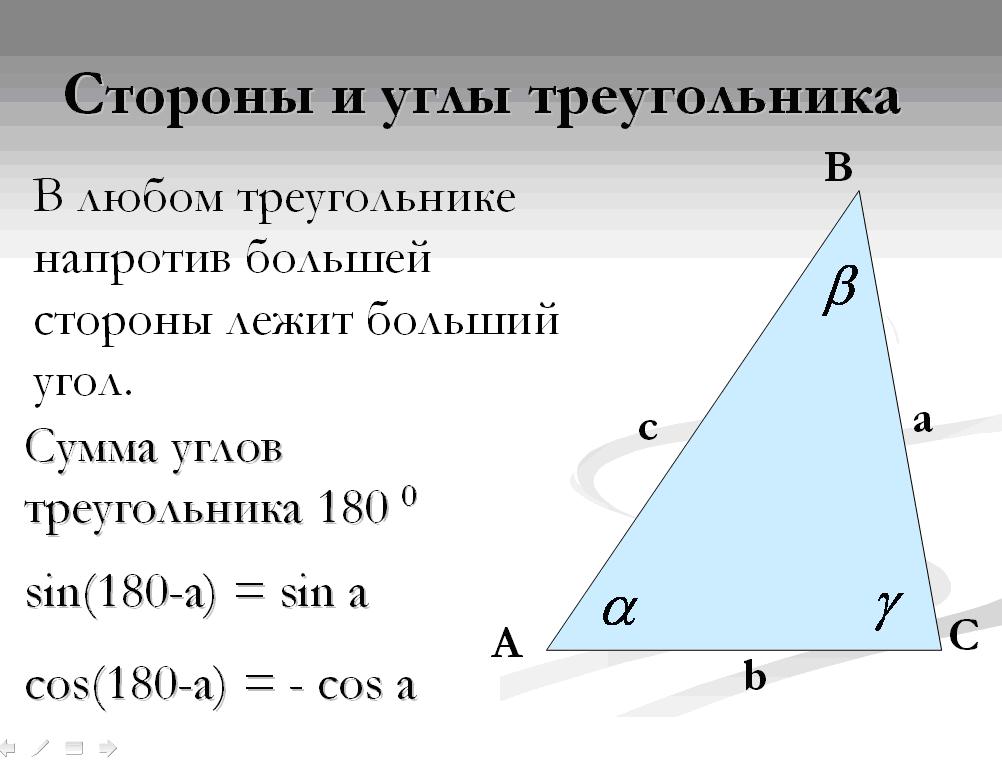 5 футов
5 футов
Вам может быть интересно, как найти стороны или углы треугольников. когда нет прямого угла. Что ж, перейдем к теме Решение треугольников.
Синус и косинус в единичной окружности
Часто всплывает один важный особый случай. Предположим, что гипотенуза c = 1; тогда мы называем треугольник a прямоугольный треугольник . Из параграфов выше видно, что если c = 1, то a = sin A и b = cos A .Другими словами, в прямоугольный треугольник с противоположной стороной будет равен синусу, а соседняя сторона будет равна косинусу угла.
Треугольник часто рисуют
в единичном круге , круге
радиус 1, как показано справа.
Угол A находится в центре окружности, а на соседней стороне
лежит по оси x.
Если вы сделаете это, гипотенуза будет радиусом, равным 1.
Координаты ( x , y ) внешнего конца гипотенузы
являются сторонами треугольника x и y :
( x , y ) = (cos A , sin A ).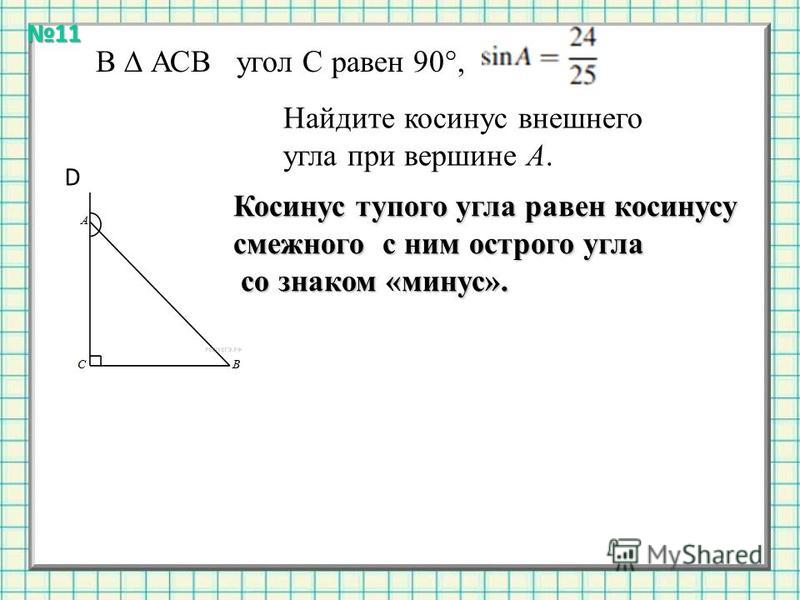 Единичный круг — ваш друг : он может помочь вам визуализировать участки
триггерных тождеств.
Единичный круг — ваш друг : он может помочь вам визуализировать участки
триггерных тождеств.
Остальные четыре: касательная, котангенс, секанс, косеканс
Остальные четыре функции не имеют реальной самостоятельной жизни; theyre просто комбинация первых двух . Вы могли бы сделать все тригонометрия, не зная ничего больше, чем синусы и косинусы. Но зная что-то в остальных четырех, особенно касательное, часто может спасти вас шаги в вычислении, и ваш учитель будет ожидать, что вы знаете о них к экзаменам.
Мне проще запомнить (извините!) Определение касательной через синус и косинус:
(3) Запомнить:
tan A = (sin A ) / (cos A )
Вы будете использовать функцию тангенса (tan) намного чаще чем последние три функции. (Я доберусь до них через минуту.)
Существует альтернативный способ запомнить значение касательной .
Помните из схемы
что sin A = противоположный / гипотенуза и cos A =
смежный / гипотенуза. Подставьте их в уравнение 3, определение
функция tan, и у вас есть tan A =
(противоположный / гипотенуза) / (смежный / гипотенуза) или
Подставьте их в уравнение 3, определение
функция tan, и у вас есть tan A =
(противоположный / гипотенуза) / (смежный / гипотенуза) или
(4) касательная = (противоположная сторона) / (смежная сторона)
Обратите внимание, что это , а не с пометкой запомнить: вам не нужно запомнить, потому что он вытекает непосредственно из определения уравнение 3, и фактически эти два утверждения эквивалент. Я решил представить их в таком порядке, чтобы минимизировать беспорядок opp, adj и hyp среди sin, cos и загар.Однако, если хотите, можете запомнить уравнение 4, а затем вывести эквивалентное тождество уравнение 3, когда вам это нужно.
Пример: Оттяжка закреплена в земле и прикреплена на вершину 45-футового флагштока. Как далеко якорь от базы флагштока, если провод встречается с землей в угол 63?
Решение: Это вариант
предыдущий пример. Этот
время, вы хотите знать сторону, прилегающую к углу A , а не
гипотенуза.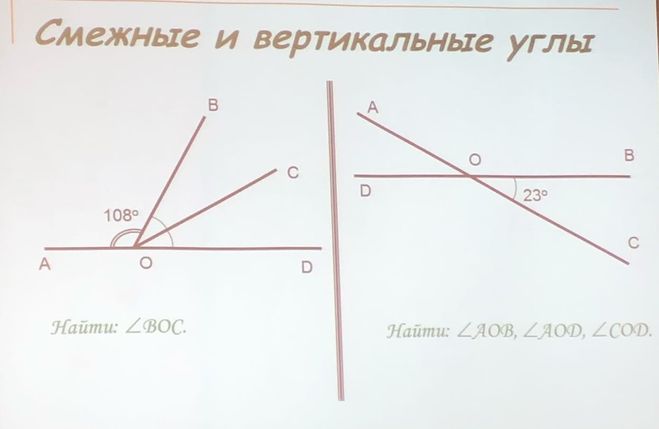 Как и раньше, предположим, что флагшток вертикальный, поэтому
это прямоугольный треугольник с A = 63, a = 45 футов,
и прилегающая сторона б неизвестный. Какая функция задействует соседнюю сторону и противоположную сторону?
Это касательная. Вы знаете, что
Как и раньше, предположим, что флагшток вертикальный, поэтому
это прямоугольный треугольник с A = 63, a = 45 футов,
и прилегающая сторона б неизвестный. Какая функция задействует соседнюю сторону и противоположную сторону?
Это касательная. Вы знаете, что
tan A = a / b
Следовательно,
b = a / tan A = 45 / tan 63 = около 22,9 футов
Итак, я сказал, что вы можете выполнить все триггеры только с синусами и косинусы.Как это сработает для этой проблемы? Ну синус и косинус обеим нужна гипотенуза, так что у вас будет
sin A = a / c ⇒ c = a / sin A и
cos A = b / c ⇒ c = b / cos A . Следовательно,
b / cos A = a / sin A
b = a × cos A / sin A =
45 × cos 63 / sin 63 = около
22. 9 футов
9 футов
В конце концов, вы попали в то же место, но путь был дольше. Итак, хотя это и не обязательно, касательная может облегчить вашу работу.
Остальные три триггера функции котангенс, секанс и косеканс являются определяется в терминах первых трех . Они используются реже, но упрощают некоторые проблемы в исчисление. В практических задачах, не связанных с исчислением, они вам практически никогда не понадобятся.
(5) Запомнить:
детская кроватка A = 1 / (tan A )
сек A = 1 / (cos A )
csc A = 1 / (sin A )
Угадайте что! Это последняя триггерная идентификация, которую вам нужно запомнить.
(Вы, вероятно, обнаружите, что в конечном итоге запомните некоторые другие
личности, даже не намереваясь, просто потому, что вы их используете
часто. Но уравнение 5 делает последние, что
вам придется сесть и запомнить только их
собственн. )
)
К сожалению, определения в уравнении 5 не являются самая легкая вещь в мире для запоминания. Равен ли секанс на 1? синус или 1 над косинусом? Вот два полезных совета : Каждое из этих определений имеет совместную функцию с одной и только с одной стороны. уравнения, поэтому у вас не возникнет соблазна подумать, что sec A равно 1 / sin A .А секанс и косеканс идут вместе, как синус и косинус, поэтому вы не подумаете, что детская кроватка A равно 1 / sin A .
Для альтернативного подхода к запоминанию выше идентификаторов, вам может понравиться:
Вы можете сразу заметить важную связь между касательной и котангенс. Каждый является совместной функцией другого, как синус и косинус:
(6) коричневый A = детская кроватка (90 — A ) или детская кроватка (π / 2 — A )
детская кроватка A = коричневый (90 — A ) или коричневый (π / 2 — A )
Если вы хотите это доказать, это легко определения и уравнение 2:
детская кроватка A = 1 / tan A
Примените определение tan:
детская кроватка A = 1 / (sin A / cos A )
Упростим дробь:
детская кроватка A = cos A / sin A
Примените уравнение 2:
детская кроватка A = sin (90 — A ) / cos (90 — A )
Наконец, признайте, что эта дробь соответствует определению функция tan, уравнение 3:
детская кроватка A = коричневый (90 — A )
Касательная и co тангенс — это такие же функции, как синус и co синус.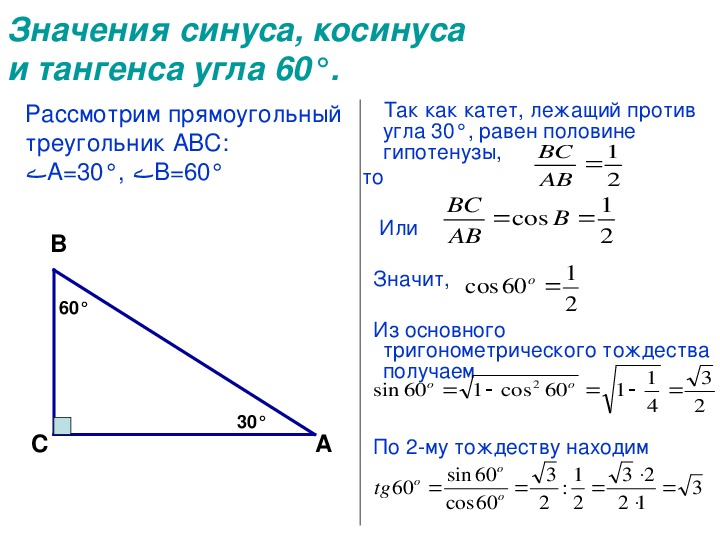 Выполняя такую же замену, вы можете показать, что секанс и
Секанс co также являются совместными функциями:
Выполняя такую же замену, вы можете показать, что секанс и
Секанс co также являются совместными функциями:
(7) сек A = csc (90 — A ) или csc (π / 2 — A )
csc A = сек (90 — A ) или сек (π / 2 — A )
Шесть функций в одном изображении
Вы видели ранее, как синус и косинус угла — стороны треугольника в единичной окружности. Оказывается что все шесть функций могут быть изображены таким образом геометрически.
единичный круг (радиус = AB = 1)
sin θ = BC;
cos θ = AC;
загар θ = ED
csc θ = AG;
сек θ = AE;
детская кроватка θ = FG
Изображение предоставлено TheMathPage
На рисунке справа треугольник ABC имеет угол θ при центр единичной окружности (AB = радиус = 1). Вы уже знайте, что BC = sin θ и AC = cos θ .
А как насчет tan θ ? Ну, так как DE касается единицы
круг, вы можете догадаться, что его длина — загар θ , и вы
правильно. Треугольники ABC и AED похожи, поэтому
Треугольники ABC и AED похожи, поэтому
ED / AD = BC / AC
ED / 1 = sin θ / cos θ
ED = тангенс угла θ
Больше информации исходит от той же пары похожих треугольники:
AE / AB = AD / AC
AE / 1 = 1 / cos θ
AE = сек θ
Длины, которые представляют кроватку θ и csc θ , придут. из другого треугольника, GAF.Этот треугольник также похож на треугольник AED. (Почему? FG перпендикулярно FA, а FA перпендикулярно ОБЪЯВЛЕНИЕ; следовательно, FG и AD параллельны. В начале геометрии вы узнал, что когда параллельные линии разрезаются третьей линией, соответствующие углы обозначены θ в диаграммы равны. Таким образом, FG касается единицы окружности, поэтому углы G и θ равны. )
Используя аналогичные треугольники GAF и AED,
FG / FA = AD / ED
FG / 1 = 1 / tan θ
FG = детская кроватка θ
В этом есть смысл: FG касается единичной окружности и является
тангенс дополнения угла θ , а именно угла GAF.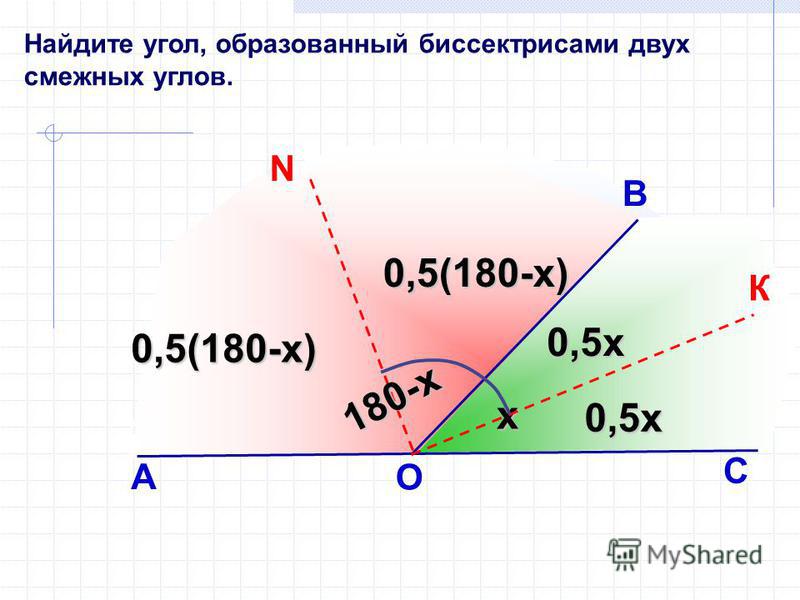 Следовательно, FG
— котангенс исходного угла θ (или угла GAD).
Следовательно, FG
— котангенс исходного угла θ (или угла GAD).
Наконец, снова используя ту же пару похожих треугольников, вы также можно сказать, что
AG / FA = AE / ED
AG / 1 = сек θ / tan θ
AG = (1 / cos θ ) / (sin θ / cos θ )
AG = 1 / sin θ
AG = csc θ
Эта диаграмма прекрасно передает геометрическое значение всех шести триггерных функций, когда угол θ проведен в центре единичный круг:
sin θ = BC; cos θ = переменный ток; загар θ = ED
csc θ = AG; сек θ = AE; детская кроватка θ = FG
Практические задачи
Чтобы извлечь максимальную пользу из этих проблем, решите их без предварительного просмотра решений.Вернитесь к главе текст, если вам нужно освежить память.
Рекомендация : Работайте на бумаге
труднее обмануть себя, действительно ли ты
полностью разобраться в проблеме.
Вы найдете полный решения всех проблем. Не просто проверяй свой ответы, но проверьте и свой метод.
1 Найдите все шесть функций угла 30. Найдите синус, косинус, и тангенс 60. 2 Найдите sin A , sin B , tan A и tan B .3 А ≈ 53,13. Найдите примерную площадь треугольник. Подсказка: площадь треугольника равна основание × высота /2.BTW: Зачем называть это синусом?
Очевидно, почему название тангенс имеет смысл: тангенс угла — это длина отрезка, касательного к единичной окружности. А как же синус функция? Как он получил свое название?
Посмотрите на
изображение еще раз, и обратите внимание, что
sin θ = BC — половина хорды окружности.Индуистский математик Арьябхата старший (о
475550) использовал слово jya или jiva для этого полуаккорда.
В арабском переводе это слово осталось без изменений, но в арабской системе
письма джива было написано так же, как арабское слово джайб,
означает грудь, складку или залив.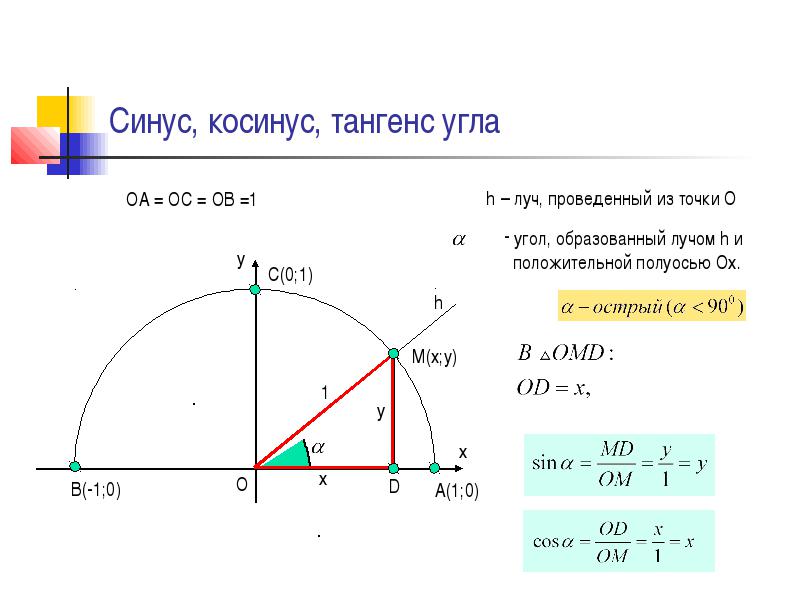 Латинское слово, обозначающее грудь, залив или кривую.
синус или синус на английском языке, и начинается с Gherardo из
Кремона (ок. 11141187), ставшая общепринятым термином.
Латинское слово, обозначающее грудь, залив или кривую.
синус или синус на английском языке, и начинается с Gherardo из
Кремона (ок. 11141187), ставшая общепринятым термином.
Эдмунд Гюнтер (15811626), кажется, был первым опубликовать аббревиатуры sin и tan для sin и касательная.
Мой источник этой истории — Эли Маорс Тригонометрический Наслаждения (1998, Princeton University Press), страницы 3536. Я призываю вас обратиться к книге для более полного отчета.
Что нового
- 27 сентября 2017 г. : откорректировать 29,2 футов до 22,9 футов, здесь и здесь, спасибо Райану МакПарлану.
- 29 октября 2016 г. :
- (промежуточные изменения подавлены)
- 19 февраля 1997 г. : Новый документ.
следующий: 3 / Специальные уголки
косинусов
;point;vertex;ABC,2″/>Затем рассмотрим углы 30 ° и 60 °.В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения сторон равны 1: √3: 2. Отсюда следует, что sin 30 ° = cos 60 ° = 1/2, и sin 60 ° = cos 30 ° = √3 / 2.
Эти результаты занесены в эту таблицу.
| Угол | Градусов | Радианы | косинус | синус | |||||
|---|---|---|---|---|---|---|---|---|---|
| 90 ° | π /2 | 0 | 060 ° | 0 | 0 | 040/3 | 1/2 | √3 / 2 | |
| 45 ° | π /4 | √2 / 2 | √2 / 2 | ||||||
| 30 ° | π /6 | √3 / 2 | 1/2 | ||||||
| 0 ° | 0 | 1 | 0 |
Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой.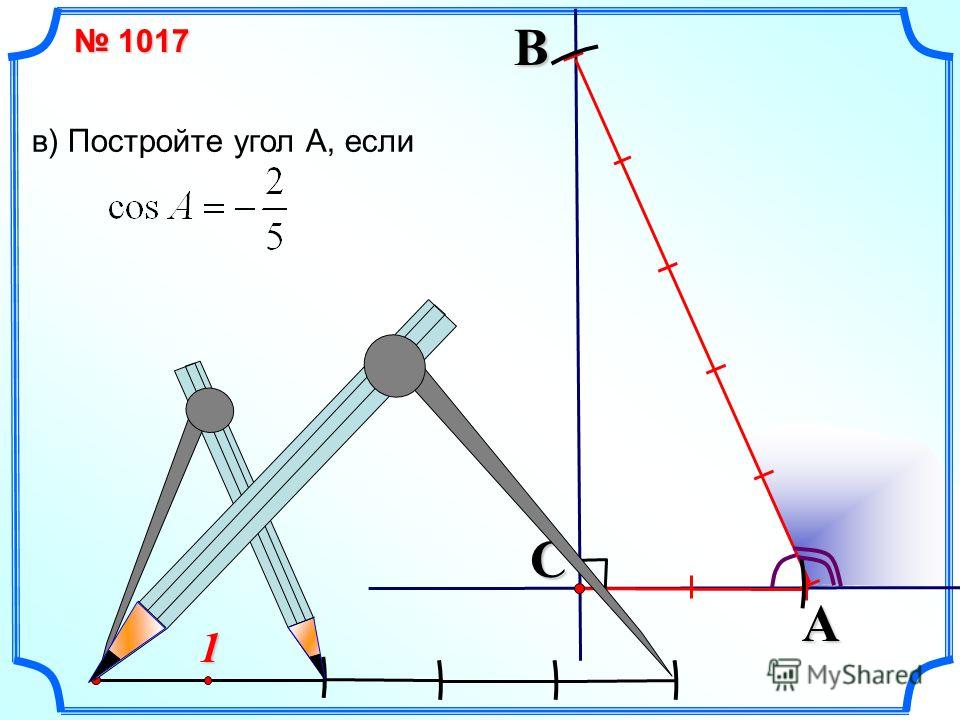
30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. b = 6,4, c = 7,8. Найдите A и a.
36. A = 23 ° 15 ‘, c = 12.15. Найдите a и b.
Подсказки
30. Косинус A связывает b с гипотенузой c, , поэтому сначала вы можете вычислить c. Если вы знаете b и c, , вы можете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух сторон, которых вы не знаете, а именно a / c. Тем не менее, это дает вам уравнение, с которым можно работать: 1/3 = a / c. Тогда c = 3 a. Из теоремы Пифагора тогда следует, что a 2 + 144 = 9 a 2 . Вы можете решить это последнее уравнение для a , а затем найти c.
Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
ответов
30. c = b / cos A = 2,25 / 0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 ‘или 4’3 «.
c = 3 a , что равно 12.73 ‘или 12’9 «.
35. cos A = b / c = 6,4 / 7,8 = 0,82. Следовательно, A = 34,86 ° = 34 ° 52 ‘, или около 35 °.
a 2 = 7,8 2 — 6,4 2 = 19,9, поэтому a составляет около 4,5.
36. a = c sin A = 12,15 sin 23 ° 15 ‘= 4,796.
b = c cos A = 12,15 cos 23 ° 15 ‘= 11.17.
Раздел 4.3: Тригонометрия прямоугольного треугольника
Результаты обучения
- Используйте прямоугольные треугольники для вычисления тригонометрических функций.
- Найдите значения функции для 30 ° (π / 6), 45 ° (π / 4) и 60 ° (π / 3).
- Используйте функции дополнительных углов.
- Используйте определения тригонометрических функций любого угла.
- Используйте тригонометрию прямоугольного треугольника для решения прикладных задач.
Использование прямоугольных треугольников для вычисления тригонометрических функций
В предыдущих разделах мы использовали единичную окружность для определения тригонометрических функций .В этом разделе мы расширим эти определения, чтобы применить их к прямоугольным треугольникам. Значение функции синуса или косинуса [latex] t [/ latex] — это его значение в [latex] t [/ latex] радианах. Сначала нам нужно создать прямоугольный треугольник. На рисунке 1 показана точка на единичной окружности радиуса 1. Если мы опустим вертикальный отрезок линии из точки [латекс] \ влево (x, y \ вправо) \\ [/ latex] на ось x , у нас есть прямоугольный треугольник, вертикальная сторона которого имеет длину [латекс] y [/ латекс], а горизонтальная сторона имеет длину [латекс] x [/ латекс].Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.
Сначала нам нужно создать прямоугольный треугольник. На рисунке 1 показана точка на единичной окружности радиуса 1. Если мы опустим вертикальный отрезок линии из точки [латекс] \ влево (x, y \ вправо) \\ [/ latex] на ось x , у нас есть прямоугольный треугольник, вертикальная сторона которого имеет длину [латекс] y [/ латекс], а горизонтальная сторона имеет длину [латекс] x [/ латекс].Мы можем использовать этот прямоугольный треугольник, чтобы переопределить синус, косинус и другие тригонометрические функции как отношения сторон прямоугольного треугольника.
Рисунок 1
Мы знаем
[латекс] \ cos t = \ frac {x} {1} = x [/ латекс]
Точно так же мы знаем
[латекс] \ sin t = \ frac {y} {1} = y [/ латекс]
Эти соотношения по-прежнему применяются к сторонам прямоугольного треугольника, когда не задействован единичный круг и когда треугольник находится не в стандартном положении и не отображается на графике с использованием координат [латекс] \ left (x, y \ right) [/ latex] . Чтобы иметь возможность свободно использовать эти соотношения, мы дадим сторонам более общие имена: вместо [latex] x [/ latex] мы назовем сторону между заданным углом и прямым углом смежной стороной к углу [ латекс] т [/ латекс]. («Соседний» означает «рядом с.») Вместо [латекс] y [/ латекс] мы назовем сторону, наиболее удаленную от данного угла, противоположной стороной под углом [латекс] t [/ латекс]. И вместо [latex] 1 [/ latex] назовем сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой , гипотенузой .Эти стороны обозначены на Рисунке 2.
Чтобы иметь возможность свободно использовать эти соотношения, мы дадим сторонам более общие имена: вместо [latex] x [/ latex] мы назовем сторону между заданным углом и прямым углом смежной стороной к углу [ латекс] т [/ латекс]. («Соседний» означает «рядом с.») Вместо [латекс] y [/ латекс] мы назовем сторону, наиболее удаленную от данного угла, противоположной стороной под углом [латекс] t [/ латекс]. И вместо [latex] 1 [/ latex] назовем сторону прямоугольного треугольника, противоположную прямому углу, гипотенузой , гипотенузой .Эти стороны обозначены на Рисунке 2.
Рис. 2. Стороны прямоугольного треугольника по отношению к углу [латекс] t [/ латекс].
Понимание отношений прямоугольного треугольника
Дан прямоугольный треугольник с острым углом [латекс] т [/ латекс],
[латекс] \ begin {align} & \ sin \ left (t \ right) = \ frac {\ text {напротив}} {\ text {hypotenuse}} & \ csc \ left (t \ right) = \ frac { \ text {hypotenuse}} {\ text {напротив}} \\ & \ cos \ left (t \ right) = \ frac {\ text {смежный}} {\ text {hypotenuse}} & \ sec \ left (t \ справа) = \ frac {\ text {hypotenuse}} {\ text {смежный}} \\ & \ tan \ left (t \ right) = \ frac {\ text {противоположный}} {\ text {смежный}} & \ кроватка \ left (t \ right) = \ frac {\ text {смежный}} {\ text {противоположный}} \ end {align} [/ latex]
Распространенным мнемоническим символом для запоминания этих отношений является SohCahToa, образованный из первых букв « S ine is o pposite over h ypotenuse, C osine a djacent over h ypotenuse, Угол равен o pposite над a djacent.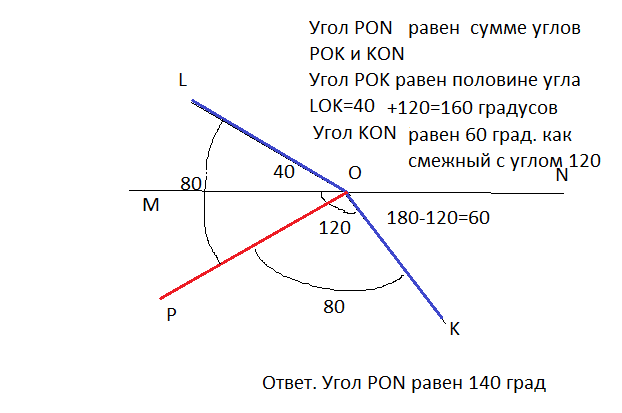 ”
”
Как сделать: учитывая длины сторон прямоугольного треугольника и один из острых углов, найдите синус, косинус и тангенс этого угла.
- Найдите синус как отношение противоположной стороны к гипотенузе
- Найдите косинус как отношение смежной стороны к гипотенузе.
- Найдите касательную — это отношение противоположной стороны к соседней.
Пример 1: Вычисление тригонометрической функции прямоугольного треугольника
Для треугольника, показанного на рисунке 3, найдите значение [latex] \ cos \ alpha [/ latex].
Рисунок 3
Показать решениеСторона, примыкающая к углу, равна 15, а гипотенуза треугольника равна 17, поэтому:
[латекс] \ begin {align} \ cos \ left (\ alpha \ right) = \ frac {\ text {смежный}} {\ text {hypotenuse}} = \ frac {15} {17} \ end {align} [/ латекс]
Попробуйте
Для треугольника, показанного на рисунке 4, найдите значение [latex] \ text {sin} t [/ latex].
Рисунок 4
Показать решение[латекс] \ frac {7} {25} [/ латекс]
Взаимосвязь углов и их функций
При работе с прямоугольными треугольниками применяются одни и те же правила независимо от ориентации треугольника.Фактически, мы можем оценить шесть тригонометрических функций любого из двух острых углов в треугольнике на рисунке 5. Сторона, противоположная одному острому углу, является стороной, смежной с другим острым углом, и наоборот.
Рис. 5. Сторона, прилегающая к одному углу, противоположна другой.
Нас попросят найти все шесть тригонометрических функций для заданного угла в треугольнике. Наша стратегия состоит в том, чтобы сначала найти синус, косинус и тангенс углов. Затем мы можем легко найти другие тригонометрические функции, потому что мы знаем, что величина, обратная синусу, является косекансной, обратная величина косинуса — секущей, а обратная величина касательной — котангенсом.
Как сделать: учитывая длины сторон прямоугольного треугольника, оцените шесть тригонометрических функций одного из острых углов.
- При необходимости нарисуйте прямоугольный треугольник и обозначьте полученный угол.
- Определите угол, прилегающую сторону, сторону, противоположную углу, и гипотенузу прямоугольного треугольника.
- Найдите нужную функцию:
- синус как отношение противоположной стороны к гипотенузе
- Косинус как отношение смежной стороны к гипотенузе
- касательная как отношение противоположной стороны к соседней
- секанс как отношение гипотенузы к смежной стороне
- косеканс как отношение гипотенузы к противоположной стороне
- котангенс как отношение соседней стороны к противоположной
Пример 2: Оценка тригонометрических функций углов, отличных от стандартного положения
Используя треугольник, показанный на рисунке 6, оцените [латекс] \ sin \ alpha [/ latex], [latex] \ cos \ alpha [/ latex], [latex] \ tan \ alpha [/ latex], [latex] \ sec \ alpha [/ latex], [latex] \ csc \ alpha [/ latex] и [latex] \ cot \ alpha [/ latex].
Рисунок 6
Показать решение[латекс] \ begin {align} & \ sin \ alpha = \ frac {\ text {напротив} \ alpha} {\ text {hypotenuse}} = \ frac {4} {5} \\ & \ cos \ alpha = \ frac {\ text {примыкает к} \ alpha} {\ text {hypotenuse}} = \ frac {3} {5} \\ & \ tan \ alpha = \ frac {\ text {напротив} \ alpha} {\ text {примыкает к} \ alpha} = \ frac {4} {3} \\ & \ sec \ alpha = \ frac {\ text {hypotenuse}} {\ text {примыкает к} \ alpha} = \ frac {5} { 3} \\ & \ csc \ alpha = \ frac {\ text {hypotenuse}} {\ text {напротив} \ alpha} = \ frac {5} {4} \\ & \ cot \ alpha = \ frac {\ text {рядом с} \ alpha} {\ text {противоположностью} \ alpha} = \ frac {3} {4} \ end {align} [/ latex]
Попробуйте
Используя треугольник, показанный на рисунке 7, оцените [латекс] \ sin t [/ latex], [latex] \ cos t [/ latex], [latex] \ tan t [/ latex], [latex] \ sec t [ / latex], [латекс] \ csc t [/ latex] и [латекс] \ cot t [/ latex].
Рисунок 7
Показать решение[латекс] \ begin {align} & \ sin t = \ frac {33} {65}, \ cos t = \ frac {56} {65}, \ tan t = \ frac {33} {56}, \ \ & \ sec t = \ frac {65} {56}, \ csc t = \ frac {65} {33}, \ cot t = \ frac {56} {33} \ end {align} [/ latex]
Нахождение тригонометрических функций специальных углов по длинам сторон
Мы уже обсуждали тригонометрические функции в связи с особыми углами на единичной окружности.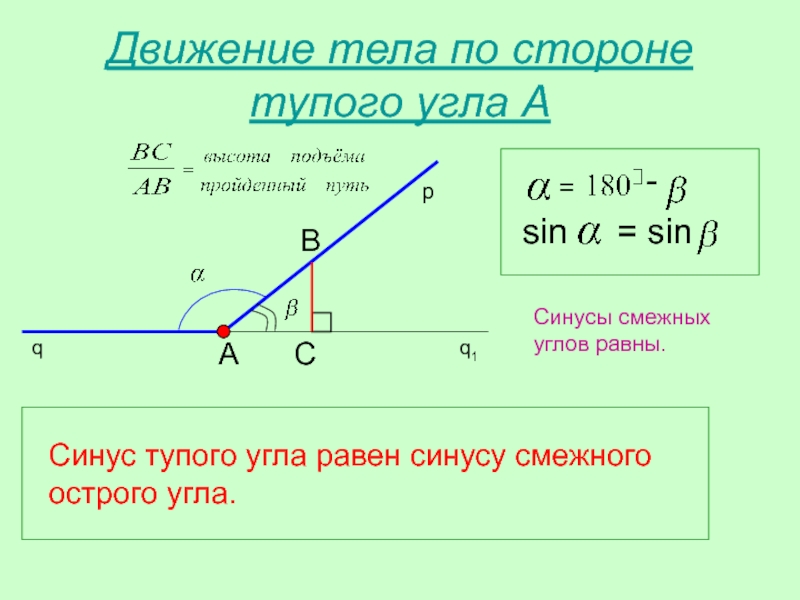 Теперь мы можем использовать эти отношения для оценки треугольников, содержащих эти особые углы.треугольник \ circ [/ latex], который также можно описать как [latex] \ frac {\ pi} {4}, \ frac {\ pi} {4}, \ frac {\ pi} {2} [/ latex ] треугольник, имеют длины в соотношении [latex] s, s, \ sqrt {2} s [/ latex]. Эти отношения показаны на рисунке 8.
Теперь мы можем использовать эти отношения для оценки треугольников, содержащих эти особые углы.треугольник \ circ [/ latex], который также можно описать как [latex] \ frac {\ pi} {4}, \ frac {\ pi} {4}, \ frac {\ pi} {2} [/ latex ] треугольник, имеют длины в соотношении [latex] s, s, \ sqrt {2} s [/ latex]. Эти отношения показаны на рисунке 8.
Рисунок 8. Длины сторон специальных треугольников
Затем мы можем использовать отношения длин сторон для оценки тригонометрических функций специальных углов.
Практическое руководство. Учитывая тригонометрические функции специального угла, оцените длину сторон.
- Используйте длины сторон, показанные на рисунке 8, для особого угла, который вы хотите оценить.
- Используйте соотношение длин сторон, соответствующее функции, которую вы хотите оценить.
Пример 3: Оценка тригонометрических функций специальных углов с использованием длин сторон
Найдите точное значение тригонометрических функций [latex] \ frac {\ pi} {3} [/ latex], используя длины сторон.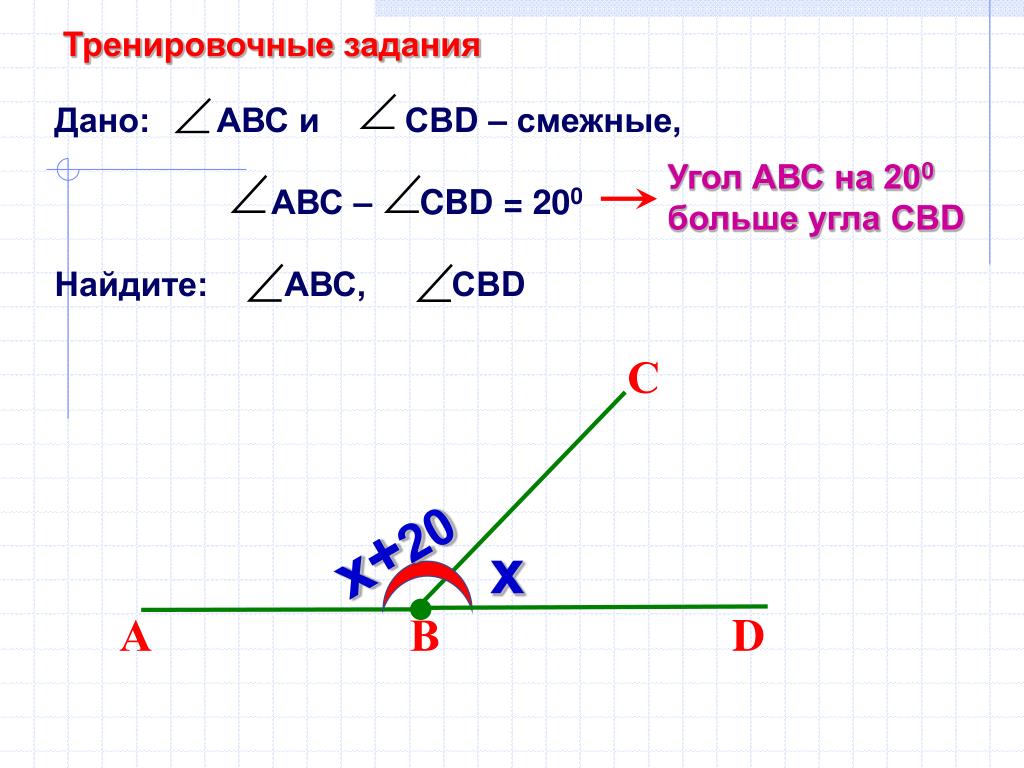
[латекс] \ begin {align} & \ sin \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {opp}} {\ text {hyp}} = \ frac {\ sqrt {3} s} {2s} = \ frac {\ sqrt {3}} {2} \\ & \ cos \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {adj} } {\ text {hyp}} = \ frac {s} {2s} = \ frac {1} {2} \\ & \ tan \ left (\ frac {\ pi} {3} \ right) = \ frac { \ text {opp}} {\ text {adj}} = \ frac {\ sqrt {3} s} {s} = \ sqrt {3} \\ & \ sec \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {hyp}} {\ text {adj}} = \ frac {2s} {s} = 2 \\ & \ csc \ left (\ frac {\ pi} {3} \ right ) = \ frac {\ text {hyp}} {\ text {opp}} = \ frac {2s} {\ sqrt {3} s} = \ frac {2} {\ sqrt {3}} = \ frac {2 \ sqrt {3}} {3} \\ & \ cot \ left (\ frac {\ pi} {3} \ right) = \ frac {\ text {adj}} {\ text {opp}} = \ frac { s} {\ sqrt {3} s} = \ frac {1} {\ sqrt {3}} = \ frac {\ sqrt {3}} {3} \ end {align} [/ latex]
Попробуйте
Найдите точное значение тригонометрических функций [latex] \ frac {\ pi} {4} [/ latex], используя длины сторон. {\ circ} [/ latex]
{\ circ} [/ latex]
Теперь, когда у нас есть эта таблица, мы можем использовать ее для нахождения точных значений тригонометрических выражений.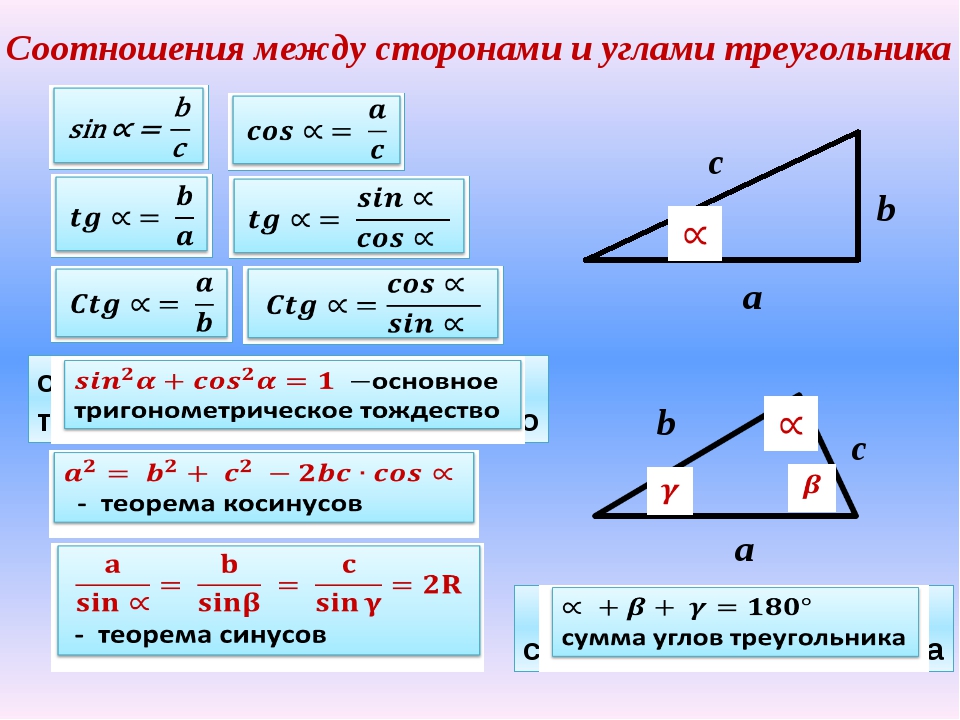 \ circ \ right) [/ latex], используя таблица выше.
\ circ \ right) [/ latex], используя таблица выше.
Использование равных функций дополнений
Если мы посмотрим на таблицу выше, мы заметим закономерность. В прямоугольном треугольнике с углами [latex] \ frac {\ pi} {6} [/ latex] и [latex] \ frac {\ pi} {3} [/ latex] мы видим, что синус [latex] \ frac {\ pi} {3} [/ latex], а именно [latex] \ frac {\ sqrt {3}} {2} [/ latex], также является косинусом [latex] \ frac {\ pi} { 6} [/ latex], тогда как синус [latex] \ frac {\ pi} {6} [/ latex], а именно [latex] \ frac {1} {2} [/ latex], также является косинусом [латекс] \ frac {\ pi} {3} [/ латекс].
[латекс] \ begin {align} & \ sin \ frac {\ pi} {3} = \ cos \ frac {\ pi} {6} = \ frac {\ sqrt {3} s} {2s} = \ frac {\ sqrt {3}} {2} \\ & \ sin \ frac {\ pi} {6} = \ cos \ frac {\ pi} {3} = \ frac {s} {2s} = \ frac {1 } {2} \ end {align} [/ latex]
Рис. 9. Синус [latex] \ frac {\ pi} {3} [/ latex] равен косинусу [latex] \ frac {\ pi} {6} [/ latex] и наоборот.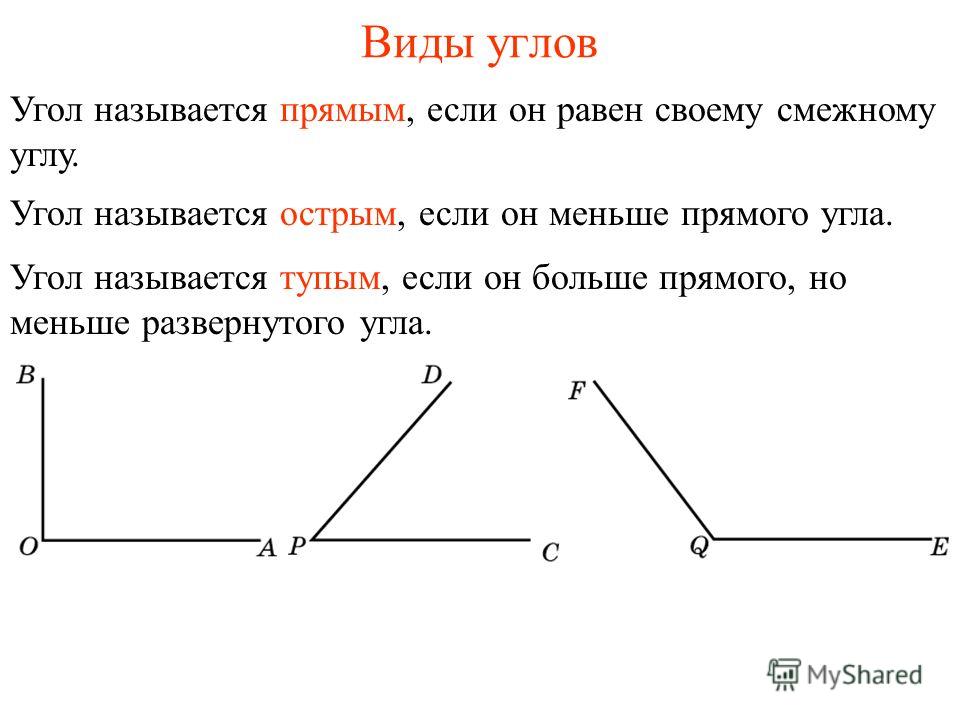
Этот результат не должен вызывать удивления, потому что, как мы видим на рисунке 9, сторона, противоположная углу [latex] \ frac {\ pi} {3} [/ latex], также является стороной, смежной с [latex] \ frac { \ pi} {6} [/ latex], поэтому [latex] \ sin \ left (\ frac {\ pi} {3} \ right) [/ latex] и [latex] \ cos \ left (\ frac {\ pi } {6} \ right) [/ latex] — это точно такое же соотношение тех же двух сторон, [latex] \ sqrt {3} s [/ latex] и [latex] 2s [/ latex].Аналогично, [latex] \ cos \ left (\ frac {\ pi} {3} \ right) [/ latex] и [latex] \ sin \ left (\ frac {\ pi} {6} \ right) [/ latex ] также имеют такое же соотношение с использованием тех же двух сторон, [латекс] [/ латекс] и [латекс] 2 [/ латекс].
Взаимосвязь между синусами и косинусами [latex] \ frac {\ pi} {6} [/ latex] и [latex] \ frac {\ pi} {3} [/ latex] также сохраняется для двух острых углов в любой прямоугольный треугольник, так как в любом случае отношение одних и тех же двух сторон будет составлять синус одного угла и косинус другого. Поскольку три угла треугольника складываются в [латекс] \ pi [/ latex], а прямой угол равен [latex] \ frac {\ pi} {2} [/ latex], оставшиеся два угла также должны составлять [латекс] \ frac {\ pi} {2} [/ латекс]. Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, которые складываются с [latex] \ frac {\ pi} {2} [/ latex], другими словами, любыми двумя дополнительными углами. Таким образом, мы можем сформулировать идентичность кофункции : Если любые два угла дополняют друг друга, синус одного является косинусом другого, и наоборот.Эта идентичность проиллюстрирована на рисунке 10.
Поскольку три угла треугольника складываются в [латекс] \ pi [/ latex], а прямой угол равен [latex] \ frac {\ pi} {2} [/ latex], оставшиеся два угла также должны составлять [латекс] \ frac {\ pi} {2} [/ латекс]. Это означает, что прямоугольный треугольник может быть образован любыми двумя углами, которые складываются с [latex] \ frac {\ pi} {2} [/ latex], другими словами, любыми двумя дополнительными углами. Таким образом, мы можем сформулировать идентичность кофункции : Если любые два угла дополняют друг друга, синус одного является косинусом другого, и наоборот.Эта идентичность проиллюстрирована на рисунке 10.
Рисунок 10. Идентичность кофункций синуса и косинуса дополнительных углов
Используя это тождество, мы можем утверждать, не вычисляя, например, что синус [latex] \ frac {\ pi} {12} [/ latex] равен косинусу [latex] \ frac {5 \ pi} {12 } [/ latex], и что синус [latex] \ frac {5 \ pi} {12} [/ latex] равен косинусу [latex] \ frac {\ pi} {12} [/ latex]. Мы также можем утверждать, что если для определенного угла [латекс] t [/ латекс], [латекс] \ cos \ text {} t = \ frac {5} {13} [/ latex], то [латекс] \ sin \ left (\ frac {\ pi} {2} -t \ right) = \ frac {5} {13} [/ latex].
Мы также можем утверждать, что если для определенного угла [латекс] t [/ латекс], [латекс] \ cos \ text {} t = \ frac {5} {13} [/ latex], то [латекс] \ sin \ left (\ frac {\ pi} {2} -t \ right) = \ frac {5} {13} [/ latex].
A Общее примечание: идентификаторы совместных функций
Идентификаторы совместных функций в радианах перечислены в таблице ниже.
| [латекс] \ cos t = \ sin \ left (\ frac {\ pi} {2} -t \ right) [/ latex] | [латекс] \ sin t = \ cos \ left (\ frac {\ pi} {2} -t \ right) [/ latex] |
| [латекс] \ tan t = \ cot \ left (\ frac {\ pi} {2} -t \ right) [/ latex] | [латекс] \ cot t = \ tan \ left (\ frac {\ pi} {2} -t \ right) [/ latex] |
| [латекс] \ sec t = \ csc \ left (\ frac {\ pi} {2} -t \ right) [/ latex] | [латекс] \ csc t = \ sec \ left (\ frac {\ pi} {2} -t \ right) [/ latex] |
Практическое руководство.
 Зная синус и косинус угла, найдите синус или косинус его дополнения.
Зная синус и косинус угла, найдите синус или косинус его дополнения.- Чтобы найти синус дополнительного угла, найдите косинус исходного угла.
- Чтобы найти косинус дополнительного угла, найдите синус исходного угла.
Пример 5: Использование идентификаторов совместных функций
Запишите следующее как эквивалентное выражение косинуса: [latex] \ sin \ left (\ frac {5 \ pi} {12} \ right) [/ latex].
Показать решениеСогласно идентификаторам совместных функций для синуса и косинуса,
[латекс] \ sin t = \ cos \ left (\ frac {\ pi} {2} -t \ right) [/ latex].\ circ \ right) [/ латекс]
Использование тригонометрических функций
В предыдущих примерах мы вычисляли синус и косинус в треугольниках, где мы знали все три стороны. Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон.
Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон.
Как сделать: у прямоугольного треугольника, длины одной стороны и меры одного острого угла найдите остальные стороны.
- Для каждой стороны выберите тригонометрическую функцию с неизвестной стороной в качестве числителя или знаменателя.Известная сторона, в свою очередь, будет знаменателем или числителем.
- Напишите уравнение, устанавливающее значение функции известного угла, равное отношению соответствующих сторон.
- Используя значение тригонометрической функции и известную длину стороны, найдите недостающую длину стороны.
Пример 7: Нахождение недостающих длин сторон с помощью тригонометрических соотношений
Найдите неизвестные стороны треугольника на рисунке 11.
Рисунок 11
Показать решение Мы знаем угол и противоположную сторону, поэтому можем использовать касательную, чтобы найти прилегающую сторону. \ circ \ right)} \\ & = 14 \ end {align} [/ latex]
\ circ \ right)} \\ & = 14 \ end {align} [/ latex]
Попробуйте
Прямоугольный треугольник имеет один угол [латекс] \ frac {\ pi} {3} [/ latex] и гипотенузу 20. Найдите неизвестные стороны и угол треугольника.
Показать решение[латекс] \ text {смежный} = 10 [/ латекс]; [латекс] \ текст {напротив} = 10 \ sqrt {3} [/ латекс]; отсутствующий угол [латекс] \ frac {\ pi} {6} [/ latex]
Тригонометрия прямоугольного треугольника имеет множество практических применений. Например, способность вычислять длины сторон треугольника позволяет определить высоту высокого объекта, не взбираясь на вершину и не протягивая рулетку по его высоте.Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом. Угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. Правый треугольник, создаваемый этим положением, имеет стороны, которые представляют неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол прямой видимости, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем образовать треугольник из вершины высокого объекта, глядя вниз. Угол наклона объекта под наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. На рисунке ниже [латекс] \ alpha [/ latex] представляет угол подъема , а [латекс] \ beta [/ latex] представляет угол углубления .
Зная измеренное расстояние до основания объекта и угол прямой видимости, мы можем использовать тригонометрические функции для вычисления неизвестной высоты. Точно так же мы можем образовать треугольник из вершины высокого объекта, глядя вниз. Угол наклона объекта под наблюдателем относительно наблюдателя — это угол между горизонталью и линией от объекта до глаза наблюдателя. На рисунке ниже [латекс] \ alpha [/ latex] представляет угол подъема , а [латекс] \ beta [/ latex] представляет угол углубления .
Рисунок 12
Практическое руководство. Для высокого объекта измерьте его высоту косвенно.
- Сделайте набросок проблемной ситуации, чтобы отслеживать известную и неизвестную информацию.
- Разместите измеренное расстояние от основания объекта до точки, где верхняя часть объекта будет хорошо видна.
- Посмотрите на верхнюю часть объекта на другом конце измеренного расстояния. Измерьте угол, под которым линия визирования образует горизонталь.
 \ circ \ right) && \ text {Умножение}. \\ & h \ приблизительно 46,2 && \ text {Используйте калькулятор}. \ end {align} [/ latex]
\ circ \ right) && \ text {Умножение}. \\ & h \ приблизительно 46,2 && \ text {Используйте калькулятор}. \ end {align} [/ latex]Дерево примерно 46 футов в высоту.
Попробуйте
Какова длина лестницы, чтобы подняться на подоконник на высоте 50 футов над землей, если лестница упирается в здание под углом [латекс] \ frac {5 \ pi} {12} [/ latex]? Округлите до ближайшего фута.
Обратная тригонометрическая функция на калькуляторе
Если заданы две стороны прямоугольного треугольника, обратная тригонометрическая функция может использоваться для нахождения острого угла в треугольнике.{-1} [/ латекс]. Калькулятор вернет угол в радианах или градусах, в зависимости от того, в каком режиме находится ваш калькулятор. Нам понадобится функция арктангенса для пеленга.

Подшипник
Пеленг — это направление, в котором вы движетесь по компасу. На большинстве карт N вверху, S внизу, W слева, а E справа. Подшипники записываются в такой форме: (N или S) (Острый угол) (E или W). Угол отсчитывается от севера или юга, в зависимости от того, какая буква идет первой в вашем азимуте.\ circ E [/ latex] означает, что вы пойдете на север, а затем на 20 градусов на восток или вправо. На рисунке ниже показан пример рисования подшипников. Как видите, каждый угол измеряется либо от N, либо от S в зависимости от первой буквы подшипника. Подшипники НЕ нарисованы в стандартном положении, что означает, что НЕ отрисовываются от положительной оси x.
Теперь мы рассмотрим некоторые прикладные задачи, связанные с пеленгами и прямоугольными треугольниками.
Пример 9: Найти подшипник
Полуавтомат движется на восток на 8 миль, делает поворот направо, а затем едет на юг еще 11 миль.\ circ E [/ latex] на 5 миль. Как далеко на восток и как далеко на юг бегун от исходной точки? Округлите ответы до ближайшей мили.
Показать решение
4 мили на восток, 3 мили на юг
Преобразовать процентную оценку в градусы
Процент уклона часто встречается на дорогах или тропах, и это показатель крутизны. Например, если дорога имеет уклон 6%, это означает, что дорога поднимается на 6 футов на горизонтальное расстояние (пробег) в 100 футов. Процентный уклон определяется путем деления прибавки за пробег, как показано на Рисунке 14.Подъем и бег — это тоже противоположные и смежные стороны. Мы можем найти [latex] \ theta [/ latex], взяв арктангенс.
Рисунок 14
Чтобы вычислить градусное измерение степени в процентах, сначала измените процент на десятичный разделитель, разделив его на 100. Затем возьмите арктангенс этого десятичного числа, и это даст угол в градусах. На самом деле это угол места относительно , который мы изучали ранее в этом разделе!
Как: преобразовать процентную оценку в градусы
Убедитесь, что ваш калькулятор работает в градусном режиме.
 {- 1} \ left (\ dfrac {\ text {процентная оценка}} {100} \ right) [/ latex]
{- 1} \ left (\ dfrac {\ text {процентная оценка}} {100} \ right) [/ latex]Ключевые понятия
- Мы можем определить тригонометрические функции как отношения длин сторон прямоугольного треугольника.
- Можно использовать одинаковые длины сторон для оценки тригонометрических функций любого острого угла в прямоугольном треугольнике.
- Мы можем оценить тригонометрические функции особых углов, зная длины сторон треугольников, в которых они встречаются.
- Любые два дополнительных угла могут быть двумя острыми углами прямоугольного треугольника.
- Если два угла дополняют друг друга, тождества совместных функций указывают, что синус одного равен косинусу другого, и наоборот.
- Мы можем использовать тригонометрические функции угла, чтобы найти неизвестные длины сторон.
- Выберите тригонометрическую функцию, представляющую отношение неизвестной стороны к известной стороне.
- Тригонометрия прямоугольного треугольника позволяет измерять недоступные высоты и расстояния.

- Неизвестную высоту или расстояние можно найти, создав прямоугольный треугольник, в котором неизвестная высота или расстояние является одной из сторон, а другая сторона и угол известны.
- Подшипники измеряются от N или S, в зависимости от первой буквы подшипника.
- Процентный уклон можно выразить в градусах, которые представляют собой угол подъема.
Глоссарий
- смежная сторона
- в прямоугольном треугольнике, сторона между заданным углом и прямым углом
- угол наклона
- угол между горизонталью и линией от объекта до глаза наблюдателя, предполагая, что объект расположен ниже, чем наблюдатель
- угол возвышения
- угол между горизонталью и линией от объекта до глаза наблюдателя, предполагая, что объект расположен выше, чем наблюдатель
- противоположная сторона
- в прямоугольном треугольнике со стороной, наиболее удаленной от заданного угла
- гипотенуза
- сторона прямоугольного треугольника напротив прямого угла
- процентное содержание
- Коэффициент роста за период, выраженный в процентах.
 Это мера крутизны.
Это мера крутизны.
Раздел 4.3 Домашние упражнения
1. Для данного прямоугольного треугольника пометьте прилегающую сторону, противоположную сторону и гипотенузу для указанного угла.
2. Когда прямоугольный треугольник с гипотенузой 1 помещается в единичный круг, какие стороны треугольника соответствуют координатам x и y?
3. Тангенс угла сравнивает стороны прямоугольного треугольника?
4. Как соотносятся два острых угла в прямоугольном треугольнике?
5.\ circ \ right) [/ латекс]
13. [латекс] \ tan \ left (\ frac {\ pi} {4} \ right) = \ cot \ left (\ text {__} \ right) [/ latex]
Для следующих упражнений найдите длины недостающих сторон, если сторона [латекс] a [/ латекс] находится под противоположным углом [латекс] A [/ латекс], сторона [латекс] b [/ латекс] находится под противоположным углом [латекс] B [/ latex], а side [latex] c [/ latex] — гипотенуза.
14. [латекс] \ cos B = \ frac {4} {5}, a = 10 [/ латекс]
15.
 [латекс] \ sin B = \ frac {1} {2}, a = 20 [/ латекс]
[латекс] \ sin B = \ frac {1} {2}, a = 20 [/ латекс]16. [латекс] \ tan A = \ frac {5} {12}, b = 6 [/ latex]
17.{\ circ} [/ латекс]
Для следующих упражнений используйте Рисунок 14, чтобы оценить каждую тригонометрическую функцию угла [латекс] A [/ латекс].
Рисунок 14
21. [латекс] \ sin A [/ латекс]
22. [латекс] \ cos A [/ латекс]
23. [латекс] \ tan A [/ латекс]
24. [латекс] \ csc A [/ латекс]
25. [латекс] \ сек A [/ латекс]
26. [латекс] \ кроватка A [/ латекс]
Для следующих упражнений используйте рисунок 15, чтобы оценить каждую тригонометрическую функцию угла [латекс] A [/ латекс].
Рисунок 15
27. [латекс] \ sin A [/ латекс]
28. [латекс] \ cos A [/ латекс]
29. [латекс] \ tan A [/ латекс]
30. [латекс] \ csc A [/ латекс]
31. [латекс] \ сек A [/ латекс]
32. [латекс] \ кроватка A [/ латекс]
Для следующих упражнений решите неизвестные стороны данного треугольника.

33.
34.
35.
Для следующих упражнений используйте калькулятор, чтобы найти длину каждой стороны с точностью до четырех знаков после запятой.\ circ [/ латекс]. Насколько высоко лестница поднимается к стене здания?
58. Угол поднятия к верху здания в Нью-Йорке составляет 9 градусов от земли на расстоянии 1 мили от основания здания. Используя эту информацию, найдите высоту здания.
59. Угол поднятия к вершине здания в Сиэтле составляет 2 градуса от земли на расстоянии 2 миль от основания здания. Используя эту информацию, найдите высоту здания.\ circ [/ latex], как далеко я от основания дерева?
61. Автомобиль едет на запад 5 миль, поворачивает налево и затем 9 миль на юг. Каков пеленг от исходного положения автомобиля до его текущего положения? Округлите ответ до двух десятичных знаков.
62. Грузовик едет на восток 4 мили, поворачивает налево, а затем едет на север 6 миль. Каков подшипник от исходного положения грузовика до его текущего положения? Округлите ответ до двух десятичных знаков.

63.\ circ W [/ latex] на 20 дюймов. Как далеко на запад и как далеко на юг находится паук от начальной точки? Округлите ответы до двух десятичных знаков.
65. Построен в 1901 году полковником Дж. У. Эдди, «Рейс ангелов» в Лос-Анджелесе, как говорят, является самой короткой в мире железнодорожной магистралью. Машины с противовесом, управляемые тросами, преодолевают уклон 33% на расстояние 315 футов. Какой угол образует дорожка с горизонтальной линией, округленной до одного десятичного знака?
66. Saluda Grade — это самый крутой уклон магистральных железных дорог стандартной колеи в Соединенных Штатах.Между Мелроузом и Салудой, Северная Каролина, максимальный уклон составляет 4,9% на расстоянии около 300 футов. Какой угол образует дорожка с горизонтальной линией, округленной до одного десятичного знака?
Тригонометрические отношения
«Тригон» в переводе с греческого означает треугольник , а «метрика» по-гречески означает «измерение».
 В тригонометрические соотношения специальные измерения прямоугольный треугольник (треугольник с одним
угол
измерение
90
°
).Помните, что две стороны прямоугольного треугольника, образующие прямой угол, называются ноги , а третья сторона (напротив прямого угла) называется
гипотенуза
.
В тригонометрические соотношения специальные измерения прямоугольный треугольник (треугольник с одним
угол
измерение
90
°
).Помните, что две стороны прямоугольного треугольника, образующие прямой угол, называются ноги , а третья сторона (напротив прямого угла) называется
гипотенуза
.Существует три основных тригонометрических соотношения: синус , косинус , и касательная . Для прямоугольного треугольника вы можете найти синус (или косинус, или тангенс) любого из не- 90 ° углы.
синус знак равно длина ножки противоположная углу длина гипотенузы сокращенно «грех» косинус знак равно длина ноги, прилегающей к углу длина гипотенузы сокращенно «cos» касательная знак равно длина ножки противоположная углу длина ноги, прилегающей к углу сокращенно «загар»
Пример:
Напишите выражения для синуса, косинуса и тангенса ∠ А .

Длина ноги напротив ∠ А является а . Длина ноги, прилегающей к ∠ А является б , а длина гипотенузы равна c .
Синус угла задается соотношением «противоположность гипотенузы». Так,
грех ∠ А знак равно а c
Косинус определяется отношением «смежность по гипотенузе».»
потому что ∠ А знак равно б c
Касательная задается соотношением «противоположные по соседним».
загар ∠ А знак равно а б
Поколения студентов использовали мнемонику » SOHCAHTOA «чтобы запомнить какое соотношение есть какое. ( S ине: О pposite over ЧАС ипотенуза C осин: А расслабиться ЧАС ипотенуза Т угловатый: О pposite over А djacent.
 )
)Другие тригонометрические соотношения
Другие распространенные тригонометрические соотношения:секущий знак равно длина гипотенузы длина ноги, прилегающей к углу сокращенно «сек» сек ( Икс ) знак равно 1 потому что ( Икс ) косеканс знак равно длина гипотенузы длина ножки противоположная углу сокращенно «csc» csc ( Икс ) знак равно 1 грех ( Икс ) секущий знак равно длина ноги, прилегающей к углу длина ножки противоположная углу сокращенно «детская кроватка» детская кроватка ( Икс ) знак равно 1 загар ( Икс )
Пример:
Напишите выражения для секанса, косеканса и котангенса ∠ А .

Длина ноги напротив ∠ А является а . Длина ноги, прилегающей к ∠ А является б , а длина гипотенузы равна c .
Секанс угла определяется отношением «гипотенуза к смежным». Так,
сек ∠ А знак равно c б
Косеканс определяется отношением «гипотенуза к противоположной».
csc ∠ А знак равно c а
Котангенс задается отношением «смежные к противоположным».
детская кроватка ∠ А знак равно б а
Треугольник 30 ° -60 ° -90 °. Темы по тригонометрии.
Темы | Дом
4
В тригонометрии ЕСТЬ ДВА особых треугольника.Один из них — треугольник 30 ° -60 ° -90 °.
 Другой — равнобедренный прямоугольный треугольник. Они особенные, потому что с помощью простой геометрии мы можем узнать соотношение их сторон.
Другой — равнобедренный прямоугольный треугольник. Они особенные, потому что с помощью простой геометрии мы можем узнать соотношение их сторон.Теорема. В треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении 1: 2:.
Мы докажем это ниже.
(Определение углов измерения «градусами» см. В теме 12.)
Обратите внимание, что наименьшая сторона, 1, противоположна наименьшему углу, 30 °; в то время как наибольшая сторона, 2, противоположна наибольшему углу, 90 °.(Теорема 6). (Ибо 2 больше, чем. Кроме того, хотя 1: 2 правильно соответствует сторонам, противоположным 30 ° -60 ° -90 °, многие считают, что последовательность 1: 2: легче запомнить.)
Приведенные теоремы взяты из Приложения, Некоторые теоремы плоской геометрии.
Вот примеры того, как мы пользуемся знанием этих соотношений. Во-первых, мы можем оценить функции 60 ° и 30 °.
Пример 1. Оценить cos 60 °.
Ответ .
 Для решения любой задачи, связанной с треугольником 30 ° -60 ° -90 °, ученик не должен использовать стол. Ученик должен нарисовать треугольник и указать числа отношения.
Для решения любой задачи, связанной с треугольником 30 ° -60 ° -90 °, ученик не должен использовать стол. Ученик должен нарисовать треугольник и указать числа отношения.Поскольку косинус — это отношение соседней стороны к гипотенузе, вы можете видеть, что cos 60 ° = ½.
Пример 2. Оценить sin 30 °.
Ответ . По свойству совместных функций (Тема 3), sin 30 ° равен , что равно , а cos 60 °.грех 30 ° = ½.
Вы можете видеть это прямо на рисунке выше.
Задача 1. Оценить sin 60 ° и tan 60 °.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).Синус — это отношение противоположной стороны к гипотенузе.
sin 60 ° =
2= ½. Урок 5 алгебры
Касательная — это отношение противоположной стороны к соседней.

загар 60 ° =
1=. Задача 2. Оценить кроватку 30 ° и cos 30 °.
Котангенс — это отношение соседней стороны к противоположной.
Следовательно, при осмотре рисунка выше, детская кроватка 30 ° =
1=.
Или, проще говоря, раскладушка 30 ° = загар 60 °.
Проблема 1
Что касается косинуса, это отношение смежной стороны к гипотенузе. Следовательно,
cos 30 ° =
2= ½. Прежде чем мы перейдем к следующему примеру, вот как мы соотносим стороны и углы треугольника:
Если угол обозначен заглавной буквы A, то противоположная сторона будет обозначена малым a .Аналогично для угла B и стороны b , угла C и стороны c .
Пример 3. Решите прямоугольный треугольник ABC, если угол A равен 60 °, а сторона c равна 10 см.

Решение. Решить треугольник — значит знать все три стороны и все три угла. Поскольку это прямоугольный треугольник, а угол A равен 60 °, то оставшийся угол B является его дополнением, 30 °.
Теперь в каждом треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении 1: 2:, как показано справа.Когда мы узнаем соотношение сторон, мы можем решить треугольник методом подобных фигур.
Итак, в треугольнике ABC сторона, соответствующая 2, умножена на 5. Следовательно, каждая сторона будет умножена на 5. Сторона b будет 5 × 1, или просто 5 см, а сторона a будет равна 5 см. .
В качестве альтернативы мы могли бы сказать, что сторона, прилегающая к 60 °, всегда равна половине гипотенузы. Следовательно, сторона b будет 5 см.Теперь сторона b — это сторона, соответствующая 1. И она была умножена на 5. Следовательно, сторона nI> a также должна быть умножена на 5. Она будет равна 5 см.
Всякий раз, когда мы знаем числа отношения, ученик должен использовать этот метод подобных фигур для решения треугольника, а не тригонометрическую таблицу.

(В теме 6 мы будем решать прямоугольные треугольники, отношения сторон которых нам неизвестны.)
Задача 3. В прямоугольном треугольнике DFE угол D равен 30 °, а сторона DF — 3 дюйма.Какова длина сторон d и f ?
Студент должен нарисовать аналогичный треугольник в той же ориентации. Затем посмотрите, что сторона, соответствующая, была умножена на.
Урок 26 алгебры
Задача 4. В прямоугольном треугольнике PQR угол P равен 30 °, а сторона r равна 1 см. Какова длина сторон p и q ?
Сторона, соответствующая 2, была разделена на на 2.Следовательно, каждая сторона должна быть разделена на 2. Сторона p будет равна 1/2, а сторона q будет равна 1/2.
Задача 5. Решите прямоугольный треугольник ABC, если угол A равен 60 °, а гипотенуза равна 18,6 см.
Сторона, прилегающая к 60 °, всегда равна половине гипотенузы, поэтому сторона b равна 9,3 см.

Но это сторона, которая соответствует 1.И это было умножено на 9,3. Следовательно, сторона на будет умножена на 9,3.
Будет 9,3 см.Пример 4. ABC — равносторонний треугольник, высота AD которого равна 4 см.
Найдите длину стороны x .
Решение 1 . Поскольку треугольник равносторонний, он также равноугольный, поэтому угол в точке B равен 60 °
Высота треугольника — это прямая линия, проведенная от вершины под прямым углом к основанию.Следовательно, треугольник ADB — это треугольник 30-60-90.
Для этой задачи будет удобно формировать пропорцию дробными символами:
x
4= 2 Это означает
х = 4 · 2 = 8 . 
Приняв примерно 1 . 732,
_8_
1 . 7324 . 619 см. Решение 2. Сторона, соответствующая умноженной, стала 4. Как она умножалась?
По 4 : 4 · = 4. Сравните предыдущую тему.
Следовательно, гипотенуза 2 также будет умножена на .4 : 4 · 2 = 8 , , что опять же составляет примерно 4 . 619 см.
Задача 6.
 Проверьте значения 30 °, 60 ° и 45 ° — то есть посмотрите на два треугольника —
Проверьте значения 30 °, 60 ° и 45 ° — то есть посмотрите на два треугольника —— и в каждом уравнении решите, какой из этих углов имеет значение x .
а) sin x = cos x . x = 45 °. б) загар x = 1. x = 45 °. в) sin x = ½. х = 30 ° г) cos x = ½. х = 60 °. д) sin x = ½. x = 60 ° е) cos x = ½. x = 45 °. x = 30 °. ч) csc x = 2.  x = 30 °.
x = 30 °.Пример 5.Решите это уравнение относительно угла x :
2 sin ( x — 10 °) — = 0. Решение. 2 sin ( x — 10 °) — = 0 подразумевает sin ( x — 10 °) = ½. Итак, синус какого угла равен ½?
грех 60 ° = ½. Следовательно, x — 10 ° = 60 °. х = 70 °. 
Задача 7. Решите это уравнение для угла x :
.3 csc (2 x + 6 °) — 6 = 0. 3 csc (2 x + 6 °) — 6 = 0 подразумевает csc (2 x + 6 °) = 2. 2 x + 6 ° = 30 ° х + 3 ° = 15 ° х = 12 °. 
Задача 8. Доказательство: Площадь A равностороннего треугольника со стороной s равна
.A = ¼ с 2 .
Площадь любого треугольника равна половине синуса любого угла, умноженному на произведение двух сторон, составляющих угол. (Тема 2, проблема 6.)
В равностороннем треугольнике каждая сторона равна с , а каждый угол равен 60 °.Следовательно,
A = ½ sin 60 ° с 2 .
Так как sin 60 ° = ½,
Проблема 1
A = ½ · ½ с 2 = ¼ с 2 .
Задача 9. Доказательство: Площадь A равностороннего треугольника, вписанного в круг радиуса r, равна
А = 3
4r 2 . Три радиуса делят треугольник на три равных треугольника.

Сторона Сторона
Следовательно, каждый радиус делит каждую вершину пополам на два угла по 30 °.
Если мы расширим радиус AO, то AD будет серединным перпендикуляром стороны CB.Теорема 2
Triangle OBD, следовательно, треугольник 30-60-90.
Если называть каждую сторону равностороннего треугольника s , то в прямоугольном треугольнике OBDСледовательно,
с = r
так что
с 2 = 3 r 2 .
Теперь площадь равностороннего треугольника A равна
.A = ¼ с 2 .
Проблема 8
Следовательно,
A = ¼ с 2 = ¼ · 3 r 2 = 3
4r 2 . Это то, что мы хотели доказать.
Задача 10. Доказательство: Биссектрисы равностороннего треугольника пересекаются в точке, которая составляет две трети расстояния от вершины треугольника до основания.

Пусть ABC — равносторонний треугольник, AD, BF, CE — биссектрисы углов A, B, C соответственно; тогда эти биссектрисы пересекаются в точке P, так что AP составляет две трети AD.
Во-первых, треугольники BPD, APE конгруэнтны.
Поскольку, поскольку треугольник равносторонний, а BF, AD — биссектрисы, тогда углы PBD, PAE равны и каждый 30 °;
, а сторона BD равна стороне AE, потому что в равностороннем треугольнике биссектриса угла является серединным перпендикуляром основания.Теорема 2
Тогда углы PDB, AEP прямые и равны.
Следовательно,
Уголок боковой
треугольников BPD, APE конгруэнтны.
Сейчас, БП
ПД= csc 30 ° = 2. Задача 2
Следовательно, BP = 2PD.
Но AP = BP, потому что треугольники APE, BPD соприкасаются, а это стороны, противоположные равным углам.

Следовательно, AP = 2PD.
Следовательно, AP составляет две трети всего AD.
Это то, что мы хотели доказать.Доказательство
Вот доказательство того, что в треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении 1: 2:. Он основан на том факте, что треугольник 30 ° -60 ° -90 ° равен половине равностороннего треугольника.
Нарисуйте равносторонний треугольник ABC. Тогда каждый из его равных углов равен 60 °. (Теоремы 3 и 9)
Проведите прямую AD, разделяющую угол A пополам на два угла по 30 °.
Тогда AD — серединный перпендикуляр к BC (теорема 2). Таким образом, треугольник ABD представляет собой треугольник 30 ° -60 ° -90 °.Теперь, поскольку BD равно DC, то BD составляет половину BC.
Это означает, что BD также является половиной AB, потому что AB равно BC. То есть
BD: AB = 1: 2
Из теоремы Пифагора мы можем найти третью сторону AD:
AD 2 + 1 2 = 2 2 н.  э. 2
э. 2 = 4 — 1 = 3 н.э. = . Следовательно, в треугольнике 30 ° -60 ° -90 ° стороны находятся в соотношении 1: 2:; что мы и пытались доказать.
Следствие. Квадрат, нарисованный на высоте равностороннего треугольника, составляет три четверти квадрата, нарисованного сбоку.
Следующая тема: Равнобедренный прямоугольный треугольник
Темы | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.2} {2bc} \ right] \)
A = угол A
B = угол B
C = угол C
a = сторона a
b = сторона b
c = сторона c
P = периметр
с = полупериметр
K = площадь
r = радиус вписанной окружности
R = радиус описанной окружности* Единицы длины приведены только для справки, поскольку значение результирующих длин всегда будет одинаковым, независимо от единиц.

Использование калькулятора
Использует закон косинусов для вычисления неизвестных углов или сторон треугольника. Чтобы вычислить неизвестные значения, вы должны ввести 3 известных значения.
Чтобы вычислить любой угол, A, B или C, введите 3 длины стороны a, b и c. Это тот же расчет, что и Теорема сторона-сторона-сторона (SSS). Например, чтобы рассчитать сторону a, введите противоположный угол A и две другие смежные стороны b и c.2} {2ab} \ right] \)
Характеристики треугольника
Периметр треугольника, P = a + b + c
Полупериметр треугольника, s = 0,5 * (a + b + c)
Площадь треугольника, K = √ [s * (s-a) * (s-b) * (s-c)]
Радиус вписанной окружности в треугольник, r = √ [(s-a) * (s-b) * (s-c) / s]
Радиус описанной окружности вокруг треугольника, R = (abc) / (4K)
Ссылки / Дополнительная литература
Вайсштейн, Эрик В.
 «Закон косинусов» из MathWorld — Интернет-ресурс Wolfram.
Закон косинусов.
«Закон косинусов» из MathWorld — Интернет-ресурс Wolfram.
Закон косинусов.Цвиллинджер, Даниэль (главный редактор). Стандартные математические таблицы и формулы CRC, 31-е издание New York, NY: CRC Press, p. 512, 2003 г.
http://hyperphysics.phy-astr.gsu.edu/hbase/lcos.html
http: // гиперфизика.phy-astr.gsu.edu/hbase/lsin.html
.

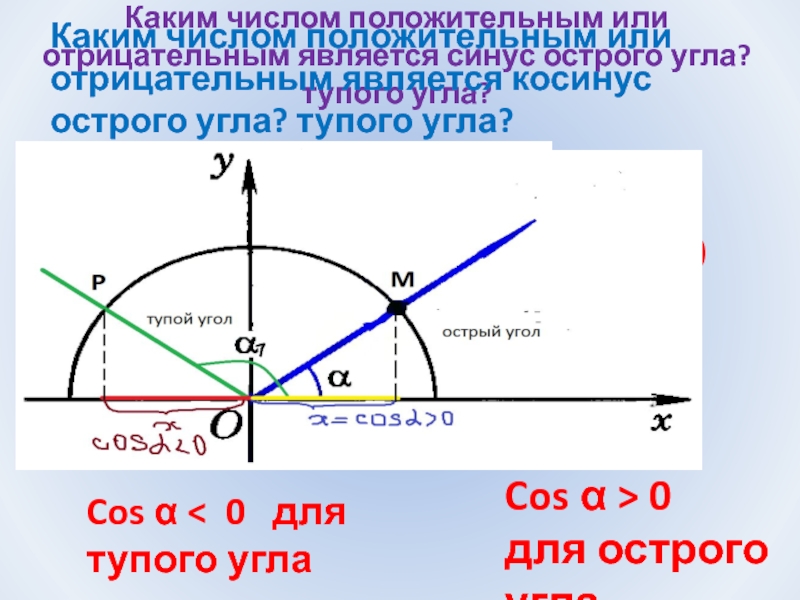
 Найдите все образовавшиеся углы.
Найдите все образовавшиеся углы. Отношение между двумя сторонами в одном треугольнике равно
соотношение между соответствующими сторонами в другом треугольнике.
Отношение между двумя сторонами в одном треугольнике равно
соотношение между соответствующими сторонами в другом треугольнике.
 \ circ \ right) && \ text {Умножение}. \\ & h \ приблизительно 46,2 && \ text {Используйте калькулятор}. \ end {align} [/ latex]
\ circ \ right) && \ text {Умножение}. \\ & h \ приблизительно 46,2 && \ text {Используйте калькулятор}. \ end {align} [/ latex]

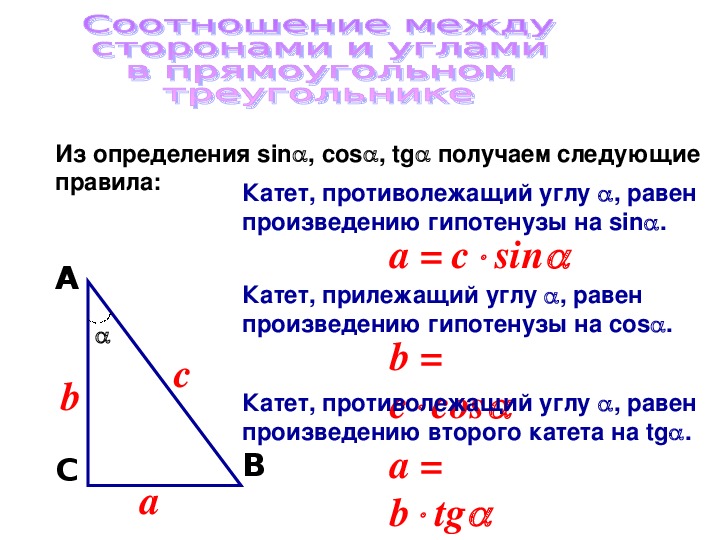 {- 1} \ left (\ dfrac {\ text {процентная оценка}} {100} \ right) [/ latex]
{- 1} \ left (\ dfrac {\ text {процентная оценка}} {100} \ right) [/ latex]
 Это мера крутизны.
Это мера крутизны. [латекс] \ sin B = \ frac {1} {2}, a = 20 [/ латекс]
[латекс] \ sin B = \ frac {1} {2}, a = 20 [/ латекс]
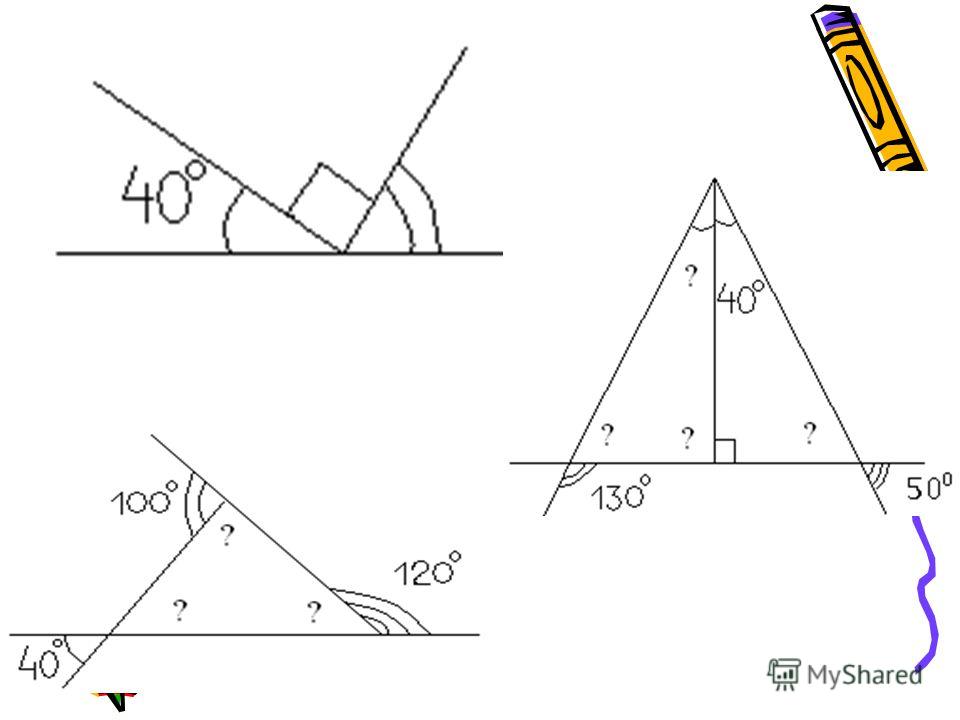
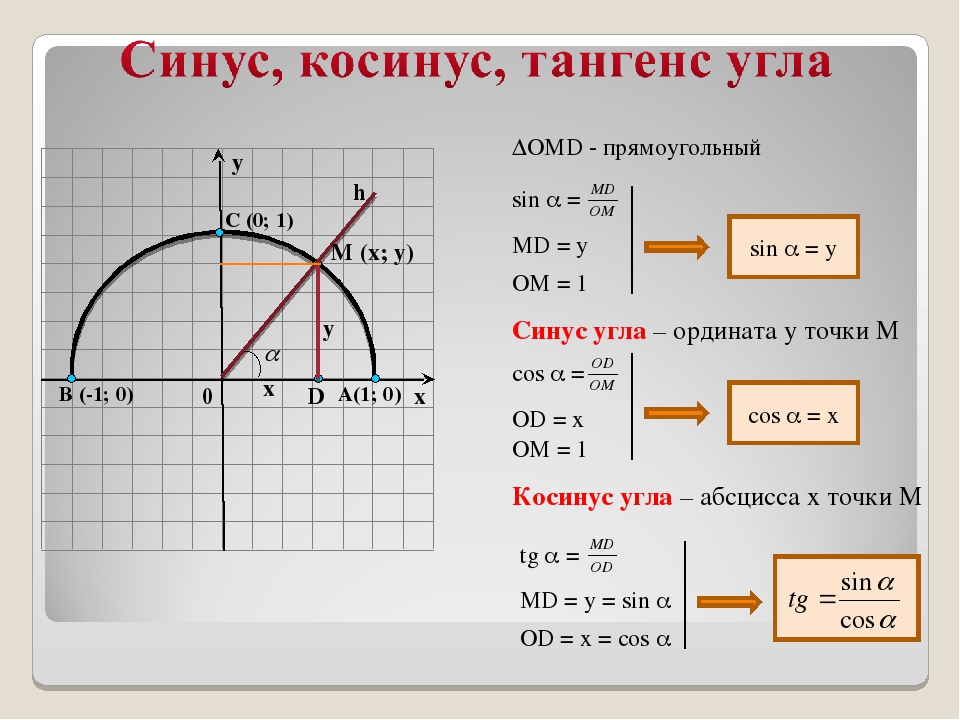 В тригонометрические соотношения специальные измерения прямоугольный треугольник (треугольник с одним
угол
измерение
90
°
).Помните, что две стороны прямоугольного треугольника, образующие прямой угол, называются ноги , а третья сторона (напротив прямого угла) называется
гипотенуза
.
В тригонометрические соотношения специальные измерения прямоугольный треугольник (треугольник с одним
угол
измерение
90
°
).Помните, что две стороны прямоугольного треугольника, образующие прямой угол, называются ноги , а третья сторона (напротив прямого угла) называется
гипотенуза
.
 )
)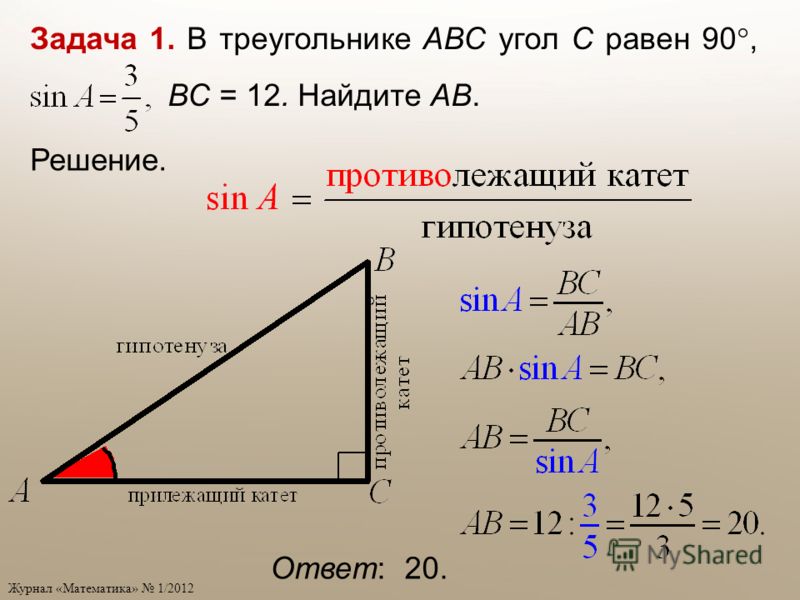
 Другой — равнобедренный прямоугольный треугольник. Они особенные, потому что с помощью простой геометрии мы можем узнать соотношение их сторон.
Другой — равнобедренный прямоугольный треугольник. Они особенные, потому что с помощью простой геометрии мы можем узнать соотношение их сторон. Для решения любой задачи, связанной с треугольником 30 ° -60 ° -90 °, ученик не должен использовать стол. Ученик должен нарисовать треугольник и указать числа отношения.
Для решения любой задачи, связанной с треугольником 30 ° -60 ° -90 °, ученик не должен использовать стол. Ученик должен нарисовать треугольник и указать числа отношения.




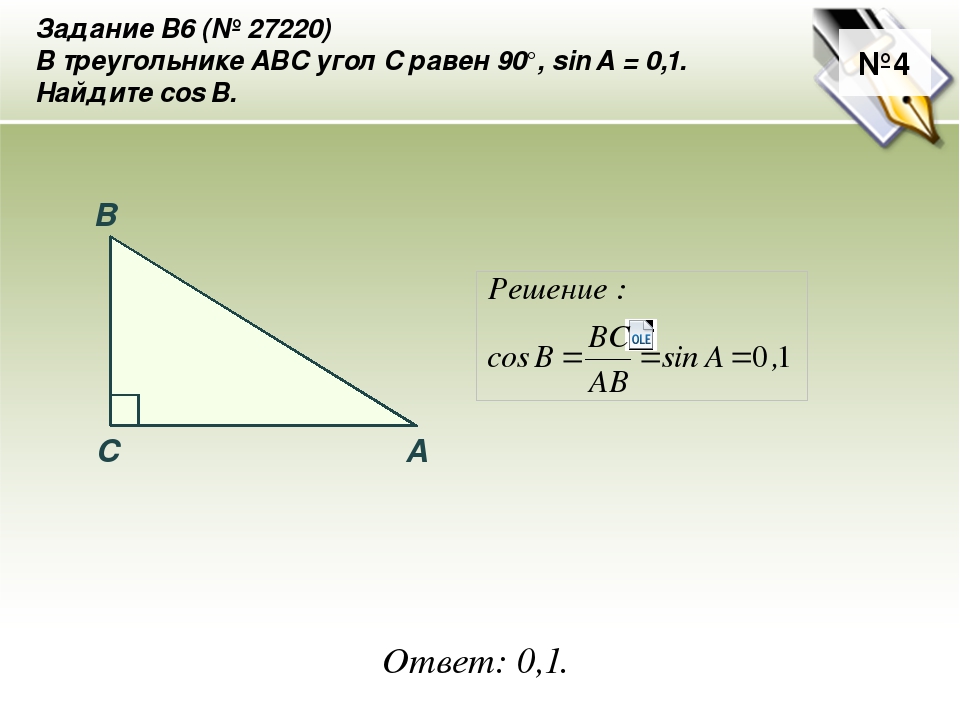 Проверьте значения 30 °, 60 ° и 45 ° — то есть посмотрите на два треугольника —
Проверьте значения 30 °, 60 ° и 45 ° — то есть посмотрите на два треугольника — x = 30 °.
x = 30 °.
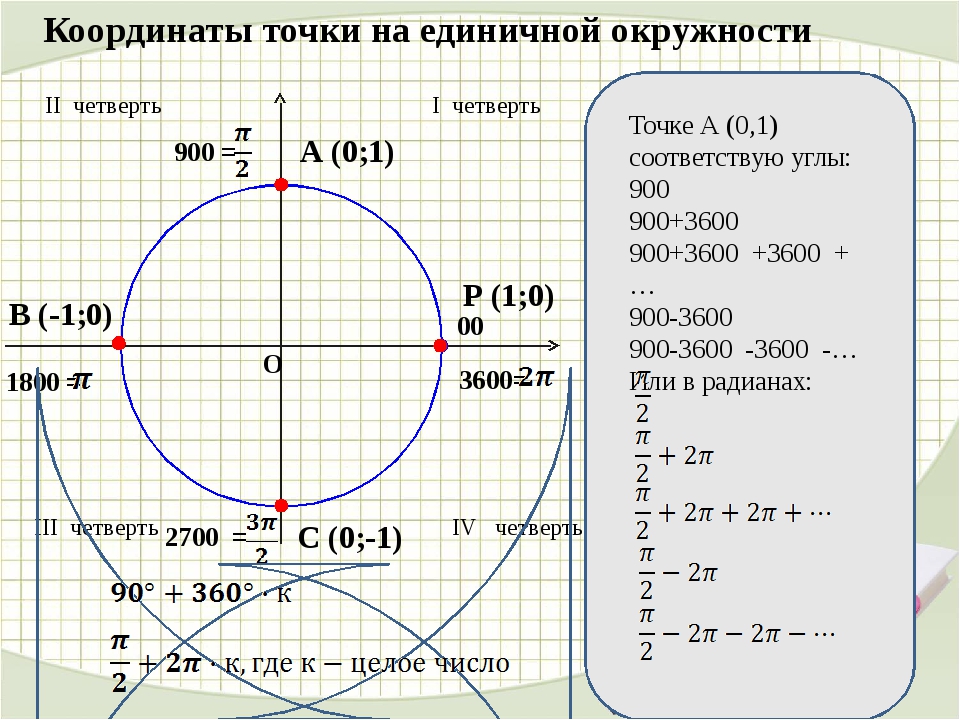
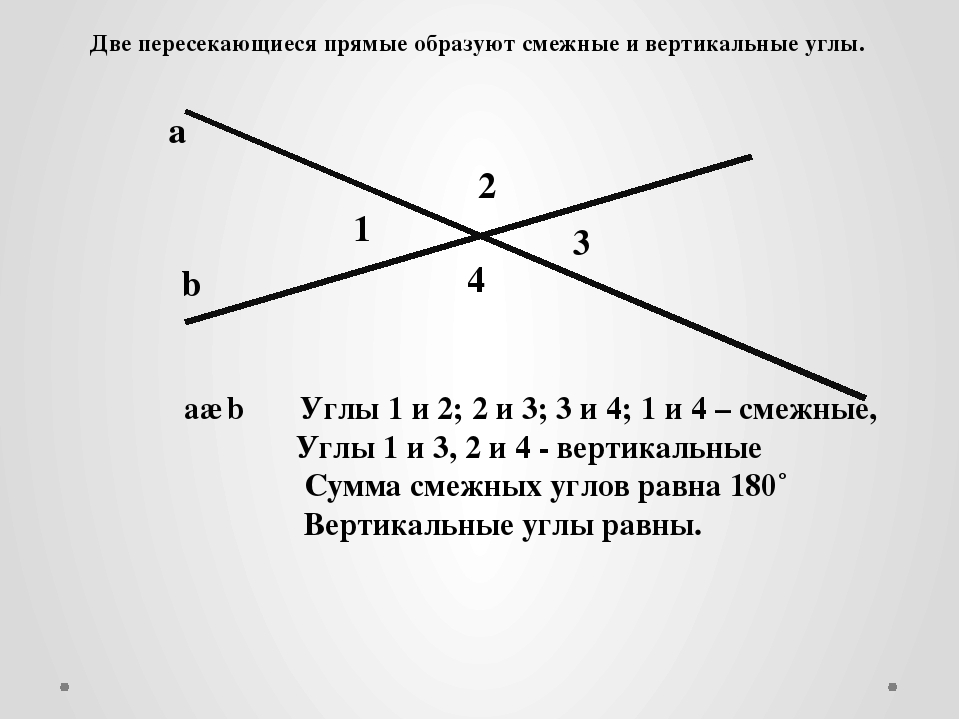


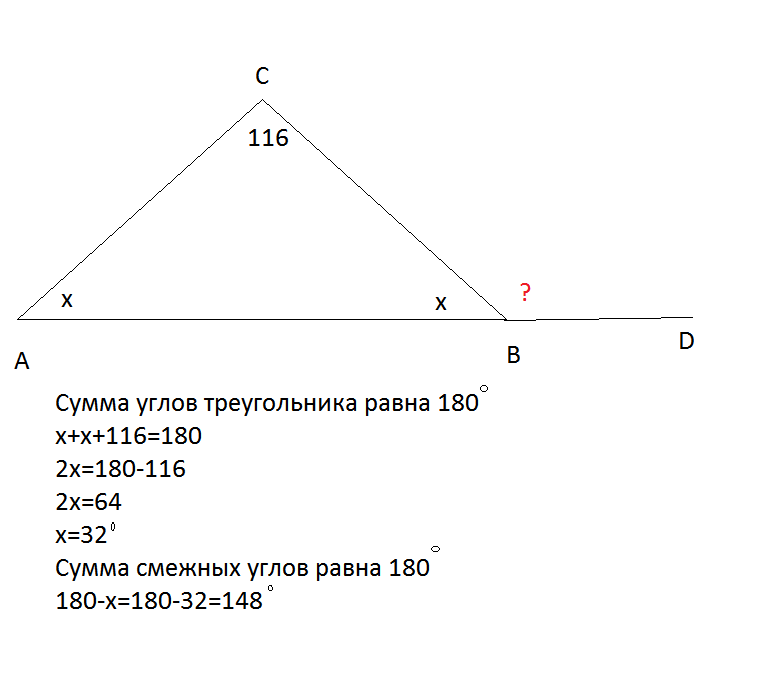 э. 2
э. 2 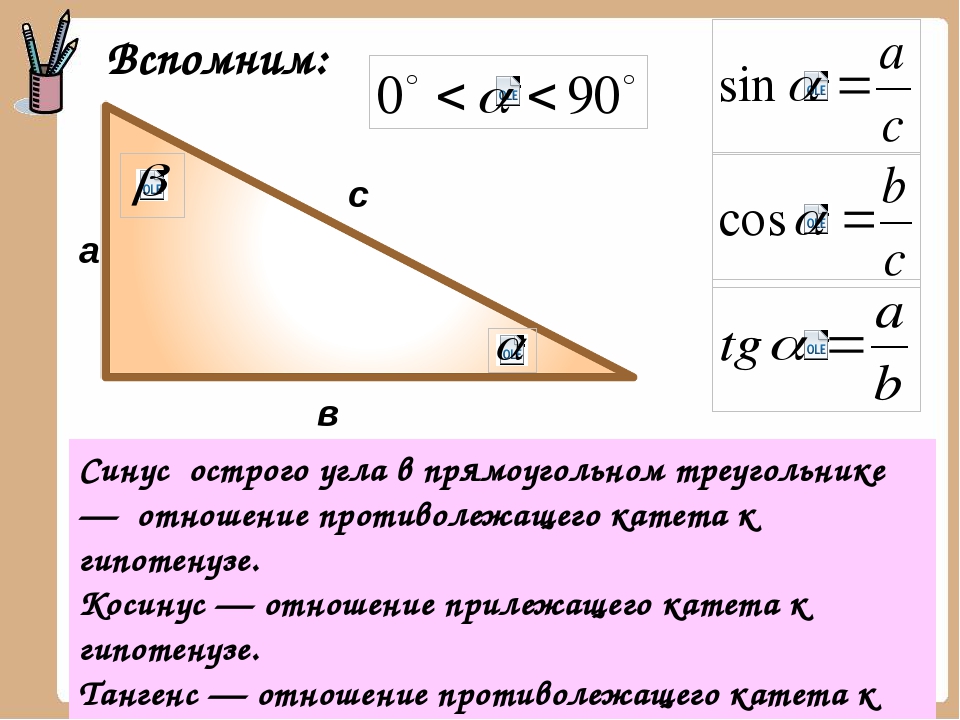
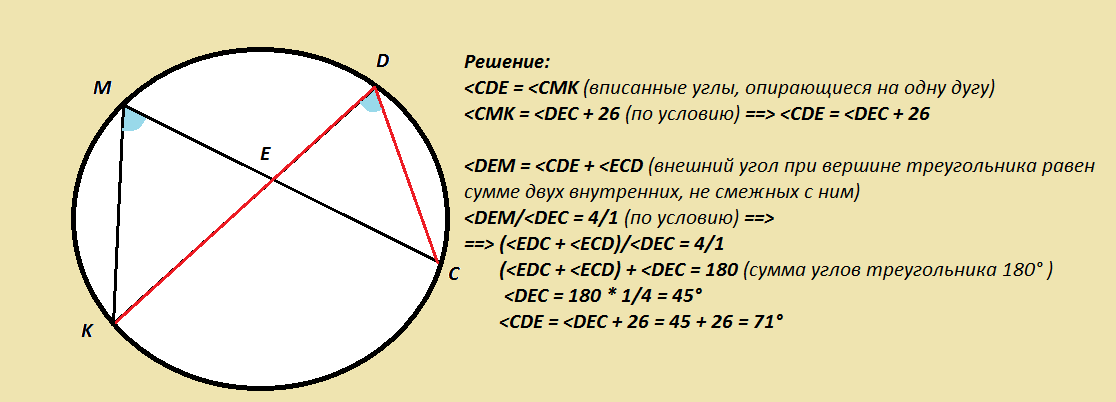 «Закон косинусов» из MathWorld — Интернет-ресурс Wolfram.
Закон косинусов.
«Закон косинусов» из MathWorld — Интернет-ресурс Wolfram.
Закон косинусов.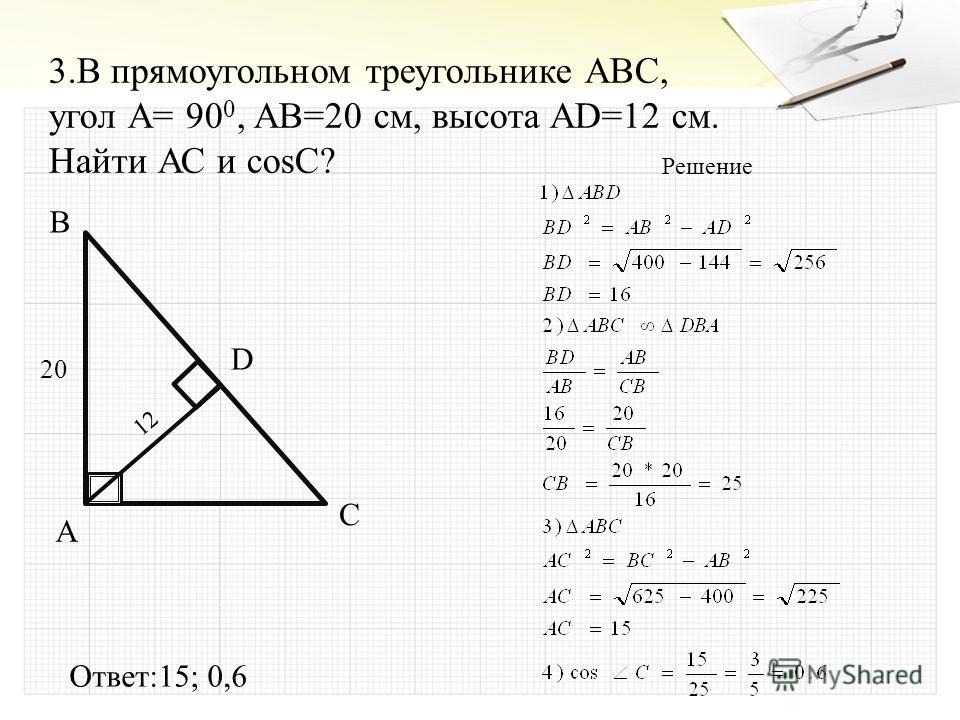
Leave A Comment