Линейная функция y = kx — урок. Алгебра, 7 класс.

Рассматривая линейную функцию вида \(y=kx + m\), особо выделяют случай, когда \(m=0\).

Тогда линейная функция принимает вид \(y=kx\).

Графиком линейной функции \(y=kx\) является прямая, проходящая через начало координат.

Важно уметь переходить от аналитической модели \(y=kx\) к геометрической и, наоборот, от геометрической к аналитической модели.

 

Например, рассмотрим прямую, изображённую на рисунке.

 

 

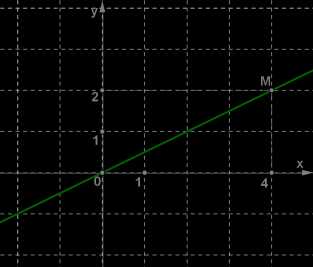
Эта прямая является графиком линейной функции \(y=kx\), так как проходит через начало координат. Нужно лишь определить значение коэффициента \(k\).

Из формулы линейной функции \(y=kx\) получим, что k=yx.

 

Поэтому для определения коэффициента \(k\) достаточно взять любую точку на прямой и найти отношение ординаты этой точки к её абсциссе.

 

Прямая проходит через точку \(M(4; 2)\), а для этой точки имеем 24=0,5. Значит, \(k=0,5\), и данная прямая является графиком линейной функции \(y=0,5x\).

 

График линейной функции \(y=kx\) обычно строят так: берут точку \((1; k)\) (если \(x = 1\), то из равенства \(y=kx\) выводим, что \(y=k\)) и проводят прямую через эту точку и начало координат.

Иногда вместо точки \((1; k)\) можно взять другую точку, более удобную.

От коэффициента \(k\) зависит угол, который построенная прямая образует с положительным направлением оси \(x\).

 

Если \(k>0\), то этот угол острый (как на первом рисунке), а

если \(k<0\), то этот угол тупой (как на втором рисунке).

 

Поэтому коэффициент \(k\) в записи \(y=kx\) называют угловым коэффициентом.

 

Обобщая сведения о линейных функциях, можно сделать вывод:

прямая, служащая графиком линейной функции \(y=kx + m\), параллельна прямой, служащей графиком линейной функции \(y=kx\).

 

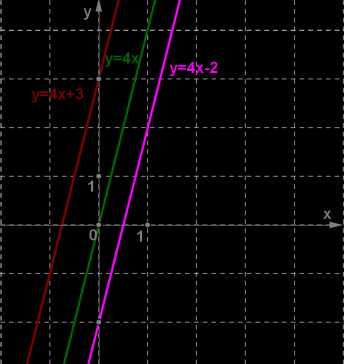
На рисунке показаны параллельные прямые с одним и тем же коэффициентом \(k = 4\).

Поэтому коэффициент \(k\) в записи \(y=kx + m\) также называют угловым коэффициентом, и

если \(k>0\), то прямая \(y=kx + m\) образует с положительным направлением оси \(x\) острый угол;

если \(k<0\), то этот угол тупой.

www.yaklass.ru

Функция у = кх ее свойства и график.

Цель работы: систематизировать и развивать у  учащихся знания      по  теме  функция,  ввести понятие области    определения   функции,     графика функции;   ввести понятие прямой пропорциональности.   Сформировать умение строить   и   читать график     функции,    заданной    формулой у = кх;   научиться определять: положение   графика   на    координатной плоскости,     принадлежность данной точки графику;    научиться  по   графику   задавать формулой прямую    пропорциональность;   способствовать развитию познавательного интереса учащихся

Просмотр содержимого документа
«Функция у = кх ее свойства и график.»

Урок 1 .

Функция у=кх

и ее график.

Учитель математики школы № 92

Павловская Нина Михайловна

  • систематизировать и развивать у учащихся знания

по теме функция, область определения функции,

график функции;

  • ввести понятие прямой пропорциональности;
  • сформировать умение строить и читать график

функции, заданной формулой у = кх;

  • научиться определять:

— положение графика на координатной плоскости,

— принадлежность данной точки графику;

  • научиться по графику задавать формулой прямую

пропорциональность;

  • способствовать развитию познавательного интереса

учащихся

  • побуждать учеников к само-, взаимоконтролю,

вызывать у них потребность в обосновании своих

высказываний.

Цели урока:

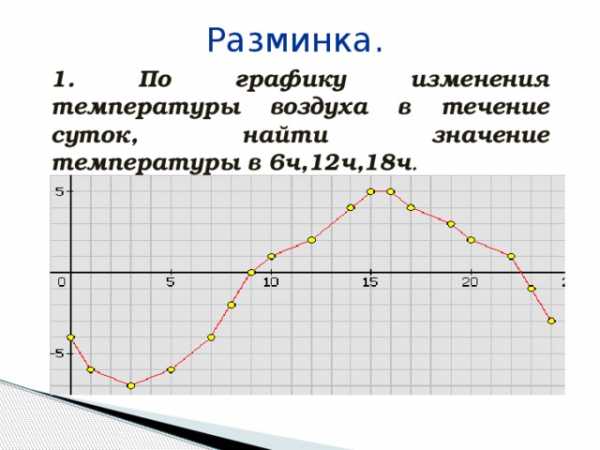
Разминка.

1. По графику изменения температуры воздуха в течение суток, найти значение температуры в 6ч,12ч,18ч .

2. Что называют областью допустимых значений переменной алгебраической дроби?

3. Найдите допустимые значения переменной для дроби:

а)

б)

г)

в)

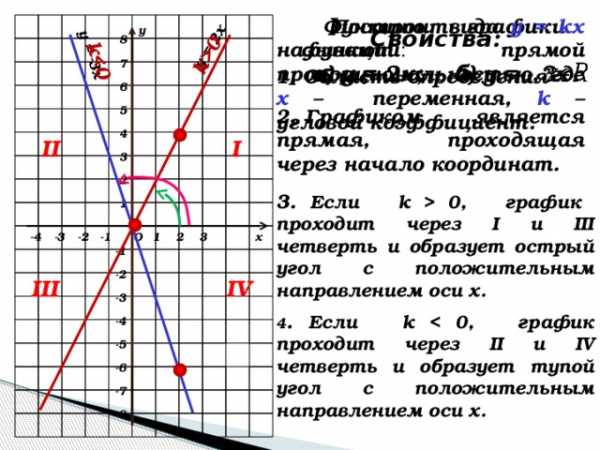0 k Функцию вида у = kх называют прямой пропорциональностью, где х – переменная, k – угловой коэффициент. Построить графики функций : у Свойства : 8 7 а) у = 2х; б) у = — 3х. 1. Область определения 6 5 2. Графиком является прямая, проходящая через начало координат. 4 II I 3 2 3. Если k 0, график проходит через I и III четверть и образует острый угол с положительным направлением оси х. 1 -3 -2 -1 3 2 1 х -4 О -1 -2 III IV -3 4 . Если k -4 -5 -6 -7 -8″

у = 2х

у = -3х

k0

k

Функцию вида у = kх называют прямой пропорциональностью, где х – переменная, k – угловой коэффициент.

Построить графики

функций :

у

Свойства :

8

7

а) у = 2х; б) у = — 3х.

1. Область определения

6

5

2. Графиком является прямая, проходящая через начало координат.

4

II

I

3

2

3. Если k 0, график проходит через I и III четверть и образует острый угол с положительным направлением оси х.

1

-3

-2

-1

3

2

1

х

-4

О

-1

-2

III

IV

-3

4

. Если k

-4

-5

-6

-7

-8

1 график вытягивается вдоль оси у. 2. Если |k| вдоль оси х.»

Построй графики функций в одной и той же системе координат. Найди особенность расположения графиков и сделай вывод.

а) у = 5х;

б) у = — 4х;

г) у = – 0,5х.

в) у = 0,2х;

Вывод:

  • Если |k|1 график вытягивается

вдоль оси у.

2. Если |k|

вдоль оси х.

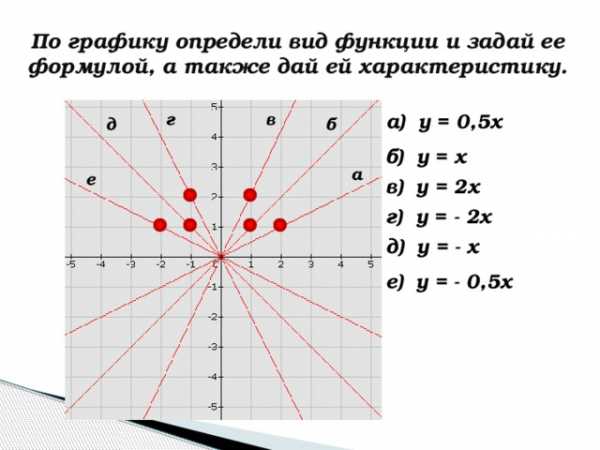
По графику определи вид функции и задай ее формулой, а также дай ей характеристику.

в

г

а) у = 0,5х

б

д

б) у = х

а

е

в) у = 2х

г) у = — 2х

д) у = — х

е) у = — 0,5х

Решить из учебника

  • Устно: № 490, 491.
  • Письменно: № 493, 494(а,в), 495(а,в)

Подведение итогов урока:

  • Что является графиком функции у = kх ?
  • Что называют угловым коэффициентом прямой у = kх ?
  • В каких координатных четвертях расположен график функции у = kх при k 0, при k 0?

 

Запишите домашнее задание:

п.6.1, 6.2 учебника,

№ 494(б, г), 495(б, г), 496.

№ 644 – по желанию.

kopilkaurokov.ru

Функция y=kx + b , её свойства и график !

Это линейная функция 1) Область определения — множество R 2) Область значений — множество R, если к не равно 0, а если к =0, то число b 3) При к не равно 0, функция ни парная ни непарная; если к =0, то функция парная; если b =0, то функция непарная 4) При к&gt;0 функция возрастает, при к &lt;0 функция убывает, при к =0 постоянная 5) Функция не имеет экстремумов 6) График — прямая, не проходящая через начало координат 7) При b =0 функция имеет вид у = кх. график — прямая, проходящая через начало координат

Обычная линейная функция, график — прямая

Это прямая, сдвинутая вправо (в сторону +) на величину b

y=kx+b При k&gt;0 y(x) строго монотонно возрастает; при k&lt;0 y(x) строго монотонно убывает; при k=0: y=b=const График y(x) — прямая. Этим уравнением описываются все прямые, за исключение вертикальных (Доказательство. Пусть прямая проходит через точки A(x1,y1) и B(x2,y2), x1&ne;x2. Подставляя в уравнение прямой y=kx+b, получаем систему линейных уравнений: {y1 = kx1 + b, {y2 = kx2 + b. Решая эту систему, получаем: k = (y2&minus;y1)/(x2&minus;x1), b = (x2*y1 &minus; x1*y2)/(x2&minus;x1).) Коэффициент k равен тангенсу угла наклона прямой к оси x b = y(o) &rArr; прямая пересекает ось y в точке (0;b) y=0 &rArr; x=&minus;b/k (k&ne;0). Прямая пересекает ось x в точке (&minus;b/k;0) <img src=»//otvet.imgsmail.ru/download/110a79559497dbdc98e649ce1160ca10_i-278.jpg» >

touch.otvet.mail.ru

8 класс. Алгебра. Квадратичная функция. Функция у = к/х. — Функция у =кх² , ее свойства и график.

Комментарии преподавателя

На данном уроке мы познакомимся с квадратичной функцией вида  и свойствами этой функции. Ранее мы уже знакомились с простейшей квадратичной функцией , сегодня же мы подробно рассмотрим влияние введенного коэффициента , рассмотрим принципиальные примеры, когда  и , и увидим закономерность построения параболы для таких двух случаев. Весь урок будет посвящен рассмотрению положительных значений коэффициента .

 Введение

Урок: Функ­ция , ее свой­ства и гра­фик

Еще в про­шлом году мы изу­ча­ли по­стро­е­ние гра­фи­ков про­стей­ших функ­ций:  (кон­стант­ная),  (ли­ней­ная),  (про­стей­шая квад­ра­тич­ная). На се­го­дняш­нем уроке мы рас­смот­рим услож­нен­ный ва­ри­ант квад­ра­тич­ной функ­ции , где ко­эф­фи­ци­ент  может быть каким угод­но чис­лом, на­при­мер,  или . Важно разо­брать­ся и по­нять, каким об­ра­зом этот ко­эф­фи­ци­ент вли­я­ет на по­стро­е­ние квад­ра­тич­ной функ­ции в част­но­сти и любой функ­ции в целом. На дан­ном уроке мы будем рас­смат­ри­вать толь­ко по­ло­жи­тель­ные зна­че­ния этого ко­эф­фи­ци­ен­та .

Изоб­ра­зим в одной си­сте­ме ко­ор­ди­нат (рис. 1) гра­фи­ки трех функ­ций:  (синий пунк­тир), 

www.kursoteka.ru

Методическая разработка по алгебре (7 класс) на тему: Линейная функция у=кх | скачать бесплатно

Разработка открытого урока по алгебре в 7 классе Годуновой Ирины Викторовны, учителя математики МБОУ «СШ № 11».

Линейная функция у=kx

Цели урока: (формирование УУД):

Личностные:

  • формирование у учащихся готовности и способности к самообразованию на основе мотивации к обучению и познанию;
  • формирование уважительного и доброжелательного отношения к другому человеку, его мнению;
  • формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в процессе учебно-исследовательской деятельности.

Метапредметные: развитие у учащихся умений:

  • находить  необходимую информацию;
  • анализировать информацию;
  • формулировать гипотезы;
  • устанавливать причинно-следственные связи, проводить умозаключение и делать выводы;
  • соотносить свои действия с планируемыми результатами.

Предметные: планируется, что к окончанию урока ученики будут распознавать линейную функцию у= kx, её график и задавать ее по принадлежащей графику этой функции точке.

способствовать развитию у обучаемых исследовательских умений и навыков; создать условия,

Тип урока:  урок «открытия» нового знания.

Форма урока:  урок-исследование.

Оборудование: проектор, компьютер; карточки для индивидуальной работы.

Ход урока:

I.Организационный момент. Здравствуйте, ребята! Сегодня на уроке у нас   присутствуют гости. Не волнуйтесь, т.к. «Дорогу осилит идущий, а математику — мыслящий»!

 II. Актуализация опорных знаний учащихся (УС на действия с дес.дробями) – 3 минуты.

 — Ребята, сейчас у нас, как обычно, тренаж устного счета на 3 минуты, Напоминаю, начинает опрос более сильный ученик. Соблюдайте рабочую обстановку, пож-ста!

 III. Актуализация опорных знаний учащихся (тренаж на знание определений) – 5 минут

— Ребята, сейчас у нас, как обычно, тренаж по изученной теме на 5 минут. Напоминаю, начинает опрос более сильный ученик. Соблюдайте рабочую обстановку, пож-ста!

(актуализировать знания учащихся, необходимые для «открытия нового знания»: определение линейной функции, значение коэффициентов m и  k; график линейной функции)

— Итак, с помощью тренажа вы напомнили друг другу, теперь напомните мне:

  • определение линейной функции, (учитель записывает на доске уравнение линейной функции у=kx+m)
  • что является графиком линейной функции? (прямая)
  • как влияет значение коэффициента k на возрастание и убывание функции (при k>0 функция у=kx+m возрастает, а при k
  • как располагается график линейной функции при k=0 (он расположен параллельно оси абсцисс)

     IV. Изучение нового материала.

 — как выглядит уравнение, задающее линейную функцию, если m=0?

— сформулируйте тему урока, запишите её в тетрадях (и на доске): «Линейная функция у=kx»(СЛАЙД1)

 — Давайте придадим коэффициенту k некоторые конкретные значения и построим соответствующие графики. Возьмём одно значение k положительное, например 2, другое отрицательное, пусть это будет -3, а третье дробное 1/2. Получим функции: у = 2х, у = -3х, у = 0,5х.

 — Давайте с помощью нашего алгоритма построим графики этих функций (3 ученика у доски строят на заранее начерченных координатных плоскостях ХОУ)

 — Сверим построенные графики с графиками на слайде (СЛАЙД 2)

—  Что интересного можно заметить на рисунках? (:На всех изображены прямые, проходящие через начало координат.) И такое расположение не зависело от выбора коэффициента k.  Таким образом, что является графиком функции у = kх ? (Графиком функции у = kх является прямая, проходящая через начало координат.) 

— Иногда математики такой вид линейной функции называют прямой пропорциональностью. Что это значит? (Это значит, что если мы в несколько раз увеличиваем х, то во столько же раз увеличивается у). В обычной жизни какие из примеров являются прямой пропорциональностью (СЛАЙД 2)?

 — Давайте снова внимательно посмотрим на построенные нами прямые. На каких из них функция возрастает и что влияет на возрастание и убывание функции? (На 1 и 3 рисунке изображены графики возрастающих функций, у которых коэффициент k положительный:  k = 2 и k = 0,5).

— Верно: если двигаться вдоль графика слева направо, то мы как бы поднимаемся вверх. В таком случае математики говорят, что функция возрастает и бОльшему значению аргумента соответствует бОльшее значение функции. (А на втором рисунке изображён график убывающей функции, у которой коэффициент k отрицательный:  k = — 3).

 — Верно, Если двигаться вдоль этого графика слева направо, то мы как бы опускаемся вниз. В этом случае говорят, что функция убывает и бОльшему значению аргумента соответствует меньшее значение функции. 

Так как прямая пропорциональность является частным случаем линейной функции, то и у прямой пропорциональности знак коэффициента k влияет на возрастание и убывание функции. Кроме того, от него зависит угол, который составляет прямая с положительным направлением оси x.

В случае возрастания функции этот угол острый, в случае убывания – тупой. Поэтому математики называют коэффициент k – угловым коэффициентом. (Я отмечаю на доске углы, а все – в тетрадях! И пишут: K – угловой коэффициент.)

График функции y=kx располагается во 1 и 3 координатных углах при k >0

График функции y=kx располагается во 2 и 4 координатных углах при kЯ отмечаю на доске четверти, а все – в тетрадях!) (СЛАЙД 4)

V. Физминутка!!!

Быстро встали, улыбнулись,

Выше-выше потянулись,

Ну-ка плечи распрямите,

Поднимите, опустите,

Вправо, влево повернитесь,

Рук коленями коснитесь.

Сели, встали, сели, встали

И на месте побежали!

VI. Выполнение упражнений.

1. Примеры по теме урока.

Пример 1. Построить график функции у =  — 0,2х, используя уже измененный наш алгоритм (я раздаю клише-алгоритм).

— Что в нем изменилось? (если m=0, то вторую точку искать не нужно)

(ученик – у доски, все – в тетрадях)

1.Так как это линейная функция, то графиком будет являться прямая.

2.Поскольку коэффициент m=0, то прямая будет проходить через начало координат.

3.Причём k 

4.Для построения графика нам необходимо, кроме точки (0;0), найти ещё одну точку.

Пусть х = 5, тогда у =- 0,2·5= — 1.

Через точки (0; 0) и (5; — 1) проведём прямую.

Пример 2. Записать уравнение прямой, проходящей через начало координат и точку с координатами (2;8).

Так как прямая проходит через начало координат, то функция будет задана формулой у = kх. Поскольку прямая проходит через точку (2;8), то её координаты удовлетворяют этому уравнению. Подставим число 2 вместо х и число 8 вместо у. Получим 8 = k ∙ 2, отсюда k = 4. Значит уравнение прямой будет иметь вид: у = 4х.

 

2. Устная работа (слайды)

1.Найди ошибку в построении графика: (слайд 3) 

2. Задание: найти соответствующие формулам графики.  (слайд 4)

  1. у = 3
  1. у = 3х
  1. у = -2х-2
  2. у = -3х

3. Письменная работа

№ 9.1(а,б), № 9.6(а).

А теперь самостоятельно постройте графики функций:

1 вариант: 9.1(а)

2 вариант: 9.1(б) 

А теперь обменяйтесь тетрадями и сверьтесь с построенными графиками на слайде (СЛАЙД 5)

№ 9.6(а) Задайте лин.ф-цию ф-лой s=kt, если известно, что ее график проходит через точку А(5;7)

Решение: 7=к∙5     к==1=1,4      S=1,4t

VII. Подведение итогов урока

Еще раз давайте повторим:

— Какую функцию мы сегодня рассмотрели на уроке? (мы рассмотрели частный случай линейной функции, а именно прямую пропорциональность у = kх)

— Что влияет на возрастание и убывание прямой пропорциональности и как эта величина называется? (Угловой коэффициент. Если он >0, то ф-ция возрастает, а если

 —  Почему коэффициент к называют угловым? (потому, что от него зависит угол, который составляет прямая с положительным направлением оси Ох. Если ф-ция возрастает, то он острый, а если убывает, то он тупой.)

— Чему научились? (строить графики прямой пропорциональности и задавать функцию формулой по принадлежащей ее графику точке)

 — Что показалось особенно трудным?

VIII. Рефлексия.

1. Оцените свою деятельность на уроке: большой палец — вверх, если вы все поняли, или — вниз, если не все понятно.

2. Выставление оценок за урок в журнал.

IX. Домашнее задание: (учитель записывает на доске: 9.1(в), 9.6(в),

                                                                                           «на 4 и 5 – 9.14(в)»).

nsportal.ru