Тригонометрия задания: Задачи с тригонометрическими функциями — задачи с решениями

Задачи с решением — Тригонометрические уравнения

1.       Решить уравнение cos2x = 1/2.

Используем метод решения простейших тригонометрических уравнений и получаем:

2x = ±arccos(1/2) + 2πn = ±π/3 + 2πn (здесь и далее, n ∈ Z).

Откуда x = ±π/6 + πn.

Ответ: x = ±π/6 + πn.

2.       Решить уравнение sin(3 — 2x) = -1/2.

Используем формулу из методов решений, имеем:

3 — 2x = (-1)n(arcsin(-1/2)) + πn = (-1)n(-π/6) + πn (здесь и далее n ∈ Z).

Делаем преобразование и получаем x = 3/2 + π/12(-1)n — πn/2.

Ответ: x = 3/2 + π/12(-1)n — πn/2.

3.       Решить уравнение cos2x — 3sinx = 2.

 

Воспользуемся формулой удвоенного угла косинуса (cos2a = 1 — 2sin2a) и получим:

1 — 2sin2x — 3sinx = 2.

Воспользуемся методом замены, обозначим sinx = y. Уравнение примет вид:

2y2 + 3y + 1 = 0.

Находим его корни: y1 = -1, y2 = -1/2.

Возвращаемся к исходной переменной и получаем совокупность sinx = -1 и sinx = -1/2.

Из первого получаем решение — x = -π/2 + 2πn, из второго — x = (-1)m(-π/6) + πm (m, n ∈ Z).

Ответ: x = -π/2 + 2πn или x = (-1)m(-π/6) + πm.

4.       Решить уравнение 2tgx — 3ctgx = 1.

Так как ctgx = 1/tgx при x ≠ πn/2 (n ∈ Z) получаем уравнение

2tgx — 3/tgx = 1 или 2tg2x — tgx — 3 = 0.

Вводим новую переменную tgx = y и решаем квадратное уравнение 2y2 — y — 3 = 0 относительно y.

Оно имеет два решения y1 = 3/2, y2 = -1.

Возвращаемся к исходной переменной и решаем два уравнения:

tgx = 3/2, откуда x = arctg(3/2) + πn, n ∈ Z.

tgx = -1, откуда x = arctg(-1) + πm = -π/4 + πm, m ∈ Z.

Ответ: x = arctg(3/2) + πn или x = -π/4 + πm.

5.       Решить уравнение 3cosx — sin2x = 1 — sin3x.

Сделаем следующее преобразование 3(cosx + sinx) = 1 + sin2x.

Замена cosx + sinx = t приведет к уравнению 3t = t2. Оно имеет корни t1 = 0, t2 = 3.

Берем первый корень, возвращаем замену и получаем cosx + sinx = 0, делим на cosx ≠ 0, откуда tgx = -1, x = -π/4 + πn (n ∈ Z).

Второй корень t2 дает уравнение cosx + sinx = 3. Это уравнение не имеет решений, т.к. и cosx, и cosx меньше равны 1, в сумме меньше равны 2.

Ответ: x = -π/4 + πn.

6.       Решить уравнение cos2x + cos4x + cos6x = 0.

Проделаем следующие преобразования

(cos2x + cos6x) + cos4x = 0;

2cos4xcos2x + cos4x = 0;

cos4x(2cos2x + 1) = 0.

Имеем два случая:

cos4x = 0, откуда 4x = π/2 + πn, x = π/8 + πn/4 (n

Тригонометрия для чайников. Урок1. Тригонометрия с нуля

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

 

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

 

Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

 

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат. 

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

 

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).

 

Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.

Рассмотрим прямоугольный треугольник AOB:

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

 

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

 

Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x.  (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.

 

Координата по оси x – косинус угла, координата по оси y – синус угла.

Пример:

cos 150 ° = − 3 2

sin 150 ° = 1 2

 

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.

 

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

 

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

 

	0°	30°	45°	60°	90°
sinα	0	12	22	32	1
cosα	1	32	22	12	0
tgα	0	33	1	3	нет
ctgα	нет	3	1	33	0

 

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

 

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

 

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

 

Рассмотрим тупой угол β:

 

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

 

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

 

a sin ∠ A = b sin ∠ B = c sin ∠ C

 

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

 

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

 

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

 

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

 

Модуль геометрия: задания, связанные с тригонометрией.

 

Скачать домашнее задание к уроку 1.

 

Урок 3: Задачи тригонометрические — 100urokov.ru

План урока:

Основное тригонометрическое тождество

Тригонометрические функции суммы и разности

Формулы двойного угла

Формулы понижения степени

Формулы приведения

Сумма тригонометрических функций

Произведение тригонометрических функций

 

Основное тригонометрическое тождество

Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:

Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:

АВ² + ОВ² = ОА²

Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:

sin²α + соs²α = 1

Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.

 

Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?

Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:

sin²α + соs²α = 1

0,8² + соs²α = 1

0,64 + соs²α = 1

соs²α = 1 – 0,64

соs²α = 0,36

соsα = – 0,6 или соsα = 0,6

Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.

Ответ: 0,6.

 

Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:

По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.

 

Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит

IV четверти.

Решение.

sin²α + соs²α = 1

0,28² + sin²α = 1

0,0784 + sin²α = 1

sin²α = 1 – 0,0784

sin²α = 0,9216

sin α = –0,96 или sin α = 0,96

Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.

Ответ: – 0,96.

 

Задание. Найдите tgα, если

sinα = 5/13 и π/2 < α < π.

Решение. Здесь задача уже в два действия! Сначала определим соsα:

sin²α + соs²α = 1

соs²α = 1 – sin²α = 1 – (5/13)² = 169/169 – 25/169 = 144/169

соsα = – 12/13 или соsα = 12/13

Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.

Далее находим тангенс, просто деля синус на косинус:

tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12

Ответ: 5/12

 

Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.

Запишем тождество

sin²α + соs²α = 1

Далее поделим его на величину соs²α:

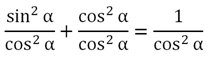
Крайнее левое слагаемое – это величина tg²α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:

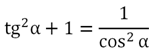
В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin

2α:

 

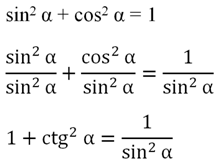
Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.

Решение.

Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:

Так как угол относится к III четверти, где косинус отрицателен, то

соsα = – 0,8

Синус угла найдем, используя основное тригон-кое тождество:

sin²α + соs²α = 1

sin²α = 1 – соs²α = 1 – (– 0,8)² = 1 – 0,64 = 0,36

sinα = – 0,6 или sinα = 0,6

С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6

Ответ: sinα = – 0,6; соsα = – 0,8.

 

Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin²α + соs²α = 1 несложно получить из выражения

sin²α = 1 – соs²α

и

соs²α = 1 – sin²α

которые помогают в работе с длинными ф-лами.

 

Задание. Упростите выражение

4sin²α + 9соs²α – 6

таким образом, чтобы в нем не содержалось синуса.

Решение. Произведем замену sin²α = 1 – соs²α:

4sin²α+ 9соs²α – 6 = 4(1 – соs²α)+ 9соs²α – 6 =

= 4 – 4 соs²α + 9соs²α – 6 = 5соs²α – 2

Видим, что получилось значительно более простое выражение.

Ответ: 5соs²α – 2.

 

Задание. Избавьтесь от синуса в выражении

sin⁴α – соs⁴α

Решение. Воспользуемся ф-лой разности квадратов:

sin⁴α – соs⁴α = (sin²α – соs²α)(sin²α + соs²α) = (sin²α – соs²α)•1 =

= 1 – соs²α– соs²α = 1 – 2 соs²α

Ответ:1 – 2 соs²α.

 

Задание. Упростите дробь

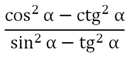
Решение.

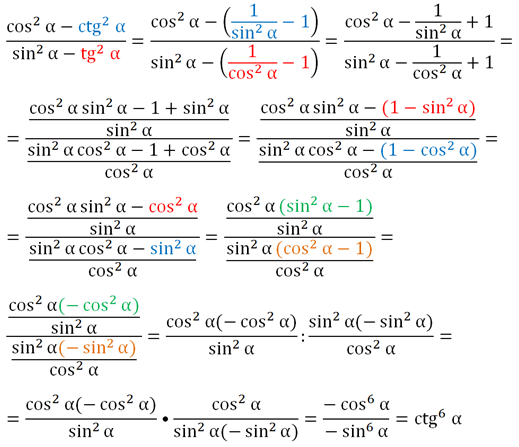
Ответ: ctg⁶α.

Для достижения наилучшего результата важно структурировать знания. В этом вам помогут онлайн-курсы по математике

Перейти

 

Тригонометрические функции суммы и разности

Легко проводить вычисления, когда все тригонометрические действия выполняются над одним углом α. Однако иногда в задачах добавляется ещё один угол, который обычно обозначают как β. Существуют ф-лы, с помощью которых можно вычислять тригон-кие ф-ции от суммы и разности углов α и β.

Вывод этих ф-л достаточно сложен, поэтому сначала мы просто без доказательства приведем две из них, позволяющие вычислять синус суммы и косинус суммы:

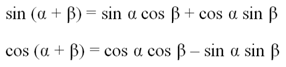
Достаточно запомнить их, а далее следующие формулы можно выводить из них. Так, если вместо β подставить угол (–β), то получим формулы для разности. При этом мы используем тот факт, что синус – нечетная ф-ция, то естьsin (– β) = – sinβ, а косинус – четная ф-ция, то есть соs (– β) = соsβ:

Теперь поступим также с ф-лой для косинуса разности:

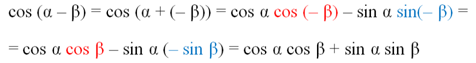
Итак, нам удалось получить ф-лы для нахождения синуса и косинуса суммы и разности углов.

С помощью этих формул возможно вычислить значение тригон-ких ф-ций для некоторых нестандартных углов. (Стандартными считаются углы в 0°, 30°, 45°, 60° и 90°, ведь для них значение тригон-ких ф-ций можно узнать из таблички.)

 

Задание. Вычислите соs 150°.

Решение. В табличке стандартных углов есть углы, равные 90° и 60°. Их сумма как раз равна 150°. Поэтому запишем:

 

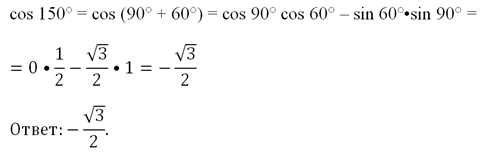
Задание. Вычислите синус, косинус и тангенс для угла 15°.

Решение. Угол в 15° можно представить как разность 45° – 30°. Тогда синус будет вычисляться так:

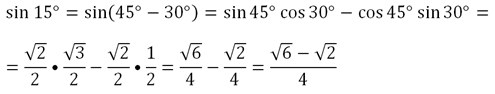
Далее вычислим косинус:

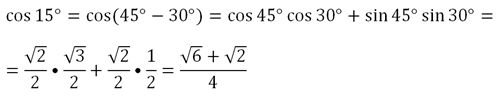
Можно выполнить проверку. Полученные значения должны удовлетворять основному тригон-кому тождеству. И действительно:

Проверка пройдена: сумма квадратов синуса и косинуса оказалась равной единице. Теперь посчитаем tg 15°, используя определение тангенса:

 

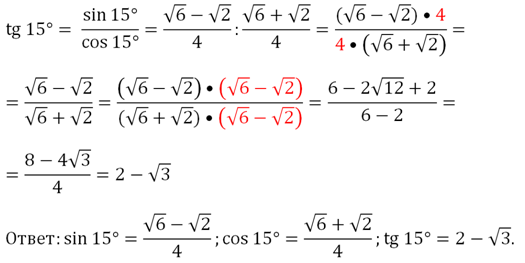
Задание. Вычислите значение тригонометрического выражения

sinπ/7 соsπ/42 + sinπ/42 соsπ/7

Решение: Значение тригон-ких ф-ций для углов π/7 и π/42 мы не знаем, однако это не помешает вычислениям. Можно заметить, что исходное выражение представляет собой синус суммы π/7 и π/42:

sinπ/7 соsπ/42 + sinπ/42 соsπ/7 = sin (π/7 + π/42) = sinπ/6 = 1/2

Ответ: 1/2.

 

Задание. Упростите выражение

Решение.

Вынесем за скобки множитель 2:

Теперь произведем замену:

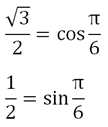
C учетом этого можно переписать выражение и использовать ф-лу суммы косинусов:

Ответ: 2соs (π/6 + α).

 

Формулы двойного угла

Что будет, если формулу синуса суммы подставить не два различных угла α и β, а два одинаковых угла α и α? Получится ф-ла для синуса двойного угла:

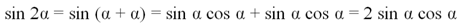
Аналогично можно составить ф-лу и для косинуса двойного угла:

Итак, справедливы следующие ф-лы:

 

Задание. Вычислите sin 120° и соs 120°.

Решение.

 

Задание. Упростите выражение

соs²t– соs 2t

Решение.

соs²t – соs 2t = соs²t – (соs² t – sin²t) = соs²t – соs² t + sin²t = sin²t

Ответ: sin²t.

 

Задание. Докажите, что функция

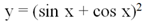
является периодической и имеет период, равный π.

Решение. Используем ф-лу квадрата суммы:

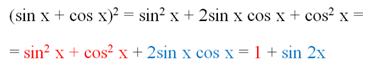
Таким образом, исходную ф-цию можно переписать в виде

у = 1 + sin 2x

По определению, ф-ция является периодической с периодом Т, если выполняется условие у(х + Т) = у(х). Поэтому подставим в нашу ф-цию величину х + π:

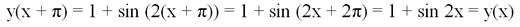
Получили, что у(х + π) = y(x), то есть ф-ция имеет период, равный π.

 

Задание. Выведите формулы синуса и косинуса тройного угла.

Решение. Для их получения следует использовать ф-лу синуса суммы углов, в которую подставляют вместо β величину 2α:

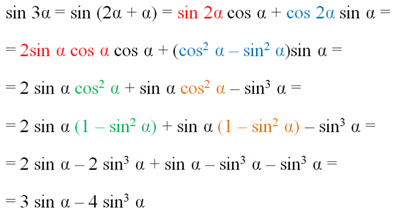
Аналогично можно получить и ф-лу для косинуса тройного угла:

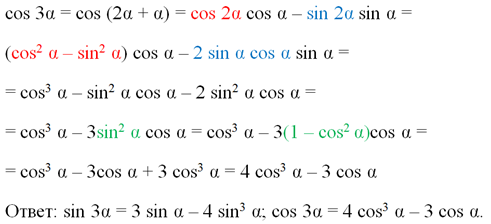
Эффективно подготовиться к ЕГЭ по математике помогут тщательно продуманные онлайн-курсы

Перейти

 

Формулы понижения степени

Если нам необходимо узнать косинус угла, который вдвое больше табличного, мы используем ф-лу:

соs 2α = соs²α – sin²α

А что делать, если нам надо вычислить косинус угла, который вдвое меньше известного? Попробуем преобразовать ф-лу косинуса двойного угла:

В результате нам удалось получить тождество, позволяющее по косинусу удвоенного угла найти косинус самого угла! Однако значительно чаще в тригонометрии это равенство записывают в обратном порядке:

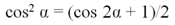
и называют ф-лой понижения степени. Действительно, в левой части стоит косинус в квадрате, а справа – косинус без квадрата, но вычисляется он от угла 2α, а не α.

Попробуем получить аналогичную ф-лу и для синуса. Для этого используем основное тригон-кое тождество:

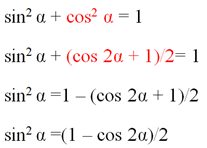
С помощью этих ф-л можно вычислять тригон-кие ф-ции для некоторых малых углов. Так, ранее мы с использованием ф-лу разности синусов определили, что

При этом мы представляли угол 15° как разность 45° – 30°. Но как посчитать соs 7,5°? Этот угол невозможно представить как разницу или сумму известных нам табличных углов (0°, 30°; 45°; 60° и 90°). Однако поможет ф-ла понижения степени. Действительно, ведь 2•7,5° = 15°. Тогда можно записать:

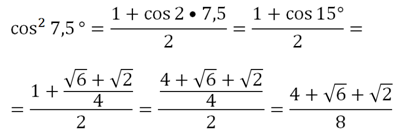
Мы нашли соs² 7,5°. Чтобы узнать соs 7,5°, необходимо извлечь квадратный корень:

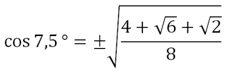
Так как угол 7,5° принадлежит I четверти, то его косинус должен быть положительным, поэтому можно записать:

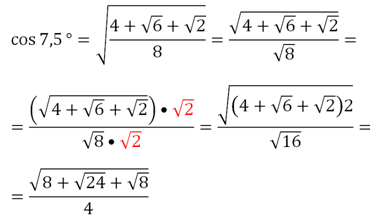
Видно, что получается довольно громоздкое выражение. Используя ф-лу понижения степени, можно найти косинус и угла, который ещё вдвое меньше, то есть равен 3,75°, но в результате получится ещё более громоздкое выражение.

 

Задание. Вычислите sinπ/8.

Решение. Угол π/4 является табличным (его градусная мера составляет 45°). Поэтому можно записать:

Эти примеры показывают, что тригон-кие ф-ции многих нестандартных углов можно выразить, используя квадратные корни. Возникает вопрос – а любую ли тригонометрическую ф-цию можно выразить таким способом? Оказывается, что нет. Например, sin 10° невозможно найти ни в одной, даже самой подробной тригонометрической таблице. Мы не будем это доказывать, но эту величину невозможно представить в виде выражения, используя арифметические операции и корни. Однако существуют приближенные методы, позволяющие с любой наперед заданной точностью вычислять значение тригонометрических ф-ций.

Формулы приведения

Возможно, вы уже заметили, что синусы и косинусы принимают одинаковые значения в углах, чья сумма равна 90°. Например, sin30° = соs60° = 1/2, и при этом 30° + 60° = 90°. Также мы знаем, чтоsin 45° = соs 45° (45° + 45° = 90°) и sin60° = соs30° (60° + 30°). В чем причина такой закономерности и справедлива ли она для нестандартных углов?

Используя ф-лу синуса разности, мы можем записать, что

Полученная ф-ла sin (90° – α) = соsα называется формулой приведения. При ее выводе мы использовали тот факт, что sin 90° = 1, а соs 90° = 0, поэтому формула получилась очень простой. Однако синусы и косинусы других углов, кратных 90° (или кратных π/2, если измерять углы в радианах), также равны 0, 1 или – 1, поэтому для них тоже можно получить подобные простые ф-лы, например:

Похожих ф-л можно написать несколько десятков! Все их запоминать не надо, так как существует особое мнемоническое правило, позволяющее записать необходимую ф-лу.

Пусть есть некоторое тригон-кое выражение вида

f(k ± α)

где f – тригонометрическая ф-ция (sin; соs; tg; ctg)

k– угол, кратный π/2 (π/2, π, 3π/2, 2π)

Мы хотим заменить ее другой ф-цией, только от угла α. На первом шаге мы смотрим на слагаемое k. Если оно кратно π (– π, π, 2π), то ф-ция f остается неизменной. Если же слагаемое k – это число π/2 или 3π/2, то ф-цию f надо поменять на так называемую кофункцию (синус меняем на косинус, тангенс на котангенс и наоборот).

Далее надо определить знак, стоящий перед новой ф-цией. Для этого мы предполагаем, что α – это острый угол, то есть он принадлежит I четверти. Далее с учетом этого предположения смотрим, в какую четверть попадает угол k ± α, и какое значение принимает там исходная тригонометрическая ф-ция. Если она отрицательна, то перед новой тригонометрической ф-цией надо поставить минус. В противном случае ничего ставить не надо.

Лучше всего изучить это алгоритм на примерах.

 

Задание. Упростите выражение соs (π/2 + α).

Решение. Первый шаг – смотрим на слагаемое под знаком косинуса. Это число π/2. Оно НЕ кратно π, а потому мы должны поменять косинус на синус:

sinα

Второй шаг – надо определить, надо ли ставить минус перед синусом. Если α – это острый угол, то угол (π/2 + α) попадет во II четверть:

Во второй четверти косинус отрицателен, а потому перед синусом следует поставить минус:

соs (π/2 + α) = – sinα

Ответ: – sinα.

 

Важное примечание. В этом примере для составления формулы приведения мы «предположили», что угол α является острым. В результате нам удалось получить формулу соs (π/2 + α) = – sinα. Однако отметим, что полученная нами формула выполняется для абсолютно любых значений угла α, а не только для 0° < α < 90°. Предположение об остроте угла – это лишь часть мнемонического правила для составления формул приведения, позволяющая быстро определить, надо ли в ней перед тригонометрической функцией ставить знак минус или не надо.

Это мнемоническое правило работает абсолютно точно, однако надо понимать, что всё-таки для строгого вывода формул приведения следует использовать формулу косинуса суммы

соs (π/2 + α) = cosπ/2 cos α – sin π/2 sin α = 0•cos α – 1•sin α = – sin α

Получили тот же результат, что и с помощью формулы приведения. При этом нам не потребовалось предположение об остроте угла α, то есть формула верна для любых α. Но практика показывает, что люди просто не могут запомнить формулу косинусов суммы. Поэтому для «упрощения жизни» школьникам рассказывают об относительно простом мнемоническом правиле.

 

Задание. Составьте ф-лу приведения для выражения tg (α – π).

Решение. Сначала смотрим на слагаемое под знаком тангенса. Это число (– π), кратное π. Поэтому сама ф-ция не меняется на кофункцию:

tgα

Примем, что угол α принадлежит I четверти, тогда угол α – π будет ему противоположен и окажется в III четверти:

Тангенс в III четверти положителен. Значит, минуса перед тангенсом ставить не надо:

tg (α– π) = tgα

 

Задание. Вычислите sin 7π/6.

Решение. Представим угол 7π/6 как сумму: 7π/6 = π + π/6. Получается, нам надо вычислить величину sin (π + π/6). Составим ф-лу приведения для выражения π + α Так как в скобках стоит слагаемое π, то ф-ция sin остается, а не меняется на косинус:

sinα

Угол (π + α) относится к III четверти, где синус отрицателен. Следовательно, надо добавить знак минус:

sin (π + α) = – sinα

Остается подставить вместо α величину π/6:

sin (π + π/6) = – sinπ/6 = – 1/2

Ответ: – 1/2.

 

Задание. Чему равен ctg7π/4?

Решение. Угол 7π/4 можно представить как 3π/2 + π/4. Найдем ф-лу приведения для ctg (3π/2 + α). Из-за слагаемого 3π/2, не кратного π, ф-ция должна измениться с котангенса на тангенс:

ctg (3π/2 + α) = tgα

Угол 3π/2 + α попадает в IV четверть, где котангенс отрицателен. Поэтому необходимо добавить знак минуса перед ф-цией:

ctg (3π/2 + α) = –tgα

Ф-ла приведения получена. Осталось подставить в неё значение α = π/4:

ctg (7π/4) = ctg (3π/2 + π/4) = – tgπ/4 = – 1

Ответ: – 1.

 

Откуда же возникло название «формула приведения»? Дело в том, что с их помощью вычисление тригонометрических ф-ций от углов из диапазона 0 ≤ π ≤ 2π можно привести к вычислению ф-ций от углов из I четверти, то есть из диапазона 0 ≤ α ≤ π/2. Это означает, что нет смысла заучивать большие таблицы, в которых указаны синусы и косинусы углов, больших 90°. Достаточно знать ф-ции от стандартных углов: 0, π/6; π/4, π/3 и π/2.

Если всё же использование ф-л приведения вызывает сложности, то вместо них всегда можно использовать обычные ф-лы косинуса и синуса суммы, которые дадут такой же результат.

В прошлом уроке, строя графики косинуса, мы заметили, что он представляет собой синусоиду, смещенную на π/2 единиц:

Теперь становится ясна причина этого смещения. Дело в ф-ле приведения

соsx = sin (x + π/2)

Она показывает, что точки графика косинуса могут быть получены параллельным переносом точек синусоиды на π/2 единиц влево.

Мы сделали подборку лучших онлайн-курсов по школьным предметам

Перейти

 

Сумма тригонометрических функций

Мы видим, что тригон-ких формул довольно много. Надо ли все их учить? Этого делать не надо. Достаточно иметь под рукой справочник при решении задач, связанных с преобразованием тригонометрических выражений, в котором все эти ф-лы можно посмотреть. В крайнем случае можно всегда самостоятельно вывести все ф-лы, используя только основное тригон-кое тождество и ф-лы синуса и косинуса суммы. Они, кстати, выдаются в качестве раздаточного материала учащимся при сдаче ЕГЭ. Ещё важно помнить определение тангенса, которое в раздаточном материале не записано.

Пусть есть два произвольных угла s и t. Найдем синусы их разности и суммы:

Сложим эти два уравнения:

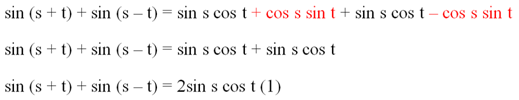
Теперь произведем замену. Будем считать, что

x = s + t

у = s – t

Это значит, чтох + у = 2s, или

s = (x + y)/2

С другой стороны

х – у = s + t– (s– t) = 2t

то есть

t = (x – у)/2

Подставляем всё это в ф-лу (1):

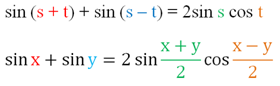
Получили формулу, с помощью которой можно найти сумму любых двух синусов! Теперь попытаемся составить аналогичную ф-лу и для их разности синусов. При этом мы учтем нечетность синуса (это значит, что sin (– у) = – sinу):

 

Задание. Упростите выражения

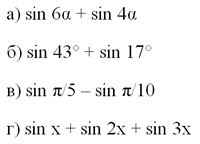
Решение.

Теперь попробуем составить ф-лы для сложения и вычитания косинусов. Для этого запишем ф-лы для произвольных величин s и t:

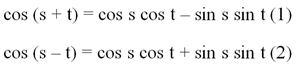
Сложив уравнения, мы получим тождество

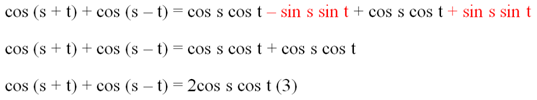
Далее произведем замены, которые выполняли и ранее:

x = s + t

у = s – t

s = (x + y)/2

t = (x – у)/2

Подставляя всё это в (3), получим:

Получили ф-лу, с помощью которой можно складывать косинусы. Чтобы их можно было вычитать, вычтем из (1) уравнение (2):

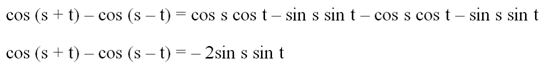
Снова произведем замены переменных s и t:

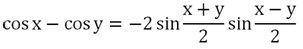
Получили ф-лу и для разности косинусов.

 

Задание. Упростить тригонометрические выражения

Решение.

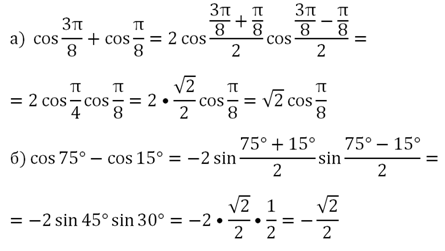
в) Здесь мы сталкиваемся с более сложным случаем, так как из косинуса надо вычесть синус. У нас нет готовой ф-лы для такого действия. Однако вспомним, что с помощью формул приведения легко заменить синус на косинус:

sinx = соs (π/2 – х)

Тогда исходное выражение уже можно будет преобразовать:

 

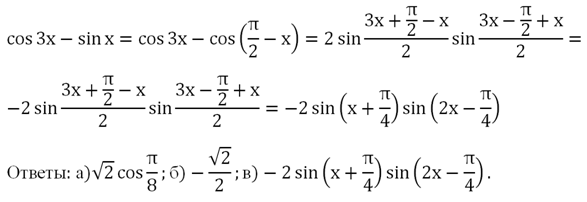
Произведение тригонометрических функций

В предыдущем разделе, когда мы выводили ф-лы для вычисления суммы синусов и косинусов, мы сначала получали уравнения:

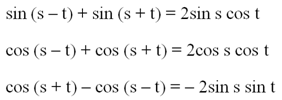
Далее мы производили замену переменных sи t. Однако давайте вместо этого просто поделим первые два уравнения на двойку, а третье – на (– 2):

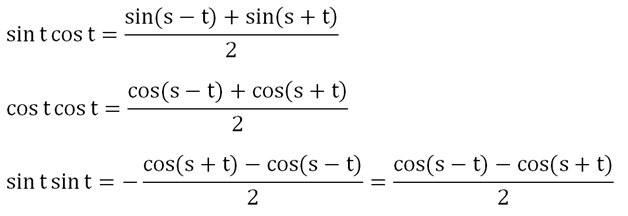
В случае с последней формулой мы воспользовались правилом, по которому знак минус перед дробью можно убрать, если в числителе поменять местами вычитаемое и уменьшаемое.

Получили ф-лы, которые позволяют заменять произведение тригонометрических ф-ций их суммой.

 

Задание. Преобразуйте произведение в сумму:

Решение.

На этом наше знакомство с основными тригонометрическими формулами заканчивается. Ещё раз напомним, что в рамках школьного курса заучивать все ф-лы не нужно, можно при необходимости пользоваться смотреть в справочник. Тригон-кие преобразования помогут в будущем при решении сложных тригон-ких уравнений.

В самом конце приведем перечень всех формул, выведенными в этом уроке:

Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы

Перейти

 

Mathway | Решение тригонометрических задач

Mathway | Решение тригонометрических задач

New Messages

User is Typing

Для функционирования Mathway необходим javascript и современный браузер.

Этот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.

Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:

• число
• буква
• специальный символ: @$#!%*?&

Практические задачи с использованием тригонометрии.

Практические задачи с использованием тригонометрии.

Существует ряд практических ситуаций, в которых необходимо использовать тригонометрию для определения неизвестных сторон и углов треугольников.

Пример 1

Здание шириной 10 м имеет двускатную крышу с наклоном 35^o с одной стороны и 41^o — с другой. Найти длину скатов крыши с точностью до сантиметра.

Пример 2

На рис. показаны два вектора напряжения, V₁=50В и V₂=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V₁

Пример 3

На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.

Пример 4

Поле имеет форму четырехугольника ABCD, показанного на рис. ниже. Определить площадь поля.

 

Пример 1

Здание шириной 10 м имеет двускатную крышу с наклоном 35^o с одной стороны и 41^o — с другой. Найти длину скатов крыши с точностью до сантиметра.

 

Решение:

Угол конька крыши В=180^o — 35^o— 41^o=104^o

По теореме синусов

,

Откуда

.

Также по теореме синусов:

Откуда

.

(используется таблица синусов)

Следовательно, длины скатов крыши равны 6 м и 7 м с точностью до см.

Примечание: сторона а — сторона против угла А, сторона с — сторона против угла С.

Пример 2

На рис. показаны два вектора напряжения, V₁=50В и V₂=90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V₁.

 

Решение:

<CAB=180^o — 45^o=135^o.

Согласно теореме косинусов:

СА² = V₁²+V₂² — 2V₁V₂ cosCBA=

=50² + 90² — 2*50*90cos135^o=16963.(по таблице косинусов)

Результирующий вектор CA=(16963)^1/2 =130,2B.

Cогласно теореме синусов,

,

Откуда

,

Следовательно угол АСВ приблизительно равен 29^о. (по таблице синусов)

Итак, результирующий вектор напряжения равен 130,2В и составляет угол в 29^о с V₁

Пример 3

На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.

Решение:

По теореме синусов,

, откуда

Значит, В=arcsin0,2431≈ 14 ^o (по таблице синусов )

Следовательно, шатун AB составляет угол 14 ^o с горизонталью.

<ОАВ=180^o-45^o-14^o=121^o

По теореме синусов:

, откуда

Пример 4

Поле имеет форму четырехугольника ABCD, показанного на рис. Определить площадь поля.

Проведенная из В в D диагональ делит четырехугольник на два треугольника.

 

 Решение:

 Площадь четырехугольника ABCD= площадь треугольника ABD+площадь треугольника BCD, т.е.

 S_ABCD =1/2*(40)*(21)*sin115^o + 1/2*(45)*(23)*sin55^o=804,582 м²

 

Тригонометрические уравнения | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Поэтому ответ:

3. Бывает, что перед разложением суммы или разности тригонометрических функций в произведение надо проделать обратную процедуру: превратить произведение в сумму (разность).

Решим уравнение:

Домножаем обе части на 2, преобразуем левую часть в разность косинусов, а правую часть — в сумму косинусов:

Ответ:

4. Ещё пример, где финальное разложение на множители поначалу замаскировано:
Здесь используем формулу понижения степени:
(которая является ни чем иным, как переписанной в другом виде формулой косинуса двойного
угла). Получаем:
и дальше ясно.

5. Многие оказываются в ступоре при виде следующего уравнения:
Переносим косинус влево и применяем формулу приведения
Дальше — дело техники.

6. А в этом примере нужны совсем другие манипуляции:
Раскладываем синус двойного угла, всё собираем в левой части и группируем:
Цель достигнута.

Рассмотрим уравнение:
Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене
степень каждого слагаемого равна двум (степень одночлена — это сумма степеней входящих в него сомножителей).
Поскольку степени всех слагаемых одинаковы, такое уравнение называют однородным. Для однородных уравнений существует стандартный приём решения — деление обеих его частей на . Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?

Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.

Предположим, что . Тогда в силу уравнения и , что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию , и мы можем поделить обе его части на .

В результате деления приходим к равносильному квадратному уравнению относительно тангенса:

и дальнейший ход решения трудностей не представляет

1. Рассмотрим уравнение
Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение :
и дело сделано.

2. Неожиданным образом сводится к однородному следующее уравнение:
Казалось бы, где тут однородность? Переходим к половинному углу!
откуда

(3)

Мы не случайно довели это уравнение до ответа. В следующем разделе оно будет решено другим методом, и ответ окажется внешне непохожим на этот.

Введение дополнительного угла

Этот метод применяется для уравнений вида . Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.

1. Рассмотрим уравнение
Делим обе части на 2:
Замечаем, что  :

В левой части получили синус суммы:
,
откуда и

2. Другой пример:
Делим обе части на
Сделаем теперь для разнообразия в левой части косинус разности:
3. Рассмотрим теперь общий случай — уравнение
Делим обе части на :

(4)

Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:

Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :

Соотношение (4) тогда приобретает вид:
,
или

Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол .

4. Снова решим уравнение
Делим обе части на :
Существует угол такой, что . Например, . Получаем:
,
,
,
,

В предыдущем разделе мы решили это уравнение, сведя его к однородному, и получили в качестве ответа выражение (3). Сравните с полученным только что выражением. А ведь это одно и то же множество решений!

Универсальная подстановка

Запомним две важные формулы:

Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной подстановки. Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.

1. Решим уравнение
Выражаем , используя универсальную подстановку:
Делаем замену :
Получаем кубическое уравнение:
Оно имеет единственный корень . Стало быть, , откуда .
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало .

2. Рассмотрим уравнение
А вот здесь использование универсальной подстановки сужает ОДЗ. Поэтому сначала непосредственно подставляем в уравнение и убеждаемся, что это — решение.
Теперь обозначаем  и применяем универсальную подстановку:
После простых алгебраических преобразований приходим к уравнению:
Следовательно, и .
Ответ: .

Метод оценок

В некоторых уравнениях на помощь приходят оценки .

3. Рассмотрим уравнение
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в
том случае, когда они равны единице одновременно:
Таким образом, должны одновременно выполняться следующие равенства:
Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:
Умножаем обе части на 90 и сокращаем на π:
Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.

Искать k, в принципе, уже не нужно. Сразу находим x:

Ответ: .

4. Рассмотрим уравнение
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.

Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:
Тем самым мы сокращаем работу вдвое, получая лишь одну систему:
Имеем:
Ищем пересечение:
Умножаем на 21 и сокращаем на π:
Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.

5. Страшное с виду уравнение
также решается методом оценок. В самом деле, из неравенств следует, что . Следовательно, , причём равенство возможно в том и только в том случае, когда
Остаётся решить полученную систему. Это не сложно.

Учёт тригонометрических неравенств

Рассмотрим уравнение:

Перепишем его в виде, пригодном для возведения в квадрат:

Тогда наше уравнение равносильно системе:

Решаем уравнение системы:

,
,

Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:

Теперь нужно произвести отбор решений в соответствии с неравенством . Серия  не удовлетворяет этому неравенству, а серия удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия .
Ответ: .

Специальные приёмы

В этом разделе рассматриваются некоторые типы уравнений, приёмы решения которых нужно знать обязательно.

1. Рассмотрим уравнение

Это сравнительно редкий случай, когда используется исходная формула косинуса двойного угла:
,
,
,

Каждое из уравнений полученной совокупности мы решать умеем.

2. Теперь рассмотрим такое уравнение:

Метод решения будет совсем другим. Сделаем замену . Как выразить  через t? Имеем:
,
откуда . Получаем:
,
,
,

Как действовать дальше, мы знаем.

3. Надо обязательно помнить формулы косинуса и синуса тройного угла (чтобы не изобретать их на экзамене):
,

Вот, например, уравнение:

Оно сводится к уравнению относительно :
,
,

Дальше всё понятно.

4. Как бороться с суммой четвёртых степеней синуса и косинуса? Рассмотрим уравнение

Выделяем полный квадрат!
,
,
,
,
,
,

5. А как быть с суммой шестых степеней? Рассмотрим такое уравнение:

Раскладываем левую часть на множители как сумму кубов: .
Получим:
,

С суммой четвёртых степеней вы уже умеете обращаться.

Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.

В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.

 

Методическая разработка по алгебре (10 класс) по теме: Задания для устной работы по теме «Тригонометрические функции»

Покропаева О.Б.

учитель математики

ГБОУ СОШ №47 г. Санкт-Петербург

Задания для устной работы по теме

«Тригонометрические функции»

Одной из главных особенностей осуществляемого в настоящее время преобразования школьной системы образования является его нацеленность на всестороннее развитие личности каждого ученика. А это требует коренного обновления прежних форм, методов, средств обучения, характерных для уроков, главной целью которых является научить школьников еще одному способу решения какого-либо типа задач или ознакомить их с еще одним, никак «не связанным» со всеми предыдущими, новым понятием.

Главной целью школьного математического образования должно быть развитие не шаблонного, а логического, творческого мышления учащихся. А основным средством достижения этой цели являются задачи. Собственно, одно из основных назначений задач и упражнений и заключается в том, чтобы активизировать мыслительную деятельность учеников на уроке. Математические задачи должны прежде всего будить мысль учеников, заставлять ее работать, развиваться, совершенствоваться.

Вот почему целью настоящей работы было создание системы устных заданий для изучения темы «Тригонометрические функции», которые удовлетворяли бы всем вышеуказанным требованиям.

В учебнике «Алгебра-10» (Алимова Ш.А.)  большее число задач ориентировано на вычислительную деятельность для ответа, тогда как задачи с элементами исследования и задачи на усвоение математических понятий представлены в недостаточном количестве. В связи с этим мною была разработана система устных заданий, дополняющих задачи учебника, по наиболее содержательно богатым разделам темы «Тригонометрические функции», которая представлена в работе. К каждому заданию системы приводятся методические комментарии (в каких учебных ситуациях его целесообразно использовать, в том числе, учитывая профильную дифференциацию).

Задания для устной работы и методические комментарии к ним

Одним из средств, способствующих лучшему усвоению математики, являются устные задания (не путать с устным счетом). С их помощью учащиеся отчетливее понимают сущность математических понятий, теорем, математических преобразований.

Устные задания активизируют мыслительную деятельность учащихся, развивают внимание, наблюдательность, память, речь, быстроту реакции, повышают интерес к изучаемому материалу. Они дают возможность изучить большой по объему материал за более короткий промежуток времени, позволяют учителю судить о готовности класса к изучению нового материала, о степени его усвоения, помогают выявлять ошибки учащихся.

Проводимые в начале урока устные упражнения помогают учащимся быстро включаться в работу, в середине или конце урока служат своеобразной разрядкой после напряжения и усталости, вызванной письменной или практической работой. В ходе выполнения этих заданий учащиеся чаще, чем на других этапах урока получают возможность устно отвечать, что, в свою очередь, способствует формированию их грамотной математической речи. При этом они сразу проверяют правильность своего ответа. В отличие от письменных заданий содержание устных таково, что решение их не требует большого числа рассуждений, преобразований, громоздких вычислений. Но между тем они отражают важные элементы курса.

При организации устных фронтальных упражнений, с целью экономии времени на уроке, целесообразно использовать проектор или другую мультимедийную технику.

Здесь будет представлена система устных заданий, дополняющих задачи учебника, по наиболее содержательно богатым разделам темы «Тригонометрические функции». К ним можно отнести:

1. Поворот точки вокруг начала координат.

2. Определения синуса, косинуса и тангенса.

3. Формулы приведения.

4. Простейшие тригонометрические уравнения  и неравенства.

5. Исследование тригонометрических функций.

6. Преобразования графиков тригонометрических функций.

7. Обратные тригонометрические функции.

8. Производные тригонометрических функций

Эта система включает в себя:

— качественные вопросы;

— задачи.

Первые могут быть использованы не только для фронтальной устной работы, но и для самостоятельной индивидуальной и групповой работы.

Предлагаемые задания могут быть использованы учителем и при подготовке к изучению нового материала, и при первичном ознакомлении, закреплении, и при ликвидации пробелов в знаниях учащихся.

При построении задач системы часто использовались обратные задачи, когда по решению нужно представить объект. Например, по решению уравнения сконструировать само уравнение. Такие задачи будут способствовать лучшему осознанию учащимися рассматриваемых понятий.

Кроме того, во многих задачах используются наглядные образы, что тоже дает возможность воспринимать изучаемый объект как целостное явление и как совокупность его свойств. Это тоже должно способствовать лучшему осознанию изучаемых понятий, свойств, явлений.

Задания, составляющие систему, соответствуют разному уровню сложности. Сложность задания указывается заглавными латинскими буквами А, В или С. Соответственно задание с индексом С имеет самый высокий уровень сложности.

Задания в системе представлены в соответствии с выделенными ранее разделами. И для заданий каждого раздела приводятся методические комментарии (в каких учебных ситуациях их целесообразно использовать, в том числе, учитывая профильную дифференциацию).

1. Поворот точки вокруг начала координат

Качественные вопросы:

1. На какой вопрос следует дать утвердительный ответ:

    а) Может ли величина   АОВ быть равной 2    радиан ?

    б) Может ли величина дуги АВ быть равной 0 радиан ?

    в) Верно ли, что R11π= R-10π ?

    г) Верно ли, что   R9π= R-7π ?

2. Какое из высказываний ложно:

    а) Если  t2 = t1+π, то ординаты точек  Pt2 и Pt1 —  противоположные числа.

    б) Если  t2 = t1+π, то абсциссы точек  Pt2 и Pt1  — противоположные числа.

    в) Если  t1 = π-α, t2 = π+α, где α  , то ординаты точек  Pt1  и Pt2  — противоположные числа.

     г) Если точки    Pt1  и Pt2  совпадают, то числа  t1  и  t2    равны.

Устные задания:

3. Определите координаты точек единичной окружности:

    а) Р90   ; б) Р180   ; в) Р270   ; г) Р-90   ; д) Р-180   ; е) Р-270   .

4. Пусть А(1;0), В(0;1), С(-1;0), Д(0;-1). Какая из данных точек получена поворотом точки (1;0) на угол:

   а) 450o ; б) 540o ; в) -720o ?

Комментарии:

Задания 3 и 4 (сложности А) носят тренировочный характер и могут быть предложены учащимся сразу после изучения данной темы. Кроме того, задание 3 может быть использовано при подготовке к изучению темы «Определения синуса, косинуса и тангенса» в начале урока (если определения вводятся с помощью единичной окружности).

Вопросы 1 и 2 — сложности С — поэтому их нецелесообразно выносить на устную фронтальную работу в общеобразовательном классе. Но их можно использовать в качестве дополнительных вопросов на обобщающем уроке темы «Элементы тригонометрии». Однако в математическом классе такие вопросы можно использовать при фронтальной работе с учащимися сразу после изучения темы.

2. Определения синуса, косинуса и тангенса

Качественные вопросы:

1.  Может ли синус угла быть равным:

       а) -3,7;  б) 3,7;  в) ;  г)  ?

2.  Может ли косинус угла быть равным:

       а) 0,75;    б)  ;   в) -0,35;    г)    ?

3. При каких значениях а и b справедливы следующие равенства:

        cos       sin         tg

        sin         ctg        cos  ?

4. Возможны ли равенства:

        2 — sin=1,7                   tg

                         ?

Устные задания:

5. Глядя на рисунок, определите букву, которой соответствует:

   а) sin 220o                                                                                                                                      

       cos

                                                       

  б)                                                              cos 80o               sin80o

                                                                   cos (-280o)         sin800o 

                                                                   cos 380o             sin (-340o)

Комментарии:

Задания 1-5 (сложности соответственно А, А, С, В, В) целесообразно предлагать учащимся сразу после введения определений основных тригонометрических функций на единичной окружности. Задание 3 может вызвать трудность у учащихся общеобразовательного класса в связи с тем, что надо оперировать параметрами а и b, поэтому его не стоит выносить на устную фронтальную работу, но можно, разобрав один пример на доске, включить указанное задание в письменную работу на уроке.

Методическая ценность задания 5,а состоит в множественном выборе правильного ответа. Задание 5,б, кроме указанной темы, может быть использовано при подготовке к изучению темы «Формулы приведения»:

cos 80o = cos(80o-2π) = cos(-280o)

sin 80o = sin(80o+4π) = sin 800o

В связи с наглядностью и доступностью задания 5 его можно использовать при работе с гуманитарным классом.

3. Формулы приведения

Устные задания:

1. Найдите α, если   0oαo    и  

   а)  sin 182o = — sin α;             б)  cos 295o = cos α.

2. Найдите несколько значений  α, если:

а)   sin α = sin 20o;   б)  cos α = — cos 50o;  в)  tg α =  tg 70o.  

Комментарии:

Предлагаемые задания (сложности В) предполагают использование формул приведения в нестандартной ситуации. В связи с этим, указанные задания могут быть предложены учащимся на этапе закрепления данной темы. Кроме того, их можно использовать при изучении темы «Периодичность». Для гуманитарного класса задания 1,2 можно упростить, используя единичную окружность:

Аналогично 1, а).                                Аналогично 2, б), в).

4. Простейшие тригонометрические уравнения и неравенства

Устные задания:

1.1. Назовите хотя бы одно уравнение, решением которого являются числа:

       а)    πn, n ;             в) ;               д)     π+2πn, n 

       б)   2πn, n;            г)   ;                        

1.2. Решения каких тригонометрических уравнений изображены на следующих схемах:

2. Является ли число  π   корнем уравнения:

   а)   ;                  б)   ?

3. Запишите с помощью неравенств множество всех точек x, лежащих на дуге:

        а) BmC  ;   в) BCD;

        б) CnD  ;   г)  CDA.

4. Решения каких тригонометрических неравенств изображены на следующих схемах:

Комментарии:

Задания 1.1, 1.2 (сложности А) носят репродуктивный характер и могут быть использованы для контроля знаний учащихся после изучения темы «Простейшие тригонометрические уравнения». Для гуманитарного класса целесообразнее использовать задание 1.2 ввиду его наглядности. Задание 1.2 является обратным к заданиям типа: «Решить уравнение:  sin x = -1, имеющимся в учебниках. Оно формирует у учащихся умение читать подобные схемы и раскрывает смысл тригонометрических уравнений на единичной окружности.

Задание 2 (сложности В) можно использовать при первичном закреплении указанной темы в математическом классе или на обобщающем уроке в общеобразовательном (или гуманитарном) классе.

Задание 3 (сложности А) можно предложить учащимся в начале урока, непосредственно пред изучением темы «Простейшие тригонометрические неравенства».

Задание 4 (сложности В) является обратным к заданиям типа: «Решить неравенство:  sinx ≤ 0,5», имеющимися в учебниках, оно формирует у учащихся умение читать подобные схемы и раскрывает смысл тригонометрических неравенств на единичной окружности. С таких заданий можно начинать изучение темы «Тригонометрические неравенства» как в гуманитарном, так и в математическом классах.

5. Исследование тригонометрических функций.

5.1. Периодичность.

Качественные вопросы:

1. Может ли данный промежуток (или объединение промежутков) являться областью определения периодической функции:

а) (-;                в) ;                д)  ?

б) ;                 г) ;

2.  Верно ли утверждение:

а) периодическая функция может иметь конечное число периодов;

б) если число Т – период функции f(x), то число 2Т также период этой функции;

в) если Т1 и Т2 – периоды функции f(x), то число Т1 + Т2 также период этой функции ?

Укажите ложное высказывание:

а) возрастающая функция не может быть периодической;

б) убывающая функция не может быть периодической;

в) периодическая функция имеет бесконечное множество корней;

г) у периодической функции не может быть конечного множества корней.

Устные задания:

4. Какая из функций не является периодической:

а)       в)       д) ;

б) ;  г) ;       е)  ?

5. У какой функции наименьший положительный период больше 2π:

а)

б)

в)

г)   ?

6. Определите период функции, график которой изображен на рисунке:

Комментарии:

Вопросы 1-3 (сложности С) могут быть предложены учащимся математического класса сразу после введения понятия периодической функции. Учитель с их помощью может выяснить степень осознания учащимися данного понятия.

Задание 4 (сложности В) носит обобщающий характер и поэтому может быть предложено учащимся обычного класса на обобщающем уроке темы «Периодичность тригонометрических функций».

Задание 5 (сложности С) может быть использовано для устной фронтальной работы только в математическом классе. В общеобразовательном классе это задание следует вынести на письменную работу.

Задание 6 (сложности А) предназначено для учащихся гуманитарного класса. Оно носит тренировочный характер и может быть предложено учащимся сразу после изучения данной темы.

5.2. Чётность

Качественные вопросы:

1. Какое высказывание ложно:

а) сумма двух чётных на R функций есть функция чётная;

б) разность двух четных на R функций есть функция четная;

в) произведение двух четных на R функций есть функция четная;

г) всякая функция либо чётная, либо нечетная.

Устные задания:

2. Укажите график чётной функции:

3. Укажите график нечётной функции:

4. Какая из указанных функций является нечётной:

;                        ;

;                     ?

Комментарии:

Задание 1 (сложности В) может быть использовано учителем на обобщающем уроке темы «Чётность». Оно ещё раз акцентирует внимание учащихся на том, что множество всех функций не разбивается на множество чётных и множество нечётных функций. Кроме того, учащихся математического класса после устной работы, включающей данное задание, можно в качестве упражнения попросить доказать утверждения 1-3.

Задания 2,3 (сложности А) можно использовать и как тренировочное (при первичном закреплении), и как контролирующее в любом из типов классов.

Задание 4 (сложности С) может быть вынесено на устную фронтальную работу только в математическом классе. Причем целесообразно перед ним предложить учащимся задание 1. В обычном или гуманитарном классе это задание следует вынести на письменную работу.

Задание на обобщающий урок по теме

«Исследование тригонометрических функций»

С помощью графиков функций, изображенных на рисунке, ответьте на следующие вопросы:

1. Графики каких тригонометрических функций изображены на рисунке?
2. Каковы значения x, для которых ?
3. Каковы промежутки возрастания, убывания функции?
4. Укажите значения x, при которых функция принимает максимальное, минимальное значения?
5. Обратима ли функция на R? на ? на ?
6. Каков период данной функции?
7. Выясните чётность данной функции.

а)

б)

в)

Комментарии:

Отдельные части (1-6) рассматриваемого (или подобного ему) задания могут быть предложены учащимся в качестве тренировочного устного упражнения при первичном закреплении соответствующих тем. Подобные задания формируют у учащихся навык чтения графика функции и являются хорошей иллюстрацией основных свойств тригонометрических функций.

6. Преобразования графиков тригонометрических функций

Устные задания:

1. С помощью каких преобразований из графика функции  можно получить график функции:

а)  ;          в)   ;          д)   ?

б)  ;          г) ;

Комментарии:

Это задание (сложности В) формирует у учащихся навык преобразования графиков функций вообще, и тригонометрических, в частности. Раскрывает суть понятий: амплитуда, начальная фаза, частота колебаний. В гуманитарном классе подготовительными для такого задания могут служить упражнения типа:

С помощью какого преобразования из графика функции  можно получить график функции  (см. рис.) ?

7. Обратные тригонометрические функции

1. Какие значения может принимать выражение:

а) ;       в) ;      д) ;

б) ;  г) ;   е) ?

Комментарии:

Указанные задания (сложности В) носят тренировочный характер и могут быть предложены учащимся на этапе закрепления темы «Обратные тригонометрические функции». Они акцентируют внимание учащихся на области определения и области значений тригонометрических функций.

8. Производные тригонометрических функций

Устные задания:

1. Графики производных каких тригонометрических функций изображены на рисунке:

Комментарии:

Подобные задания (сложности В) могут быть предложены учащимся на этапе закрепления указанной темы. Но лишь в том случае, если тема «Преобразования графиков функций» была изучена ранее.

Литература

1.  Заочные математические олимпиады./Н.Б.Васильев и др. — М.:Наука, 1981.

3. Алгебра:  Учеб. для 10 кл.   общеобразоват.   учреждений/    

Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. — 2 изд.-М.: Просвещение, 2010.

4. Макарычев Ю.Н. и др. О преподавании темы «Тригонометрические выражения и их преобразования» в курсе алгебры 8 класса. — Математика в школе, 1986, №1.

5. Рыбников К.А. Тригонометрия в школе и в системе наук. — Математика в школе, 1984, №6.

6. Цукарь А.Я. Упражнения практического характера по тригонометрии. — Математика в школе, 1993, №3.

Тригонометрия

Тригонометрия (от греч. Тригонон «треугольник» + метрон «мера»)

Хотите изучить тригонометрию? Вот краткое изложение.
Чтобы узнать больше, перейдите по ссылкам или перейдите в Индекс тригонометрии

Тригонометрия … всего около треугольника.

Тригонометрия помогает нам находить углы и расстояния и часто используется в науке, технике, видеоиграх и многом другом!

Прямоугольный треугольник

Наибольший интерес представляет прямоугольный треугольник.Прямой угол показан маленькой рамкой в ​​углу:

Другой угол часто обозначается как θ, и тогда три стороны обозначаются:

• Соседний : рядом (рядом) угол θ
• Напротив : напротив угла θ
• , а самая длинная сторона — Гипотенуза

Почему прямоугольный треугольник?

Почему этот треугольник так важен?

Представьте, что мы можем измерять по длине и вверх, но хотим знать прямое расстояние и угол:

Тригонометрия может найти недостающий угол и расстояние.

Или, может быть, у нас есть расстояние и угол, и нам нужно «нарисовать точку» вдоль и вверх:

Подобные вопросы часто встречаются в инженерии, компьютерной анимации и т. Д.

И тригонометрия дает ответы!

Синус, косинус и тангенс

Основные функции в тригонометрии: Синус, косинус и тангенс

Это просто одна сторона прямоугольного треугольника, разделенная на другую.

Для любого угла « θ «:

(Синус, косинус и тангенс часто сокращаются до sin, cos и tan.)

Пример: Что такое синус 35 °?

Используя этот треугольник (длины до одного десятичного знака):

sin (35 °) = Напротив Гипотенуза = 2,8 4,9 = 0,57 …

Треугольник может быть больше, меньше или перевернут, но этот угол всегда будет иметь соотношение .

У калькуляторов

есть sin, cos и tan, чтобы помочь нам, поэтому давайте посмотрим, как их использовать:

Пример: Насколько высокое дерево?

Мы не можем добраться до вершины дерева, поэтому мы уходим и измеряем угол (с помощью транспортира) и расстояние (с помощью лазера):

• Нам известна гипотенуза
• И мы хотим знать напротив

Синус — это отношение Противоположность / Гипотенуза :

грех (45 °) = Напротив Гипотенуза

Возьмите калькулятор, введите «45», затем нажмите клавишу «sin»:

sin (45 °) = 0.7071 …

Что означает 0,7071 … ? Это отношение длин сторон, так что Противоположность примерно на 0,7071 в раз длиннее Гипотенузы.

Теперь мы можем поставить 0,7071 … вместо sin (45 °):

0,7071 … = Напротив Гипотенуза

И мы также знаем, что гипотенуза равна 20 :

0,7071 … = Напротив 20

Чтобы решить, сначала умножьте обе части на 20:

20 × 0.7071 … = Напротив

Наконец:

Напротив = 14,14 м (с точностью до 2 знаков после запятой)

Когда вы наберетесь опыта, вы сможете сделать это быстро следующим образом:

Пример: Насколько высокое дерево?

Начать с: sin (45 °) = Напротив Гипотенуза

Мы знаем: 0,7071 … = Напротив 20

Поменять местами: Напротив 20 = 0.7071 …

Умножить обе стороны на 20 : Противоположное = 0,7071 … × 20

Вычислить: Противоположное = 14,14 (до 2 знаков после запятой)

Дерево 14,14 м высотой

Попробуйте Sin Cos and Tan

Поиграйте с этим некоторое время (перемещайте мышь) и познакомьтесь со значениями синуса, косинуса и тангенса для разных углов, таких как 0 °, 30 °, 45 °, 60 ° и 90 °.

Также попробуйте 120 °, 135 °, 180 °, 240 °, 270 ° и т. Д. И обратите внимание, что позиции могут быть положительными или отрицательными по правилам декартовых координат, поэтому синус, косинус и тангенс также изменяются между положительным и отрицательным ,

Итак, тригонометрия — это тоже окружности !

Единичный круг

То, с чем вы только что играли, — это Unit Circle.

Это круг с радиусом 1 с центром в 0.

Поскольку радиус равен 1, мы можем напрямую измерить синус, косинус и тангенс.

Здесь мы видим синусоидальную функцию единичной окружности:

Примечание: вы можете увидеть красивые графики, состоящие из синуса, косинуса и тангенса.

градусов и радианов

Углы могут быть в градусах или радианах. Вот несколько примеров:

Уголок	градусов	Радианы
Прямоугольный	90 °	π / 2
__ Уголок прямой	180 °	π
Полное вращение	360 °	2π

Повторяющийся узор

Поскольку угол вращается вокруг окружности , функции синуса, косинуса и тангенса повторяются один раз при каждом полном вращении (см. Амплитуда, Период, Фазовый сдвиг и Частота).

Когда мы хотим вычислить функцию для угла, большего, чем полный оборот на 360 ° (2π радиан), мы вычитаем столько полных оборотов, сколько необходимо, чтобы вернуть его ниже 360 ° (2π радиан):

Пример: каков косинус 370 °?

370 ° больше 360 °, поэтому вычтем 360 °

370 ° — 360 ° = 10 °

cos (370 °) = cos (10 °) = 0,985 (до 3 знаков после запятой)

А когда угол меньше нуля, просто добавьте полные обороты.

Пример: какой синус у −3 радиана?

−3 меньше 0, поэтому добавим 2π радиан

−3 + 2π = −3 + 6,283 … = 3,283 … радиан

sin (−3) = sin (3,283 …) = −0,141 (до 3 знаков после запятой)

Решение треугольников

Тригонометрия также полезна для обычных треугольников, а не только для прямоугольных.

Это помогает нам разгадывать треугольники. «Решение» означает поиск недостающих сторон и углов.

Мы также можем найти недостающие стороны.Общее правило:

Когда мы знаем какие-либо 3 стороны или углы, мы можем найти остальные 3
(за исключением случая с тремя углами)

См. Раздел «Решение треугольников» для более подробной информации.

Другие функции (котангенс, секанс, косеканс)

Подобно синусу, косинусу и касательности, есть еще три тригонометрические функции , которые выполняются делением одной стороны на другую:

Косеканс, функция:	csc ( θ ) = Гипотенуза / Напротив
Секущая функция:	сек ( θ ) = Гипотенуза / Соседний
Функция котангенса:	детская кроватка ( θ ) = рядом / напротив

Тригонометрические и треугольные идентичности

И по мере того, как вы станете лучше разбираться в тригонометрии, вы сможете выучить эти:

Наслаждайтесь становлением экспертом по треугольникам (и кругам)!

,

тригонометрия | Определение, формулы, соотношения и тождества

Слово тригонометрия происходит от греческих слов trigonon («треугольник») и metron («измерять»). Примерно до XVI века тригонометрия в основном занималась вычислением числовых значений недостающих частей треугольника (или любой формы, которую можно разрезать на треугольники), когда были даны значения других частей. Например, если известны длины двух сторон треугольника и мера внутреннего угла, можно вычислить третью сторону и два оставшихся угла.Такие вычисления отличают тригонометрию от геометрии, которая в основном исследует качественные отношения. Конечно, это различие не всегда является абсолютным: например, теорема Пифагора представляет собой утверждение о длинах трех сторон прямоугольного треугольника и, таким образом, носит количественный характер. Тем не менее, в своем первоначальном виде тригонометрия в целом была порождением геометрии; только в 16 веке эти два направления стали отдельными разделами математики.

Древний Египет и Средиземноморский мир

Несколько древних цивилизаций, в частности египетская, вавилонская, индуистская и китайская, обладали значительными познаниями в практической геометрии, включая некоторые концепции, которые были прелюдией к тригонометрии.Папирус Райнда, египетский сборник из 84 задач по арифметике, алгебре и геометрии, датируемый примерно 1800 годом до нашей эры, содержит пять задач, связанных с секедом . Тщательный анализ текста с сопровождающими его рисунками показывает, что это слово означает наклон склона — важное знание для огромных строительных проектов, таких как пирамиды. Например, в задаче 56 задается вопрос: «Если высота пирамиды 250 локтей, а длина стороны ее основания — 360 локтей, то каково ее шекэда ?» Решение дается как 5 ¹ / ₂₅ пальм на локоть, и, поскольку один локоть равен 7 пальмам, эта доля эквивалентна чистому соотношению ¹⁸ / ₂₅ .На самом деле это отношение «подъем к подъему» рассматриваемой пирамиды — по сути, котангенс угла между основанием и гранью. Это показывает, что египтяне имели хоть какое-то представление о числовых отношениях в треугольнике, своего рода «прото-тригонометрии».

Египетский сек Египтяне определили секед как отношение пробега к подъему, что является обратной величиной современного определения наклона. Британская энциклопедия, Inc. Получите эксклюзивный доступ к контенту нашего 1768 First Edition с подпиской.Подпишитесь сегодня

Тригонометрия в современном понимании началась с греков. Гиппарх ( c. 190–120 до н. Э.) Был первым, кто построил таблицу значений для тригонометрической функции. Он считал каждый треугольник — плоский или сферический — вписанным в круг, так что каждая сторона становится хордой (то есть прямой линией, соединяющей две точки на кривой или поверхности, как показано вписанным треугольником A B C на рисунке). Чтобы вычислить различные части треугольника, нужно найти длину каждой хорды как функцию центрального угла, который его образует, или, что то же самое, длину хорды как функцию от соответствующей ширины дуги.Это стало главной задачей тригонометрии на следующие несколько столетий. Как астроном, Гиппарх в основном интересовался сферическими треугольниками, такими как воображаемый треугольник, образованный тремя звездами на небесной сфере, но он также был знаком с основными формулами плоской тригонометрии. Во времена Гиппарха эти формулы были выражены в чисто геометрических терминах как отношения между различными хордами и углами (или дугами), которые их соединяют; современные символы для тригонометрических функций не были введены до 17 века.

треугольник, вписанный в круг Этот рисунок иллюстрирует взаимосвязь между центральным углом θ (угол, образованный двумя радиусами в круге) и его хордой A B (равной одной стороне вписанного треугольника). Encyclopædia Britannica, Inc. Изучите, как Птолемей пытался использовать деференты и эпициклы для объяснения ретроградного движения. Теория Птолемея о солнечной системе. Encyclopædia Britannica, Inc. Смотрите все видео к этой статье

Первой крупной древней работой по тригонометрии, которая дошла до Европы нетронутой после Средневековья, была Альмагест Птолемея ( ок. 100–170 гг. Н. Э.). Он жил в Александрии, интеллектуальном центре эллинистического мира, но о нем мало что известно. Хотя Птолемей написал работы по математике, географии и оптике, он в основном известен Альмагест , сборником из 13 книг по астрономии, который стал основой картины мира человечества до тех пор, пока гелиоцентрическая система Николая Коперника не начала вытеснять геоцентрическую систему Птолемея. в середине 16 века. Чтобы создать эту картину мира, суть которой заключалась в неподвижной Земле, вокруг которой Солнце, Луна и пять известных планет движутся по круговым орбитам, Птолемею пришлось использовать элементарную тригонометрию.Главы 10 и 11 первой книги Альмагест посвящены построению таблицы хорд, в которой длина хорды в окружности дается как функция от центрального угла, который ее образует, для углов в диапазоне от От 0 ° до 180 ° с интервалом в полградуса. По сути, это таблица синусов, которую можно увидеть, обозначив радиус r , дугу A и длину удлиненной хорды c , чтобы получить c = 2 r sin ^{. А} / ₂ .Поскольку Птолемей использовал вавилонские шестидесятеричные числа и системы счисления (основание 60), он проводил вычисления со стандартным кругом радиуса r = 60 единиц, так что c = 120 sin ^A / ₂ . Таким образом, помимо коэффициента пропорциональности 120, это была таблица значений sin ^A / ₂ и, следовательно, (путем удвоения дуги) sin A . С помощью своей таблицы Птолемей усовершенствовал существующие геодезические измерения мира и усовершенствовал модель движения небесных тел Гиппарха.

построение таблицы хорд Обозначив на рисунке центральный угол A , радиусы r и хорду c , можно показать, что c = 2 r sin ( A /2). Следовательно, таблица значений хорд в круге фиксированного радиуса также является таблицей значений синуса углов (путем удвоения дуги). Британская энциклопедия, Inc. .

Mathway | Решение задач тригонометрии

Mathway | Решение задач тригонометрии

Новые сообщения

Пользователь набирает

Mathway требует javascript и современного браузера.

Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство работы с ним.

Убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждое из следующих значений:

• номер
• письмо
• специальный символ: @ $ #!% *? &

,

Практические задачи по тригонометрии

Постарайтесь решить эти проблемы самостоятельно, а если вам понадобится помощь, посмотрите на скрытые решения. Вы можете использовать калькулятор. Вы можете загрузить копии всех этих вопросов (Acrobat (PDF) 108kB Jul25 09), чтобы использовать их самостоятельно. Если у вас возникли трудности, попробуйте страницу с примерами основных триггерных функций.

Расчет длины стороны

Длина тропы в гору

Вы поднимаетесь на 500.метровая горка. Тропа имеет уклон 12 градусов. Как далеко вы пройдете, чтобы добраться до вершины? Первым шагом обычно является создание эскиза. Однако это уже было сделано, поэтому мы перейдем к шагу 2 и определим, какую функцию триггера использовать. Мы знаем угол А (12 градусов) и длину противоположной стороны (500 м). Мы хотим знать длину гипотенузы (H), поэтому воспользуемся формулой для синуса:

Подставляя соответствующие значения,

Шаг 3 — перестроить уравнение так, чтобы то, что вы знаете, было с одной стороны, а то, чего вы не знали, — с другой, а затем подставьте известные значения.Изолирующая Н,

Наконец, мы воспользуемся калькулятором, чтобы определить значение тригонометрической функции (в данном случае синус) и найти неизвестное значение. Используя калькулятор,

sin (12) = 0,21, значит,

Тропа в гору , длина 2400 м, .

Глубина залегания угля

Вы заметили, что пластовой уголь наклонен под углом 12 градусов и выходит на поверхность в 6 километрах от вашего участка.Насколько глубоко вам придется копать, чтобы добраться до угольного пласта на вашем участке?
Это может помочь нарисовать картину этого. Попробуйте сами, а затем посмотрите, похоже ли это на то, что скрыто ниже Здесь у нас есть угол 12 градусов, и мы знаем прилегающую сторону (6 км), и мы хотим знать длину противоположной стороны (O). Формула, которая нам поможет, — это касательная:

Подставив соответствующие значения,

Перестановка для изоляции O,

O = загар (12) * 6 км

Используя калькулятор, значение tan (12) равно 0.213. Так

O = 0,213 * 6 км

Таким образом, противоположная сторона треугольника, глубина угольного пласта, составляет 1,275 км или 1275 метров .

Расчет радиуса внешнего ядра (сейсмология)

Зона тени S-волн возникает из-за того, что внешнее ядро ​​не пропускает S-волны. Он пересекает на Земле дугу в 105 градусов (см. Диаграмму слева). Оцените радиус внешнего ядра. Радиус всей Земли — 6370 км.

Опять же, будет полезно нарисовать схему.
Здесь у нас есть прямоугольный треугольник с одним углом 52,5 градуса (половина 105 градусов) и гипотенуза длиной 6370 км. Нам нужно найти прилегающую сторону, которая является приблизительным радиусом внешнего ядра, поэтому мы будем использовать косинус.

Подставляя в,

Перестановка для A,

A = cos (52,5) * 6370 км
, поэтому
A = 3877 км

Так что приблизительный радиус ядра 3877 км .
Обратите внимание, что это приблизительное значение из-за искривления сейсмических волн при отражении через мантию. Фактический радиус составляет около 3500 км.

---

Расчет угла

Градиент потока

Река Колорадо опускается с 3200 футов у озера Мид до высоты 500 футов у Ли-Ферри, на расстоянии 270 миль от реки. Что такое градиент в градусах?

У треугольника две стороны, и нам нужен угол. Расстояние до реки — это гипотенуза, а вертикальный перепад — это противоположный угол.Однако есть загвоздка. Единицы измерения не совпадают, и они должны соответствовать нашим тригонометрическим формулам. Итак, сначала мы конвертируем падение в мили (мы могли бы конвертировать расстояние в футы — это не имеет значения).

(Примечание — если вам нужна помощь на этом этапе, вы можете перейти на страницу преобразования единиц измерения)
Теперь мы можем использовать формулу для синуса, чтобы вычислить угол x
.
подставляя в,

так

грех (х) = 0.00189

чтобы найти угол x, возьмите обратный синус каждого

sin ^-1 (sin (x)) = sin ^-1 (0,00189)

поскольку sin ^-1 (sin (x)) = x, наш результат равен

x = 0,11 градуса

Итак, уклон реки Колорадо 0,11 градуса.

Угол естественного откоса

Угол естественного откоса — это самый крутой угол, при котором сухой рыхлый осадок стабилен. Вы создаете конусообразную кучу песка настолько крутой, насколько это возможно.Высота ворса 11 см, радиус 16 см. Каков угол естественного откоса этого песка?

Если смотреть на коническую сваю сбоку, это два сложенных прямоугольных треугольника. Высота — это сторона, противоположная углу естественного откоса, а радиус сваи — прилегающая сторона. Итак, у нас есть информация для уточнения тангенса угла естественного откоса, который мы можем назвать x.

так

тангенс (х) =.6875

Отсюда мы можем найти x угол естественного откоса

чтобы найти x, нам нужно будет взять арктангенс от обеих частей уравнения

тангенс (х) =. 6875

так

tan ^-1 (tan (x)) = tan ^-1 (0,6875)

поскольку tan ^-1 (tan (x)) = x

x = 34,5 градуса , угол естественного откоса для этого песка.

Тектоника плит и угол субдукции

Погружение океанических плит может круто или неглубоко погрузиться под перекрывающую плиту.В современных зонах субдукции расположение землетрясений может показать, насколько круто погружающаяся плита погружается в мантию, однако в древних зонах субдукции мы не можем использовать этот метод. Вместо этого мы можем использовать наблюдение, что вулканическая дуга обычно возникает выше точки, в которой погружающаяся плита достигает глубины 100 км. Если древняя вулканическая дуга находилась в 200 км от желоба, знаменующего начало субдукции, каков угол субдукции?

В этом случае нужно найти угол, под которым известны смежная сторона (расстояние до вулканической дуги) и противоположная сторона (глубина плиты ниже вулканической дуги), поэтому нам нужно будет использовать касательную, чтобы найти угол субдукции.

т.

Разделив, находим, что

тангенс (х) = 0,5

Отсюда мы можем найти x, угол субдукции

чтобы найти x, нам нужно будет взять арктангенс от обеих частей уравнения

тангенс (х) = 0,5

так

tan ^-1 (tan (x)) = tan ^-1 (0,5)

поскольку tan ^-1 (tan (x)) = x

х = 26.6 градусов , угол субдукции.

Следующие шаги

Если вы чувствуете себя комфортно с тригонометрией, можете переходить к экзамену.

Или вы можете вернуться на страницу объяснения тригонометрии. ,