Олимпиадные задачи 2 тура с решениями и ответами — 2006 год
Главная › Олимпиады школьников › Математические олимпиады школьников
Олимпиадные задачи 2 тура с решениями и ответами — 2006 год
- Просмотр
- Следить
Втр, 30/03/2010 — 16:22 — Татьяна Алексан…
Олимпиадные задачи 2 тура с решениями и ответами — 2006 год6 класс
- Разность двух чисел на 17 меньше уменьшаемого и на 9 больше вычитаемого. Найдите уменьшаемое и вычитаемое.
- Будет ли сумма чисел 1 + 2 + 3 + …..+ 2005 + 2006 + 2007 делиться на 2007? Ответ обоснуйте.
- Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов. Какое наибольшее число клеток понадобится?
- На выставку привезли 25 собак. 12 из них большие, 8 – маленькие, остальные средние. Только 10 из участников выставки породистые, остальные – дворняжки.
 Среди дворняжек поровну больших, маленьких и средних. Сколько больших породистых собак привезли на выставку?
Среди дворняжек поровну больших, маленьких и средних. Сколько больших породистых собак привезли на выставку?
7 класс
- Восстановите пример: АВС × СВА = 692443.
- За весну Обломов похудел на 25%, затем за лето поправился на 20%, затем за осень похудел на 10%, а за зиму прибавил 20%. Похудел он в итоге или поправился? Ответ обоснуйте.
- Какой цифрой оканчивается число 20072006?
- На клетчатой бумаге со стороной клетки 1 см нарисован треугольник. Чему равна его площадь?
- У мамы четыре дочери Поля, Валя, Катя и Маша. Девочки играли и разбили вазу. На вопрос: «Кто это сделал?» Поля, Валя и Катя ответили: «Не я», а Маша – «не знаю».

8 класс
- Решите уравнение x — 6 = |x — 3|/(x — 3).
- Верно ли равенство 3100 + 7100 = 8100? Ответ обоснуйте.
- Дворники получают грабли и метлы. Если каждый возьмет одну метлу или одни грабли, то останется 14 метел. А чтобы дать каждому дворнику и одну метлу, и одни грабли, не хватает 10 грабель. Сколько было дворников, сколько метел и сколько грабель?
- На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы всегда лгут. Путешественник, приехавший на остров, нанял островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал туземца узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал: «Туземец говорит, что он абориген». Кем был проводник: пришельцем или аборигеном? Ответ обоснуйте.

- В окружности с центром в точке О проведены радиусы ОВ и ОА так, что ﮮАОВ=60°, ОВ = DС. Найдите величину ﮮАDО.
9 класс
- В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°. Докажите, что трапеция – равнобедренная.
- Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой. Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д., причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде, из которого вода отливается. Сколько воды будет в сосудах после 2007 переливаний?
- Решите неравенство .
- Решите уравнение x2 + 2005x – 2006 = 0.
- Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?
10 класс
- Решите уравнение (x-2)(x-3)(x+4)(x+5) = 1320.

- На плоскости дан отрезок АВ. Где может быть расположена точка С, чтобы ∆АВС был остроугольным?
- Найти все натуральные числа, оканчивающиеся на 2006, которые после зачеркивания последних четырех цифр уменьшаются в целое число раз.
- Вычислить сумму a2006 + 1/a2006, если a2– a + 1 = 0.
- Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей, и т. д. Может ли за некоторое число разрезаний получиться 2006 листка бумаги?
11 класс
- Докажите, что уравнение xy = 2006 (x+y) имеет решения в целых числах.
- Докажите, что если α, β, γ — углы произвольного треугольника, то справедливо тождество cos2α + cos2β + cos2γ + 2 cos
- Три шара радиуса R касаются друг друга и плоскости α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных шаров.
 Определите высоту «горки» из четырех шаров.
Определите высоту «горки» из четырех шаров. - Докажите неравенство x2 — 3x3 < 1/6 на луче [1/4; +∞).
- В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.
2006 год
6 класс
- Ответ: 43 – 17.
- Ответ: будет. Представим данную сумму в виде следующих слагаемых: (1 + 2006) + (2 + 2005) + …..+ (1003 + 1004) + 2007. Так как каждое слагаемое делится на 2007, то и вся сумма будет делиться на 2007.
- Ответ: 5 клеток.
- Ответ: 7 больших породистых собак.
- Ответ: 64 см
7 класс
- Ответ: 739 ×937 = 692443.
- Ответ: Обломов похудел.
- Ответ: число оканчивается цифрой 9.

- Ответ: 25,5 см2
- Среди ответов Поли, Вали и Кати может быть только один ложный ответ, иначе при двух ложных ответах получается, что стекло разбили двое. Тогда вторым ложным ответом будет ответ Маши. Значит, Маша знала, кто разбил стекло.
8 класс
- Ответ: 7.
- Решение: Нет. 3100 оканчивается 1, 7100 оканчивается 1, а 8100 оканчивается 6.
- Ответ: 24 дворника, 24 метлы и 14 грабель.
- Ответ: Проводник был аборигеном.
- Ответ: ﮮCDO = 20°.
- Пусть AD = a, BC = b, AC = a + b. Продолжим AD за точку D на расстояние DM = BC. Тогда очевидно, что ∆АСМ — равносторонний. Но это значит, что ∆АОD и ∆ВОС — тоже равносторонние. Отсюда непосредственно следует, что ∆АОВ = ∆СОD, откуда имеем, что AB = CD.
- «Просчитав» несколько первых переливаний, нетрудно обнаружить, что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды.
 Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/ 2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k+1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/ 2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k+1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды. - Заметим, что все решения исходного неравенства существуют, если подкоренные выражения неотрицательны. Одновременно эти неравенства выполняются лишь при условии x2 – 4x + 3 = 0. Это уравнение имеет два корня 1 и 3. Проверка показывает, что исходное неравенство имеет единственное решение 3.

- Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные шесть выстрелов, то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка. Тогда за оставшиеся 3 выстрела надо набрать 26 очков. Что возможно при единственной комбинации 8+9+9=26. Итак, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, в девятку – 3 раза.
10 класс
- Ответ: -8; 6.
- Построим на АВ как на диаметр окружность и проведем через А и В две прямые, перпендикулярные отрезку АВ. Точка С может находится между этими прямыми вне круга.
- Пусть натуральные числа имеют вид x∙10000 + 2006, где x € N. После вычеркивания последних цифр получим число x. По условию , где n € N. Отсюда имеем, что должно быть натуральным числом, т. е. x — делитель числа 2006. Число 2006 имеет делители: 1; 2; 17; 34; 59; 118; 2006. Следовательно, имеются числа, отвечающие условию задачи: 12006; 22006; 172006; 342006; 592006; 1182006; 20062006.

- Так как a<>0, то, разделив обе части исходного уравнения на a, получим a + 1/a = 1. Заметим, что a3 + 1 = 0, т. к. a3 + 1 = (a + 1)(a2 – a + 1). Таким образом, a3 = -1. Тогда a2006 + 1/a2006 = (a3)6682 = a2 +1/a2 = — 1.
- Замечаем, что при каждом разрезании из одного листка получаем пять, т. е. число листков увеличивается на 4. Следовательно, из исходного листа может получиться число листков вида 1 + 4n, где n € N, т. е. это число при делении на 4 дает остаток 1. Но 2006 = 4∙501 + 2. Следовательно, 2006 листков получиться не может.
11 класс
- Преобразуем уравнение к следующему виду: (х – 2006)(у — 2006) = 20062. Уравнение имеет решения, например, х = у = 4012.

- Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π, и применяя формулы: cos2x = (1 + cos2x)/2, cosx = — cos(π — x), cosx + cosy = (2cos((x + y)/2))cos((x — y)/2), получим справедливое тождество.
- Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости a в точках A1, B1, C1 (см. рис). Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R. Вершина D этой пирамиды проектируется в центр основания О., .
- Пусть y = x2 – 3x3. Тогда y’ = 2x – 9x2 и с помощью метода интервалов получаем, что y’ < 0 при всех x>2/9. Но 1/4>2/9, следовательно, функция y(x) убывает на луче [1/4; +∞]. Это значит, что x2 — 3x3 < 1/16 — 3/64 = 1/64 < 1/64.
- Окружим каждый квадрат полоской шириной 1/2. Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4.
 Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов.
Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов.
‹ Олимпиадные задачи 2 тура с решениями и ответами — 2005 год Вверх Олимпиадные задачи 2 тура с решениями и ответами — 2007 год ›
СправочникиУчебникиПодготовка к ГИАЖурналыПодготовка к ЕГЭО водеАктуальные документы по вопросам образованияЭкологияЭлектронные тренажёрыМетодическая литератураСовременные технологииГалереяАльтернативная энергетикаРефератыКнигиКаталог ресурсов
Все теги
Стереометрия. Геометрия в пространстве
Стереометрия. Геометрия в пространстве
ОглавлениеПРЕДИСЛОВИЕ К ЧИТАТЕЛЮВВЕДЕНИЕ ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ § 1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ 1.2. Двугранный угол. Угол между плоскостями. 1.3. Плоскость и прямая в пространстве. 1.4. Аксиомы стереометрии. 1.5. Взаимное расположение двух прямых в пространстве. 1.6. Признаки скрещивающихся прямых. 1.7. Параллельные прямые. 1.8. Параллельное проектирование.  § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 2.2. О значении перпендикуляра. 2.3. Теорема о трех перпендикулярах. 2.4. Признак перпендикулярности прямой и плоскости. 2.5. Построение плоскости, перпендикулярной данной прямой. 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости. 2.7. Теорема о прямой, перпендикулярной плоскости. 2.8. Перпендикулярность плоскостей. 2.9. Ортогональное проектирование. § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 3.2. Параллельность и перпендикулярность. 3.3. Основная теорема о параллельных плоскостях. 3.4. Второй признак параллельности плоскостей. 3.5. Расстояние и параллельность. 3.6. Сонаправленность лучей и угол между прямыми. 3.7. Параллельность и углы. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ § 4. СФЕРА И ШАР 4.2. Взаимное положение шара и плоскости. 4.3. Сфера и многранники. 4.4. Вид и изображение шара и сферы.  4.5. Опорная плоскость. 4.6. Ограниченные фигуры. Диаметр фигуры. 4.7. Опорные плоскости в концах диаметра. 4.8. Сфера — фигура вращения. 4.9. Симметрия сферы и шара. 4.10. Сфера — центрально симметричная фигура. 4.11. Сфера — зеркально симметричная фигура. 4.12. Отражение в плоскости и отражение в зеркале. § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ 5.2. Тригонометрия трехгранного угла. 5.3. Равенство трехгранных углов. 5.4. Сферические треугольники. 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников. § 6. ЦИЛИНДР 6.2. Другой подход к определению цилиндра. 6.3. Цилиндр вращения. 6.4. Эллипс как сечение цилиндра вращения. 6.5. Винтовые линии. 6.6. Цилиндры в практике. § 7. ПРИЗМА 7.2. Параллелепипед. 7.3. Прямоугольный параллелепипед. 7.4. Симметрия параллелепипеда. 7.5. Симметрия правильных призм. Поворот вокруг прямой. § 8. КОНУС 8.2. Сечение конуса плоскостью, параллельной плоскости основания.  8.3. Конус вращения. 8.4. Усеченный конус. § 9. ПИРАМИДА 9.2. Правильная пирамида. 9.3. Симметрия правильной пирамиды. 9.4. Конусы и пирамиды в практике. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ 10.2. Граница и внутренность. 10.3. Определение тела и замкнутой плоской области. 10.4. Выпуклые фигуры. 10.5. Выпуклые тела. § 11. МНОГОГРАННИКИ 11.2. Выпуклые многогранники. 11.3. Теорема Эйлера. 11.4. Выпуклые многогранники и выпуклые оболочки. 11.5. Многогранная поверхность и развертка. 11.6. Развертка выпуклого многогранника. § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ 12.2. Классификация правильных многогранников. 12.3. Полуправильные многогранники. 12.4. Симметрия правильных многогранников. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ § 13.  ПОНЯТИЕ ОБЪЕМА ПОНЯТИЕ ОБЪЕМА13.2. Определение объема. 13.3. Геометрические величины. § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА 14.2. Объем прямой призмы. § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ 15.2. Выражение объема через площади сечений. § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА 16.2. Объем конуса 16.3. Объем шара. 16.4. Объем тел вращения. 16.5. Объем шарового сегмента и шарового сектора. § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ 17.2. Площадь сферы. 17.3. Площадь сферических многоугольников. 17.4. Площадь сферического сегмента и сферического пояса. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 5. КООРДИНАТЫ И ВЕКТОРЫ § 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ 18.2. Другой способ нахождения координат точки. 18.3. Построение точки с данными координатами. 18.4. Выражение расстояния между точками. § 19. МЕТОД КООРДИНАТ 19.2. Уравнения без одной или двух координат. 19.3. Некоторые применения метода координат. § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ 20.  2. Полярные координаты. 2. Полярные координаты.20.3. Цилиндрические координаты. 20.4. Сферические координаты. 20.5. Координатная сеть. § 21. ПОНЯТИЕ ВЕКТОРА 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов. 21.3. Сонаправленность и равенство векторов. 21.4. Признаки равенства векторов. 21.5. Радиус-вектор. § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 22.2. Разложение вектора на составляющие. 22.3. Умножение вектора на число. 22.4. Координаты вектора. 22.5. Равенство координат векторов и координат точек. 22.6. Разложение векторов по базису. 22.7. Ориентация базиса. § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ 23.2. Выражение скалярного произведения через координаты. 23.3. Свойства скалярного умножения. 23.4. Применения скалярного умножения. 23.5. Скалярное произведение и проекции. § 24. ВЕКТОРНЫЙ МЕТОД 24.2. Общее уравнение плоскости. 24.3. Векторное задание отрезка. 24.4. Некоторые теоремы о треугольниках и тетраэдрах.  24.5. Центр масс системы материальных точек. 24.6. Центры масс и выпуклые многогранники. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 6. ПРЕОБРАЗОВАНИЯ 25.1. Преобразования фигур. 25.2. Определения движения и равенства фигур. 25.3. Преобразования симметрии. 25.4. Параллельный перенос. 25.5. Поворот. § 26. СВОЙСТВА ДВИЖЕНИЙ 26.2. Общие свойства движений. 26.3. Теоремы о задании движений. 26.4. Неподвижные точки движений. 26.5. Два рода движений. 26.6. Теорема подвижности пространства. 26.7. Композиция отражений в плоскости. § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА 27.2. Движения первого рода как винтовые движения. 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот. 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения. § 28. ПОДОБИЕ 28.2. Гомотетия. 28.3. Свойства подобия. 28.4. Группы преобразований. § 29. ИНВЕРСИЯ 29.  2. Аналитическое задание инверсии. 2. Аналитическое задание инверсии.29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии. 29.4. Сохранение величин углов при инверсии. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ОТВЕТЫ И УКАЗАНИЯ ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ |
Три одинаковых металлических шара радиусом r каждый лежат на горизонтальной поверхности так, что при соединении центров трех шаров образуется равносторонний треугольник. Центр масс системы расположен по адресу
CP SINGH-ЦЕНТР МАССОВЫХ Упражнений
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro and dekho sari videos bina kisi ad ki rukaavat ke!
Дата обновления: 27 июня 2022 г.
लिखित उत्तर
A
Горизонтальная поверхность
B
Центр Один из шаров
C
Связанные центры из любых двух шаров
D
пункт пересечения медиасов
Ответ
Правильный ответ Medians
. is D
is D
Раствор
c.m. будет в центре равностороннего треугольника.
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
संबंधित वीडियो
Три тонких однородных круглых диска массой M и радиусом R расположены на горизонтальной поверхности, касаясь друг друга так, что при соединении центров трех дисков образуется равносторонний треугольник. Найдите М.И. вокруг оси, проходящей через центр масс системы дисков и перпендикулярной плоскости.
13025667
तीन सम| निकाय के द्रव्यमान केन्द्र की स्थिति ज्ञात कीतज |
94855961
Три одинаковых шара радиусом 10 см каждый и массой 1 кг лежат на горизонтальной поверхности, касаясь друг друга. Где находится их центр масс?
112986969
धातु के तीन गोले ( प्रत्येक की त्रिज्या r ) एक क्षैतिज तल पर एक — दूसरे से सटाकर इस प्रकार रखे गए हैं की उनके केंद्रों को मिलाने पर एक समबाहु त्रिभुज प्राप्त होता है निकाय का द्रव्यमान — केंद्र होगा —
234020652
Три шара из одного и того же металла радиусом r соприкасаются на горизонтальной поверхности так, что их центры соединяются в равносторонний треугольник.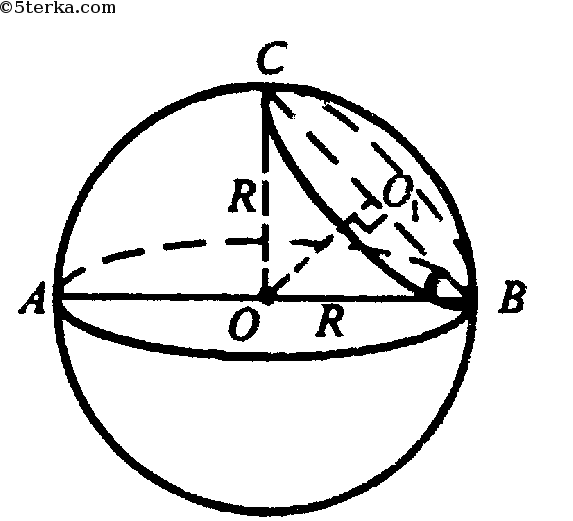 Положение центра масс тела будет
Положение центра масс тела будет
641278532
Три одинаковых шара радиусом R лежат на горизонтальном столе, касаясь друг друга. Центр масс системы расположен
642674527
Три одинаковых кольца массой M и радиусом R расположены в одной плоскости и касаются друг друга так, что их центры лежат в вершинах равностороннего треугольника. М.И системы относительно оси, проходящей через центр одного из колец и перпендикулярной его плоскости, равен
642674760
Три одинаковых металлических шара, радиусом r каждый, соприкасаются друг с другом на горизонтальной поверхности так, что при соединении центров трех шаров образуется равносторонний треугольник. Тогда где же их центр масс?
642687317
Три одинаковых шара радиусом R лежат на горизонтальном столе, касаясь друг друга. Центр масс системы расположен
642708369
Три одинаковых кольца массой M и радиусом R расположены в одной плоскости и касаются друг друга так, что их центры образуют вершины равностороннего треугольника. М.И системы относительно оси, проходящей через центр одного из колец и перпендикулярной его плоскости, равен
М.И системы относительно оси, проходящей через центр одного из колец и перпендикулярной его плоскости, равен
642708547
Текст Решение
Три одинаковых металлических шара, каждый радиусом r, соприкасаются друг с другом на горизонтальной поверхности так, что при соединении центров трех шаров образуется равносторонний треугольник. Центр масс системы расположен в точке
642793012
Текст Решение
На горизонтальном столе лежат три одинаковых шара радиусом R каждый, касаясь друг друга. Центр масс системы расположен
642845514
Текст Решение
Три одинаковых кольца массой M и радиусом R расположены в одной плоскости и касаются друг друга так, что их центры лежат в вершинах равностороннего треугольника. М.И системы относительно оси, проходящей через центр одного из колец и перпендикулярной его плоскости, равен
642845721
. Три одинаковых шара массой m касаются друг друга на горизонтальной поверхности. какова позиция C. M. системы?
M. системы?
643069096
R त्रिज्या वाली एक ध ध की की गेंदों को क्षैतिज सतह प प प जैसी ध ध की गेंदों क क्षैतिज सतह प प выполнительный निकाय के द्रव्यमान केन्द्र की स्थिति होगी
643234720
Геометрия — 4 сфер все касаются друг друга ??
$\begingroup$
Если есть 4 сферы, все соприкасающиеся друг с другом, и 3 из них имеют диаметры 4, 6 и 12, каков диаметр четвертой? Я представляю это как 3 шара на плоском столе, соприкасающиеся друг с другом, а затем мы должны положить еще один поверх них, но в моем воображении верхняя сфера может быть любого размера, верно?
- геометрия
- сферы
- объемная геометрия
$\endgroup$
4
$\begingroup$
Не любого размера . Если четвертая сфера достаточно мала, она может поместиться в отверстие посередине, также опираясь на стол, не касаясь ни одной из трех других сфер.
Я предполагаю, что эта проблема требует минимального диаметра четвертой сферы, который гарантирует контакт со всеми остальными тремя.
$\endgroup$
2
$\begingroup$
Просто дополняю только что опубликованный ответ. Если новая сфера достаточно мала, она поместится в отверстие посередине, поэтому у нас есть нижняя граница размера новой сферы. Точно так же, если новая сфера достаточно велика, она может также сделать размер одной из предыдущих сфер «достаточно малым», таким образом, 0145 может быть верхней границей.
$\endgroup$
2
$\begingroup$
Подсказка
Слово cirsphe может относиться к кругу, сфере гиперсферы.
Теорема Декарта для $n\geq 2$ измерений говорит нам, что нам нужно $n+1$ цирф, чтобы иметь возможность определить радиус $n+2$-го цирф…
Теперь, как сделать это? 92$$
Зная $k_1, k_2,…,k_{n+1}$, можно определить кривизну $n+2$-й окружности и, следовательно, ее радиус.
Об этой формуле даже есть стихотворение!
$\endgroup$
1
$\begingroup$
Если стол является обязательным, то достаточно большая четвертая сфера может быть предотвращена (столом) от соприкосновения с самой маленькой другой сферой. И если гравитация не исключена, крупный может упасть с насеста. 🙂
$\endgroup$
$\begingroup$
Представьте, что все три шара касаются друг друга. Четвертый должен ровно помещаться в середину этих трех шаров.

 Среди дворняжек поровну больших, маленьких и средних. Сколько больших породистых собак привезли на выставку?
Среди дворняжек поровну больших, маленьких и средних. Сколько больших породистых собак привезли на выставку?

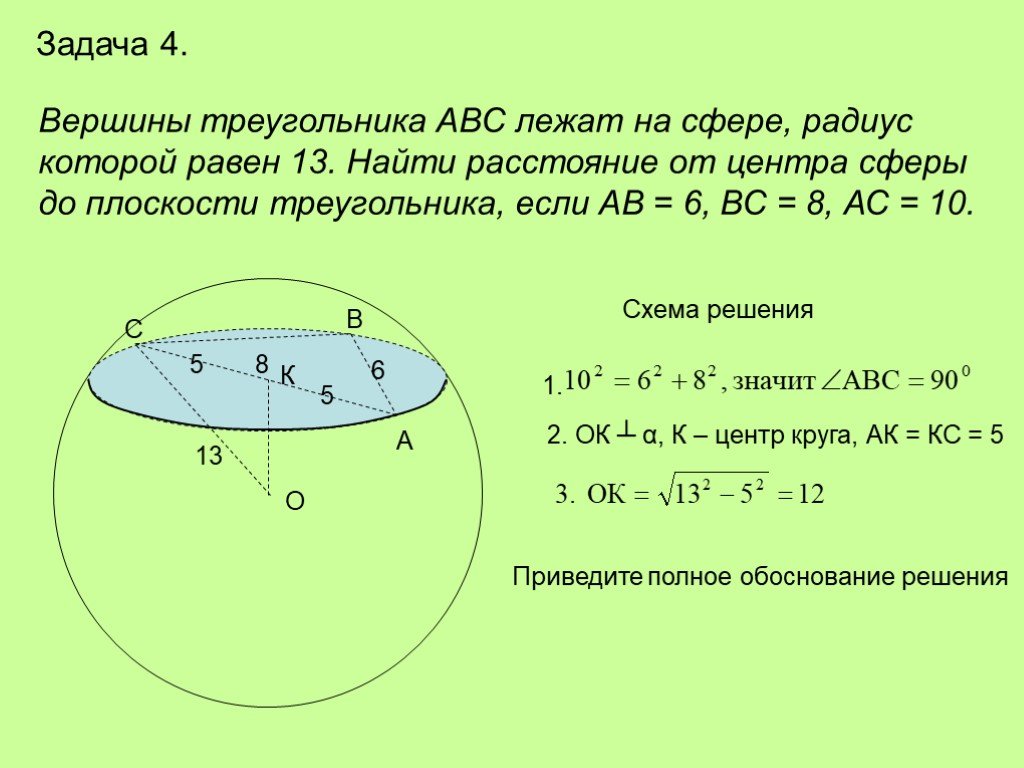
 Определите высоту «горки» из четырех шаров.
Определите высоту «горки» из четырех шаров.
 Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/ 2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k+1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/ 2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k+1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды. 
 Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов.
Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов. Д., Вернер А. Л., Рыжик В. И. Стереометрия. Геометрия в пространстве: Учеб. пособие для уч. ст. кл. и абитуриентов. — Висагинас, Alfa, 1998.— 576 с.
Д., Вернер А. Л., Рыжик В. И. Стереометрия. Геометрия в пространстве: Учеб. пособие для уч. ст. кл. и абитуриентов. — Висагинас, Alfa, 1998.— 576 с.
Leave A Comment