Значения функции и точки максимума и минимума
Значения функции и точки максимума и минимума
 Наибольшее значение функции
Наибольшее значение функции
Наменьшее значение функции
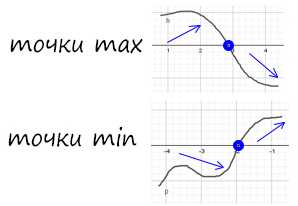
Точки max
Точки min
Как говорил крестный отец: «Ничего личного». Только производные!
Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Найти точку максимума / минимума
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ:
Найдите точку максимума функции
- Берем производную:
- Приравняем ее к нулю:
- Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15
Найдите точку минимума функции
- Преобразуем и возьмем производную:
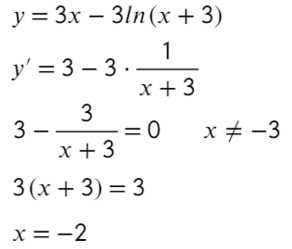
- Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.
- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.
- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]
- Преобразуем и возьмем производную:

- «3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?
- Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:
Ответ: −6
Найдите наибольшее значение функции на отрезке [0; 1,5π]
- Берем производную:
- Находим, чему равняется sin(x):
- Но такое невозможно! Sin(x)…
- Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
- В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
Будь в курсе новых статеек, видео и легкого математического юмора.
ik-study.ru
Как найти точки минимума и максимума функции: особенности, способы и примеры
Функция и исследование ее особенностей занимает одно из ключевых глав в современной математике. Главная составляющая любой функции — это графики, изображающие не только ее свойства, но также и параметры производной данной функции. Давайте разберемся в этой непростой теме. Итак, как лучше искать точки максимума и минимума функции?
Функция: определение
Любая переменная, которая каким-то образом зависит от значений другой величины, может называться функцией. Например, функция f(x2) является квадратичной и определяет значения для всего множества х. Допустим, что х = 9, тогда значение нашей функции будет равно 92= 81.
Функции бывают самых разных видов: логические, векторные, логарифмические, тригонометрические, числовые и другие. Их изучением занимались такие выдающиеся умы, как Лакруа, Лагранж, Лейбниц и Бернулли. Их труды служат оплотом в современных способах изучения функций. Перед тем как найти точки минимума, очень важно понять сам смысл функции и ее производной.
Производная и ее роль
Все функции находятся в зависимости от их переменных величин, а это значит, что они могут в любой момент изменить свое значение. На графике это будет изображаться как кривая, которая то опускается, то поднимается по оси ординат (это все множество чисел «y» по вертикали графика). Так вот определение точки максимума и минимума функции как раз связано с этими «колебаниями». Объясним, в чем эта взаимосвязь.
Производная любой функции изображается на графике с целью изучить ее основные характеристики и вычислить, как быстро изменяется функция (т.е. меняет свое значение в зависимости от переменной «x»). В тот момент, когда функция увеличивается, график ее производной будет также возрастать, но в любую секунду функция может начать уменьшаться, и тогда график производной будет убывать. Те точки, в которых производная переходит со знака минуса на плюс, называются точками минимума. Для того чтобы знать, как найти точки минимума, следует лучше разобраться с понятием производной.
Как вычислять производную?
Определение и вычисление производной функции подразумевает под собой несколько понятий из дифференциального исчисления. Вообще, само определение производной можно выразить следующим образом: это та величина, которая показывает скорость изменения функции.

Математический способ ее определения для многих учеников кажется сложным, однако на самом деле все гораздо проще. Необходимо лишь следовать стандартному плану нахождения производной любой функции. Ниже описано, как можно найти точку минимума функции, не применяя правила дифференцирования и не заучивая таблицу производных.
- Вычислить производную функции можно с помощью графика. Для этого необходимо изобразить саму функцию, затем взять на ней одну точку (точка А на рис.) Вертикально вниз провести линию к оси абсцисс (точка х0), а в точке А провести касательную к графику функции. Ось абсцисс и касательная образуют некий угол а. Для вычисления значения того, насколько быстро возрастает функция, необходимо вычислить тангенс этого угла а.
- Получается, что тангенс угла между касательной и направлением оси х является производной функции на маленьком участке с точкой А. Данный метод считается геометрическим способом определения производной.
Способы исследования функции
В школьной программе математики возможно нахождение точки минимума функции двумя способами. Первый метод с помощью графика мы уже разобрали, а как же определить численное значение производной? Для этого потребуется выучить несколько формул, которые описывают свойства производной и помогают преобразовать переменные величины типа «х» в числа. Следующий метод является универсальным, поэтому его можно применять практически ко всем видам функций (как к геометрическим, так и логарифмическим).
- Необходимо приравнять функцию к функции производной, а затем упростить выражение, используя правила дифференцирования.
- В некоторых случаях, когда дана функция, в которой переменная «х» стоит в делителе, необходимо определить область допустимых значений, исключив из нее точку «0» (по простой причине того, что в математике ни в коем случае нельзя делить на ноль).
- После этого следует преобразовать изначальный вид функции в простое уравнение, приравняв все выражение к нулю. Например, если функция выглядела так: f(x) = 2x3+38x, то по правилам дифференцирования ее производная равна f'(x) = 3x2+1. Тогда преобразуем это выражение в уравнение следующего вида: 3x2+1 = 0.
- После решения уравнения и нахождения точек «х», следует изобразить их на оси абсцисс и определить, является ли производная в этих участках между отмеченными точками положительной или отрицательной. После обозначения станет ясно, в какой точке функция начинает убывать, то есть меняет знак с минуса на противоположный. Именно таким способом можно найти как точки минимума, так и максимума.
Правила дифференцирования
Самая основная составляющая в изучении функции и ее производной — это знание правил дифференцирования. Только с их помощью можно преобразовывать громоздкие выражения и большие сложные функции. Давайте ознакомимся с ними, их достаточно много, но все они весьма просты благодаря закономерным свойствам как степенных, так и логарифмических функций.
- Производная любой константы равна нулю (f(х) = 0). То есть производная f(х) = x5+ х — 160 примет такой вид: f’ (х) = 5x4+1.
- Производная суммы двух слагаемых: (f+w)’ = f’w + fw’.
- Производная логарифмической функции: (logad)’ = d/ln a*d. Эта формула применима ко всем видам логарифмов.
- Производная степени: (xn)’= n*xn-1. Например,(9x2)’ = 9*2x = 18x.
- Производная синусоидальной функции: (sin a)’ = cos a. Если sin угла а равен 0,5, то ее производная равна √3/2.
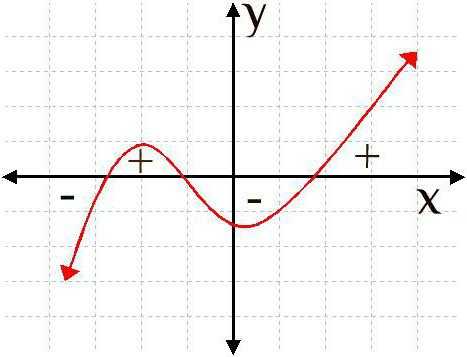
Точки экстремума
Мы уже разобрали, как найти точки минимума, однако существует понятие и точек максимума функции. Если минимум обозначает те точки, в которых функция переходит со знака минуса на плюс, то точками максимума являются те точки на оси абсцисс, на которых производная функции меняется с плюса на противоположный — минус.
Находить точки максимума можно по вышеописанному способу, только следует учесть, что они обозначают те участки, на которых функция начинает убывать, то есть производная будет меньше нуля.
В математике принято обобщать оба понятия, заменяя их словосочетанием «точки экстремумов». Когда в задании просят определить эти точки, это значит, что необходимо вычислить производную данной функции и найти точки минимума и максимума.
fb.ru
Максимумы, минимумы и экстремумы функций
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).
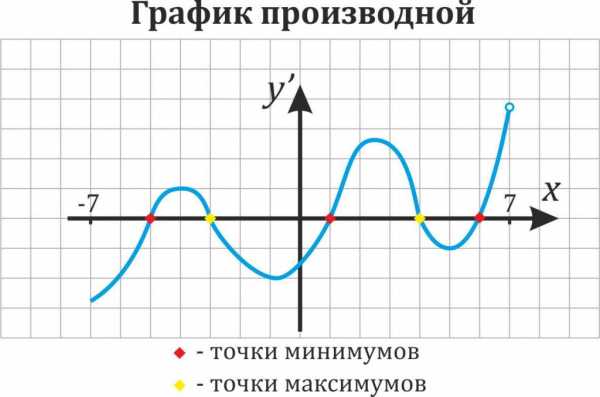
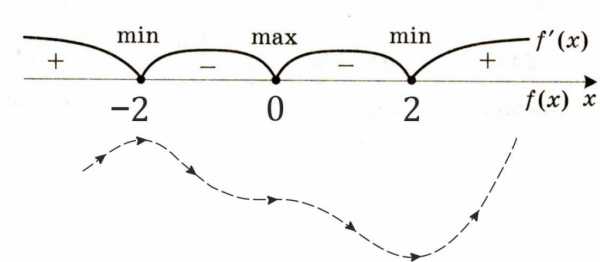
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки \(-13\), \(-11\), \(-9\),\(-7\) и \(3\). Количество точек экстремума функции – \(5\).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
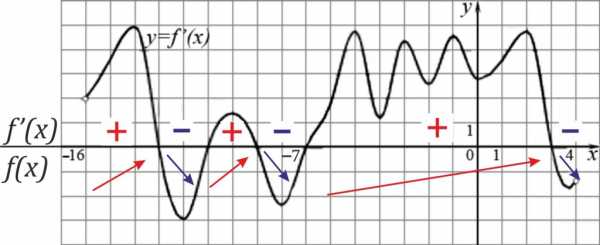
Начнем с \(-13\): до \(-13\) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что \(-13\) – точка максимума.
\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.
\(- 9\): функция возрастает, а потом убывает – максимум.
\(-7\): минимум.
\(3\): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции \(f'(x)\).
- Найдите корни уравнения \(f'(x)=0\).
- Нарисуйте ось \(x\) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью \(f'(x)\), а под осью \(f(x)\).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если \(f’(x)\) изменила знак с «\(+\)» на «\(-\)», то \(x_1\) – точка максимума;
— если \(f’(x)\) изменила знак с «\(-\)» на «\(+\)», то \(x_3\) – точка минимума;
— если \(f’(x)\) не изменила знак, то \(x_2\) – может быть точкой перегиба.
Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.
Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:
\(15x^4-60x^2=0\) \(|:15\)
\(x^4-4x^2=0\)
\(x^2 (x^2-4)=0\)
\(x=0\) \(x^2-4=0\)
\(x=±2\)
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является \(-2\).
Ответ. \(-2\).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
cos-cos.ru
Экстремумы функции, максимум и минимум
ОПРЕДЕЛЕНИЕЭкстремумами (максимумами и минимумами) функции называются значения функции в точках максимума и минимума.
Точки экстремума функции
Говорят, что в точке максимум (минимум), если существует такая -окрестность точки — , что для всех из этой окрестности, отличных от выполняется неравенство .
ОПРЕДЕЛЕНИЕТочки максимума и минимума называются точками экстремума.
ОПРЕДЕЛЕНИЕ Точки области определения, в которых производная функции равна нулю или не существует, называются критическими точками.Необходимое условие существования экстремума функции. Пусть функция дифференцируема в промежутке . Если в некоторой точке функция имеет экстремум, то в этой точке производная равна нулю: .
Достаточное условие существования экстремума функции. Если производная функции равна нулю в точке и при переходе через эту точку в сторону возрастания меняет знак с «+» («-») на «-» («+»), то в точке функция имеет максимум (минимум). Если же при переходе через точку производная функции не меняет знак, то в этой точке функция экстремума не имеет.
Для исследования функции на экстремум необходимо:
- найти критические точки функции;
- проверить, изменяет ли знак производная функции при переходе через критическую точку;
- вычислить значения максимума или минимума .
Примеры исследования функции на экстремум
ПРИМЕР 1| Задание | Найти экстремум функции |
| Решение | Найдем критические точки функции, для этого вычислим производную заданной функции
приравняем её к нулю и найдем корни полученного квадратного уравнения
Получили две критические точки . Обозначим найденные корни на числовой оси и определим знак производной на полученных интервалах. В точке производная меняет знак с «+» на «-», значит в этой точке максимум. Вычислим значение максимума
В точке производная меняет знак с «-» на «+», значит, — точка минимума. Значение минимума соответственно равно
|
| Ответ |
| Задание | Найти экстремум функции
|
| Решение | Область определения функции — вся числовая прямая, за исключением точки , то есть .
Вычислим производную заданной функции и найдем критические точки
Приравниваем к нулю производную
Получаем одну критическую точку . Обозначим на числовой оси область определения функции и найденную критическую точку и определим знак производной на полученных интервалах В точке производная меняет знак с «-» на «+», значит, в этой точке минимум. Значение минимума соответственно равно
|
| Ответ |
Монотонность функции
Нули функции
Наибольшее и наименьшее значение функции
Точки перегиба функции
Промежутки выпуклости и вогнутости функции
Исследование функции
ru.solverbook.com
Как найти экстремум (точки минимума и максимума) функции
Простой алгоритм нахождения экстремумов. Учимся находить с bugaga.net.ru.- Находим производную функции
- Приравниваем эту производную к нулю
- Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)
- Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум
- Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.
Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.
Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.
https://bugaga.net.ru/ege/math/ekstremum.html bugaga.net.ru
Рассмотрим примерНаходим производную и приравниваем её к нулю:
Полученные значения переменных наносим на координатную прямую и высчитываем знак производной на каждом из промежутков. Ну например, для первого возьмём -2, тогда производная будет равна -0,24, для второго возьмём 0, тогда производная будет 2 , а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.
Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума.
Смотрите также:
Еще больше материалов для подготовки к ЕГЭ
bugaga.net.ru
матан коллоквиум / 12.Понятие экстренума.Определение максиимума,минимума,понятие критической точки,графическая иллюстрация критических точек
Экстре́мум (лат. extremum — крайний) в математике —максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть дана функция и— внутренняя точка области определенияТогда
Если неравенства выше строгие, то называется точкой строгого локального максимума или минимума соответственно.
Значение функции называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
Достаточные условия существования локальных экстремумов
является точкой строгого локального максимума. А если
то является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке
и
является точкой локального максимума. А если
и
то является точкой локального минимума.
Если чётно и, то- точка локального максимума. Есличётно и, то- точка локального минимума. Еслинечётно, то экстремума нет.
Максимум и минимум функции.
Приведем
точные определения точек
экстремума. Определение. Точка
x0 называется
точкой минимума функции f, если для всех
x из некоторой окрестности x0 выполняется
неравенство f(x) ≥ f(x0. Это
наглядно показано на рисунке 1: 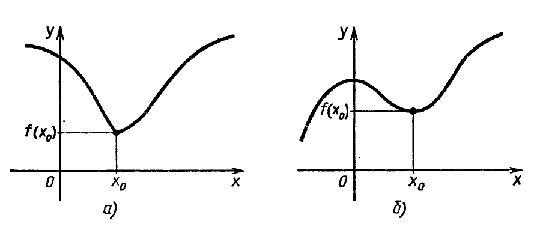 рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2:
рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2: 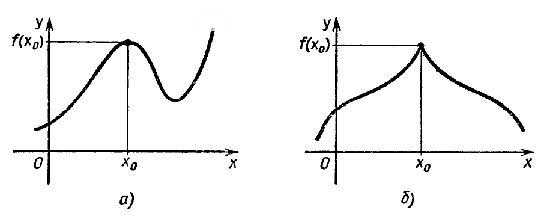 рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже: Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin.
рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже: Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin.
Критической точкой дифференцируемой функции , где — область в , называется точка, в которой все её частные производные обращаются в ноль. Это условие эквивалентно обращению в ноль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.
studfiles.net
Исследование графика функции. Минимум и максимум
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.
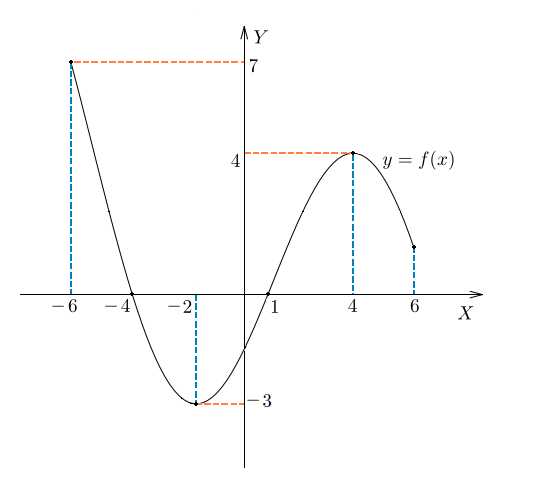
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru

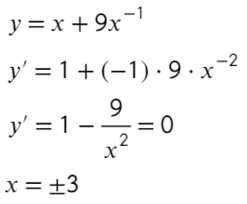
Leave A Comment