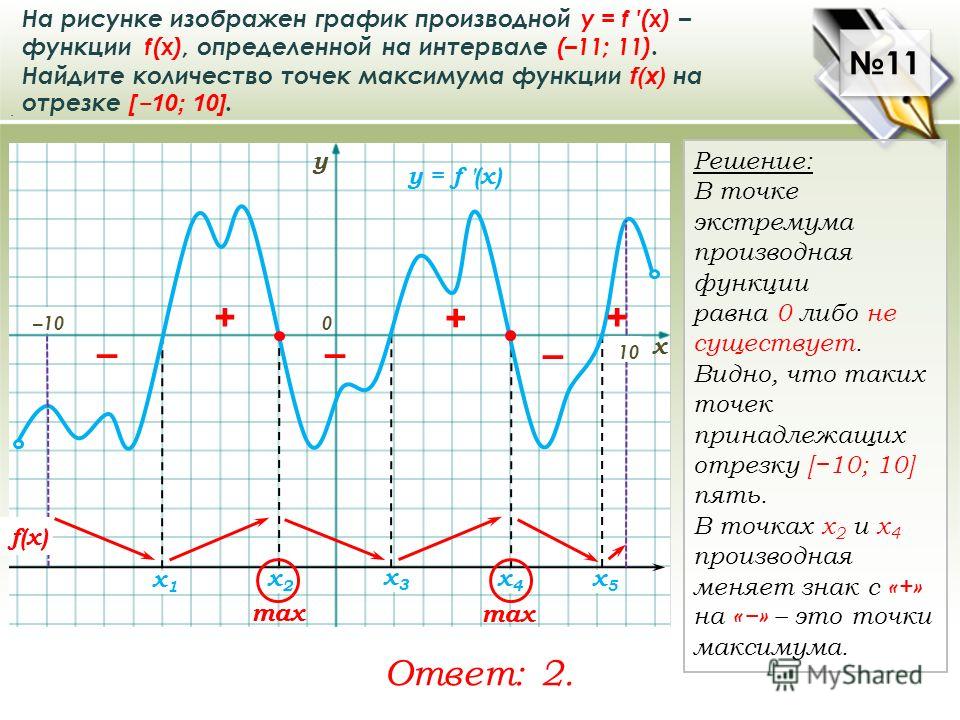
Экстремумы функции онлайн
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word. Если же задана функция f(x,y), следовательно, необходимо найти экстремум функции двух переменных. Также можно найти интервалы возрастания и убывания функции.- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
y =
на отрезке [;]Включать теорию
Правила ввода функций:
Вместе с этим калькулятором также используют следующие:
Асимптоты функции
Уравнение касательной к графику функции
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Необходимое условие экстремума функции одной переменной
Уравнение f’0(x*) = 0 — это необходимое условие экстремума функции одной переменной, т. е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
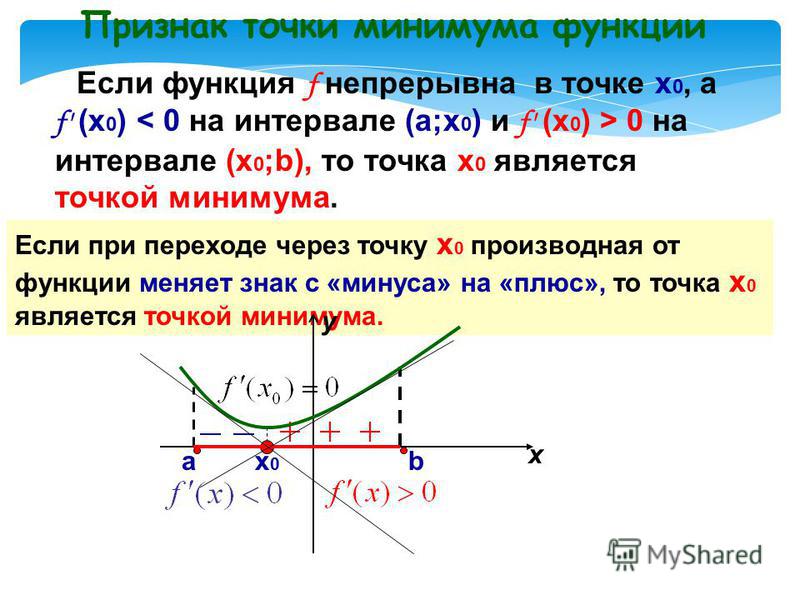
Достаточное условие экстремума функции одной переменной
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:f’0(x*)
f»0(x*) > 0 то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f’0(x*) = 0
f»0(x*) < 0
Пример №1. Найти наибольшее и наименьшее значения функции:
на отрезке [1; 3].
Решение.
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)=5/2, f(3)=3 8/81
Ответ: fmin=5/2 при x=2; fmax=9 при x=1
Пример №2. С помощью производных высших порядков найти экстремум функции y=x-2sin(x).
Решение.
Находим производную функции: y’=1-2cos(x). Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=±π/3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x=
Пример №3. Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение.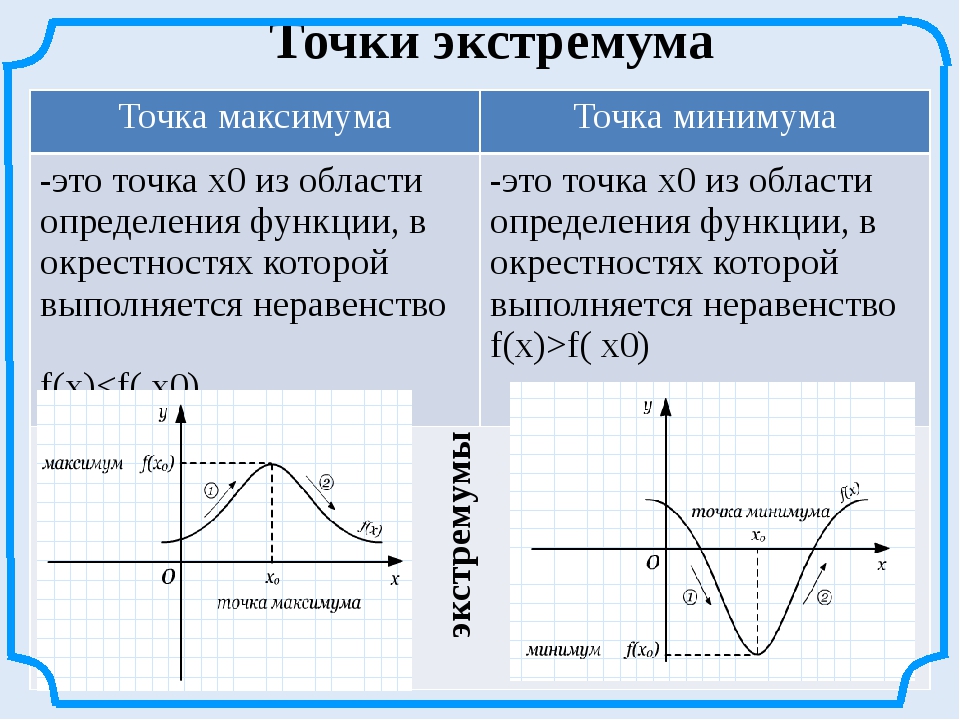 Здесь необходимо найти экстремумы функции. Если экстремум
Здесь необходимо найти экстремумы функции. Если экстремум x=0, то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x
Пример №4. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x2
Наибольший объем цилиндра
Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R.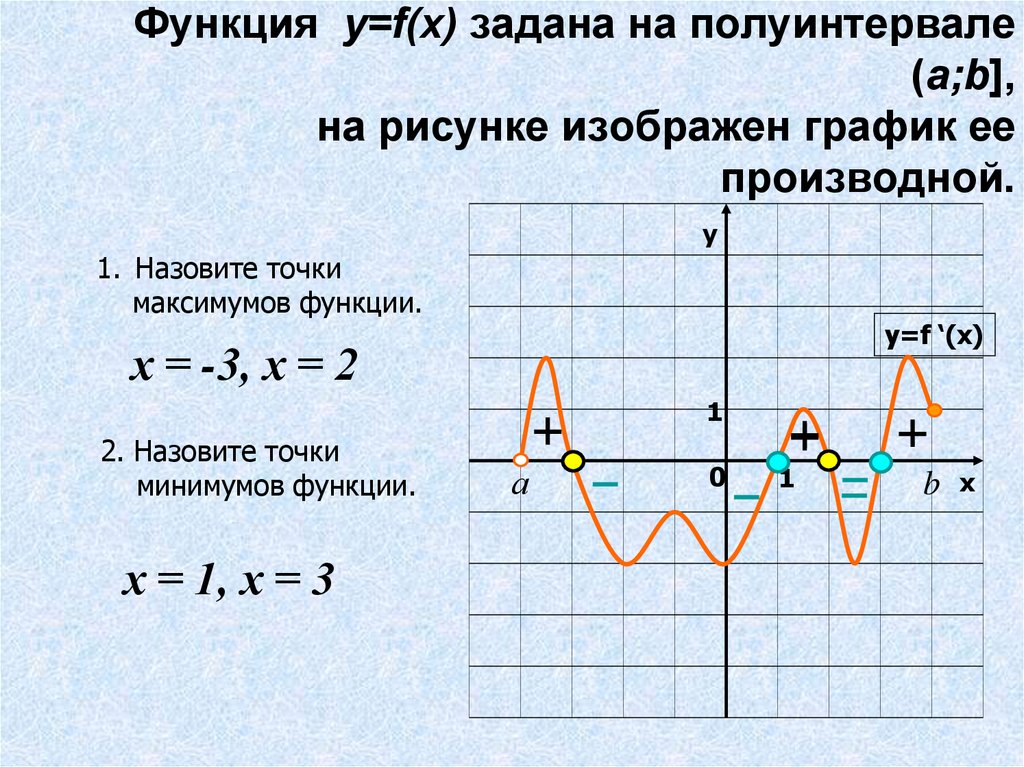
Решение:
Объем цилиндра равен: V = πr2H
где H = 2h,
Подставим эти значения в целевую функцию.
V → max
Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервиса
Производная онлайни приравняем ее к нулю.
dV/dh = 2πR2 — 6πh2
dV/dh = 0
2πR2 — 6πh2 = 0 или R2 = 3h2
Откуда
При высоте и радиусе основания размеры цилиндра будут наибольшими.
Как найти точки минимума и максимума функции, анализируя функцию, её производную и область определения
Поиск точки максимума и минимума функции — довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом «экстремум» подразумевают наибольшее или наименьшее значение функции. Это не совсем верно.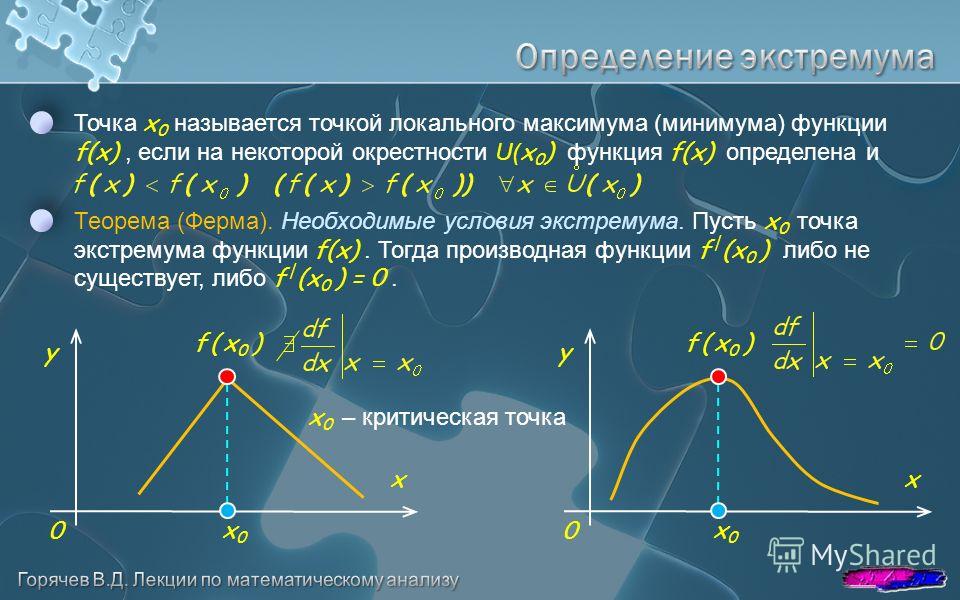 Значение может быть наибольшим или минимальным, но не являться экстремумом.
Значение может быть наибольшим или минимальным, но не являться экстремумом.
Содержание:
- Глобальный и локальный максимум
- Исследование
- Область допустимых аргументов
- Асимптоты
- Производная и экстремумы
- Концы интервала и сравнение результатов
- Видео
Глобальный и локальный максимум
Максимум бывает локальным или глобальным
Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.
Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.
Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:
- экстремума, если она попадает в указанный отрезок,
- разрыва,
- ограничивающей заданный отрезок.
Исследование
Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):
- Найти область допустимых аргументов и пересечения этой области с областью исследования.
- Выявить асимптоты. Они равны пределу при стремлении аргумента к точкам разрыва.
- Определить первую производную и вычислить экстремальные точки и выяснить поведение функции в окрестности этих точек.
- Рассчитать значение f(x) в точках, ограничивающих область исследования.
 2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.
Асимптоты
Асимптота — это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.
Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется.
 3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
3. У неё не может быть экстремумов, она убывает на всей оси аргументов.2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной.
После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).
Концы интервала и сравнение результатов
При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.
Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.

Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.
Видео
Как найти максимальные значения
Все ресурсы AP Расчет AB
3 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
AP Calculus AB Справка » Как найти максимальные значения
Каков локальный максимум когда ?
Возможные ответы:
Локального максимума нет.
Правильный ответ:
Пояснение:
Чтобы найти максимум, нам нужно посмотреть на первую производную.

Чтобы найти первую производную, мы можем использовать правило степени. Для этого мы уменьшаем показатель степени переменных на единицу и умножаем на исходный показатель степени.
Мы будем считать, что все в нулевой степени равно единице.
Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.
Глядя на первую производную, помните, что если результат этого уравнения положительный, исходная функция возрастает. Если производная отрицательна, то функция убывает.
Обратите внимание, что меняется с положительного на отрицательное, когда .
Мы можем найти этот корень, используя квадратное уравнение:
Поскольку мы ищем отрицательное значение, мы вычтем.
Таким образом, максимальное значение равно .
Сообщить об ошибке
Каков локальный максимум между и ?
Возможные ответы:
Между этими двумя точками нет максимума.

Объяснение:
Чтобы найти максимум, мы должны найти, где график смещается от возрастания к убыванию. Чтобы узнать скорость, с которой график смещается с увеличения на уменьшение, мы смотрим на вторую производную и видим, когда значение меняется с положительного на отрицательное.
Другими словами, мы посмотрим на вторую производную и увидим, где (если вообще) график пересекает ось x и движется от положительного значения y к отрицательному значению y.
Теперь надо найти вторую производную. К сожалению, производные триггерных функций нужно запоминать. Первая производная:
.
Чтобы найти вторую производную, мы берем производную нашего результата.
.
Следовательно, вторая производная будет .
Пересекает ли наше новое уравнение ось x и движется ли оно от положительного к отрицательному между и ? Да.
 Это происходит один раз, когда . Поэтому наш локальный максимум будет при . Подставьте это значение обратно в наше первое уравнение, чтобы найти, что максимум будет в точке .
Это происходит один раз, когда . Поэтому наш локальный максимум будет при . Подставьте это значение обратно в наше первое уравнение, чтобы найти, что максимум будет в точке .Сообщить об ошибке
Найдите координату x максимума за интервал .
Возможные ответы:
6
0
5
-2
2
Правильный ответ:
2
Объяснение:
Сначала найдите производную, а именно:
Приравняйте ее к нулю, чтобы получить критические точки:
Вы также должны принять во внимание -1 и 2 как критические точки, поскольку они являются вашими конечными точками. . Оцените каждую из этих критических точек в исходной функции:
Максимум — ваш максимум. Координата x равна 2,9.0005
Сообщить об ошибке
Найдите значение, при котором функция достигает своего локального максимума.

Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти максимум, нам нужно найти критические точки. Для этого нужно найти производную функции.
И мы видим, что и являются критическими точками для этой функции.
Простой способ узнать, что является максимальным, а какое — минимальным, состоит в том, чтобы подставить значения критических точек в исходное уравнение.
и
Следовательно, максимальное значение равно 3, а значение, при котором функция достигает максимума, равно 0.
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы AP Calculus AB
3 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
Локальный максимум и минимум, поиск локального максимума и минимума
LearnPracticeDownload
Локальные максимум и минимум — это точки функций, которые дают максимальный и минимальный диапазон.
 Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума.
Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума.Давайте узнаем больше о том, как найти локальный максимум и минимум, о методах поиска локального максимума и минимума, а также о примерах локального максимума и минимума.
1. Что такое локальный максимум и минимум? 2. Методы поиска локального максимума и минимума 3. Важные условия для местных максимумов и минимумов 4. Примеры локальных максимумов и минимумов 5. Практические вопросы 6. Часто задаваемые вопросы о локальном максимуме и минимуме Что такое локальный максимум и минимум?
Локальные максимумы и минимумы — это входные значения, для которых функция выдает максимальное и минимальное выходные значения соответственно.
 Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции.
Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции.Рассмотрим функцию f(x). Входное значение \(x_1\), для которого \(f(x_1)\) > 0, называется локальным максимумом, а \(f(x_1)\) — локальным максимальным значением, а входное значение \( x_1\), для которых \(f(x_2)\) < 0, называется локальным минимумом, а \(f(x_2)\) - локальным минимальным значением. Локальный максимум и минимум рассчитываются только для определенного интервала и не применяются ко всему диапазону функции.
методов поиска локального максимума и минимума
Локальный максимум и минимум можно определить, взяв производную от заданной функции. Проверка первой производной и проверка второй производной полезны для нахождения локального максимума и минимума. Давайте разберемся подробнее в каждом из этих тестов.
Проверка первой производной
Проверка первой производной помогает найти поворотные точки, в которых выход функции имеет максимальное или минимальное значение.
 Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.
Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.- Если f ′(x) меняет знак с положительного на отрицательный по мере увеличения x через c, т. е. если f ′(x) > 0 в каждой точке, достаточно близкой к c и слева от нее, и f ′(x) < 0 в каждой точке, достаточно близкой и правее от c, то c является точкой локальных максимумов.
- Если f ′(x) меняет знак с отрицательного на положительный по мере увеличения x через c, т. е. если f ′(x) < 0 в каждой точке, достаточно близкой к c и слева от нее, и f ′(x) > 0 в каждой точке, достаточно близкой и правее от c, то c является точкой локального минимума.
- Если f ′(x) существенно не изменяется при увеличении x через c, то c не является ни точкой локальных максимумов, ни точкой локальных минимумов. Фактически такая точка называется точкой перегиба.

Следующие шаги помогут выполнить тест первой производной и найти предельные точки.
- Найдите первую производную заданной функции и найдите предельные точки, приравняв выражение первой производной к нулю.
- Найдите по одной точке на соседней левой и правой стороне предельной точки и подставьте эти соседние точки в функции первой производной.
- Если для соседней точки слева производная функции положительна, а для соседней точки справа отрицательна, то предельной точкой являются локальные максимумы.
- Если производная функции отрицательна для соседней точки слева, а положительна для соседней точки справа, то предельной точкой являются локальные минимумы.
Проверка второй производной
Проверка второй производной — это систематический метод нахождения абсолютного максимума и абсолютного минимума значения функции с действительным знаком, заданной на замкнутом или ограниченном интервале. Здесь мы рассматриваем дважды дифференцируемую функцию f(x), определенную на отрезке I, и точку x=k, принадлежащую этому отрезку (I).
 Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной.
Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной.- x = k, является точкой локальных максимумов, если f'(k) = 0 и f»(k) < 0. Точка при x = k является локальным максимумом, а f(k) называется локальное максимальное значение f(x).
- x = k является точкой локальных минимумов, если f'(k) = 0 и f»(k) >0 . Точка при x = k является локальным минимумом, а f(k) называется локальным минимальным значением f(x).
- Тест не пройден, если f'(k) = 0 и f»(k) = 0. А точка x = k называется точкой перегиба.
Следующая последовательность шагов облегчает проверку второй производной, чтобы найти локальные максимумы и локальные минимумы функции с действительным знаком.
- Найти первую производную f'(x) функции f(x) и приравнять первую производную к нулю f'(x) = 0, к предельным точкам \(x_1, x_2\).
- Найдите вторую производную функции f»(x) и подставьте предельные точки во вторую производную\(f»(x_1), f»(x_2)\).
 .
. - Если вторая производная больше нуля\(f»(x_1) > 0\), то предельная точка \((x_1)\) является локальным минимумом.
- Если вторая производная меньше нуля \(f»(x_2)<0\), то предельной точкой \((x_2)\) являются локальные максимумы.
Важные условия для местного максимума и минимума
Следующие важные термины полезны для лучшего понимания локальных максимумов и минимумов.
- Максимум: Максимальное входное значение x, при котором функция f(x) имеет максимальный выход, называется максимумом функции. Обычно он определяется в пределах интервала и также называется локальным максимумом.
- Абсолютный максимум: Абсолютный максимум — это точка x во всем диапазоне функции f(x), в которой она имеет максимальное значение. Абсолютный максимум также иногда называют глобальным максимумом.
- Минимум: Минимальное входное значение x, при котором функция f(x) имеет минимальный выход, называется минимумом функции.
 Обычно он определяется в пределах интервала и также называется локальным минимумом.
Обычно он определяется в пределах интервала и также называется локальным минимумом. - Абсолютный минимум: Абсолютный минимум — это точка x во всем диапазоне функции f(x), в которой она имеет минимальное значение. Абсолютный минимум также иногда называют глобальным минимумом.
- Точка инверсии: Значение x в области определения f(x), которое не является ни локальным максимумом, ни локальным минимумом, называется точкой инверсии. Точки в непосредственной близости слева и справа от точки инверсии имеют нулевой наклон.
- Максимальное значение: Выход, полученный функцией f(x) при подстановке значения точки локального максимума вместо x, называется максимальным значением функции. Это максимальное значение функции во всем диапазоне функции.
- Минимальное значение: Выход, полученный функцией f(x) при подстановке значения точки локального минимума вместо x, называется минимальным значением функции.
 Это минимальное значение функции во всем диапазоне функции.
Это минимальное значение функции во всем диапазоне функции. - Теорема об экстремальном значении: Для функции f, заданной на отрезке [a, b] и непрерывной на этом отрезке, существуют точки c, d на интервале [a, b], в которых эта функция f достигает максимального и минимального значения. ф(с) > f(x) > f(d).
Связанные темы
Следующие темы помогают лучше понять локальные максимум и минимум.
- Производная формула
- Дифференциация
- Теорема о среднем значении
- Теорема Ролля
- Формула дифференциальных уравнений
- Применение деривативов
Примеры локального максимума и минимума
Пример 1: Найдите локальные максимумы и локальные минимумы функции f(x) = 2x 3 + 3x 2 — 12x + 5, используя критерий первой производной.
Решение:
Данная функция такова: f(x) = 2x 3 + 3x 2 — 12x + 5
f'(x) = 6x 2 6′ 9004 + (х) = 0; 6x 2 — 6x — 12 = 0, 6(x 2 + x — 2) = 0, 6(x — 1)(x + 2) = 0
Следовательно, предельные точки x = 1 и x = -2.

Возьмем точки в непосредственной близости от x = 1. Это точки {0, 2}.
f'(0) = 6(0 2 + 0 — 2) = 6(-2) = -12 и f'(2) = 6(2 2 + 2 — 2) = 6( 4) = +24
Производная функции отрицательна слева от x = 1 и положительна справа. Следовательно, x = 1 — локальные минимумы.
Теперь возьмем точки в непосредственной близости от x = -2. Очки равны {-3, -1}.
f'(-3) = 6((-3) 2 + (-3) — 2) = 6(4) = +24 и f'(-1) = 6((-1) 2 + (-1) -2) = 6(-2) = -12
Производная функции положительна слева от x = -2 и отрицательна справа. Следовательно, x = -2 — локальные максимумы.
Следовательно, локальные максимумы равны -2, а локальные минимумы -1.
Пример 2: Найти локальные максимумы и локальные минимумы функции f(x) = x 3 — 6x 2 +9x + 15. с использованием теста второй производной.
Решение:
Данной функцией является f(x) = x 3 — 6x 2 +9x + 15.

f'(x) = 3x + 2 90×78 — 12 Пусть us найти нули выражения. f'(x) = 0.
f'(x) = 3(x 2 — 4x + 3)
x 2 — 4x + 3 = 0 или (x — 1)(x — 3) =0.
Здесь х = 1, а х = 3
f»(x) = 6x — 12
f»(1) = 6(1) — 12 = 6 — 12 = -6., f» (1) < 0, а x = 1 — максимумы.
f»(3) = 6(3) — 12 = 18 — 12 = 6, f»(3) > 0, x = 3 — минимумы.
Следовательно, при использовании теста второй производной локальные максимумы равны 1 с максимальным значением f(1) = 19, а локальные минимумы равны 3 с минимальным значением f(3) = 15
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по локальному максимуму и минимуму
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о локальном максимуме и минимуме
Как найти локальный минимум и максимум?
Локальный минимум и максимум можно найти, продифференцировав функцию и найдя точки поворота, в которых наклон равен нулю.


 2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0. 3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
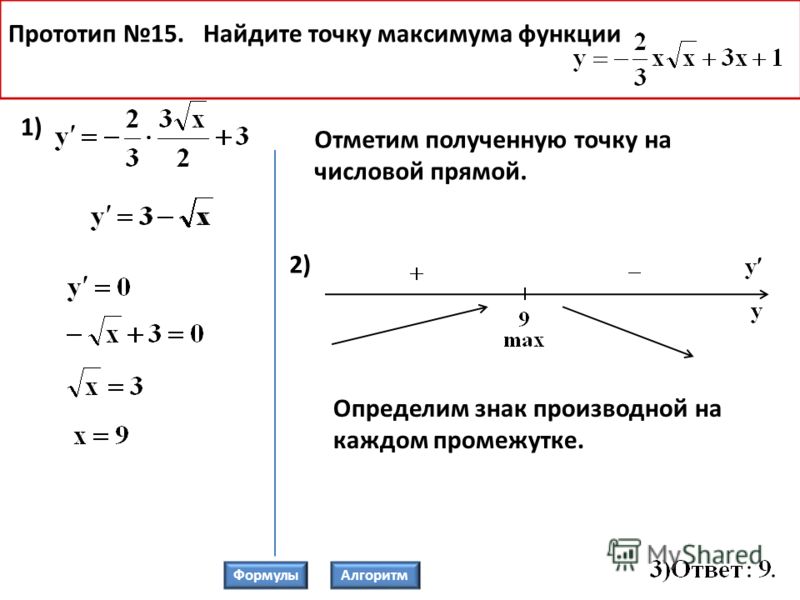

 Это происходит один раз, когда . Поэтому наш локальный максимум будет при . Подставьте это значение обратно в наше первое уравнение, чтобы найти, что максимум будет в точке .
Это происходит один раз, когда . Поэтому наш локальный максимум будет при . Подставьте это значение обратно в наше первое уравнение, чтобы найти, что максимум будет в точке .
 Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума.
Локальные максимумы и локальные минимумы можно вычислить, найдя производную функции. Тест первой производной и тест второй производной являются двумя важными методами нахождения локального максимума и локального минимума.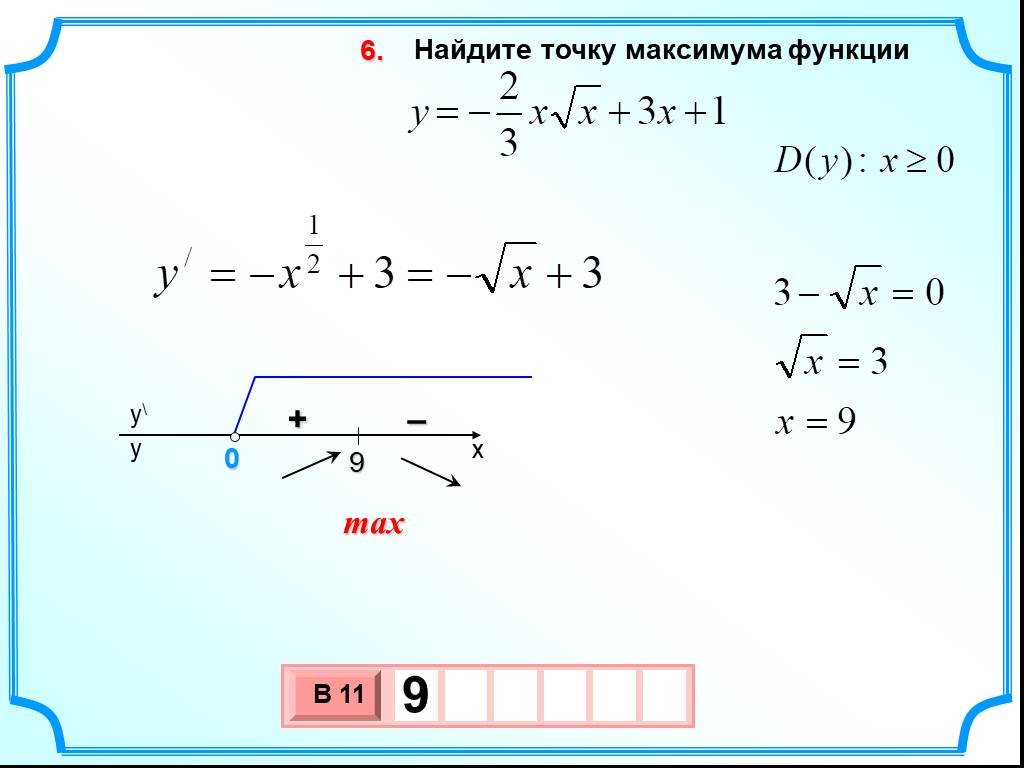 Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции.
Функциональное уравнение или графики недостаточно полезны для нахождения точек локальных максимумов и локальных минимумов. Производная функции очень полезна при нахождении локального максимума и локального минимума функции. Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.
Для теста первой производной. определим функцию f(x) на открытом интервале I. Пусть функция f(x) непрерывна в критической точке c интервала I. Здесь мы имеем следующие условия для отождествления локального максимума и минимума от первой производной тест.
 Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной.
Здесь у нас есть следующие условия для определения локального максимума и минимума из теста второй производной. .
. Обычно он определяется в пределах интервала и также называется локальным минимумом.
Обычно он определяется в пределах интервала и также называется локальным минимумом.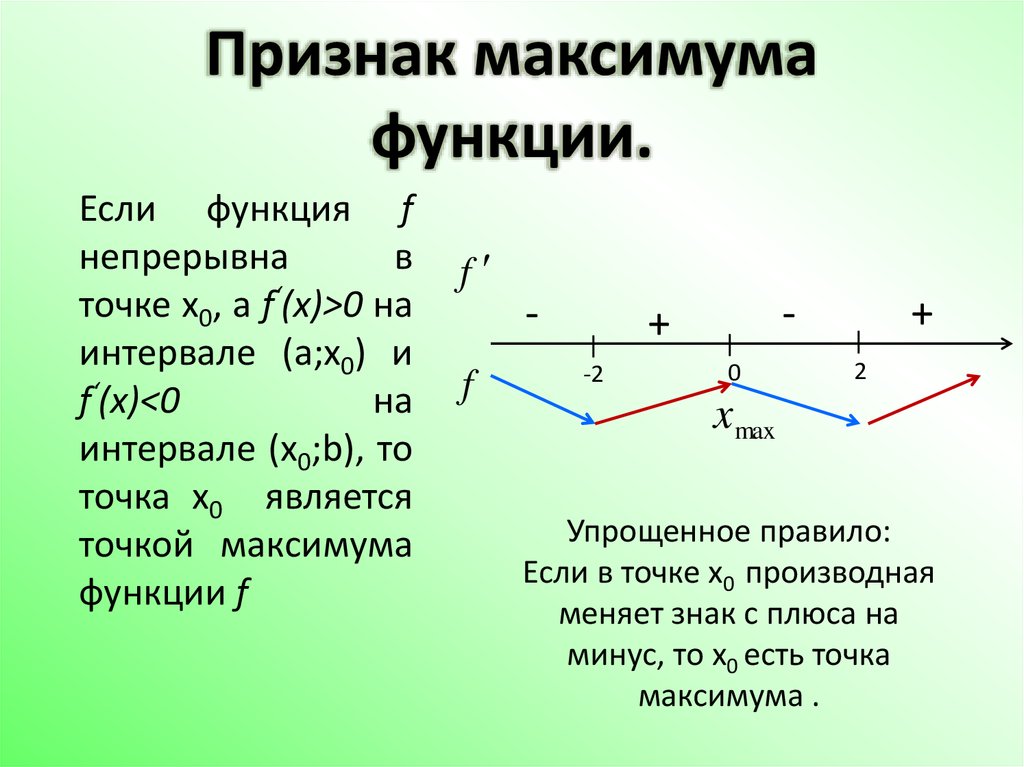 Это минимальное значение функции во всем диапазоне функции.
Это минимальное значение функции во всем диапазоне функции.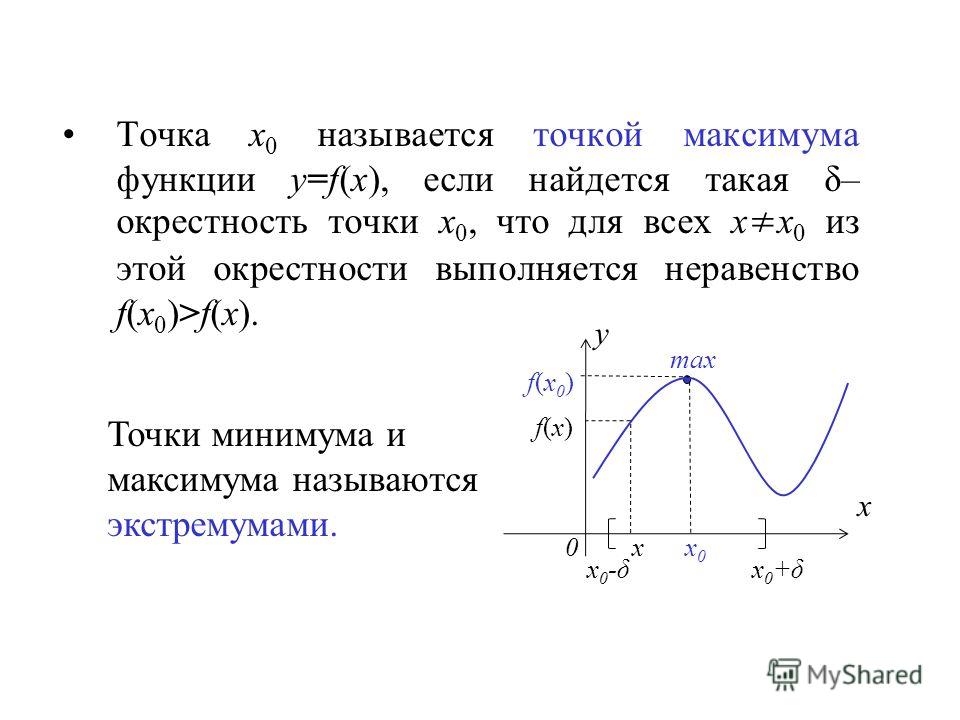

Leave A Comment