Ответ. $\mathrm{S}_{\Delta A B C}=3 \sqrt{3}$ (м2)
Остались вопросы?
Здесь вы найдете ответы.
Как можно вычислить площадь равсностороннего треугольника?
Согласно формуле, по которой вычисляется площадь S треугольника с равными сторонами, она равна:
S = √3/4*а, в которой а – это длина стороны фигуры.
Площадь можно также найти следующим образом:
S = a*h/2, где h – это высота.
Высоту можно вычислить, используя теорему Пифагора:
h = а² — (а/2)².
Как можно рассчитать площадь равностороннего треугольника, если известно, что площадь треугольной фигуры, отсекаемой от него средней линией, составляет 6 см. кв.?
Обозначим имеющийся треугольник с равными сторонами как АВС. Обозначим
длину стороны как а, и получим, что АВ=ВС=АС=а. Среднюю линию обозначим
как МК.
В случае с равносторонним треугольником:
S = а²√3/4
Зная свойство средней линии треугольника, можно записать следующее равенство:
МК = АС/2 = а/2.
В этом случае площадь отсекаемого треугольника равна:
Sмвк = (а/2)²*√3/4 = а²√3/16 см.кв.
В условии дано, что Sмвк = 6 см.кв., тогда:
а²√3/16 = 6
а² = 96/√3.
Площадь равностороннего треугольника:
S = а²√3/4 = (96√3)/(4√3) = 96/4 =24 см.кв.
Как можно вычислить площадь равностороннего треугольника при условии, что его периметр составляет 24 см.?
Найдем сторону равносторонней треугольной фигуры, разделив его периметр на 3:
а = 24:3 = 8 см.
Тогда площадь этой фигуры равна:
S =1/2a²sin 60° = 1/2*64*√3/2 = 16√3 см.кв.
Что представляет собой формула площади равностороннего треугольника?
Обозначив одну из сторон равносторонней треугольной фигуры как а, а высоту, проведенную к ней, — как h, то формула расчета площади этой фигуры будет выглядеть так:
S=ah/2.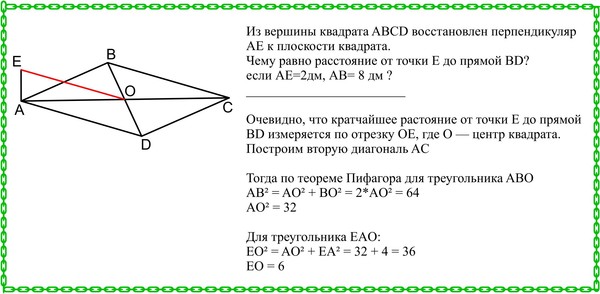
Принимая во внимание то, что все стороны данной треугольной фигуры равны, то его высоту можно выразить через сторону и вычислить, используя теорему Пифагора:
h² = а²-(а/2)² = h² = а²- а²/4 = 3а²/4
h = (а√3)/2
Тогда площадь данной фигуры равна:
S = ½ a* h = ½ a*(а√3)/2 = (a²√3)/4
Как выразить длину стороны а из формулы площади равностороннего треугольника?
Для расчета площади треугольника, длины всех сторон которого равны, используется формула:
S=a²√3/4
Перенесем 4 в правую часть равенства:
4S=a²√3.
Тогда:
a² = 4S/√3
а = √4S/√3.
Какая формула используется для вычисления площади равностороннего треугольника с длиной стороны а?
Если известно, что сторона равносторонней треугольной фигуры равна а, то его площадь рассчитывается так:
S = а²√3/4.
Треугольник имеет два катета – АВ и ВС. Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС.
Его гипотенуза – ВС. Так как
фигура является равносторонней, то АВ = АС.
Требуется доказать, что площадь треугольной фигуры, стороны которой одинаковы, равна произведению длин его катетов, разделенному на два.
Превратим имеющийся треугольник в квадрат, проведя перпендикуляр из его углов, и получим что:
ΔВАС = ΔВСD.
Площадь квадрата равна:
S = а*b.
Диагональ квадрата ВС является гипотенузой треугольника, которая делит квадрат на 2 равные части. Из этого следует, что площадь треугольника равна половине площади квадрата. Что и требовалось доказать.
Как вычислить площадь равностороннего треугольника со стороной длиной 9 см.?
Имеется треугольник АВС с равным сторонами.
ВН = 9 см.
Площадь данной фигуры находится по формуле:
S=1/2*АС*ВН,
в которой АС – основание треугольной фигуре, по длине равное любой из сторон (равносторонний Δ), ВН – высота.
Предположим, что АС = 2а см. Тогда:
Тогда:
АН = АС/2 = ½*2а = а см.
Согласно теореме Пифагора:
АВ² = ВН²+АН².
В данном случае:
(2а)² = 9²+а²
Переносим а² в правую часть уравнения:
4а²-а² = 81
Упрощаем:
3а² = 81.
Отсюда:
а² = 81/3 = 27
а=√27=√9×3=3√3 см.
Теперь можно найти площадь:
S=1/2*9*3√3=1/2*27/√3=27√3/2=13,5√3 см.кв.
Какому числу равна площадь равностороннего треугольника с основанием длиной 6 см.?
Известна формула расчета площади треугольника:
S=1/2*h*b.
Проведем высоту h, которая в равностороннем треугольнике представляет собой также биссектрису и медиану.
Воспользуемся теоремой Пифагора для вычисления высоты:
h = √(36-9) = √27 см.
Тогда:
S = h*3 = 3√27 см.кв.
Возможно ли привести доказательство того, что площадь равностороннего треугольника равна √3*a²/4, в которой длина его стороны обозначена как а?
Доказать, что приведенное в задании утверждение является верным, можно,
если превратить имеющуюся треугольную фигуру в параллелограмм/, площадь
которого равна произведению длины стороны и высоты. 2√3/4?
2√3/4?
Известно, что площадь любого треугольника можно найти по формуле:
S = 1/2*a*b*sinA,
в которой стороны треугольника обозначены как а и b, а угол, образованный ими, — как А.
Доказано, что каждый угол равносторонней треугольной фигуры составляют 60 градусов (sin60 =sqrt(3)/2), а его стороны имеют одинаковые длины. Если подставить эти значения в формулу, то получим:
S = a22√3/4.
Как найти площадь равностороннего треугольника при условии, что длина каждой его стороны составляет 12 см.?
Площадь треугольника с равными сторонами вычисляется по формуле:
S = √3/4*a².
В данном случае:
S= √3/4*12²= √3*144 /4*1 = 36√3 ≈ 62,35 см.кв.
Согласно формуле Герона:
S = √(р(р-а)(р-a)(p-a))
Для данного треугольника:
Р = 12*3 = 36 см.
Р = р/2 = 36/2 = 18 см.
Тогда:
S = √ (18× (18-12)³) = √(18*6³) = √(18×216)=√3888 ≈ 62,35 см. кв.
Как вычислить площадь правильного равностороннего треугольника, зная радиус круга R?
Площадь треугольника с одинаковыми сторонами считается как:
S = a²√3/4.
Радиус r окружности, которая вписана в данный Δ, равен a√3/6. Значит:
а = 2√3r.
Считаем площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильной треугольной фигуры, равен a/√3. Следовательно, а = R√3.
В этом случае:
S = R²*3√3/4 = 3√3R²/4.
Известно, что площадь правильного треугольника равна 100√3 м.кв. Как вычислить его сторону?
Площадь треугольника равна:
(a²√3)/4.
В данном случае:
100√3=(a²√3)/4
Тогда:
a²√3=400√3.
Находим а:
a²√3 = 400√3
a² = 400
a = 20 см.
Чему равна площадь правильного треугольника при условии, что диаметр окружности, вписанной в него, = 10 см.?
Если d = 10 см., то r = 10/2 = 5 см.
Известно, что:
r = а√3/6, где а – это длина стороны правильного Δ.
Значит:
5 = а√3/6.
Отсюда:
а = 30/√3 = 10√3 см.
Тогда:
SΔ = a²√3/4 =(10√3)³ *√3/4 = 75√3 см. кв.
кв.
Чему равна площадь правильного треугольника со стороной 4 дм.?
Известно, что:
S = 1/2 * a * a sin 60 = 1/2 * 4 * 4 * √3/2 = 4√3 дм.кв.
Площадь также можно найти так:
S = a²√3/4 = 16√3/4 = 4√3 дм.кв.
Как найти площадь правильного треугольника, зная, что длина описанной около него окружности равна 4Пи см.?
Длина окружности через радиус находится так:
L=2πR.
Значит:
R=L/2π=4π/2π=2 у.е.
Имеем правильный треугольник, значит длина его стороны:
a=R*√3=2√3 у.е.
Можем найти SΔ:
S = √3/4a² = √3/43*3 = 3√3 у.е.кв.
Чему равна площадь правильного треугольника и его стороны, если его высота = 14 см.?
В правильном треугольнике длины всех сторон одинаковы. Это значит, что каждую из них можно обозначить как х. Тогда:
Р (периметр) = х + х + х = 3х см.
Площадь будет равна:
S = 1/2 h * x = 14/2*x = 7х см.кв.
Как найти площадь правильного треугольника с равными сторонами при условии, что радиус круга R?
Площадь треугольной фигуры с равными сторонами считается как:
S = a²√3/4.
Радиус окружности, вписанной в этот Δ, составляет a√3/6. Тогда а = 2√3r.
Находим площадь треугольника:
S = 4*3r²√3/4 = 3√3r².
Радиус R окружности, которая описана около правильного Δ, составляет a/√3. Это означает, что а = R√3.
S = R²*3√3/4 = 3√3R²/4.
Как найти площадь правильного треугольника при условии, что расстояние от его центра до вершины составляет 2 м.?
Центр правильно треугольной фигуры также является центральной точкой описанной около нее окружности. Ее радиус представляет собой расстояние от центра до вершины фигуры:
а=R√3=2√3
Все углы в правильном треугольнике являются одинаковыми и равны по 60 градусов (180/3).
Площадь треугольной фигуры рассчитывается как:
а²sin60°/2=(2√3)²√3/2/2=6√3 м.кв.
Как найти площадь правильного треугольника, если определено, что сторона
имеет длину, аналогичную длине стороны ромба с диагоналями 10 см. и 12 см.?
и 12 см.?
Предположим, что BD = 10 см., а АС = 12 см.
Диагонали ромба перпендикулярны и делятся на две равные части, пересекаясь в определенной точке.
ΔАВО: ∠АОВ = 90°, АО = АС/2 = 6, ВО = BD/2 = 5.
Согласно теореме Пифагора:
АВ = √(АО² + ВО²) = √(36 + 25) = √41.
Треугольник имеет равные стороны, длина каждой из которых аналогична длине стороны ромба:
а = √41.
Тогда:
SΔ = a²√3/4 = 41√3/4 см.кв.
Как найти площадь правильного треугольника периметром 6 см.?
Если длина стороны правильного треугольника указана, то его площадь вычисляется следующим образом:
S = a²√3/4.
Согласно определению правильного треугольника, длины всех его сторон одинаковые. Исходя из этого можно найти его сторону, разделив периметр на три:
а = 6/3 = 2 см.
Ищем площадь, подставив в равенство значение а:
S = 2²√3/4 = S 4√3/4 = √3 см.кв.
Как найти площадь правильного треугольника при условии, что окружность,
которая вписана в него, имеет радиус длиной 4 см.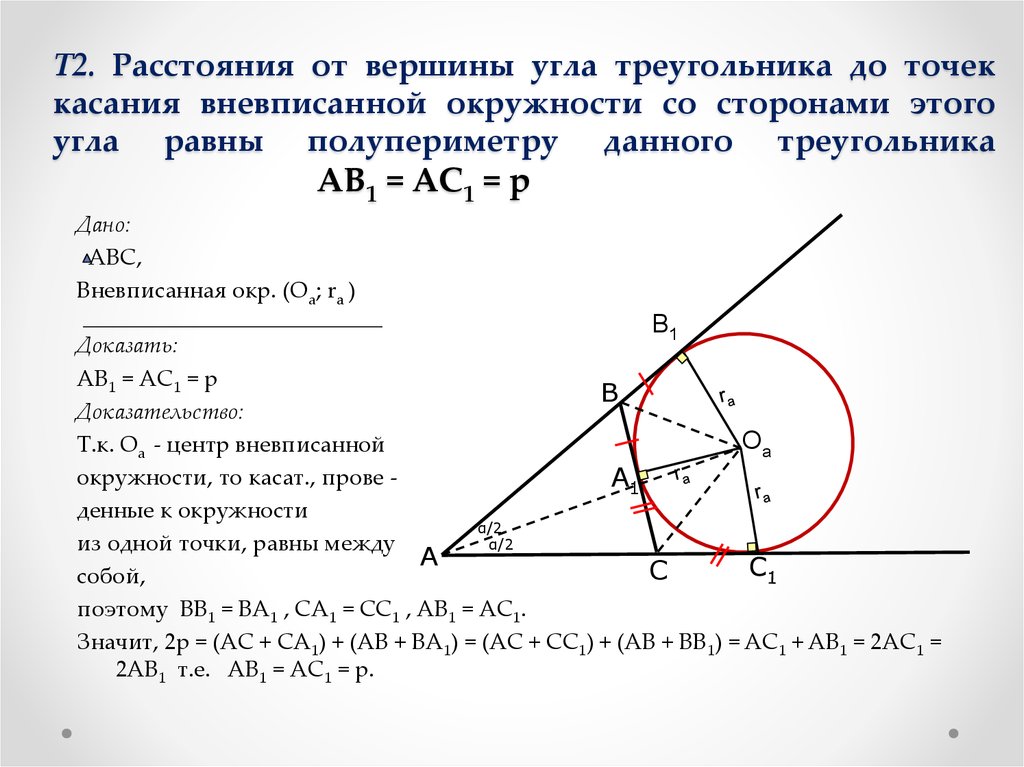 ?
?
Площадь треугольника, имеющего стороны одинаковой длины, может быть рассчитана через длину его стороны без применения формулы радиуса окружности, которая вписана в него. Для данной фигуры верно утверждение о том, что высота, биссектриса и медиана делятся в точке пересечения в отношении 2:1. При схематичном изображении можно увидеть, что треугольная фигура АВС включает 6 треугольников с прямыми углами, которые имеют одинаковый катет (R) и гипотенузу (АО=ВО=СО). Следовательно, площадь треугольника АВС будет представлять собой сумму площадей всех 6 треугольников, формирующих его.
Какова формула вычисления площади равностороннего треугольника со стороной а?
Если сказано, что сторона равносторонней треугольной фигуры равна а, то его площадь можно найти:
S = a²√3/4.
Как определить, чему равна длина стороны треугольника с равными сторонами, зная формулу, по которой вычисляется площадь равностороннего треугольника (S=√3/4 а²) и то, что она равна 9√3см²?
Если S=√3/4 а², то в данном случае S=9√3, что означает: 9√3=√3/4 а².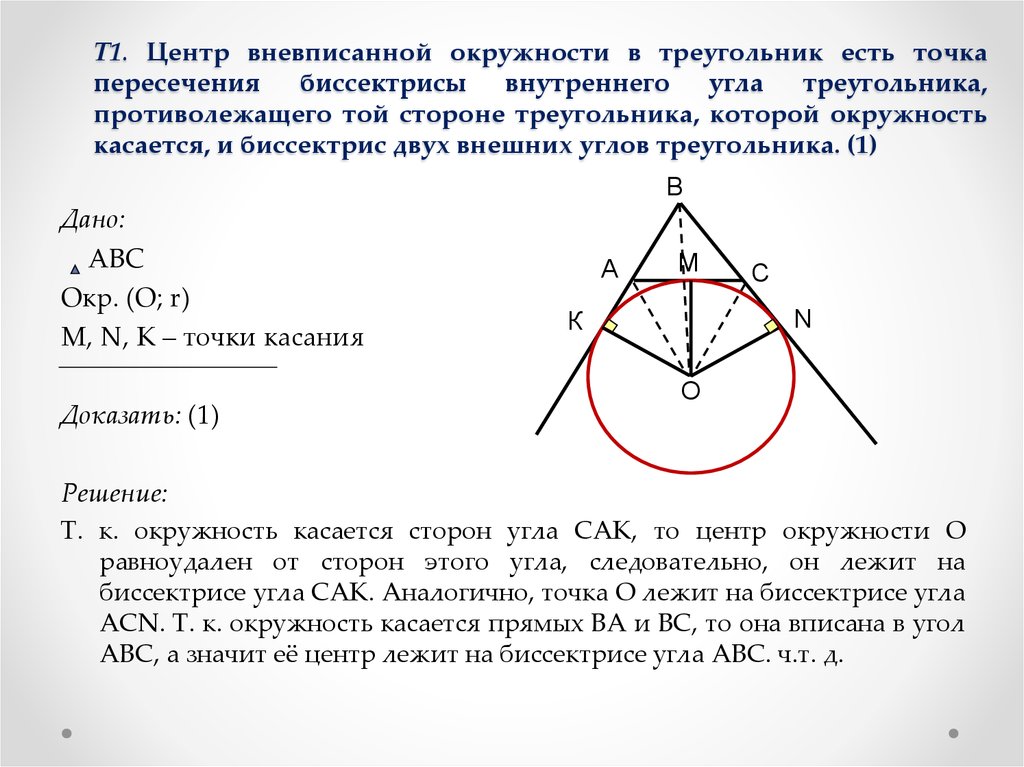
Выразим а²:
а² = 9√3:√3/4 = 9√3 x 4√3 = 36
а = +-√36 = +- 6.
Так как длина стороны не может быть отрицательным числом, то a = 6 см.
Какой вид имеет формула, которая отражает зависимость площади равностороннего треугольника от длины его сторон?
Доказано, что равносторонний треугольник имеет равные углы по 60 градусов. Также известна формула вычисления площади данной фигуры путем умножения длин двух его сторон и синуса угла, который они образуют:
S = 1/2*a*a*sin 60 = a²√3/4 см.кв.
Чему равна площадь равностороннего треугольника и длина его медианы, если известно, что его сторона составляет а?
Если указано, что длина стороны равностороннего треугольника составляет а, то его площадь равна:
S=a²√3/4.
Медиана, проведенная в треугольнике с равными сторонами, также представляет собой его биссектрису и высоту. Из этого следует, что:
h=a√3/2.
Ответ: Площадь треугольника = a²√3/4 см. кв., его медиана = a√3/2 см.
кв., его медиана = a√3/2 см.
Как определить площадь равностороннего треугольника со стороной, длина которой составляет 8√2 см?
В случае с треугольником с равными сторонами, высота представляет собой также медиану, делящую на две равные части сторону, на которую она опущена. Если применить в данном случае теорему Пифагора, то высота равна:
h = √((8√2)²-(4√2)²)=4√6 см.
Теперь есть возможность найти площадь:
S = (1/2)*8√2*4√6 = 32√3 см. кв.
Площадь также можно найти по формуле для треугольника с равными сторонами:
S =(√3/4)*a² или S =(√3/4)*128 = 32√3 см. кв.
Дано два равносторонних треугольника, площадь одного из которых превышает площадь другого в три раза. Чему будет равна сторона второго равностороннего треугольника, при условии, что сторона первого из них составляет 1 см.?
Для расчета площади треугольника с равными сторонами есть формула:
S = a²√3/4.
Найдем площадь меньшего из треугольников, подставив значение а:
S₁ = 12 √3/4 = √3/4 см. кв.
кв.
Известно, что площадь второго треугольника больше площади первой фигуры в три раза. Тогда:
S₂ = 3√3/4.
Очевидно, что сторона большего треугольника составляет √3 см.
Сторона равностороннего треугольника равна 14 см. Чему будет равна его площадь, умноженная на √3?
Формула площади для треугольника с равными сторонами:
S = а²*√3/4.
Подставляем значение а:
S = 14²*√3/4 = 49√3 см. кв.
Умножаем полученное число на √3:
49√3*√3 = 49*3 = 147 см.
Читать дальше: как найти площадь круга.
Равносторонний треугольник | ЮКлэва
И вот мы снова изучаем треугольники. Это всё больше похоже на заговор…
Не волнуйся: после прочтения этой статьи тайн не останется, ведь ты будешь знать всё о равностороннем треугольнике!
Тема простая, но очень важная!
Поехали!
Свойства равностороннего треугольника
Свойство 1.
{o }}\)
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не \(12\) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной.
{o}}=\frac{a\sqrt{3}}{2}\)
Радиус вписанной окружности равностороннего треугольника
\(r=\frac{a\sqrt{3}}{6}\)
Это уже теперь должно быть совсем ясно:
Бонус 2: Вебинары о треугольниках, чтобы набить руку в решении задач
А в этих видео из нашего курса подготовки к ЕГЭ по математике вы можете потренироваться, решая задачи вместе с нашим репетитором Алексеем Шевчуком.
Это не просто вебинары, «бла-бла-бла» о теории математики. Это разбор задач в режиме реального времени.
Вы точно научитесь решать любые задачи на эти темы, если их прослушаете.
Хотите получить максимум от этих вебинаров? Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.

Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но в этом видео мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
На этом уроке мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Также мы научимся решать и «обычные» треугольники. Убедимся в утверждении из прошлого урока — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
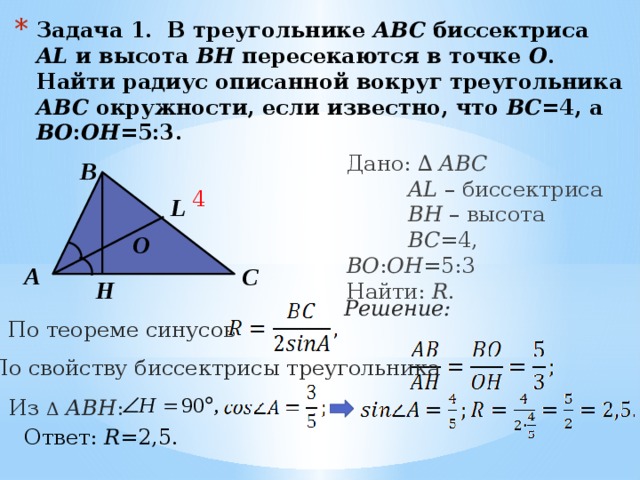
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Итак, задача 16 профильного ЕГЭ.
Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Калькулятор равностороннего треугольника
Автор: Hanna Pamuła, PhD
Отзыв от Bogna Szyk и Adena Benn
Последнее обновление: 02 февраля 2023 г.
Содержание:
- Что такое равносторонний треугольник?
- Площадь и высота равностороннего треугольника
- Периметр равностороннего треугольника, радиус описанной и вписанной окружности
- Как я могу использовать калькулятор равностороннего треугольника?
- FAQ
Калькулятор равностороннего треугольника поможет вам в расчетах стандартных параметров треугольника. Независимо от того, ищете ли вы площадь равностороннего треугольника, его высоту, периметр, радиус описанной окружности или внутренний радиус, этот великолепный инструмент является надежным выбором. Прокрутите вниз, чтобы узнать больше о полезных формулах (например, для расчета высоты равностороннего треугольника) и узнать, что такое равносторонний треугольник.
Что такое равносторонний треугольник?
Равносторонний треугольник, также называемый правильным треугольником, представляет собой треугольник, у которого все три стороны равны. Каковы другие важные свойства этой конкретной правильной формы?
- Все три внутренних угла равны друг другу, и все они равны 60°.
- Высоты, биссектрисы углов, биссектрисы перпендикуляров и медианы совпадают.
Равносторонний треугольник — это частный случай равнобедренного треугольника, у которого равны не только две, но и все три стороны. Если вы хотите узнать больше о равнобедренном треугольнике, наш калькулятор равнобедренного треугольника — это именно то, что вам нужно.
Площадь и высота равностороннего треугольника
Формула площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленный на 4:
площадь = (a² × √3)/4и уравнение высоты равностороннего треугольника выглядит следующим образом:
h = a × √3 / 2, гдеa— сторона треугольника.А знаете ли вы, откуда берутся формулы? Вы можете найти их по крайней мере двумя способами: вывести из теоремы Пифагора (обсуждается в нашем калькуляторе теоремы Пифагора) или с помощью тригонометрии.
1.
Использование теоремы Пифагора
Основная формула площади треугольника: сторона
a(основание) умножить на высотуh, разделить на 2:
площадь = (а × ч) / 2Высота равностороннего треугольника получается путем разделения равностороннего треугольника на два прямоугольных треугольника. Посмотрите наш калькулятор прямоугольного треугольника, чтобы узнать больше о прямоугольных треугольниках.
Один катет этого прямоугольного треугольника равен высоте, другой катет — половине стороны, а гипотенуза — стороне равностороннего треугольника.
`(а/2)² + h² = а²` После нехитрых преобразований получаем формулу высоты равностороннего треугольника:
h = a × √3 / 22. Использование тригонометрии
Начнем с тригонометрической формулы площади треугольника:
площадь = (1/2) × a × b × sin(γ), гдеγ— угол между сторонами.Мы помним, что в равностороннем треугольнике все стороны и все углы равны, поэтому формула упрощается до:
площадь = 0,5 × a × a × sin(60°)Более того, мы знаем, что синус 60° равен √3/2, поэтому формула площади равностороннего треугольника:
площадь = (1/2) × a² × (√3/2) = a² × √3/4Высота равностороннего треугольника получается из определения синуса:
h / a = sin(60°), значит,h = a × sin(60°) = a × √3 / 2Периметр равностороннего треугольника, радиус описанной и вписанной окружности
Вы можете легко найти периметр равностороннего треугольника, сложив все его стороны вместе. У этого правильного треугольника все стороны равны, поэтому формула для периметра:
периметр = 3 × aКак найти радиус окружности, описывающей три вершины, и радиус вписанной окружности?
окружность_радиус = 2 × h / 3 = a × √3 / 3.
incircle_radius = h / 3 = a × √3 / 6.Как пользоваться калькулятором равностороннего треугольника?
Возьмем пример из повседневной жизни: мы хотим найти все параметры знака доходности.
Введите данное значение в правильное поле . Предположим, у нас есть знак с длиной стороны 36 дюймов.
Калькулятор равностороннего треугольника быстро находит остальные значения . Теперь мы знаем, что:
- Высота знака доходности 31,2 дюйма;
- Его площадь равна 561 дюйм²;
- Периметр: 108 дюймов;
- Радиус окружности составляет 20,8 дюйма; и
- Радиус вписанной окружности 10,4 дюйма
Оцените гибкость нашего инструмента . Обновите калькулятор и введите другой параметр, например, периметр. Это работает и таким образом. Разве это не круто?
Часто задаваемые вопросы
Как найти площадь равностороннего треугольника?
Чтобы найти площадь равностороннего треугольника, следуйте данным инструкциям:
Возьмите квадратный корень из 3 и разделите его на 4 .
Умножьте на квадрат стороны на результат шага 1 .
Поздравляем! Вы вычислили площадь равностороннего треугольника.
Как найти высоту равностороннего треугольника?
Чтобы найти высоту равностороннего треугольника, выполните следующие действия:
Возьмите квадратный корень из 3 и разделите на 2 .
Умножьте результат шага 1 на длину стороны .
Вы получите высоту равностороннего треугольника.
Как найти периметр равностороннего треугольника со стороной 8 см?
Периметр данного треугольника равен 24 см .
Чтобы вычислить периметр равностороннего треугольника, нам нужно умножить длину его стороны на 3 . Длина каждой стороны данного треугольника равна 8 см.
Следовательно, его периметр будет равен 3 × 8 см = 24 см .
Может ли прямоугольный треугольник быть равносторонним?
Нет, прямоугольный треугольник не может быть равносторонним . Один из углов прямоугольного треугольника равен 90°. Так как сумма всех внутренних углов треугольника равна 180°, то два других угла прямоугольного треугольника всегда меньше 9.0°.
Согласно определению равносторонних треугольников все внутренние углы равны. Следовательно, прямоугольный треугольник никогда не может быть равносторонним треугольником.
Hanna Pamuła, PhD
Сторона (A)
Высота (H)
Периметр
Радиус округа
9000 4050 45 45 45 45 45 45 45 455 455 455 455 455 450 45 455 450 45 450 405 450 450 450 450 405 450 405045 405 405 450 450 405. прямоугольный треугольник… 15 подробнее
Нарисуйте равносторонний треугольник, одна из сторон которого равна 7 см…
Перейти к
- Конструкции.
Упражнение 17.1.
- Конструкции. Упражнение 17.2.
- Конструкции. Упражнение 17.3.
- Конструкции. Упражнение 17.4.
- Конструкции. Упражнение 17.5.
- Целые числа
- Фракции
- Десятичные
- Рациональное число
- Операции над рациональными числами
- Экспоненты
- Алгебраические выражения
- Линейные уравнения с одной переменной
- Соотношение и пропорция
- Унитарный метод
- Процент
- Доходы и расходы
- Простой интерес
- Линии и углы
- Свойства треугольника
- Конгруэнтность
- Конструкции
- Симметрия
- Визуализация твердых фигур
- Измерение 1
- Измерение 2 Площадь круга
- Данные организации по обработке и сбору данных
- Обработка данных — основные ценности
- Обработка данных — построение гистограмм
- Обработка данных-вероятность
Главная > РД Шарма Решения Класс 7 Математика > Глава 17 — Конструкции > Конструкции.
Упражнение 17.2. > Вопрос 3
Вопрос 3 Построения Упражнение 17.2
Нарисуйте равносторонний треугольник, одна из сторон которого имеет длину 7 см.
Ответ:
Этапы построения:
Нарисуйте отрезок АВ длиной 7 см.
С центром А нарисуйте дугу радиусом 7 см.
С центром B нарисуйте дугу радиусом 7 см, пересекающую ранее начерченную дугу в точке C.
Соедините AC и BC, чтобы получить требуемый треугольник.
Стенограмма видео
эй, дети, добро пожаловать на небольшую домашнюю работу, меня зовут Хема, и я немного дота, давайте начнем с вопроса. равно 7 на 9, умноженное на тире, поэтому давайте сделаем это первое, что у нас здесь минус 4, умноженное на 7 на 9, что будет равно 7 на 9, умноженное на пробел, поэтому, если вы внимательно посмотрите на это число, это что-то в форме здесь на b, умноженное на c на d, что будет равно c на d, умноженном на a на b, поэтому, когда вы умножаете два рациональных числа в любом порядке, мы получим тот же результат, который мы получили благодаря свойству коммутативности, поэтому здесь, в пробел мы получим минус 4 и свойство, которое мы здесь используем, является коммутативным свойством, давайте перейдем ко второму во втором вопросе, который они задали 5 на 11 равно минус 3 на 8, что равно минус 3 на 8, умноженное на тире так что снова мы запишем вопрос, так что если вы наблюдаете второй, он похож на первый, поэтому снова, используя товарное свойство, мы получим ответ будет равен минус 3 при умножении 8 на у нас здесь есть пробел, поэтому, когда вы умножаете числа в любом порядке, получите обратно то же самое, так что минус 3 на 8 умножить на 5 на 11 и как мы это получили мы получили это с помощью коммутативного свойства хорошо теперь давайте перейдем к третьему вопросу в третьем у нас есть 1 на 2 умножить на 3 на 4 плюс минус 5 на 12 равно 1 на 2 умножить на тире плюс тире умножить на минус 5 на 12 сначала запишем вопрос так что в третьем у нас 1 на 2 умножить на 3 на 4 плюс минус 5 на 12 в скобках и это равно 1 на 2, умноженное на у нас здесь пробел, давайте снова у нас есть пробел, умноженный на минус 5 на 12, если вы заметили, что мы применяем здесь распределительное свойство, и что такое распределительное свойство, так что это а на b, умноженное на c на d плюс e на f будет равно, поэтому вам нужно умножить y здесь a на b с c на d, а затем сложите и снова умножьте a на b с e на f, чтобы это было равно a на b, умноженное на c на d, это попадет в скобки, а затем снова умножьте a на b с e на f, так что это с использованием распределительного свойства, поэтому, если мы сравним это в пробеле, мы получим 1 на 2, умноженное на 3 на 4, плюс у нас есть пробел, который умножается на 5 на 12, так что здесь мы будем получить 1 на 2, и это мы получили, используя свойство распределения, поэтому давайте запишем это, используя свойство распределения, теперь давайте перейдем к четвертому в четвертом вопросе, у нас есть минус четыре на пять, умноженное на пять на семь плюс минус 8 на 9эти два числа в скобках, которые равны 4,5, умноженные на тире плюс минус 4 на 9, умноженные на минус 8 на i, поэтому, когда этот вопрос аналогичен третьему, мы снова применяем распределительное свойство, поэтому давайте сделаем это, поэтому четвертый вопрос и четвёртый у нас минус 4 на 5 умножить на в скобках у нас 5 на 7 плюс минус 8 на 9 это в скобках что будет равно здесь у нас минус 4 на 5 умножить на тире а потом плюс у нас минус 4 на 5 умножить на минус 8 на 9поэтому у нас здесь только один пробел, так что в этом пробеле, очевидно, как я упоминал ранее, используется распределительное свойство, поэтому минус 4 на 5 будет умножаться на 5 на 7 и снова умножается на минус 8 на 9, так что последняя скобка полностью заполнена в первой скобке мы получим здесь 5 на 7, и снова, как мы это получили, мы получили это, используя дистрибутивное свойство, вот и все, поэтому мы решили здесь все четыре проблемы, данные нам, мы применили здесь коммутативное свойство и дистрибутивное свойство, чтобы решить их поэтому, если у вас есть какие-либо вопросы, пожалуйста, оставьте комментарий ниже и подпишитесь на этот канал для получения дополнительных уведомлений, большое спасибо за просмотр
Связанные вопросы
Нарисуйте △ABC, в котором AB = 5,5 см.
ВС = 6 см и СА = 7 см. Также проведите серединный перпендикуляр к стороне B…
Нарисуйте ΔPQR, в котором PQ = 3 см, QR = 4 см и RP = 5 см. Также нарисуйте биссектрису ∠Q
Начертите треугольник, стороны которого равны 4 см, 5 см и 7 см. Начертите серединный перпендикуляр к…
Начертите треугольник ABC со сторонами AB = 6 см, BC = 7 см и CA = 8 см. Используя только линейку и циркуль, начертите (i)…
Нарисуйте △DEF так, чтобы DE= DF= 4 см и EF = 6 см. Измерьте ∠E и ∠F. Решение:
Нарисуйте любой треугольник ABC. Разделите сторону АВ пополам в точке D. Через D проведите прямую, параллельную ВС, с пересечением АС в точке Е. …
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение на построение 17.

 {o }}\)
{o }}\) {o}}=\frac{a\sqrt{3}}{2}\)
{o}}=\frac{a\sqrt{3}}{2}\)
 Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.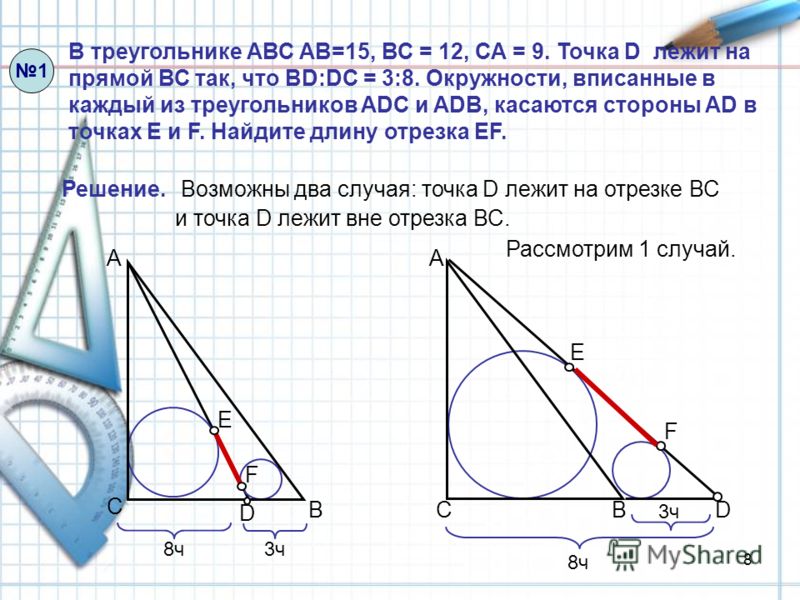
 Использование теоремы Пифагора
Использование теоремы Пифагора 


 Следовательно, его периметр будет равен 3 × 8 см = 24 см .
Следовательно, его периметр будет равен 3 × 8 см = 24 см . Упражнение 17.1.
Упражнение 17.1. Упражнение 17.2.
>
Вопрос 3
Упражнение 17.2.
>
Вопрос 3 ВС = 6 см и СА = 7 см. Также проведите серединный перпендикуляр к стороне B…
ВС = 6 см и СА = 7 см. Также проведите серединный перпендикуляр к стороне B…
Leave A Comment