Урок по математики в 10-11 классе по теме: «Точки максимума и минимума».
Тема урока: Точки максимума и минимума.
Эпиграф урока:
«Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает настойчивость
и упорство в достижении цели».
(А. Маркушевич.)
Цели урока:
образовательные
— ввести понятие критических точек функции, точек максимума и минимума функции; рассмотреть необходимое и достаточное условие существования экстремума, признаки максимума и минимума функции; алгоритм исследования функции на экстремум; продолжить усвоение понятий, формул и правил; продолжить подготовку учащихся к ЕГЭ.
развивающие
— способствовать формированию умений применять полученные знания в новой ситуации; развивать математическое мышление, внимание, речь учащихся.
воспитательные
— содействовать воспитанию интереса к математике, активности, мобильности, умения общаться..
В результате изучения темы учащиеся должны
Знать определения точек максимума и минимума;
Знать необходимый признак экстремума (теорема Ферма) и достаточный признак максимума и минимума;
Знать определения стационарных и критических точек функции;
Уметь находить критические точки функции по графику и определять их вид;
Уметь находить точки экстремума функции аналитическим путем.
Тип урока: комбинированный.
Техническое обеспечение: проектор, компьютер.
План урока:
Организационный момент.
Актуализация знаний.
Изучение нового материала.
Отработка определений.
Закрепление новой темы.
Домашнее задание.

Подведение итогов.
Ход урока
Организационный момент.
Ребята, как вы знаете, нам предстоит сдача ЕГЭ. Чтобы пройти это испытание успешно, необходимо много работать, повторять пройденный материал. Сегодня мы продолжаем изучать приложение производной и рассмотрим вопрос о её применении, т.е. введём понятие критических точек функции, точек максимума и минимума функции; рассмотрим необходимое и достаточное условие существования экстремума, признаки максимума и минимума функции; алгоритм нахождения точек экстремума. Итак, запишем тему сегодняшнего урока:
2. Актуализация знаний.
Для решения поставленных задач, нам необходимо вспомнить некоторые вопросы, рассмотренные ранее. Фронтальный опрос.
Найти область определения и производную функции: (Слайд 3)
у = 3х4 – 2х + 5; 2) у = е-2х + 1; 3) у = х2 ;
4) у = ; 5) у = ; 6) у = .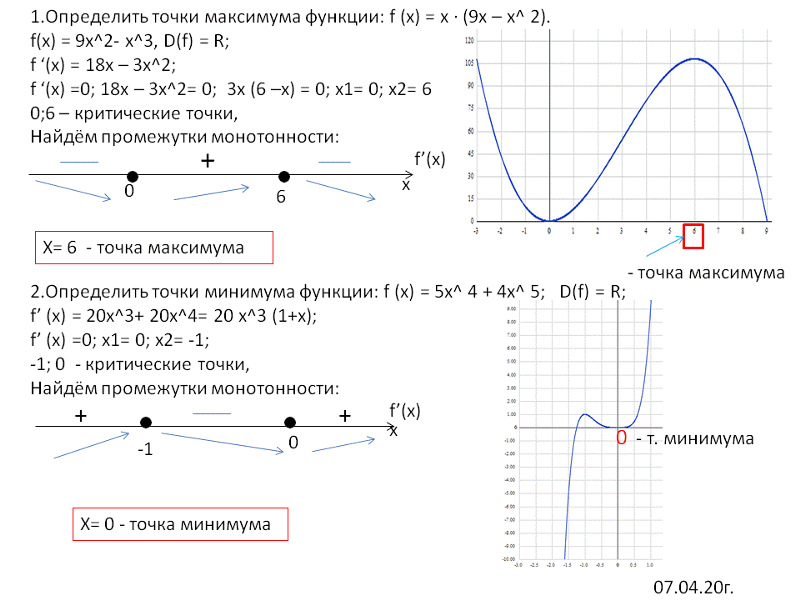
2. Найти значения х, при которых значение f(x) равно 0, если (Слайд 4)
1) f(x) =5х2 + 3х; 2) f(x) = хех; 3) f
3. Решить неравенство: (Слайд 5)
1) 15х + 1 > 0; 2) х2 – 5х + 6 < 0; 3) (х + 2)ех < 0.
4. По графику функции определите, на каких промежутках производная отрицательна, положительна. (Слайд 6)
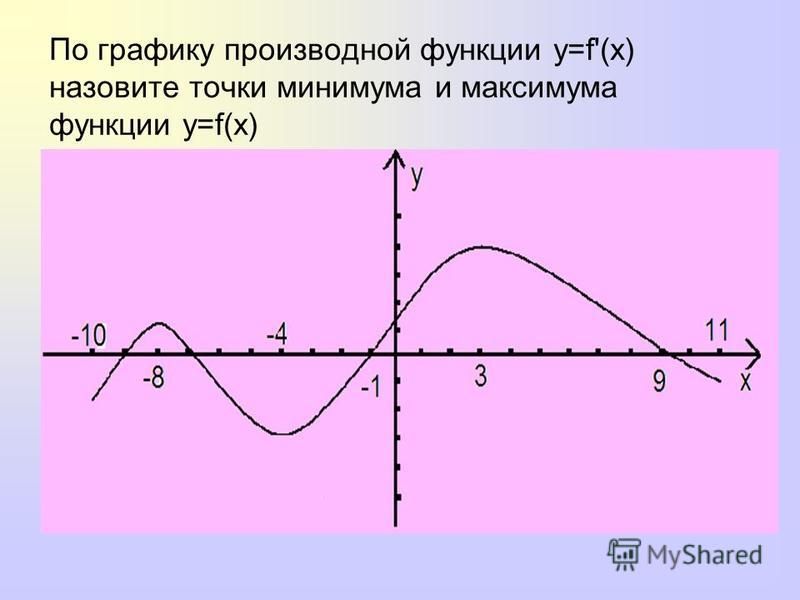
5. По графику производной функции определите, на каких промежутках функция возрастает, на каких убывает. (Слайд 7)
3. Изучение нового материала.
Пусть график некоторой функции имеет вот такой вид.
а) Если рассмотреть значение функции в точке х0 на этом графике (Слайд 8), то оно будет наибольшим (максимальным), чем в любой другой точке из близлежащей окрестности.
Точка х0 из области определения функции называется точкой максимума, если для любого из окрестности точки х0 выполняется неравенство f(x) < f(x0)
б) Попробуйте сформулировать определение точки минимума. (Слайд 9)
Если рассмотреть значение функции в точке х0, то оно будет наименьшим (минимальным), чем в любой другой из близлежащей окрестности. В этом случае говорят, что
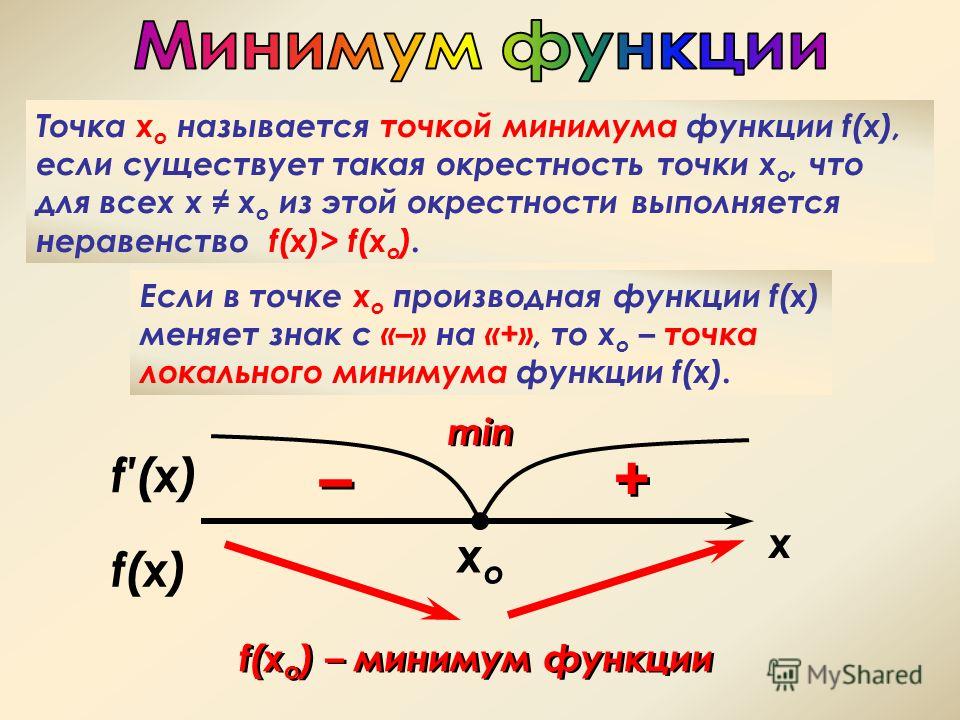
Точка х0 из области определения функции называется точкой минимума, если для любого х из окрестности точки х0 выполняется неравенство > .
(Слайд 10) Максимум и минимум функции объединяют словом экстремум ( с латинского — крайний), а точки максимума и минимума называют точками экстремума (экстремальными точками)
(Слайд 11)
Теорема Ферма: Пусть функция f(х) определена в некоторой окрестности х0 и дифференцируема в этой точке.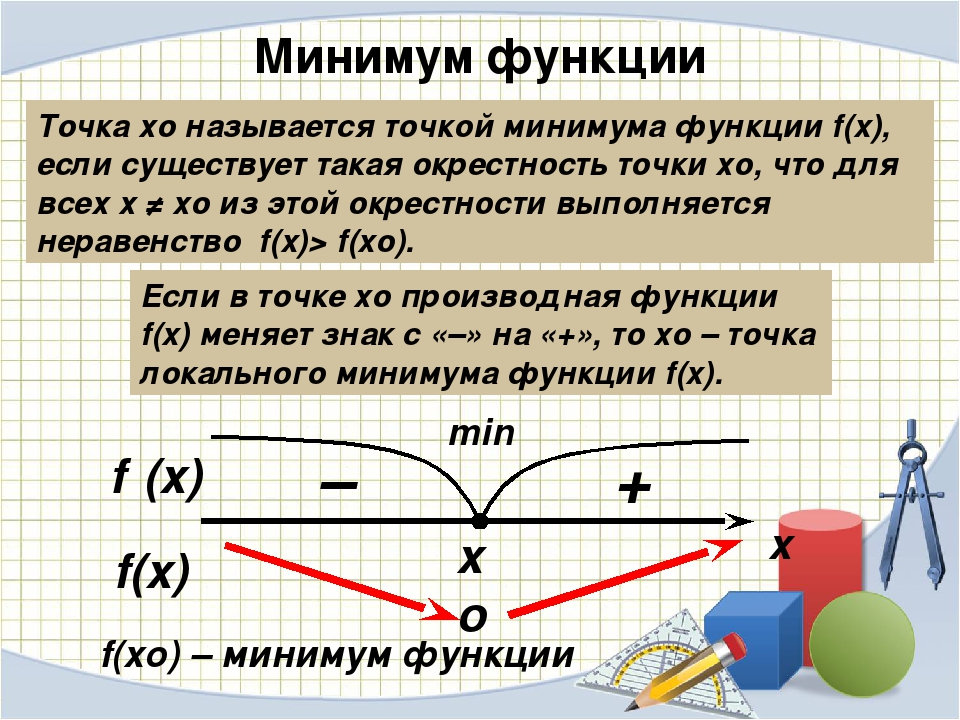
Теорема имеет наглядный геометрический смысл: в точках экстремума касательная к графику функции параллельна оси абсцисс, и поэтому её угловой коэффициент f ´(х)=0. (Слайд 12)
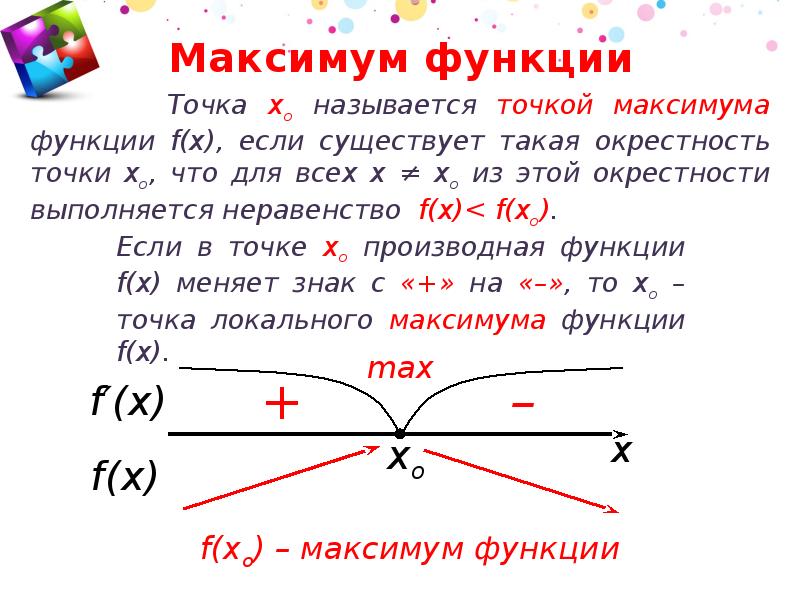
Необходимое условие существования экстремума функции в точке: Если -точка экстремума функции и в этой точке функция дифференцируема, то производная в этой точке равна нулю.
Точки в которых производная равна нулю называют стационарными.
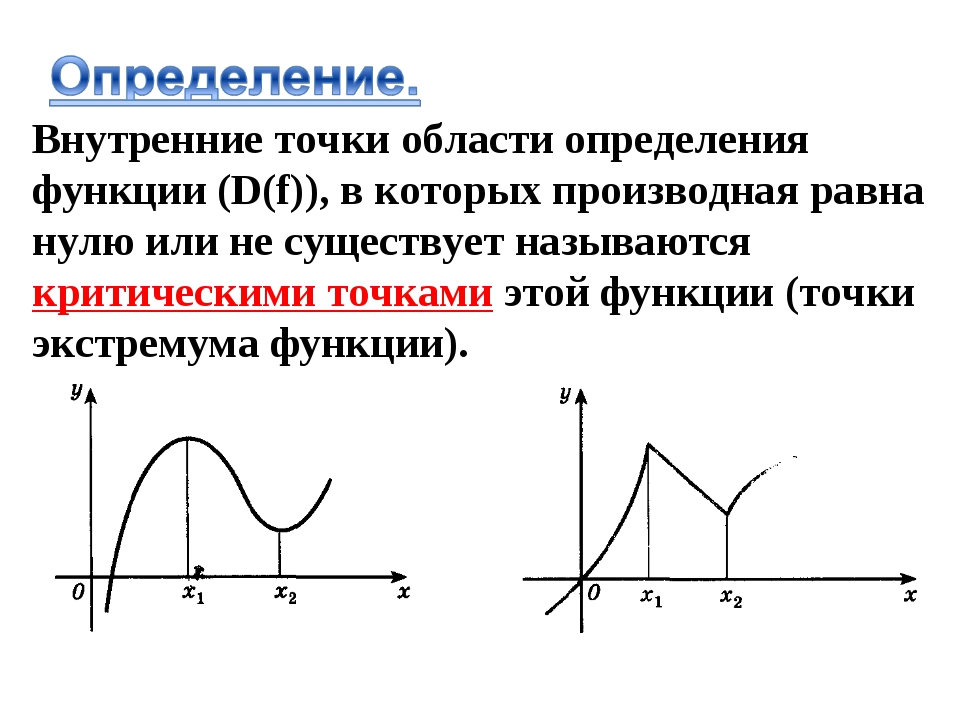
Определение критических точек (Слад 13)
Необходимое условие не является достаточным, (Слайд 14) т.е. из того факта, что производная равна нулю в некоторой точке, не следует, что функция в этой точке имеет экстремум (например, функция ).
Какие условия необходимо добавить, чтобы утверждать, что некоторая критическая точка является точкой максимума или минимума? Видно, что точка максимума служит границей перехода от возрастания к убыванию функции (слайд 15), а точка минимума — от убывания к возрастанию
(Слайд 16).
Достаточное условие существования максимума состоит в смене знака производной при переходе через критическую точку с «+» на «-«, а для минимума с «-» на «+». Если при переходе через критическую точку смены знака производной не происходит, то в данной точке экстремума нет. (Слайд 17)
Необходимое и достаточное условие экстремума. (Слайд 18)
Для того, чтобы точка х0 была точкой экстремума функции f(х), необходимо , чтобы х
достаточно, чтобы при переходе через критическую точку х0 производная меняла знак.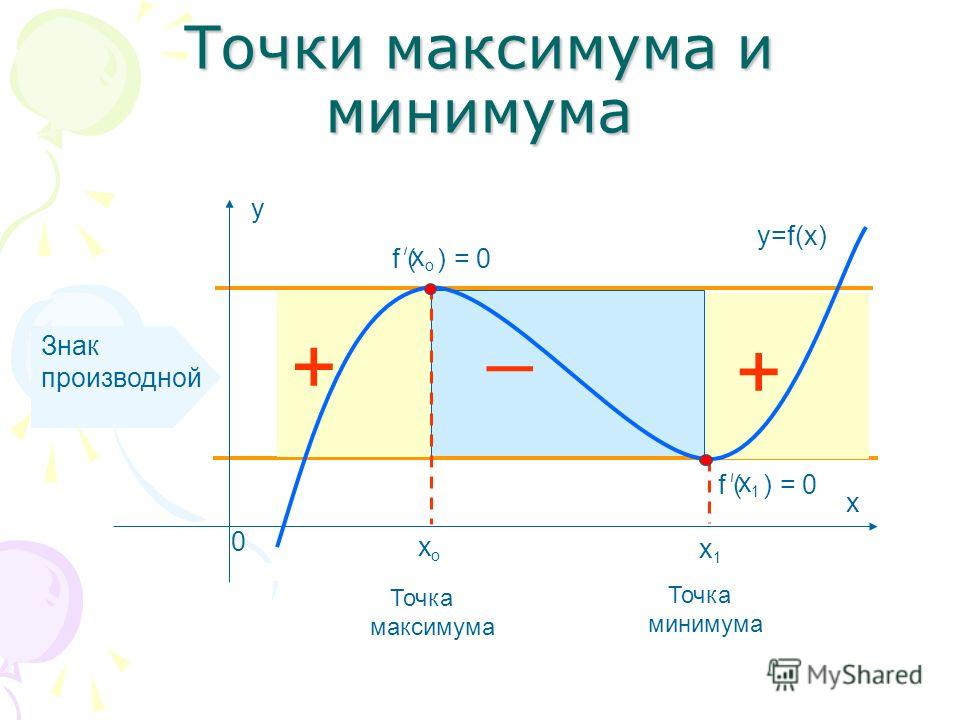
Выписать в тетрадь необходимый и достаточный признак экстремума.
Алгоритм нахождения точек экстремума: (Слайд 19) алгоритм раздается детям
Найти производную функции.
Решить уравнение f ´(х)=0, и найти тем самым стационарные точки.
Методом интервалов установить промежутки знакопостоянства производной.
Если при переходе через точку х0
— производная не меняет знак, то х0 – точка перегиба;
— производная меняет знак с «+» на «-», то х0 точка максимума;
— производная меняет знак с «-» на «+», то х0 точка минимума.
4. Отработка определений. (один к доске, остальные с сигнальными карточками).
Используются слайды презентации.
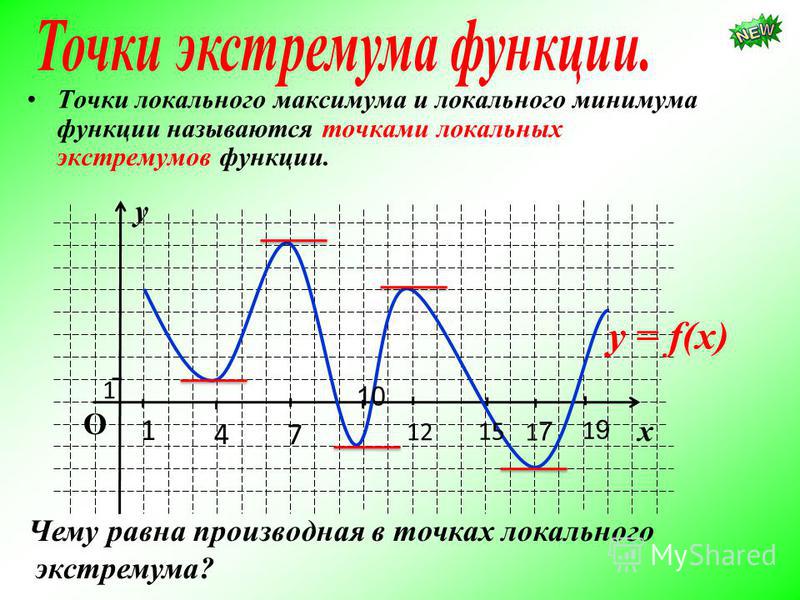
Вопрос к слайду 20
Найти по графику функции точки, с определениями которых вы только, что познакомились.

Вопросы к слайду 21
2. Укажите:
1) в каких точках графика касательные к нему параллельны оси абсцисс;
2) чему равна производная в этих точках;
3) как называются такие точки;
4) чему равна производная в точке х4;
5) как называется такая точка;
6) какие точки можно назвать точками экстремума.
5. Закрепление новой темы.
1. Найдём точки экстремума функций. (Слайд 22)
а) у = 2х – 3
1) Найдём производную функции = 2
2) Найдём стационарные точки: 2 = 0 решений нет, значит, стационарных точек нет.
3) Данная функция линейная и возрастает на всей числовой оси, поэтому не имеет точек экстремума.
Ответ: точек экстремума нет.
б) у = х2 — 2х – 1 (Слайд 23)
1) = 2х — 2
2) 2х — 2 = 0
2х = 2
х = 1,5
— +
у 1,5 х
Ответ: функция имеет максимум в точке х = 1,5
2. Решение задач (Слайд 24)
Решение задач (Слайд 24)
№ 9(1,3) решение у доски с комментарием
№ 11 (1,5) решение у доски с комментарием
№11(2) самостоятельно
3. Резерв: Решение задания В8 из сборника ЕГЭ 3000 задач №1683,1741, 1751 – устно
6. Домашнее задание (Слайд 25)
§ 2 № 9(2) №11(4)
Решение В8 (сборник ЕГЭ 3000 задач) №1685, №1743, №1752, №1942 — устно
7. Итог урока
На сегодняшнем уроке мы с вами познакомились с новыми понятиями, научились находить точки максимума и минимума. Умение применять полученные знания вам пригодятся при сдаче экзаменов и при дальнейшем учении. Поэтому, все, что вам дается на уроках, всегда вам пригодится.
формулы, пример с решением по высшей математике
Максимум и минимум функцийТочка
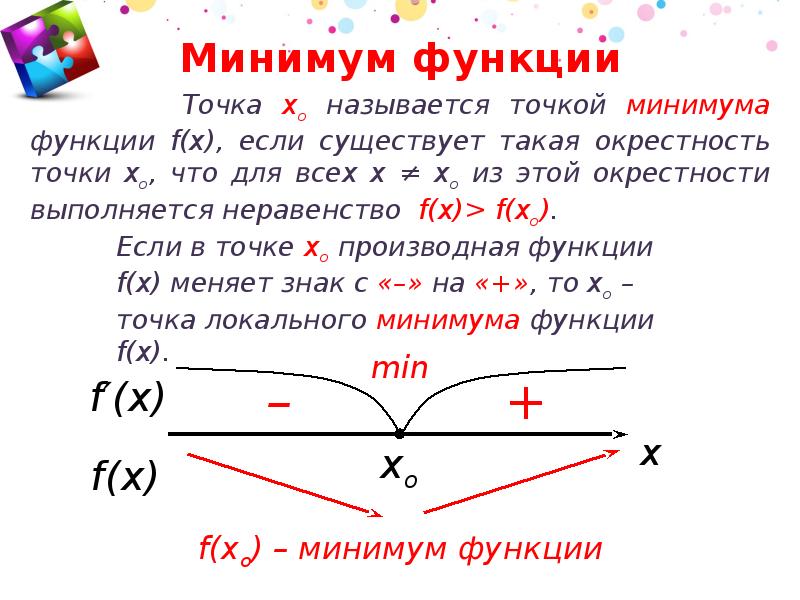
называется точкой максимума функции , если существует такая -окрестность точки , что для всех из этой окрестности выполняется неравенство .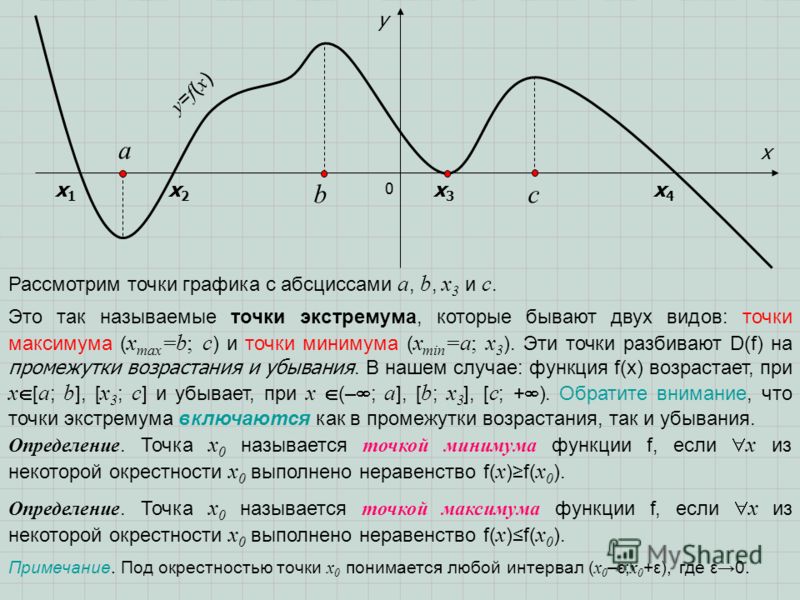
Аналогично определяется точка минимума функции:
— точка минимума функции, если . На рисунке 146 — точка минимума, а точка — точка максимума функции .Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.
Понятие экстремума всегда связано с определенной окрестностью точки из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения. Рассмотрим условия существования экстремума функции.
Теорема 25.8 (необходимое условие экстремума). Если дифференцируемая функция
имеет экстремум в точке , то ее производная в этой точке равна нулю: .Пусть, для определенности,
— точка максимума. Значит, в окрестности точки выполняется неравенство . Но тогда , если , и , если . По условию теоремы производнаясуществует. Переходя к пределу, при
, получим , если , и , если . Поэтому . Аналогично доказывается утверждение теоремы 25. 8, если — точка минимума функции .
8, если — точка минимума функции .Геометрически равенство
означает, что в точке экстремума дифференцируемой функции касательная к ее графику параллельна оси (см. рис. 147).Отметим, что обратная теорема неверна, т. е. если
, то это не значит, что — точка экстремума. Например, для функции ее производная равна нулю при , но не точка экстремума (см. рис. 148).Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция
в точке производной не имеет, но точка — точка минимума (см. рис. 149).Таким образом, непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.
Теорема 25.9 (достаточное условие экстремума). Если непрерывная функция
дифференцируема в некоторой -окрестности критической точки и при переходе через нее (слева направо) производная меняет знак с плюса на минус, то есть точка максимума; с минуса на плюс, то — точка минимума.
Рассмотрим
-окрестность точки . Пусть выполняются условия: и . Тогда функция возрастает на интервале , а на интервале она убывает. Отсюда следует, что значение в точке является наибольшим на интервале , т. е. для всех . Это и означает, что — точка максимума функции.Графическая интерпретация доказательства теоремы 25.9 представлена на рисунке 150.
Аналогично теорема 25.9 доказывается для случая, когда
и .Исследовать функцию на экстремум означает найти все ее экстремумы. Из теорем 25.8 и 25.9 вытекает следующее правило исследования функции на экстремум:
1) найти критические точки функции
;2) выбрать из них лишь те, которые являются внутренними точками области определения функции;
3) исследовать знак производной
слева и справа от каждой из выбранных критических точек;4) в соответствии с теоремой 25.9 (достаточное условие экстремума) выписать точки экстремума (если они есть) и вычислить значения функции в них.
Найти экстремум функции
.Решение:
Очевидно,
. Находим , т.е. .Производная не существует при
и равна нулю при . Эти точки разбивают всю область определения данной функции на три интервала . Отметим на рисунке 151 знаки производной слева и справа от каждой из критических точек.Следовательно,
— точка максимума, , и — точка минимума, .Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.
Теорема 25.10. Если в точке
первая производная функции равна нулю (), а вторая производная в точке существует и отлична от нуля (), то при в точке функция имеет максимум и минимум — при .Пусть для определенности
. Так както
в достаточно малой окрестности точки . Если , то ; если , то .Таким образом, при переходе через точку
первая производная меняет знак с минуса на плюс. 3 возрастает на всей числовой оси.
3 возрастает на всей числовой оси.Таким образом, точки минимума и максимума всегда будут находиться среди корне уравнения f’(x) = 0. Но не все корни этого уравнения будут являться точками максимума или минимума.
Стационарные и критические точки
Точки, в которых значение производной функции равно нулю, называются стационарными точками. Точки максимума или минимума могут иметься и вточках, в которых производной у функции вообще не существует. Например, у = |x| в точке х = 0 имеет минимум, но производной в этой точке не существует. Эта точка будет являться критической точкой функции.
Критическими точками функции называются точки, в которых производная равна нулю, либо производной в этой точке не существует, то есть функция в этой точке недифференцируема. Для того чтобы найти максимум или минимум функции необходимо выполнение достаточного условия.
Пусть f(x) некоторая дифференцируемая на интервале (a;b) функция. Точка х0 принадлежит этому интервалу и f’(x0) = 0.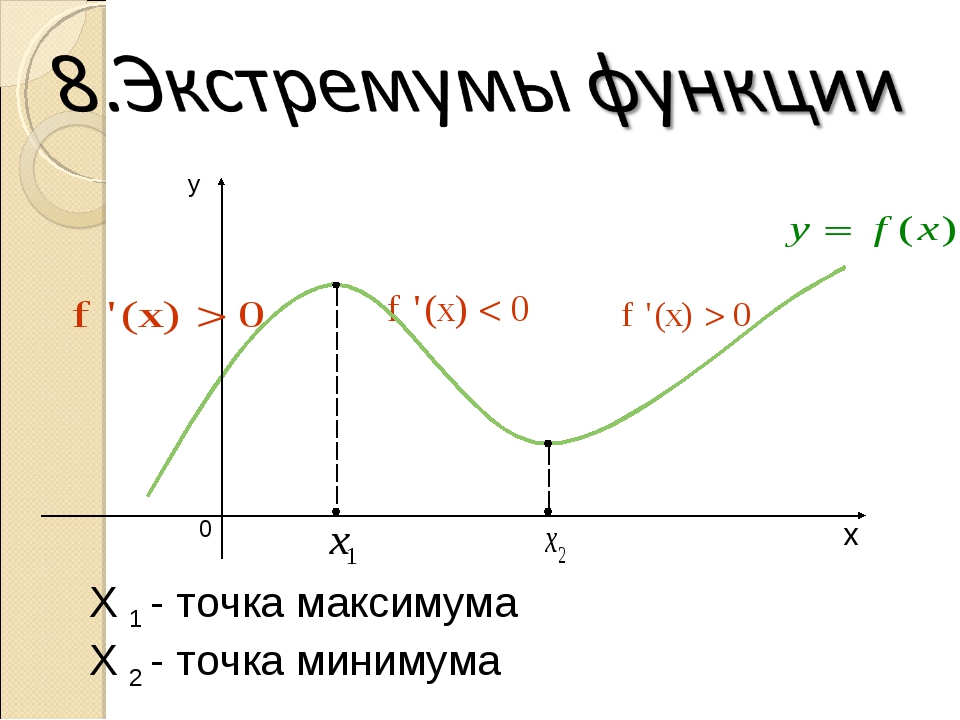 Тогда:
Тогда:
1. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «плюса» на «минус», тогда точка х0 является точкой максимума функции.
2. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «минуса» на «плюс», тогда точка х0 является точкой минимума функции.
Нужна помощь в учебе?
Предыдущая тема: Касательная к графику ункции: уравнение касательной
Следующая тема:   Примеры применения производной к исследованию функции: ↑ и ↓
3.2.5 Точки экстремума (локального максимума и минимума) функции
Видеоурок 1: Экстремумы функции
Видеоурок 2: Экстремум функции двух переменных
Лекция: Точки экстремума (локального максимума и минимума) функции
Некое значение аргумента х0 функции будет называться точкой, в которой наблюдается локальный максимум, в том случае, если функция в данной точке будет больше, чем в любой другой точке данной окрестности:
f(x0) > f(x).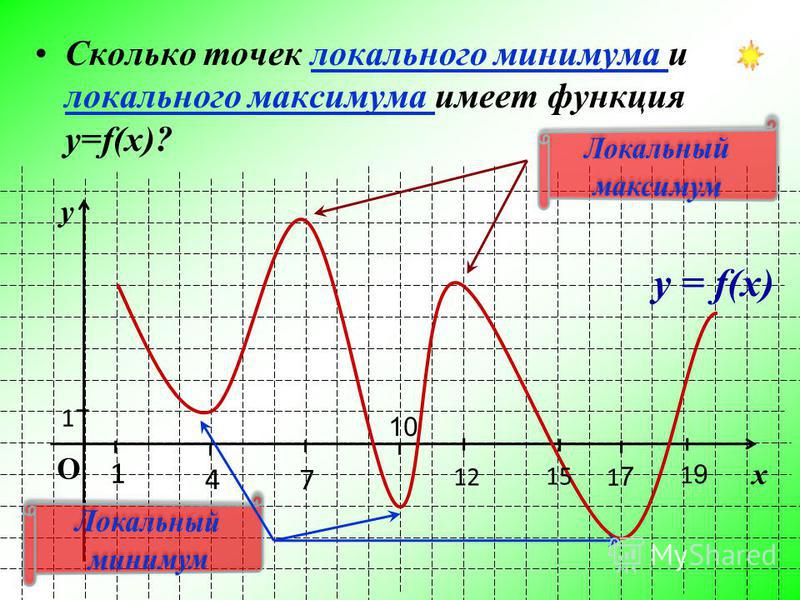
Некое значение аргумента х0 функции будет называться точкой, в которой наблюдается локальный минимум, в том случае, если функция в данной точке будет меньше, чем в любой другой точке данной окрестности:
f(x0) < f(x).
В точке локального максимума функция будет принимать наибольшие значения в данной окрестности, и будет называться локальным максимумом.
В точке локального минимума функция будет принимать наименьшие значения в данной окрестности, и будет называться локальным минимумом.
Если функция принимает максимальное или минимальное значение на рассматриваемом диапазоне области значения функции, то она будет называться глобальным экстремумом.
Для того, чтобы точку можно было назвать экстремумом, должно выполняться некое необходимое условие:
Чтобы убедиться, что точка является экстремумом необходимо определить значение производной в данной точке. Если производная равна нулю или не существует, то точка является экстремумом.

Обратите внимание, не каждая критическая точка является экстремумом.
Точка будет считать экстремальной, если:
рассматриваемая функция непрерывна;
если производная в рассматриваемой точке равна нулю или не существует;
а также, если при переходе через данную точку функция меняет свой знак.
критические точки максимума и минимума
77419.Найдите точку максимума функции у=х 3 –48х+17
Найдем нули производной:
Получим корни:
Определим знаки производной функции подставляя значения из интервалов в полученную производную, и изобразим на рисунке поведение функции:
Получили, что в точке –4 производная меняет свой знак в положительного на отрицательный. Таким образом, точка х=–4 это искомая точка максимума.
Ответ: –4
77423. Найдите точку максимума функции у=х 3 –3х 2 +2
Найдём производную заданной функции:
Приравняем производную к нулю и решим уравнение:
В точке х=0 производная меняет знак с положительного на отрицательный, значит это есть точка максимума.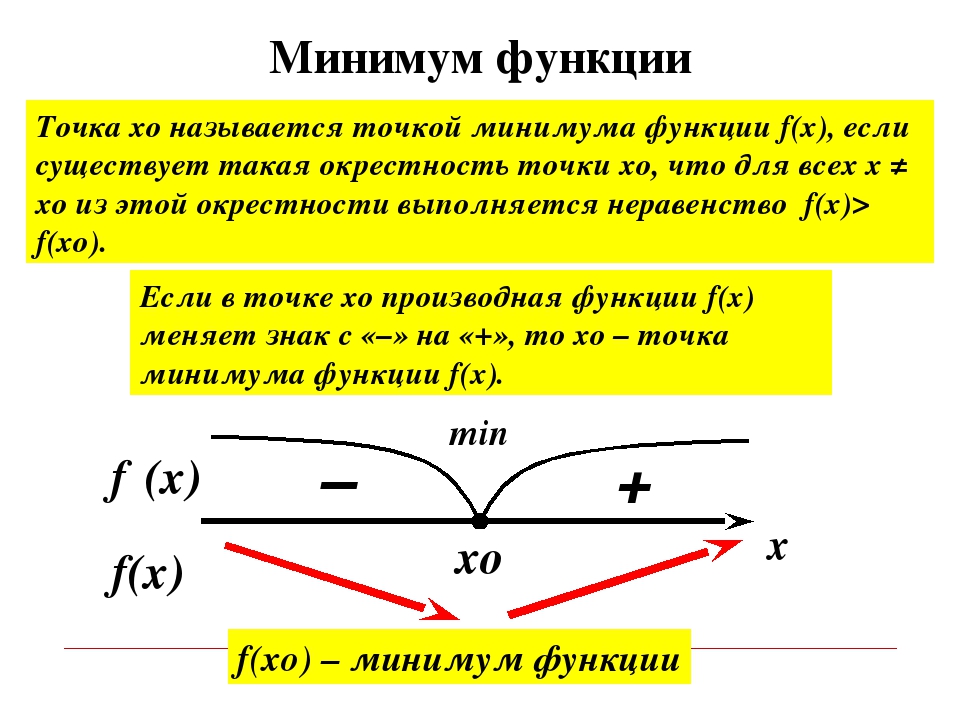
77427. Найдите точку максимума функции у=х 3 +2х 2 +х+3
Найдём производную заданной функции:
При равняем производную к нулю и решим уравнение:
Определим знаки производной функции и изобразим на рисунке интервалы возрастания и убывания функции подставляя значения из каждого интервала в выражение производной:
В точке х=–1 производная меняет знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: –1
77431. Найдите точку максимума функции у=х 3 –5х 2 +7х–5
Найдём производную функции:
Найдем нули производной:
3х 2 – 10х + 7 = 0
3∙0 2 – 10∙0 + 7 = 7 > 0
3∙2 2 – 10∙2 + 7 = – 1
3∙3 2 – 10∙3 + 7 = 4 > 0
В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
77435. Найдите точку максимума функции у=7+12х–х 3
Найдём производную функции:
Найдем нули производной:
12 – 3х 2 = 0
Решая квадратное уравнение получим:
*Это точки возможного максимума (минимума) функции.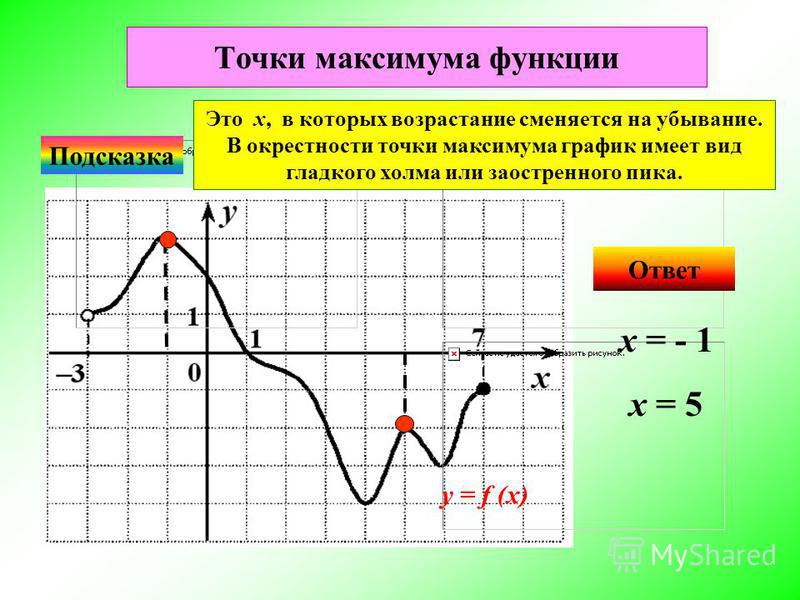
Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:
12 – 3∙(–3) 2 = –15
12 – 3∙0 2 = 12 > 0
12 – 3∙3 2 = –15
В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
*Для этой же функции точкой минимума является точка х = – 2.
77439. Найдите точку максимума функции у=9х 2 –х 3
Найдём производную функции:
Найдем нули производной:
18х –3х 2 = 0
3х(6 – х) = 0
Решая уравнение получим:
*Это точки возможного максимума (минимума) функции.
Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:
18 (–1) –3 (–1) 2 = –21
18∙1 –3∙1 2 = 15 > 0
18∙7 –3∙7 2 = –1
В точке х=6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
*Для этой же функции точкой минимума является точка х = 0.
Значения функции и точки максимума и минимума
Наибольшее значение функции
Наменьшее значение функции
Как говорил крестный отец: «Ничего личного». Только производные!
12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.
12 задание бывает двух видов:
- Найти точку максимума / минимума (просят найти значения «x»).
- Найти наибольшее / наименьшее значение функции (просят найти значения «y»).
Найти точку максимума / минимума
- Приравнять ее к нулю.
- Найденный или найденные «х» и будут являться точками минимума или максимума.
- Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.
Задания с ЕГЭ:
Найдите точку максимума функции
- Берем производную:
Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15
Найдите точку минимума функции
- Преобразуем и возьмем производную:
- Отлично! Сначала функция убывает, затем возрасает — это точка минимума!
Найти наибольшее / наименьшее значение функции
- Взять производную от предложенной функции.

- Приравнять ее к нулю.
- Найденный «х» и будет являться точкой минимума или максимума.
- Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
- В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
- Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.
Задания с ЕГЭ:
Найдите наибольшее значение функции на отрезке [−4; −1]
Ответ: −6
Найдите наибольшее значение функции на отрезке
- Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».
Ответ: 11
Выводы:
- 70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y» , а на точку максимума/минимума написать «х».
- Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
- Ответ всегда может быть записан в виде числа или десятичной дроби.
 Нет? Тогда перерешивай пример.
Нет? Тогда перерешивай пример. - В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
- А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.
В этой статье мы рассмотрим несколько примеров на нахождение точек максимума (минимума) иррациональной функции. Алгоритм решения был уже неоднократно изложен в статьях с подобными заданиями, в одной из прошлых статей.
У вас может возникнуть вопрос – а чем рациональная функция отличается от иррациональной? У иррациональной функции, говоря простыми словами, аргумент находится под корнем, или степень у него это дробное число (несокращаемая дробь). Другой вопрос — в чём отличия в нахождении их точек максимума (минимума)? Да ни в чём.
Сам принцип и алгоритм решения заданий на определения точек максимума (минимума) един. Просто для удобства и систематизации материала я разбил его на несколько статей – отдельно рассмотрел рациональные, логарифмические, тригонометрические и прочие, осталось ещё несколько примеров на нахождение наибольшего (наименьшего) значения иррациональной функции на отрезке. Их мы тоже рассмотрим.
Просто для удобства и систематизации материала я разбил его на несколько статей – отдельно рассмотрел рациональные, логарифмические, тригонометрические и прочие, осталось ещё несколько примеров на нахождение наибольшего (наименьшего) значения иррациональной функции на отрезке. Их мы тоже рассмотрим.
Давайте здесь подробно опишу нахождение производной, когда у аргумента имеется степень, во всех примерах ниже это используется.
Сама формула:
То есть, если у нас аргумент стоит в некоторой степени и требуется найти производную, то мы записывает это значение степени, умножаем его на аргумент, а его степень будет на единицу меньше, например:
Если же степень дробное число, то всё тоже самое:
Следующий момент! Конечно же, вы должны помнить свойства корней и степеней, а именно:
То есть, если в примере вы увидите, например, выражение (или подобное с корнем):
То при решении, чтобы вычислить производную, его необходимо представить как х в степени, будет так:
Остальные табличные производные и правила дифференцирования вы должны знать!!!
Правила дифференцирования:
Рассмотрим примеры:
77451. Найдите точку минимума функции y = x 3/2 – 3x + 1
Найдите точку минимума функции y = x 3/2 – 3x + 1
Найдем нули производной:
Решаем уравнение:
В точке х = 4, производная меняет знак с отрицательного на положительный, это означает, что данная точка является точкой минимума.
Ответ: 4
77455. Найдите точку максимума функции
Найдём производную заданной функции:
Найдем нули производной:
Решаем уравнение:
Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:
В точке х = 4, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.
Ответ: 4
77457. Найдите точку максимума функции
Найдём производную заданной функции:
Найдем нули производной:
Решая уравнение:
Определим знаки производной функции и изобразим на рисунке поведение функции. Для этого подставим произвольные значения из полученных интервалов в производную:
Для этого подставим произвольные значения из полученных интервалов в производную:
В точке х = 9, производная меняет знак с положительного на отрицательный, это означает, что данная точка является точкой максимума.
Ответ: 9
Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
Вконтакте
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно.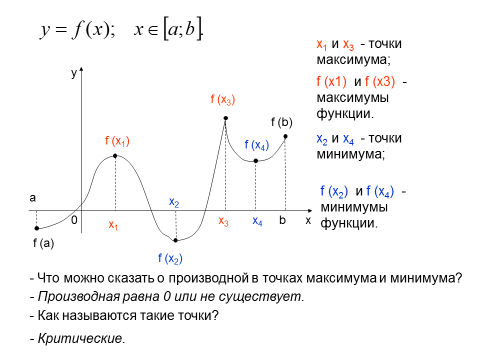 Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
- статистика;
- машинное управление;
- эконометрика.
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения.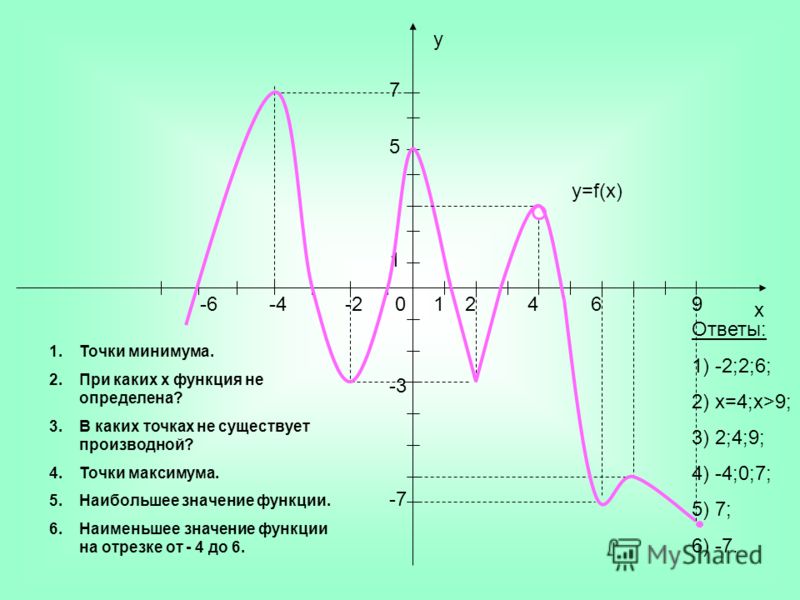 В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
- Нахождение точной области определения на графике.
- Поиск производной функции и точки экстремума.
- Решать стандартные неравенства на область нахождения аргумента.

- Уметь доказывать, в каких функциях точка на графике определена и непрерывна.
Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
| Полное исследование значения | Построение графика значения |
| 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3. Процесс определения изменений положения на графике. 4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5. Создание сводной таблицы исследования с точки зрения определения ее координат. 6. Нахождение промежутков возрастания и убывания крайних и острых точек. 7. Определение выпуклости и вогнутости кривой. 8. Построение графика с учетом исследования позволяет найти минимум либо максимум. | Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике. Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. |
как найти критическую точку максимума и минимума
Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
Основные науки, в которых используют данный концепт:
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
Производная функция
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения. В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством
Острый экстремум
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
Острый экстремум
[stop]Важно! Процесс нахождения точек острого экстремума функции называется дифференцированием и используется как в школьном курсе изучения алгебры и начала анализа, так и в ходе освоения высшей математики в университете.[/stop]
Экстремальное значение функции
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде.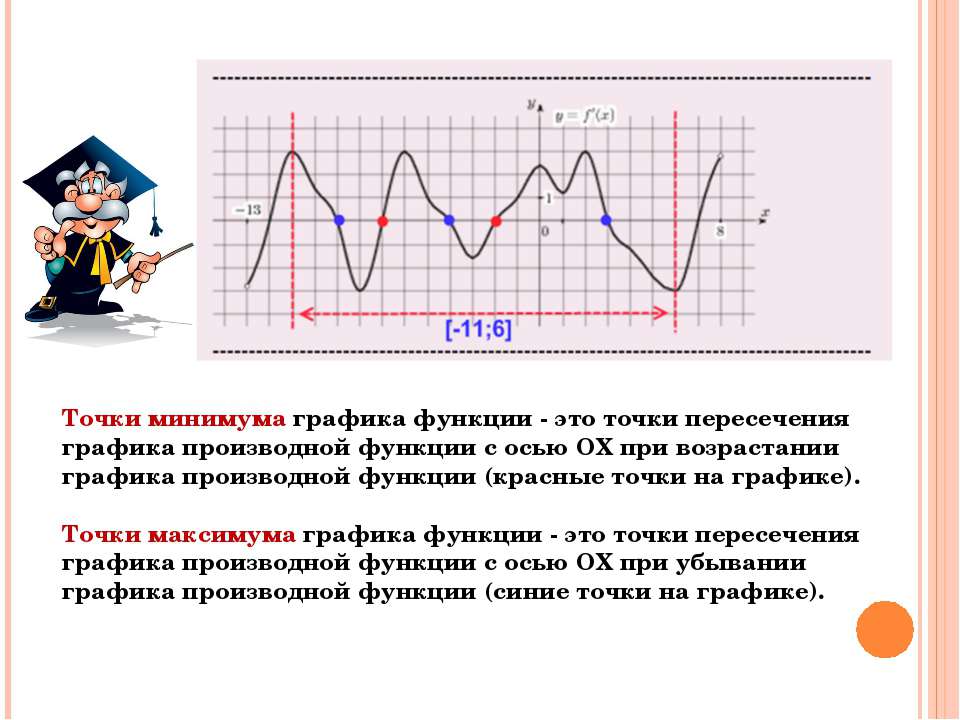 Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
- Нахождение точной области определения на графике.
- Поиск производной функции и точки экстремума.
- Решать стандартные неравенства на область нахождения аргумента.
- Уметь доказывать, в каких функциях точка на графике определена и непрерывна.
Экстремальное значение функции
[warning]Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.[/warning]
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
Точки минимума и максимума
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
| Полное исследование значения | Построение графика значения |
| 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3. Процесс определения изменений положения на графике. 4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5. Создание сводной таблицы исследования с точки зрения определения ее координат. 6. Нахождение промежутков возрастания и убывания крайних и острых точек. 7. Определение выпуклости и вогнутости кривой. 8. Построение графика с учетом исследования позволяет найти минимум либо максимум.
| Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике. Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума. Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума.
|
Экстремум функционала
Для того чтобы отыскать вышеозначенное значение, необходимо придерживаться следующих правил:
- определить необходимое условие экстремального отношения;
- учитывать достаточное условие крайних точек на графике;
- осуществлять расчет острого экстремума.
Используются также такие понятия, как слабый минимум и сильный минимум. Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Это интересно! Легкие правила округления чисел после запятой
Экстремумы функции. 10 класс.
youtube.com/embed/mcfux8f7Q94″ frameborder=»0″ allowfullscreen=»allowfullscreen»/>
Исследование функции. Экстремумы функции — bezbotvy
Вывод
После прочтения и осознания данной статьи любой новичок в математике имеет возможность понять возможности острых экстремумов в том виде, в каком они используются в образовательном процессе. Вышеперечисленные моменты позволяют разобраться в крайних точках без помощи репетиторов.
Точки экстремума — rajak.rs
Экстремумом функции называется максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума.
Точка ${x_0}$ называется точкой локального максимума функции $f$, если выполняется условие: $\exists {U_\delta }\left( {{x_0}} \right):\forall x \in {U_\delta }\left( {{x_0}} \right)$ $f\left( {{x_0}} \right) \geqslant f\left( x \right). $
$
Аналогично точка ${x_0}$ называется точкой локального минимума функции $f$ , если выполняется условие: $\exists {U_\delta }\left( {{x_0}} \right):\forall x \in {U_\delta }\left( {{x_0}} \right)$ $f\left( {{x_0}} \right) \leqslant f\left( x \right).$
Точки, в которых производная равна нулю, называются стационарными точками.
Точки, в которых функция непрерывна, а её производная либо равна нулю, либо не существует, называются критическими точками.
Теорема (необходимое условие экстремума)
Если точка ${x_0}$ – точка экстремума функции $f$, то она критическая.
Замечаниe:
Не всякая критическая точка является точкой экстремума.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция $f$ определена и дифференцируема в некоторой окрестности точки ${x_0}$, кроме, быть может, самой точки ${x_0}$ и непрерывна в этой точке. Тогда:
- Если производная ${f’}$ меняет знак с » — » на «+» при переходе через точку ${x_0}$: $\forall x \in \left( {{x_0} — \delta ;{x_0}} \right)$ $f’\left( x \right) < 0$ и $\forall x \in \left( {{x_0};{x_0} + \delta } \right)$ $f’\left( x \right) > 0$, то ${x_0}$ – точка строго минимума функции $f$.

- Если производная ${f’}$ меняет знак с «+» на » — » при переходе через точку ${x_0}$: $\forall x \in \left( {{x_0} — \delta ;{x_0}} \right)$ $f’\left( x \right) > 0$ и $\forall x \in \left( {{x_0};{x_0} + \delta } \right)$ $f’\left( x \right) < 0$, то ${x_0}$ – точка строго максимума функции $f$.
Замечание:
Если ${x_0}$ – точка строго экстремума, то из этого не следует, что производная ${f’}$ меняет знак при переходе через точку ${x_0}$.
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть дана функция $f$, она определена в некоторой окрестности точки ${x_0}$, ее первая производная $f’\left( x \right) = 0$ и пусть существует $f»\left( {{x_0}} \right)$, тогда:
- Если $f»\left( {{x_0}} \right) > 0$, то точка ${x_0}$ – точка строгого минимума;
- Если $f»\left( {{x_0}} \right) < 0$, то точка ${x_0}$ – точка строгого максимума.
Замечаниe:
Если $f’\left( x \right) = 0$ и $f»\left( x \right) = 0$ , то функция $f$ может и не иметь экстремум в точке ${x_0}$. {\left( n \right)}}\left( {{x_0}} \right) > 0$, то ${x_0}$ – точка локального минимума;
{\left( n \right)}}\left( {{x_0}} \right) > 0$, то ${x_0}$ – точка локального минимума;
Максимальные и минимальные точки — Математическая энциклопедия
Точки в области определения вещественнозначной функции, в которой она принимает свои наибольшие и наименьшие значения; такие точки также называются точками абсолютного максимума и абсолютного минимума. Если $ f $
определено на топологическом пространстве $ X $,
затем точка $ x _ {0} $
называется точкой локального максимума (локального минимума), если существует окрестность $ U \ substeq X $
из $ x _ {0} $
такие, что $ x _ {0} $
является точкой абсолютного максимума (минимума) ограничения $ f $
в этот район.Различают строгие и нестрогие точки максимума (минимума) (как абсолютные, так и локальные). Например, точка $ x _ {0} \ in \ mathbf R $
называется нестрогой (строгой) точкой локального максимума функции $ f $
если есть окрестность $ U $
из $ x _ {0} $
такое, что для всех $ x \ in U $
$ f (x) \ leq f (x _ {0}) $ (
$ f (x)
Для функций, определенных в конечномерных областях, существуют условия и тесты, в терминах дифференциального исчисления, для того, чтобы данная точка была точкой локального максимума (минимума).{(} 0) $
— точка строгого локального максимума (минимума). Условия для точек максимума и минимума дифференцируемых функций известны, когда наложены ограничения на изменение аргументов в области: должны выполняться уравнения связи. В специальных разделах математики получены необходимые и достаточные условия максимума (минимума) вещественной функции с более сложной структурой области ее определения; например, в выпуклом анализе и математическом программировании (см. также Максимизация и минимизация функций).Точки максимума и минимума функций на многообразиях изучаются в вариационном исчислении в целом, а точки максимума и минимума функций на функциональных пространствах, т. Е. Для функционалов, изучаются в вариационном исчислении. Также существуют различные методы численной аппроксимации для нахождения точек максимума и минимума.
Список литературы
| [1] | В.А. Ильин, Э. Позняк, «Основы математического анализа», 1 , МИР (1982) |
| [2] | Л.Д. Кудрявцев, «Курс математического анализа», 1-2 , Москва (1981) |
| [3] | С.М. Никольский, «Курс математического анализа», 1 , МИР (1977) |
| [4] | Н.С. Бахвалов, «Численные методы: анализ, алгебра, обыкновенные дифференциальные уравнения», МИР (1977) |
Список литературы
| [a1] | K.Р. Стромберг, «Введение в классический реальный анализ», Wadsworth (1981) |
Как процитировать эту запись:
Максимальные и минимальные точки. Математическая энциклопедия. URL: http://encyclopediaofmath. org/index.php?title=Maximum_and_minimum_points&oldid=47806
org/index.php?title=Maximum_and_minimum_points&oldid=47806
. Найти максимальное значение функции: практика и обзор — видео и стенограмма урока
Как определить максимальное значение
Есть три метода определения максимального значения квадратного уравнения.Каждый из них можно использовать в своей уникальной настройке для определения максимума.
Первый способ — это построение графика . Вы можете найти максимальное значение визуально, построив уравнение и найдя максимальную точку на графике. Это особенно просто, когда у вас есть графический калькулятор, который может сделать всю работу за вас. Опять же, используя этот график, вы можете видеть, что максимальная точка графика находится в точке y = 5.
Второй способ определения максимального значения — использовать уравнение y = ax 2 + bx + c .
Если ваше уравнение имеет вид ax 2 + bx + c , вы можете найти максимум, используя уравнение:
max = c — ( b 2/4 a ).
Первый шаг — определить, дает ли ваше уравнение максимум или минимум. Это можно сделать, посмотрев на член x 2. Если этот член положительный, точка вершины будет минимальной. Если он отрицательный, вершина будет максимальной.
Определив, что у вас действительно будет точка максимума, используйте уравнение, чтобы найти ее.Например, давайте найдем максимальную точку:
-x 2 + 4 x — 2.
Поскольку член с x 2 отрицательный, вы знаете, что будет максимальная точка. Чтобы найти его, подставьте значения в уравнение:
max = c — ( b 2/4 a )
Это даст нам:
max = -2 — (42/4 * ( -1))
4 в квадрате равно 16, а 4 умножить на -1 равно -4. 16 разделить на -4 равно -4. И -2 минус -4 становится -2 плюс 4, потому что два отрицательных значения становятся положительными, поэтому мы получаем максимальное значение 2.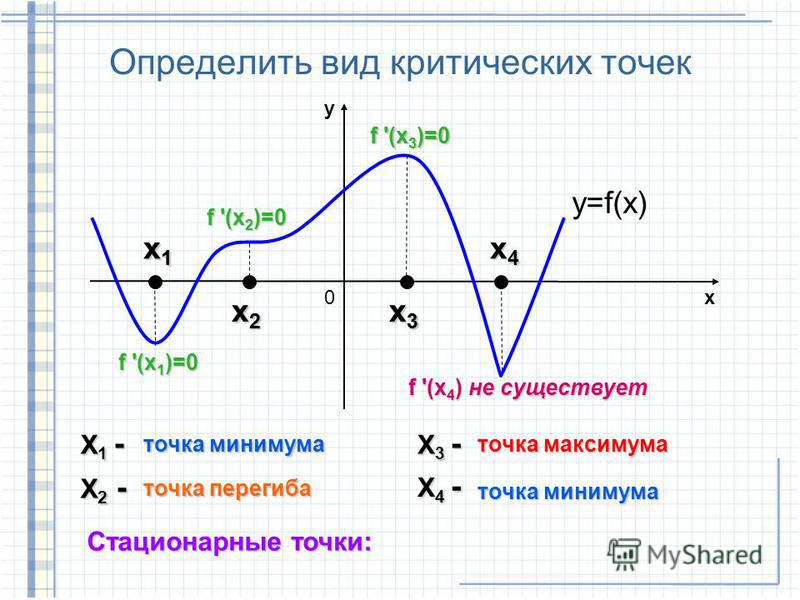
Есть еще один способ определить максимальное значение функции, и это из уравнения:
y = a ( x — h ) 2 + k
As в последнем уравнении член a в этом уравнении должен быть отрицательным, чтобы был максимум. Если член a отрицателен, максимум может быть найден при k . Никаких уравнений или вычислений не требуется — ответ — k .
Например, давайте найдем максимум уравнения:
-3 ( x — 5) 2-7
Поскольку член a равен -3, максимум будет равен -7.
Примеры из реального мира
Теперь давайте рассмотрим несколько примеров того, как эта информация может быть полезна в реальном мире.
Допустим, у вас есть 250 футов ограды и большое поле. Вы хотите построить прямоугольную игровую площадку. Какова максимальная площадь вашей игровой площадки? Используйте уравнение:
y = — x 2 + 125 x
Поскольку член a отрицательный, мы знаем, что для этого квадратного уравнения будет максимум. Чтобы найти этот максимум, который является максимальной площадью, мы можем использовать уравнение:
Чтобы найти этот максимум, который является максимальной площадью, мы можем использовать уравнение:
max = c — ( b 2/4 a )
Подставляя наши числа, мы получаем max = 0 — ( (1252) / (4 * -1)), или max = -15625 / -4, что становится max = 3906 футов2. И это будет максимальная площадь нашей игровой площадки с использованием 250 футов ограждения.
Давайте посмотрим на еще один. Высота h в футах, на которой объект находится над землей, задается уравнением: h = -16 t 2 + 64 t + 190, где t — время в секундах.Какая максимальная высота объекта?
Используя уравнение max = c — ( b 2/4 a ), мы можем найти максимальную высоту.
Сначала мы подставляем наши числа, чтобы получить max = 190 — ((642) / (4 * -16))
Затем возводим в квадрат 64 и умножаем знаменатель, чтобы получить max = 190 — (4096 / (-64)) , которое мы можем упростить до max = 190 + 64 или max = 254 футов.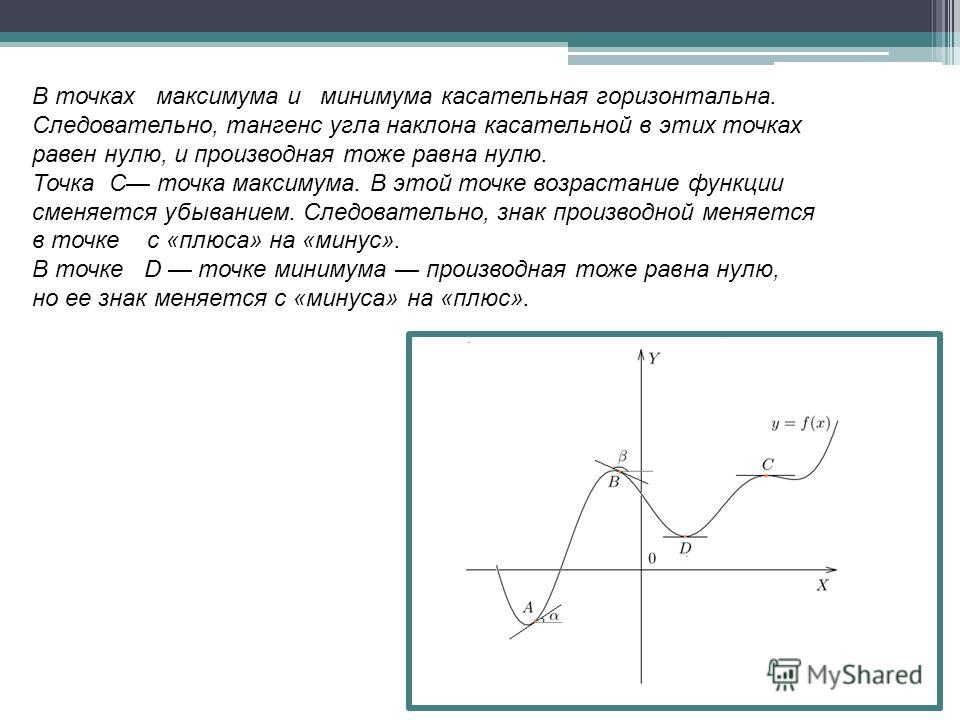
Краткое содержание урока
Максимальное значение функции — это место, где функция достигает своей наивысшей точки или вершины на графике.Если ваше квадратное уравнение имеет отрицательное значение или , оно также будет иметь максимальное значение. Есть три способа найти этот максимум, в зависимости от того, какая у вас форма квадратичной. Если у вас есть график или вы можете нарисовать график, максимум — это просто значение y в вершине графика. Если вы не можете нарисовать график, есть формулы, которые можно использовать, чтобы найти максимум. Если дана формула y = ax 2 + bx + c , то максимальное значение можно найти по формуле max = c — ( b 2/4 a ).Если у вас есть уравнение y = a ( x — h ) 2 + k и член a отрицателен, то максимальное значение будет k .
Максимум и минимум задач — Precalculus
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Относительные максимумы и минимумы — Концепция
Найти относительные максимумы и минимумы функции можно, посмотрев на график функции. Относительный максимум — это точка, которая выше, чем точки непосредственно рядом с ней с обеих сторон, а относительный минимум — это точка, которая ниже, чем точки непосредственно рядом с ней с обеих сторон. Относительные максимумы и минимумы являются важными точками при построении кривых, и их можно найти с помощью теста первой или второй производной.
Относительный максимум — это точка, которая выше, чем точки непосредственно рядом с ней с обеих сторон, а относительный минимум — это точка, которая ниже, чем точки непосредственно рядом с ней с обеих сторон. Относительные максимумы и минимумы являются важными точками при построении кривых, и их можно найти с помощью теста первой или второй производной.
Я хочу поговорить о двух новых понятиях относительного максимума и относительного минимума.Вот определения, относительный максимум, который иногда называют локальным максимумом, f имеет относительный максимум при x = c, если c является наибольшим значением f около c, а относительный минимум f имеет относительный минимум при x = c, если f of c — наименьшее значение f рядом с c. Теперь вам важно знать, потому что вы можете услышать, как я использую эти термины в видео. Множественное число от максимума — это максимум, множественное число от минимума — это минимум.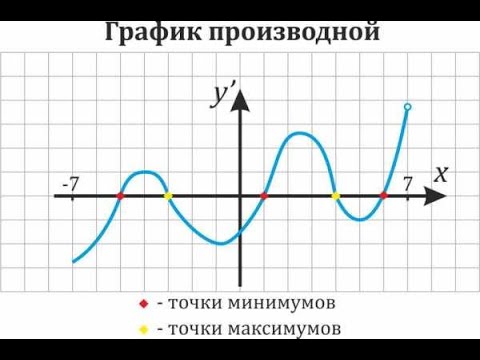
Давайте посмотрим на пример, проблема гласит: определить относительные max и min f в интервале от 1 до 15, теперь это та часть, которую я нарисовал здесь, так что это мой график y равен f от x, и я хочу определить, где происходят относительные максимумы и относительные минимумы.Что ж, их много, теперь помните, что относительный максимум, если значение f из c, которое больше, чем любое соседнее значение, поэтому здесь это значение 42 является относительным максимумом для функции f, если вы посмотрите на это маленькое соседство здесь это самая высокая точка, которая делает его относительным максимумом. Таким образом, есть относительный максимум при x = 1, и мы можем аналогичным образом пройтись и найти другие относительные максимумы, есть один прямо здесь, вы просто покроете остальную часть графика руками и заметите, что в этом небольшом интервале здесь 35 — это самый высокий точка справа 35 — это наибольшее значение, которое принимает функция, поэтому имеется относительный максимум при x = 9.
И, наконец, в этой конечной точке график, кажется, достигает еще одного максимума, если вы посмотрите на него. 52 — это значение функции здесь, и это самое высокое значение в некотором интервале вокруг этой точки. Итак, x = 15, мы получили относительный максимум, так что у нас есть 1, 9 и 15 — это положения относительных максимумов, а как насчет относительных минимумов? Что ж, похоже, что эти 2, и я хочу, чтобы вы обратили пристальное внимание на тот факт, что многие из этих, прежде всего, 2 относительных максимума происходят в конечных точках. Конечные точки важно проверять, но также не обязательно должны выглядеть относительные максимумы и минимумы, они не должны выглядеть извилистыми, вы на самом деле можете иметь точку минимума или максимума, поэтому это считается минимумом.Это самая низкая точка в окрестностях. Это значение 18 будет самой низкой точкой, а минимум на самом деле происходит при x = 11, и здесь у нас есть минимальное значение 11, а это минимум происходит при x = 5.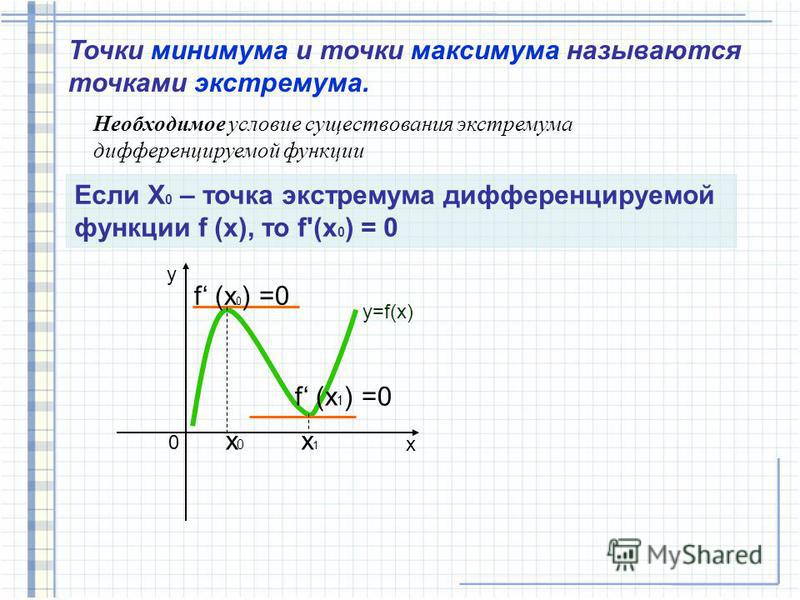 Таким образом, их относительные минимумы при x = 5 и x = 11 эти 2 точки.
Таким образом, их относительные минимумы при x = 5 и x = 11 эти 2 точки.
Теперь вам также важно знать новый термин «относительные максимумы» и «относительные минимумы», которые вместе называются относительными экстремумами. Итак, если я говорю найти относительные экстремумы, я имею в виду найти относительные максимумы и минимумы.
применений дифференциации — математика A-Level Revision
В этом разделе рассматривается использование дифференциации, стационарных точек, точек максимума и минимума и т. Д.
Функции увеличения и уменьшения
Возрастающая функция — это функция, в которой: если x 1 > x 2 , то f (x 1 )> f (x 2 ), поэтому при увеличении x увеличивается f (x). Уменьшающая функция — это функция, которая уменьшается с увеличением x. Конечно, в одних местах функция может увеличиваться, а в других — уменьшаться. Точка, в которой функция изменяется с возрастающей на убывающую или наоборот, называется поворотной точкой. Точка поворота — это тип стационарной точки (см. Ниже).
Точка поворота — это тип стационарной точки (см. Ниже).
Мы можем использовать дифференцирование, чтобы определить, увеличивается или уменьшается функция:
Функция возрастает, если ее производная всегда положительна. Функция убывает, если ее производная всегда отрицательна.
Примеры
y = -x имеет производную -1, которая всегда отрицательна, поэтому -x уменьшается.
y = x 2 имеет производную 2x, которая отрицательна, когда x меньше нуля, и положительна, когда x больше нуля.Следовательно, x 2 уменьшается при x <0 и увеличивается при x> 0.
Стационарные точки
Стационарные точки — это точки на графике, где градиент равен нулю. Есть три типа стационарных точек: максимумы, минимумы и точки перегиба (/ inflexion). Эти три показаны здесь:
Пример
Найдите координаты стационарных точек на графике y = x 2 .
Мы знаем, что в стационарных точках dy / dx = 0 (поскольку градиент равен нулю в стационарных точках).
Путем дифференцирования получаем: dy / dx = 2x. Следовательно, стационарные точки на этом графике возникают, когда 2x = 0, то есть когда x = 0.
Когда x = 0, y = 0, поэтому координаты стационарной точки равны (0,0) . В данном случае это единственная неподвижная точка. Если вы думаете о графике y = x 2 , вы должны знать, что он имеет U-образную форму с самой низкой точкой в начале координат.Это то, что мы только что обнаружили.
Максимум, минимум или точка перегиба?
Во всех стационарных точках градиент одинаков (= ноль), но часто бывает необходимо знать, нашли ли вы точку максимума, точку минимума или точку перегиба. Следовательно, необходимо учитывать градиент по обе стороны от стационарной точки (в качестве альтернативы мы можем использовать вторую производную).
В точках максимума градиент положительный непосредственно перед максимумом, он равен нулю в максимуме и отрицателен сразу после максимума.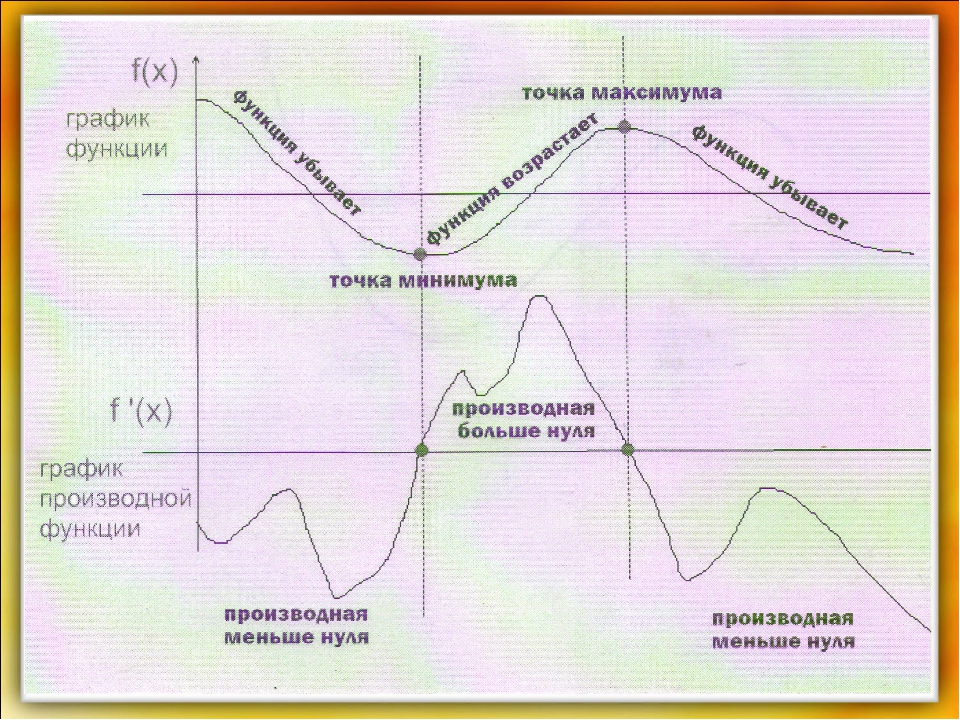 В минимальных точках градиент отрицательный, затем ноль, затем положительный. Наконец, в точках перегиба градиент может быть положительным, нулевым, положительным или отрицательным, нулевым или отрицательным. Это проиллюстрировано здесь:
В минимальных точках градиент отрицательный, затем ноль, затем положительный. Наконец, в точках перегиба градиент может быть положительным, нулевым, положительным или отрицательным, нулевым или отрицательным. Это проиллюстрировано здесь:
Пример
Найдите стационарные точки на графике y = 2x 2 + 4x 3 и укажите их природу (то есть являются ли они максимумами, минимумами или точками перегиба).
dy / dx = 4x + 12x 2
В стационарных точках dy / dx = 0
Следовательно, 4x + 12x 2 = 0 в стационарных точках
Следовательно, 4x (1 + 3x) = 0
Следовательно, либо 4x = 0 или 3x = -1
Следовательно, x = 0 или -1/3
Когда x = 0, y = 0
Когда x = -1/3, y = 2x 2 + 4x 3 = 2 (-1/3) 2 + 4 (-1/3) 3 = 2/9 — 4/27 = 2/27
Если смотреть на градиент по обе стороны от x = 0:
Когда x = -0. 0001, dy / dx = отрицательный
0001, dy / dx = отрицательный
Когда x = 0, dy / dx = ноль
Когда x = 0,0001, dy / dx = положительный
Таким образом, градиент идет -ve, ноль, + ve, что показывает минимальную точку.
Глядя на градиент по обе стороны от x = -1/3.
Когда x = -0,3334, dy / dx = + ve
Когда x = -0,3333 …, dy / dx = ноль
Когда x = -0,3332, dy / dx = -ve
Таким образом, градиент идет + ve, ноль , -ve, который показывает максимальную точку.
Следовательно, существует максимальная точка в (-1/3, 2/27) и минимальная точка в (0,0) .
Решение практических задач
Этот метод нахождения максимумов и минимумов очень полезен и может использоваться для определения максимальных и минимальных значений всех видов вещей.
Пример
Найдите наименьшую площадь металла, необходимую для изготовления закрытого цилиндрического контейнера из тонкого листового металла, чтобы он мог иметь вместимость 2000 п / см 3 .
Общая площадь цилиндра S составляет 2pr 2 + 2prh
Объем = pr 2 h = 2000p
Следовательно, pr 2 h = 2000p.
Следовательно, h = 2000 / r 2
Следовательно, S = 2pr 2 + 2pr (2000 / r 2 )
= 2pr 2 + 4000p
r
Итак, у нас есть выражение для площади поверхности. Чтобы найти, когда площадь поверхности минимальна, нам нужно найти dS / dr.
dS = 4pr — 4000p
dr r 2
Когда dS / dr = 0:
4pr — (4000p) / r 2 = 0
Следовательно, 4pr = 4000p
r 2
Итак, 4pr 3 = 4000p
Итак, r 3 = 1000
Итак, r = 10
Затем вы должны проверить, действительно ли это минимум, используя описанную выше методику.
Таким образом, минимальная площадь возникает при r = 10. Эта минимальная площадь находится путем подстановки в уравнение для площади значения r = 10.
S = 2pr 2 + 4000p
r
= 2p (10) 2 + 4000p
10
= 200p + 400p
= 600p
Следовательно, минимальное необходимое количество металла составляет 600p см 2
Максимум / Минимум проблем
Многие прикладные задачи в исчислении связаны с функциями, для которых вы хотите найти максимальные или минимальные значения.Ограничения, указанные или подразумеваемые для таких функций, будут определять домен, из которого вы должны работать. Функция вместе с ее доменом предложит, какой метод подходит для определения максимального или минимального значения — теорема об экстремальном значении, тест первой производной или второй тест производной.Пример 1: Прямоугольная коробка с квадратным основанием без верха должна иметь объем 108 кубических дюймов. Найдите размеры коробки, требующие наименьшего количества материала.
Функция, которая должна быть минимизирована, — это площадь поверхности ( S ), в то время как объем ( V ) остается фиксированным на уровне 108 кубических дюймов (Рисунок 1).
Рисунок 1 Коробка с открытым верхом для Примера 1.
Положив x = длину квадратного основания и h = высоту коробки, вы обнаружите, что
с областью f (x) = (0, + ∞), потому что x представляет длину.
, следовательно, критическая точка возникает, когда x = 6. Использование теста второй производной:
и f имеет локальный минимум x = 6; следовательно, размеры коробки, требующие наименьшего количества материала, составляют: длина и ширина 6 дюймов, а высота 3 дюйма.
Пример 2: Правый круговой цилиндр вписан в правый круговой конус, так что центральные линии цилиндра и конуса совпадают.Конус имеет 8 см и радиус 6 см. Найдите максимально возможный объем вписанного цилиндра.
Функция, которая должна быть максимизирована, — это объем ( V ) цилиндра, вписанного в конус высотой 8 см и радиусом 6 см (рисунок).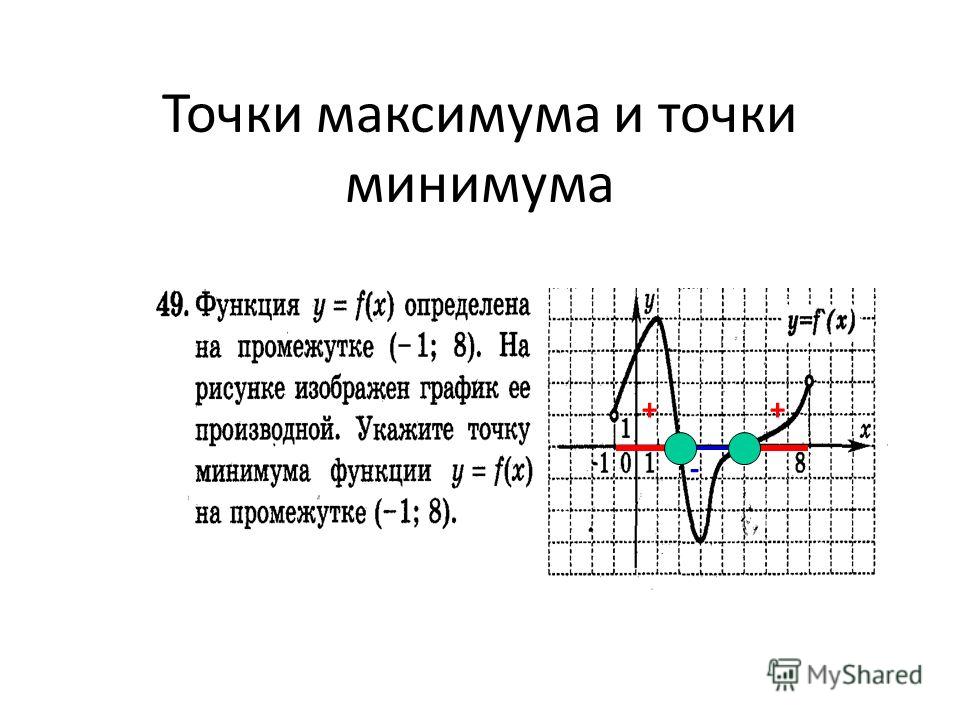
Рисунок 2 Поперечное сечение конуса и цилиндра для Примера 2.
Положив r = радиус цилиндра и h = высоту цилиндра и применяя аналогичные треугольники, вы обнаружите, что
Поскольку V = π r 2 h и h = 8 — (4/3) r , получается, что
с областью f (r) = [0,6], потому что r представляет радиус цилиндра, который не может быть больше, чем радиус конуса.
Поскольку f (r ) непрерывно на [0,6], используйте теорему об экстремальных значениях и оцените функцию в ее критических точках и ее конечных точках; следовательно,
, следовательно, максимальный объем составляет 128π / 3 см 3 , что будет, когда радиус цилиндра равен 4 см, а его высота равна 8/3 см.
Видео с вопросом: Нахождение локальных максимальных и минимальных значений квадратичной функции
Стенограмма видео
Определите локальный максимум и
минимальные значения функции равны отрицательным трем 𝑥 в квадрате минус шесть 𝑥
минус четыре.
Прежде всего напомним, что при критических точек, первая производная функции — в данном случае d𝑦 на d𝑥 — равна нуль. Итак, нашим первым шагом будет найти первую производную этой функции. Применяя правило силы дифференцирования, мы находим, что d𝑦 на d𝑥 равно отрицательным шести 𝑥 минус шесть. Затем мы задаем выражение для d𝑦 на d𝑥 равное нулю и решим относительно 𝑥, давая равно отрицательному. Таким образом, наша функция имеет один критическая точка, которая возникает, когда 𝑥 равно отрицательному.
Далее нам нужно оценить
функция в критической точке, которую мы делаем, подставляя 𝑥, равно отрицательному
в уравнение, которое нам дано. Получаем, что равно трем отрицательным
умножить на минус один квадрат минус шесть умножить на минус четыре
что упрощается до отрицательного. Это говорит нам тогда, что единственный
критической точкой этой функции является точка с координатами отрицательная, отрицательная
один. Но нам нужно определить,
это локальный минимум или локальный максимум, который мы сделаем, применив второй
производный тест.
Чтобы найти вторую производную, мы нужно дифференцировать нашу первую производную по. Итак, мы находим производную от отрицательные шесть 𝑥 минус шесть по отношению к 𝑥. Применяя правило силы, мы видим что эта производная просто равна отрицательной шестерке. Теперь эта вторая производная равна на самом деле просто константа, потому что мы дифференцировали квадратное выражение дважды. Поэтому нам не нужно заменять 𝑥-координата в нашей критической точке, чтобы оценить, потому что вторая производная постоянна для всех значений 𝑥.Отметим, что отрицательная шестерка меньше чем ноль. Напомним, что если второй производная функции отрицательна в критической точке, то критическая точка это локальный максимум. Итак, точка отрицательная, отрицательная один действительно является локальным максимумом этой функции.
Итак, мы можем сделать вывод, что это
функция не имеет локального минимального значения, но имеет локальное максимальное значение отрицательное
один. Обратите внимание, что это значение
функция, которую мы здесь даем, а не значение, хотя они оба
то же самое и в этом случае.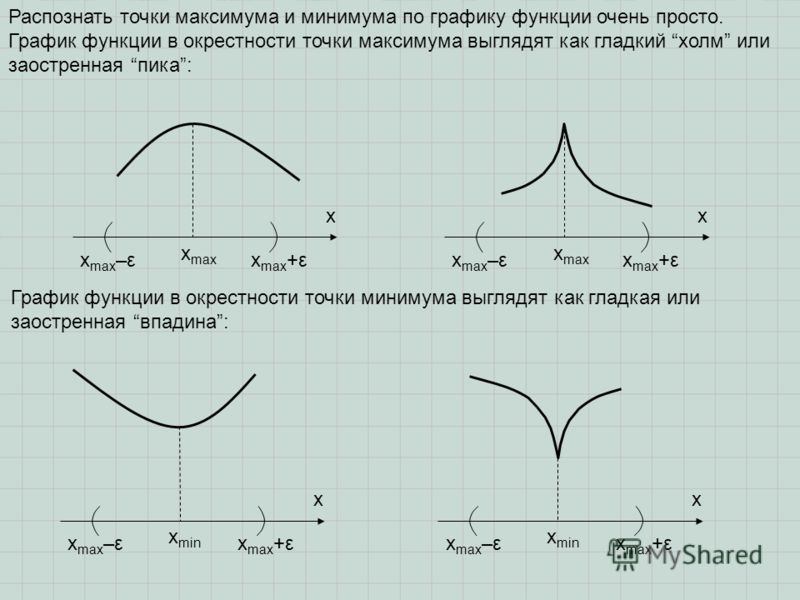



 Нет? Тогда перерешивай пример.
Нет? Тогда перерешивай пример.


Leave A Comment