Стереометрия на ЕГЭ
Математика — гимнастика для ума, Стереометрия — витамин для мозга
_
_
_
_
Стереометрия (от др.-греч. στερεός, «стереос» — «твёрдый, пространственный» и μετρέω — «измеряю») — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.
Вики
Стереометрия вокруг нас: в быту и в профессиональной деятельности. Мы, безусловно, не можем «увидеть» науку, но можем ежедневно лицезреть объемные тела в пространстве, которые она изучает. Например, капли жидкости в невесомости принимают форму геометрического тела, называемого шаром. Такую же форму имеет и маленький теннисный шарик, и более крупные предметы — наша планета и многие другие космические объекты. А консервная банка — это цилиндр.
Для начала посмотрим на это с точки зрения психологии. С самого рождения и до 2 лет, ребенок не может воспринимать предметы объемные, а видит только одну сторону, несмотря на то, что мы живем в трехмерном пространстве. Если от ребенка спрятать игрушку, он будет считать, что она пропала. Поэтому, когда мама уходит, дети начинают искать ее и пугаться, что она исчезла. Сами они не могут догадаться, что игрушка под подушкой, а мама просто вышла за дверь.
Психологами был проведен опыт. На стол поставили макет горы, задачей детей было нарисовать ее с той стороны, с которой они ее видят. С этим заданием все справились великолепно, но, когда их попросили нарисовать гору со стороны соседа, они нарисовали то же самое, что и в первый раз. Отсюда вывод — наше подсознание, наш мозг не способны воспринимать вещи в полном объеме до определенного возраста, вот почему стереометрия преподается в старших классах
Аксиомы стереометрии
Аксио́ма (др.-греч. ἀξίωμα — утверждение, положение), постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое в основе доказательства других ее положений
Аксиомы планиметрии описывают свойства простейших геометрических фигур на плоскости. Так как стереометрия изучает фигуры в пространстве и так, как в пространстве может быть великое множество плоскостей, то аксиомы стереометрии состоят из аксиом планиметрии с уточнением «на» или «в заданной плоскости» и 3-х дополнительных аксиом. Плоскости обозначаются греческими буквами α, β, γ.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей
Расстояние между любыми двумя точками пространства одно и то же на всех плоскостях, содержащих эти точки
Основные теоремы стереометрии
Теоре́ма (др.-греч.θεώρημα — «доказательство, вид; взгляд; представление, положение») — утверждение, для которого в рассматриваемой теории существует доказательство
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость
Если две прямые параллельны третьей прямой, то они параллельны
Векторы в стереометрии
Векторное решение многих стереометрических задач значительно проще их решения средствами элементарной геометрии («чисто геометрически»). Причина этого «упрощения» заключается в том, что при векторном методе решения можно обойтись без тех дополнительных построений, которые следует выполнять (аргументированно!) при «чисто геометрическом» решении даже простых задач.
Вместе с тем, чтобы векторы стали аппаратом решения геометрических задач, необходимо уметь переводить условие геометрической задачи в векторную терминологию и символику (на «векторный язык»), затем выполнять соответствующие алгебраические операции над векторами и, наконец, полученный в векторной форме результат переводить «обратно», на «геометрический язык».
Знание условий коллинеарности двух векторов и компланарности трех векторов позволяет в векторной форме решать аффинные задачи стереометрии — задачи, в которых изучаются вопросы взаимного расположения прямых и плоскостей. Свойства скалярного произведения двух векторов, условия перпендикулярности двух векторов позволяют легко перевести в векторную форму отношения перпендикулярности прямых и плоскостей и с помощью векторов решать метрические задачи — задачи, в которых находят расстояния, углы, площади, объемы геометрических фигур.
Одним словом, векторы — мощный аппарат решения стереометрических задач
Компланарными векторами называют вектора, параллельные одной плоскости или лежащие на одной плоскости
Коллинеарными векторами называют вектора, параллельные одной прямой или лежащие на одной прямой
Стереометрия на ЕГЭ
И вот наконец то мы добрались до самого главного вопроса, который возникает при изучении стереометрии: как решать задачи по стереометрии на ЕГЭ?
Как правило задание заключается в поиске углов между прямыми, плоскостями, или между прямой и плоскостью. Или поиск синуса, косинуса или тангенса этого угла. Часто в этом задании просят найти расстояние между точками, прямыми, или прямой и плоскостью.
Существует три основных метода решения задач C2 из ЕГЭ по математике. Условно назовем их «методом построений», «векторным методом» и «методом объемов». Каждый из них удобен в том или ином случае, поэтому лучше знать и уметь использовать все три.
Наиболее универсальным является «метод построений», с его помощью можно решить практически любую задачу по стереометрии из тех, что предлагаются в вариантах ЕГЭ по математике. Обычно это поиск углов между прямыми, плоскостями, или между прямой и плоскостью. Или поиск синуса, косинуса или тангенса этого угла. Зачастую в этом задании просят найти расстояние между точками, прямыми, или прямой и плоскостью.Читать далее: http://4ege.ru/video-matematika/4606-stereometriya-klassicheskiy-metod-s2.html Обычно это поиск углов между прямыми, плоскостями, или между прямой и плоскостью. Или поиск синуса, косинуса или тангенса этого угла. Зачастую в этом задании просят найти расстояние между точками, прямыми, или прямой и плоскостью.Читать далее: http://4ege.ru/video-matematika/4606-stereometriya-klassicheskiy-metod-s2.html Обычно это поиск углов между прямыми, плоскостями, или между прямой и плоскостью. Или поиск синуса, косинуса или тангенса этого угла. Зачастую в этом задании просят найти расстояние между точками, прямыми, или прямой и плоскостьюЧитать далее: http://4ege.ru/video-matematika/4606-stereometriya-klassicheskiy-metod-s2.html Обычно это поиск углов между прямыми, плоскостями, или между прямой и плоскостью. Или поиск синуса, косинуса или тангенса этого угла. Зачастую в этом задании просят найти расстояние между точками, прямыми, или прямой и плоскостьюЧитать далее: http://4ege.ru/video-matematika/4606-stereometriya-klassicheskiy-metod-s2.htmlСледствия аксиом стереометрии. Теоремы 1,2.
Аксиомы стереометрии.
Стереометрия-раздел геометрии, в котором изучаются фигуры в пространстве.
Основные фигуры стереометрии:
1. Точка А
2. Прямая
3. Плоскость
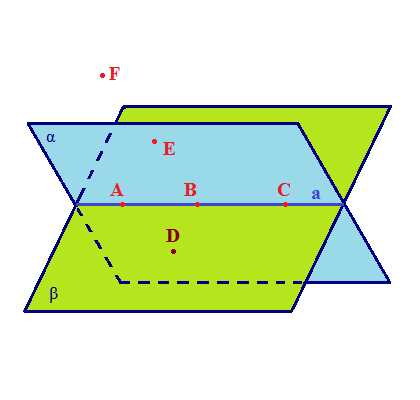
Свойство 1. Какова бы не была плоскость, существуют точки, принадлежащие этой плоскости и принадлежащие ей. ∃α: А∈ α; В∈α; D∉α. ∃-существует.
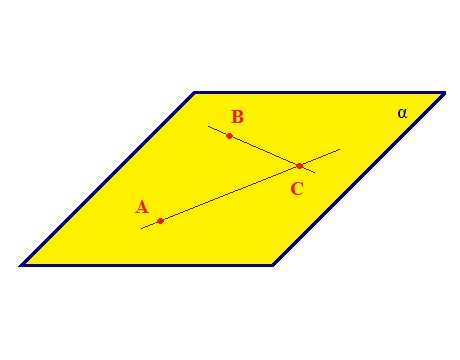
Свойство 2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Если А∈ α; А∈β, то ∃α: а ∈ α; α ∈ β, А∈а
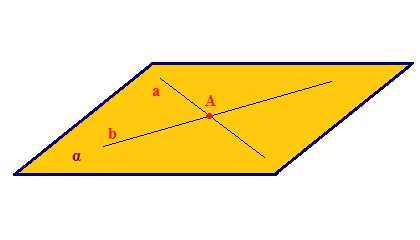
Свойство 3. Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну. Если А∈а; А∈в, то ∃!α: а∈α; в∈α; А∈α
Свойство 4. Если две различны точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. Если А∈α; В∈α, то АВ∈α
Следствия аксиом стереометрии. Теоремы 1,2.
Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну. Дано: а; С∉а. Доказать: ∃!α: а∈α; С∈α. Доказательство: 1. В∈а (по аксиоме о том, что существует точки принадлежащие прямой и не принадлежащие ей). 2. ВС (по аксиоме о том, что через две точки можно провести одну прямую). 3. Т.к. В∈ВС, В∈а, то по Свойству 3 ∃α:ВС∈α, а∈α. 4. Пусть ∃α
Теорема 2. Через 3 любые точки, не лежащие на 1 прямой можно провести плоскость и притом только 1. Дано: точка А, точка В, точка С. Доказать: ∃!α: А∈α; В∈α; С∈α. Доказательство:1. АВ, АС (по аксиоме о том, что через 2 точки можно провести 1 прямую). 2. Т.к. А∈АВ, А∈АС, то по Свойству 3 ∃α:АВ∈α, ВС∈α. 4. Пусть ∃α2: а∈α1; А∈α1, тогда В∈α1; С∈α1, тогда по свойству 2 А, В, С лежат на одной прямой, но это противоречит условию, значит α-единственная. чтд.
Взаимное расположение прямых в пространстве.
2 прямые не лежащие в одной плоскости могут: пересекаться, быть параллельными, совпадать. Две прямые лежащие в одной плоскости называются параллельными, если они не пересекаются. Если прямые не лежат в одной плоскости и не пересекаются, то они будут параллельными.
Теорема 3. Через точку вне данной прямой можно провести прямую, параллельную этой прямой и притом только одну. Дано: а; А; А∉а. Доказать: ∃!а1: А∈а1, а1| |а. Доказательство: 1. По Т1 ∃!α: А∈α; а∈α. 2. А∈а1, а1| |а (по аксиоме планиметрии о том, что через точку к заданной прямой можно провести параллельную прямую и притом только одну). 3. Пусть ∃а2: А∈а2, а2| |а, тогда через прямые а и а2 проведем плоскость α, но по Т1 эта плоскость проходит через а и А, значит а1 и а2 совпадут, а1-единственная. чтд.
Теорема 4. Признак параллельности прямых (теорема о транзитивности). Если две прямые параллельны третьей, то они параллельны друг другу. Дано: а,в,с. а| |в, а| |с. Доказать: в| |с. Доказательство:1. β: а∈β; в∈β. 2. α: а∈α; С∈α. 3. В∈в (по акстоме С1). 4. По Т1 ∃!α: С∈α1; В∈α1. 5. Т.к. В∈β, В∈α1, то по аксиоме С2 ∃в: в∈β; в∈α1; В∈в.
Взаимное расположение прямой и плоскости. Признак параллельности прямой и плоскости.
Прямая и плоскость будут параллельны, если они не пересекаются.
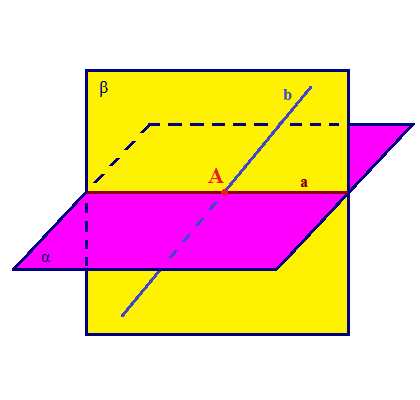
Теорема 5. Если прямая не лежащая в плоскости параллельна, какой нибудь прямой в этой плоскости, то она параллельна и самой плоскости. Дано: α; а; а∈α; в∈α; а| |в. Доказать: а| |α. Доказательство:1. ∃β: а∈β; в∈β (Т1). 2. Пусть а непараллельная α, тогда ∃М: М∈а, М∈β; М∈α; значит по С2 М∈в. 3. Получим что М∈а, М∈в, но по условию а| |в, значит наше предположение не верно, ; а| |α. чтд.
Теорема 6. Справедлива обратная теорема: Если плоскость β, проходящая через прямую а, параллельную плоскости α, пересекает эту плоскость по прямой в, то прямые а и в параллельны. Дано: а; в; α; β; а∈β; а| |α; в∈α; в∈β. Доказать: а| |в. Доказательство:Пусть а непараллельная в, тогда ∃М: М∈а; М∈в; М∈β; М∈α. 2. Получит что М∈а, М∈α, значит а пересекает α, но по условию а| |в, значит наше предположение не верно. чтд.
Параллельность двух плоскостей. Две плоскости называются параллельными, если они не пересекаются.
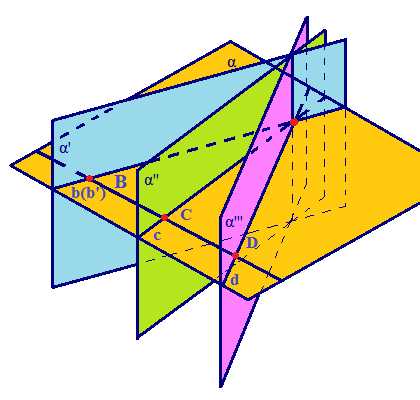
Признаки параллельности плоскостей. Теорема 7. Если плоскость параллельна двум пересекающимся прямым лежащим в другой плоскости, то эти плоскости параллельны.Дано: α; β; а∈β; в∈β; а| |α; в| |α; А∈а; А∈в. Доказать: α| |β. Доказательство:1. Пусть α не параллельна β, тогда ∃С: С∈α; С∈β. 2. Тк а| |α и в| |α, имеем а| |с и в| |с (Т5). 3. Тк а| |с и в| |с то Т4 (о транзитивности) имеем а| |в, но по условию а не параллельна в, значит наше предположение не верно α| |β. чтд.
Теорема 8. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Если А∈а; А∈в; а∈β; в∈β; А1∈а1; А1∈в1; а1∈α; в1∈α; а| |а1; в| |в1, то α| |β.
Параллельное проектирование и его свойства. Изображение фигур в стереометрии.
Для изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием. Этот способ состоит в следующем. Берем произвольную прямую h, пересекающую плоскость чертежа а, проводим через произвольную точку А фигуры прямую, параллельную h. Точка А1 пересечение этой прямой с плоскостью чертежа будет изображением точки А.
Свойства:1. Прямолинейные отрезки фигуры изображаются на плоскости чертежа отрезками.
2. Параллельные отрезки изображаются на плоскости чертежа параллельными отрезками.
3. Отношение отрезков одной прямой или параллельных прямых сохраняется при параллельном проектировании.
Изображение фигур в стереометрии.1. Прямоугольные, равнобедренные и равносторонние треугольники изображаются в стереометрии произвольными треугольниками.
2. Квадрат, прямоугольник, ромб изображаются в стереометрии в виде параллелограмма.
3. Окружность или круг изображаются в стереометрии в виде эллипса.
Перпендикуляр и наклонная. Свойства перпендикуляра и наклонной проведенных из одной точки.
1. Перпендикуляром (АВ) опущенным из данной точки на плоскость, называют отрезок соединяющий данную точку с точкой плоскости и лежащей на прямой перпендикулярной этой плоскости. Точка В называется основанием перпендикуляра.
2. Расстоянием от точки до плоскости называют длину перпендикуляра опущенного из этой т очки на плоскость.
3. Наклонной проведенной из данной точки к плоскости называют любой отрезок не перпендикулярный плоскости, соединяющий данную точку с плоскостью (АС; АС1). Точки С и С1 называют основаниями наклонных.
4. Отрезок на плоскости соединяющий основание перпендикуляра (В) с основанием наклонной (АС, АС1) проведенных из одной точки называется проекцией наклонной на плоскость (ВС, ВС1).
Свойства наклонных и проекций.
1. Длина перпендикуляра к плоскости меньше длины любой наклонной к плоскости. (АВ<АС; АВ<АС1)
2. Большей наклонной соответствует большая проекция. Если АС1<АС, то ВС1>ВС.
3. Длины наклонных равны тогда и только тогда, когда равны длины их проекций.
Теорема о трех перпендикулярах.
Теорема 16. Прямая проведенная на плоскости через основание наклонной перпендикулярна ее проекции перпендикулярна и самой наклонной.
Обратная теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции этой наклонной.
Дано: АВ┴α; АС-наклонная. С∈с. Доказать: 1. с┴АС; 2.с┴ВС. Доказательство:1.А,С┴α; А,С| |АВ (по Т15). 2. β:АВ∈β; А,С∈β (по определению параллельных прямых). 3. Пусть СВ ┴с, А,С┴с (по определению перпендикуляра к плоскости), значит по Т13 имеем, что прямая С┴β, значит по определению с┴АС. 4. Пусть АС┴с, А,С┴с (по определ. перпендикуляра к плоскости), значит по Т13 имеем, что прямая с┴β, значит по определению с┴СВ. чтд.
Признак перпендикулярности двух плоскостей.
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Доказательство: Пусть — плоскость , b — перпендикулярная ей прямая, — плоскость проходящая через прямую b, и с — прямая по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны.
Проведем в плоскости через точку пересечения прямой b с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и b плоскость . Она перпендикулярна прямой с, так как прямые а и b перпендикулярны, то плоскости и перпендикулярны. Теорема доказана.
Трехгранный угол. Теорема о свойстве плоских углов многогранного угла.
Трехгранный угол – это фигура состоящая из 3 плоских углов. Точка S-вершина угла, a, b, c-ребра. Углы между прямыми ab; bc; ac-это плоские углы трехгранного угла.
Теорема 20. Величина каждого плоского угла, трехгранного угла меньше суммы величин двух других его плоских углов.
Теорема 20. Сумма величин всех трех плоских углов трехгранного угла меньше 3600.
Теорема о сумме плоских углов многогранника.
Теорема 20. Сумма величин всех трех плоских углов трехгранного угла меньше 3600.
Призма. Ее элементы.
Призма – это многогранник, образованный двумя параллельными плоскостями соединенными параллельными отрезками.
Элементы призмы.
Высота призмы – расстояние между плоскостями оснований. Диагональ призмы (CF1; BE1; BF1) – отрезок соединяющий две вершины, не принадлежащие одной грани. Диагональное сечение (FCC1F1) – сечение призмы плоскостью, проходящей через два боковых ребра не принадлежащие одной грани.
1. Основания (ABCDEF, А1В1С1В1Е1А1)
2. Ребра оснований (АВ, ВС, СD, DE, EF, A1D1, D1C1, C1D1, D1E1, E1F1)
3. Боковые ребра (AA1, FF1, EE1, DD1, CC1, BB1)
4. Боковые грани (параллелограммы) (ABB1A1, BCC1B1, CDD1C1, DEE1D1, EFF1E1, AFF1A1)
Виды призм.
1. n-угольная призма (треугольная, четырехугольная).
2. Пряма призма-это призма у которой боковые ребра перпендикулярны основаниям, иначе призма наклонная.
3. Прямая призма называется правильной, если в ее основании лежит правильный многоугольник.
Sполн=Sбок + Sосн.
Боковой поверхностью призмы называют сумму площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и двух площадей оснований.
Теорема 23. Боковая поверхность правильной (прямой) призмы равна произведению периметра основания на высоту, т.е. длину бокового ребра.
Виды пирамиды.
1. n-угольная пирамида (треугольная, четырехугольная)
2. Правильная пирамида-это пирамида в основании которой лежит правильный многоугольник и ее вершина проектируется в центр данного многоугольника.
Апофема-высота боковой грани правильной пирамиды. (SK)
Теорема27. Плоскость параллельная основанию пирамиды и пересекающая ее отсекает подобную пирамиду.
Sполн=Sбок+Sосн.
Теорема 28. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
Правильные многогранники.
Многогранником называется тело ограниченное конечным числом плоскостей. Многогранник называется выпуклым, если он лежит по одну сторону каждой из ограниченных его плоскостей.
Элементы многогранника.
1. Вершины (точки)
2. Ребра (отрезки)
3. Грани (плоскости)
Многогранник называется правильным если его грани являются правильными многоугольниками и в каждой вершине сходится одинаковое число ребер.
Существует 5 видов многогранников:
1. Тетраэдр — грани правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
2. Куб – все грани квадраты; в каждой вершине сходятся по три ребра. Куб представляет собой треугольный параллелепипед с равными ребрами.
3. У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.
4. У додекаэдра грани — правильные пятиугольники.
5. У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.
Теорема 22. Теорема Эйлера. Для любого выпуклого многогранника с числом вершин β, числом граней Г и числом ребер Р выполняется следующие равенство: В+Г-Р=2.
Для тетраэдра В=4, Г=4, Р=6. Имеем: 4+4-6=2. Для куба В=8, Г=6, Р=12. Имеем 8+6-12=2. Для октаэдра В=6, Г=8, Р=12. Имеем:6+8-12=2. Для додекаэдра В=20, Г=12, Р=30. Имеем: 20+12-30=2. Для икосаэдра В=12, Г=20, Р=30. Имеем: 12+20-30=2.
Объем шара и его частей.
V= ПR3
Аксиомы стереометрии.
Стереометрия-раздел геометрии, в котором изучаются фигуры в пространстве.
Основные фигуры стереометрии:
1. Точка А
2. Прямая
3. Плоскость
Свойство 1. Какова бы не была плоскость, существуют точки, принадлежащие этой плоскости и принадлежащие ей. ∃α: А∈ α; В∈α; D∉α. ∃-существует.
Свойство 2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Если А∈ α; А∈β, то ∃α: а ∈ α; α ∈ β, А∈а
Свойство 3. Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну. Если А∈а; А∈в, то ∃!α: а∈α; в∈α; А∈α
Свойство 4. Если две различны точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. Если А∈α; В∈α, то АВ∈α
Следствия аксиом стереометрии. Теоремы 1,2.
Теорема 1. Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну. Дано: а; С∉а. Доказать: ∃!α: а∈α; С∈α. Доказательство: 1. В∈а (по аксиоме о том, что существует точки принадлежащие прямой и не принадлежащие ей). 2. ВС (по аксиоме о том, что через две точки можно провести одну прямую). 3. Т.к. В∈ВС, В∈а, то по Свойству 3 ∃α:ВС∈α, а∈α. 4. Пусть ∃α1: а∈α1; С∈α1, тогда С∈α; С∈α1, по свойству 2 имеем, что С ∈а, но по условию С∉а, значит наше предположение не верно и α1 совпадают с Сα, т.е. α-единственная. чтд.
Теорема 2. Через 3 любые точки, не лежащие на 1 прямой можно провести плоскость и притом только 1. Дано: точка А, точка В, точка С. Доказать: ∃!α: А∈α; В∈α; С∈α. Доказательство:1. АВ, АС (по аксиоме о том, что через 2 точки можно провести 1 прямую). 2. Т.к. А∈АВ, А∈АС, то по Свойству 3 ∃α:АВ∈α, ВС∈α. 4. Пусть ∃α2: а∈α1; А∈α1, тогда В∈α1; С∈α1, тогда по свойству 2 А, В, С лежат на одной прямой, но это противоречит условию, значит α-единственная. чтд.
Рекомендуемые страницы:
lektsia.com
|
||||
www.mathtask.ru
Введение в стереометрию — урок. Геометрия, 10 класс.
Школьный курс геометрии состоит из планиметрии и стереометрии.
Планиметрия изучает фигуры и их свойства на плоскости. Образно говоря, планиметрия изучает всё, что можно нарисовать или начертить на листе бумаги.
Основные объекты планиметрии — это точки, линии и замкнутые фигуры (например: квадрат, треугольник, круг, трапеция, ромб). Множество всех точек, рассматриваемых в планиметрии, образует плоскость. Множество точек в планиметрии называется фигурой. Замкнутая фигура в планиметрии — это множество точек, ограниченных линией. Стереометрия изучает фигуры и их свойства в пространстве. Образно говоря, стереометрия изучает всё, что можно склеить из бумаги, сколотить из досок, построить из кирпичей и т.п.Основными объектами стереометрии являются точки, прямые, плоскости и замкнутые пространственные фигуры (например: куб, пирамида, параллелепипед, шар, конус). Множество всех точек, рассматриваемых в стереометрии, называется пространством. Любое множество точек называется фигурой. Замкнутая фигура в стереометрии — это множество точек, ограниченных поверхностью.
Пример:
На анимированных иллюстрациях наглядно показаны связь и различие плоских и пространственных фигур.

Ваш браузер не поддерживает HTML5 видео
 Ваш браузер не поддерживает HTML5 видео
Ваш браузер не поддерживает HTML5 видео
Так как каждая прямая и каждая плоскость содержат какие-либо точки, то прямая и плоскость тоже являются фигурами стереометрии.
Плоскость бесконечна и делит пространство на две части.
Точки обозначаются прописными латинскими буквами \(A, B, C, D, E, F…\).
Прямые обозначаются строчными латинскими буквами \(a, b, c, d, e, f…\).
Плоскости обозначаются греческими буквами α,β,γ и т.д.
www.yaklass.ru
Параллельность прямых, прямой и плоскости — урок. Геометрия, 10 класс.
Параллельность прямых \(a\) и \(b\) обозначается так: a∥b илиb∥a.
Teорема 1. Через две параллельные прямые можно провести плоскость, и при том только одну.
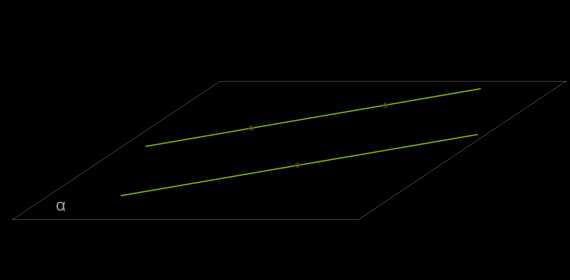
Доказательство:
1. Так как прямые \(a\) и \(b\) параллельны, из определения следует, что через них можно провести плоскость α.
2. Чтобы доказать, что такая плоскость только одна, на прямой \(a\) обозначаем точки \(B\) и \(C\), а на прямой \(b\) точку \(A\).
3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость (2 аксиома), то α является единственной плоскостью, которой принадлежат прямые \(a\) и \(b\).
Теорема 2. Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и при том только одну.
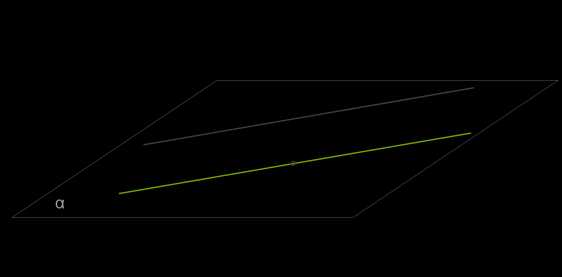
Доказательство:
1. Через данную прямую \(a\) и точку \(M\), которая не лежит на прямой, проводится плоскость α.
2. Такая плоскость только одна (т.к. через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну).
3. А в плоскости α через точку \(M\) можно провести только одну прямую \(b\), которая параллельна прямой \(a\).
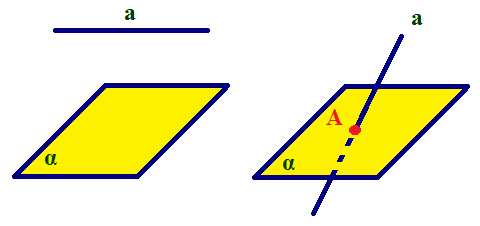
Теорема 3. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
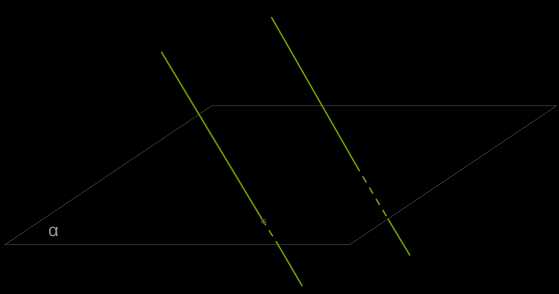
(1. рис.)
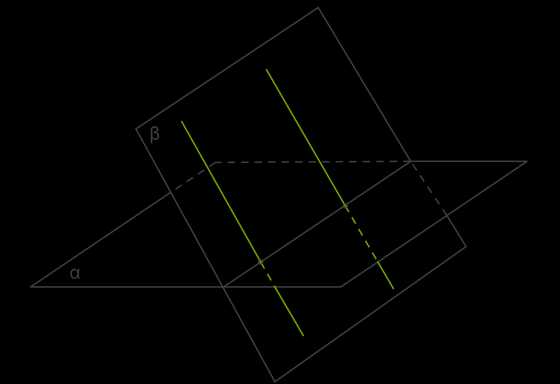
(2. рис.)
Доказательство:
Рассмотрим две параллельные прямые \(a\) и \(b\) и допустим, что прямая \(b\) пересекает плоскость α в точке \(M\) (1. рис.).
Из 1-ой теоремы известно, что через параллельные прямые \(a\) и \(b\) можно провести только одну плоскость β.
Так как точка \(M\) находится на прямой \(b\), то \(M\) также принадлежит плоскости β(2. рис.). Если у плоскостей α и β есть общая точка \(M\), то у этих плоскостей есть общая прямая \(c\), которая является прямой пересечения этих плоскостей (4 аксиома).
Прямые \(a\), \(b\) и \(c\) находятся в плоскости β.
Если в этой плоскости одна из параллельных прямых \(b\) пересекает прямую \(c\), то вторая прямая \(a\) тоже пересекает \(c\).
Точку пересечения прямых \(a\) и \(c\) обозначим за \(K\).
Так как точка \(K\) находится на прямой \(c\), то \(K\) находится в плоскости α и является единственной общей точкой прямой \(a\) и плоскости α.
Значит, прямая \(a\) пересекает плоскость α в точке \(K\).
Теорема 4. Две прямые, параллельные третьей прямой, параллельны.
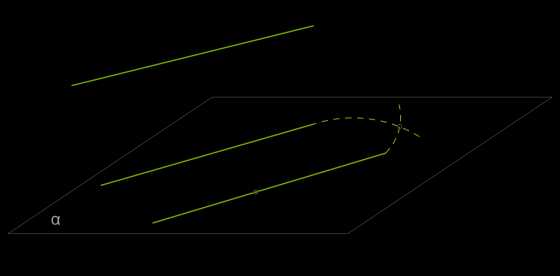
Дано: a∥cиb∥c
Доказать: a∥b
Доказательство:
Выберем точку \(M\) на прямой \(b\).
Через точку \(M\) и прямую \(a\), которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая \(b\) пересекает плоскость α или 2) прямая \(b\) находится в плоскости α.
Пусть прямая \(b\) пересекает плоскость α.
Значит, прямая \(c\), которая параллельна прямой \(b\), тоже пересекает плоскость α. Так как a∥c, то получается, что \(a\) тоже пересекает эту плоскость. Но прямая \(a\) не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая \(b\) пересекает плоскость α, является неверным.
Значит, прямая \(b\) находится в плоскости α.
Теперь нужно доказать, что прямые \(a\) и \(b\) параллельны.
Пусть у прямых \(a\) и \(b\) есть общая точка \(L\).
Это означает, что через точку \(L\) проведены две прямые \(a\) и \(b\), которые параллельны прямой \(c\). Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые \(a\) и \(b\) не имеют общих точек.
Так как прямые \(a\) и \(b\) находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Всё множество прямых в пространстве, которые параллельны данной прямой, называется пучком параллельных прямых.
Выводы:
1) Любые две прямые пучка параллельных прямых параллельны между собой.
2) Параллельности прямых в пространстве присуща транзитивность: еслиa∥bиb∥c,тоa∥c.
Пример:
Одна сторона параллелограмма пересекает плоскость. Докажите, что прямая, которая содержит противоположную сторону параллелограмма, тоже пересекает эту плоскость.
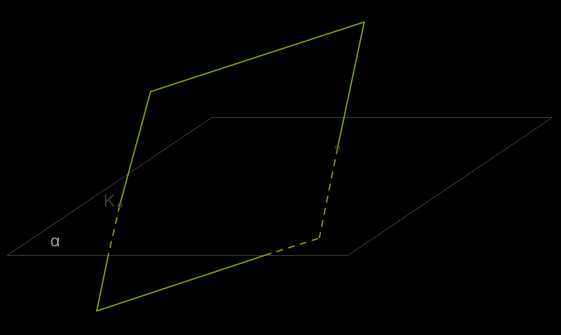
Допустим, что у параллелограмма \(ABCD\) сторона \(AD\) пересекает плоскость α в точке \(K\).
Так как противоположные стороны параллелограмма параллельны, то, согласно третьей теореме, прямая, которая содержит сторону \(CD\), тоже пересекает плоскость α.
2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются)
Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит прямая \(a\) должна быть параллельна плоскости α.
www.yaklass.ru
|
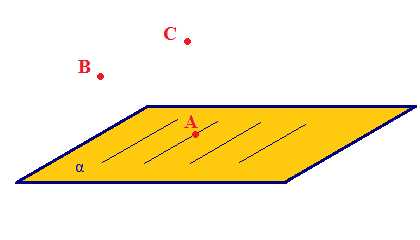
Плоскость. | |
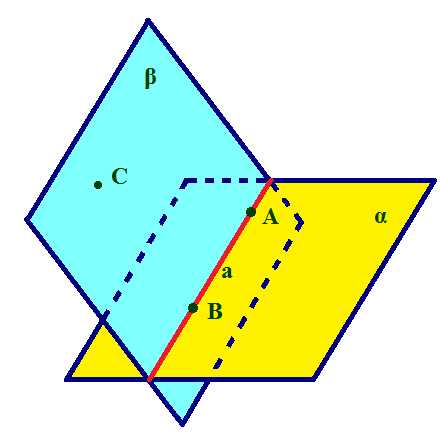
| На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д.
Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β, |
|
Аксиомы стереометрии и их следствия
Аксиома 1. |
|
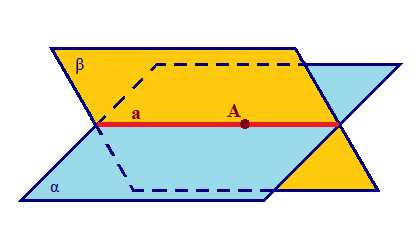
Аксиома 2. |
|
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются. |
|
Аксиома 3. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты. |
Некоторые следствия из аксиом
Теорема 1. |
|
Теорема 2.
|
Параллельные прямые в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. |
|
| Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. |
|
Теорема о трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b). |
|
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
|
|
Теорема. Теорема. |
|
Взаимное расположение прямых в пространстве
| ||
Пересекающиеся прямые: | Параллельные прямые: | Скрещивающиеся прямые: |
Параллельность плоскостей |
Признак параллельности двух плоскостей Теорема. |
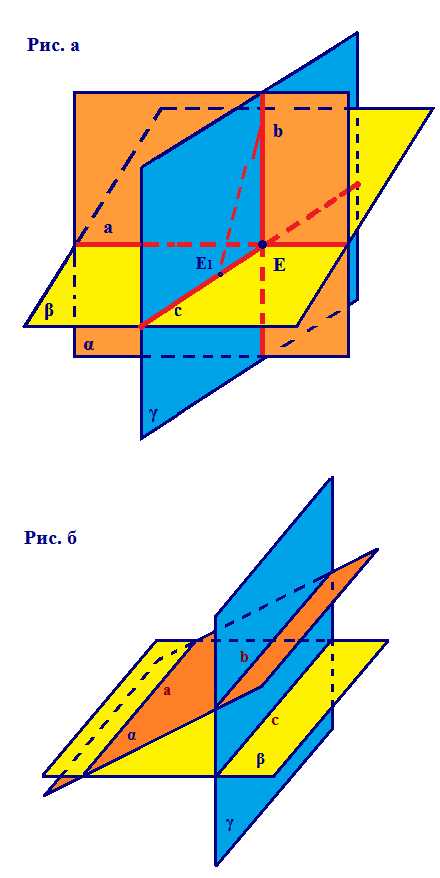
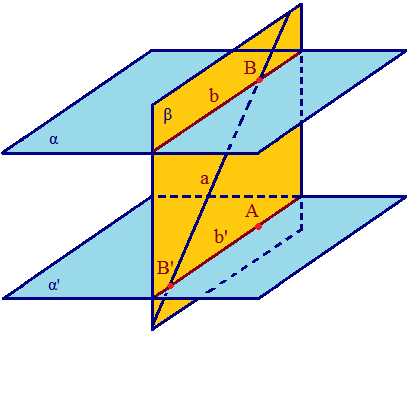
Свойства параллельных плоскостей
Вели α∥β и они пересекаются с γ, то а∥b. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. | Если α∥β и AB∥CD, то АВ = CD. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. |
osiktakan.ru
Формулы стереометрии
Александр | 2012-10-26
Формулы стереометрии. В этой статье общий обзор формул для решения задач по стереометрии. Нужно сказать, что задачи по стереометрии довольно разнообразны, но они несложны. Это задания на нахождение геометрических величин: длин, углов, площадей, объёмов.
Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 80% таких задач решаются элементарно, практически устно.
Остальные требуют небольших усилий, наличия знаний и специальных приёмов. В будущих статьях мы с вами будем рассматривать все эти задачи, не пропустите!
Для решения необходимо знать формулы площадей поверхности и объёмов параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Ещё раз подчеркну, что сложных задач нет, все они решаются в 2-3 действия (максимум). Важно «увидеть» какую формулу необходимо применить, только и всего.
Все необходимые формулы представлены ниже:
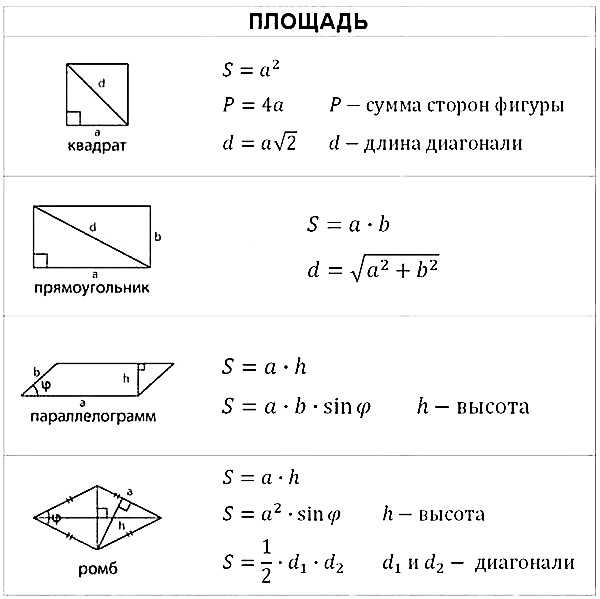
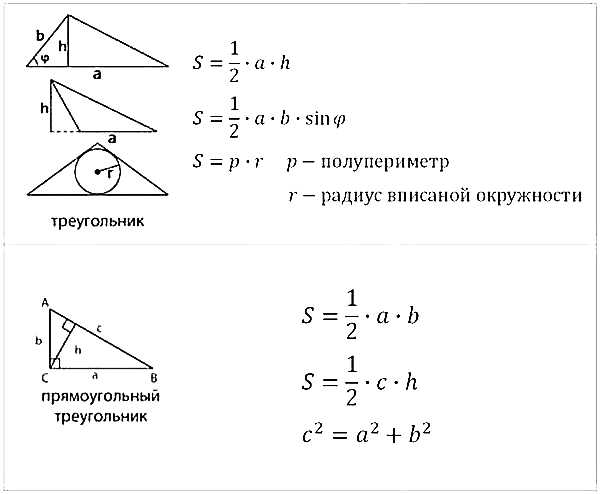
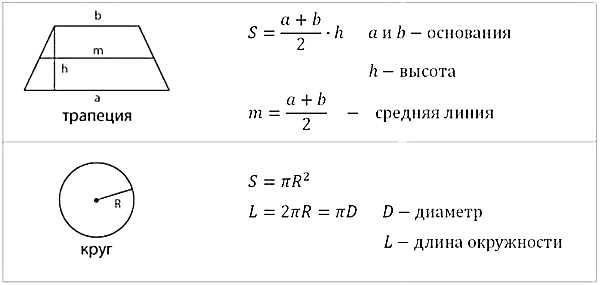
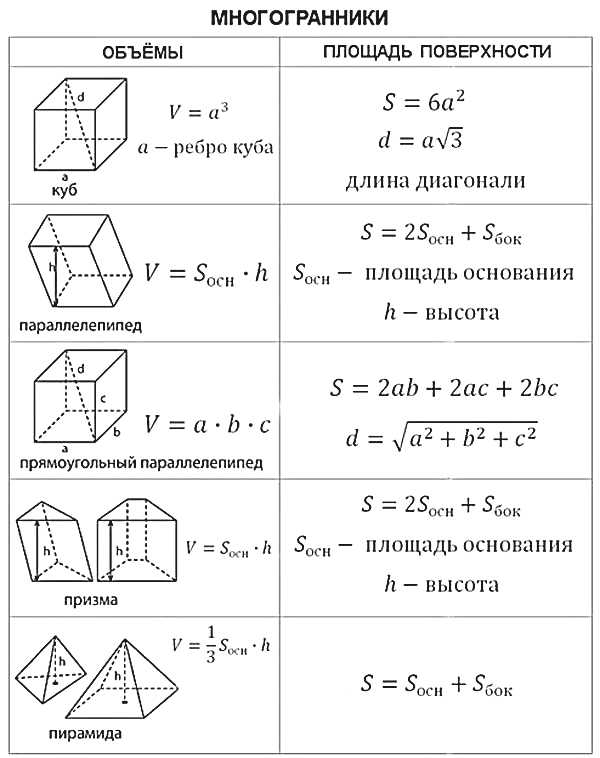
 Конечно, кроме указанных формул необходимо знать теорему Пифагора, определения тригонометрических функций, понятие средней линии треугольника и ещё немного теоретических фактов, о которых мы поговорим в следующей статье.
Конечно, кроме указанных формул необходимо знать теорему Пифагора, определения тригонометрических функций, понятие средней линии треугольника и ещё немного теоретических фактов, о которых мы поговорим в следующей статье.С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Формулы Теория | ЕГЭ-№8Формулы
Подготовка к ОГЭ по математике. Полный курс!
Школа репетиторов Анны Малковой!
Онлайн-обучение, подготовка к ЕГЭ и ОГЭ по предметам!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
matematikalegko.ru



Leave A Comment