Движение тела с ускорением свободного падения
ОпределениеСвободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
Внимание!В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как
Обозначается как
Единица измерения ускорения свободного падения — 1 м/с2.
Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с2. При решении задач это значение округляется до целых: g = 10 м/с2.
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
Скоростьv = gt
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
v = gt = 10∙3 = 30 (м/с).
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Высота паденияЕсли известна скорость падения тела в момент времени
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
Два этапа движения тела, брошенного вертикально вверхЭтап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях (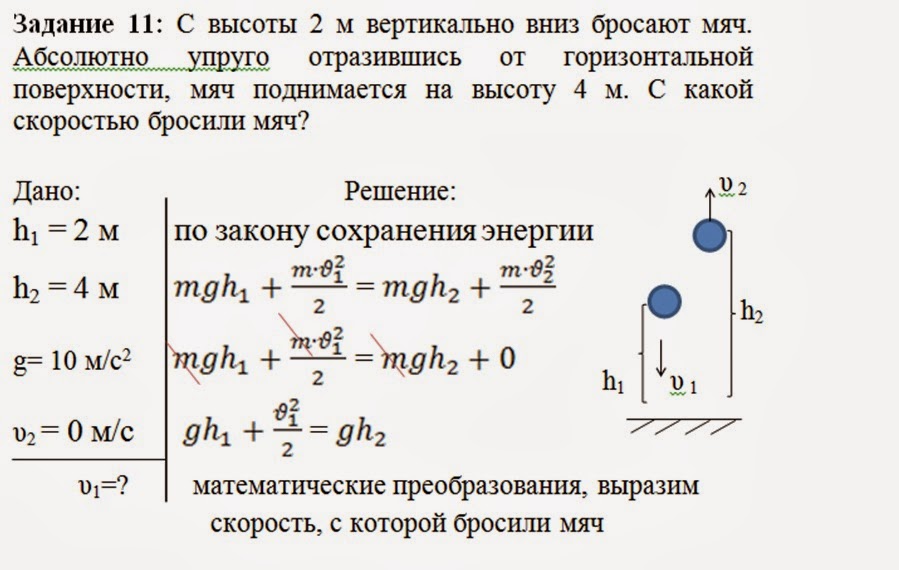 Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:
Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (
По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).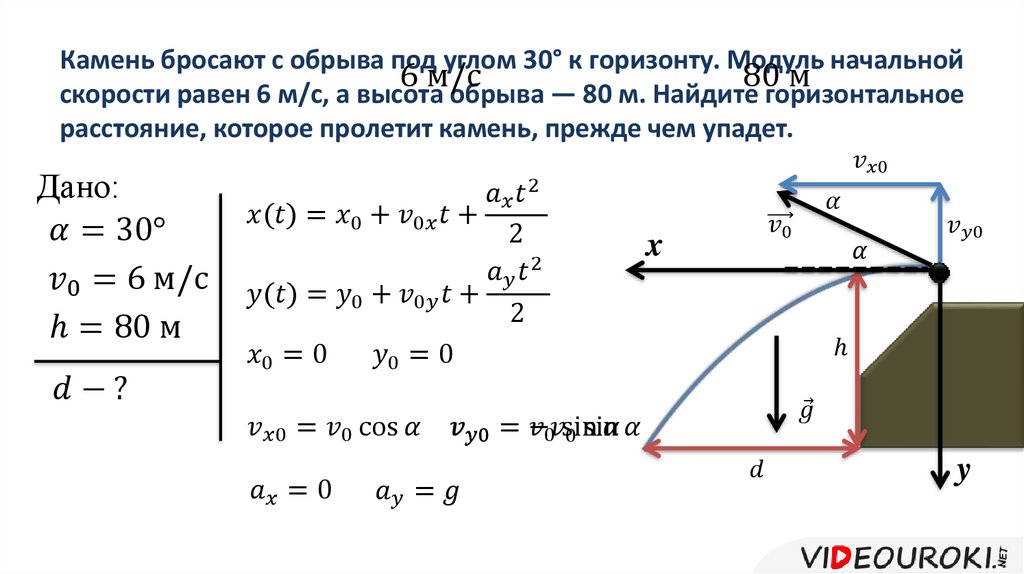
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты- В момент падения тела на землю y = 0.
- В момент броска тела от земли y0 = 0.
- Когда тело достигает наибольшей высоты v = 0.
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа- Чертится ось ОУ.
 Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории. - Отмечаются начальная и конечная координаты тела (y и y0).
- Указываются направления векторов.
Свободное падение на землю с некоторой высоты
Чертеж:
Уравнение скорости:
–v = v0 – gtпад
Уравнение координаты:
Тело подбросили от земли и поймали на некоторой высоте
Чертеж:
Уравнение скорости:
–v = v0 – gt
Уравнение координаты:
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
Через 3 с после падения тело окажется на высоте 5 м.
Задание EF17519 С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.

Делаем чертеж:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Ответ: 500pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17483 Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.

- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 19.7k
Задачи по кинематике с подробными решениями
Путь, перемещение, скорость, ускорение
1. 3
3
1.1.2 Из точек A и B, расположенных на расстоянии 300 м, навстречу друг другу
1.1.3 Скорость тела меняется по закону v=10+2t. Чему равен путь, пройденный
1.1.4 График зависимости скорости тела от времени имеет вид полуокружности
1.1.5 Поезд начинает двигаться по прямой, параллельной оси x. Зависимость
1.1.6 Какова скорость транспортера, если за 5 с он перемещается на 10 м?
1.1.7 Расстояние между двумя городами автомашина проехала со скоростью 60 км/ч
1.1.8 Расход воды в канале за секунду составляет 0,27 м3. Найти скорость воды
1.1.9 В трубопроводе с площадью поперечного сечения 100 см2 в течение часа
1.1.10 Тело прошло половину пути со скоростью 6 м/с, а другую половину пути
1.1.11 Точка движется по прямой в одну сторону. На рисунке показан график зависимости
Прямолинейное равномерное движение
1.2.1 Первую половину пути автомобиль двигается со скоростью 60 км/ч, а вторую
1.2.2 Один автомобиль, двигаясь равномерно со скоростью 12 м/с, в течение 10 с прошел
1. 2.3 За минуту человек делает сто шагов. Определить скорость движения человека, если
2.3 За минуту человек делает сто шагов. Определить скорость движения человека, если
1.2.4 Поезд движется на подъеме со скоростью 10 м/с, а на спуске со скоростью 25 м/с
1.2.5 Автобус третью часть пути шел со скоростью 20 км/ч, половину оставшегося пути
1.2.6 Движение грузового автомобиля описывается уравнением x=-270+12t (м). Когда
1.2.7 Поезд первую половину пути шел со скоростью в 1,5 раза большей, чем вторую
1.2.8 С какой постоянной скоростью должна двигаться нефть в трубопроводе с площадью
1.2.9 Катер прошел первую половину пути со скоростью в 2 раза большей, чем вторую
1.2.10 Тело первую половину пути двигалось со скоростью 12 км/ч. После этого половину
1.2.11 Первую половину пути велосипедист проехал со скоростью в 8 раз большей, чем
1.2.12 Мотоциклист за первые 5 минут проехал 3 км, за последующие 8 минут – 9,6 км и
1.2.13 Автобус прошел первые 4 км со средней скоростью 20 км/ч, а следующие 0,3 ч он
1.2.14 Какое расстояние пробежит конькобежец за 40 с, если он будет двигаться
1. 2. Через какое время
2. Через какое время
1.3.8 Тело, двигаясь равноускоренно, проходит 80 м за 4 с. Чему равна мгновенная
1.3.9 Поезд начинает равноускоренное движение и через 10 с имеет скорость 8 м/с
1.3.10 Мотоциклист, подъезжая к уклону, имеет скорость 10 м/с и начинает двигаться
1.3.11 Автобус движется равнозамедленно, проходя при этом до остановки расстояние
1.3.12 Вычислить тормозной путь автомобиля, имеющего начальную скорость 60 км/ч
1.3.13 Машинист локомотива, движущегося со скоростью 72 км/ч, начал тормозить
1.3.14 Поезд, имеющий скорость 90 км/ч, стал двигаться с замедлением 0,3 м/с2. Найти
1.3.15 Пуля со скоростью 200 м/с ударяет в земляной вал и проникает в него на глубину
1.3.16 Пуля со скоростью 400 м/с ударяет в земляной вал и проникает в него. Чему
1.3.17 Ружейная пуля движется внутри ствола длиной 60 см в течение 0,004 с. Найти
1.3.18 Самолет при взлете проходит взлетную полосу за 15 с и в момент отрыва от земли
1.3.19 Скорость поезда возросла с 15 до 19 м/с на расстоянии 340 м. С каким
С каким
1.3.20 Тело движется равноускоренно из состояния покоя. Во сколько раз путь
1.3.21 Тело, двигаясь с места равноускоренно, проходит за четвертую секунду
1.3.22 Теплоход, двигаясь равноускоренно из состояния покоя с ускорением 0,10 м/с2
1.3.23 Тормозной путь автомобиля, двигавшегося со скоростью 30 км/ч, равен 7,2 м. Чему
1.3.24 Скорость движения автомобиля от времени задана уравнением v=3+2t. Какой
1.3.25 По одному направлению из одной точки одновременно начали двигаться два тела
1.3.26 Скорость движения тела, равная 10 м/с, за 17 с уменьшилась в 5 раз. Определить
1.3.27 У светофора трактор, движущийся равномерно со скоростью 18 км/ч, обогнал
1.3.28 Автомобиль двигался со скоростью 4 м/с, затем был выключен двигатель
1.3.29 Автомобиль начал двигаться с ускорением 1,5 м/с2 и через некоторое время
1.3.30 Автомобиль, двигаясь равноускоренно, прошел два смежных участка пути
1.3.31 За первую секунду равноускоренного движения тело проходит путь 1 м, а за
1. 3.32 За седьмую секунду равноускоренного движения модуль вектора скорости
3.32 За седьмую секунду равноускоренного движения модуль вектора скорости
1.3.33 К концу первой секунды равнозамедленного движения модуль скорости тела
1.3.34 На некотором отрезке пути скорость тела увеличилась с 12 см/с до 16 см/с
1.3.35 Ракета летит со скоростью 4 км/с. Затем она движется с постоянным ускорением
1.3.36 Тело движется прямолинейно с ускорением 4 м/с2. Начальная скорость тела
1.3.37 Тело движется с начальной скоростью 4 м/с вдоль прямой, причем его скорость
1.3.38 Тело, двигаясь с места равноускоренно, проходит за четвертую секунду
1.3.39 Тело, имея некоторую начальную скорость, движется равноускоренно. За время
1.3.40 Точка движется равноускоренно. За 4 с она проходит путь 24 м. За следующие
1.3.41 Частица, начав двигаться из состояния покоя и пройдя некоторый путь
1.3.42 Велосипедист начал свое движение из состояния покоя и в течение первых
1.3.43 Два велосипедиста едут навстречу: один из них, имея скорость 7,2 км/ч, спускается
1. 2 (м). Найти
2 (м). Найти
1.3.49 Пуля, летящая со скоростью 141 м/с, попадает в доску и проникает на глубину
1.3.50 Пробежав с постоянным ускорением по взлетной полосе 750 м, самолет
1.3.51 Поезд метрополитена разгоняется от остановки с постоянным ускорением
1.3.52 При торможении автомобиль, двигаясь равнозамедленно, проходит за пятую
1.3.53 Поезд, двигаясь от остановки с постоянным ускорением, прошел 180 м за 15 с
1.3.54 Точка движется вдоль оси x со скоростью, проекция которой v_x как функция
1.3.55 Какие из приведенных зависимостей от времени пути S и модуля скорости v
Свободное падение тел. Движение тела, брошенного вертикально
1.4.1 Высота Исаакиевского собора в Ленинграде 101,8 м. Определить время
1.4.2 Высота свободного падения молота 2,5 м. Определить его скорость
1.4.3 На какую высоту поднимется тело, брошенное вертикально вверх
1.4.4 Тело брошено вертикально вверх со скоростью 50 м/с. Через какое время
1.4.5 При свободном падении время полета первого тела больше в 2 раза, чем
1.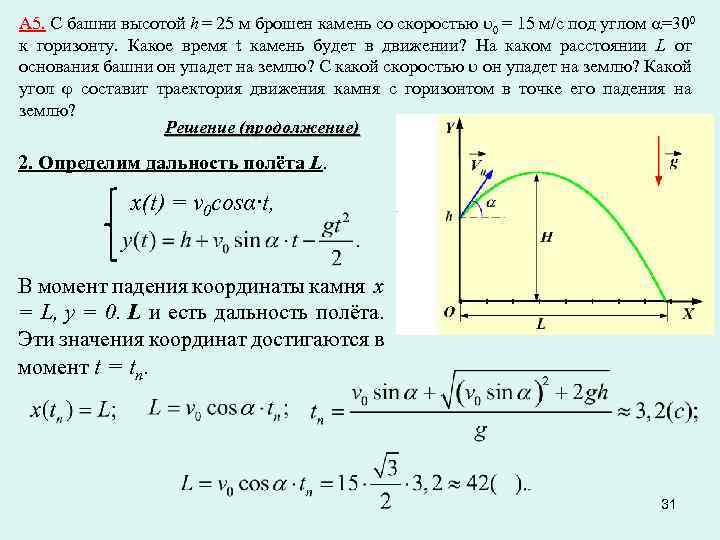 4.6 Определить скорость падения тела с высоты 10 м, если его начальная скорость
4.6 Определить скорость падения тела с высоты 10 м, если его начальная скорость
1.4.7 Тело падает с высоты 5 м. Какую скорость оно будет иметь в момент падения
1.4.8 Тело, брошенное вертикально вверх, через 4 с упало на Землю. На какую
1.4.9 Тело брошено со скоростью 40 м/с. Определить высоту подъема тела
1.4.10 Камень брошен вертикально вниз со скоростью v0=5 м/с. Определить
1.4.11 Камень, брошенный вертикально вверх со скоростью 12 м/с, через 1 с
1.4.12 Мяч брошен вверх со скоростью 10 м/с. На каком расстоянии от поверхности
1.4.13 Мяч брошен с некоторой высоты вертикально вниз со скоростью 5 м/с. Какова
1.4.14 Мяч брошен вверх со скоростью 20 м/с. На какое расстояние от поверхности
1.4.15 Вертикально вверх с высоты 392 м с начальной скоростью 19,6 м/с брошено
1.4.16 Тело, свободно падающее из состояния покоя, в конце первой половины пути
1.4.17 Камень, брошенный вертикально вверх, упал на Землю через 2 с. Определить
1.4.18 Из точки A вертикально вверх брошено тело с начальной скоростью 10 м/с
1. 4.19 Камень упал в шахту. Определить глубину шахты, если звук от падения камня
4.19 Камень упал в шахту. Определить глубину шахты, если звук от падения камня
1.4.20 Мяч брошен с земли вертикально вверх. На высоте 10 м он побывал два раза
1.4.21 Тело бросают вертикально вверх. Наблюдатель замечает промежуток времени
1.4.22 Тело, брошенное вертикально вверх, за третью секунду прошло 5 м. Определить
1.4.23 Определите время равноускоренного движения снаряда в стволе длиной 3 м
1.4.24 При равноускоренном движении тело проходит за четвертую секунду 16 м. Определить
1.4.25 С вертолета, находящегося на высоте 500 м, упал камень. Через какое время
1.4.26 С какой высоты падало тело, если за последние 2 с прошло путь 60 м?
1.4.27 Свободно падающее тело прошло последние 30 м за 0,5 с. С какой высоты
1.4.28 Тело падает с высоты 10 м. За какое время тело прошло последний метр пути?
1.4.29 Тело падает с высоты 4,9 м. Какова средняя скорость движения тела?
1.4.30 Тело свободно падает без начальной скорости с высоты 45 м. Какой путь
1. 4.31 Человек, стоящий на краю высохшего колодца, бросает вертикально вверх
4.31 Человек, стоящий на краю высохшего колодца, бросает вертикально вверх
1.4.32 Аэростат поднимается вертикально вверх с ускорением 2 м/с2. Через 5 с от
1.4.33 С аэростата, опускающегося со скоростью 5 м/с, бросают вертикально вверх тело
1.4.34 С вертолета, находящегося на высоте 300 м, сброшен груз. Через какое время
1.4.35 В последнюю секунду свободного падения тело прошло путь вдвое больше
1.4.36 Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 100 м
1.4.37 Вертолет двигался равномерно вниз. Из вертолета выпал груз. Когда
1.4.38 Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 50 м
1.4.39 Двигатель ракеты, запущенной с поверхности Земли, сообщает ей постоянное
1.4.40 Над шахтой глубиной 40 м вертикально вверх бросили камень со скоростью 12 м/с
1.4.41 Парашютист сразу после прыжка пролетает расстояние 50 м с пренебрежимо
1.4.42 При падении камня в колодец его удар о поверхность воды доносится через 5 с
1. 4.43 Свободно падающий камень пролетел последние три четверти пути за одну
4.43 Свободно падающий камень пролетел последние три четверти пути за одну
1.4.44 Тело начинает свободно падать с высоты 45 м. В тот же момент с высоты 24 м
1.4.45 Тело падает без начальной скорости с высоты 45 м. Определить среднюю скорость
1.4.46 Тело свободно падает с высоты 5 м. Найти среднюю скорость тела на нижней
1.4.47 Упругий шар, падая с высоты 80 м, после удара о Землю, отскакивает вертикально
1.4.48 Цепочка шаров висит над поверхностью стола: первый шар – на высоте 1 м, второй
1.4.49 Свободно падающее без начальной скорости тело пролетело мимо точки A
1.4.50 За последнюю секунду свободно падающее без начальной скорости тело
1.4.51 Мяч, брошенный вертикально вверх, упал на землю через 3 с. Чему равна величина
Движение тела, брошенного горизонтально
1.5.1 Камень брошен горизонтально со скоростью 5 м/с. Через 0,8 с он упал
1.5.2 Камень брошен с некоторой высоты в горизонтальном направлении и упал
1.5.3 В горизонтальном направлении со скоростью 10 м/с брошено тело, которое
1.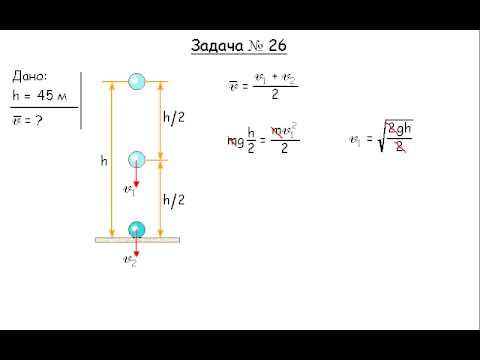 5.4 Дальность полета тела, брошенного горизонтально со скоростью 4,9 м/с
5.4 Дальность полета тела, брошенного горизонтально со скоростью 4,9 м/с
1.5.5 Два тела брошены с высоты 100 м, первое – с горизонтальной скоростью 5 м
1.5.6 Камень, брошенный горизонтально с вышки, через 3 с упал на землю
1.5.7 Камень, брошенный горизонтально с обрыва высотой 10 м, упал на расстоянии
1.5.8 Понижение траектории снаряда, выпущенного из горизонтально расположенного
1.5.9 Тело брошено с высоты 2 м горизонтально так, что к поверхности земли
1.5.10 Спортсменка, стоящая на вышке, бросает мяч с горизонтальной скоростью
1.5.11 Тело брошено горизонтально с высоты h=20 м. Траектория его движения
Движение тела, брошенного под углом к горизонту
1.6.1 Тело брошено со скоростью 10 м/с под углом 30 градусов к горизонту
1.6.2 Баскетболист бросает мяч в кольцо. Скорость мяча после броска
1.6.3 Камень, брошенный с земли под углом 45 градусов к горизонту
1.6.4 Минимальная скорость при движении тела, брошенного под углом
1.6.5 На некоторой высоте одновременно из одной точки брошены
1.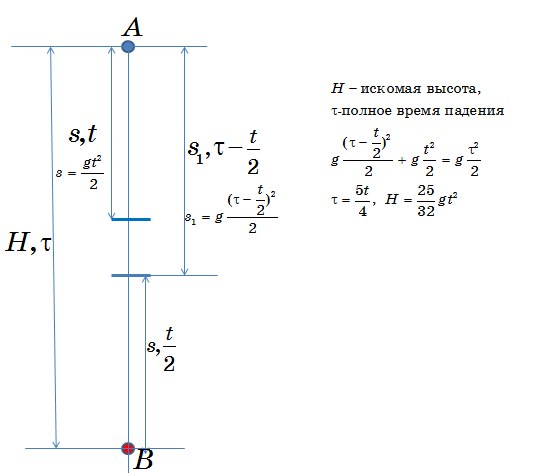 6.6 Под каким углом к горизонту нужно бросить тело, чтобы высота
6.6 Под каким углом к горизонту нужно бросить тело, чтобы высота
1.6.7 Мяч, брошенный под некоторым углом к горизонту с начальной
1.6.8 Мяч, брошенный со скоростью 10 м/с под углом 45 градусов
1.6.9 Пуля вылетает из ствола под углом 45 градусов к горизонту
1.6.10 Снаряд вылетает из орудия со скоростью 1000 м/с под углом 60
1.6.11 Тело бросили под углом 60 градусов к горизонту со скоростью 10 м/с
1.6.12 Тело брошено с начальной скоростью 40 м/с под углом 30 градусов
1.6.13 Бомбардировщик пикирует на цель под углом 60 градусов к горизонту
1.6.14 Игрок посылает мяч с высоты 1,2 м над землей так, что угол
1.6.15 Камень, брошенный под углом к горизонту, упал на землю
1.6.16 Из орудия сделан выстрел вверх по склону горы. Угол наклона горы
1.6.17 Из шланга, лежащего на земле, бьет под углом 45° к горизонту вода
1.6.18 Какое расстояние по горизонтали до первого удара о пол
1.6.19 Какой скоростью обладал мальчик при прыжке с трамплина
1.6.20 С вершины холма бросают камень с начальной скоростью
1. 2 и x2=80-4t
2 и x2=80-4t
1.7.4 Лодка, двигаясь перпендикулярно берегу, оказалась на другом берегу на расстоянии
1.7.5 По оси x движутся две точки: первая по закону x1=10+2t, а вторая – по закону
1.7.6 Скорость велосипедиста 36 км/ч, а скорость встречного ветра 4 м/с. Какова
1.7.7 Танк движется со скоростью 20 км/ч. С какими скоростями относительно дороги
1.7.8 Два поезда идут навстречу друг другу со скоростями 36 и 54 км/ч. Пассажир
1.7.9 Автомобиль, двигаясь равномерно со скоростью 45 км/ч, в течение 10 с прошел
1.7.10 Акула и подводная лодка начали двигаться одновременно из одной точки
1.7.11 В течение какого времени скорый поезд длиной 280 м, следуя со скоростью
1.7.12 Катер проходит расстояние между двумя пунктами на реке в обе стороны за 14 ч
1.7.13 Катер, переправляясь через реку шириной 600 м, двигался перпендикулярно
1.7.14 Когда нет ветра, капли дождя оставляют на окне равномерно движущегося вагона
1.7.15 Моторная лодка проходит расстояние между двумя пунктами A и B по течению реки
1. 7.16 Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду
7.16 Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду
1.7.17 Пловец переплывает реку по прямой, перпендикулярной берегу. Определить
1.7.18 Пассажирский поезд идет со скоростью 72 км/ч. По соседнему пути движется
1.7.19 Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду
1.7.20 Вертолет летит на высоте 500 м со скоростью 100 м/с. Навстречу ему по реке
1.7.21 В момент, когда тронулся поезд, провожающий стал равномерно бежать по ходу поезда
1.7.22 Кран равномерно поднимает груз со скоростью 0,3 м/с и одновременно движется
1.7.23 Катер, плывущий вниз по реке, догоняет спасательный круг. Через 30 мин после
1.7.24 Автомобиль движется со скоростью 12 м/с. Чему равен модуль линейной скорости верхней
1.7.25 Человек бежит со скоростью 5 м/с относительно палубы теплохода в направлении
1.7.26 При движении моторной лодки по течению реки ее скорость относительно берега
1.7.27 При движении моторной лодки по течению реки ее скорость относительно берега
Движение по окружности
1. 8.1 Какова линейная скорость точек на ободе колеса паровой турбины с диаметром
8.1 Какова линейная скорость точек на ободе колеса паровой турбины с диаметром
1.8.2 Какова угловая скорость вращения колеса, делающего 240 оборотов
1.8.3 Найти скорость движения автомобиля, если его колесо диаметром 1,1 м делает
1.8.4 С какой скоростью едет велосипедист, если колесо делает 100 об/мин. Радиус
1.8.5 Угол поворота колеса радиусом 0,2 м изменяется по закону phi=9,42t (рад)
1.8.6 На повороте вагон трамвая движется с постоянной по модулю скоростью 5 м/с
1.8.7 С какой скоростью автомобиль должен проходить середину выпуклого моста
1.8.8 Во сколько раз изменится центростремительное ускорение тела, если оно будет двигаться
1.8.9 Колесо велосипеда делает 100 об/мин. Каков радиус колеса, если скорость
1.8.10 Минутная стрелка часов в 3 раза длиннее секундной. Во сколько раз линейная скорость
1.8.11 Тело движется по окружности с постоянной по модулю скоростью. Во сколько раз
1.8.12 Тело движется равномерно по окружности. Во сколько раз увеличится
1. 8.13 Тело равномерно движется по окружности радиусом 2 м с частотой 0,5 с-1. Определить
8.13 Тело равномерно движется по окружности радиусом 2 м с частотой 0,5 с-1. Определить
1.8.14 Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его
1.8.15 К валу, радиус которого 5 см, прикреплена нить. Через 5 с после начала равномерного
1.8.16 Велосипедист начинает двигаться делать поворот по кругу со скоростью 10 м/с
1.8.17 Вертолет начал снижаться вертикально вниз с ускорением 0,2 м/с2. Лопасть винта
1.8.18 Вычислить путь, который проехал за 30 с велосипедист, двигающийся с угловой
1.8.19 Материальная точка движется по окружности. Угол поворота радиуса, соединяющего
1.8.20 Найти радиус вращающегося колеса, если линейная скорость точки на ободе
1.8.21 Обруч катится по горизонтальной плоскости без проскальзывания со скоростью
1.8.22 Точки окружности вращающегося диска имеют линейную скорость по модулю
1.8.23 Угловая скорость лопастей вентилятора 20pi рад/с. Найти число оборотов
1.8.24 Частота вращения воздушного винта самолета 1500 об/мин. Сколько оборотов
Сколько оборотов
1.8.25 Шкив радиусом 10 см приводится во вращение грузом, подвешенным на нити. Груз
1.8.26 Определить радиус колеса, если при вращении скорость точек на ободе колеса
1.8.27 Для того чтобы повернуть трактор, движущийся со скоростью 18 км/ч, тракторист
1.8.28 Колесо, имеющее 12 равноотстоящих спиц, во время вращения фотографируют
1.8.29 Точка движется по окружности с постоянной по величине скоростью 50 см/с
1.8.30 С какой скоростью будет перемещаться ось катушки, если конец нити тянуть
1.8.31 Стержень длиной 50 см вращается с частотой 30 об/мин вокруг перпендикулярной
1.8.32 Гладкий горизонтальный диск вращается вокруг вертикальной оси с частотой
1.8.33 Линейная скорость точки на ободе равномерно вращающегося колеса диаметром
1.8.34 Маховое колесо вращается с угловой скоростью 10 рад/с. Модуль линейной скорости
1.8.35 Колесо имеет угловую скорость вращения 2pi рад/с. За какое время оно делает
1.8.36 У паровой турбины радиус рабочего колеса в 8 раз меньше, а число оборотов
Пожалуйста, поставьте оценку
( 115 оценок, среднее 4. 63 из 5 )
63 из 5 )
Вы можете поделиться с помощью этих кнопок:
Свободно падающие предметы
Свободно падающие предметыСвободное падение
Систематические эксперименты со свободно падающими объектами проводились Галилео Галилей (1564-1642). У поверхности земли все свободно падающие предметы разгоняться примерно с той же скоростью. Это ускорение обозначается г . Его направление вниз, к центру земли. Свободно падающие предметы движутся с постоянным ускорением. г = 9,8 м/с 2 вниз.
Проблема:
Вы бросаете мяч из окна на верхнем этаже здания. Это ударяется о землю со скоростью v. Теперь вы повторяете падение, но у вас есть друг на улице, который бросает еще один мяч вверх тем же скорость v. Ваш друг подбрасывает мяч вверх одновременно с тем, как вы бросаете свой из окна. В каком-то месте шары проходят друг мимо друга. Это расположение на полпути между окном и землей, над этим точки или ниже этой точки?
Решение:
- Рассуждение:
Оба мяча ускоряются. Мяч, брошенный вверх
достигнет окна в то же время, когда упавший мяч коснется земли.
Скорость брошенного мяча линейно возрастает со временем. Мяч
движется с наименьшей скоростью у окна и с наибольшей скоростью у окна
момент, когда он падает на землю. За половину времени, необходимого для достижения
на земле он покрывает менее половины расстояния и все еще находится выше средней точки
между окном и землей. Скорость мяча, подброшенного вверх
линейно уменьшается со временем. Он движется быстрее всего у земли и
медленнее всего возле окна. За половину времени, необходимого для достижения
окно, оно уже выше средней точки. Таким образом, два шара
встречаются выше средней точки.
Мяч, брошенный вверх
достигнет окна в то же время, когда упавший мяч коснется земли.
Скорость брошенного мяча линейно возрастает со временем. Мяч
движется с наименьшей скоростью у окна и с наибольшей скоростью у окна
момент, когда он падает на землю. За половину времени, необходимого для достижения
на земле он покрывает менее половины расстояния и все еще находится выше средней точки
между окном и землей. Скорость мяча, подброшенного вверх
линейно уменьшается со временем. Он движется быстрее всего у земли и
медленнее всего возле окна. За половину времени, необходимого для достижения
окно, оно уже выше средней точки. Таким образом, два шара
встречаются выше средней точки.Мы также можем работать с нашими кинематические уравнения.
Предположим, что мяч падает в течение 1 секунды. Скорость падающего мяча как функция времени v = 9,8 (м/с 2 ) t , а пройденное расстояние d = ½ 9,8 (м/с 2 ) t 2 . За одну секунду мяч проходит 4,9 м. Скорость падающего мяча как функция времени равна v = -9,8 (м/с 2 ) t j и его положение как функция времени r = (4,9м — ½ 9,8 (м/с 2 ) т 2 ) j .
Скорость поднимающегося мяча как функция времени равна v = (9,8 (м/с) — 9,8 (м/с 2 ) t) j и его положение как функция времени равно r = (9,8 (м/с) t — ½ 9,8( м/с 2 ) t 2 ) j . Графики скорость и положение в зависимости от времени для двух шаров показаны ниже.
Проблема:
Камень брошен прямо вверх с начальной скоростью 4 м/с. с высоты 20 м. Через какой промежуток времени камень упадет на землю?
Решение:
- Обоснование:
У нас есть движение в одном измерении с постоянным ускорением. Положите начало вашей системы координат в положении камня в t = 0 и пусть ось x направлена прямо вниз. Тогда мы знаем, что
x i = 0, v xi = -4 м/с, t i = 0,
х f = 20 м, v xf = ?, t f = ?,
a x = 9,8 м/с 2 .
Нас просят решить для t = t f . - Детали расчета:
Имеем x f — х i = v xi ∆t + ½a x ∆t 2 , 20 м = -4 (м/с) t + 4,9 (м/с 2 ) t 2 .
Перепишем это уравнение как t 2 — (4 с/4,9) t — (20 с 2 /4,9) = 0 или t 2 — (0,816 с)t — 4,08 с 2 = 0,
Это квадратное уравнение с двумя решениями.
t = (0,816 с)/2 ± sqrt[((0,816 с)/2) 2 + 4,08) = 0,408 с ± 2,061 с
Имеет смысл только знак +. Находим t = 2,47 с
Проблема:
Какова скорость камня в предыдущей задаче при ударе о земля?
Решение:
- Обоснование:
Есть разные способы найти ответ. Один из способов заключается в использовании уравнение v xf 2 = v xi 2 + 2а х (х f — х i ).
Все величины в правой части известны, мы можем найти v xf .
- Детали расчета:
Здесь (x f — x i ) = 20 м, a x = 9,8 м/с 2 , и v xi = -4 м/с.
Следовательно, v xf 2 = (16 + 2*9,8*20)(м/с) 2 , v xf = 20,2 м/с.
Примечание. Если камень брошен прямо вниз с начальной скоростью 4 м/с, он ударяется о землю с той же скоростью, но в более позднее время.
Когда камень, брошенный вверх, возвращается в исходное положение
положение, его скорость — v i .
Величина равна начальной скорости, но знак
скорость изменилась.
Теперь скорость уменьшается.
С этого момента камень ведет себя точно так же, как бросок камня вниз
с той же начальной скоростью.
Проблема:
Галилей экспериментировал с шарами, катящимися по наклонным плоскостям, чтобы
уменьшить ускорение по плоскости и тем самым уменьшить скорость снижения
шаров. Предположим, угол, который образует наклонная плоскость с
горизонталь равна θ. Как бы вы ожидали ускорение вдоль плоскости
уменьшаться по мере уменьшения θ. Какая специфическая тригонометрическая зависимость от
θ вы ожидаете для ускорения?
Предположим, угол, который образует наклонная плоскость с
горизонталь равна θ. Как бы вы ожидали ускорение вдоль плоскости
уменьшаться по мере уменьшения θ. Какая специфическая тригонометрическая зависимость от
θ вы ожидаете для ускорения?
Решение:
- Обоснование:
Ускорение — это вектор. Гравитационное ускорение вектор g указывает прямо вниз. Векторы можно записать в терминах их компонентов вдоль осей системы координат. Если мы выберем наш системе координат, как показано, то x-компонента g параллельна и y-компонент g перпендикулярен поверхности наклонного самолет.
У нас есть g x = g sinθ. Объект ограничен двигаться по поверхности самолета, а потому будет ускоряться в x-направление. Мы ожидаем, что величина ускорения будет равна g x и зависит от θ как sinθ .
Проблема:
В колодец брошен камешек, слышен всплеск 16 с позже. Каково приблизительное расстояние от края колодца до поверхность воды?
Решение:
- Обоснование:
Если предположить, что камешек — это свободно падающий предмет, то расстояние, пройденное галькой за время t, равно d = ½gt 2 , где g = 9,8 м/с 2 — ускорение свободного падения. Если
галька падали 16 с, d = ½9,8 (м/с 2 ) 256 с 2 = 1254 м и его скорость в это время будет v = gt = 9,8 (м/с 2 )
16 с = 156 м/с = 351 миля в час. Однако, поскольку скорость звука равна 343 м/с, мы
всплеск услышишь только после 19.6 с. Поэтому камень должен быть
падение в течение более короткого времени и путешествие на более короткое расстояние. Он должен упасть на
где-то между 13 и 14 с. Предположим, что оно падает за 13,5 с. Тогда д
= 893 м. Звук преодолевает это расстояние за 2,6 с. Так что 890 м примерно правильно,
пока у нас есть основания пренебрегать сопротивлением воздуха.
Если
галька падали 16 с, d = ½9,8 (м/с 2 ) 256 с 2 = 1254 м и его скорость в это время будет v = gt = 9,8 (м/с 2 )
16 с = 156 м/с = 351 миля в час. Однако, поскольку скорость звука равна 343 м/с, мы
всплеск услышишь только после 19.6 с. Поэтому камень должен быть
падение в течение более короткого времени и путешествие на более короткое расстояние. Он должен упасть на
где-то между 13 и 14 с. Предположим, что оно падает за 13,5 с. Тогда д
= 893 м. Звук преодолевает это расстояние за 2,6 с. Так что 890 м примерно правильно,
пока у нас есть основания пренебрегать сопротивлением воздуха.
Проблема:
Мяч из твердой резины, выпущенный на уровне груди, падает на тротуар и
возвращается почти на ту же высоту. Когда он соприкасается с
дорожного покрытия нижняя сторона мяча временно сплющена. Предположим, что
максимальная глубина вмятины на шаре около 1 см. Сделать заказ
оценка величины максимального ускорения мяча. Сформулируйте свой
предположения, количества, которые вы оцениваете, и значения, которые вы оцениваете для них.
Сформулируйте свой
предположения, количества, которые вы оцениваете, и значения, которые вы оцениваете для них.
Решение:
- Обоснование:
Мяч падает с высоты груди, поэтому он падает на расстояние примерно 1,3 м при постоянном ускорении g . Это падает на время t = (2d/g) ½ и касается земли со скоростью v = gt.
Центр шара теперь перемещается еще на сантиметр до того, как мяч остановится, и v = 0, - Детали расчета:
Мяч падает на время т = (2д/г) ½ = 0,51 с и касается земли со скоростью v = gt = 5 м/с.
Центр шара теперь перемещается еще на сантиметр до того, как мяч остановится, и v = 0.
Мы можем использовать v xf 2 — v xi 2 = 2a x (x f — x i ), чтобы найти среднее ускорение мяча в течение этот временной интервал.
-(5 м/с) 2 = 2 a x 0,01 м. х = -1205 м/с 2 .
Проблема:
Мяч катится вверх по склону, а затем скатывается обратно в исходное положение. Какой из следующих графиков лучше всего представляет скорость мяча как функция времени?
Решение:
- Обоснование:
Если мы ориентируем ось X нашей системы координат так, указывает вверх по склону, то при t = 0 v x положительно. Скорость v x уменьшается линейно, начиная с x точек в отрицательном направлении x. Когда мяч достигает высшей точки, v x = 0, когда он откатывается назад, наклон v x отрицателен. график (С) лучше всего представляет скорость мяча как функцию времени.
Модуль 2: Вопрос 2
Предмет падает с крыши здания высотой h. В течение В последнюю секунду спуска он падает на расстояние h/3. Рассчитать высоту здания.
Обсудите подходы к решению этой проблемы с однокурсниками на форуме!
Тело, свободно падающее из покоя, имеет скорость v после падения через высота «ч».
 Расстояние, на которое он должен упасть, чтобы его скорость удвоилась,
составляет (1) 2 часа (2) 4 часа (3) 6 часов (4) 8 часов Практические вопросы NEET, MCQ, вопросы прошлого года (PYQ), вопросы NCERT, банк вопросов, вопросы класса 11 и класса 12 и решение PDF с ответами
Расстояние, на которое он должен упасть, чтобы его скорость удвоилась,
составляет (1) 2 часа (2) 4 часа (3) 6 часов (4) 8 часов Практические вопросы NEET, MCQ, вопросы прошлого года (PYQ), вопросы NCERT, банк вопросов, вопросы класса 11 и класса 12 и решение PDF с ответамиВыбор субъекта:
Ботаника Химия Физика ZOOLOGIOL99. падает с высоты ‘ х ‘. Расстояние, на которое он должен упасть, чтобы его скорость удвоилась, составляет
(1) 2 ч
(2) 4 ч
(3) 6 h
(4) 8 h
Q119:
79
% From NCERT
(1)
(2)
(3)
(4)
Подтема: Равномерно ускоренное движение |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для XI th и XII th Физика, химия и биология
Скорость тела точка, из которой он был спроецирован вверх, равна1. v=0
2. v=2u
3. v=0.5u
4. v=-u
Q120:
72
% From NCERT AIIMS — 1999
(1)
(2)
(3)
(4)
Подтема: Ускоренное движение |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для XI th и XII th Физика, химия и биология с вертикально проецируемыми телами
0 A скорость
u возвращается в исходную точку через 4 секунды. Если g = 10 m / sec 2 , the value of u is(1) 5 m/sec
(2) 10 m/sec
( 3) 15 m/sec
(4) 20 m/sec
Q121:
87
% From NCERT
(1)
(2)
(3)
(4)
Подтема: Равномерно ускоренное движение |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
NEET MCQ Books для XI TH & XII TH Физика, химия и биология
Время, взятое объектом с отдыха, чтобы покрыть высоту H 1 и H 2 1 и H 2 1 и H 2 и H 2 и H 2 9007 составляет соответственно т 1 и т 2 . Тогда отношение t 1 к t 2 равно
(1) ч 1 : h 2
(2) h2 : h3
(3) h 1 : 2 h 2
(4) 2 h 1 : h 2
Q122:
88
% From NCERT PMT — 1999
(1)
(2)
(3)
(4)
Подтема: Равномерно ускоренное движение |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, указанный ниже.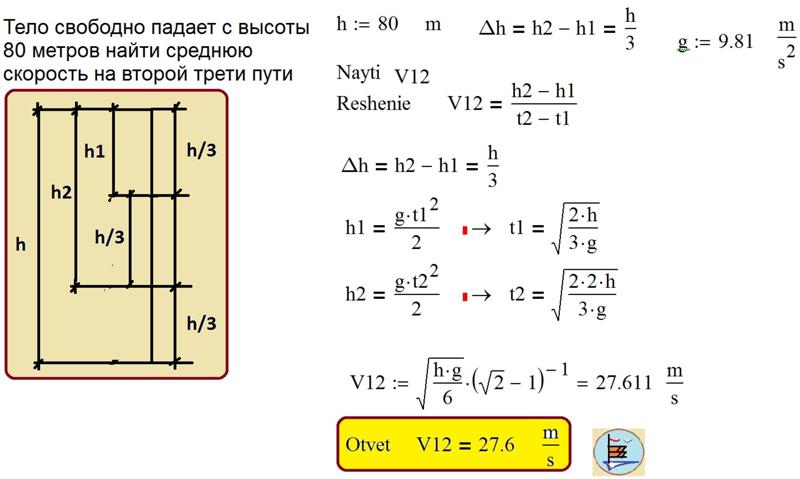
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
NEET MCQ Books для XI th & XII th Физика, химия и биология
Тело брошено с земли вертикально вверх. Он достигает максимальной высоты 100 м за 5 секунд. Через какое время он достигнет земли из положения максимальной высоты?
1. 1,2 сек
2. 5 сек
3. 10 сек
4. 25 сек
Q123:
80
% Из NCERT PMT — 2000
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
111111111111119(1)
(2)
(3)
(4)
(1)
(2)
(3)
(4)
0 |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальные книги MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для XI th и XII th Физика, химия и биология с поднятым вверх телом
0 A начальная скорость
и достигает максимальной высоты за 6 секунд. Отношение расстояний, пройденных телом за первую и седьмую секунды, равно(1) 1: 1
(2) 11: 1
(3) 1: 2
(4) 1: 11
Q124:
54
%от NCERT
- Подтема:
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, указанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для XI th и XII th Физика, химия и биология
0 Частицы брошены вертикально вверх. Если его скорость на половине максимальной высоты равна 10
m/s , then maximum height attained by it is (Take g = 10 m / s 2 )(1) 8 m
(2) 10 m
(3) 12 m
(4) 16 m
Q125:
87
% From NCERT PMT — 2001
Подтема: Равномерно ускоренное движение |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
NEET MCQ Books for XI th & XII th Физика, химия и биология
Тело, брошенное вверх с некоторой скоростью, достигает максимальной высоты 20 м . Другое тело с удвоенной массой, подброшенной вверх, с удвоенной начальной скоростью достигнет максимальной высоты ) 40 м
Q126:
80
%от NCERT
(4).
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
Книги NEET MCQ для XI th и XII th Физика, химия и биология
0 Воздушный шар начинает подниматься с земли с ускорением 1,25
м / с 2 . Через 8 секунд из шара вылетает камень. Камень будет ( г = 10 м / с 2 )(1) Достигнуть земли за 4 секунды
(2) Начать движение вниз после освобождения m
(4) Cover a distance of 40 m in reaching the ground
Q127:
From NCERT
Подтема: Равномерно ускоренное движение |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, указанный ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Чтобы просмотреть объяснение, пожалуйста, пройдите пробную версию курса ниже.
NEET 2023 — Целевая партия — Арьян Радж Сингх
Пожалуйста, сначала попробуйте ответить на этот вопрос.
Предпочитаете книги для практики вопросов? Получите уникальных книг MCQ от NEETprep с онлайн-решениями для аудио/видео/текста через Telegram Bot
NEET MCQ Books для XI th & XII th Физика, химия и биология
Тело брошено вертикально вверх со скоростью u . Найдите верное утверждение из следующего:
(1) И скорость, и ускорение равны нулю в высшей точке
(2) Скорость максимальна, а ускорение равно нулю в высшей точке
(3) Скорость максимальна, а ускорение равно г вниз в самой высокой точке
(4) Скорость равна нулю в самой высокой точке, а максимальная достигнутая высота равна u2/2g
Q128:
87
% From NCERT
Subtopic: Uniformly Ускоренное движение |
Чтобы просмотреть объяснение, пожалуйста, пройдите пробный курс, описанный ниже.

 Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.

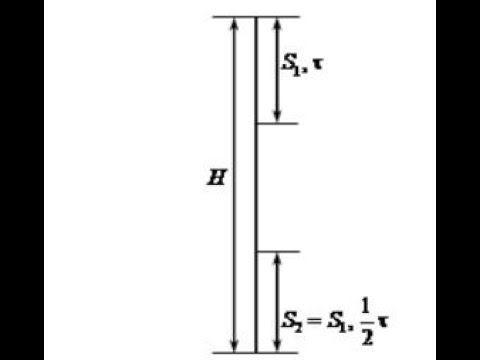 Мяч, брошенный вверх
достигнет окна в то же время, когда упавший мяч коснется земли.
Скорость брошенного мяча линейно возрастает со временем. Мяч
движется с наименьшей скоростью у окна и с наибольшей скоростью у окна
момент, когда он падает на землю. За половину времени, необходимого для достижения
на земле он покрывает менее половины расстояния и все еще находится выше средней точки
между окном и землей. Скорость мяча, подброшенного вверх
линейно уменьшается со временем. Он движется быстрее всего у земли и
медленнее всего возле окна. За половину времени, необходимого для достижения
окно, оно уже выше средней точки. Таким образом, два шара
встречаются выше средней точки.
Мяч, брошенный вверх
достигнет окна в то же время, когда упавший мяч коснется земли.
Скорость брошенного мяча линейно возрастает со временем. Мяч
движется с наименьшей скоростью у окна и с наибольшей скоростью у окна
момент, когда он падает на землю. За половину времени, необходимого для достижения
на земле он покрывает менее половины расстояния и все еще находится выше средней точки
между окном и землей. Скорость мяча, подброшенного вверх
линейно уменьшается со временем. Он движется быстрее всего у земли и
медленнее всего возле окна. За половину времени, необходимого для достижения
окно, оно уже выше средней точки. Таким образом, два шара
встречаются выше средней точки.

 Если
галька падали 16 с, d = ½9,8 (м/с 2 ) 256 с 2 = 1254 м и его скорость в это время будет v = gt = 9,8 (м/с 2 )
16 с = 156 м/с = 351 миля в час. Однако, поскольку скорость звука равна 343 м/с, мы
всплеск услышишь только после 19.6 с. Поэтому камень должен быть
падение в течение более короткого времени и путешествие на более короткое расстояние. Он должен упасть на
где-то между 13 и 14 с. Предположим, что оно падает за 13,5 с. Тогда д
= 893 м. Звук преодолевает это расстояние за 2,6 с. Так что 890 м примерно правильно,
пока у нас есть основания пренебрегать сопротивлением воздуха.
Если
галька падали 16 с, d = ½9,8 (м/с 2 ) 256 с 2 = 1254 м и его скорость в это время будет v = gt = 9,8 (м/с 2 )
16 с = 156 м/с = 351 миля в час. Однако, поскольку скорость звука равна 343 м/с, мы
всплеск услышишь только после 19.6 с. Поэтому камень должен быть
падение в течение более короткого времени и путешествие на более короткое расстояние. Он должен упасть на
где-то между 13 и 14 с. Предположим, что оно падает за 13,5 с. Тогда д
= 893 м. Звук преодолевает это расстояние за 2,6 с. Так что 890 м примерно правильно,
пока у нас есть основания пренебрегать сопротивлением воздуха.
Leave A Comment