Тело падает без начальной скорости с высоты 45 м. Определить среднюю скорость
Условие задачи:
Тело падает без начальной скорости с высоты 45 м. Определить среднюю скорость падения на второй половине пути.
Задача №1.4.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=45\) м, \(S_1=\frac{1}{2}H\), \(\upsilon_{ср}-?\)
Решение задачи:
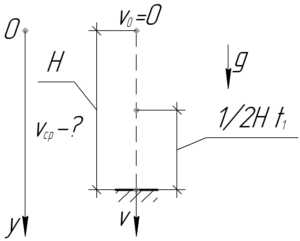 Чтобы определить среднюю скорость на второй половине пути, необходимо поделить пройденный путь, равный \(\frac{1}{2}H\), на время \(t_1\), сколько летело тело эту половину пути.
Чтобы определить среднюю скорость на второй половине пути, необходимо поделить пройденный путь, равный \(\frac{1}{2}H\), на время \(t_1\), сколько летело тело эту половину пути.
\[{\upsilon _{ср}} = \frac{H}{{2{t_1}}}\]
Найдем время \(t_1\). Для этого воспользуемся следующими рассуждениями. Если тело прошло весь путь \(H\) за время \(t\), а последнюю половину пути за \(t_1\) секунд, то первую половину пути \(\frac{1}{2}H\) оно прошло за \(\left( {t — {t_1}} \right)\). Так как тело двигалось без начальной скорости с ускорением \(g\), то верно записать следующую систему:
\[\left\{ \begin{gathered}
H = \frac{{g{t^2}}}{2} \hfill \\
\frac{1}{2}H = \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2} \hfill \\
\end{gathered} \right.\]
Поделим верхнее выражение в системе на нижнюю.
\[{\left( {\frac{t}{{t — {t_1}}}} \right)^2} = 2\]
Извлечем квадратный корень из обеих частей равенства.
\[\left[ \begin{gathered}
\frac{t}{{t — {t_1}}} = \sqrt 2 \hfill \\
\frac{t}{{t — {t_1}}} = — \sqrt 2 \hfill \\
\end{gathered} \right.\]
Второе выражение можно «выкинуть», так как очевидно, что отношение времен не может быть отрицательным.
\[t = \sqrt 2 t — \sqrt 2 {t_1}\]
\[{t_1} = t\frac{{\sqrt 2 — 1}}{{\sqrt 2 }}\]
Полное время падения \(t_1\) тела найдем из первой формулы приведенной системы.
\[H = \frac{{g{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2H}}{g}} \]
Значит:
\[{t_1} = \frac{{\sqrt 2 — 1}}{{\sqrt 2 }}\sqrt {\frac{{2H}}{g}} \]
В итоге средняя скорость на второй половине пути найдется по формуле:
\[{\upsilon _{ср}} = \frac{{\sqrt 2 H}}{{2\left( {\sqrt 2 — 1} \right)}}\sqrt {\frac{g}{{2H}}} \]
\[{\upsilon _{ср}} = \frac{{\sqrt {gH} }}{{2\left( {\sqrt 2 — 1} \right)}}\]
Подсчитаем численный ответ, используя инженерный калькулятор.
\[{\upsilon _{ср}} = \frac{{\sqrt {10 \cdot 45} }}{{2\left( {\sqrt 2 — 1} \right)}} = 25,61\; м/с = 92,18\; км/ч \]
Ответ: 92,18 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделиться ею с друзьями с помощью этих кнопок.
easyfizika.ru
Тело свободно падает без начальной скорости с высоты 45 м. Какой путь
Условие задачи:
Тело свободно падает без начальной скорости с высоты 45 м. Какой путь оно пройдет в последнюю секунду падения?
Задача №1.4.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=45\) м, \(t_1=1\) с, \(S-?\)
Решение задачи:
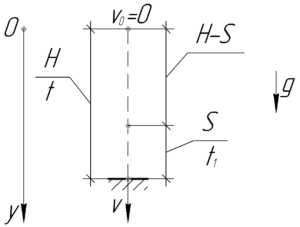 В условии говорится, что тело падает свободно без начальной скорости, поэтому мы можем легко определить время падения \(t\) благодаря формуле:
В условии говорится, что тело падает свободно без начальной скорости, поэтому мы можем легко определить время падения \(t\) благодаря формуле:
\[H = \frac{{g{t^2}}}{2} \Rightarrow t = \sqrt {\frac{{2H}}{g}}\;\;\;\;(1)\]
Если тело пройдет за последнюю \(t_1\) секунду путь \(S\), то за время \(\left( {t — {t_1}} \right)\) оно пройдет \(H-S\) метров. Запишем формулу, аналогичную формуле (1).
\[H — S = \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2}\]
Выразим из последнего выражения искомый путь \(S\).
\[S = H — \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2}\]
Раскроем скобки и подставим выражение (1) для \(H\) (а не для времени).
\[S = \frac{{g{t^2}}}{2} — \frac{{g{{\left( {t — {t_1}} \right)}^2}}}{2}\]
\[S = \frac{{g{t^2}}}{2} — \frac{{g{t^2}}}{2} + gt{t_1} — \frac{{gt_1^2}}{2}\]
\[S = gt{t_1} — \frac{{gt_1^2}}{2}\]
\[S = g{t_1}\left( {t — \frac{{{t_1}}}{2}} \right)\]
Осталось только подставить формулу для полного времени падения \(t\) и получим ответ в общем виде.
\[S = g{t_1}\left( {\sqrt {\frac{{2H}}{g}} — \frac{{{t_1}}}{2}} \right)\]
\[S = 10 \cdot 1\left( {\sqrt {\frac{{2 \cdot 45}}{{10}}} — \frac{1}{2}} \right) = 25\; м \]
Кстати, ответ легко подсчитывается и без калькулятора. Такой навык необходим развивать обязательно, если Вы хотите хорошо написать ЕГЭ или какую-нибудь олимпиаду по физике.
Ответ: 25 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделиться ею с друзьями с помощью этих кнопок.
easyfizika.ru
1)Тело падает с высоты 45 м без начальной скорости. Определите его скорость в момент достижения поверхности Земли.
5-9 класс
2)Найдите силу гравитационного притяжения двух соприкасающихся свинцовых шаров диаметром 1 м и массой 160 кг каждый.
3) Тело падало без начальной скорости с высоты 20 м. Определите время падения.
4)С какой силой притягиваются два бруска массой 6 кг каждый находясь на расстоянии 1 м друг от друга.
5)Скорость электропоезда 200000 кг при его торможении с постоянным ускорением уменьшилась на 12 м/с за 24 с. Определите равнодействующую сил , действующих на электровоз в указанный промежуток времени.
02 мая 2016 г., 21:06:48 (2 года назад)
1)U^2=2*g*h
U^2=882
U=29.7 м/c
2)Используя закон всемирного тяготения:
Fгр=y(m/R)^2=6.67*10^(-11)(160 кг/1 м)^2=1.7*10^(-6)H
3)Определим все время падения из формулы h = g*t^2 / 2 ,
t =корень квадратный из 2*h / g ( h — высота =20м, g — ускорение свободного падения=10м/c^2). t = кор. кв. из 2*20 / 10 =2c. определим путь за первую секунду
S1 = g*t1^2 / 2, S1=10*1 / 2 = 5м. Значит за вторую ( последнюю) секунду оно прошло путь S2 = S — S1. S2 = 20 — 5 =15м. Чтобы определить среднюю скорость на
всем пути нужно весь путь разделить на все время: vср=S / t, vср =20 / 2 =10м/c.
Определим время на первой половине пути ( S3=S / 2 =10м) , из формулы
S3 = g*t3^2 / 2, t3=кор. кв. из 2*S3 / g . t3=кор. кв. из 2*10 / 10=1,4c. Вторую половину он пролетел за время t2= t — t3. t2 = 2 — 1,4 =0,6c, Определим среднюю ксорость на 2 половине v1ср=S / 2*t2. v1ср=40 / 2*0,6 =33,3м/c.
S2=15м (за последнюю секунду) , vср=10м/c( на всем пути) , v1ср=33,3м/c(на второй половине пути).
4)
Ответить
fizika.neznaka.ru
1)Тело падает с высоты 45 м без начальной скорости. Определите его скорость в момент достижения поверхности Земли.
5-9 класс
2)Найдите силу гравитационного притяжения двух соприкасающихся свинцовых шаров диаметром 1 м и массой 160 кг каждый.
3) Тело падало без начальной скорости с высоты 20 м. Определите время падения.
4)С какой силой притягиваются два бруска массой 6 кг каждый находясь на расстоянии 1 м друг от друга.
5)Скорость электропоезда 200000 кг при его торможении с постоянным ускорением уменьшилась на 12 м/с за 24 с. Определите равнодействующую сил , действующих на электровоз в указанный промежуток времени.
02 мая 2016 г., 21:06:48 (2 года назад)
1)U^2=2*g*h
U^2=882
U=29.7 м/c
2)Используя закон всемирного тяготения:
Fгр=y(m/R)^2=6.67*10^(-11)(160 кг/1 м)^2=1.7*10^(-6)H
3)Определим все время падения из формулы h = g*t^2 / 2 ,
t =корень квадратный из 2*h / g ( h — высота =20м, g — ускорение свободного падения=10м/c^2). t = кор. кв. из 2*20 / 10 =2c. определим путь за первую секунду
S1 = g*t1^2 / 2, S1=10*1 / 2 = 5м. Значит за вторую ( последнюю) секунду оно прошло путь S2 = S — S1. S2 = 20 — 5 =15м. Чтобы определить среднюю скорость на
всем пути нужно весь путь разделить на все время: vср=S / t, vср =20 / 2 =10м/c.
Определим время на первой половине пути ( S3=S / 2 =10м) , из формулы
S3 = g*t3^2 / 2, t3=кор. кв. из 2*S3 / g . t3=кор. кв. из 2*10 / 10=1,4c. Вторую половину он пролетел за время t2= t — t3. t2 = 2 — 1,4 =0,6c, Определим среднюю ксорость на 2 половине v1ср=S / 2*t2. v1ср=40 / 2*0,6 =33,3м/c.
S2=15м (за последнюю секунду) , vср=10м/c( на всем пути) , v1ср=33,3м/c(на второй половине пути).
4)
Ответить
algebra.neznaka.ru

Leave A Comment