9. Графические задачи
А 1 | На рисунках изображены графики зависимости модуля ускорения от времени для разных видов движения. Какой график соответствует равномерному движению? | |||||||||||||||
1 0 t ) | 2 0 t ) | 3 0 t ) | 4 0 t ) | |||||||||||||
А 2 | Тело,
двигаясь вдоль оси ОХ прямолинейно и
равноускоренно, за некоторое время
уменьшило свою скорость в 2 раза. | |||||||||||||||
1 0 t ) | 2 0 t ) | 3 0 t ) | 4 0 t ) | |||||||||||||
Равноускоренному движению соответствует график зависимости модуля ускорения от времени, обозначенный на рисунке буквой
| ||||||||||||||||
А 4 | Автомобиль
движется по прямой улице. Модуль ускорения максимален в интервале времени
| |||||||||||||||
А 5 | Автомобиль
движется по прямой улице. Модуль ускорения максимален в интервале времени
| |||||||||||||
А 6 | Автомобиль
движется по прямой улице. На графике
представлена зависимость скорости
автомобиля от времени. | |||||||||||||
1) от 0 с до 10 с | 2) от 10 с до 20 с | |||||||||||||
4) от 30 с до 40 с | ||||||||||||||
А 7 | Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Модуль ускорения минимален в интервале времени | |||||||||||||
1) от 0 с до 10 с | 2) от 10 с до 20 с | |||||||||||||
3) от 20 с до 30 с | 4) от 30 с до 40 с | |||||||||||||
А 8 | Стрела
пущена вертикально вверх. | |||||||||||||
1)1,5 с | 2) 3 с | |||||||||||||
3) 4,5 с | 4) 6 с | |||||||||||||
А 9 | Стрела пущена вертикально вверх. Проекция ее скорости на вертикальное направление меняется со временем согласно графику на рисунке. Через сколько секунд стрела упадет на Землю? | |
1)1,5 с | 2) 3 с | |
3) 4,5 с | 4) 6 с |
А 10 | На
рисунке приведен график зависимости
проекции скорости тела от времени. | |||||||||
Проекция ускорения тела в интервале времени от 0 до 2 с представлена графиком | ||||||||||
-5 | 1 0 t 5 -5 ) | 2 0 t 5 -5 ) | 3 0 t 5 -5 ) | 4 0 t 5 ) | ||||||
А 11 | На
рисунке приведен график зависимости
проекции скорости тела от времени. | |||||||||
Проекция ускорения тела в интервале времени от 2 до 4 с представлена графиком | ||||||||||
-5 | 1 0 t 5 -5 ) | 2 0 t 5 -5 ) | 3 0 t 5 -5 ) | 4 0 t 5 ) | ||||||
А 12 | На
рисунке приведен график зависимости
проекции скорости тела от времени. | |||||||||
Проекция ускорения тела в интервале времени от 8 до 12 с представлена графиком | ||||||||||
-5 | 1 0 t 5 -5 ) | 2 0 t 5 -5 ) | 3 0 t 5 -5 ) | 4 0 t 5 ) | ||||||
А 13 | На
рисунке приведен график зависимости
проекции скорости тела от времени. | |||||||||
Проекция ускорения тела в интервале времени от 8 до 12 с представлена графиком | ||||||||||
-5 | 1 0 t 5 -5 ) | 2 0 t 5 -5 ) | 3 0 t 5 -5 ) | 4 0 t 5 ) | ||||||
А 14 | Тело
начинает двигаться из начала координат
вдоль оси ОХ,
причем проекция скорости
меняется
с течением времени по закону,
приведенному на графике. | 11 1 21 | ||||||||
1) 0 м/c2 | 2) 0,5 м/c2 | |||||||||
3) 1 м/c2 | 4) 2 м/c2 | |||||||||
А 15 | П о графику зависимости модуля скорости от времени, представленному на рисунке, определите ускорение прямолинейно движущегося тела в момент времени 2 с. | 3 6 21 9 31 41 1 | ||||||||
1) 2 м/c2 | 2) 3 м/c2 | |||||||||
3) 9 м/c2 | 4) 27 м/c2 | |||||||||
А 16 | Тело
движется по оси ОХ.
Проекция его скорости
меняется по закону, приведенному на
графике. | 1 0,5 1 0,5 | ||||||||
1) 0,25 м | 2) 0,5 м | |||||||||
3) 1 м | 4) 2 м | |||||||||
А 17 | Тело движется по оси ОХ. Проекция его скорости меняется по закону, приведенному на графике. Путь, пройденный телом за 2 с, равен | 2 1 2 1 | ||||||||
1) 1 м | 2) 2 м | |||||||||
3) 4 м | 4) 8 м | |||||||||
А 18 | На
рисунке представлены графики скорости
трех тел, движущихся прямолинейно. | 5 10 15 1 2 3 I II III | |||||
1) I | 2) II | ||||||
3) III | 4) пути трех тел одинаковые | ||||||
А 19 | По графику зависимости модуля скорости от времени определите путь, пройденный телом за 2 с. | 4 1 2 3 | |||||
1) 6 м | 2) 8 м | ||||||
3) 5 м | 4) 4 м | ||||||
А 20 | На
графике показана зависимость скорости
тела от времени. | ||||||
1) 7 м | 2) 6 м | ||||||
3) 5 м | 4) 4 м | ||||||
А 21 | На графике изображена зависимость проекции скорости тела, движущегося вдоль оси ОХ, от времени. Какой путь прошло тело к моменту времени t = 6 с? | ||||||
1) 0 м | 2) 6 м | ||||||
3) 8 м | 4) 10 м | ||||||
А 22 | На
графике изображена зависимость
проекции скорости тела, движущегося
вдоль оси ОХ,
от времени. | ||||||
1) 0 м | 2) 6 м | ||||||
3) 8 м | 4) 10 м | ||||||
А 23 | На рисунке представлен график зависимости пути велосипедиста от времени . Определите интервал време-ни, когда велосипедист двигался со скоростью 5 м/с. | ||||||
1) от 5 с до 7 с | 2) от 3 с до 5 с | ||||||
3) от 1 с до 3 с | 4) от 0 с до 1 с | ||||||
А 24 | На
рисунке представлен график зависимости
пути
велосипедиста от времени
. | ||||||
1) от 0 с до 1 с | 2) от 1 с до 3 с | ||||||
3) от 3 с до 5 с | 4) от 5 с и далее | ||||||
А 25 | На рисунке изображен график изменения координаты тела с течением времени. В какой промежуток времени скорость тела была равна нулю? | ||||||
1) только при 0 с | 2) только от 2 до 5 с | ||||||
3) только от 5 до 8 с | 4) от 2 до 8 с | ||||||
А 26 | На
рисунке изображен график изменения
координаты тела с течением времени. | ||||||
1) не изменялась 2) увеличивалась 3) уменьшалась 4) для ответа на вопрос не хватает данных | |||||||
А 27 | На рисунке представлен график движения тела. Определите значение его координаты и скорости движения в момент времени 5 с. | ||||||
1) 2 м; 1,6 м/с 2) 10 м; 2 м/с 3) 10 м; 1,6 м/с 4) 2 м; 2 м/с | |||||||
А 28 | На
рисунке представлен график зависимости
координаты тела, движущегося вдоль
оси OX,
от времени.
| |||||||||||||
А 29 | На рисунке представлен график движения автобуса из пункта А в пункт В и обратно. Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна скорость автобуса на пути из А в Б? | |||||||||||||
1) 40 км/ч | 2) 50 км/ч | |||||||||||||
3) 60 км/ч | 4) 75 км/ч | |||||||||||||
А 30 | На
рисунке представлен график движения
автобуса из пункта А в пункт В и обратно. | |||||||||||||
1) 40 км/ч | 2) 50 км/ч | |||||||||||||
3) 60 км/ч | 4) 75 км/ч | |||||||||||||
А 31 | На рисунке представлен график движения автобуса из пункта А в пункт В и обратно. Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? | |||||||||||||
1) 40 км/ч | 2) 50 км/ч | |||||||||||||
3) 60 км/ч | 4) 75 км/ч | |||||||||||||
А 32 | На
рисунке представлен график движения
автобуса из пункта А в пункт В и обратно. | |||||||||||||
1) 40 км/ч | 2) 50 км/ч | |||||||||||||
3) 60 км/ч | 4) 75 км/ч | |||||||||||||
А 33 | На рисунке изображен график зависимости координаты бусинки, движущейся по горизонтальной спице, от времени. На основании графика можно утверждать, что
| |||||||||||||
№ п/п | Задания | ответ | |||||||||||||||||||||||||
ОБЯЗАТЕЛЬНАЯ ЧАСТЬ | |||||||||||||||||||||||||||
Часть А. | |||||||||||||||||||||||||||
А.1 | Какое тело, из перечисленных ниже, оставляет видимую траекторию? 1) Камень, падающий в горах | ||||||||||||||||||||||||||
А.2 | Материальная точка, двигаясь прямолинейно, переместилась из точки с координатами (-2; 3) в точку с координатами (1; 7). Определите модуль вектора перемещения. 1) 1 м 2) 2 м 3) 5 м 4) 7 м | ||||||||||||||||||||||||||
А.3 | Что образует систему отсчета? 1) тело отсчета и система координат 3) тело отсчета и часы 4) тело отсчета, система координат и часы | ||||||||||||||||||||||||||
А.4 | Санки съехали с одной горки и въехали на другую. 1) -2,5 м/с2 2) 2,5 м/с2 3) -9,0 м/с2 4) 3,5 м/с2 | ||||||||||||||||||||||||||
А.5 | Гору длиной 50 м лыжник прошел за 10 с, двигаясь с ускорением 0,4 м/с2. Чему равна скорость лыжника в начале и в конце горы? 1) 3 м/с и 6 м/с 2) 2 м/с и 8 м/с 3) 4 м/с и 7 м/с 4) 3 м/с и 7 м/с | ||||||||||||||||||||||||||
А.6 | Тело, двигаясь вдоль оси ОХ прямолинейно и равноускоренно, за некоторое время уменьшило свою скорость в 2 раза. Какой из графиков зависимости проекции ускорения от времени соответствует такому движению? | ||||||||||||||||||||||||||
А. | По графику зависимости модуля скорости от времени определите путь, пройденный телом за 20 с. 1) 60 м 4) 40 м | ||||||||||||||||||||||||||
ДОПОЛНИТЕЛЬНАЯ ЧАСТЬ | |||||||||||||||||||||||||||
Часть В. Задание на установление соответствия позиций | |||||||||||||||||||||||||||
В.1 |
| ||||||||||||||||||||||||||
Решить задачу на применение закона (формулы) по данной теме и записать ответ. | |||||||||||||||||||||||||||
В.2 | Аварийное торможение автомобиля заняло 4 с и происходило с постоянным ускорением 4 м/с2. Найдите тормозной путь. | ||||||||||||||||||||||||||
В.3 | Трамвай движется на повороте по закруглению радиусом 40 м. Рассчитайте линейную скорость трамвая, если центростремительное ускорение равно 0,4 м/с2. | ||||||||||||||||||||||||||
Часть С. Задача на применение одного — двух законов (формул), показать полную запись логики решения задачи. | |||||||||||||||||||||||||||
С.1 | Пост ГИБДД находится за городом на расстоянии 500 м от городской черты. Автомобиль выезжает из города и, проехав мимо поста со скоростью 5 м/с, начинает разгоняться с постоянным ускорением 1 м/с2 на прямолинейном участке шоссе. | ||||||||||||||||||||||||||
Прямолинейное движение — Равноускоренное движение
Неравномерное движение : “ Тело говорят, что он имеет неравномерную скорость (или движение), если он охватывает неравные перемещений за равные промежутки времени». Среднее его скорость остается навсегда меняется. Если скорость увеличивается с постоянной скоростью, то говорят, что она находится в равноускоренный. Если скорость продолжает уменьшаться с постоянной скоростью, то говорят, что она находится в равномерная задержка. УСКОРЕНИЕ: «Время изменения скорости объект называется ускорением объекта». Если мы считать скорости объекта равными против и v’ в моменты времени t & t’ соответственно тогда a = ( v’ – v )/ (t’ – t) векторная величина и ее единица СИ м/с 2 (мс -2 ) Кинетические уравнения равноускоренного движения : начальная скорость (u), конечная скорость (v), время, необходимое для того, чтобы u стало v (t), ускорение (a) и расстояние, пройденное за это время (s), равны соотносится с помощью трех уравнений движения: (I) Скорость – Время : Как мы знаем, что a = (v’ –v ) / (t’ – t ), переставляя это уравнение, получаем a (t’ – t) = v’ – v Или. Если исходный скорость принимается как u, окончательная как v , начальное время как ноль и конечное as t Тогда v = u + at Это 1 st уравнение движение. (II) Должность – Отношение времени : Если взять тело, начальная скорость которого v & и конечная скорость равна v’, тогда его средняя скорость V ср = (1/2) (v + v’) ———— (2) Предположим первоначально (в момент времени = t) положение тела равно x и в t = O оно равно x’, то средняя скорость Vср = (x’ – x )/ (t’ – t ) Или x’- x = (t ’ – t) v ср ————————- ( 3 ) Установка значение V av из (2) в (3) X’ – x = (1/2) (t’ – t) (v + v’) ———— (4) От уравнения (1), мы знаем, что v’ = v + a (t’ – t) Помещение этого значение равно уравнению (4) x’ – x = (1/2) (t’ – t) [v + v +a (t’ – t)] x’ – x = (1/2) (t’ – t) 2v +(1/2) a (t’ – t) 2 x’ – x = v (t’ – t ) + (1/2) a (t’ – т) 2 ——— (5) Если принять начальная скорость как u, начальное время как ноль, конечное время как t и x’ – x как перемещение S, тогда S = ut + (1/2)at 2 Это второе уравнение движения Уравнение (5) дает x’ – x = v (t’ – t) + ( 1 / 2 ) a (t’ – t) 2 Мы должны заменить время на скорость. Таким образом, используя a = ( v’ – v)/( t’ – t), мы получаем t’ – t =( v’ – v ) / a Подставив это значение в уравнение (5), мы получаем x’ – x = v (v’ – v)/(a) + (1/2) a{ v’ – v)/(a)} 2 x’ – x = (v ‘ 2 – v 2 ) / 2a Или v’ 2 – v = 2a (x’ – x) Если принять u за начальная скорость v как конечная скорость & x’ – x как смещение S, тогда v 2 – u 2 = 2as = => v 2 = у 2 + 2as Это 3 рд уравнение движения. (IV) Рабочий объем в n th second: Предположим, что тело перемещается на расстояние S. в n секунды и S n-1 в n – 1 секунда. Затем, используя S = ut + ( 1 / 2 ) при 2 получаем, S n = un + (½)an 2 & S n-1 = u (n – 1) + ( 1 / 2 ) (n – 1) 2 Итак, пройденное расстояние в n th секунда = S n – S n-1 S n – S n-1 = un + (1/2) an 2 – {u (n – 1) + (1/2) a (n – 1) 2 } S nth = un + (1/2) ан 2 – ип + и — (1/2) a (n 2 + 1 – 2n) =
(1/2) 2 + u — (1/2) 2 -(1/2) а +(1/2) а (2n) = u + ан -(1/2) а. S n-й = u + (1/2) а (2n – 1 ) ФОРМУЛА РАВНОУСКОРЕННОГО ДВИЖЕНИЯ РАСЧЕТНЫМ МЕТОДОМ (а) Скорость – Связь времени : Предположим, что тело двигаясь с ускорением «а» и за малое время «dt», оно меняет свое скорость на небольшую величину «dv». Тогда согласно определению ускорения: A = dv/dt => dv = a dt ——— (1) Теперь предположим, что мы хотим узнать общее изменение скорости за весь путь. Тогда мы должны интегрируем обе части уравнения (1) Предположим, что начальная скорость есть & конечная скорость v, начальное время равно нулю и конечное время t, затем интегрируем уравнение (1) u ∫ v dv = 0 ∫ t а dt = а 0 ∫ t dt [v} v u = a[t] t 0 => v- u = a (t – o) => v = u + at 3 8 9003 уравнение движения.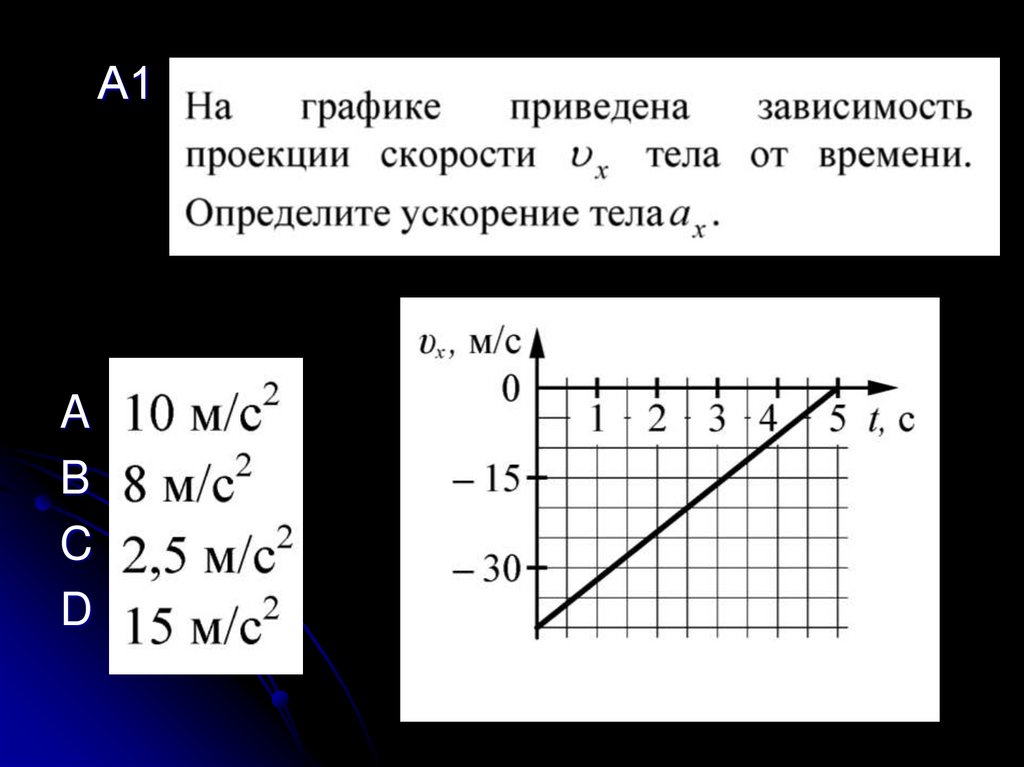 (b) Положение – отношение времени : Предположим, что одно и то же тело подвергается небольшому смещению «dx» за небольшой интервал времени «dt», тогда мгновенная скорость определяется как x = dx/ dt или dx = v dt Использование 1 st уравнение движения получаем dx = (u + at) dt = u.dt + at dt ——— (2) Если его начальный перемещение x o и время считается нулевой начальной скоростью как u, то интегрируя уравнение (2) x0 ∫ x dx = 0 ∫ t ( u + at) dt = u 0 ∫ t dt + a 0 ∫ t tdt [x] x xo = u [t] t 0 + (a) [t 2 /2] t 0 x – x 0 = u (t – 0 ) + a {(T 2 /2) — 0} AS x — x 0 = S, SO, S = UT + ( 1 / 2 ) на 2 . (с) скорость — Отношение смещения : Поскольку мы знаем, что ускорение определяется как a = dv/dt Но у нас есть найти скорость — перемещение связь. Итак, мы умножаем правую часть приведенного выше соотношения на dx/dx, чтобы ввести смещение в нем. Итак, a = (dv/dt)(dx/dx) = v(dv/dt) { as dx/dt = v} => v dv = a dx ————— (3) начальная позиция как x o , конечная как x, начальная скорость как u & final как v, а затем, интегрируя уравнение (3) по всему маршруту, получаем и ∫ v v DV = XO ∫ x A DX => [V 2 /2} V U = A [x] x 1 3 3 9139137791377 3 13 13 13 1 3 1 3 1913 . v 2 /2) – (u 2 /2) = a (x -x o )=> ( 1 / 2 )(v 2 – u 2 ) = aS => v 2 – и 2 = 2аС => v 2 = u 2 + 2as Это 2 и уравнение движения. Скорость – График равномерности во времени Ускоренное движение : Скорость – график времени
Равноускоренное движение представляет собой прямую линию, наклоненную к оси времени. В случае
положительного ускорения, график наклонен вверх, а в случае отрицательного
ускорение, график наклонен вниз. .Наклон графика дает ускорение. (Наклон = tan0) Позиция – временной график Равномерно Ускорение Движение : Если у нас есть положение тела в разное время, то есть движется с равномерным ускорением, то можно построить его положение – временной график, который оказывается изогнутым, наклон которого увеличивается вверх направление. С другой стороны, если мы построим тот же график равномерно запаздывающего тело, то мы получаем кривую, наклон которой продолжает уменьшаться. Доказательство кинематических уравнений движения Использование графического метода : I Уравнение движения «Можно доказать, что расстояние
покрываемое равномерно ускоренным телом, может быть задана площадью, ограниченной
его скорость — временной график со временем
ось. Предположим, что начальная скорость (OA) равна u, время (OB) равно «t», ускорение равно «a», тогда изменение скорости во времени ‘t’ равно CD = ускорение x время = a x t = at Итак, скорость после времени t = BD = BC + CD v = u + at, что равно 1 st Уравнение движения II Уравнение движения Теперь площадь на графике OADB = Площадь прямоугольника OBCA + Площадь ∆ACD A = OA x OB + 1 / 2 AC x CD = u x t + 1 / 2 t x at Итак, Площадь вложенный = ut + 1 / 2 at 2 Но мы знаем эта область под графиком x-t и осью времени дает смещение, следовательно, S = ut + 1 / 2 на 2 , что является вторым уравнением. из движение. III Уравнение движения Площадь График OADB также задан A = площадь трапециевого OADB => A = 1 / 2 (Сумма парильных сторон X высота) = 1 / 2 (V+U ) t} = 1 / 2 { (v+u) (v – u)/a} = 1 / 2 {(v 2 – u 2 )/a} мы знаем, что площадь под x-t графиком и осью времени дает смещение, следовательно, S = 1 / 2 {(v 2 – u 2 )/a} => 2aS = v 2 – u 2 => v 2 = u 2 + 2aS, что является третьим уравнением
движения. Очередь. . Водоизмещение (измеряется в метрах) частицы, движущейся вдоль оси X, определяется как x = 18t + 5т 2 . Рассчитайте (i) мгновенную скорость в момент времени t = 2 с (ii) среднее значение скорость между t = 2 с и t = 3 с. |
Движение в одном измерении
Предоставил:
NEO Ср, 16 марта 2022 г., 11:20 UTC
Этот pdf-файл включает следующие темы:
ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ
Динамика
Статика
Система отсчета:
Скорость и скорость
Примеры
1.
БЛОК – II
МЕХАНИКА
2.1 ДВИЖЕНИЕ В ОДНОМ ИЗМЕРЕНИИ
Механика – старейшая и наиболее фундаментальная из всех областей физики. По существу,
механика изучает состояние покоя, а также состояние движения объектов под действием силы или сил
.
Изучение механики в целом подразделяется на 1) динамику и 2) статику.
Динамика имеет дело с телами в движении.
Статика имеет дело с телами, покоящимися под действием системы сил.
Динамика снова делится на кинематику и кинетику.
Кинематика занимается описанием движения без ссылки на причину движения. (Или
Как движения?).
Кинетика имеет дело с тем, что движется и что заставляет его двигаться (т.е. имеет дело с массой движущегося тела
и силой, вызывающей движение). (Или почему движения?).
Два пассажира, сидящие в движущемся поезде, покоятся относительно друг друга, но находятся в движении
относительно неподвижного внешнего наблюдателя, другими словами, покой и движение относительны. Таким образом, нам нужна ссылка
для описания покоя и движения. Система отсчета, которую мы используем, называется «Система отсчета»
Система отсчета:
Система отсчета — это система отсчета, в которой сидит наблюдатель и ведет наблюдение.
Есть два типа.
1) Инерциальная система отсчета.
2) Неинерциальная система отсчета.
Система отсчета, которая либо находится в состоянии покоя, либо движется с постоянной скоростью, называется инерциальной
система отсчета.
Система отсчета, движущаяся с некоторым ускорением, называется неинерциальной системой отсчета.
Для наблюдения прикрепляем систему отсчета. Определенная система координат
Y состоит из трех взаимно перпендикулярных осей x, y и z, пересекающихся в общей точке
‘O’, начале координат. Когда частица движется в пространстве, ее положение в любой момент времени
может быть описано с помощью трех ее положений
координат (x, y и z), которые меняются со временем в процессе движения частицы.
O X
Движение и покой:
Говорят, что тело находится в движении, если его положение меняется относительно других тел, рассматриваемых как неподвижные
с течением времени.
Говорят, что тело находится в состоянии покоя, если оно занимает одно и то же положение относительно другого тела и не
меняет свое положение с течением времени.
Движение бывает двух видов, т. е.
1) Поступательное движение. 2) Вращательное движение.
Говорят, что тело совершает поступательное движение, когда оно движется так, что все частицы тела совершают
одно и то же движение, т. е. имеют равные скорости в любой момент и описывают сходные пути или траектории.
Bridge Course – Phy – I PUC ‐ 32 ‐
2.
Пример: стрела, выпущенная из лука, камень, упавший с высоты, поезд, движущийся по рельсам, и т. д.
Движение тела называется вращательным, если оно движется так, что частица или линия частиц в нем
остается неподвижным относительно окружающей среды.
Пример: Колесо движущегося велосипеда имеет вращательное движение. Он совершает вращательное движение вокруг своей оси.
Основными характеристиками движения частицы являются ее траектория, координаты, перемещение,
скорость, ускорение и длина пути.
Движение в одном измерении:
Говорят, что движение частицы происходит в одном измерении, если только одна из трех координат
, определяющих положение частицы, изменяется со временем.
Пример: Автомобиль движется по прямой дороге.
Расстояние и смещение:
Расстояние — это общая длина пути, описываемого частицей за данный интервал времени или
Фактическое расстояние, пройденное частицей за данный интервал времени.
Смещение — это вектор, соединяющий
начальное положение частицы с ее конечным положением за заданный интервал времени.
Рассмотрим тело, движущееся из точки А в точку В, как показано на рисунке.
C Фактическая длина криволинейного пути ACB — это расстояние, пройденное телом
, задается во временном интервале. Отрезок AB дает величину
AB смещения тела за данный интервал времени.
Направление смещения направлено от А к В через прямую линию АВ
и величина смещения равна АВ.
Важные особенности:
a. Расстояние — это скалярная величина, а перемещение — векторная величина.
б. Длина пути или расстояние есть положительная скалярная величина, которая не убывает со временем и никогда не может быть равна нулю для движущегося тела. Перемещение тела может быть нулевым.
Перемещение тела может быть нулевым.
в. Величина смещения никогда не может быть больше расстояния.
д. Когда тело возвращается в исходное положение, его перемещение равно нулю, а расстояние или длина пути
не равно нулю.
эл. При прямолинейном движении тела перемещение равно расстоянию.
Скорость и скорость:
Скорость движущейся частицы определяется как расстояние, пройденное за единицу времени.
Скорость = пройденное расстояние
Затраченное время
Это скалярная единица мс-1, всегда положительная.
Скорость равномерна, если движущийся объект проходит одинаковое расстояние за равные промежутки времени.
Для неравномерного движения мы определяем среднюю скорость как отношение всего пройденного пути к общему 906:13 затраченное время.
Средняя скорость = общее пройденное расстояние
общее затраченное время.
Скорость тела определяется как скорость его перемещения.
скорость = перемещение
время.
Bridge Course – Phy – I PUC ‐ 33 ‐
3. Скорость — это вектор, единица измерения СИ которого равна мс-1. Скорость называется равномерной, если ее величина и направление остаются неизменными, в противном случае скорость неравномерна.
Скорость — это вектор, единица измерения СИ которого равна мс-1. Скорость называется равномерной, если ее величина и направление остаются неизменными, в противном случае скорость неравномерна.
Средняя скорость определяется как отношение общего смещения к общему времени.
Средняя скорость = полное перемещение
затраченное время
Скорость тела в любой момент времени называется его мгновенной скоростью.
Важные функции
a. Скорость является скалярной величиной. Скорость является векторной величиной.
б. Скорость может быть отрицательной, нулевой или положительной, но скорость никогда не бывает отрицательной.
в. Если движение происходит в одном и том же направлении, то средняя скорость и средняя скорость
одинаковы.
д. Если частица проходит расстояние со скоростью «v1» и возвращается со скоростью «v2», то
Vavg = 2 v1v2
v1+v2
e. Если частица движется за два равных промежутка времени с разными скоростями v1 и v2
соответственно, то
Vavg = v1+v2
2
Ускорение частицы определяется как скорость изменения скорости.
Ускорение = изменение скорости
затраченное время
Это вектор, имеющий единицу измерения мс-2.
Ускорение может быть равномерным или переменным.
Ускорение частицы называется равномерным, если скорость частицы изменяется на одинаковую величину
через равные промежутки времени, какими бы малыми они ни были. В противном случае говорят, что ускорение равно
Постоянное ускорение
Равномерное ускорение, имеющее то же направление скорости, называется постоянным ускорением.
Пример: ускорение свободного падения равно g.
Уравнения движения тел с постоянным ускорением
Следующие символы используются применительно к уравнениям движения.
u Æ начальная скорость a Æ равномерное ускорение v Æ конечная скорость
s Æ расстояние, пройденное за время ‘t’ t Æ интервал времени, для которого рассматривается движение.
Скорость в момент времени ‘t’
По определению ускорение ‘a’ определяется выражением a = изменение скорости = (v – u)
время, затраченное на t
Следовательно, v = u + at.
Bridge Course – Phy – I PUC ‐ 34 ‐
4.
Пройденное расстояние за время t’
В случае движения с переменной скоростью
Средняя скорость = перемещение = с
Затраченное время t
Поскольку ускорение равномерное,
Средняя скорость = (u + v) = с
2 т
Или s = (u + v) ИЛИ s = u + u + at (Поскольку v = u + at)
2 2
Следовательно, s = ut + ½ at2
Скорость, приобретаемая при прохождении расстояния s’:
Средняя скорость = пройденное расстояние
затраченное время
(u + v) = с Или (u + v) t = 2 с
2 t
По определению, a = (v – u) Или t = (v – u)
t a
Следовательно, (u + v) (v – u) = 2 с
a
т. е. v2 – u2 = 2as
Следовательно, v2 = u2 + 2as
Важные особенности равномерного движения
• Равномерное движение – прямолинейное движение с постоянной скоростью.
• При равномерном движении перемещение и расстояние равны.
• Для равномерного движения объекта не требуется результирующая сила.
• Скорость при равномерном движении не зависит от интервала времени.
• Скорость при равномерном движении не зависит от выбора начала координат.
Равномерное движение
Говорят, что частица движется равномерно, если она совершает равные перемещения за равные промежутки времени
какими бы маленькими ни были эти интервалы.
Расстояние Sn, пройденное за n-ю секунду движения:
Расстояние, пройденное за n-ю секунду, равно разнице между расстоянием, пройденным за n
секунд и (n-1) секунд.
Sn = (un + ½ an2) – [u (n-1) + ½ a (n-1)2]
= u + an – ½ a
Следовательно, Sn = u + a (n – 1/2) .
Ускорение, выраженное в виде расстояния, пройденного за два последовательных равных интервала времени
Если s1 и s2 — расстояния, пройденные за два последовательных интервала времени «t», каждый «a», то константа
ускорение и ‘u’ начальная скорость для s1, то
S1 = ut + ½ at2 и
s1 + s2 = u (2t) + ½ a (2t)2 = 2 ut + 2 at2
Следовательно, (s1 + s2 – 2s1) = at2
т. е. s2 – s1 = at2
е. s2 – s1 = at2
Следовательно, a = (s2 – s1)
t2
Курс бриджа – Phy – I PUC – 35 –
5.
Движение под действием силы тяжести с высоты:
Любое падающее тело движется к земле с почти постоянным ускорением. Его движение является
примером одномерного движения под действием силы тяжести. Это ускорение одинаково для всех тел, которые
сбрасываются и не зависят от их размера, массы или состава и называются «ускорением из-за
». Оно всегда направлено к центру Земли и обозначается буквой «g».
Уравнения движения свободно падающего тела получаются заменой «а» на «g»
т. е. для тела, свободно падающего под действием силы тяжести,
1. V = u + gt
2. S = ut + ½ gt2
3 .V2 = u2 + 2gh
4. Snt = u + ½ g (2n–1)
Для тела, поднимающегося вертикально против силы тяжести,
1. V = u — gt
2 S = ut – ½ gt2
3. V2 = u2 – 2gh
4. Sn = u – ½ g (2n-1)
График – это графическое представление изменения одной величины по отношению к другой.
Графики широко используются в науке. Есть две основные причины для нанесения экспериментальных данных
на графики, а именно:
а) Чтобы сообщить результат в легко понятной форме.
б) Для помощи в анализе результатов.
Движение тела удобно изобразить графически.
Время откладывается по оси x, а скорость или мгновенное положение или ускорение — по оси y.
Есть три типа графиков.
График положение-время:
Когда мгновенные положения частицы строятся в зависимости от времени, результирующий график известен
как график положение-время.
1. График показывает мгновенное значение смещения в любой момент времени.
2. Наклон касательной к графику в любой момент времени дает мгновенную скорость
в этот момент.
3. График s-t не может делать резких поворотов.
Различные случаи графика смещения-времени
Sl Различные
s-t График Основные характеристики
Нет наблюдений
1 В покое Наклон ‘v’ = 0
с
t
2 Однородный θ = постоянный
движение v = постоянный
с a=0
t
Курс моста – Phy – I PUC — 36 ‐
6. 3 Равномерное θ ускоренно увеличивается в
3 Равномерное θ ускоренно увеличивается в
раз. Итак,
движений с s ‘v’ равно
u=0, s=0 при увеличении &
t=0 t ‘a’ положителен
4 Равномерный наклон s-t
ускоренный график постепенно
движение с s продолжается
u≠0, но увеличивается
s=0 при t =0 t
5 Равномерно θ
запаздывает в убывании.
движение с Итак, «v» равно
уменьшение &
‘a’ отрицательное
tÆ
График зависимости скорости от времени
1. График зависимости скорости от времени дает мгновенное значение скорости в любой момент времени.
2. Наклон касательной на графике дает мгновенное ускорение.
3. Площадь под графиком v-t с осью времени дает величину перемещения, пройденного за заданное время.
4. Кривая v-t не может делать резких поворотов.
Различные варианты графика зависимости скорости от времени
Sl
Различные варианты графика v-t Основные характеристики
Нет
1 Равномерное движение θ = 00
v v = постоянное
наклон a = 0
t
2 Равномерно θ = постоянное
ускоренное a = постоянное
движение с u=0, v v равномерно возрастает с
s=0 при t= 0 время
t
3 Равномерно Положительное постоянное ускорение
ускоряется, потому что θ постоянно, но
движение с u≠0, начальная скорость частицы
с=0 при t=0 v положительная
t
4 Равномерно Наклон графика v-t = -a
ускорение v (замедление)
движение
t
5 Неравномерно Уклон увеличивается со временем.
ускоренный То есть «а» увеличивается
движение v
t
Курс моста – Phy – I PUC ‐ 37 ‐
7.
6 Неравномерно θ убывает. Таким образом, ускорение
ускорение равно уменьшению
движения v
t
1. Наклон графика v-t никогда не может быть бесконечным в любой точке, потому что бесконечный наклон графика v-t означает
бесконечное ускорение. Точно так же бесконечный наклон графика s-t означает бесконечную скорость. Следовательно, следующие
графов невозможны.
v v
t t
2. Одновременно невозможны два значения скорости или перемещения. Следовательно, следующие графики
неприемлемы.
v
v v
tÆ tÆ
График ускорение-время:
1) Если график a-t представляет собой прямую линию, параллельную оси времени, то ускорение «a» является постоянным.
a
tÆ
2) Если график a-t представляет собой прямую линию, проходящую через начало координат, то ускорение частицы равно
и возрастает равномерно.
a
tÆ
3) Когда график a-t представляет собой прямую линию с отрицательным наклоном, ускорение уменьшается равномерно.
a
tÆ
4) График ускорение-время дает мгновенное значение ускорения в любой момент времени.
5) Площадь под графиком a-t дает значение изменения скорости за данный интервал времени.
Bridge Course – Phy – I PUC ‐ 38 ‐
8.
2.1 Вопросы:
1. Может ли смещение частицы быть равным нулю?
2. Что показывает спидометр в автомобиле: среднюю скорость или мгновенную скорость?
3. Может ли ускорение быть отрицательным?
4.В каком направлении направлена буква «g»?
5.Можно ли реализовать движение тела, в котором скорость и ускорение
направлены противоположно?
6.Может ли быть равна нулю скорость частицы, но не ее ускорение?
7. Различают среднюю скорость и среднюю скорость?
8.Что представляет наклон на графике положение-время?
9.Что представляет площадь под графиком скорость-время?
10.

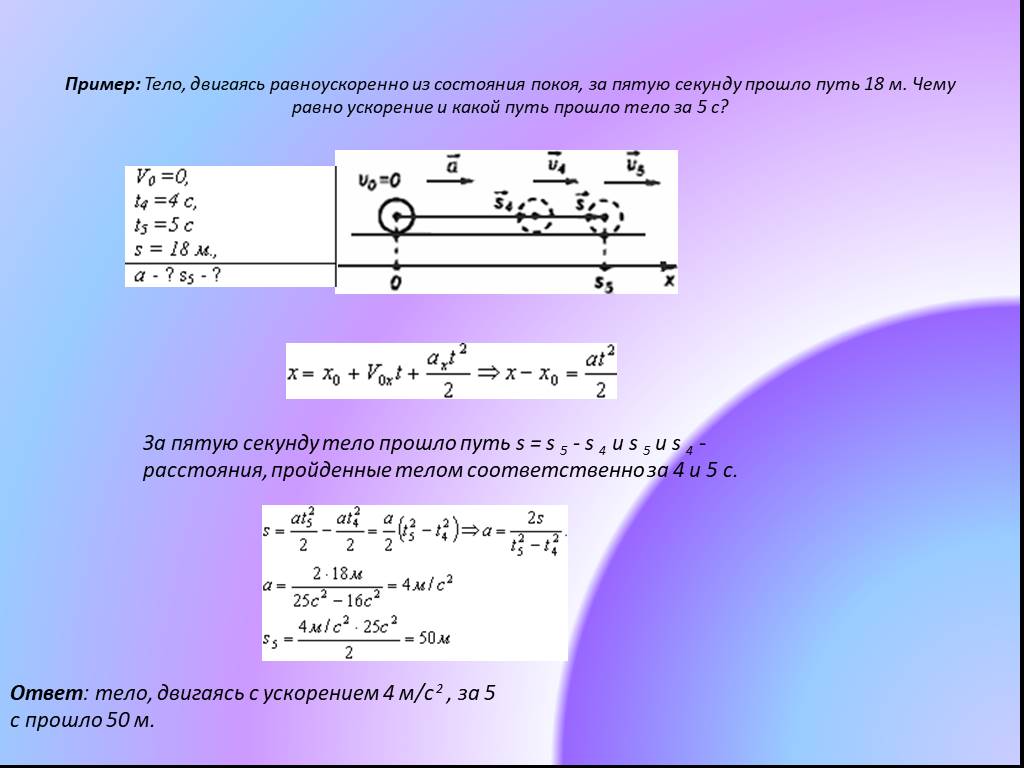 На графике
представлена зависимость проекции
скорости автомобиля от времени.
На графике
представлена зависимость проекции
скорости автомобиля от времени.
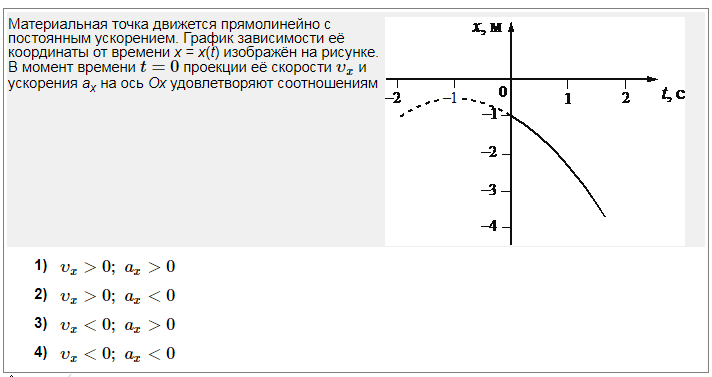 Модуль ускорения
максимален в интервале времени
Модуль ускорения
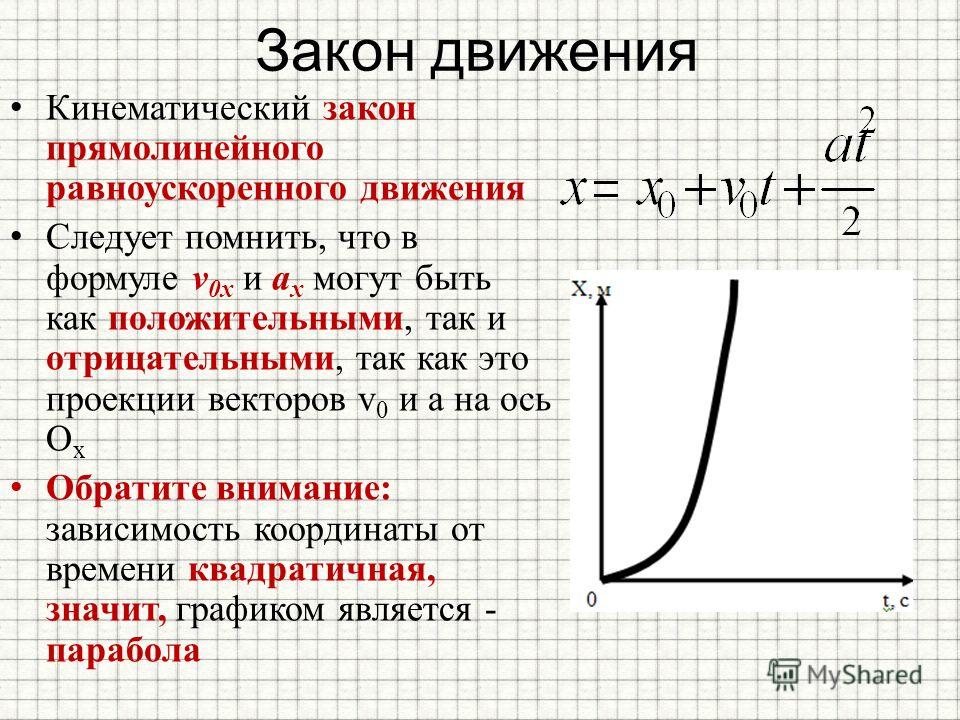
максимален в интервале времени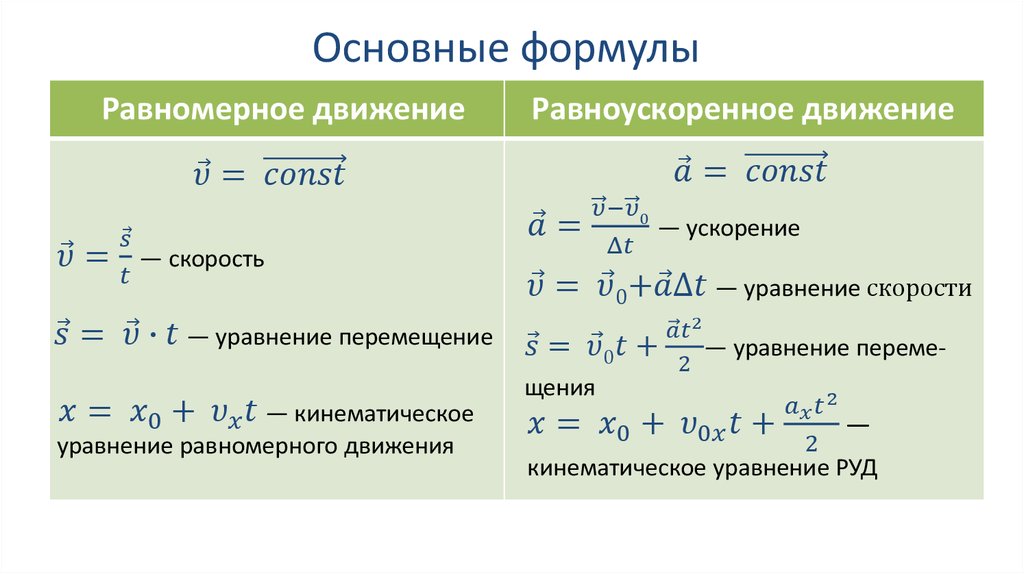 Проекция
ее скорости на вертикальное направление
меняется со временем согласно графику
на рисунке. В какой момент времени
стрела достигла максимальной высоты?
Проекция
ее скорости на вертикальное направление
меняется со временем согласно графику
на рисунке. В какой момент времени
стрела достигла максимальной высоты?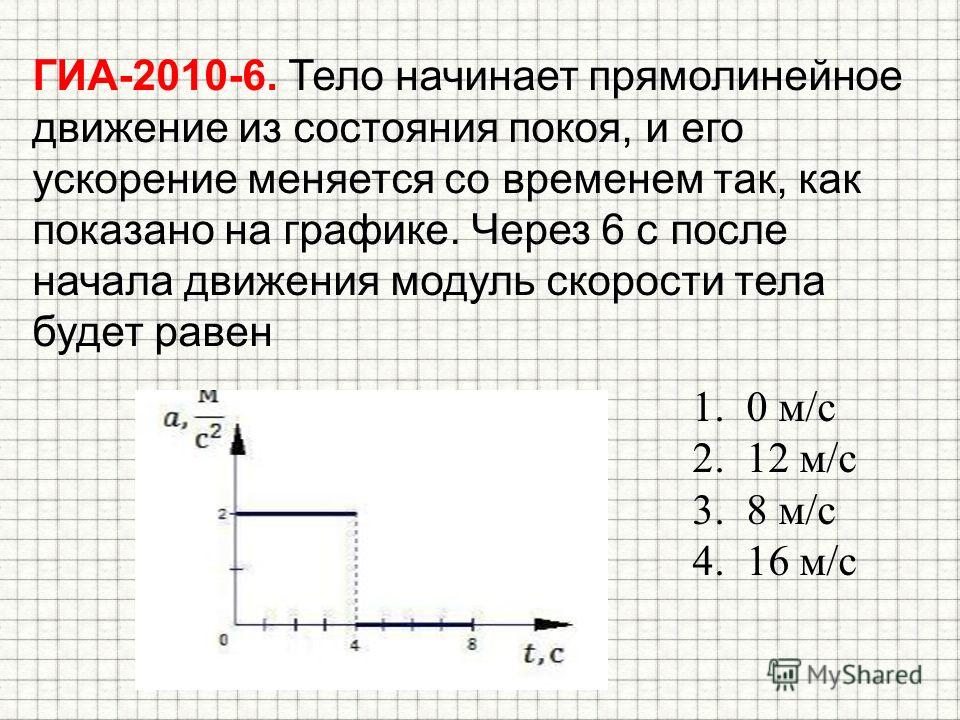


 Через 2 с
ускорение тела равно
Через 2 с
ускорение тела равно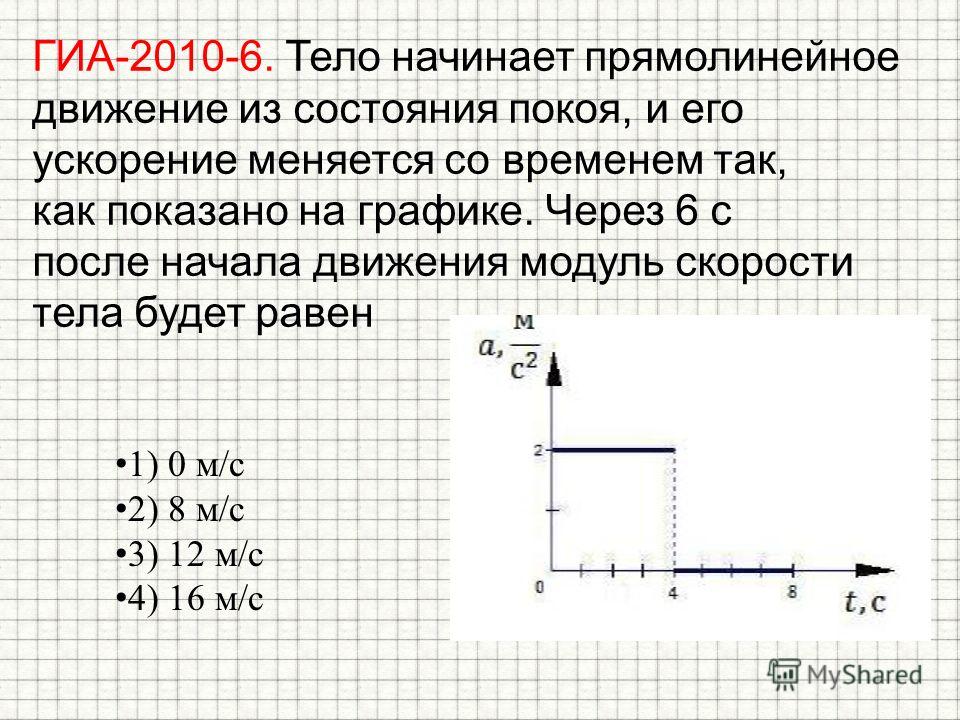 Путь, пройденный телом за 1
с, равен
Путь, пройденный телом за 1
с, равен Какое тело прошло наименьший путь за
3 с?
Какое тело прошло наименьший путь за
3 с? Каков путь, пройденный
телом к моменту времени t = 4 c?
Каков путь, пройденный
телом к моменту времени t = 4 c? Какое перемещение совершило
тело к моменту времени t = 6 с?
Какое перемещение совершило
тело к моменту времени t = 6 с?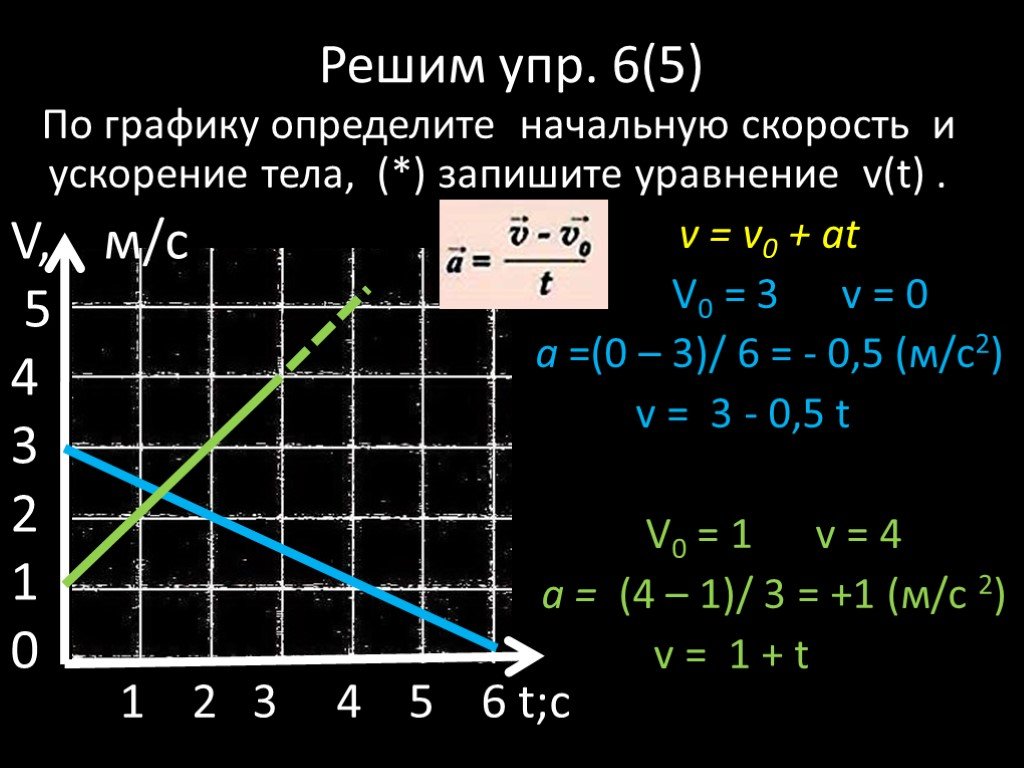 В каком интервале времени велосипедист
не двигался?
В каком интервале времени велосипедист
не двигался?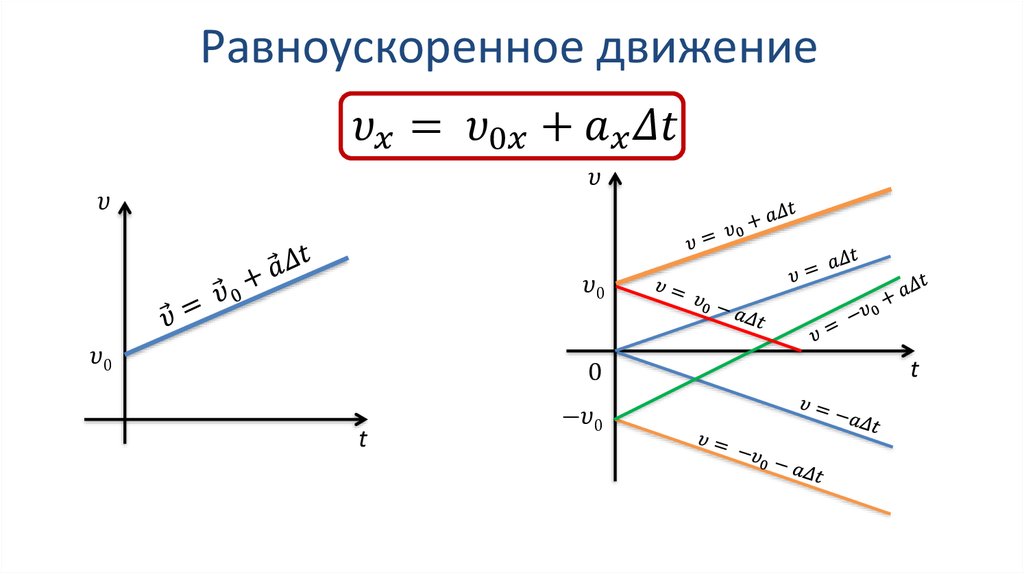 Как изменялась скорость тела в
промежуток времени от 0 до 5 с?
Как изменялась скорость тела в
промежуток времени от 0 до 5 с?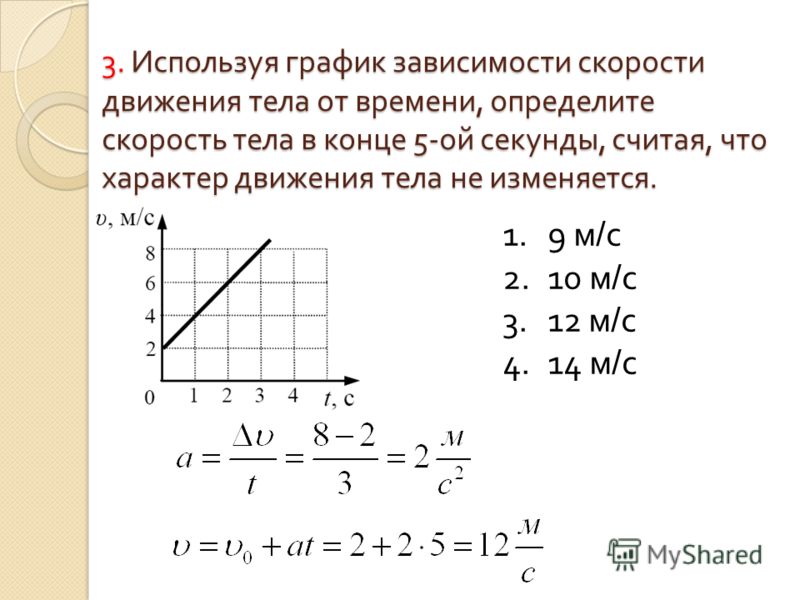 Сравните скорости
, и тела в моменты времени
.
Сравните скорости
, и тела в моменты времени
.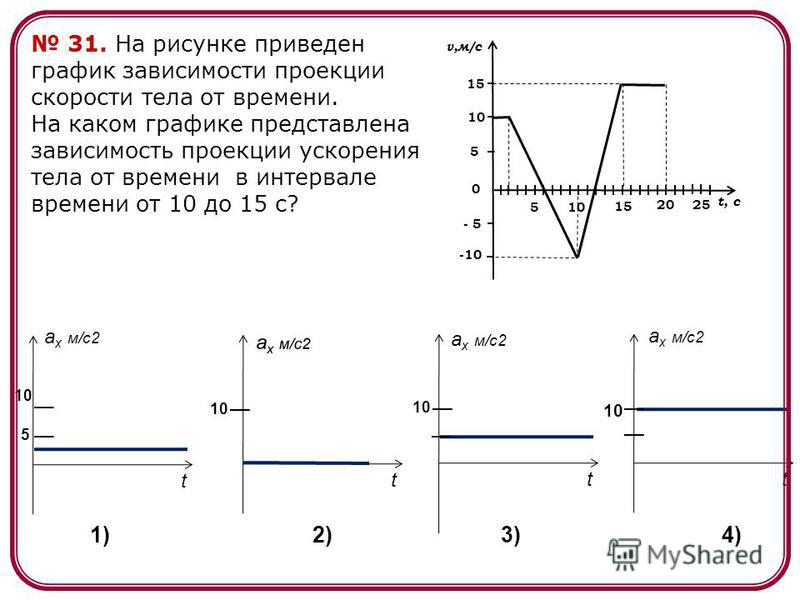 Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна скорость автобуса
на пути из Б в А?
Пункт А находится в точке х = 0, а пункт В — в точке х = 30 км. Чему равна скорость автобуса
на пути из Б в А? Пункт А находится в точке х = 0, а
пункт В — в точке х = 30 км. Чему равна минимальная скорость
автобуса на всем пути следования туда
и обратно?
Пункт А находится в точке х = 0, а
пункт В — в точке х = 30 км. Чему равна минимальная скорость
автобуса на всем пути следования туда
и обратно?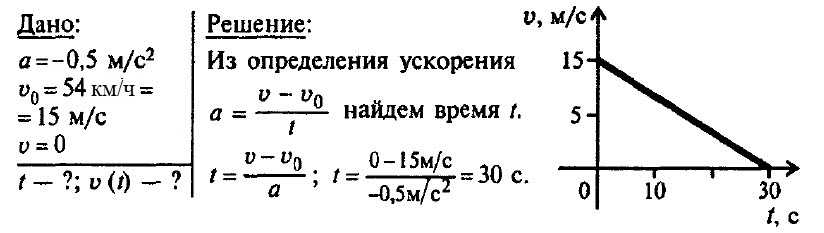 Выберите один верный ответ
Выберите один верный ответ Во время подъема на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 43,2 км/ч до 7,2 км/ч. При этом модуль ускорения был равен
Во время подъема на горку скорость санок, двигавшихся прямолинейно и равноускоренно, за 4 с изменилась от 43,2 км/ч до 7,2 км/ч. При этом модуль ускорения был равен 7
7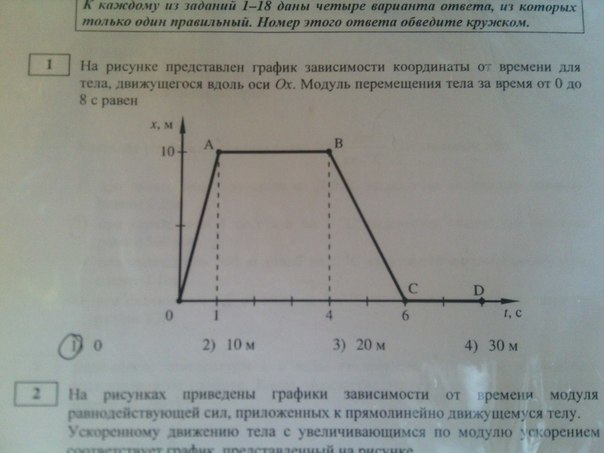
 Найдите положение автомобиля относительно городской черты через 30 с после прохождения им поста ГИБДД.
Найдите положение автомобиля относительно городской черты через 30 с после прохождения им поста ГИБДД. В’
= v + a (t’ – t ) ———-(1)
В’
= v + a (t’ – t ) ———-(1)

 nd уравнение движения.
nd уравнение движения.
 »
»
Leave A Comment