Тело бросили с поверхности Земли под углом α к горизонту. Если время его полета равно 2 с, а
ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА, НУЖНО РЕШИТЬ С ДАНО И РЕШЕНИЕМ Вычислите, каким сопротивлением обладает нихромовый проводник длиной 600 см и площадью попе … речного сечения 0,75 мм² ? ( ƿ=110 ∙ 10-8 Ом∙м ).A) 8,88 Ом B) 88,8 Ом C) 8,8 Ом D) 0,888 Ом E) 0,0888 Ом
Здраствуйте! У Меня СОР Решите пожалуйста! 100 Баллов даю!
1. Напишите, какому агрегатному состоянию соответствует данное утверждение
1) Сохраняют объ
… ем, но легко меняют форму, молекулы расположены на расстояниях,
сравнимых с размером молекулы и перемещаются свободно друг относительно друга.
_________________________________ [1]
2) Не сохраняют объем и форму, молекулы находятся на больших расстояниях друг от друга,
практически не взаимодействуют друг с другом и движутся беспорядочно.
_____________________________________ [1]
3) Сохраняют объем и форму, молекулы расположены в строгом порядке, сильно
взаимодействуют друг с другом и колеблются около определенных положений.

Общее сопротивление участка цепи АВ 8 Ом. Определите сопротивление второго проводника. Какова сила тока в участке цепи АВ? Вольтметр показывает 4 В.
| Движение тела, брошенного горизонтально или под углом к горизонту. | |
| |
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное. | |
Движение тела, брошенного горизонтально. | |
Выразим проекции скорости и координаты через модули векторов.
| |
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y: — между координатами квадратичная зависимость, траектория – парабола! | |
Движение тела, брошенного под углом к горизонту. | |
Порядок решения задачи аналогичен предыдущей. Решим задачу для случая х0=0 и y0=0. | |
. Мы получили квадратичную зависимость между координатами. | |
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0. Следовательно, для решения этой задачи необходимо решить уравнение . Оно будет иметь решение при t=0 (начало движения) и |
|
Зная время полета, найдем максимальное расстояние, которое пролетит тело: | Дальность полета:
|
Из этой формулы следует, что: — максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450; — на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории. | |
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело. | Время подъема: |
Тогда: | Максимальная высота:
|
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна | |
Угол, под которым направлен вектор скорости в любой момент времени: | |
Задачи тело брошенное под углом к горизонту
Движение тела, брошенного под углом к горизонту
Основные формулы криволинейного движения
1. Скорость движения материальной точки
где (vec r) – радиус-вектор точки.
2. Ускорение материальной точки
где (a_< au>) – тангенциальное ускорение, (a_n) – нормальное ускорение.
3. Тангенциальное ускорение
4. Нормальное ускорение
где (R) – радиус кривизны траектории.
5. для равнопеременного движения
Выразив из второго равенства (t) и подставив в первое, получим полезную формулу
Примеры решения задач
В задачах о движении тела в поле силы тяжести будем полагать (a=g=9.8) м/с 2 .
Задача 1.
Снаряд вылетает из орудия с начальной скоростью 490 м/с под углом 30 0 к горизонту. Найти высоту, дальность и время полета снаряда, не учитывая его вращение и сопротивление воздуха.
Решение задачи
Свяжем ИСО с орудием.
Составляющие скорости по осям Ox и Oy в начальный момент времени равны:
(V_<0x>=V_0cosalpha) – остается неизменной во все время полета снаряда,
(V_<0y>=V_0sinalpha) – меняется согласно уравнению равнопеременного движения
В наивысшей точке подъема (V_y=V_0sinalpha-gt_1=0) , откуда
Полное время полета снаряда
Высоту подъема снаряда определим из формулы пути равно замедленного движения
Дальность полета определим как
Задача 2.
Из точки А свободно падает тело. Одновременно из точки В под углом (alpha) к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Показать, что угол (alpha) не зависит от начальной скорости (V_0) тела, брошенного из точки В, и определить этот угол, если (frac
Решение задачи.
Свяжем ИСО с точкой В.
Оба тела могут встретиться на линии ОА (см. рис.) в точке С. Разложим скорость (V_0) тела, брошенного из точки В, на горизонтальную и вертикальную составляющие:
Пусть от начала движения до момента встречи пройдет время
За это время тело из точки А опуститься на величину
а тело из точки В поднимется на высоту
Решая последние два уравнения совместно, находим
Подставляя сюда ранее найденное время, получим
т.е. угол бросания не зависит от начальной скорости.
Задача 3.
С башни брошено тело в горизонтальном направлении со скоростью 40 м/с. Какова скорость тела через 3 с после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?
Какова скорость тела через 3 с после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?
Решение задачи.
Дано: (V_0=40) м/с. (t=3) c.
Свяжем ИСО с башней.
Тело одновременно участвует в двух движениях: равномерно в горизонтальном направлении со скоростью (V_0) и в свободном падении со скоростью (V_y=gt) . Тогда полная скорость тела есть
Направление вектора скорости определяется углом (alpha) . Из рисунка видим, что
Задача 4.
Два тела брошены вертикально вверх из одной точки одно вслед за другим с интервалом времени, равным (Delta) , с одинаковыми скоростями (V_0) . Через какое время (t) после бросания первого тела они встретятся?
Решение задачи.
Из анализа условия задачи, ясно, что первое тело поднимется на максимальную высоту и на спуске встретится со вторым телом. Запишем законы движения тел:
В момент встречи (h_1=h_2) , откуда сразу получаем
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Принцип решения этих задач заключается в разложении скорости свободно падающего тела на две составляющие – горизонтальную и вертикальную. Горизонтальная составляющая скорости постоянна, вертикальное движение происходит с ускорением свободного падения g=9.8 м/с 2 . Также может применяться закон сохранения механической энергии, согласно которому сумма потенциальной и кинетической энерги тела в данном случае постоянна.
Материальная точка брошена под углом к горизонту с начальной скоростью 15 м/с. Начальная кинетическая энергия в 3 раза больше кинетической энергии точки в верхней точке траектории. На какую высоту поднималась точка?
Тело брошено под углом 40 градусов к горизонту с начальной скоростью 10 м/с.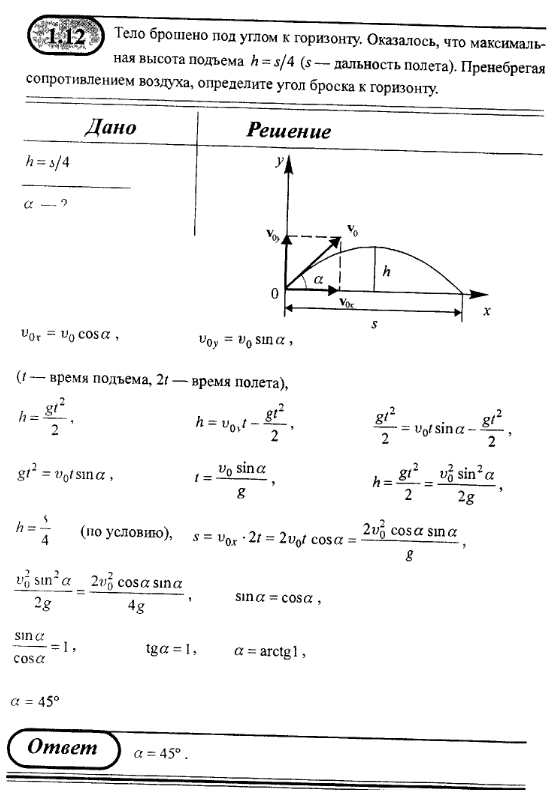 Найти расстояние, которое пролетит тело до падения, высоту подъема в верхней точке траектории и время в полете.
Найти расстояние, которое пролетит тело до падения, высоту подъема в верхней точке траектории и время в полете.
Тело брошено с башни высотой H вниз, под углом α к горизонту, с начальной скоростью v. Найти расстояние от башни до места падения тела.
Тело массой 0,5 кг брошено с поверхност Земли под углом 30 градусов к горизонту, с начальной скоростью 10 м/с. Найти потенциальную и кинетическую энергии тела через 0,4 с.
Материальная точка брошена вверх с поверхности Земли под углом к горизонту с начальной скоростью 10 м/с. Определить скорость точки на высоте 3 м.
Тело брошено вверх с поверхности Земли под углом 60 градусов с начальной скоростью 10 м/с. Найти расстояние до точки падения, скорость тела в точке падения и время в полете.
Тело брошено вверх под углом к горизонту с начальной скоростю 20 м/с. Расстояние до точки падения в 4 раза больше максимальной высоты подъема. Найти угол, под которым брошено тело.
Тело брошено с высоты 5 м под углом 30 градусов к горизонту с начальной скоростью 22 м/с. Найти дальность полета тела и время полета тела.
Найти дальность полета тела и время полета тела.
Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью 30 м/с. Найти тангенциальное и нормальное ускорения тела через 1с после броска.
Тело брошено с поверхности Зесли под углом 30 градусов к горизонту с начальной скоростью 14,7 м/с. Найти тангенциальное и нормальное ускорения тела через 1,25с после броска.
Тело брошено под углом 60 градусов к горизонту с начальной скоростью 20 м/с. Через какое время угол между скоростью и горизонтом станет равным 45 градусов?
Мяч, брошенный в спортзале под углом к горизонту, с начальной скоростью 20 м/с, в верхней точке траектории коснулся потолка на высоте 8м и упал на некотором расстоянии от места броска. Найти это расстояние и угол, под которым брошено тело.
Тело, брошеное с поверхности Земли под углом к горизонту, упало через 2,2с. Найти максимальную высоту подъема тела.
Камень брошен под углом 30 градусов к горизонту.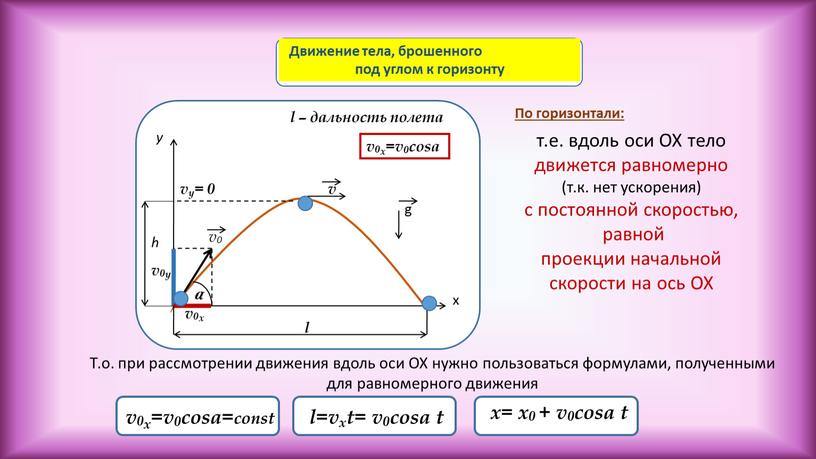 На некоторой высоте камень побывал дважды – через время 1с и 3 с после броска. Найти эту высоту и начальную скорость камня.
На некоторой высоте камень побывал дважды – через время 1с и 3 с после броска. Найти эту высоту и начальную скорость камня.
Камень брошен под углом 30 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние от точки бросания до камня через 4 с.
Снаряд выпущен в момент, когда самолет пролетает над орудием, под углом к горизонту с начальной скоростью 500 м/с. Снаряд поразил самолет на высоте 3,5 км через 10с после выстрела. Какова скорость самолета?
Ядро массой 5 кг брошено с поверхности Земли под углом 60 градусов к горизонту. На разгон гири потрачена энергия 500Дж. Определить дальность полета и время в полете.
Тело брошено с высоты 100м вниз под углом 30 градусов к горизонту с начальной скоростью 5 м/с. Найти дальность полета тела.
Тело массой 200г, брошеное с поверхности Земли под углом к горизонту, упало на расстоянии 5м через время 1,2с. Найти работу по броску тела.
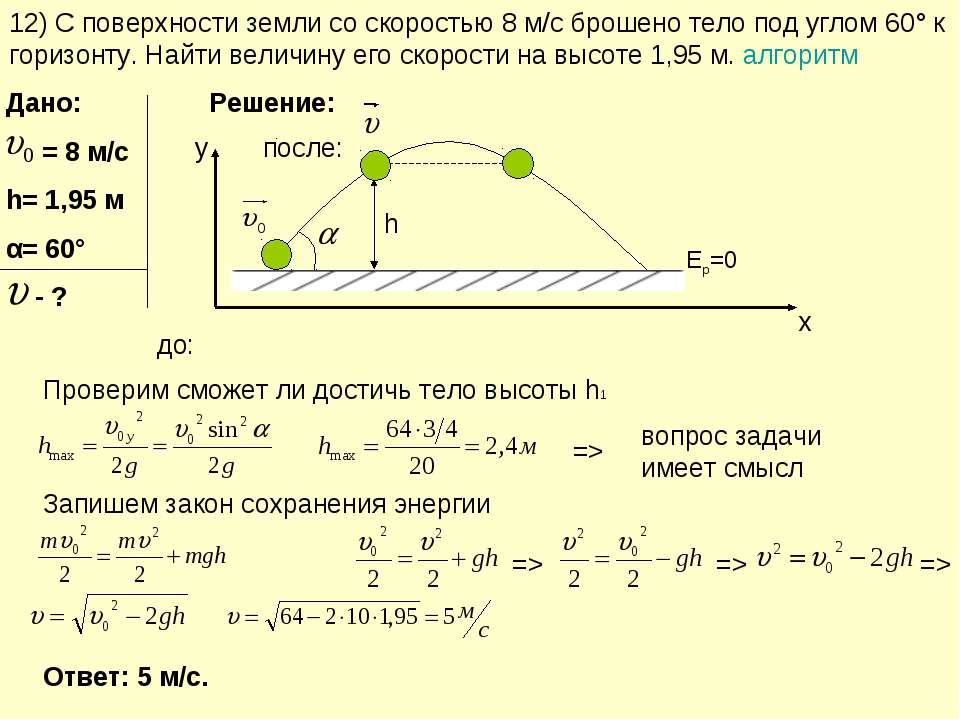
1.Тело бросили с поверхности Земли под углом= 60к горизонту с начальной скоростью v= 20 м/с.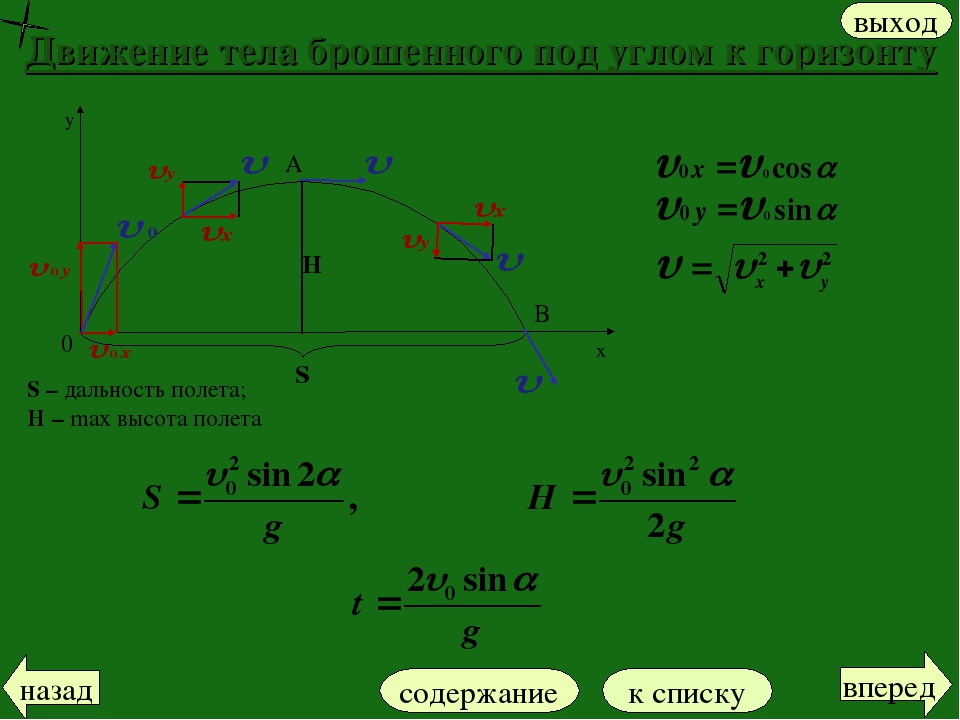 Пренебрегая сопротивлением воздуха, найти:
Пренебрегая сопротивлением воздуха, найти:
а) скорость тела через t= 2 с после начала движения;
б) время t1, через которое скорость будет составлять с горизонтом угол= 30;
в) время полета тела Тдо падения на Землю;
г) максимальную высоту подъема Ни дальность полетаL;
д) уравнение траектории y(x), гдеxиy– координаты тела.
а) Выбираем систему отсчетаxy,показанную на рисунке. По своему характеру данное движение есть движение с постоянным ускорениемПоэтому закон изменения скорости с течением времени имеет вид:
Найдем проекции вектора скорости на оси координат, спроектировав это уравнение на оси xиy:
Из связи между модулем вектора и его проекциями на декартовые оси получим:
б) Если - угол между вектором скорости и горизонтальной осью в некоторый момент времениt1, то:
в) Запишем закон движения тела в векторном виде, учтя, что в начальный момент тело находилось в начале координат.
(1)
Здесь – радиус-вектор тела в момент времениt.
Спроектируем это уравнение на ось y:
(2)
Найдем время полета тела Тиз условия, что в этот момент координатаy= 0:
Один из корней полученного уравнения Т1= 0 соответствует начальному положению тела, другой корень дает время полета тела:
г) Спроектируем уравнение (1) на ось x:
Найдем дальность полета тела Lиз условия L = x(T) :
(3)
Для того, чтобы определить максимальную высоту подъема Н, найдем время полета тела в наивысшую точку траектории из условия, что в этот момент времениТвектор скоростинаправлен горизонтально и, следовательно, проекция скорости на осьyvy= 0, т.е.
Заметим, что время подъема Т равно половине времени полетаТ. Следовательно, время подъема равно времени спуска.
д) Закон движения в координатной форме, определяемый соотношениями (2) и (3), по существу задает уравнение траектории через параметр t. Исключив этот параметр, получим уравнение траектории в явном виде:
(4)
Из (4) следует, что траектория тела, брошенного под углом к горизонту, представляет собой параболу, ветви которой направлены вниз (коэффициент при x 2 отрицателен). Парабола проходит через начало координат (один из корней уравненияy(x) = 0 равен нулю).
2.Самолет летит на высотеh= 500 м по горизонтальной прямой со скоростью v= 100 м/с. Летчик должен сбросить бомбу в цель, лежащую впереди самолета. Под каким угломк вертикали он должен видеть цель в момент сбрасывания бомбы?
Решение.Движение бомбы можно рассматривать как наложение двух движений, одно из которых происходит по горизонтали с постоянной скоростью v, а другое представляет собой свободное падение с нулевой начальной скоростью (см.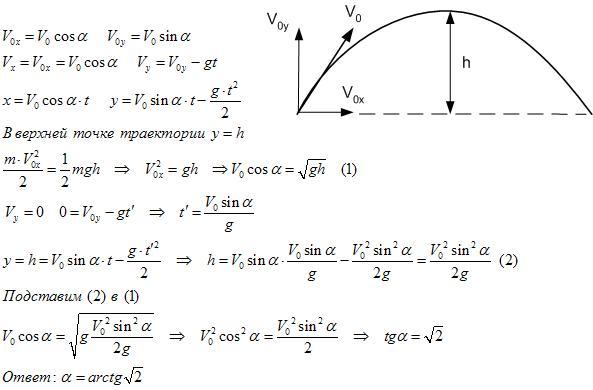 рис.).
рис.).
Искомый угол определяется очевидным соотношением:
где l– дальность полета по горизонтали. Эта величина равнаl= vt, гдеt– время полета бомбы находится из условия
;
3.Под каким угломк горизонту следует бросить камень со скоростьюv = 20 м/с, чтобы он пролетел по горизонтали до падения на землю расстояние? Сопротивление воздуха пренебречь.
Решение.Запишем соотношение между дальностью полетаL, начальной скоростьюv, угломи ускорением свободного паденияg(см.(3) задачи 1 этого раздела):
Здесь n– целые числа, значения которых найдем из очевидного условия:
Пусть n= 0. ТогдаПриn= 1
При других значениях nугол > 90. Итак, искомые углы равны:
4.Камень бросили горизонтально с большой высоты со скоростьюм/с. Определить черезс:
а) скорость камня и модуль приращения вектора его скорости;
б) модуль вектора перемещения камня.
Решение.а) В соответствии с выражением (1.12) скорость камня равна
,
где – ускорение свободного падения. Найдём построением скорость(см. рис.). Из полученного треугольника скоростей находим:
м/с.
По определению им/с.
б) Вектор перемещения равен
,
где , а, а его модуль
м.
Движение тела, брошенного под углом к горизонту. 10 класс, готовимся к олимпиадам.
Предлагаю задачи, связанные с движением тела, брошенного под углом к горизонту. Также при решении часто нужно иметь понятие об относительности движения, ведь, если оба тела падают, то почему не перейти в падающую систему отсчета?
Задача 1. Игрушечная пушка установлена на краю стола. Из нее можно стрелять с одинаковой начальной скоростью маленькими шариками в любом направлении. Шарики взрываются в воздухе через время с после выстрела. На расстоянии м от пушки, под углом к горизонту, висит воздушный шар. Под каким углом к горизонту надо стрелять, чтобы шарики разрывались как можно ближе к шару? Сопротивлением воздуха пренебречь. Ускорение свободного падения м/с В ответе выразить тангенс искомого угла, округлив до десятых.
Ускорение свободного падения м/с В ответе выразить тангенс искомого угла, округлив до десятых.
К задаче 1
Решение.
Перейдем в систему отсчета, которая в момент выстрела начинает двигаться вниз с ускорением без начальной скорости. В этой системе отсчета снаряд летит по прямой с постоянной скоростью шар поднимается вверх без начальной скорости с ускорением а время до взрыва, расстояние от точки взрыва до шара и угол между начальной скоростью снаряда и горизонтом такие же, как в системе отсчета, связанной с Землей.
Точка взрыва снаряда ввиду произвольности выбора направления выстрела находится на окружности с центром в точке где изначально находилась пушка, и радиусом (на рисунке она показана красным цветом). Ближайшая к конечному положению шара точка этой окружности лежит на отрезке то есть стреляющие должны целиться в точку, находящуюся на высоте над начальным положением шара.
Пояснение к решению
Тангенс угла , под которым следует стрелять, легко определить из рисунка:
Ответ: 3,7.
Задача 2. Небольшой мяч, брошенный с поверхности земли, через с упруго ударился о вертикальную стену дома и через с упал на землю. На какой высоте находится место удара? Ответ дать в метрах, округлив до целых. Ускорение свободного падения м/с
Решение.
В момент удара вертикальная скорость не изменяется. Воспользуемся принципом обратимости движения. Рассмотрим полет с высоты точки удара двух тел с одинаковыми вертикальными начальными скоростями. Одно тело за меньшее время летит на землю вниз, а другое с начальной скоростью вверх. Уравнения изменения вертикальной координаты тел будут выглядеть как и где — вертикальная составляющая начальной скорости.
Сложим уравнения, предварительно разделив на время. Получим
Ответ: 6 м.
Задача 3. С самолета, летящего на высоте м со скоростью км/ч, выпал груз. На какой высоте скорость груза будет направлена под углом 60 к горизонту? Ускорение свободного падения м/с Ответ дать в метрах, округлив до целых.
Решение.
Найдем время, через которое скорость будет направлена по углом 60 Воспользуемся векторным треугольником скоростей, из которого следует
Тогда высота, на которой окажется груз, равна
Подставляя время из первого уравнения во второе, получим м.
Ответ: 225 м.
Задача 4. Два камня расположены на одной горизонтали на расстоянии м друг от друга. Один камень бросают вертикально вверх со скоростью м/с, а второй одновременно бросают горизонтально по направлению к первому камню со скоростью м/с. Чему равно наименьшее расстояние между камнями в процессе движения? Ответ дать в метрах, округлив до целых.
Решение.
Задачу на совместное движение двух свободно падающих тел удобно решать в падающей с ускорением системе отсчета одного из камней. Например, пересядем в систему отсчета камня, летящего вверх. Тогда второй камень будет двигаться равномерно и прямолинейно со скоростью м/с. Наименьшее расстояние между камнями равно длине перпендикуляра, опущенного из точки, где находится «неподвижный» камень, на линию движения «подвижного».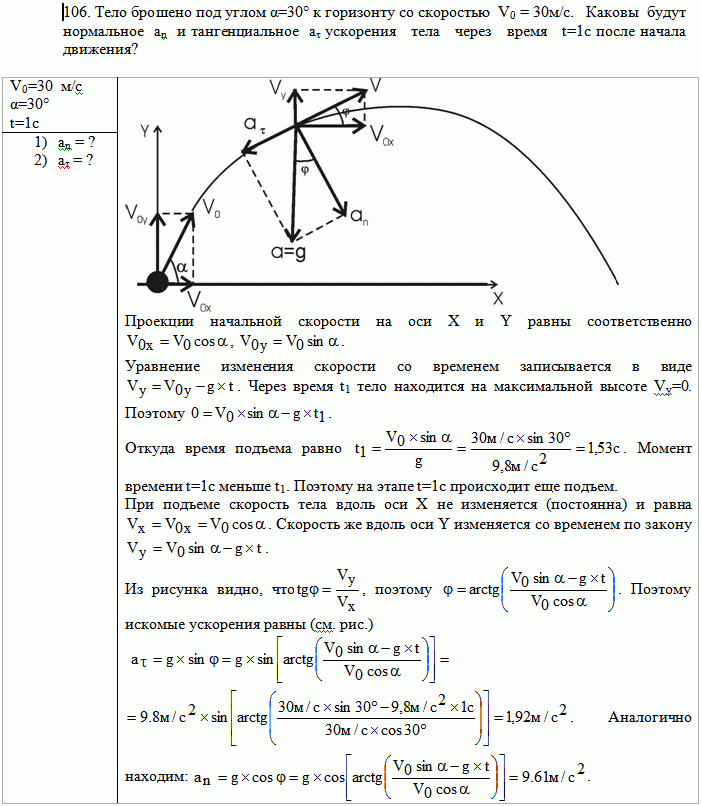 Следовательно,
Следовательно,
Ответ: 12 м.
Задача 5. Из двух точек, находящихся на расстоянии м друг от друга, одновременно бросили навстречу друг другу под углом к горизонту и два тела. При падении тела меняются местами. Чему равна относительная скорость одного тела относительно другого в момент, когда они находятся на одной вертикальной прямой? Ответ дать в м/с, округлив до целых. Считать, что м/с Сопротивлением воздуха пренебречь.
Решение.
Так как дальности полетов тел равны, а углы, под которыми они брошены к горизонту, дополняют друг друга до 90 то начальные скорости также равны по величине. Это можно доказать, используя формулу для дальности полета:
Так как то из предыдущего соотношения в силу того, что получим, что
Значение начальной скорости также можно получить из уравнения для дальности полёта
Получаем, что Зависимости скоростей обоих тел от времени имеют вид
Для определенности перейдем в систему отсчета, связанную с первым телом. Тогда из закона сложения скоростей получим, что скорость второго тела относительно первого равна Она, очевидно, не зависит от времени. Нарисовав рисунок, перенеся в одну точку вектора начальных скоростей и вычтя их, получим, что относительная скорость равна
Тогда из закона сложения скоростей получим, что скорость второго тела относительно первого равна Она, очевидно, не зависит от времени. Нарисовав рисунок, перенеся в одну точку вектора начальных скоростей и вычтя их, получим, что относительная скорость равна
Замечание: неважно, в какой системе отсчёта (первого или второго тела) вычислять относительную скорость — ее величина всё равно будет одной и той же. Можете убедиться в этом сами, сделав расчет еще раз в системе отсчёта второго тела.
Ответ: 15 м/с.
3.1 Свободное движение тела, брошенного под углом: задачи с ответами
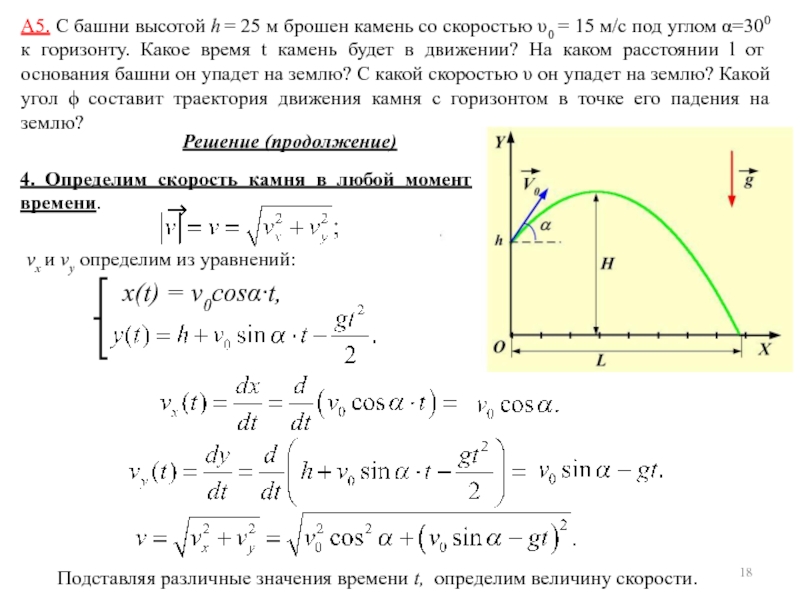
(Все задачи по кинематике и ответы к ним находятся также в zip-архиве (332 кб), который можно скачать и открыть на своем компьютере. Попробуйте решить все задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)3.1. С башни высотой 45 м горизонтально брошен камень со скоростью 10 м/с. На каком расстоянии от башни он упадет на землю? [35 м]
3. 2. Тело, брошенное под углом 45° к горизонту, через 2 c имело вертикальную составляющую скорости 10 м/с. Определить дальность полета тела. [180 м; 20 м]
2. Тело, брошенное под углом 45° к горизонту, через 2 c имело вертикальную составляющую скорости 10 м/с. Определить дальность полета тела. [180 м; 20 м]
3.3. Тело брошено со скоростью 10 м/с под углом 60° к горизонту. Определить скорость тела в верхней точки траектории. [5 м/с]
3.4. В мишень с расстояния 20 м сделано два выстрела при горизонтальной наводке винтовки. Скорость первой пули 100 м/с, а второй — 200 м/с. Определить расстояние между пробоинами в мишени. [15 см]
3.5. Камень, брошенный под углом к горизонту, упал на землю через 2 c. Чему равна дальность полета камня, если за время полета его максимальная скорость была вдвое больше минимальной? [12 м]
3.6. Тело брошено горизонтально со скоростью 4 м/с. При этом оказалось, что дальность его полета равна высоте бросания. С какой высоты бросили тело? [3,2 м]
3.7. С вышки бросили камень в горизонтальном направлении. Через 10 c он упал на расстоянии 50 м от вышки. Определить начальную скорость камня. [5 м/с]
Через 10 c он упал на расстоянии 50 м от вышки. Определить начальную скорость камня. [5 м/с]
3.8. Из горизонтально установленной винтовки стреляют в мишень, расположенную на расстоянии 300 м от винтовки. При этом пуля попадает в центр мишени. На сколько нужно передвинуть мишень по горизонтали, чтобы пуля попала в нее на 25 см выше центра? Скорость вылета пули 600 м/с. [31 м]
3.9. Камень брошен горизонтально со скоростью 15 м/с. Через какое время вектор его скорости будет направлен под углом 45° к горизонту? [1,5 c]
3.10. Камень брошен под углом 45° к горизонту со скоростью 10 м/с. Через какое время вектор его скорости будет направлен под углом 30° к горизонту? [0,3 c; 1,1 c]
3.11. Тело с высоты 4 м бросают в горизонтальном направлении так, что оно подлетает к земле под углом 45°. Какое расстояние по горизонтали пролетело тело? [8 м]
3.12. С обрыва в горизонтальном направлении бросают камень со скоростью 27 м/с. Через какое время касательное ускорение камня будет равно нормальному? [2,7 c]
Через какое время касательное ускорение камня будет равно нормальному? [2,7 c]
3.13. Миномет установлен на расстоянии 8000 м от вертикального обрыва высотой 105 м. Как близко к основанию обрыва (рисунок слева) могут «подобраться» мины, если их начальная скорость 300 м/с? [15 м]
3.14. Тело брошено со скоростью vo, под углом α к горизонту. Определить радиус кривизны траектории в точке бросания и в точке максимального подъема.
| Ответ к задаче 3.14: R1 = | vo2 | ; R2 = | vo2cos α | . |
| gcos α | g |
3.15. Тело брошено под углом к горизонту. При каком угле бросания радиус кривизны траектории в точке максимального подъема будет равен высоте этой точки? [54,7°]
3.16. На какое максимальное расстояние можно бросить мяч в спортивном зале высотой 8 м, если начальная скорость мяча 20 м/с? Рассмотреть случай H = 15 м? [39 м; 39°; 40 м]
3. 17. Какую максимальную площадь можно полить из шланга, если скорость воды на выходе из шланга 10 м/с? [314 м2]
17. Какую максимальную площадь можно полить из шланга, если скорость воды на выходе из шланга 10 м/с? [314 м2]
3.18. С вершины горы горизонтально брошен камень, который упал на расстоянии L от вершины. С какой скоростью бросили камень, если склон горы составляет угол α с горизонтом?
| Ответ к задаче 3.18: vo = √ | gLcos2 α | . |
| 2sin α |
3.19. Тело, брошенное со скоростью 10 м/с под углом 60° к горизонту, дважды проходит высоту 1,6 м. На каком расстоянии находятся точки прохождения этой высоты? [7 м]
3.20. Из шланга, лежащего на земле, под углом 45° к горизонту вытекает струя воды и падает на землю на расстоянии 10 м от шланга. Какая масса воды находится на высоте выше 2 м, если сечение выходного отверстия шланга 10 см2? [6,3 кг]
3. 21. Тело брошено с обрыва со скоростью vo под углом α к горизонту. Через какое время направление скорости тела станет перпендикулярным направлению начальной скорости?
21. Тело брошено с обрыва со скоростью vo под углом α к горизонту. Через какое время направление скорости тела станет перпендикулярным направлению начальной скорости?
| Ответ к задаче 3.21: t = | vo | . |
| gsin α |
3.22. Тело брошено со скоростью vo под углом α к горизонту. Через какое время радиус-вектор тела, проведенный из точки бросания, и вектор его скорости будут перпендикулярны?
| Ответ к задаче 3.22: t = | vo | (3sin α +− √(9sin2 α − 8)) | . |
| 2g |
3.23. Под каким углом к горизонту необходимо бросить тело, чтобы равенство его кинетической и потенциальной энергий достигалась в высшей точке траектории? [45°]
3.24. Тело брошено со скоростью vo под углом α к горизонту. На какой высоте кинетическая энергия тела будет равна потенциальной? [ h = vo2/(4g) при α ≥ 45°]
На какой высоте кинетическая энергия тела будет равна потенциальной? [ h = vo2/(4g) при α ≥ 45°]
Далее: следующие 23 задачи по свободному движению тела, брошенному под углом к горизонту. | Вернуться к списку разделов КИНЕМАТИКИ.
Физика 10 класс, школьный этап (1 этап), 2018-2019 учебный год
Содержание
- Задача 1
- Задача 2
- Задача 3
- Задача 4
- Задача 5
Задача 1
Автомобиль, едущий по шоссе с постоянной скоростью 54 км/ч, проезжает мимо второго автомобиля, стоящего на соседней полосе. В этот момент второй автомобиль трогается с места и начинает ехать за первым, двигаясь с постоянным ускорением 5 м/с2. За какое время второй автомобиль догонит первый? Какую скорость он будет иметь в момент, когда поравняется с первым? Автомобили считать материальными точками.
Возможное решение
Перемещения автомобилей с момента первой встречи до момента второй встречи равны.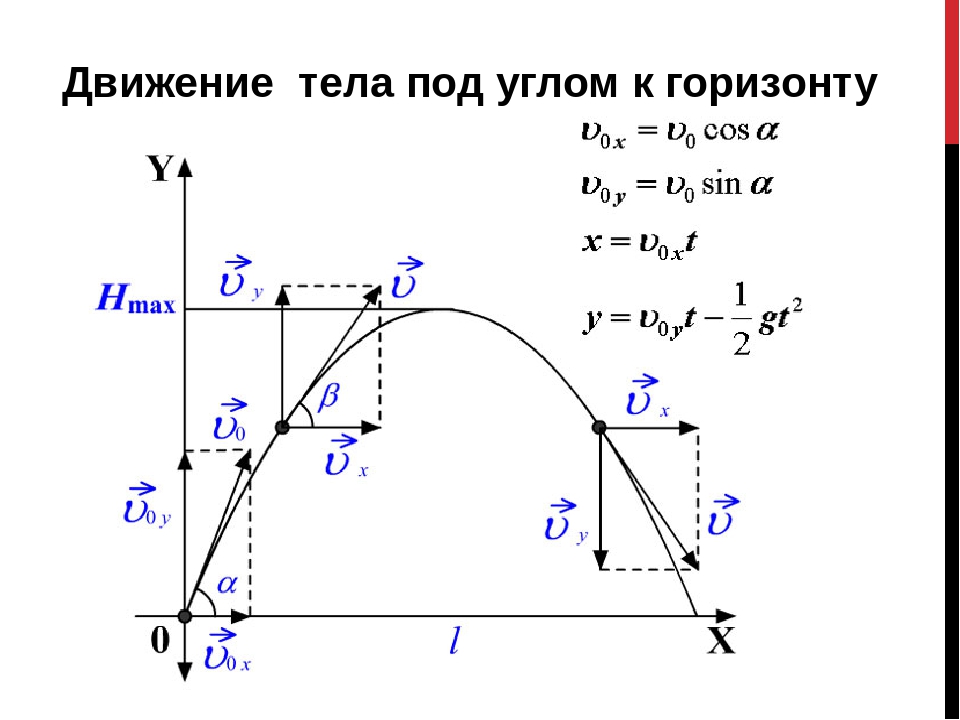 Пусть t – промежуток времени между встречами, S – модуль перемещения автомобилей за этот промежуток времени,
Пусть t – промежуток времени между встречами, S – модуль перемещения автомобилей за этот промежуток времени,
скорость первого автомобиля, a – ускорение второго автомобиля. Тогда:
Скорость второго автомобиля спустя время t равна:
Критерии оценивания
- Указано, что перемещения автомобилей между их встречами равны 2 балла
- Записано выражение для равенства перемещений 3 балла
- Найдено t 1 балл
- Записано выражение для V2 3 балла
- Найдено значение V2 1 балл
Максимум за задачу 10 баллов.
Задача 2
Полая металлическая сфера массой m и радиусом R всплывает со дна озера с постоянной скоростью. Груз какой массы нужно поместить внутрь сферы, чтобы она погружалась с такой же по модулю скоростью? Сила сопротивления, действующая на шар со стороны жидкости, зависит только от скорости шара относительно жидкости и направлена противоположно этой скорости. Плотность жидкости ρ, объём сферы равен V = (4/3)πR3
Плотность жидкости ρ, объём сферы равен V = (4/3)πR3
Возможное решение
При всплытии сферы с постоянной скоростью сумма сил, действующих на неё, равна нулю. Вертикально вниз действуют силы тяжести mg и сопротивления Fсопр , а вертикально вверх – сила Архимеда FАрх . При движении вниз с той же постоянной скоростью вертикально вниз действует сила тяжести (m + Δm)g, где Δm – масса добавленного груза, а вертикально вверх – такая же сила Архимеда FАрх , как в первом случае, и сила сопротивления Fсопр (неизменная по модулю в силу равенства модулей скоростей сферы относительно воды в обоих случаях). Таким образом:
Сложив уравнения, получим:
Критерии оценивания
- Указано, что силы Архимеда в обоих случаях равны 1 балл
- Указано, что силы сопротивления в обоих случаях равны по модулю и противоположны по направлению 2 балла
- Записаны уравнения для сил (по 3 балла за каждое) 6 балла
- Получено выражение для Δm 1 балл
Максимум за задачу 10 баллов.
Задача 3
Точечное тело бросают с поверхности Земли под некоторым углом к горизонту. Определите, при каких значениях этого угла кинетическая энергия тела в течение всего времени полёта будет больше его потенциальной энергии. Потенциальная энергия на поверхности Земли равна нулю; сопротивлением воздуха можно пренебречь.
Возможное решение
Пусть начальная скорость тела равна V0 , угол к горизонту, под которым бросают тело, равен α , масса тела – m.
Заметим, что максимальное значение потенциальной энергии достигается при максимальной высоте подъёма (в верхней точке траектории), а минимальное значение кинетической энергии достигается при минимальном значении скорости (также в верхней точке траектории). То есть, если в верхней точке траектории кинетическая энергия превышает потенциальную, то она превышает потенциальную и во всех других точках траектории.
Запишем это условие:
Критерии оценивания
- Указано, что максимальное значение потенциальной энергии достигается в верхней точке траектории тела 1 балл
- Указано, что минимальное значение кинетической энергии достигается в верхней точке траектории тела 1 балл
- Записано выражение для потенциальной энергии в верхней точке траектории 2 балла
- Записано выражение для кинетической энергии в верхней точке траектории 2 балла
- Получено условие для угла в неявном виде 2 балла
- Определены все значения a , при которых выполняется требуемое условие 2 балла
Максимум за задачу 10 баллов.
Задача 4
Идеальный вольтметр включён в цепь, схема которой изображена на рисунке. Цепь состоит из четырёх одинаковых резисторов сопротивлением R и батареи с напряжением ε = 9 В и нулевым внутренним сопротивлением. Найдите показания вольтметра.
Возможное решение
Пронумеруем резисторы, как показано на рисунке. Общее сопротивление резисторов 1, 2 и 3 равно
Полное сопротивление всей цепи равно
Сила тока, текущего через резистор 4, равна
Сопротивления участков цепи, включённых параллельно, относятся как 1:2. Следовательно, сила тока I12, текущего через резисторы 1 и 2, в два раза меньше, чем сила тока, текущего через резистор 3. Поэтому сила тока I12 составляет 1/3 часть от силы тока I, то есть
Таким образом, вольтметр показывает напряжение
Критерии оценивания
- Найдено общее сопротивление резисторов 1, 2 и 3 2 балла
- Найдено полное сопротивление всей цепи 1 балл
- Найдена сила тока I, текущего через резистор 4 1 балл
- Показано, что I12 = I3/2 2 балла
- Найдена сила тока I12, текущего через резистор 2 3 балла
- Найдены показания вольтметра 1 балл
Максимум за задачу 10 баллов.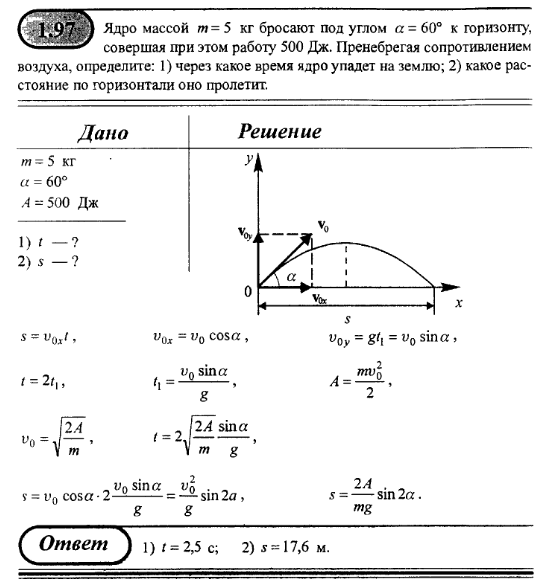
Задача 5
В частных домах иногда используют проточный водонагреватель, в случае если к дому не подведены трубы с горячей водой. Температура холодной воды, идущей из крана, равна 14 °С, а температура текущей из душа воды (которая «прошла» через нагреватель), равна 40 °С. Определите объёмный расход воды в душе (в литрах в минуту), если потребляемая мощность водонагревателя 5 кВт, а его КПД равен 80%. Удельная теплоёмкость воды 4200 (Дж)/кг ×°С, плотность воды 1000 кг/м3. При работе проточного водонагревателя вся втёкшая в него холодная вода подогревается и сразу же вытекает наружу.
Возможное решение
Введём обозначения: q – искомый объёмный расход воды, τ – время использования душа, ρ – плотность воды, с – удельная теплоемкость воды, t1 t2, – температуры воды до и после нагревания соответственно, η – КПД бойлера, N – мощность нагревателя. Запишем уравнение теплового баланса:
Критерии оценивания
- Записано уравнение теплового баланса 4 балла
- Получено выражение для объёмного расхода 4 балла
- Правильно вычислено значение объёмного расхода в л/мин 2 балла
Максимум за задачу 10 баллов.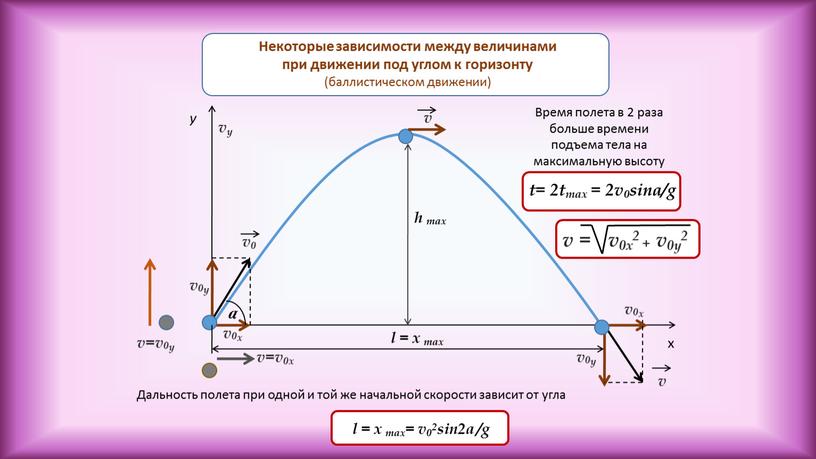
Всего за работу 50 баллов.
Статьи — Abitu.net
В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.
1. Векторный способ.
В этом способе положение материальной точки `A` задаётся с помощью так называемого радиус-вектора `vecr`, который представляет собой вектор, проведённый из точки `O`, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку `A` (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени `vecr=vecr(t)`.
Геометрическое место концов радиус-вектора `vecr(t)` называют траекторией точки `A`.
В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка `A` после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени `Delta t` тело (точка `A`) переместилось из начального положения `1` с радиус-вектором `vec r_1` в конечное положение `2` с радиус-вектором `vec r_2` (рис. 2). Приращение `Deltavec r` радиус-вектора тела в таком случае равно: `Deltavec r = vec r_2- vec r_1`.
Вектор `Deltavec r`, соединяющий начальное и конечное положения тела, называют перемещением тела.
Отношение `Delta vec r//Delta t` называют средней скоростью (средним вектором скорости) `vec v_»cp»` тела за время `Delta t`:
`vecv_»cp»=(Deltavecr)/(Delta t)` (1)
Вектор `vecv_»cp»` коллинеарен и сонаправлен с вектором `Deltavec r`, так как отличается от последнего лишь скалярным неотрицательным множителем `1//Delta t`.
Предложенное определение средней скорости справедливо для любых значений `Delta t`, кроме `Delta t=0`. Однако ничто не мешает брать промежуток времени `Delta t` сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени `t` или в конкретной точке траектории. С этой целью промежуток времени `Delta t` устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение `Delta vec r`. При этом отношение `Deltavec r//Delta t` стремится к определённому значению, не зависящему от `Delta t`.
Величина, к которой стремится отношение `Deltavec r//Delta t` при стремлении `Delta t` к нулю, называется мгновенной скоростью`vec v`:
`vec v =(Delta vec r)/(Delta t)` при `Delta t -> 0`.
Теперь заметим, что чем меньше `Delta t`, тем ближе направление `Deltavec r` к направлению касательной к траектории в данной точке. Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела.
В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости `vec v` тела (материальной точки).
Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его определяют через отношение приращения вектора скорости `Delta vec v` тела к промежутку времени `Delta t`, в течение которого это приращение произошло.
Ускорением `veca` тела называется величина, к которой стремится отношение `Delta vec v//Delta t` при стремлении к нулю знаменателя `Delta t`:
`vec a =(Delta vec v)/(Delta t)` при `Delta t -> 0` (2)
При уменьшении `Delta t` ориентация вектора`Delta vec v` будет приближаться к определённому направлению, которое принимается за направление вектора ускорения `vec a`. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!
Таким образом, зная зависимость `vec r(t)`, можно найти скорость `vec v` и ускорение $$ \overrightarrow{a}$$ тела в каждый момент времени. 2`).
2`).
2. Координатный способ.
В этом способе положение материальной точки `A` на плоскости в произвольный момент времени `t` определяется двумя координатами `x` и `y`, которые представляют собой проекции радиус-вектора $$ \overrightarrow{r}$$тела на оси `Ox` и `Oy` соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями `t`: $$ x=x\left(t\right)$$ и $$ y=y\left(t\right)$$. Если эти функции известны, то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости $$ \overrightarrow{v}$$ можно спроецировать на оси координат и определить таким образом скорости $$ {v}_{x}$$ и $$ {x}_{y}$$ изменения координат тела (рис. 4). В самом деле $$ {v}_{x}$$ и $$ {v}_{y}$$ будут равны значениям, к которым стремятся соответственно отношения `Delta x//Delta t` и `Delta y//Delta t` при стремлении к нулю промежутка времени `Delta t`.
Аналогично с помощью проецирования вектора $$ \overrightarrow{a}$$ определяются ускорения $$ {a}_{x}$$ и $$ {a}_{y}$$ тела по направлениям координатных осей. 2)`, а его направление может быть задано углом между этим вектором и любой осью координат. Так, угол $$ \alpha $$ между вектором $$ \overrightarrow{v}$$ и осью `Ox` определяется отношением `»tg»alpha=v_y//v_x`. Аналогичными формулами определяются модуль и направление вектора $$ \overrightarrow{a}$$.
2)`, а его направление может быть задано углом между этим вектором и любой осью координат. Так, угол $$ \alpha $$ между вектором $$ \overrightarrow{v}$$ и осью `Ox` определяется отношением `»tg»alpha=v_y//v_x`. Аналогичными формулами определяются модуль и направление вектора $$ \overrightarrow{a}$$.
Обратная задача – нахождение скорости и зависимостей $$ x\left(t\right)$$ и $$ y\left(t\right)$$ по заданному ускорению – будет иметь однозначное решение, если кроме ускорения заданы ещё и начальные условия: проекции скорости и координаты точки в начальный момент времени $$ t=0$$.
3. Естественный (или траекторный) способ.
Этот способ применяют тогда, когда траектория материальной точки известна заранее. На заданной траектории `LM` (рис. 5) выбирают начало отсчёта – неподвижную точку `O`, а положение движущейся материальной точки `A` определяют при помощи так называемой дуговой координаты `l`, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта `O` до точки `A`. При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.
При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.
Движение тела определено, если известны его траектория, начало отсчёта `O`, положительное направление отсчёта дуговой координаты `l` и зависимость $$ l\left(t\right)$$.
Следующие два важных механических понятия – это пройденный путь и средняя путевая скорость.
По определению, путь `Delta S` — это длина участка траектории, пройденного телом за промежуток времени `Delta t`.
Ясно, что пройденный путь – величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением `Delta vec r`, представляющим собой вектор. Сравнивать можно только путь `Delta S` и модуль перемещения `
|Delta vecr|`. Очевидно, что `Delta S >=|Deltavec r|`.
Средней путевой скоростью `v_»cp»` тела называют отношение пути `Delta S` к промежутку времени `Delta t`, в течение которого этот путь был пройден:
`v_»cp»=(Delta S)/(Delta t)` (3)
Определённая ранее средняя скорость `v_»cp»` (см.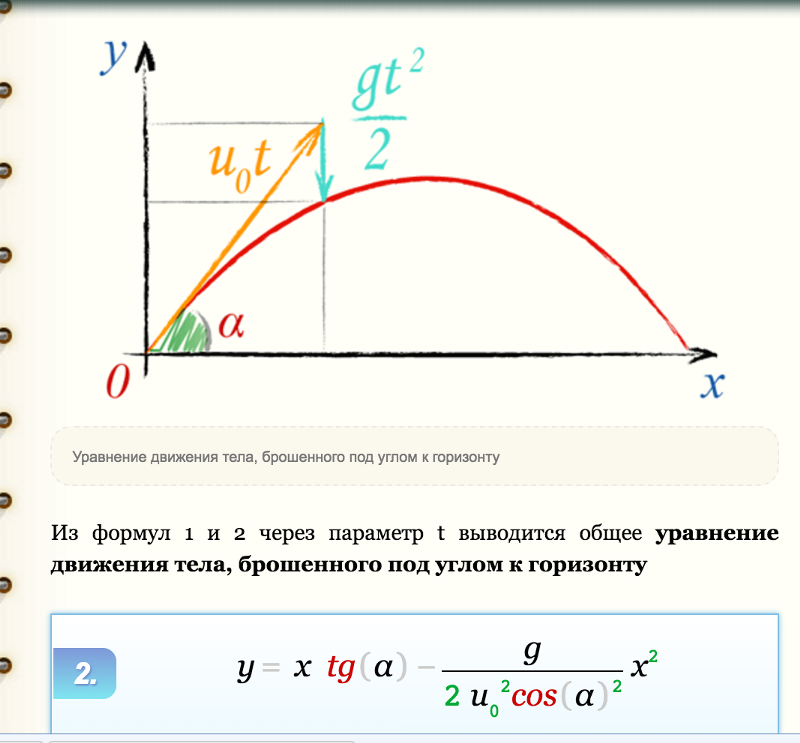 формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.
формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.
Городской троллейбус утром вышел на маршрут, а через 8часов, проехав в общей сложности `72` км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость `vec v_»cp»` и средняя путевая скорость `v_»cp»` троллейбуса?
Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение `Delta vecr` равно нулю: `Deltavecr=0`, следовательно, `vecv_»ср»=Deltavecr//Deltat=0` и `|vecv_»ср»|=0`. Но средняя путевая скорость троллейбуса не равна нулю:
`v_»cp»=(Delta S)/(Delta t)=(72 «км»)/(8 «ч»)=9 «км»//»ч»`.
2 |) `Максимальная дальность полета снаряда
Ах да. Я знаю, что уже сделал это. Однако это было очень давно с дрянными графиками. Я могу лучше.
Я могу лучше.
В учебниках сказано, что максимальная дальность движения снаряда (без сопротивления воздуха) составляет 45 градусов. Как вы это получили? Вот так.
Во-первых, чтобы прояснить, что такое движение снаряда? Типичное определение — движение объекта за счет только силы тяжести (без сопротивления воздуха, ракет и прочего).Если вам нужно подробное обсуждение движения снаряда, прочтите этот пост. В противном случае запомните ключ к движению снаряда:
Движение снаряда похоже на две одномерные задачи кинематики, которые имеют общее только время. Ускорение в вертикальном направлении — g, , а горизонтальное ускорение равно нулю.
Движение снаряда — нет сопротивления воздуха
Используя основные идеи, приведенные выше, и кинематические уравнения (для постоянного ускорения), должно быть верно следующее:
[]
Обратите внимание, что я предполагаю, что t = 0 секунд , начальные положения равны x 0 y 0 вместе с начальными скоростями.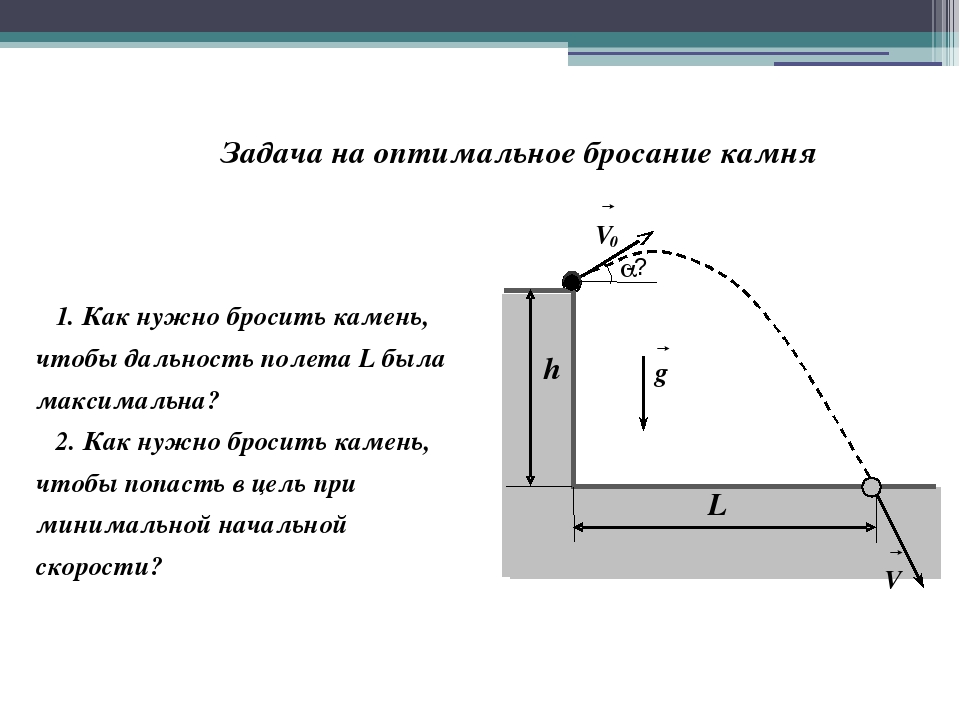 Кроме того, я использую типичное соглашение, что г = 9,8 Н / кг = 9,8 м / с 2 , так что ускорение в направлении y составляет — g . Но как далеко уйдет объект, если он начинается и заканчивается в одном и том же диапазоне y ? Вот диаграмма, показывающая скорость запуска некоторого объекта.
Кроме того, я использую типичное соглашение, что г = 9,8 Н / кг = 9,8 м / с 2 , так что ускорение в направлении y составляет — g . Но как далеко уйдет объект, если он начинается и заканчивается в одном и том же диапазоне y ? Вот диаграмма, показывающая скорость запуска некоторого объекта.
[]
Цель здесь — найти диапазон ( x — x 0 ). Для этого я сначала определю время движения, используя направление y. Помните, я знаю, что объект начинается и заканчивается на тех же и .Это дает:
[]
Быстрая проверка. Какое значение θ даст наибольшее время? Хорошо, это было бы, когда sin (θ) является наибольшим — при значении π / 2 (90 градусов — ну, вы знаете, прямо вверх). А как насчет единиц? (м / с) больше (м / с 2 ) дает единицы времени. Большой. Теперь вставим это выражение для движения по оси x.
[]
Проверка агрегата. (m 2 / s 2 ) over (m / s 2 ) действительно дает единицы измерения. Еще одна проверка. Что, если я брошу мяч прямо вверх (θ = π / 2)? Ну, cos (π / 2) = 0, так что это дает горизонтальный диапазон 0 метров.Имеет смысл.
Еще одна проверка. Что, если я брошу мяч прямо вверх (θ = π / 2)? Ну, cos (π / 2) = 0, так что это дает горизонтальный диапазон 0 метров.Имеет смысл.
Но реальный вопрос: какой угол для максимального расстояния (для данной начальной скорости). Очевидно, этот диапазон зависит от произведения синуса и косинуса. Позвольте мне сначала выделить триггерное удостоверение. Произведение синуса и косинуса (в общем):
[]
Я знаю, о чем вы думаете: мы действительно собираемся использовать триггерное тождество? Я думал, что мы просто должны были получить их в старшей школе в качестве наказания за все те плевки, которые мы бросали. О нет. Они действительно полезны.Для этого триггерного тождества θ = φ, так что:
[]
Наибольшее значение sin для чего-либо может быть равно 1. Под каким углом это будет?
[]
Готово. 45 градусов. Все как в учебнике написано. О, тебе это не нравится? Вы визуальный ученик? Я могу с этим справиться. Вот сюжет, который может вам понравиться.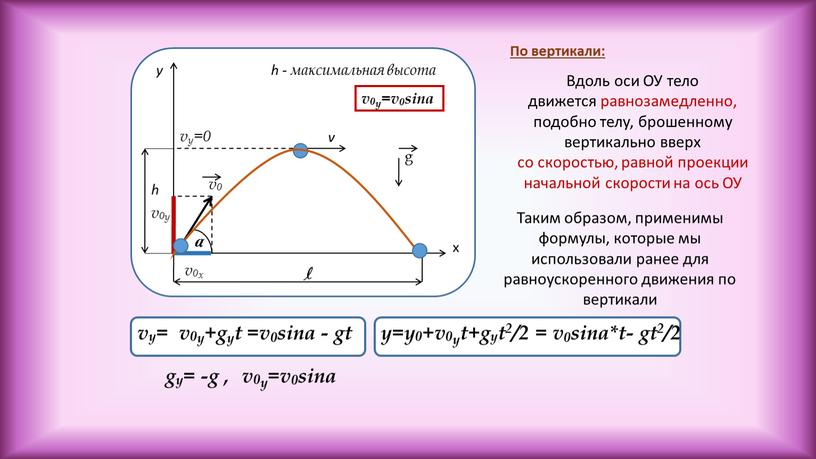 Это график sinθ cosθ и произведения двух от нуля до π / 2.
Это график sinθ cosθ и произведения двух от нуля до π / 2.
[]
Обратите внимание, что член cos * sin имеет максимальное значение при θ = π / 4? Бум.Все еще недостаточно хорошо? А как насчет того, чтобы бросить целую кучу шаров с одинаковой начальной скоростью, но под разными углами? Вот результат:
[]
Все они запускаются с одинаковой начальной скоростью, но под разными углами. Угадайте, какой из них идет дальше всего?
1.3: Приложения и решение прямоугольных треугольников
На ранних этапах развития тригонометрия часто использовалась как средство косвенного измерения, например определение больших расстояний или длин путем измерения углов и малых известных расстояний.\ circ \) от его горизонтальной линии обзора до основания дома на земле. Если предположить, что земля плоская, как далеко от земли находится дом от дирижабля?
Решение:
Пусть \ (x \) будет расстояние по земле от дирижабля до дома, как на картинке справа. Поскольку земля и горизонтальная линия обзора дирижабля параллельны, мы знаем из элементарной геометрии, что угол подъема \ (\ theta \) от основания дома до дирижабля равен углу падения дирижабля на дирижабль. цоколь дома, т.\ circ \) к горизонту океана. Используйте это, чтобы оценить радиус Земли.
Поскольку земля и горизонтальная линия обзора дирижабля параллельны, мы знаем из элементарной геометрии, что угол подъема \ (\ theta \) от основания дома до дирижабля равен углу падения дирижабля на дирижабль. цоколь дома, т.\ circ \) к горизонту океана. Используйте это, чтобы оценить радиус Земли.
Решение:
Предположим, что Земля — это сфера. Пусть \ (r \) — радиус Земли. Пусть точка \ (A \) представляет вершину горы, а \ (H \) — горизонт океана на линии прямой видимости из \ (A \), как на рисунке 1.3.1. Пусть \ (O \) будет центром Земли, и пусть \ (B \) будет точкой на горизонтальной линии обзора от \ (A \) (то есть на прямой, перпендикулярной \ (\ overline {OA} \ )).\ circ} \\
& \ Rightarrow \ quad \ boxed {r ~ = ~ 3958,3 ~ \ text {miles}} ~.
\ end {align} \]
Примечание. Этот ответ очень близок к фактическому (среднему) радиусу Земли в \ (3956,6 \) миль.
Пример 1.15
В качестве еще одного приложения тригонометрии к астрономии мы найдем расстояние от Земли до Солнца. Пусть \ (O \) будет центром Земли, пусть \ (A \) будет точкой на экваторе, и пусть \ (B \) будет представлять объект (например, звезду) в космосе, как на картинке на верно.\ circ \ приблизительно 8,8 » \), о чем мы упоминаем только потому, что некоторые устройства измерения углов действительно используют минуты и секунды.
Пусть \ (O \) будет центром Земли, пусть \ (A \) будет точкой на экваторе, и пусть \ (B \) будет представлять объект (например, звезду) в космосе, как на картинке на верно.\ circ \ приблизительно 8,8 » \), о чем мы упоминаем только потому, что некоторые устройства измерения углов действительно используют минуты и секунды.
Пример 1.16
Наблюдатель на Земле измеряет угол \ (32 ‘\; 4’ ‘\) от одного видимого края Солнца до другого (противоположного) края, как на картинке справа. Используйте это, чтобы оценить радиус солнца.
Решение:
Пусть точка \ (E \) будет землей, а \ (S \) будет центром солнца.\ circ \).
Теперь \ (ES \) — это расстояние от поверхности земли (где стоит наблюдатель) до центра Солнца. В примере 1.15 мы обнаружили, что расстояние от центра Земли до Солнца составляет \ (92 908 394 \) миль. Поскольку в этом примере мы рассматривали Солнце как точку, то мы вправе рассматривать это расстояние как расстояние между центрами Земли и Солнца. Итак, \ (ES = 924 — ~ \ text {радиус Земли} = 924 — 3956,6 = 92
Итак, \ (ES = 924 — ~ \ text {радиус Земли} = 924 — 3956,6 = 92
7.\ circ ~ = ~ \ boxed {433,293 ~ \ text {miles}} ~. \]
Примечание. Этот ответ близок к фактическому (среднему) радиусу Солнца в \ (432 200 \) миль.
Возможно, вы заметили, что для решения приведенных нами примеров требовался хотя бы один прямоугольный треугольник. В прикладных задачах не всегда очевидно, какой прямоугольный треугольник использовать, поэтому подобные задачи могут быть трудными. Часто прямоугольный треугольник не сразу бросается в глаза, поэтому вам придется его создать. Для этого не существует общей стратегии, но помните, что прямоугольный треугольник требует прямого угла, поэтому ищите места, где вы можете образовывать перпендикулярные отрезки линии.Когда задача содержит круг, вы можете создать прямые углы, используя перпендикулярность касательной к кругу в точке с линией, соединяющей эту точку с центром круга. Мы сделали именно это в примерах 1.14, 1.15 и 1.16.
Пример 1. \ circ \).\ circ} ~ = ~ 1.384 \]
\ circ \).\ circ} ~ = ~ 1.384 \]
Следовательно, диаметр большого ролика равен \ (\, d = 2 \ times OB = 2 \, (1.384) = \ boxed {2.768} \) ~.
Пример 1.18
Кривошипно-ползунковый механизм показан на Рисунке 1.3.2 ниже. Когда поршень движется вниз, шатун поворачивает кривошип по часовой стрелке, как показано.
Рисунок 1.3.2 Кривошипно-ползунковый механизм Точка \ (A \) является центром пальца шатуна и перемещается только вертикально.Точка \ (B \) является центром стержня кривошипа и движется по окружности радиуса \ (r \) с центром в точке \ (O \), которая находится непосредственно под \ (A \) и не двигаться. При вращении кривошип образует угол \ (\ theta \) с линией \ (\ overline {OA} \). Мгновенный центр вращения шатуна в данный момент времени — это точка \ (C \), где горизонтальная линия, проходящая через \ (A \), пересекает удлиненную линию, проходящую через \ (O \) и \ (B \). Из рисунка 1.3.2 видно, что \ (\ angle \, OAC = 90 ^ \ circ \), и пусть \ (a = AC \), \ (b = AB \) и \ (c = BC \) . 2} ~ \ tan \; \ theta ~. \]
2} ~ \ tan \; \ theta ~. \]
Для некоторых задач может быть полезно помнить, что когда у прямоугольного треугольника есть гипотенуза длины \ (r \) и острый угол \ (\ theta \), как на рисунке ниже, соседняя сторона будет иметь длину \ (r \, \ cos \; \ theta \), а противоположная сторона будет иметь длину \ (r \, \ sin \; \ theta \). Вы можете рассматривать эти длины как горизонтальные и вертикальные « компоненты » гипотенузы.
Обратите внимание, что в прямоугольном треугольнике выше мы получили две части информации: один из острых углов и длину гипотенузы.Клавиши {-1} \)} \) работают аналогично для синуса и косинуса соответственно. Эти клавиши используют обратные тригонометрические функции , которые мы обсудим в главе 5.
Авторы и авторство
% PDF-1.3
%
910 0 объект
>
эндобдж
xref
910 130
0000000016 00000 н.
0000002953 00000 н.
0000003172 00000 п.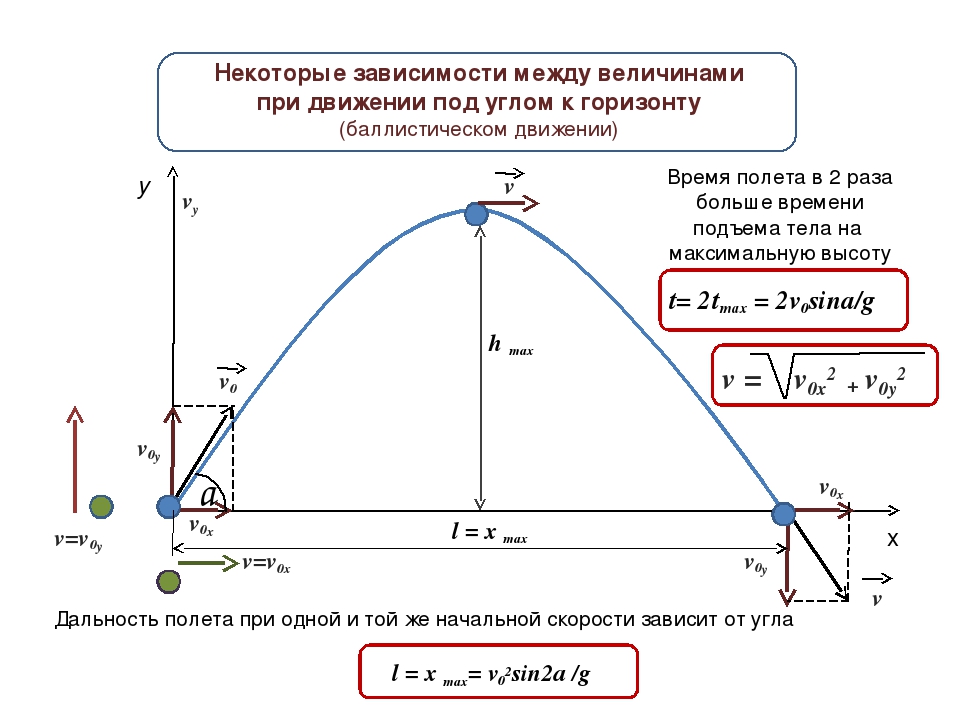 0000003203 00000 н.
0000003258 00000 н.
0000004893 00000 н.
0000005149 00000 п.
0000005215 00000 н.
0000005400 00000 н.
0000005552 00000 н.
0000005719 00000 н.
0000005881 00000 н.
0000006018 00000 н.
0000006169 00000 п.
0000006318 00000 п.
0000006451 00000 п.
0000006655 00000 н.
0000006783 00000 н.
0000006931 00000 п.
0000007135 00000 н.
0000007323 00000 н.
0000007413 00000 п.
0000007590 00000 н.
0000007740 00000 н.
0000007813 00000 н.
0000007939 00000 п.
0000008036 00000 н.
0000008148 00000 н.
0000008302 00000 н.
0000008453 00000 п.
0000008629 00000 н.
0000008832 00000 н.
0000009020 00000 н.
0000009210 00000 п.
0000009413 00000 н.
0000009601 00000 п.
0000009755 00000 н.
0000009922 00000 н.
0000010077 00000 п.
0000010226 00000 п.
0000010383 00000 п.
0000010556 00000 п.
0000010705 00000 п.
0000010878 00000 п.
0000011025 00000 п.
0000011198 00000 п.
0000011356 00000 п.
0000011535 00000 п.
0000011723 00000 п.
0000011911 00000 п.
0000012114 00000 п.
0000012320 00000 н.
0000012493 00000 п.
0000012652 00000 п.
0000003203 00000 н.
0000003258 00000 н.
0000004893 00000 н.
0000005149 00000 п.
0000005215 00000 н.
0000005400 00000 н.
0000005552 00000 н.
0000005719 00000 н.
0000005881 00000 н.
0000006018 00000 н.
0000006169 00000 п.
0000006318 00000 п.
0000006451 00000 п.
0000006655 00000 н.
0000006783 00000 н.
0000006931 00000 п.
0000007135 00000 н.
0000007323 00000 н.
0000007413 00000 п.
0000007590 00000 н.
0000007740 00000 н.
0000007813 00000 н.
0000007939 00000 п.
0000008036 00000 н.
0000008148 00000 н.
0000008302 00000 н.
0000008453 00000 п.
0000008629 00000 н.
0000008832 00000 н.
0000009020 00000 н.
0000009210 00000 п.
0000009413 00000 н.
0000009601 00000 п.
0000009755 00000 н.
0000009922 00000 н.
0000010077 00000 п.
0000010226 00000 п.
0000010383 00000 п.
0000010556 00000 п.
0000010705 00000 п.
0000010878 00000 п.
0000011025 00000 п.
0000011198 00000 п.
0000011356 00000 п.
0000011535 00000 п.
0000011723 00000 п.
0000011911 00000 п.
0000012114 00000 п.
0000012320 00000 н.
0000012493 00000 п.
0000012652 00000 п. 0000012807 00000 п.
0000012923 00000 п.
0000013076 00000 п.
0000013226 00000 п.
0000013399 00000 п.
0000013572 00000 п.
0000013760 00000 п.
0000013951 00000 п.
0000014154 00000 п.
0000014311 00000 п.
0000014459 00000 п.
0000014600 00000 п.
0000014755 00000 п.
0000014852 00000 п.
0000015016 00000 п.
0000015103 00000 п.
0000015182 00000 п.
0000015318 00000 п.
0000015454 00000 п.
0000015627 00000 н.
0000015818 00000 п.
0000016006 00000 п.
0000016171 00000 п.
0000016359 00000 п.
0000016495 00000 п.
0000016646 00000 п.
0000016835 00000 п.
0000017023 00000 п.
0000017226 00000 п.
0000017399 00000 п.
0000017589 00000 п.
0000017733 00000 п.
0000017936 00000 п.
0000018037 00000 п.
0000018240 00000 п.
0000018445 00000 п.
0000018610 00000 п.
0000018708 00000 п.
0000018900 00000 п.
0000019093 00000 п.
0000019299 00000 п.
0000019505 00000 п.
0000019623 00000 п.
0000019741 00000 п.
0000019859 00000 п.
0000019977 00000 п.
0000020095 00000 п.
0000020213 00000 н.
0000020331 00000 п.
0000020449 00000 п.
0000020567 00000 п.
0000012807 00000 п.
0000012923 00000 п.
0000013076 00000 п.
0000013226 00000 п.
0000013399 00000 п.
0000013572 00000 п.
0000013760 00000 п.
0000013951 00000 п.
0000014154 00000 п.
0000014311 00000 п.
0000014459 00000 п.
0000014600 00000 п.
0000014755 00000 п.
0000014852 00000 п.
0000015016 00000 п.
0000015103 00000 п.
0000015182 00000 п.
0000015318 00000 п.
0000015454 00000 п.
0000015627 00000 н.
0000015818 00000 п.
0000016006 00000 п.
0000016171 00000 п.
0000016359 00000 п.
0000016495 00000 п.
0000016646 00000 п.
0000016835 00000 п.
0000017023 00000 п.
0000017226 00000 п.
0000017399 00000 п.
0000017589 00000 п.
0000017733 00000 п.
0000017936 00000 п.
0000018037 00000 п.
0000018240 00000 п.
0000018445 00000 п.
0000018610 00000 п.
0000018708 00000 п.
0000018900 00000 п.
0000019093 00000 п.
0000019299 00000 п.
0000019505 00000 п.
0000019623 00000 п.
0000019741 00000 п.
0000019859 00000 п.
0000019977 00000 п.
0000020095 00000 п.
0000020213 00000 н.
0000020331 00000 п.
0000020449 00000 п.
0000020567 00000 п.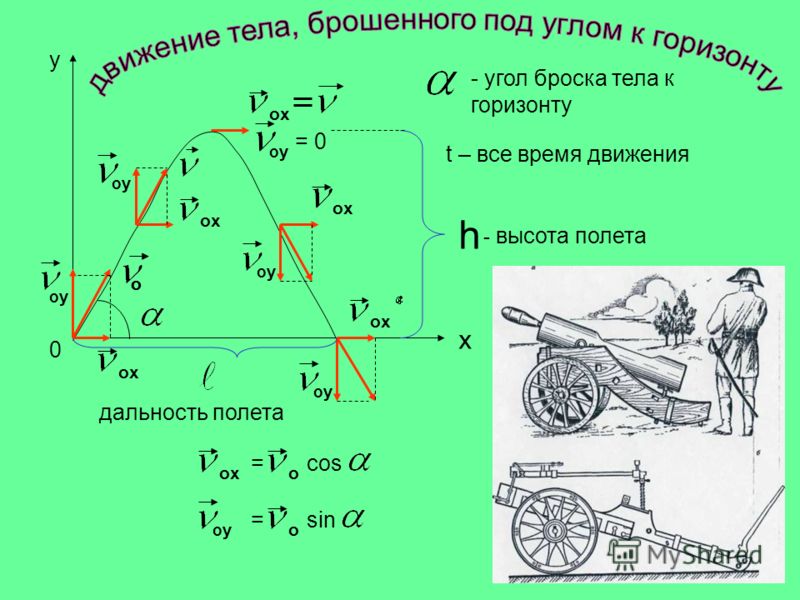 0000020779 00000 п.
0000021029 00000 п.
0000021568 00000 н.
0000021819 00000 п.
0000022357 00000 п.
0000022420 00000 н.
0000022494 00000 п.
0000023287 00000 п.
0000023532 00000 п.
0000023841 00000 п.
0000024166 00000 п.
0000024411 00000 п.
0000024495 00000 п.
0000025091 00000 п.
0000025770 00000 п.
0000026009 00000 п.
0000026242 00000 п.
0000040014 00000 п.
0000060049 00000 п.
0000065812 00000 п.
0000066654 00000 п.
0000093582 00000 п.
0000093662 00000 п.
0000003299 00000 н.
0000004869 00000 н.
трейлер
]
>>
startxref
0
%% EOF
911 0 объект
>
эндобдж
912 0 объект
[
913 0 руб.
]
эндобдж
913 0 объект
>
/ F 3 0 R
>>
эндобдж
914 0 объект
>
эндобдж
1038 0 объект
>
транслировать
HV [lUgRAB & Jc% 5fKIg.3 {Vf
bШC7IC? &> ‘g / ow
0000020779 00000 п.
0000021029 00000 п.
0000021568 00000 н.
0000021819 00000 п.
0000022357 00000 п.
0000022420 00000 н.
0000022494 00000 п.
0000023287 00000 п.
0000023532 00000 п.
0000023841 00000 п.
0000024166 00000 п.
0000024411 00000 п.
0000024495 00000 п.
0000025091 00000 п.
0000025770 00000 п.
0000026009 00000 п.
0000026242 00000 п.
0000040014 00000 п.
0000060049 00000 п.
0000065812 00000 п.
0000066654 00000 п.
0000093582 00000 п.
0000093662 00000 п.
0000003299 00000 н.
0000004869 00000 н.
трейлер
]
>>
startxref
0
%% EOF
911 0 объект
>
эндобдж
912 0 объект
[
913 0 руб.
]
эндобдж
913 0 объект
>
/ F 3 0 R
>>
эндобдж
914 0 объект
>
эндобдж
1038 0 объект
>
транслировать
HV [lUgRAB & Jc% 5fKIg.3 {Vf
bШC7IC? &> ‘g / ow
Движение снаряда — материалы исследования для IIT JEE
Теперь мы обсудим некоторый пример изогнутого движения или двумерного движения с постоянным ускорением, такого как движение с постоянным ускорением, такое как движение частицы, проецируемой под определенным углом к горизонтали в вертикальной плоскости xy (этот тип движения называется движением снаряда). движение). Предполагается, что сопротивление воздуха движению тела в этом типе движения отсутствует.
движение). Предполагается, что сопротивление воздуха движению тела в этом типе движения отсутствует.
Тело, выброшенное в космос и больше не приводимое в движение топливом, называется снарядом .
Для анализа движения снаряда мы используем следующую концепцию «Преобразование двухмерного движения в два одномерного движения», как обсуждалось ранее. Следовательно, легче анализировать движение снаряда как состоящее из двух одновременных прямолинейных движений, которые не зависят друг от друга:
(a) Вдоль вертикальной оси Y с равномерным ускорением вниз ‘g’ и
(b) Вдоль горизонтальной оси x с равномерной скоростью вперед.
Рассмотрим частицу, проецируемую с начальной скоростью u под углом θ к горизонтальной оси x, как показано на рисунке ниже. Скорость и ускорение можно разделить на две составляющие:
Скорость по оси x = u x = u cos θ
Ускорение по оси x a x = 0
Скорость по оси y = u y = u sin θ
Ускорение по оси y a y = -g
Здесь мы используем другое уравнение движения одного измерения, полученное ранее, чтобы получить разные параметры.
… … (а)
… … (б)
v 2 = v 0 2 — 2g (г-г 0 )… … (c)
Когда тело возвращается на тот же горизонтальный уровень, результирующее смещение в вертикальном направлении y равно нулю. Используйте уравнение b.
Следовательно, 0 = (u sin θ) t — (½) gt 2 ,
Так как t не может равняться нулю, то общее время полета
Горизонтальный диапазонгоризонтальная дальность (OA = X) = горизонтальная скорость × время полета
= u cos θ × 2 u sin θ / g
Так горизонтальный диапазон,
Максимальная высотаВ самой высокой точке траектории вертикальная составляющая скорости равна нулю.
Следовательно, 0 = (u sin θ) 2 — 2g H max
Итак, максимальная высота будет
. Обратитесь к этому видео, чтобы лучше понять движение снаряда: —
Обратитесь к этому видео, чтобы лучше понять движение снаряда: — Уравнение траектории
Предполагается, что точка проекции является началом координат, а горизонтальное направление — осью x, а вертикальное направление — осью y. Пусть P (x, y) будет положением частицы в момент после t секунды.
Тогда x = u cos θ.t и y = u sin θ.t — 1/2 gt 2
Исключая ‘t’ из приведенных выше уравнений, получаем
y = x tan θ — (gx 2 / 2u 2 cos 2 θ)
Это уравнение траектории, которое представляет собой параболу (y = ax + bx 2 ).
См. Это моделирование для движения снаряда: — Мяч запускается под углом и приземляется на той же высоте, с которой был запущен. Камера каждую секунду делает снимок полета на одном и том же кадре пленки. Затем изображения перемещаются вниз и вправо, чтобы показать независимость горизонтального и вертикального движения.
Затем изображения перемещаются вниз и вправо, чтобы показать независимость горизонтального и вертикального движения.
Скорость снаряда, когда он находится на максимальной высоте, в √2 / 5 раз больше его скорости на половине максимальной высоты. Узнайте угол проекции.
Решение : —
Пусть θ — угол проекции, а u — его начальная скорость. Тогда максимальная высота будет
.H = u 2 sin 2 θ / 2g
Итак, gH = u 2 sin 2 θ / 2
Теперь, v H = u cosθ
Или, v H 2 = u 2 cos 2 θ…… (1)
v H / 2 2 = u 2 -2g (H / 2) = u 2 -gH
v H / 2 2 = u 2 — (u 2 sin 2 θ / 2)… … (2)
Теперь дано, что,
v H = [√2 / 5] v H / 2
Или, v H 2 = (2/5) v H / 2 2
Подставляя значения из уравнений (1) и (2), получаем,
(u 2 cos 2 θ) = 2/5 [u 2 — (u 2 sin 2 θ / 2)]
Или, 5cos 2 θ = 2 [1- (sin 2 θ / 2)]
Или, 5 (1-sin 2 θ) = 2-sin 2 θ
Или, sin 2 θ = ¾
Или, sinθ = (√3) / 2, Или, θ = 60 o
Таким образом, из вышеприведенного наблюдения мы заключаем, что угол проецирования будет 60 o .
Задача 2 : —
Пушка, движущаяся со скоростью 30 м / с, ведет огонь под углом 30 o со скоростью 150 м / с относительно пушки. Найдите расстояние между пушкой и снарядом, когда снаряд попадает в землю. (g = 10 м / сек)
Решение : —
Вертикальная составляющая скорости = 150 sin 30 o = 75 м / с
Горизонтальная составляющая скорости относительно пушки = 150 cos 30 o = 75√3 м / с
Горизонтальная составляющая скорости относительно земли = 75√3 + 30 ≈ 160 м / с
Время полета = (275) / g = 15 с
Дальность снаряда = 160 × 15 = 2400 м
Дальность перемещения орудия и снаряда = 2400 — 450 = 1950 м.
Горизонтальная проекция: —Рассмотрим частицу, проецируемую горизонтально со скоростью из точки O, как показано на рисунке сбоку.
Предполагается, что точка проекции O является началом координат, а горизонтальное направление — осью X, а вертикальное направление — осью Y. Пусть P (x, y) будет положением частицы через t секунд.
Пусть P (x, y) будет положением частицы через t секунд.
Итак, x = горизонтальное расстояние, пройденное за время t = ut. …………… (1)
y = расстояние по вертикали, пройденное за время t = ½gt2…………… (2)
Исключим t из уравнений (1) и (2), получим
y = (1/2) (g / u 2 ) (x 2 )
Это уравнение параболы, проходящей через начало координат с вершиной в начале координат O. Следовательно, траектория является параболой.
Задача 3 : —
Камень брошен со скоростью 19,6 м / сек под углом 30 o над горизонтом с башни высотой 490 метров.Найдите время, в течение которого камень будет в воздухе. Также найдите расстояние от подножия башни до точки, где камень падает на землю?
Решение : —
Рассмотрим движение камня отдельно в горизонтальном и вертикальном направлениях.
(i) Вертикальное движение (отрицательное направление вниз):
Начальная вертикальная скорость y = 19,6 sin 30 o
Ускорение a = g = -9,8 м / с 2
Пройденное расстояние по вертикали = h = 490 м
Использование, h = ut + 1 / 2gt 2
У нас 490 = — 9. 8 т + (1/2) 9,8 т 2
8 т + (1/2) 9,8 т 2
100 = — 2t + t 2 или t 2 — 2t — 100 = 0
t = 11,05 сек
(ii) Горизонтальное перемещение:
Начальная горизонтальная скорость y = 19,6 sin 30 o = 9,8 м / с
Отсюда расстояние от подножия башни до точки падения камня на землю
= Горизонтальная составляющая × время полета
= 19,6 cos 30 o × 11,05 = 188 м
Движение снаряда по наклонной плоскости: —Пусть частица ударится о плоскость в точке A так, чтобы OA была дальностью полета снаряда на наклонной плоскости.Эту начальную скорость можно разделить на две составляющие:
(i) u cos (α — β) по плоскости
(ii) u sin (α — β) перпендикулярно плоскости.
Ускорение свободного падения g можно разделить на две составляющие:
(i) g sin β параллельно плоскости
(ii) g cos β перпендикулярно плоскости.
Пусть t будет временем, за которое частица переместится из точки A в точку B. В это время смещение снаряда к плоскости равно нулю.
Следовательно, 0 = u sin (α-β) t — ½g β t 2
=> t = 2u sin (α-β) / gcosβ
Диапазон: —Во время полета горизонтальная скорость u cos α остается постоянной.
Отсюда горизонтальное расстояние
OB = (ucosα) t = 2u 2 sin (α-β) cosα / gcosβ
Итак, OA = OB / cosβ = 2u 2 sin (α-β) cosα / gcosβ
Наибольшее расстояние снаряда от наклонной плоскости u 2 sin 2 (α-β) / 2gcosβ.
Задача 4 : —
Частица проецируется со скоростью 39,2 м / сек под углом 30 o к наклонной плоскости (наклоненной под углом 45 o к горизонтали). Найдите диапазон наклона (a), когда он проецируется вверх (b), когда он проецируется вниз.
Решение : —
Время полета будет одинаковым в обоих случаях, потому что ускорение перпендикулярно плоскости одинаково.Следовательно,
0 = 39,2 sin 30 o т — (½) g cos 45 o т 2
Или, t = (2 × 39,2 sin 30) / (g cos 45) = 4√2 с
(a) Диапазон вверх
= 39,2 cos 30 o т — (½) g sin 30 o т 2
= 39,2 × √3 / 2 × 4√2- (1/2) × 9,8 × (1/2) × (4√2) 2 = 113,7 м
(б) Диапазон вниз
= 39,2 cos 30 o × t + (½) g sin 30 o t 2
= 39.2 × √3 / 2 × 4√2 + (1/2) × 9,8 × (1/2) × (4√2) 2 = 270,5 м Ответ.
Движение вниз по плоскости: —Пусть частица будет брошена со скоростью v0 под углом «α» к горизонту, как показано на рисунке.
v 0 sin (α + β) T- 1/2 gcosβT 2 = 0 [для y ‘= 0]
=> T = (2v 0 sin (α + β)) / gcosβ
R = v 0 cos (α + β) T + 1/2 g sin βT 2 = (v 0 2 ) / g [(sin (2α + β) + sinβ) / (1- sin2β)]
Поскольку α — переменная, а максимальное значение функции sin равно 1, поэтому, чтобы R было максимальным, sin (2α + β) = 1
и Rmax (v 0 2 ) / g [(1 + sinβ) / (1-sin2β)] = (v 0 2 ) / (g (1-sinβ)) вниз по плоскости.
|
Вопрос 1 : —
Что из следующего не является снарядом:
(а) пуля, выпущенная из винтовки (б) бомба, сброшенная с самолета
(c) мяч для крикета, движущийся в пространстве (d) водородный шар, плавающий в воздухе
Вопрос 2 : —
Частица, проецируемая горизонтально из вершины башни, очищает диапазон, равный высоте башни. Описанный путь является частью a:
Описанный путь является частью a:
(а) круг (б) эллипс
(в) гипербола (г) парабола
Вопрос 3 : —
Частица брошена вертикально вверх. На самом высоком уровне он имеет:
(а) восходящая скорость (б) нисходящая скорость
(c) ускорение вверх (d) ускорение вниз
Вопрос 4 : —
Частица брошена вертикально вверх.Его скорость на половине высоты составляет 10 м / с, максимальная достигаемая им высота:
.(а) 8 м (б) 20 м
(в) 10 м (г) 16 см
Вопрос 5 : —
Тело выступает горизонтально с вершины башни высотой 19,6 метра. Он достигает земли через:
(а) 1 сек (б) 2 сек
(в) 2,5 сек (г) 5 сек
| Q.1 | Q.2 | Q.3 | Q. 4 4 | Q.5 |
б | д | д | с | б |
Чтобы узнать больше, купите учебные материалы по кинематике, включая учебные заметки, заметки о пересмотре, видеолекции, решенные вопросы за предыдущий год и т.Также поищите здесь дополнительные учебные материалы по физике.
% PDF-1.4
%
386 0 объект
>
эндобдж
xref
386 231
0000000017 00000 н.
0000005093 00000 н.
0000007361 00000 н.
0000007718 00000 н.
0000007995 00000 н.
0000008204 00000 н.
0000008548 00000 н.
0000008854 00000 н.
0000009187 00000 н.
0000009375 00000 п.
0000009556 00000 п.
0000009724 00000 н.
0000009900 00000 н.
0000010254 00000 п.
0000010536 00000 п.
0000010883 00000 п.
0000011136 00000 п. 0000011441 00000 п.
0000011809 00000 п.
0000011952 00000 п.
0000012047 00000 п.
0000012323 00000 п.
0000012700 00000 п.
0000013004 00000 п.
0000013285 00000 п.
0000013583 00000 п.
0000013850 00000 п.
0000014039 00000 п.
0000014217 00000 п.
0000014384 00000 п.
0000014593 00000 п.
0000014926 00000 п.
0000015102 00000 п.
0000015422 00000 н.
0000015692 00000 п.
0000016008 00000 п.
0000016253 00000 п.
0000016537 00000 п.
0000016860 00000 п.
0000017038 00000 п.
0000017276 00000 п.
0000017581 00000 п.
0000017950 00000 п.
0000018241 00000 п.
0000018513 00000 п.
0000018765 00000 п.
0000018931 00000 п.
0000019141 00000 п.
0000019357 00000 п.
0000019542 00000 п.
0000019824 00000 п.
0000020229 00000 п.
0000020404 00000 п.
0000020561 00000 п.
0000020726 00000 п.
0000020989 00000 н.
0000021203 00000 п.
0000021483 00000 п.
0000021651 00000 п.
0000021918 00000 п.
0000022144 00000 п.
0000022368 00000 п.
0000022591 00000 п.
0000022818 00000 п.
0000023072 00000 п.
0000011441 00000 п.
0000011809 00000 п.
0000011952 00000 п.
0000012047 00000 п.
0000012323 00000 п.
0000012700 00000 п.
0000013004 00000 п.
0000013285 00000 п.
0000013583 00000 п.
0000013850 00000 п.
0000014039 00000 п.
0000014217 00000 п.
0000014384 00000 п.
0000014593 00000 п.
0000014926 00000 п.
0000015102 00000 п.
0000015422 00000 н.
0000015692 00000 п.
0000016008 00000 п.
0000016253 00000 п.
0000016537 00000 п.
0000016860 00000 п.
0000017038 00000 п.
0000017276 00000 п.
0000017581 00000 п.
0000017950 00000 п.
0000018241 00000 п.
0000018513 00000 п.
0000018765 00000 п.
0000018931 00000 п.
0000019141 00000 п.
0000019357 00000 п.
0000019542 00000 п.
0000019824 00000 п.
0000020229 00000 п.
0000020404 00000 п.
0000020561 00000 п.
0000020726 00000 п.
0000020989 00000 н.
0000021203 00000 п.
0000021483 00000 п.
0000021651 00000 п.
0000021918 00000 п.
0000022144 00000 п.
0000022368 00000 п.
0000022591 00000 п.
0000022818 00000 п.
0000023072 00000 п.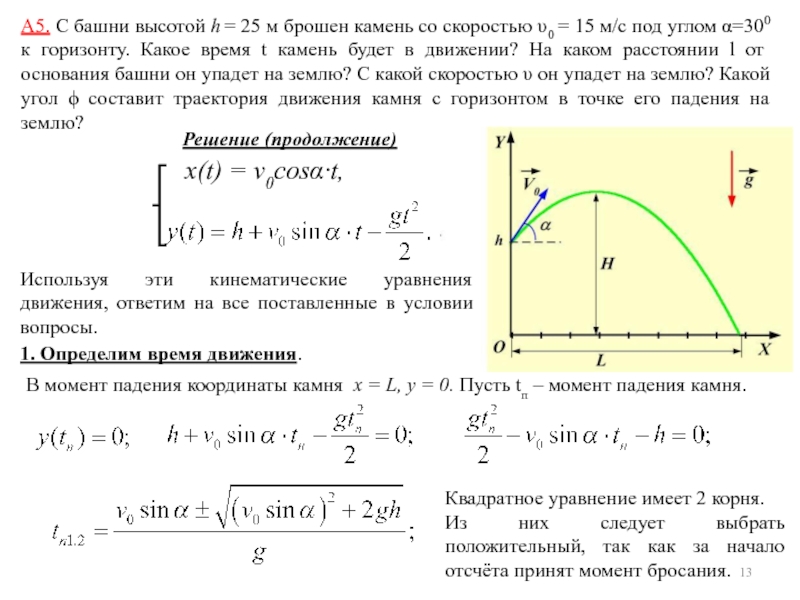 0000023239 00000 п.
0000023435 00000 п.
0000023597 00000 п.
0000023795 00000 п.
0000024018 00000 п.
0000024204 00000 п.
0000024443 00000 п.
0000024636 00000 п.
0000024831 00000 п.
0000025060 00000 п.
0000025297 00000 п.
0000025488 00000 п.
0000025743 00000 п.
0000025980 00000 п.
0000026236 00000 п.
0000026488 00000 п.
0000026672 00000 н.
0000027212 00000 н.
0000027339 00000 н.
0000027561 00000 п.
0000036258 00000 п.
0000036433 00000 п.
0000036763 00000 п.
0000036932 00000 п.
0000037148 00000 п.
0000037781 00000 п.
0000037966 00000 п.
0000038261 00000 п.
0000038487 00000 п.
0000045405 00000 п.
0000045589 00000 п.
0000045745 00000 п.
0000045968 00000 п.
0000049491 00000 п.
0000049763 00000 п.
0000050812 00000 п.
0000051073 00000 п.
0000051340 00000 п.
0000051512 00000 п.
0000051686 00000 п.
0000051858 00000 п.
0000052044 00000 п.
0000052236 00000 п.
0000052421 00000 п.
0000052579 00000 п.
0000052813 00000 п.
0000052981 00000 п.
0000053174 00000 п.
0000023239 00000 п.
0000023435 00000 п.
0000023597 00000 п.
0000023795 00000 п.
0000024018 00000 п.
0000024204 00000 п.
0000024443 00000 п.
0000024636 00000 п.
0000024831 00000 п.
0000025060 00000 п.
0000025297 00000 п.
0000025488 00000 п.
0000025743 00000 п.
0000025980 00000 п.
0000026236 00000 п.
0000026488 00000 п.
0000026672 00000 н.
0000027212 00000 н.
0000027339 00000 н.
0000027561 00000 п.
0000036258 00000 п.
0000036433 00000 п.
0000036763 00000 п.
0000036932 00000 п.
0000037148 00000 п.
0000037781 00000 п.
0000037966 00000 п.
0000038261 00000 п.
0000038487 00000 п.
0000045405 00000 п.
0000045589 00000 п.
0000045745 00000 п.
0000045968 00000 п.
0000049491 00000 п.
0000049763 00000 п.
0000050812 00000 п.
0000051073 00000 п.
0000051340 00000 п.
0000051512 00000 п.
0000051686 00000 п.
0000051858 00000 п.
0000052044 00000 п.
0000052236 00000 п.
0000052421 00000 п.
0000052579 00000 п.
0000052813 00000 п.
0000052981 00000 п.
0000053174 00000 п. 0000053360 00000 п.
0000053527 00000 п.
0000053690 00000 п.
0000053904 00000 п.
0000054157 00000 п.
0000054373 00000 п.
0000054622 00000 н.
0000054957 00000 п.
0000055251 00000 п.
0000055559 00000 п.
0000055843 00000 п.
0000056029 00000 п.
0000056212 00000 п.
0000056534 00000 п.
0000056714 00000 п.
0000056877 00000 п.
0000057227 00000 п.
0000057400 00000 п.
0000057730 00000 п.
0000057992 00000 п.
0000058332 00000 п.
0000058588 00000 п.
0000058886 00000 п.
0000059218 00000 п.
0000059398 00000 п.
0000059650 00000 п.
0000059976 00000 п.
0000060379 00000 п.
0000060644 00000 п.
0000060912 00000 п.
0000061178 00000 п.
0000061448 00000 п.
0000061729 00000 п.
0000061945 00000 п.
0000062275 00000 п.
0000062494 00000 п.
0000062662 00000 п.
0000062864 00000 п.
0000063149 00000 п.
0000063313 00000 п.
0000063559 00000 п.
0000063773 00000 п.
0000064048 00000 п.
0000064319 00000 п.
0000064599 00000 п.
0000064813 00000 п.
0000065085 00000 п.
0000065293 00000 п.
0000053360 00000 п.
0000053527 00000 п.
0000053690 00000 п.
0000053904 00000 п.
0000054157 00000 п.
0000054373 00000 п.
0000054622 00000 н.
0000054957 00000 п.
0000055251 00000 п.
0000055559 00000 п.
0000055843 00000 п.
0000056029 00000 п.
0000056212 00000 п.
0000056534 00000 п.
0000056714 00000 п.
0000056877 00000 п.
0000057227 00000 п.
0000057400 00000 п.
0000057730 00000 п.
0000057992 00000 п.
0000058332 00000 п.
0000058588 00000 п.
0000058886 00000 п.
0000059218 00000 п.
0000059398 00000 п.
0000059650 00000 п.
0000059976 00000 п.
0000060379 00000 п.
0000060644 00000 п.
0000060912 00000 п.
0000061178 00000 п.
0000061448 00000 п.
0000061729 00000 п.
0000061945 00000 п.
0000062275 00000 п.
0000062494 00000 п.
0000062662 00000 п.
0000062864 00000 п.
0000063149 00000 п.
0000063313 00000 п.
0000063559 00000 п.
0000063773 00000 п.
0000064048 00000 п.
0000064319 00000 п.
0000064599 00000 п.
0000064813 00000 п.
0000065085 00000 п.
0000065293 00000 п.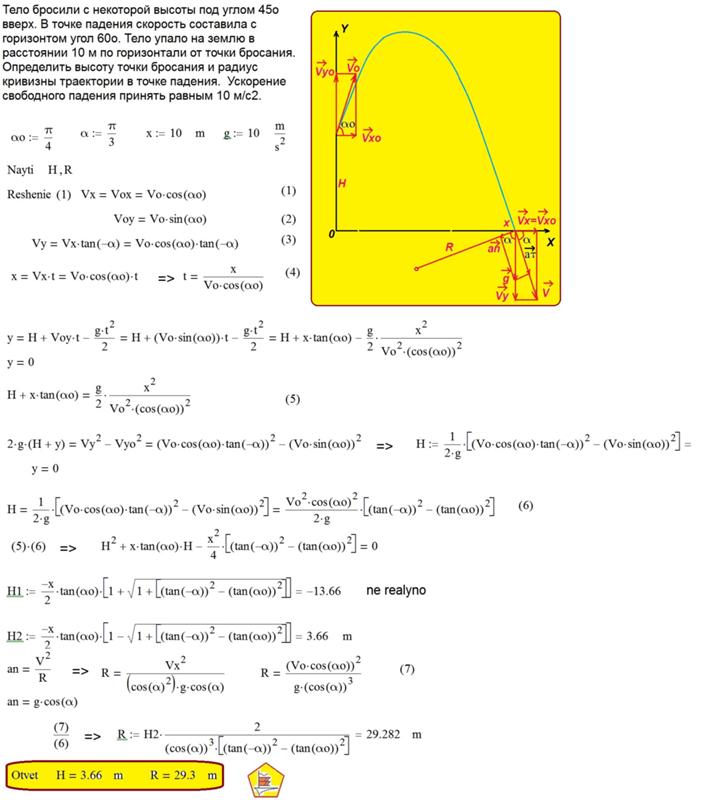 0000065499 00000 п.
0000065770 00000 п.
0000066095 00000 п.
0000066392 00000 п.
0000066697 00000 п.
0000066929 00000 п.
0000067132 00000 п.
0000067434 00000 п.
0000067756 00000 п.
0000068013 00000 п.
0000068301 00000 п.
0000068624 00000 п.
0000068870 00000 п.
0000069341 00000 п.
0000069785 00000 п.
0000070056 00000 п.
0000070503 00000 п.
0000070783 00000 п.
0000071044 00000 п.
0000071242 00000 п.
0000071412 00000 п.
0000071628 00000 п.
0000071799 00000 п.
0000072018 00000 п.
0000072371 00000 п.
0000072658 00000 п.
0000072955 00000 п.
0000073227 00000 н.
0000073524 00000 п.
0000073803 00000 п.
0000074061 00000 п.
0000074406 00000 п.
0000074672 00000 п.
0000074876 00000 п.
0000075185 00000 п.
0000075390 00000 п.
0000075672 00000 п.
0000075923 00000 п.
0000076217 00000 п.
0000076521 00000 п.
0000076758 00000 п.
0000077039 00000 п.
0000077277 00000 п.
0000077526 00000 п.
0000077788 00000 п.
0000078108 00000 п.
0000078419 00000 п.
0000078660 00000 п.
0000065499 00000 п.
0000065770 00000 п.
0000066095 00000 п.
0000066392 00000 п.
0000066697 00000 п.
0000066929 00000 п.
0000067132 00000 п.
0000067434 00000 п.
0000067756 00000 п.
0000068013 00000 п.
0000068301 00000 п.
0000068624 00000 п.
0000068870 00000 п.
0000069341 00000 п.
0000069785 00000 п.
0000070056 00000 п.
0000070503 00000 п.
0000070783 00000 п.
0000071044 00000 п.
0000071242 00000 п.
0000071412 00000 п.
0000071628 00000 п.
0000071799 00000 п.
0000072018 00000 п.
0000072371 00000 п.
0000072658 00000 п.
0000072955 00000 п.
0000073227 00000 н.
0000073524 00000 п.
0000073803 00000 п.
0000074061 00000 п.
0000074406 00000 п.
0000074672 00000 п.
0000074876 00000 п.
0000075185 00000 п.
0000075390 00000 п.
0000075672 00000 п.
0000075923 00000 п.
0000076217 00000 п.
0000076521 00000 п.
0000076758 00000 п.
0000077039 00000 п.
0000077277 00000 п.
0000077526 00000 п.
0000077788 00000 п.
0000078108 00000 п.
0000078419 00000 п.
0000078660 00000 п.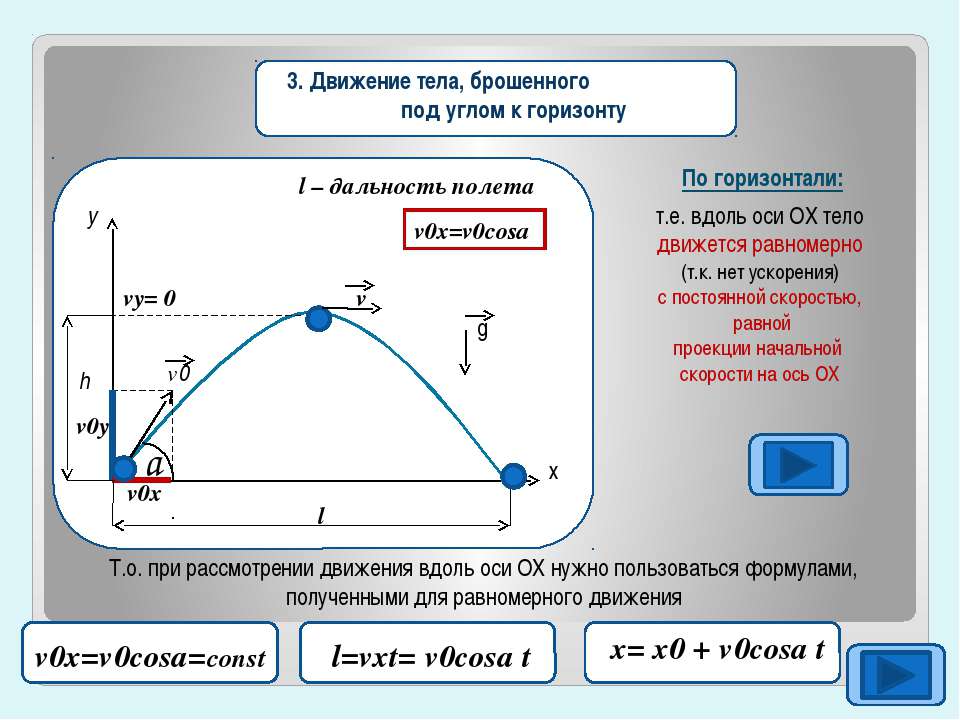 0000078990 00000 н.
0000079174 00000 п.
0000079560 00000 п.
0000079784 00000 п.
0000079999 00000 н.
0000082837 00000 п.
0000082990 00000 п.
0000083147 00000 п.
0000083356 00000 п.
0000084097 00000 п.
00000
0000078990 00000 н.
0000079174 00000 п.
0000079560 00000 п.
0000079784 00000 п.
0000079999 00000 н.
0000082837 00000 п.
0000082990 00000 п.
0000083147 00000 п.
0000083356 00000 п.
0000084097 00000 п.
00000
Как запустить мяч, чтобы достичь наибольшего расстояния?
В эпизоде «Движение снаряда» телеканала NBC Learn «Наука о футболе НФЛ» вы видите, что мячи с иглами движутся по дуге, известной математикам как парабола.
swf?VIDEO_ID=1248037″ allowscriptaccess=»always» salign=»tl» quality=»high» bgcolor=»#000000″ name=»NBC_Learn_Video» type=»application/x-shockwave-flash» allowfullscreen=»true»/>
В любом футбольном матче обе команды сражаются друг с другом, а также с общим противником — гравитацией. Гравитационное притяжение Земли делает передачу на дальние дистанции сложной задачей и сбивает даже самые сильные удары пантов и метких ударов.
Поскольку сила тяжести постоянна, опытные квотербэки и кикеры могут учитывать ее эффекты, чтобы максимально эффективно перемещать мяч вниз по полю. Как и все снаряды, футбольный мяч, будучи выпущенным, следует траекторией, известной в математических терминах как парабола — симметричная дуга, которая в конечном итоге возвращает мяч обратно на землю. (В реальной жизни на полет снаряда влияет не только сила тяжести, но и ветер, и сопротивление воздуха, поэтому парабола не будет идеальной.)
Параболы изучались тысячелетиями, и их свойства хорошо изучены. Для любого снаряда, находящегося под действием силы тяжести, расстояние, достигаемое во время полета, равно sin (2θ) X v² / g, где v — начальная скорость снаряда, g — ускорение к Земле под действием силы тяжести и θ — угол, под которым запускается снаряд.
Для любого снаряда, находящегося под действием силы тяжести, расстояние, достигаемое во время полета, равно sin (2θ) X v² / g, где v — начальная скорость снаряда, g — ускорение к Земле под действием силы тяжести и θ — угол, под которым запускается снаряд.
Это может выглядеть как сложное уравнение, но пару переменных можно игнорировать. Во-первых, поскольку сила тяжести постоянна, г и будут одинаковыми независимо от того, как игрок бьет по мячу.Во-вторых, для игрока, пытающегося как можно глубже забить мяч, вы можете предположить, что он бьет так сильно, как может физически, поэтому против зависит просто от того, насколько сильно он может ударить, а не от какого-либо стратегического решения для данного конкретного случая. плоскодонка.
Единственный выбор, который он должен сделать, чтобы максимизировать расстояние, — это угол, под которым он бьет по мячу. Из приведенного выше уравнения видно, что расстояние, пройденное мячом, будет наибольшим, когда sin (2θ) наибольший. Синусоидальная функция достигает своего наибольшего выходного значения, 1, с входным углом 90 градусов, поэтому мы можем видеть, что для пантов с наибольшим радиусом действия 2θ = 90 градусов и, следовательно, θ = 45 градусов.Другими словами, снаряд летит дальше всего, когда он запущен под углом 45 градусов.
Синусоидальная функция достигает своего наибольшего выходного значения, 1, с входным углом 90 градусов, поэтому мы можем видеть, что для пантов с наибольшим радиусом действия 2θ = 90 градусов и, следовательно, θ = 45 градусов.Другими словами, снаряд летит дальше всего, когда он запущен под углом 45 градусов.
Но как насчет попытки увеличить высоту снаряда для увеличения времени зависания? В параболе максимальная высота, достигаемая снарядом, равна (sin (θ)) ² X v² / 2g. Еще раз, мы можем игнорировать v и g, по тем же причинам, что и выше. (Любой, кто хочет поднять снаряд как можно выше, просто запустит его как можно быстрее, а гравитация будет постоянной.)
Итак, чтобы отправить снаряд так высоко, как он может лететь, вы можете увидеть, что вы хотите сделать ( sin (θ)) ² как можно больше, что означает просто сделать sin (θ) как можно большим.Как упоминалось выше, синусоидальная функция достигает своего наибольшего выходного значения, 1, с входным углом 90 градусов, поэтому мы можем видеть, что для заоблачной высоты θ = 90.


 Значит траектория — парабола.
Значит траектория — парабола.
Leave A Comment