Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Углы |
| Вписанные и центральные углы |
| Углы, образованные хордами, касательными и секущими |
| Доказательства теорем об углах, связанных с окружностью |
Вписанные и центральные углы
Определение 1. Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Рис. 1
Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Рис. 2
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема |
| Вписанный угол | Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство | |
| Вписанный угол | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |
| Вписанный угол | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |
| Вписанный угол | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды | |
| Вписанный угол | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |
| Окружность, описанная около прямоугольного треугольника | Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
| Вписанный угол |
Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство |
Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны. |
Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды |
Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |
Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
Теоремы об углах, образованных хордами, касательными и секущими
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами | Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство | ||
| Угол, образованный секущими, которые пересекаются вне круга | Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | ||
| Угол, образованный касательной и хордой, проходящей через точку касания | Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство | ||
| Угол, образованный касательной и секущей | Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | ||
| Угол, образованный двумя касательными к окружности | Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный пересекающимися хордами хордами |
| Формула: |
Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство |
| Угол, образованный секущими секущими, которые пересекаются вне круга |
| Формула: |
Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и хордой хордой, проходящей через точку касания |
| Формула: |
Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и секущей касательной и секущей |
| Формула: |
Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный двумя касательными касательными к окружности |
| Формулы: |
Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
Доказательства теорем об углах, связанных с окружностью
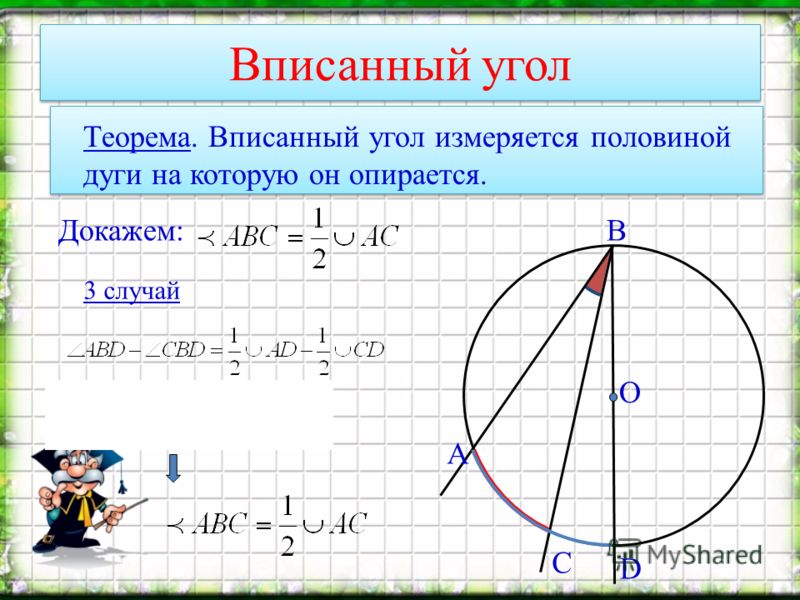
Теорема 1.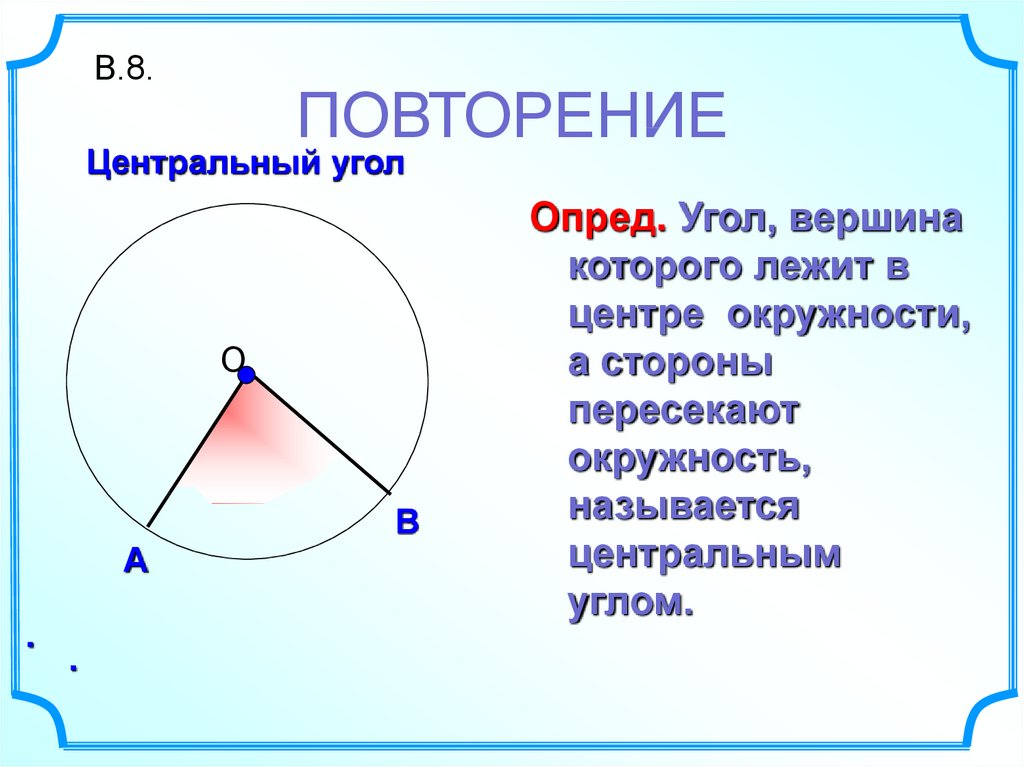 Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).
Рис. 5
Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
Рис. 6
В этом случае справедливы равенства
и теорема 1 в этом случае доказана.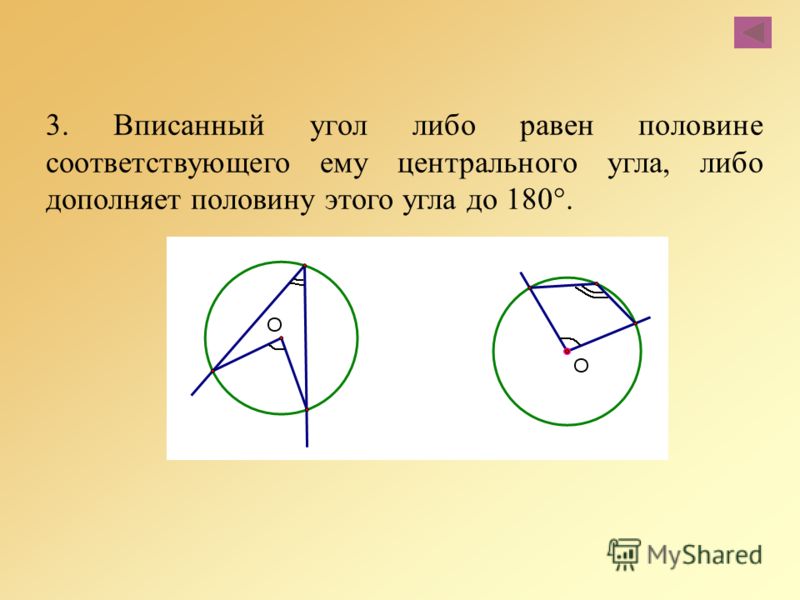
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
Рис. 7
В этом случае справедливы равенства
что и завершает доказательство теоремы 1.
Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 8.
Рис. 8
Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.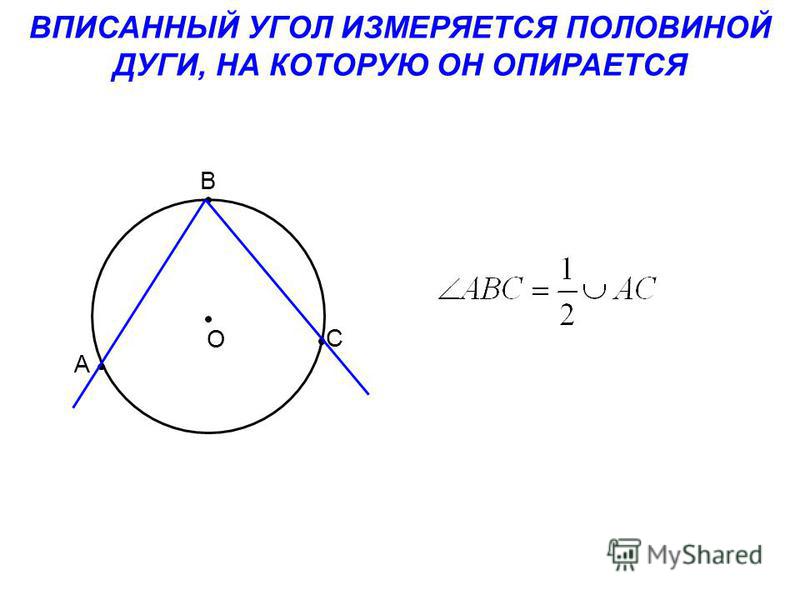
Доказательство. Рассмотрим рисунок 9.
Рис. 9
Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство. Рассмотрим рисунок 10.
Рис. 10
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать
Теорема 5.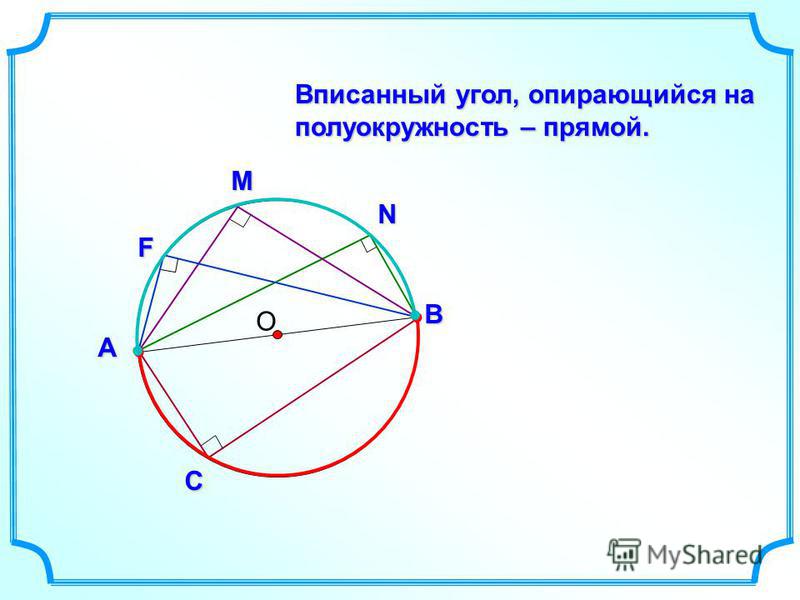 Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.
Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 11.
Рис. 11
Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать.
Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 12.
Рис. 12
Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют π радиан.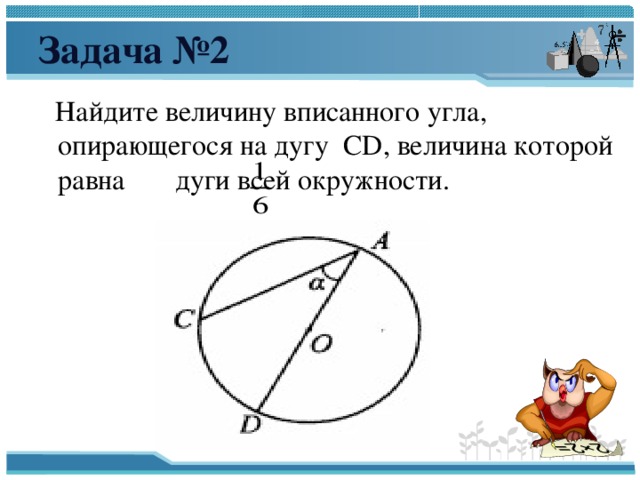 Поэтому справедливо равенство
Поэтому справедливо равенство
α = π – γ .
Далее получаем
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Теорема о вписанном угле / Окружность / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Теорема о вписанном угле
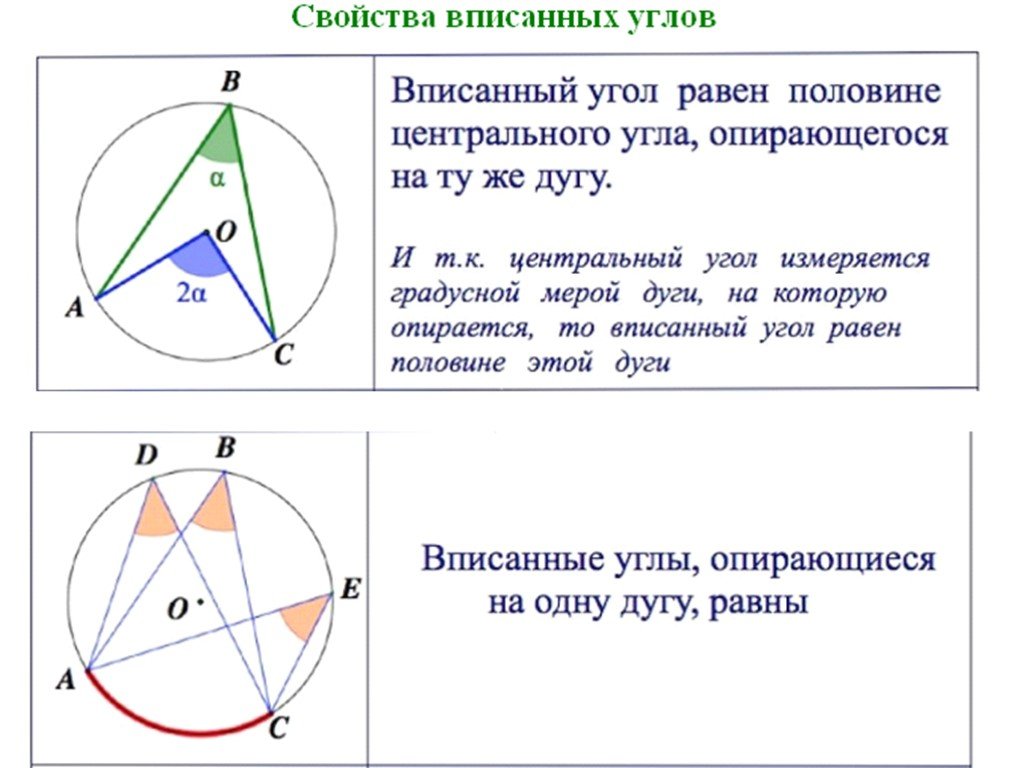
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
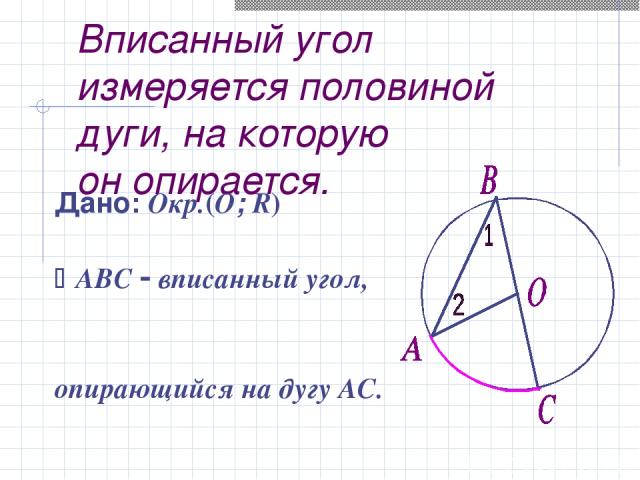
На рисунке 1 угол ВАС вписанный, дуга ВLС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу ВLC.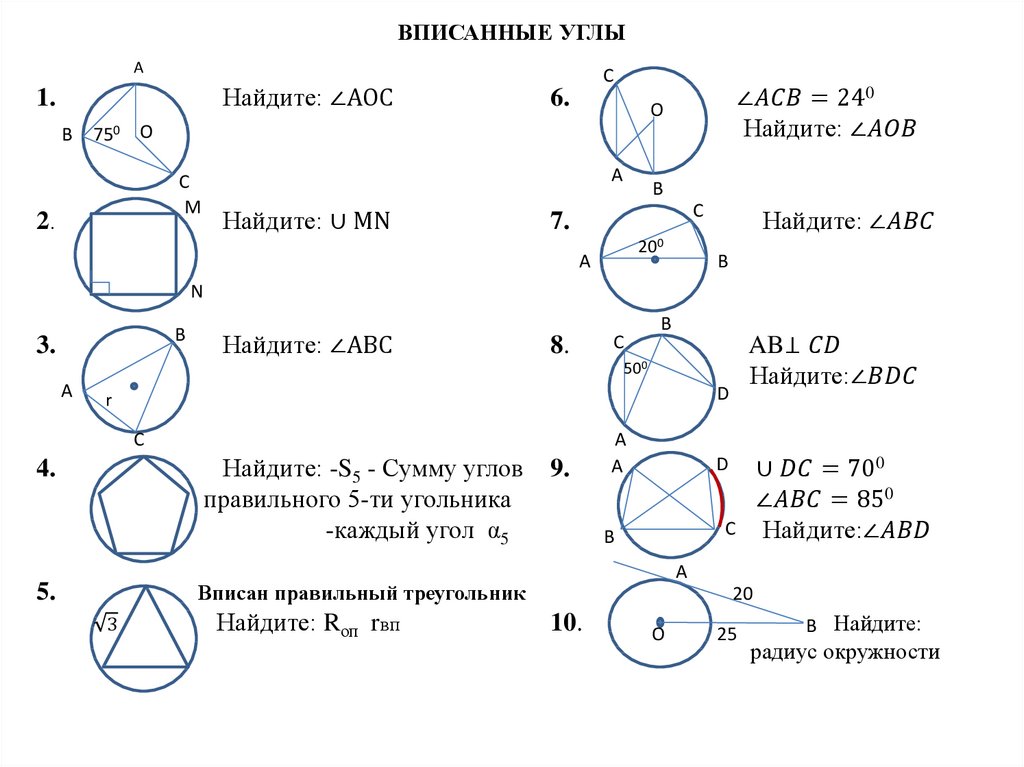
Теорема
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Доказательство
Дано: окружность (О), АВС — вписанный, АС — внутри АВС.
Доказать: АВС = АС.
Доказательство:
1 случай
Луч ВО совпадает с одной из сторон угла АВС.
Пусть ВО совпадает с ВС (Рис. 2).
В данном случае дуга АС меньше полуокружности, следовательно, АОС =АС (т.к. АОС — центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).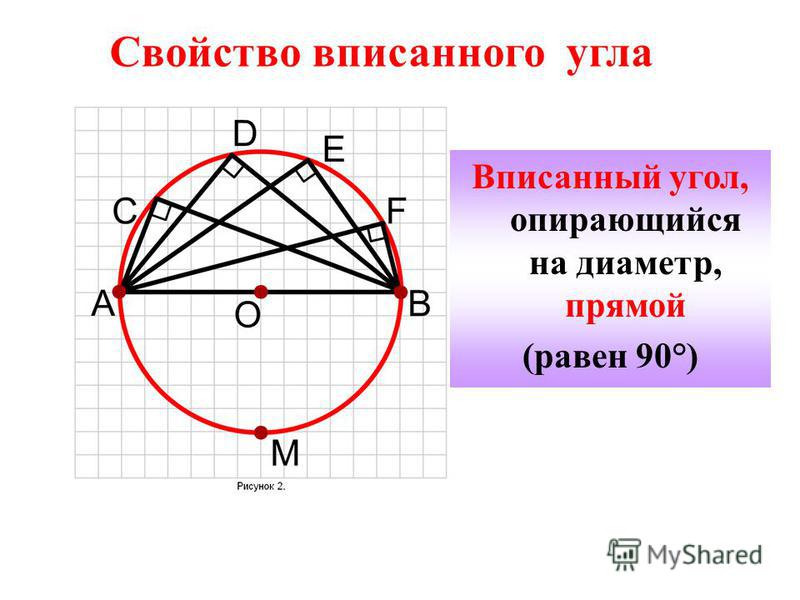
АВО — равнобедренный с основанием АВ (т.к. ОА = ОВ — радиусы), 1 = 2 (углы при основании). АОС — внешний угол АВО, АОС = 1 + 2 = 21. Следовательно, учитывая то, что АОС =АС, получим: АС = 2 1, откуда 1 = АС, т.е. АВС = АС.
2 случай
Луч ВО делит угол АВС на два угла.
В данном случае луч ВО пересекает дугу АС в некоторой точке D (Рис. 3).
Точка D разделят дугу АС на две дуги: АD и DС, поэтому АС = АD + DС.
Луч ВD разделяет угол АВС на два угла, поэтому АВС = АВD + DВС.
По доказанному в 1 случае АВD = АD и DВС = DС. Складывая эти равенства, получаем: АВD + DВС = АD + DС или АВD + DВС = (АD + DС). Следовательно, АВС = АС.
3 случай
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
В данном случае луч ВС пересекает дугу АD в точке С (Рис.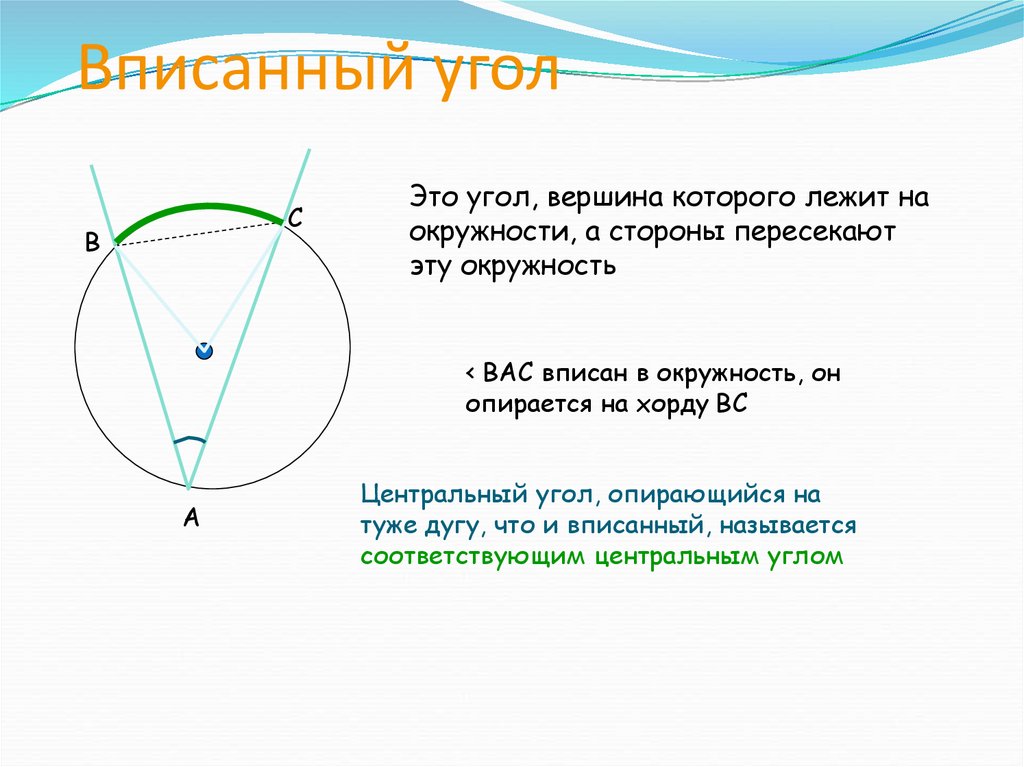 4).
4).
Точка С разделят дугу АD на две дуги: АC и CD, поэтому АD = АC + CD, откуда АC = АD — CD.
Луч ВС разделяет угол АВD на два угла, поэтому АВD = АВC + CВD, откуда АВC = АВD — CВD.
По доказанному в 1 случае АВD = АD и СВD = СD. Вычитая из первого равенства второе, получаем: АВD — СВD = АD — CD или АВD — СВD = (АD — CD).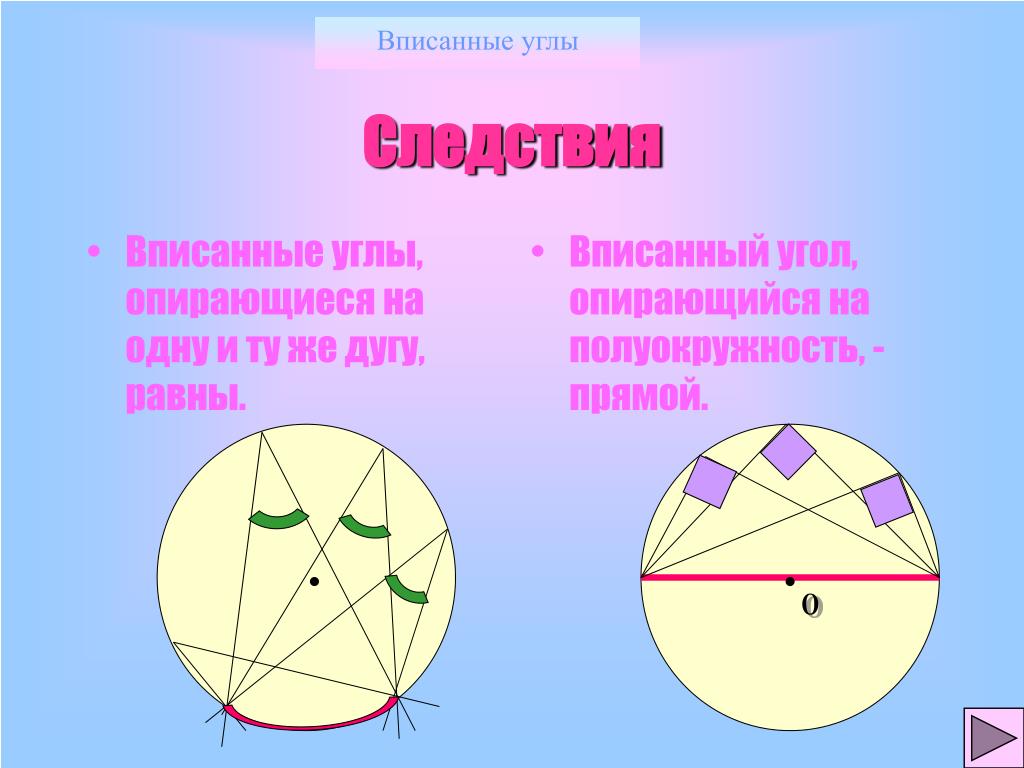 Следовательно, АВС = АС.
Следовательно, АВС = АС.
Теорема доказана.
Следствия из теоремы о вписанном угле
| 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис. 5). |
| 2. Вписанный угол, опирающийся на полуокружность, — прямой (рис. 6). |
Теорема
| Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Доказательство
Дано: окружность, АВ и СD — хорды, АВСD = Е
Доказать: АЕВЕ = СЕDЕ.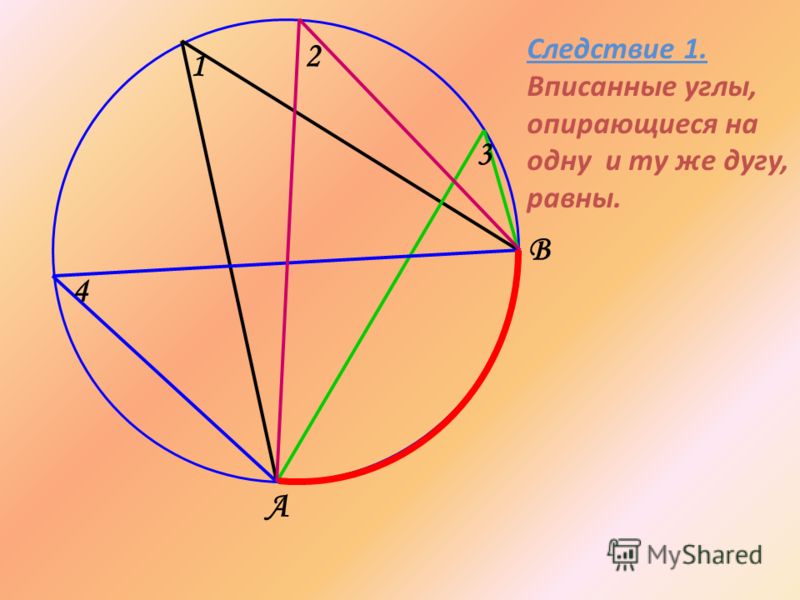
Доказательство:
В АDЕ и СВЕ: 1 = 2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле), 3 = 4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому , откуда
Теорема
| Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. |
Доказательство
Дано: окр.(О, ), АВ — хорда, АС — касательная, А — точка касания.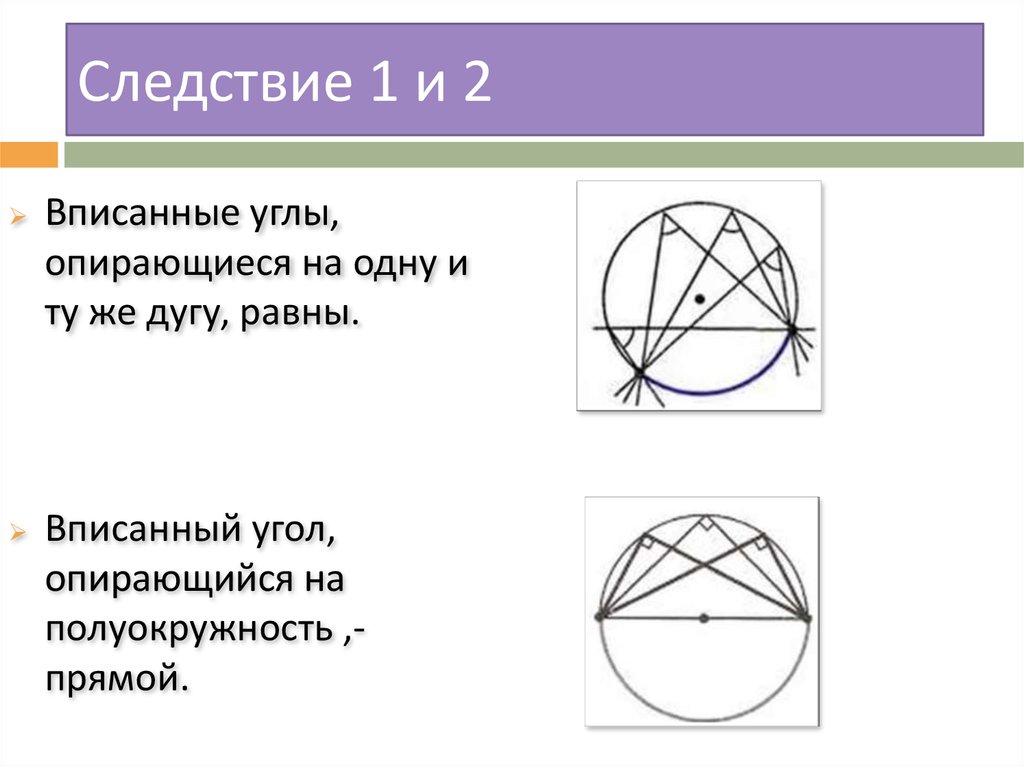
Доказать: ВАС = АВ.
Доказательство:
АОВ — равнобедренный с основанием АВ, т.к. ОА = ОВ = , значит, ОАВ = ОВА (как углы при основании), при этом ОААС (свойство касательной), поэтому ОАВ = ОВА = 900 — ВАС. Следовательно, по теореме о сумме углов треугольника: 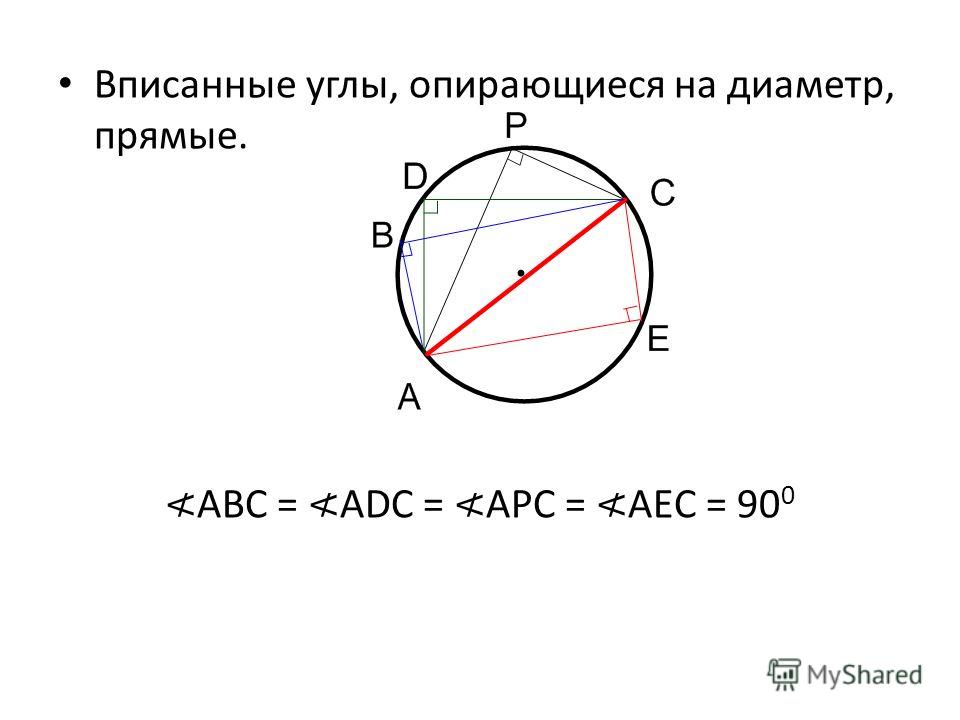 Теорема доказана.
Теорема доказана.
Советуем посмотреть:
Взаимное расположение прямой и окружности
Касательная к окружности
Градусная мера дуги окружности
Свойство биссектрисы угла
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 655, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 658, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 661, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 662, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 665, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 667, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 703, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1035, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1099, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1134, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Теорема о вписанном угле.
 Определение, теорема, доказательство, примеры
Определение, теорема, доказательство, примерыВ теореме о вписанном угле упоминается, что угол, вписанный внутрь окружности, всегда равен половине меры центрального угла или дуги, проведенной с ним, которая имеет общие концы сторон вписанного угла. В окружности угол, образованный двумя хордами с общими концами окружности, называется вписанным углом, а общий конец считается вершиной угла. В этом разделе мы узнаем о теореме о вписанном угле, доказательстве теоремы и решим несколько примеров.
| 1. | Что такое теорема о вписанном угле? |
| 2. | Свойства вписанного угла Теорема |
| 3. | Доказательство теоремы о вписанном угле |
| 4. | Часто задаваемые вопросы по теореме о вписанном угле |
Что такое теорема о вписанном угле?
Теорема о вписанном угле также называется теоремой об угле в центре, поскольку вписанный угол равен половине центрального угла.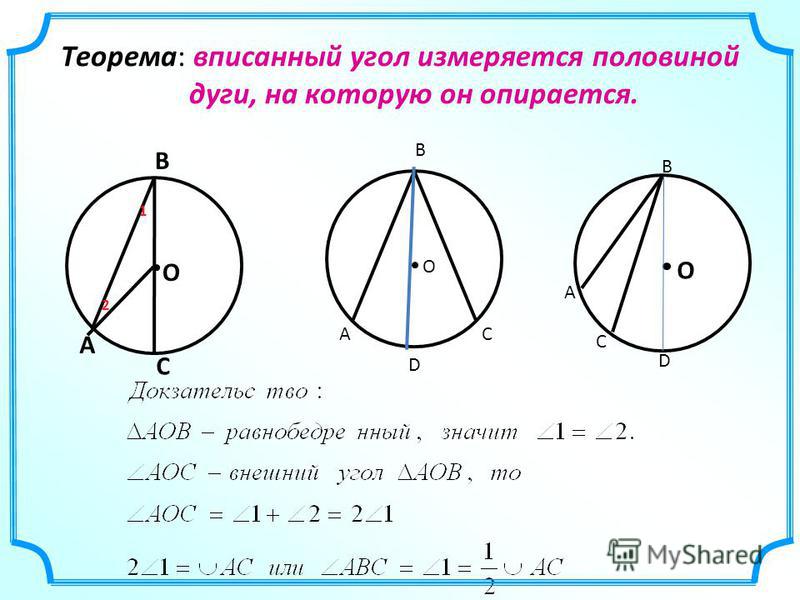 Поскольку конечные точки фиксированы, центральный угол всегда один и тот же, независимо от того, где он находится на одной дуге между конечными точками. Теорему о вписанном угле также называют теоремой о стреле или теоремой о центральном угле. Эта теорема утверждает, что: мера центрального угла равна удвоенной мере вписанного угла, опирающегося на ту же дугу. ИЛИ. Вписанный угол — это половина центрального угла, опирающегося на ту же дугу. ИЛИ. Угол в центре окружности вдвое больше любого угла на окружности, опирающейся на ту же дугу. Нам нужно помнить эти три термина для теоремы:
Поскольку конечные точки фиксированы, центральный угол всегда один и тот же, независимо от того, где он находится на одной дуге между конечными точками. Теорему о вписанном угле также называют теоремой о стреле или теоремой о центральном угле. Эта теорема утверждает, что: мера центрального угла равна удвоенной мере вписанного угла, опирающегося на ту же дугу. ИЛИ. Вписанный угол — это половина центрального угла, опирающегося на ту же дугу. ИЛИ. Угол в центре окружности вдвое больше любого угла на окружности, опирающейся на ту же дугу. Нам нужно помнить эти три термина для теоремы:
- Вписанный угол — это угол, вершина которого лежит на окружности, а две его стороны лежат на хорде этой же окружности.
- Центральный угол — это угол, вершина которого лежит в центре окружности с двумя радиусами в качестве сторон угла.
- Пересекаемая дуга представляет собой угол, образованный концами двух хорд на окружности окружности.
На изображении выше AB = пересекаемая дуга, θ = вписанный угол и 2θ = центральный угол.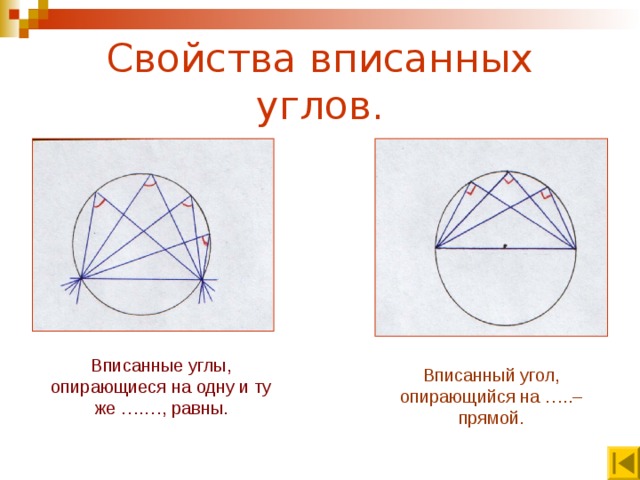
Свойства вписанного угла Теорема
Теорема о вписанном угле имеет три основных свойства, связанных с центральным углом, а именно:
- Вписанный угол, опирающийся на ту же дугу, равен. (см. изображение ниже для справки)
- Вписанный в полуокружность угол равен 90°.
- Центральные углы, опирающиеся на дуги, имеют одинаковую длину.
На изображении выше мы видим, что….
Доказательство теоремы о вписанном угле
Для доказательства теоремы о вписанном угле необходимо рассмотреть три случая:
- Вписанный угол находится между хордой и диаметром окружности.
- Диаметр находится между лучами вписанного угла.
- Диаметр вне лучей вписанного угла.
Случай 1. Вписанный угол находится между хордой и диаметром окружности.
Здесь нужно доказать, что ∠AOB = 2θ
На изображении выше давайте рассмотрим, что ∆OBD является равнобедренным треугольником, где OD = OB = радиус окружности. Следовательно, ∠ODB = ∠DBO = вписанный угол = θ. Диаметр AD представляет собой прямую линию, поэтому ∠BOD = 180 — ∠AOB (назовем это x). Согласно свойству суммы углов ∠ODB + ∠DBO + ∠BOD = 180°.
Следовательно, ∠ODB = ∠DBO = вписанный угол = θ. Диаметр AD представляет собой прямую линию, поэтому ∠BOD = 180 — ∠AOB (назовем это x). Согласно свойству суммы углов ∠ODB + ∠DBO + ∠BOD = 180°.
θ + θ + (180 — х) = 180
2θ + 180 — х = 180
2θ — х = 180 — 180
2θ — х = 0
х = 2θ.
Следовательно, ∠AOB = 2θ. Значит доказано.
Случай 2: Диаметр находится между лучами вписанного угла.
Здесь нам нужно доказать, что ∠ACB = 2θ
На изображении выше мы рисуем диаметр пунктирными линиями, которые делят пополам оба угла, как показано, т.е. а 1 + а 2 . Из случая 1 мы уже знаем, что 1 = 2θ 1 и 2 = 2θ 2 . Когда мы складываем углы, мы получаем:
a 1 + a 2 = 2θ 1 + 2θ 2
A 1 + A 2 = 2 (θ 1 + θ 2 )
A 1 + A 2 )
A 1 + A 2 )
A 1 + A 2 )
A 1 + A 2 )
a = 2θ
Отсюда доказано, что ∠ACB = 2θ.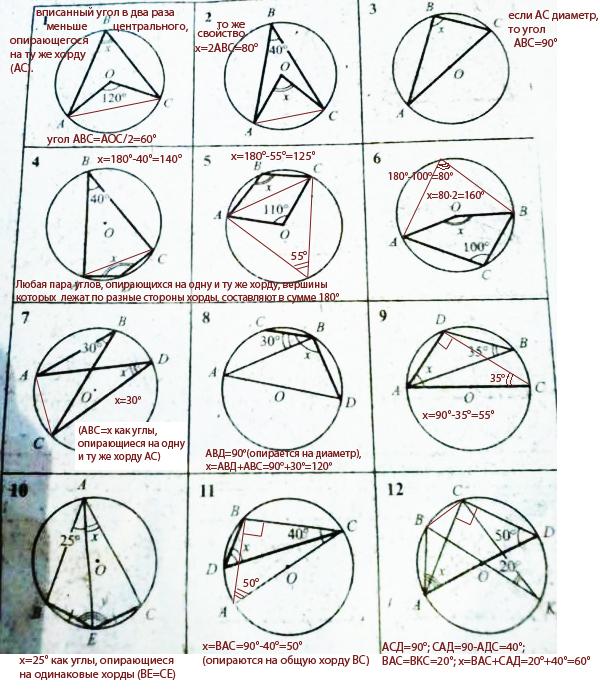
Случай 3: Диаметр вне лучей вписанного угла.
Нужно доказать, что a = 2θ в нижнем круге.
Из приведенного выше круга мы уже знаем,
a 1 = 2θ 1
2 (θ 1 + θ) = а 1 + а
Но, а 1 = 2θ 1 и а 2 9 = 10θ Подставляя, получаем
2θ 1 + 2θ = 2θ 1 + a
a = 2θ.
Отсюда доказано.
Связанные темы
Ниже перечислены некоторые темы, связанные с теоремой о вписанном угле.
- Последовательный внутренний угол
- Внешний угол Теорема
- Калькулятор центрального угла
- Биссектриса
Часто задаваемые вопросы по теореме о вписанном угле
Что подразумевается под теоремой о вписанном угле?
Теорема о вписанном угле, также называемая теоремой о центральном угле, утверждает, что угол, образуемый дугой в центре окружности, в два раза больше угла, образуемого дугой в любой другой точке окружности.
Что утверждает теорема о вписанном угле?
Теорема о вписанном угле утверждает, что угол, вписанный в окружность, равен половине центрального угла, опирающегося на ту же дугу окружности.
Что такое вписанный угол?
Угол, образуемый дугой в любой точке окружности, называется вписанным углом.
В чем разница между центральным углом и вписанным углом?
Центральный угол — это угол, образуемый дугой в центре окружности. Вписанный угол — это угол, опирающийся на дугу в любой точке окружности.
Что такое вписанный угол?
Руководство по теоремам о вписанном угле окружности и вычислениям окружности
Что такое вписанный угол?
Contents
Definition: An inscribed angle is an angle whose vertex lies on окружность круга.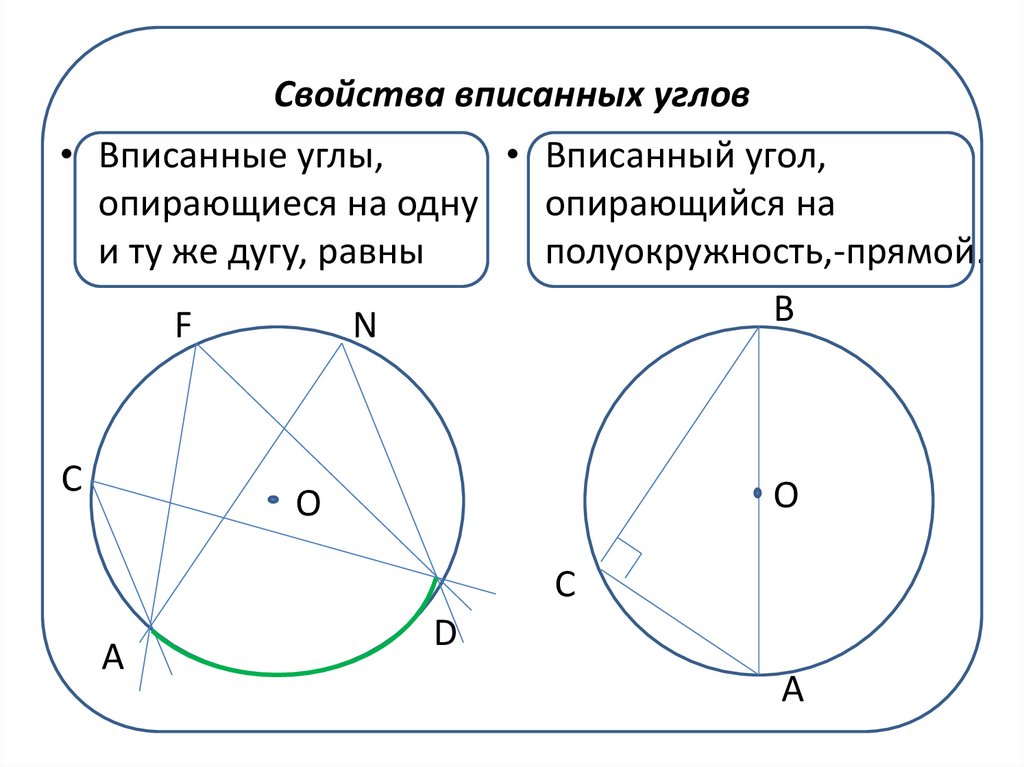 Вершина — это общая точка концов двух сторон угла.
Вершина — это общая точка концов двух сторон угла.
Вписанный угол может быть определен как угол, стягиваемый в точке на окружности двумя заданными точками на окружности. Вписанный угол — это угол, образованный внутри окружности двумя хордами, имеющими общий конец на окружности.
Эта общая конечная точка образует вершину вписанного угла.
Вписанный угол окружности
Вписанный угол Теоремы и характеристики
- Угол в центре вдвое больше угла на окружности.
Угол, образованный в центре круга линиями, исходящими из двух точек на окружности круга, в два раза больше угла, образованного на окружности круга линиями, исходящими из тех же точек. - Угол, вписанный в полуокружность, является прямым углом.
Углы, образованные проведением линий от концов диаметра круга к его окружности, всегда образуют прямой угол. - Вписанные в окружность углы, опирающиеся на одну дугу, равны.
Углы в одном сегменте равны. Углы, образованные двумя точками на окружности, равны другим углам той же дуги, образованным из этих двух точек.
Использование
Вписанный угол используется во многих доказательствах элементарной евклидовой геометрии плоскости. Вписанный угол является основой для нескольких других теорем, связанных со степенью точки относительно окружности.
Важность
Вписанный угол является очень важной частью теоремы о окружности. Теоремы о четырех кругах напрямую основаны на вписанном угле.
Угол в центре вдвое больше угла на окружности. Угол, вписанный в полуокружность, является прямым углом.
Вписанные в окружность углы, опирающиеся на одну дугу, равны.
Во вписанный четырехугольник четыре угла. Противоположные углы вписанного четырехугольника являются дополнительными.
Вписанный угол
ФормулаУгол вписан в окружность, если угол имеет вершину на этой окружности и имеет стороны, содержащие две хорды одной и той же окружности.
Вписанный угол равен половине дуги, на которую он опирается, или можно сказать, что угол в центре в два раза больше угла на окружности (вписанный угол).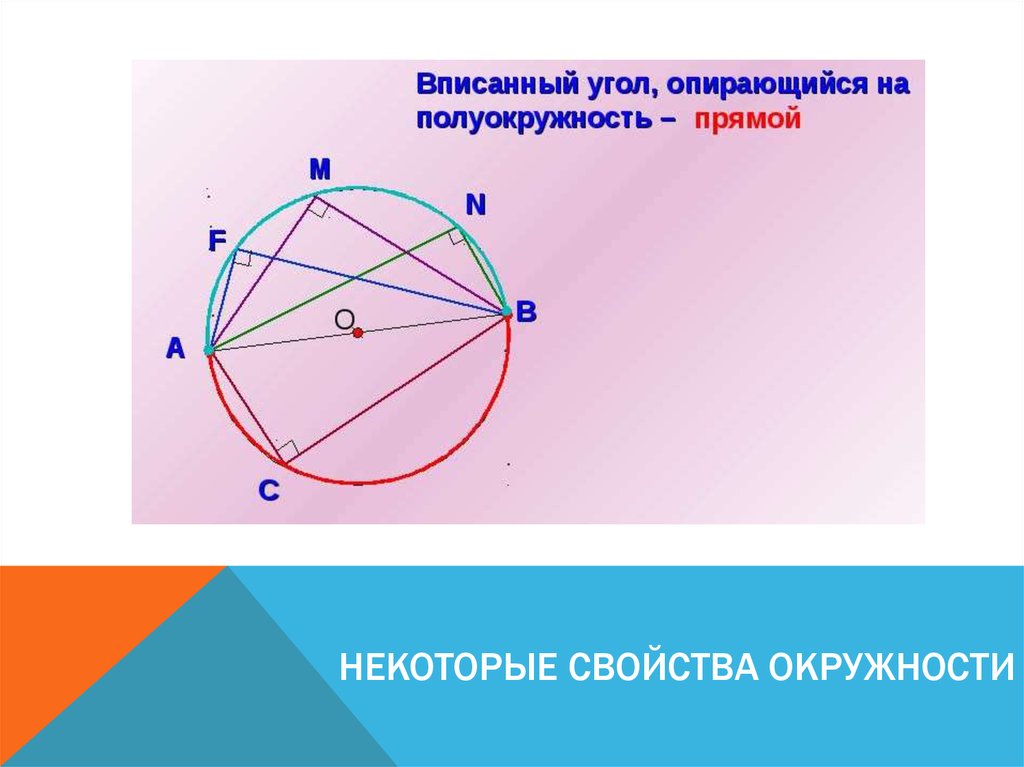
Угол, вписанный в полуокружность, является прямым углом.
Вписанные в окружность углы, опирающиеся на одну дугу, равны.
Противоположные углы вписанного четырехугольника в сумме дают 180.
Примеры вписанных углов
Вписанные углы в полукруги
Угол, вписанный в полуокружность, является прямым углом
Диаметр опирается на вписанный угол, равный 90°, всегда на окружности окружности.
Пример
В приведенном выше круге O — центральная точка, AC — диаметр. От концов диаметра проводят две линии АВ и СВ, сходящиеся на окружности окружности в точке В.
Угол В — вписанный угол, проведенный от концов диаметра окружности к ее окружности, угол B – прямой угол (90°).
В приведенном выше круге O — центральная точка, AB — диаметр. От концов диаметра проводят две линии АС и ВС, которые встречаются на окружности окружности в точке С.
Угол С — вписанный угол, проведенный от концов диаметра окружности к ее окружности, угол C — прямой угол (90°), а угол AOB равен 180°, что в два раза больше 90°.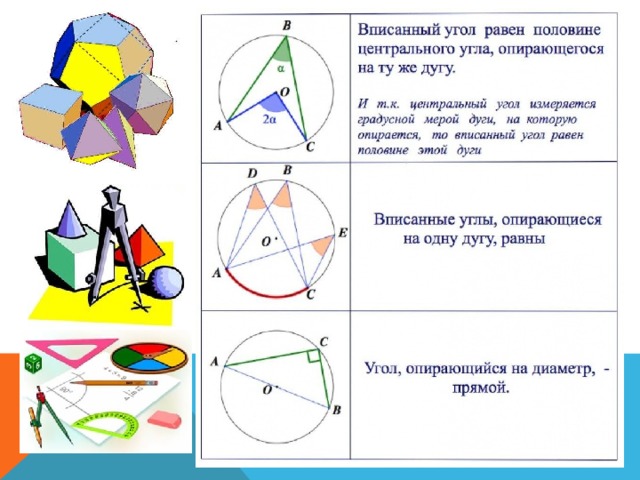 Угол в центре (∠AOB) в два раза больше угла на окружности (∠ACB).
Угол в центре (∠AOB) в два раза больше угла на окружности (∠ACB).
Вписанный угол окружности
Вписанные в окружность углы, опирающиеся на одну и ту же дугу, равны.
Любые два угла, вписанные в окружность с одинаковыми дугами, пересекаемыми, всегда конгруэнтны (равны по мере).
Пример
В приведенном выше круге О — центральная точка; угол А и угол D вписанные углы, опирающиеся на одну дугу ВС. Мера угла A равна мере угла D. Угол A равен углу D.
∠A ≅ ∠D
Вписанный угол во вписанном четырехугольнике
Противоположные углы вписанного четырехугольника являются дополнительными.
Вписанный четырехугольник имеет все вершины на окружности. Во вписанном четырехугольнике четыре вписанных угла, противоположные углы во вписанном четырехугольнике являются дополнительными. Сумма противоположных углов вписанного четырехугольника всегда равна 180°.
Пример
На рисунке выше четырехугольник вписан в окружность.



Leave A Comment