Трапеция. Определение, виды, свойства
- Содержание
- Определения
- Виды трапеций
- Свойства трапеции
- Свойства равнобокой (равнобедренной) трапеции
Определения
Определение 1. Трапецией называется четырехугольник, у которого две стороны параллельны а две другие − нет.
На Рис.1 четырехугольники ABCD и EFGH являются трапециями.
Параллельные стороны трапеции называются основаниями трапеции, а непараллельные стороны − боковыми сторонами (Рис.2).
В трапеции ABCD (Рис.1) углы A и B называют углами при основании AB, а углы C и D называют углами при основании CD.
Определение 2. Высотой трапеции называется перпендикуляр, отпущенный из любой точки прямой, проходящей через один из оснований трапеции, на прямую, проходящую через другое основание.
На Рис.3 отрезки DM, ON, QP являются вершинами трапеции ABCD. Поскольку величина каждой из этих отрезков является расстоянием между параллельными прямыми, проходящими через основания трапеции, то они равны друг другу.
Определение 3. Средней линией трапеции называется отрезок, соединяющий средние точки боковых сторон.
На рисунке Рис.4 \( \small MN \) является средней линией трапеции \( \small ABCD, \) причем \( \small AM=MD,\;\; BN=NC. \)
Виды трапеций
Если боковые стороны трапеции равны, то трапеция называется равнобокой или равнобедренной (Рис.5).
Трапеция называется прямоугольной, если одна из боковых сторон перпендикуляна основаниям трапеции (Рис.6).
Трапеция называется разносторонней, если длина всех сторон разные (т.е. если трапеция не прямоульная и не равнобедренная)(Рис.7).
Свойства трапеции
Свойство 1. Средняя линия трапеции параллельна основаниям и равна половине их суммы.
Доказательство. Пусть MN средняя линия трапеции ABCD (Рис.8). Докажем, что \( \small MN || AB, \) \( \small MN=\frac12 (AB+CD). \)
Проведем прямую DN и обозначим точку ее пересечения с прямой AB точкой P. Так как MN является средней линией трапеции ABCD, то
| CN = NB | (1) |
Углы 1 и 2 вертикальные , следовательно
| \( \small \angle 1=\angle 2. \) | (2) |
Углы 3 и 4 являются накрест лежащими, при рассмотрении параллельных прямых BP и CD пересеченные секущей CB, тогда (теорема 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей).
| \( \small \angle 3=\angle 4. \) | (3) |
Исходя из равенств (1),(2) и (3) получим, что треугольники CND и NPC равны, по второму признаку равенства треугольников.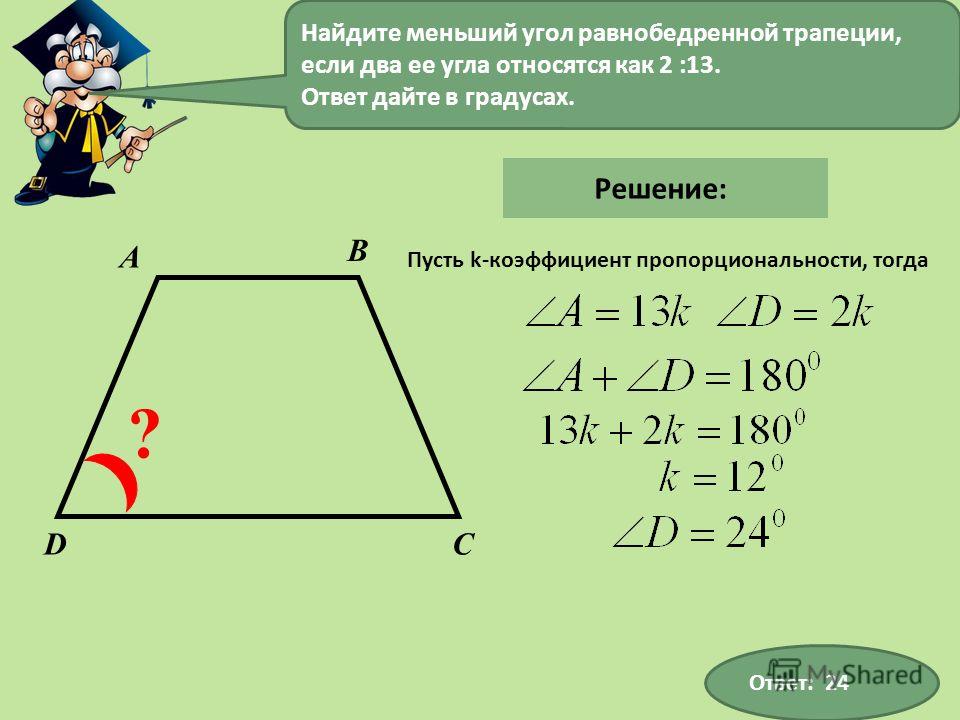 Тогда
Тогда
Свойство 2. Сумма углов трапеции, прилежащих к одной боковой стороне равна 180°.
Доказательство. Рассмотрим трапецию ABCD (Рис.9).
Углы A и D являутся односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда \( \small \angle A+ \angle D=180°.\)
Свойство 3. Отрезок, слединяющий середины диагоналей трапеции лежит на средней линии трапеции и равен половине разности оснований.
Доказательство. Рассмотрим трапецию ABCD (Рис.10).
Поскольку точки P и Q являются средними точками диагоналей AC и BD, соответственно, то:
MP − является средней линией треугольника ADC, так как , .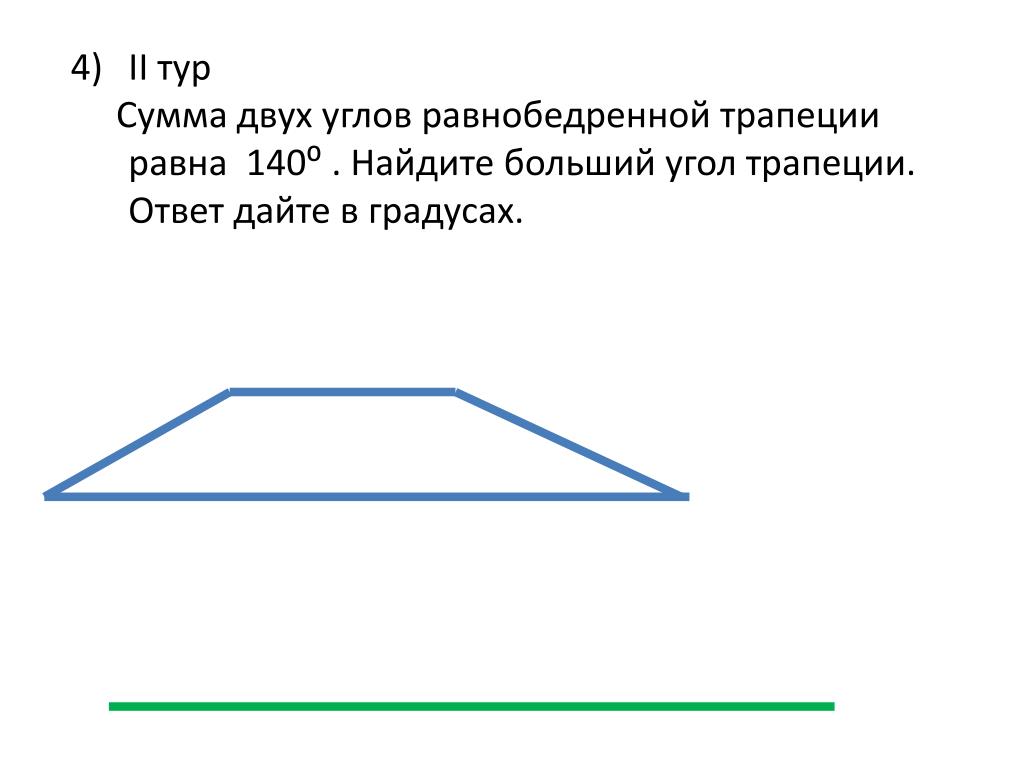 Тогда
Тогда
QN − является средней линией треугольника BCD, так как , Тогда
Из и следует, что P находится на прямой, проходящей через среднюю линию
Аналогично, из и следует, что Q находится на прямой, проходящей через среднюю линию MN, поскольку из точки N можно провести только одну прямую, параллельно CD.
Далее, учитывая (4) и (5), получим:
Откуда
Далее, учитывая свойство 1, получим:
Свойства равнобокой (равнобедренной) трапеции
Свойсво 1′. В равнобокой трапеции углы при каждом основании равны.
Доказательство. Рассмотрим равнобедренную (равнобокую) трапецию ABCD, где AD = BC (Рис.11).
Проведем высоты DM и CN. Поскольку DM = CN и AD = BC, то прямоугольники ADM и NCB равны гипотенузе и катету (см. статью Прямоугольный треугольник. Свойства, признаки равенства). Тогда \( \small \angle A=\angle B. \) Докажем, далее, что \( \small \angle ADC=\angle DCB. \) \( \small \angle A +\angle ADC=180° \) поскольку углы A и ADC являются односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle B +\angle DCB=180°. \) Учитывая, что \( \small \angle A=\angle B \), получим \( \small \angle ADC=\angle DCB. \)
статью Прямоугольный треугольник. Свойства, признаки равенства). Тогда \( \small \angle A=\angle B. \) Докажем, далее, что \( \small \angle ADC=\angle DCB. \) \( \small \angle A +\angle ADC=180° \) поскольку углы A и ADC являются односторонними углами, при рассмотрении параллельных прямых AB и CD пересеченные секущей AD (теорема 3 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle B +\angle DCB=180°. \) Учитывая, что \( \small \angle A=\angle B \), получим \( \small \angle ADC=\angle DCB. \)
Свойсво 2′. В равнобокой трапеции диагонали равны.
Доказательство. Рассмотрим треугольники ADC и DCB (Рис.12). Имеем CD общая сторона для обеих треугольников, AD = CB, \( \small \angle ADC=\angle DCB. \) Тогда треугольники равны по двум сторонам и углу между ними. Следовательно диагонали AC и DB трапеции ABCD равны.
Свойсво 3′. В равнобокой трапеции высота, приведенная из вершины тупого угла на основание, делит основание трапеции на отрезки, больший из которых равен половине суммы оснований, а меньший равен половине разности оснований.
Доказательство. Рассмотрим четырехугольник DMNC (Рис.11). Имеем:
Тогда четырехугольник DMNC является прямоугольником. Следовательно DC = MN. Поскольку треугольники ADM и NCB равны (см. доказательство следствия 1), то AM = NB. Следовательно:
Отсюда:
Далее
или
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Навигация по странице: Определение равнобедренной трапеции Признаки равнобедренной трапеции Основные свойства равнобедренной трапеции Стороны равнобедренной трапеции Средняя линия равнобедренной трапеции Высота равнобедренной трапеции Диагонали равнобедренной трапеции Площадь равнобедренной трапеции Окружность описанная вокруг равнобедренной трапеции
Формулы и свойства трапеции
Определение.
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.
Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.
| Рис.1 |
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны:
AC = BD
3. Одинаковые углы между диагоналями и основаниями:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Основные свойства равнобедренной трапеции
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
AB = CD = m
3. Вокруг равнобедренной трапеции можна описать окружность
4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):
h = m
5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
SABCD = h2
6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:
h2 = BC · AD
7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC ┴ AD
9.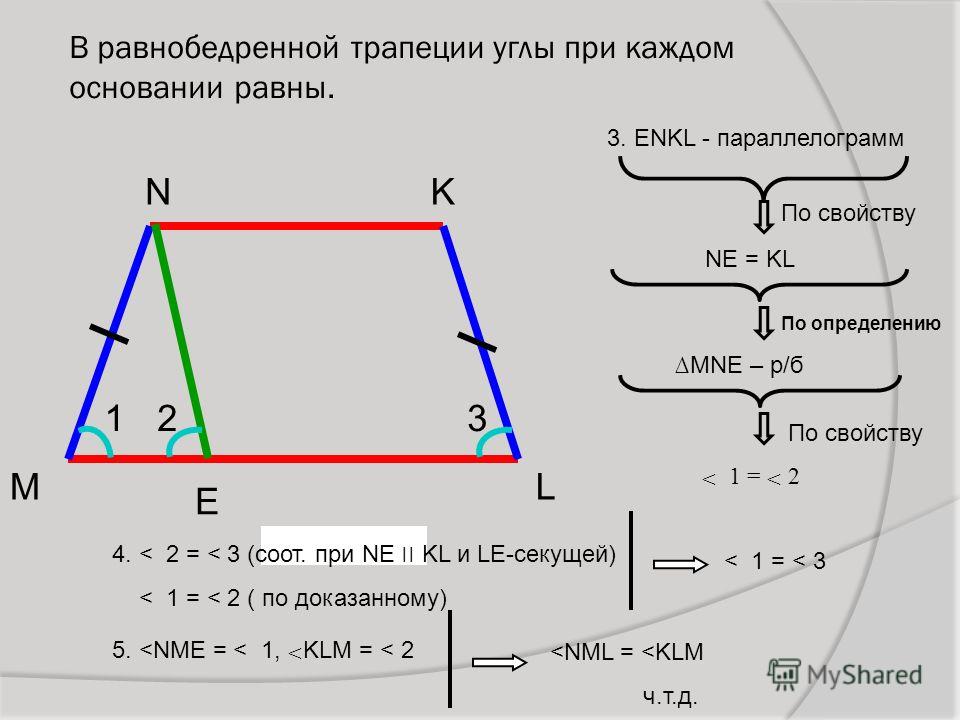 Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньшый (PD) — равен полуразности оснований:
Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньшый (PD) — равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD — BC |
| 2 |
10. Также смотрите свойства трапеции
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
1. Формулы длины сторон через другие стороны, высоту и угол:
a = b + 2h ctg α = b + 2c cos α
b = a — 2h ctg α = a — 2c cos α
| c = | h | a — b | |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d12 — c2 | b = | d12 — c2 | c = √d12 — ab |
| b | a |
3.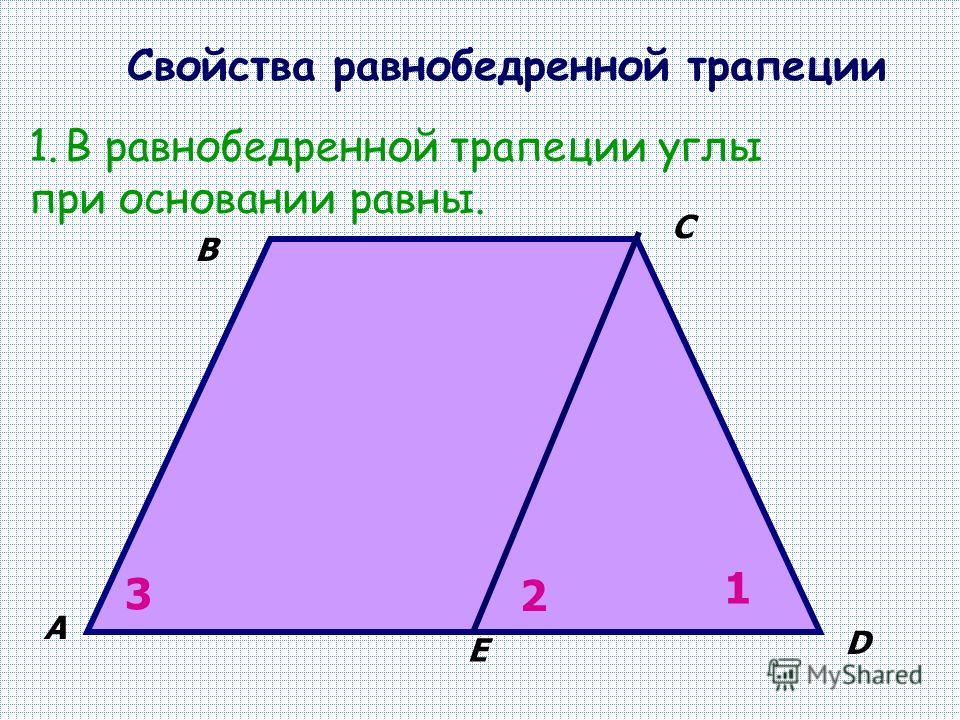 Формулы длины основ через площадь, высоту и другую основу:
Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| (a + b) sin α |
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
1. Формула определения длины средней линии через основания, высоту и угол при основании:
m = a — h ctg α = b + h ctg α = a — √c2 — h2 = b + √c2 — h2
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
Формула высоты через стороны:
| h = | 1 | √4c2 — (a — b)2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a — b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Диагонали равнобедренной трапеции равны:
d1 = d2
Формулы длины диагоналей равнобедренной трапеции:
1. Формула длины диагонали через стороны:
d1 = √с2 + ab
2. Формулы длины диагонали по теореме косинусов:
d1 = √a2 + c2 — 2ac cos α
d1 = √b2 + c2 — 2bc cos β
3.
d1 = √h2 + m2
4. Формула длины диагонали через высоту и основания:
| d1 = | 1 | √4h2 + (a + b)2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √4c2 — (a — b)2 |
| 4 |
2. Формула площади через стороны и угол:
S = (b + c cos α) c sin α = (a — c cos α) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
Формула площади через основания и угол между основой и боковой стороной:
| S = | ab | = | ab |
| sin α | sin β |
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площади через через диагонали и угол между ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площади через через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через через основания и высоту:
| S = | a + b | · h |
| 2 |
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1.
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
| p = | a + c + d1 |
| 2 |
a — большее основание
Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур
Все таблицы и формулы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Несколько ответов о пятиугольниках
Несколько ответов о пятиугольникахНекоторые соотношения в правильных пятиугольниках
Сумма углов -> Угол вершины
Общая сумма углов пятиугольника = 3*180 = 540 градусов. Таким образом, каждый угол при вершине =
540/5 = 108 градусов.
Таким образом, каждый угол при вершине =
540/5 = 108 градусов.
Равнобедренные треугольники
<-> УглыДве стороны и вершина образуют тупоугольный равнобедренный треугольник, две такие заштрихованы здесь.
Так как тупой угол EAB = 108 и два равных угла при основании имеют сумму = 180 108 = 72, острые углы при основании типа CAB = 36 градусов.
Кроме того, угол CAD = угол EAB — 2*36 = 36 градусов, поэтому 2 диагонали от вершина, такая как A, делит угол вершины на три части; то есть они делят угол при вершине на 3 равных угла по 36 градусов.
Наконец, треугольник DAC равнобедренный, так как каждый из углов при основании ACD и ADC равны 108 36 = 72 градуса.
Пентаграмма (5 звезд)
Если в правильном пятиугольнике проведены все 5 диагоналей, эти 5 сегментов образуют форму звезды, называемую правильной пентаграммой.
Суммируя то, что теперь известно о равных углах при вершинах, получаем
легко заметить, что пятиугольник ABCDE разбит на 5 равнобедренных треугольников, подобных
до треугольника ABC 36-108-36 градусов, 5 равнобедренных треугольников, подобных 72-36-72
треугольник DAC и один правильный пятиугольник в центре.
Равнобедренная трапеция и параллельные линии
Есть несколько способов убедиться, что диагональ BE параллельна CD и что CDEB — равнобедренная трапеция. Если принять знание об углах разработан выше, есть несколько быстрых способов увидеть это.
Метод поперечного и дополнительного угла: Линия BC является поперечной CD и BE. Угол DCB = 3*36 и угол CBE = 2*36, поэтому сумма углов = 5*36 = 180. Поскольку углы дополнительные, прямые CD и BE параллельны.
Метод поперечного и равноугольного метода: Линия BD является поперечной CD и БЭ. Угол BDC = 36 и угол DBE = 36. Эти конгруэнтные чередующиеся внутренние углы означают, что прямые CD и BE параллельны.
Метод симметрии линии равнобедренного треугольника: Поскольку треугольник EAB равнобедренный,
биссектриса угла EAB является серединным перпендикуляром к отрезку
БЫТЬ. Так как треугольник DAC равнобедренный, то биссектриса угла DAC
серединный перпендикуляр к CD. Но биссектрисы двух углов
углы составляют одну прямую (поскольку биссектриса DAC делит угол EAB на две
углы размером 18 + 36 градусов). Но это означает, что CD и BE имеют одинаковые
серединный перпендикуляр. Таким образом, эти прямые параллельны. Также, поскольку до н.э.
отражение ДЭ, отрезки имеют одинаковую длину.
Но биссектрисы двух углов
углы составляют одну прямую (поскольку биссектриса DAC делит угол EAB на две
углы размером 18 + 36 градусов). Но это означает, что CD и BE имеют одинаковые
серединный перпендикуляр. Таким образом, эти прямые параллельны. Также, поскольку до н.э.
отражение ДЭ, отрезки имеют одинаковую длину.
Ромбы и равные длины
Теперь мы знаем, что каждая диагональ параллельна одной из сторон. Итак, если мы нарисуем две диагонали, они образуют с параллельными сторонами параллелограмм. Но с тех пор стороны правильного пятиугольника равны, параллелограмм является ромбом. (В любом параллелограмме противоположные стороны равны; если две смежные стороны равны, тогда все четыре стороны равны.)
Это означает, что определенные длины внутри формы звезды равны сторонам пятиугольника.
Золотое сечение в правильном пятиугольнике
Теперь у нас есть много способов найти вложенные, подобные равнобедренные треугольники в пентаграмме.
Мы можем использовать эти треугольники, чтобы найти отношение длины диагонали к стороне длина пятиугольника. Примем длину стороны за единицу длины а длина диагонали должна быть d. Тогда отношение будет d с этой единичной стороной.
Из ромба DEAF мы видим, что AF = FD = DE = DC. 92 д 1 = 0,
Положительный корень этого квадратного уравнения равен (1/2)*(1 + sqrt 5). Это называется золотым сечением .
Для любого правильного пятиугольника со стороной s и диагональю d отношение d/s = золотое сечение.
Построение правильного пятиугольника из стороны
Мы узнали, как по единичной длине s построить длину sqrt 5, так что это можно использовать для построения длины d, которая является золотым сечением * s.
Тогда, используя s и d, можно начать с отрезка AB и построить все треугольники ABC, ABD, ABE и таким образом построить правильный пятиугольник со стороной AB.
Этот метод также строит случайные углы, равные 36 градусам и целым числам.

Leave A Comment