Сумма углов прямоугольного треугольника – чему равна
4.5
Средняя оценка: 4.5
Всего получено оценок: 252.
Обновлено 9 Июля, 2021
4.5
Средняя оценка: 4.5
Всего получено оценок: 252.
Обновлено 9 Июля, 2021
Сумма углов любого треугольника – величина устойчивая. Но прямоугольный треугольник выделяется среди прочих набором специфических свойств. Сумма углов не является исключением, поэтому стоит поговорить об этом свойстве прямоугольных треугольников, чтобы не возникало вопросов в дальнейшем изучении.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Треугольник
Несмотря на свою обособленность от прочих фигур, треугольник является таким же многоугольником, как и прямоугольник, квадрат или ромб. Все отличие только в количестве углов. Существует формула, по которой определяется сумма углов любого многоугольника в зависимости от количества сторон, поговорим о ней немного позже.
Итак, треугольник это фигура, имеющая три стороны и три угла. Традиционно, одна из сторон считается основанием, а две другие стороны зовутся боковыми. Обозначение не является принципиальным, поэтому любая из сторон треугольника принимается за условное основание. Такое обозначение нужно только для облегчения понимания чертежа.
Треугольник в математике считается минимально возможно фигурой. Любая из возможных фигур может быть разбита на треугольники. Это свойство иногда используется при решении задач.
Рис. 1. Фигура, разбитая на треугольникиСумма углов треугольника
Есть два варианта нахождения общей суммы углов треугольника:
- Математический анализ. За столь страшными словами кроется обычная простая формула:
180*(n-2)- где n – количество сторон многоугольника.
- Второй способ – геометрический. Именно таким образом было в первый раз выведено утверждение о том, что сумма углов треугольника равна 180 градусам.
Рассмотрим его подробнее.
Рассмотрим его подробнее.Пусть треугольник АВС – произвольный треугольник с основанием АС. Тогда построим прямую ВD, проходящую через точку В, параллельно основанию. Тогда получается две параллельные прямые: АС и ВD с двумя секущими АВ и ВС.
Рассмотрим углы при секущих прямых. Сумма трех углов при вершине В будет равна 180 градусам, так как они представляют собой развернутый угол. Тогда внутренние углы треугольника будут равные накрест лежащим наружным углам. То есть сумма углов треугольника равняется градусной мере развернутого угла и равняется 180 градусам.
Важно понимать, что наружные углы нельзя называть внешними углами треугольника, так как внешние углы получаются с помощью продолжения одной из сторон треугольника, а прямая ВD продолжением стороны треугольника не является.
Общая формула суммы углов многоугольника получается с помощью разбиения фигуры на треугольники и подсчета сумм углов получившихся малых фигур.
Прямоугольный треугольник
Прямоугольный треугольник содержит угол в 90 градусов.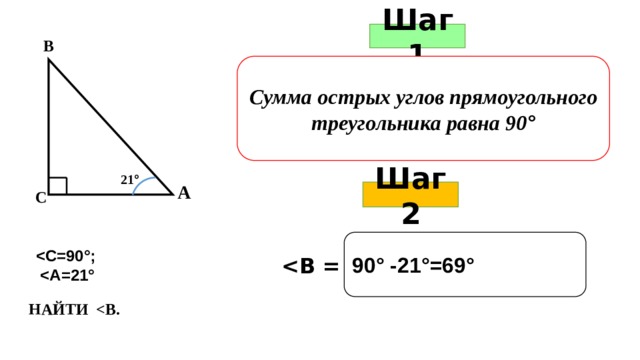
180-90=90 – то есть сумма непрямых углов прямоугольного треугольника равна 90 градусам.
Но непрямые углы это нематематическое определение. Может ли в прямоугольном треугольнике еще один угол быть прямым? Если бы такой угол мог существовать, то он был бы равен 90 градусам. То есть оставшийся третий угол:
90-90=0 – и третий угол в этом случае был бы нулевым, что невозможно. Так же, как и невозможно существование тупого угла в прямоугольном треугольнике. Потому что тупой угол всегда больше 90 градусов.
Значит, можно сделать вывод о том, что в прямоугольном треугольнике сумма острых углов равна 90 градусам.
Рис. 3. Острые углы прямоугольного треугольникаЧто мы узнали?
Мы поговорили о формуле суммы углов прямоугольного треугольника.
Вывели ее геометрическим способом и определили аналитический способ вывода, который вытекает из геометрического. Рассказали, почему невозможно существование тупоугольного прямоугольного треугольника.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 252.
А какая ваша оценка?
Сумма углов треугольника: чему равна и как найти?
Доказательство теоремы:
Нарисуем треугольник. Через одну из его вершин проведем прямую, параллельную противоположной стороне, и найдем на рисунке равные углы.
Угол 1 равен углу BAC, они накрест лежащие. Угол 2 равен углу ACB, они тоже накрест лежащие.
Сумма угла 1, угла ABC и угла 2 составляет развернутый угол.
A развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.
Разберем задачи ЕГЭ и ОГЭ, в которых фигурирует сумма углов треугольника.
Заметим, что они похожи друг на друга. Одна и та же задача на тему «Сумма углов треугольника» может встретиться и на ОГЭ, и на ЕГЭ по математике. И уровень сложности заданий по этой теме в ЕГЭ и ОГЭ примерно одинаковый.
Задачи ЕГЭ по теме: Сумма углов треугольника
Задача 1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Решение:
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х.
Получим уравнение:
и найдем x = 17.
Тогда .
Ответ: 51.
Обратите внимание, что это даже не геометрия, а алгебра. Мы составили уравнение и решили его.
Задача 2.
Один из углов равнобедренного треугольника равен 98 градусов.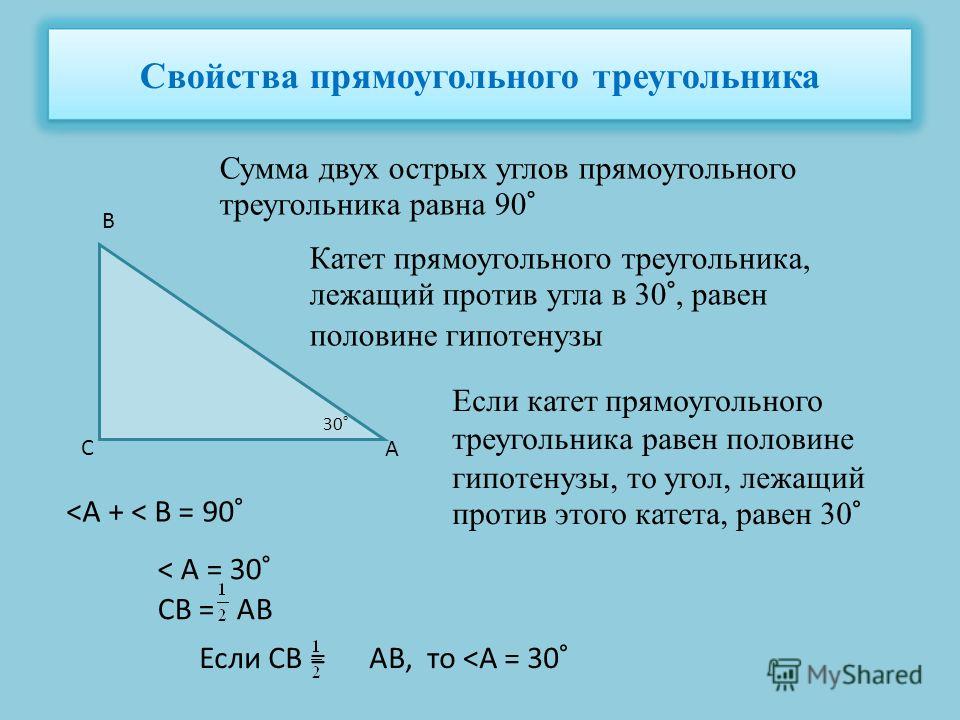
Найдите один из других его углов. Ответ дайте в градусах.
Решение:
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны .
Ответ: 41.
Задача 3.
На рисунке угол 1 равен , угол 2 равен , угол 3 равен . Найдите угол 4. Ответ дайте в градусах.
Решение:
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Сначала найдем угол 5.
Он равен
Тогда
Угол 4, смежный с углом 7 равен
Ответ:
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Задача 4.
Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.
Решение:
Пусть углы треугольника равны 2x, 3x и 4x. Запишем, чему равна сумма углов этого треугольника.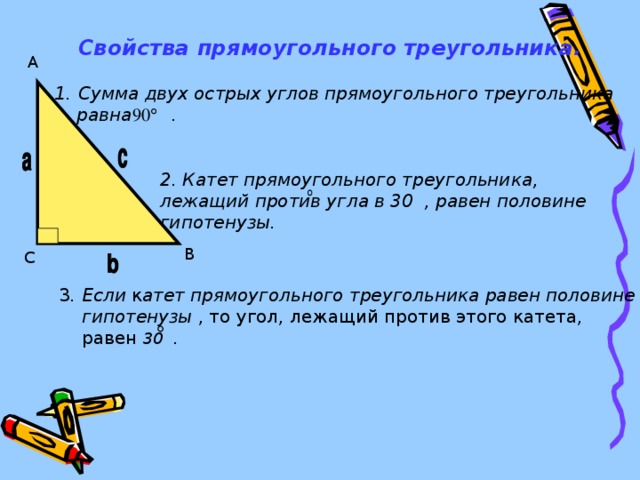
Тогда
Здесь мы тоже составили уравнение и решили его. Так же, как на уроках алгебры.
Ответ: 40.
Задача 5. В треугольнике ABC проведена биссектриса AL, угол ALC равен , угол ABC равен . Найдите угол ACB. Ответ дайте в градусах.
Решение:
ALC — внешний угол и он равен сумме двух внутренних углов, не смежных с ним. Значит, .
AL — биссектриса , а это значит, что .
По теореме о сумме углов треугольника получаем:
Ответ: 125.
Задача 6. В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, B=61D=151 Найдите величину угла A. Ответ дайте в градусах.
Решение:
Если соединить точки B и D, получим два равных треугольника. Они равны по трем сторонам. В равных треугольниках напротив равных сторон лежат равные углы.
В треугольнике ABD сумма двух углов
Тогда , по теореме о сумме углов треугольника.
Ответ: 74.
Задача 7. Отрезки AC и BD — диаметры окружности с центром O.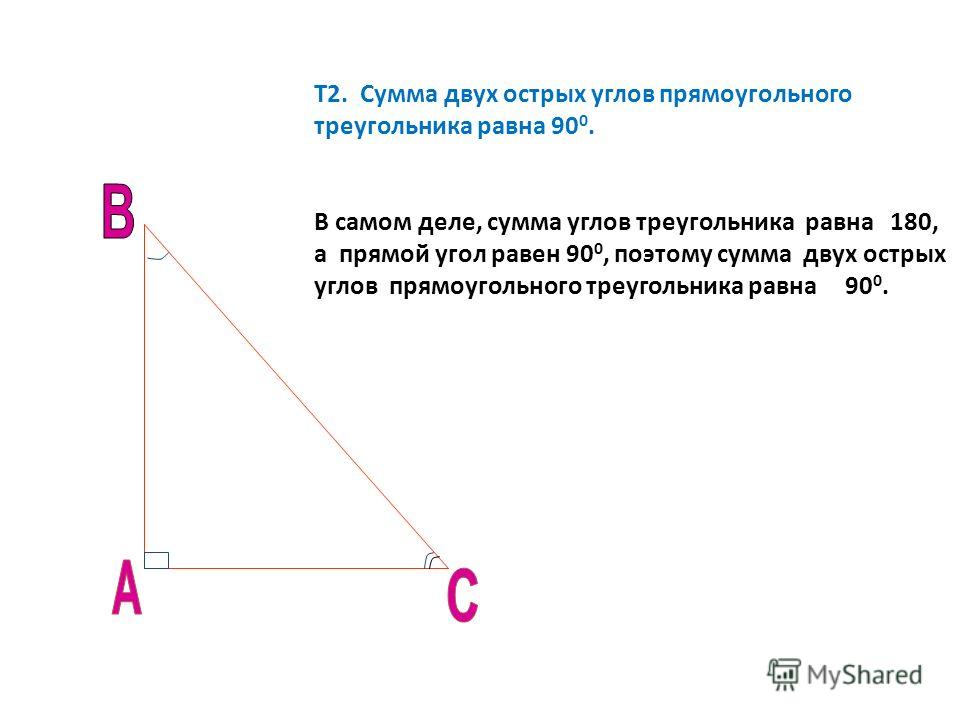
Угол AOD равен . Найдите вписанный угол ACB. Ответ дайте в градусах.
Решение:
AC и BD — диаметры окружности. Значит, — равнобедренный, в нем — как радиусы.
как вертикальные углы, тогда по теореме о сумме углов в треугольнике:
.
Ответ: 28.
Задача 8. В треугольнике ABC AD — биссектриса, угол C равен , угол CAD равен . Найдите угол B. Ответ дайте в градусах.
Решение:
AD — биссектриса, отсюда следует, что .
Тогда по теореме о сумме углов треугольника .
Ответ: 66.
Задача 9. В треугольнике ABC CD — медиана, угол C равен , угол B равен . Найдите угол ACD. Ответ дайте в градусах.
Решение:
В треугольнике ABC угол C равен , угол B равен , тогда угол A равен .
CD — медиана. А медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Значит, .
Поэтому треугольник ADC равнобедренный и .
Ответ: 55.
Задача 10. В треугольнике ABC угол C равен , биссектрисы AD и BE пересекаются в точке O.
Найдите угол AOB. Ответ дайте в градусах
Решение:
В треугольнике ABC угол C равен , отсюда по теореме о сумме углов треугольника .
Биссектрисы AD и BE пересекаются в точке O. Угол OAB — это половина угла CAB, угол OBA — это половина угла CBA. Теперь применим теорему о сумме углов треугольника к треугольнику AOB.
Ответ: 119.
Задача 11. В треугольнике ABC угол A равен , углы B и C — острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
Решение:
BD — высота тогда — прямоугольный,
CE — высота тогда — прямоугольный и .
Углы и — смежные, поэтому .
Ответ: 124.
Задача 11. В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.
Решение:
Обозначим на рисунке вершины треугольника ABC, биссектрису CК и высоту CН. Биссектриса CК делит прямой угол на два угла по .
Угол BCН равен разности углов BCК и КCН, то есть .
Треугольники BCН и BAC подобны по двум углам. Значит, угол BAC равен углу BCН, то есть
Ответ: 31.
Задача 12. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Обозначим на рисунке медиану CМ и высоту CН.
Пусть и . Высота CН разбивает прямоугольный треугольник на два треугольника, подобных исходному. Значит, угол BCН равен углу BAC, то есть .
у которых углы равны т. е. угол C разбился на углы
и
Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Получили два равнобедренных треугольника, BCМ и ACМ. В треугольнике ACМ углы A и C равны 6 градусов каждый.
Тогда угол МCН между высотой и медианой равен:
Ответ: 78.
Задачи ОГЭ по математике по теме: Сумма углов треугольника.
Задача 13. В треугольнике два угла равны и .
Найдите его третий угол. Ответ дайте в градусах.
Решение:
Сумма углов в треугольнике равна , поэтому
третий угол равен .
Ответ: 37.
Задача 14. Один из острых углов прямоугольного треугольника равен 34. Найдите его другой острый угол. Ответ дайте в градусах.
Решение:
Сумма острых углов прямоугольного треугольника равна . Поэтому второй острый угол равен: .
Ответ: 56.
Задача 15.
В треугольнике ABC известно, что AB=BC, . Найдите угол BCA. Ответ дайте в градусах.
Решение:
В треугольнике ABC известно, что AB=BC. Значит, треугольник ABС равнобедренный, и углы при основании AС равны,
т.е. .
Ответ: 36.
Задача 16. В остроугольном треугольнике ABC проведена высота BH, . Найдите угол ABH. Ответ дайте в градусах.
Решение:
BH — высота , тогда — прямоугольный, в нем и Используя теорему о сумме углов в треугольнике, найдем угол ABH:
Ответ: 53.
Задача 17. В треугольнике ABC угол C равен .
Найдите внешний угол при вершине C. Ответ дайте в градусах.
Решение:
Внешний угол треугольника AВC при вершине C является смежным углом с углом ACB, а сумма смежных углов равна .
Значит, внешний угол треугольника ABC при вершине C равен: .
Ответ: 47.
Задача 18. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и . Найдите угол BOC. Ответ дайте в градусах.
Решение:
— равнобедренный, .
— вписанный угол и опирается на дугу BC, а — центральный угол и также опирается на дугу BC. Центральный угол в два раза больше вписанного опирающегося на ту же дугу, .
Ответ: 155.
Задача 19. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ABC=123. Найдите угол BOC. Ответ дайте в градусах.
Решение:
— равнобедренный треугольник, отсюда .
— вписанный угол, он опирается на дугу BC, а — центральный угол и также опирается на дугу BC.
Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу, значит, .
Ответ: 57.
Задача 20. В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен . Найдите угол ACB. Ответ дайте в градусах.
Решение:
AC и BD — диаметры, отсюда следует, что — равнобедренный, — радиусы.
как вертикальные углы, тогда по теореме о сумме углов в треугольнике .
Ответ: 33.
Задача 21. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен . Ответ дайте в градусах.
Решение:
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. A это означает, что AB — диаметр. Угол, опирающийся на диаметр, равен , и треугольник ABC — прямоугольный. И если , то второй острый угол этого треугольника равен:
Ответ: 15.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Сумма углов треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 06.02.2023
Как найти угол в прямоугольном треугольнике
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Справка по базовой геометрии » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти угол в прямоугольном треугольнике
Найти угол С.
Возможные ответы:
C = 72
C = 65
C = 70
Ни один из этих
C = 53
Правильный ответ:
C = 65
Пояснение:
Во-первых, знайте, что сумма всех углов треугольника равна 180 градусам.
У каждого треугольника 3 угла. Таким образом, у нас есть сумма трех углов, как показано на рисунке:
, где у нас есть углы A, B и C. В нашем прямоугольном треугольнике один угол равен 25 градусам, и мы назовем этот угол A. Другой известный угол 90 градусов, и мы назовем этот угол B. Таким образом, у нас есть
Упростите и решите для C.
Сообщить об ошибке
Какое из следующихможет быть двумя мерами угла прямоугольного треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
В прямоугольном треугольнике не может быть тупого угла; это исключает выбор между 100 и 10.
Острые углы прямоугольного треугольника должны составлять 90 градусов. По этому критерию можно исключить три варианта:
Оставшийся вариант правильный:
Сообщить об ошибке
Угол прямоугольного треугольника в 15 раз больше, чем у другого.
Чему равен меньший угол?
Возможные ответы:
Правильный ответ:
Объяснение:
Сумма углов треугольника равна 180. В прямоугольном треугольнике один угол равен 90. Таким образом, сумма двух других углов будет равна 90.
Пусть = первый угол и = второй угол
Таким образом, уравнение для решения становится или
Таким образом, первый угол равен, а второй угол равен .
Таким образом, меньший угол равен
Сообщить об ошибке
Угол в треугольнике, показанном ниже (не в масштабе), равен 35 градусам. Что такое угол?
Возможные ответы:
градусы
градусы
градусы
градусы
Правильный ответ:
градусы
Пояснение:
Сумма внутренних углов треугольника всегда равна 180 градусам.
Нам дан угол и, поскольку указано, что это прямоугольный треугольник, мы знаем, что угол равен 90 градусам. Таким образом, мы знаем 2 из 3 и можем определить третий угол.
Угол равен 55 градусам.
Сообщить об ошибке
Что из следующего нельзя верно для прямоугольного треугольника?
Возможные ответы:
Прямоугольный треугольник может быть равносторонним.
Меры углов прямоугольного треугольника могут суммироваться.
Один катет может быть длиннее гипотенузы.
Прямоугольный треугольник может иметь тупой угол.
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Правильный ответ:
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Объяснение:
Все этих утверждений ложны.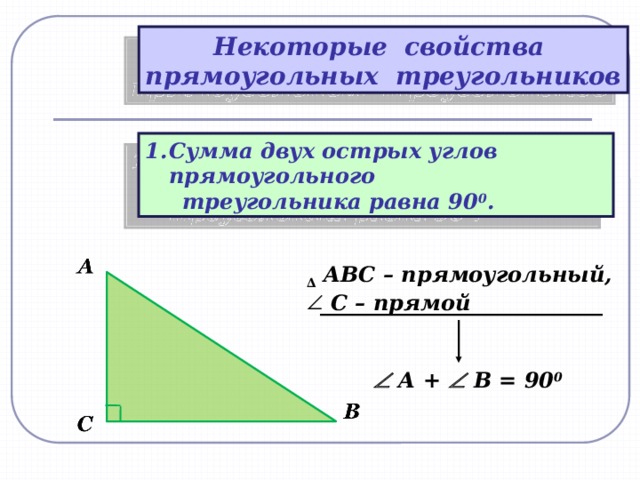
Прямоугольный треугольник может быть равносторонним.
Неверно: Равносторонний треугольник должен иметь три угла, каждый из которых измеряется.
Один катет может быть длиннее гипотенузы.
Ложь: Каждый катет на короче, чем гипотенуза на .
Прямоугольный треугольник может иметь тупой угол.
Ложь: Оба угла прямоугольного треугольника не являются прямыми должно быть острым.
Меры углов прямоугольного треугольника могут суммироваться.
Ложь: Меры любой суммы треугольников .
Сообщить об ошибке
Чему равен угол в треугольнике?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для нахождения всех углов треугольника:
Чтобы найти меру угла, мы подставляем значения и .
Поскольку угол прямой, мы знаем, что мера будет равна .
Сообщить об ошибке
Найдите градусную меру недостающего угла.
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна 180º.
Чтобы найти значение остаточного угла, вычтите известные углы из 180º:
Следовательно, третий угол равен 43º.
Сообщить об ошибке
Прямоугольный треугольник имеет два равных угла, какова их мера?
Возможные ответы:
Правильный ответ:
Пояснение:
Внутренние углы треугольника всегда составляют в сумме 180 градусов, и было дано, что треугольник прямоугольный, а это означает, что один из углов равен 90 градусов.
Это оставляет 90 градусов, чтобы равномерно разделить два оставшихся угла, как было показано в вопросе.
Следовательно, каждый из двух равных углов имеет размер 45 градусов.
Сообщить об ошибке
Какого угла не хватает в этом прямоугольном треугольнике?
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна .
Это означает, что .
Используя тот факт, что 90 — это половина 180, мы можем вычислить, что недостающий угол x плюс 34 добавляется к оставшимся 90, и мы можем просто вычесть
.
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма углов треугольника составляет 180 градусов.
Мы уже знаем, что один из углов равен 9.0 градусов, поэтому мы можем вычесть 90 из 180: два других угла должны добавиться к 90 градусам.
Теперь мы можем вычесть, чтобы получить x:
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты4 164 практических теста Вопрос дня Карточки Learn by ConceptПрямоугольные треугольники | GMAT бесплатно
Прямоугольные треугольники — это треугольники, в которых один из внутренних углов равен 90 градусов, то есть прямой угол. Поскольку три внутренних угла треугольника в сумме составляют 180 градусов, в прямоугольном треугольнике, поскольку один угол всегда равен 90 градусам, два других всегда должны в сумме давать 90 градусов (они дополняют друг друга).
Сторона, противолежащая прямому углу, называется гипотенузой. Стороны, примыкающие к прямому углу, являются катетами.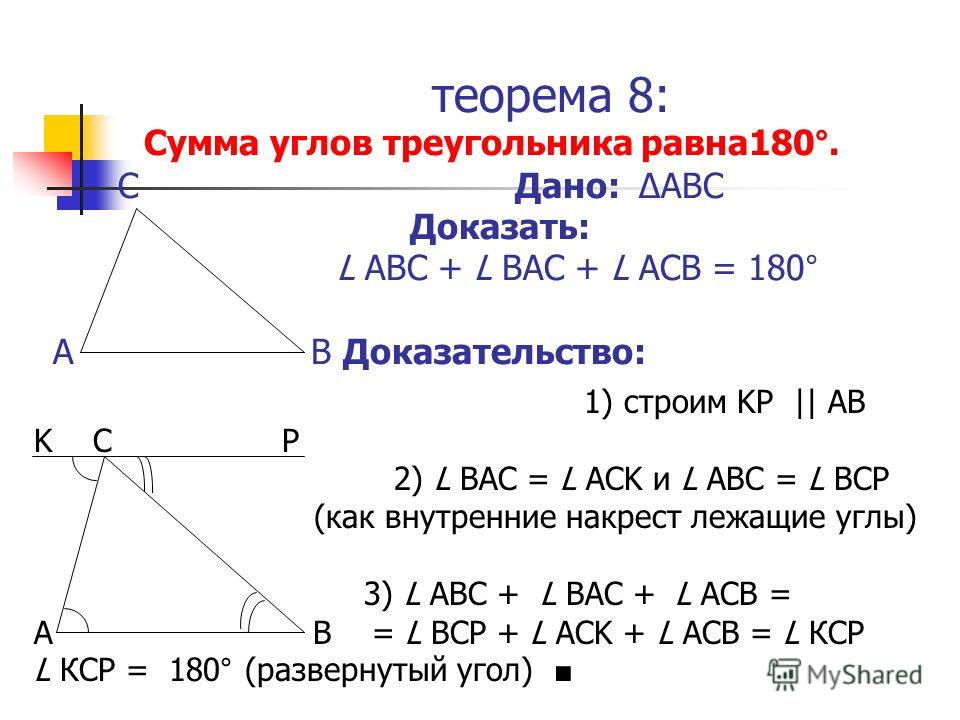
При использовании теоремы Пифагора гипотенуза или ее длина часто обозначаются строчными буквами 9.0356 с . Ноги (или их длины) обычно маркируются a и b .
Любой из катетов можно считать основанием, а другой катет считать высотой (или высотой), потому что прямой угол автоматически делает их перпендикулярными. Если известны длины обоих катетов, то, приняв одну из этих сторон за основание b , а другую за высоту h , площадь прямоугольного треугольника легко вычислить по стандартной формуле для треугольника. площадь:
Это интуитивно логично, потому что против него можно расположить другой конгруэнтный прямоугольный треугольник так, что гипотенузы будут одним и тем же отрезком, образуя прямоугольник со сторонами, имеющими длину b и ширину h . Площадь прямоугольника равна ( b )( h ), поэтому любой из образующих его конгруэнтных прямоугольных треугольников имеет площадь, равную половине этого прямоугольника.
Теорема Пифагора
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон.
The Pythagorean Theorem
The sides that we referred to as b and h above are now labeled as b and a , since the custom when using the Pythagorean Theorem is to используйте переменные a, b и c . Тем не менее, важно признать, что обе формулы относятся к одним и тем же сторонам. Например, в типичном вопросе GMAT вы можете использовать теорему Пифагора, чтобы определить основание и высоту треугольника, а затем в конечном итоге найти его площадь.
Довольно часто на GMAT вы оказываетесь в ситуации, когда знаете, что конкретный треугольник является прямоугольным, и знаете длины двух из трех сторон. Затем вы сможете найти длину третьей стороны, подставив две известные длины в
Ранее мы обсуждали, как можно использовать теорему Пифагора для вычисления расстояния между любыми двумя точками на координатной плоскости.
Общие пифагорейские тройки
Определенные тройки чисел, удовлетворяющие теореме Пифагора, часто появляются на GMAT. Вы должны запомнить хотя бы первые три тройки здесь. Вам не нужно знать углы этих треугольников, только отношения длин сторон:
На GMAT вы должны знать углы и отношения сторон для 45-45-90 и 30 -60-90 треугольников, но вы , а не , как ожидается, запомните или сможете определить углы для пифагорейских троек, перечисленных выше; Вы можете определить длины сторон, просто используя формулу Пифагора.
45-45-90 Треугольник
Поскольку прямоугольный треугольник является особым треугольником, треугольник 45-45-90 является вдвойне особенным. К нему применимы все общие правила треугольника, к нему применима теорема Пифагора, а затем он обладает некоторыми собственными особыми свойствами.
Треугольник 45-45-90
Треугольник 45-45-90 — это то, что вы получите, если у вас есть равнобедренный прямоугольный треугольник.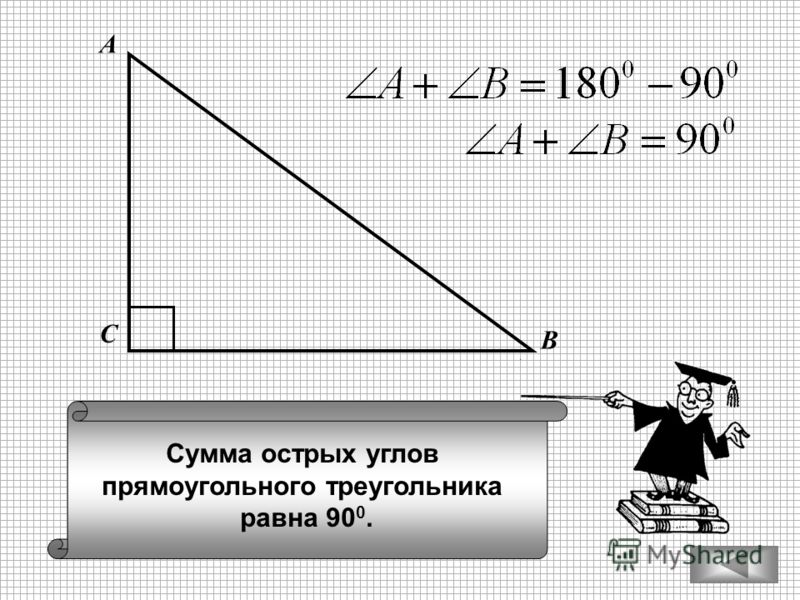
Если треугольник прямоугольный и равнобедренный, то сумма двух сторон, отличных от прямого угла, должна быть равна 9.0 градусов, и они должны быть равны, поэтому каждый должен равняться 45 градусам.
Кроме того, поскольку это прямоугольный треугольник, мы знаем, что
верно, но если a = b (поскольку мы говорим о равнобедренном треугольнике), мы можем подставить это в теорему Пифагора, чтобы получить :
Если вы попытаетесь установить a = 1, то вы получите c = √2, как на диаграмме выше. Стороны в каждом треугольнике 45-45-90 имеют длины в соотношении 1:1:√2.
Отношение сторон не означает, что стороны, противоположные углам в 45 градусов, обязательно равны 1, как указано выше. Скорее, любая длина, расположенная поперек 45 градусов, назовем ее длиной x , будет сопровождаться поперек гипотенузы стороной, которая в √2 больше, или x √2.
Треугольник 30-60-90
Треугольник 30-60-90 похож на треугольник 45-45-90 тем, что это «двойной особый» прямоугольный треугольник.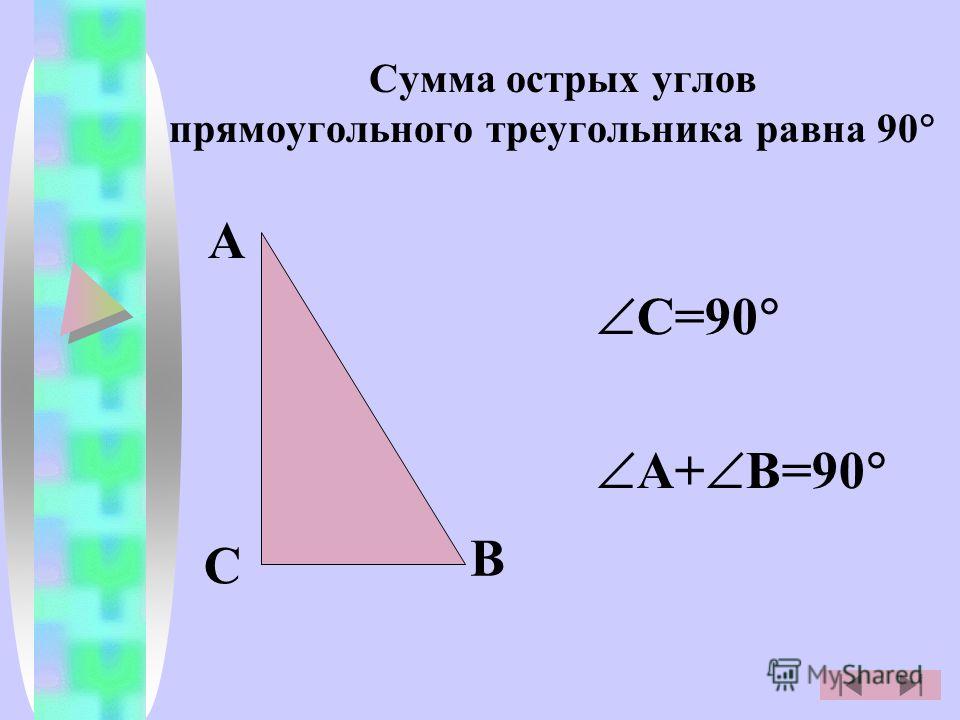
Также, как и в случае с 45-45-90 треугольник, когда у нас есть один из этих треугольников, мы знаем меру углов и знаем отношение длин сторон.
Треугольник 30-60-90 внутри равностороннего треугольника
Треугольник 30-60-90 имеет углы, которые измеряют 30 градусов, 60 градусов и 90 градусов, и стороны, обращенные к этим углам с длинами в отношении 1: √3:2 соответственно. Как и в случае с любым отношением, мы можем представить, что отсутствует число x , так что длины равны x 9.0357 : х √3: 2 х .
Если мы попытаемся подставить эти длины в теорему Пифагора, мы получим следующее:
Наш результат подтверждает, что теорема верна, а лучше бы так, поскольку мы имеем дело с прямоугольным треугольником.
Вы можете запомнить, какая сторона проходит через какой угол, используя тот факт, что большие длины сторон в треугольнике обращены к большим углам. Это означает, что сторона, расположенная напротив угла 30 градусов, будет наименьшей стороной, сторона, расположенная напротив угла 60 градусов, будет стороной средней длины, а сторона, расположенная напротив угла 9 градусов.
Угол 0 градусов будет самой длинной стороной. При использовании этого трюка с памятью иногда люди задаются вопросом, что больше: √3 или 2. Вы можете помнить, что √3 меньше 2, потому что 2 равно √4, а √3 меньше √4.
На рисунке выше показано свойство, которое иногда встречается на GMAT: обратите внимание, что изображенный треугольник 30-60-90 находится внутри равностороннего треугольника. Изучив диаграмму, вы можете убедиться, что любой равносторонний треугольник содержит два 30-60-9Внутри него «спрятано» 0 треугольников. Этот факт может появиться в более тонких вопросах геометрии на GMAT, поэтому приготовьтесь видеть два треугольника 30-60-90, когда присутствует равносторонний треугольник.
Тригонометрия?
Вам не нужно знать тригонометрию для GMAT. Помните синусы, косинусы и тангенсы углов? Может быть, вы знаете, а может и нет, но вам не нужно знать их для GMAT. И если вы изучали эти предметы и они свежи в вашей памяти, не поддавайтесь искушению попробовать их использовать.
Leave A Comment