Чему равна сумма углов?
Лев Емельянов
«Квантик» №3, 2020
Просто мне нужно объяснить… Но не просто объяснить, а чтобы ещё стало понятно!
Е. Гришковец «Одновременно»
Для математического уха разговор выглядит комично. То, что сумма углов треугольника равна 180°, знают даже школьники, не очень увлечённые математикой. А что такое 180° и почему именно 180? Ясно, скажет умный школьник, это половина от 360, то есть полного оборота.
Невозможно точно сказать, почему окружность была разбита на 360 одинаковых частей и когда это произошло. То ли это персы придумали, у которых год длился 360 дней, то ли вавилоняне, которым удобно было делить окружность на 6 равных частей с помощью равностороннего треугольника.
Была, правда, попытка ввести более логичную, с точки зрения современных представлений о счёте, шкалу для угловых мер. Она делила окружность на 400 равных частей — градов. В этой шкале величина прямого угла равнялась 100 градам. Однако шкала эта не прижилась. Трудно одним желанием изменить пятитысячелетнюю историю цивилизации. Да впрочем, какая разница, в чём мерить, хоть в попугаях, главное — понять, что угол — это некоторая доля от полного оборота.
Трудно одним желанием изменить пятитысячелетнюю историю цивилизации. Да впрочем, какая разница, в чём мерить, хоть в попугаях, главное — понять, что угол — это некоторая доля от полного оборота.
Почему же сумма углов любого треугольника равна в точности половине полного оборота? Давайте представим себе, что у нас есть три прожектора. Каждый освещает внутренность некоторого угла до бесконечности (жить мы будем временно в двумерном мире). Если мы, стоя в одной точке, включим три прожектора (зелёный, розовый и жёлтый на рисунке), сумма «световых углов» которых равна 180°, и направим их без наложений освещаемой площади, то осветим ровно половину нашего двумерного пространства.
Теперь рассмотрим произвольный треугольник и в вершинах его поставим трёх помощников (Али, Бен и Сирил по буквам вершин, но можно попросить Анну, Варвару и Светлану), доверив им по прожектору. Каждый помощник должен осветить внутренность треугольника лучами света, которые выходят из вершины и продолжаются до бесконечности.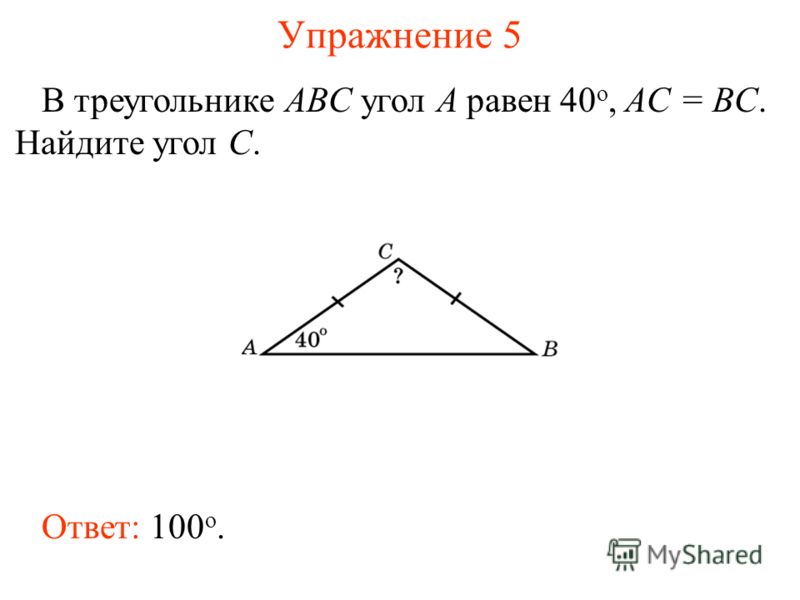 Таким образом, каждый прожектор будет освещать внутренность своего угла и не будет освещать внутренность такого же угла, вертикального выбранному. При этом каждая точка плоскости либо попадёт внутрь освещённого угла, либо не будет освещена, попав в вертикальный угол к углу треугольника. Точки же самого треугольника будут освещены трижды. Теперь давайте посмотрим на нашу частично освещённую плоскость с большой высоты (мы-то, как люди трёхмерные, имеем на это право). Если закрыть глаза на небольшой участок перекрытия внутри треугольника, то нетрудно понять, что мы осветили «ровно» половину плоскости. Из чего и можно заключить, что сумма углов произвольного треугольника равна 180°!
Таким образом, каждый прожектор будет освещать внутренность своего угла и не будет освещать внутренность такого же угла, вертикального выбранному. При этом каждая точка плоскости либо попадёт внутрь освещённого угла, либо не будет освещена, попав в вертикальный угол к углу треугольника. Точки же самого треугольника будут освещены трижды. Теперь давайте посмотрим на нашу частично освещённую плоскость с большой высоты (мы-то, как люди трёхмерные, имеем на это право). Если закрыть глаза на небольшой участок перекрытия внутри треугольника, то нетрудно понять, что мы осветили «ровно» половину плоскости. Из чего и можно заключить, что сумма углов произвольного треугольника равна 180°!
Если наше маленькое жульничество внутри треугольника режет глаз, давайте отойдём далеко-далеко от плоскости и забудем, что где-то стоят наши помощники. Нарисуем окружность огромного радиуса с центром где-то внутри треугольника. Какая часть окружности освещена? Ровно (почти) половина. И чем больше радиус нашей окружности, тем меньше будут отличаться освещённая и тёмная части окружности.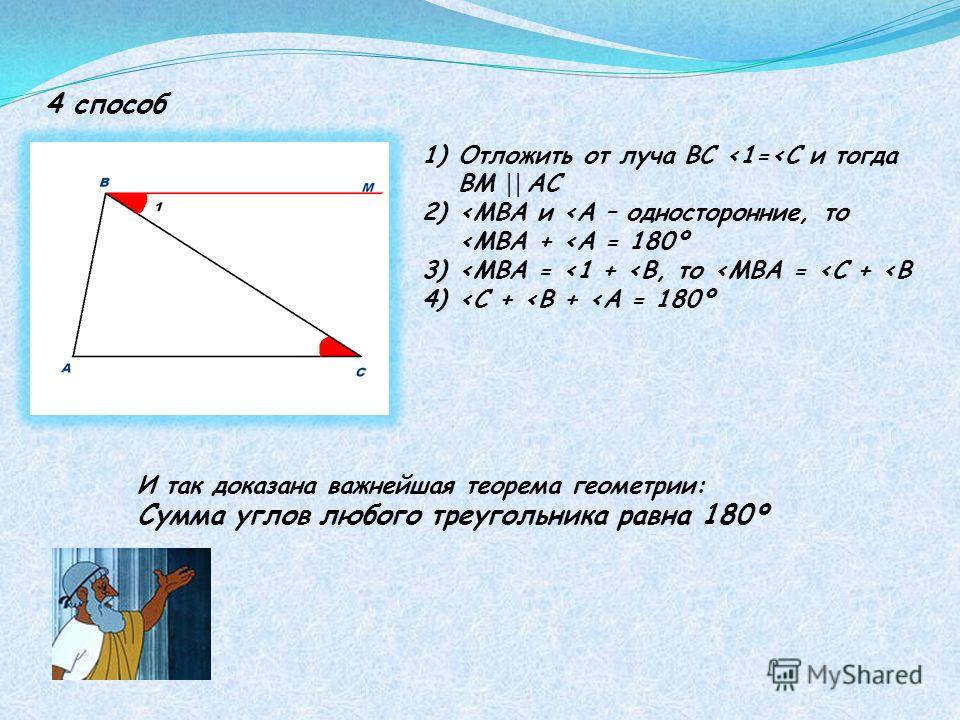 Ведь каждой светлой дуге будет в пару поставлена такая же тёмная.
Ведь каждой светлой дуге будет в пару поставлена такая же тёмная.
Не будем останавливаться на сумме углов треугольника, а попробуем развить эту идею. Самое естественное продолжение — четырёхугольник. Нетрудно понять, что четыре помощника, выполняя аналогичное задание, осветят всю плоскость, что значит: сумма углов четырёхугольника равна 360°. Стоп! Давайте не торопиться, отойдём подальше. Что мы видим? Ужас! Некоторые точки плоскости вообще не освещены. Всё пропало? Не будем паниковать преждевременно. Продолжим наши прямые до бесконечности. На рисунке серым цветом закрашена неосвещённая часть плоскости. Посмотрим внимательно на вертикальный с ней угол. Он освещён, конечно, но освещён дважды! А значит, и здесь всё сходится. Так и должно быть, ведь четырёхугольник можно просто разрезать на два треугольника. Думаем дальше.
Нарисуем пятиконечную звёздочку (не обязательно правильную). Теперь позовём пять фонарщиков, поставим их в вершинах «лучиков» нашей звёздочки, и пусть каждый освещает внутренность того угла, в котором стоит. Соответственно, вертикальный угол освещён не будет. Что мы видим? Картина почти такая же, как у треугольника. Половина плоскости светлая, половина тёмная, а значит, сумма углов пятиконечной звезды равна 180°!
Соответственно, вертикальный угол освещён не будет. Что мы видим? Картина почти такая же, как у треугольника. Половина плоскости светлая, половина тёмная, а значит, сумма углов пятиконечной звезды равна 180°!
При этом мы нигде не пользовались какими-то особенностями формы этой звёздочки. Более того, а где мы считали количество углов? Давайте внимательно посмотрим на 7-конечную звезду. А потом на 2021-конечную (нарисовать непросто, а представить можно). Что изменится для суммы? Да ничего — половина светлого, половина тёмного. Правда, для большого числа углов нужно «правильно» рисовать звёздочку. Например, для семиугольной конструкции можно привести два примера. Подсчитайте самостоятельно сумму для «более тупоугольной» звёздочки.
Теперь давайте немного развернём наших фонарщиков и дадим им задание осветить один из своих внешних углов. Для начала позовём четверых, поставим их в вершинах выпуклого четырёхугольника. Нетрудно понять, что они осветят всё, кроме самого четырёхугольника.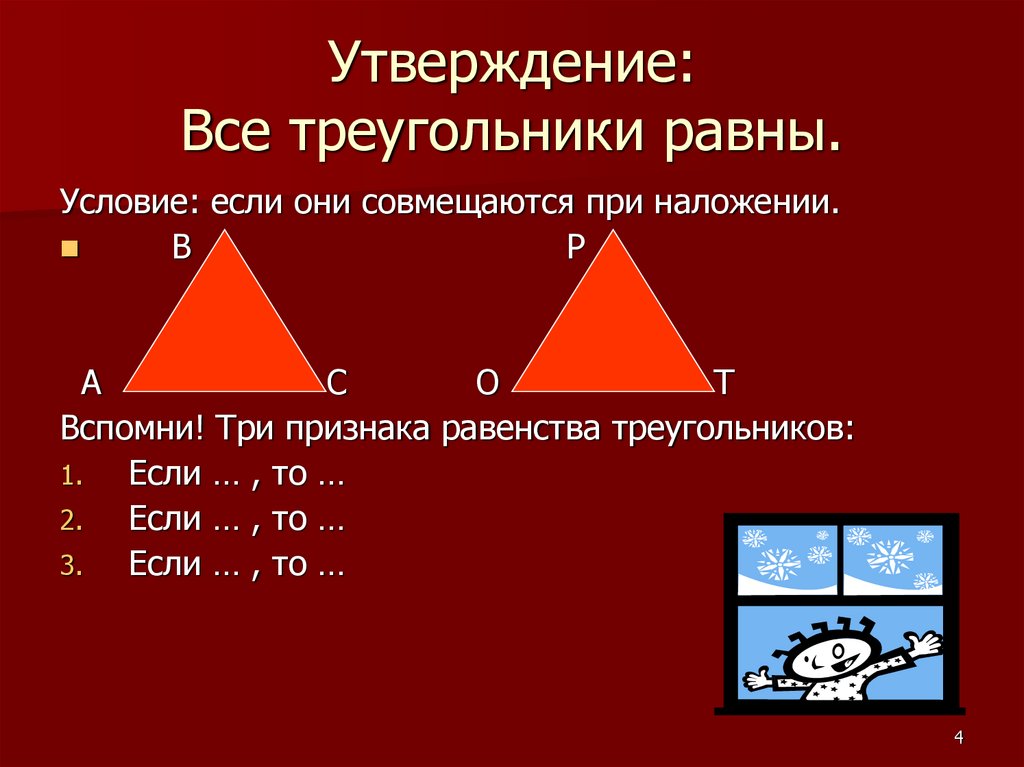 Удаляясь от них, мы поймём, что сумма внешних углов выпуклого четырёхугольника равна 360°.
Удаляясь от них, мы поймём, что сумма внешних углов выпуклого четырёхугольника равна 360°.
Также при достаточном удалении мы забудем о количестве помощников, а когда вспомним, поймём, что это совершенно неважно. Сколько бы их ни было, плоскость будет освещена полностью и без перекрытий. Из этого следует чрезвычайно важный и удивительный вывод: сумма внешних углов выпуклого многоугольника равна 360°!
Продолжая применять этот метод, можно получить и другие формулы для суммы углов. То есть если внимательно посмотреть на количество перекрытий, можно вывести формулу для суммы углов выпуклого многоугольника. Но даже без вывода становится понятно, почему сумма внутренних углов зависит от их количества, а сумма внешних нет. Попробуйте развить эту идею на случай невыпуклых многоугольников. Можно, немного поломав голову, найти сумму внутренних углов, а вот для суммы внешних надо сначала понять: что такое внешний угол невыпуклого многоугольника? Успехов в вашем исследовании!
P. S. А угольник 45°, 60° и 90°, оказывается, существует! Это специальный портновский угольник — треугольник, в котором сделаны треугольные дырки с другими углами. И речь в магазине «Ткани», оказывается, совсем не шла о сумме углов треугольника.
S. А угольник 45°, 60° и 90°, оказывается, существует! Это специальный портновский угольник — треугольник, в котором сделаны треугольные дырки с другими углами. И речь в магазине «Ткани», оказывается, совсем не шла о сумме углов треугольника.
Художник Алексей Вайнер
Сумма углов треугольника — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
ИНТЕРАКТИВНАЯ ПРАКТИЧЕСКАЯ РАБОТА
«СУММА УГЛОВ ТРЕУГОЛЬНИКА»
ЦЕЛЬ РАБОТЫ:
• Доказать практическим путем, что сумма всех углов
треугольника равна 180°.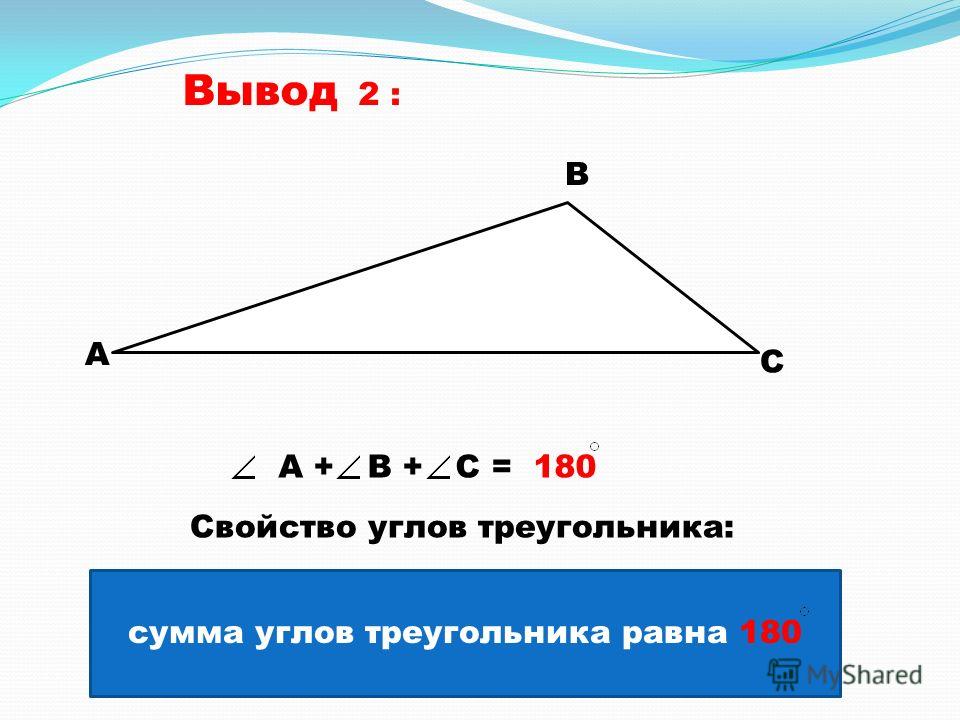
• Доказать теорему о сумме углов треугольника с
применением уже имеющихся знаний.
ОБОРУДОВАНИЕ:
1) Три листа формата А4
2) Транспортир
4) Карандаш
ХОД РАБОТЫ:
1) Начертите на первом листе формата А4 остроугольный
треугольник:
Начертите на втором листе формата А4 тупоугольный
треугольник:
Начертите на третьем листе формата А4 прямоугольный
треугольник:
2) ИЗМЕРИТЬ ТРАНСПОРТИРОМ УГЛЫ ОСТРОУГОЛЬНОГО
ТРЕУГОЛЬНИКА И СЛОЖИТЬ ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ
65°
60°
60°+55°+65°=
55°
180°
ИЗМЕРИТЬ ТРАНСПОРТИРОМ УГЛЫ ТУПОУГОЛЬНОГО
ТРЕУГОЛЬНИКА И СЛОЖИТЬ ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ
115°+32°+33°=
180°
33°
115°
32°
ИЗМЕРИТЬ ТРАНСПОРТИРОМ УГЛЫ ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА И СЛОЖИТЬ ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ
40°
90°
90°+50°+40°=
180°
50°
Согласно практическим измерениям сумма углов
любого треугольника получается 180 градусов.
Для того, чтобы убедиться в этом утверждении
проведем еще один практический эксперимент:
ВЫРЕЗАТЬ ТРИ НАРИСОВАННЫХ
ТРЕУГОЛЬНИКА ПРИ ПОМОЩИ НОЖНИЦ
ПОЛОЖИТЕ ПЕРЕД СОБОЙ ТРЕУГОЛЬНИК:
1-ЫЙ РЯД-ОСТРОУГОЛЬНЫЙ
2-ОЙ РЯД – ТУПОУГОЛЬНЫЙ
3-ИЙ РЯД – ПРЯМОУГОЛЬНЫЙ
И ПРОНУМЕРУЙТЕ ЕГО УГЛЫ
2
1
3
ПРИ ПОМОЩИ НОЖНИЦ ОТРЕЖЬТЕ УГЛЫ
ТРЕУГОЛЬНИКА
2
1
3
2
1
3
ПРИЛОЖИТЬ ОТРЕЗАННЫЕ УГЛЫ К ЛИНЕЙКЕ
ДРУГ ЗА ДРУГОМ
2
ВЫВОД:
Т.
 К. линейка образует развернутый угол,
К. линейка образует развернутый угол,исследуемого треугольника равна 180°
ДОКАЖЕМ ДАННОЕ УТВЕРЖДЕНИЕ:
D
В
К
Дано: ∆АВС
Доказать:
∟А+∟В+∟С=180°
Доказательство:
А
С
1) Через вершину В проведем прямую DK, параллельную
основанию АС.
2) ∠CBK=∠C как внутренние накрест лежащие при
параллельных DK и AC, и секущей BC
3) ∠DBA=∠A внутренние накрест лежащие при DK∥AC и секущей
AB. Угол DBK развернутый ∠DBK=∠DBA+∠B+∠CBK
4) Так как развернутый угол равен 180∘, а ∠CBK=∠C и ∠DBA=∠A, то
получим 180°=∠A+∠B+∠C
ВЫВОД:
Сумма углов любого треугольника равна 180°.
Знание этой теоремы поможет в решении
СПИСОК ИСТОЧНИКОВ:
1) Учебник Геометрия 7-9 классы авторы: Л.С.Атанасян,
В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина
Год издания: 2013
2) Изображение листа формата А4:
https://naurok.com.ua/metodichni-rekomendaci-movlennevasituaciya-yak-metodichniy-priyom-navchannya-56384.
 html
html3)
Изображение транспортита:
https://cartaterra.com.ua/shop/kanctovary/pribory-dlacercenia/linejki/transportiry/transportiry-irbis-miks-180gr-plastproz-pecatn-blpak
4)
Изображение ножниц:
https://yandex.ru/clck/jsredir?from=yandex.ru%3Bimages%2Fse
arch%3Bimages%3B%3B&text=&etext=8893.1pA74xrucVasEMS
5)
Изображение карандаша:
https://www.freepngimg.com/png/14515-pencil-png-picture
English Русский Правила
Доказательство того, что треугольник равен 180 градусам (видео)
Часто задаваемые вопросы
Сколько градусов в треугольнике?
Первое, что мы узнали о треугольниках, это то, что сумма внутренних углов равна 180 градусов.
Вы могли бы использовать эти знания, чтобы найти недостающий угол в треугольнике, когда вы знали два других, и все было хорошо. Но тогда, возможно, закралось зерно сомнения или любопытства.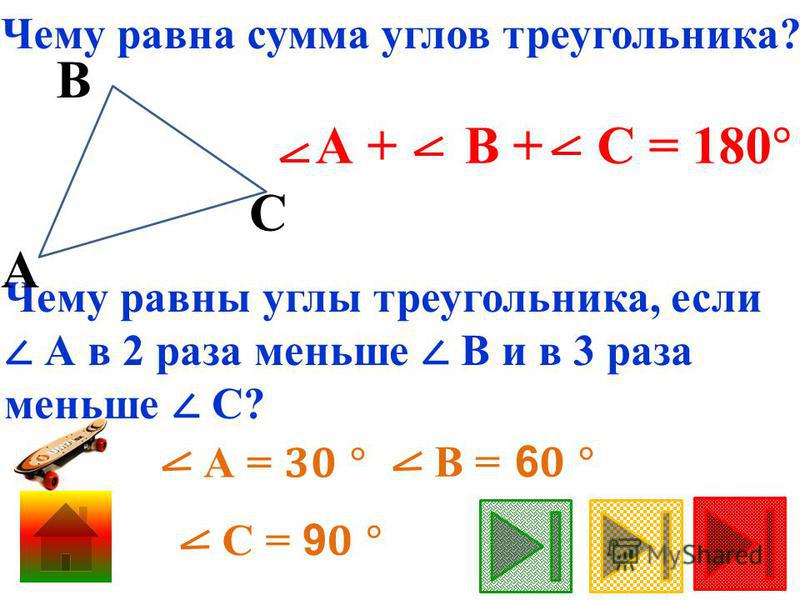 Откуда мы знаем, что сумма углов равна
Откуда мы знаем, что сумма углов равна
всегда
180? Есть ли способ, которым мы можем окончательно доказать это? Ответ — да!
Чтобы математически доказать, что сумма углов треугольника всегда равна 180 градусам, нам нужно установить некоторые основные факты об углах.
Углы треугольника
Первое, что нам нужно повторить, это определение прямого угла.
Прямой угол — это просто прямая линия, отсюда и его название.
Мы разместили на нем три точки, обозначающие три угла треугольника. Прямой угол АВС равен 180 градусам. Это будет важно позже.
Чтобы увидеть наши следующие углы, давайте возьмем два прямых угла и проведем через них другую линию:
Это то, что мы называем секущей. Мы можем видеть, что в этом случае есть только две различные угловые меры. Если мы посмотрим между параллельными линиями , мы увидим, что два угла с каждой стороны поперечной линии в сумме составляют 180 градусов.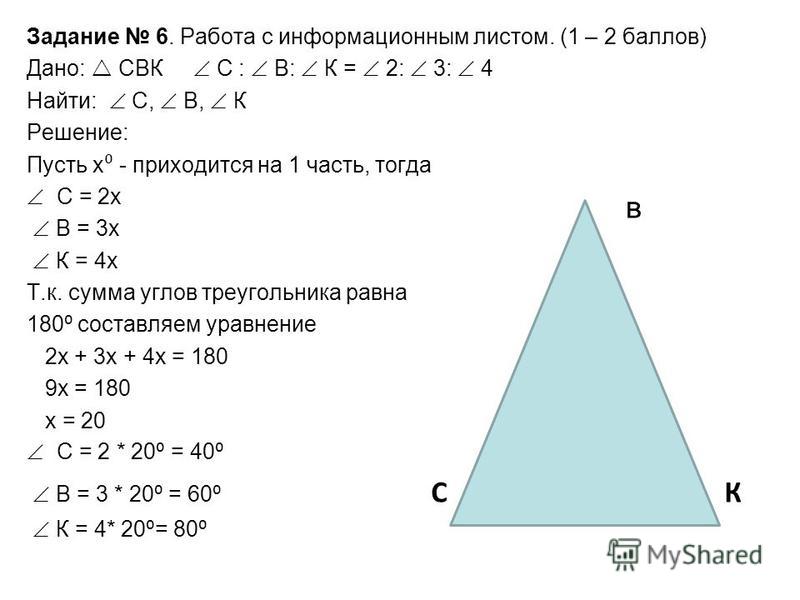
Это потому, что поперечная линия разрезает каждую из параллельных линий на две части. Поскольку прямая линия представляет собой прямой угол, при разрезании ее пополам две ее половины должны составлять исходную меру. Это похоже на то, как если вы отрежете метровую палку в любой точке, когда вы снова соедините две части палки, они все равно будут составлять один метр.
Если провести еще одну линию, пересекающую параллельные линии, то получится треугольник.
Наша верхняя группа углов была изменена с группы из четырех на группу из шести, потому что каждый из больших углов был разрезан новой линией.
Группа углов в левом нижнем углу не изменилась, и есть новая группа углов, созданная новой линией, пересекающей нижнюю параллельную линию.
Давайте добавим несколько меток ко всем углам между параллельными прямыми:
Мы видим, что углы A, B и C образуют прямой угол, а это значит, что их сумма должна быть 180 градусов. Теперь мы можем установить, что три угла внутри треугольника (B, E и F) также дают в сумме 180.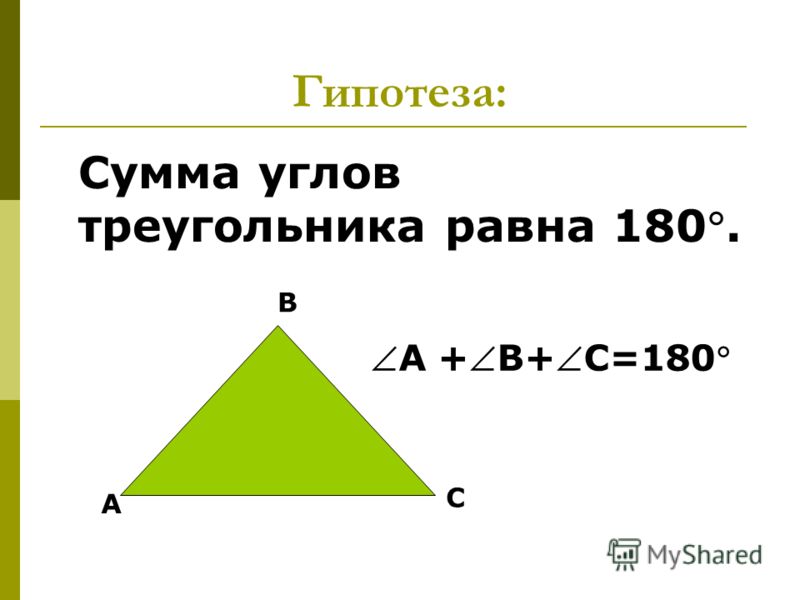
Углы A и E равны конгруэнтные углы , что означает, что они имеют одинаковую меру, потому что они являются альтернативными внутренними углами секущей с параллельными прямыми.
Угол C и угол F равны по одной и той же причине.
Угол B равен самому себе. Следовательно, сумма углов A, B и C должна быть равна сумме углов B, E и F. А так как известно, что сумма углов A, B и C равна 180, то сумма углов углы B, E и F также должны быть равны 180. Вот таблица, в которой нам все показано: 9{\circ}\)
Прямой угол определяется так: «мера угла А плюс мера угла В плюс мера угла C, равняется 180 градусам».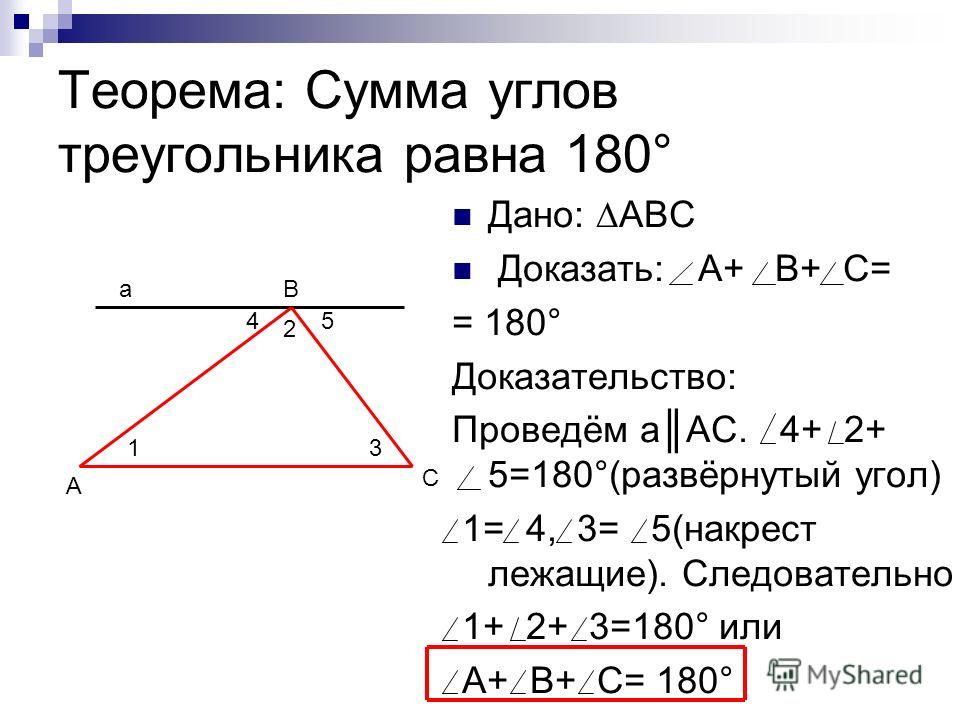 «Мера угла А равна мере угла Е» верно, потому что два угла конгруэнтны, чередующиеся внутренние углы. То же самое относится к углам C и F.
«Мера угла А равна мере угла Е» верно, потому что два угла конгруэнтны, чередующиеся внутренние углы. То же самое относится к углам C и F.
Давайте теперь посмотрим на это с угловыми мерами:
Когда мы посмотрим на три угла под линией 1, мы увидим, что их сумма составляет 180 градусов, как мы и знаем, они должны быть.
И три угла в треугольнике имеют одинаковые три угловые меры. Это всегда будет правдой. Если мы повернем добавленную линию и снова посмотрим на измерения, то увидим, что она все еще работает:
У нас есть 55, 75 и 50 внутри треугольника, а также 55, 75 и 50 под первой линией. Сложите их вместе, и вы получите, к удивлению, угол 180 градусов.
Обзор
Хорошо, прежде чем мы начнем, давайте ответим на пару вопросов для быстрого обзора!
1. Какова мера прямого угла?
- 360 °
- 180 °
- 90 °
- 0 °
2. Если два раковины — чередующиеся внутренние углы трансверсальных линий, это означает, что это означает, что это также 9000 районы.
Это все для этого обзора! Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Как доказать, что треугольник равен 180 градусам?
A
В прямом угле, таком как \(∠A+∠B+∠C\) в красном круге, три угла образуют \(180°\). Секущие, образованные длинами сторон треугольника, образуют пары углов, которые конгруэнтны. Например, \(∠A\) и \(∠A\) конгруэнтны, потому что они являются альтернативными внутренними углами. \(∠B\) и \(∠B\) также конгруэнтны, потому что они также являются альтернативными внутренними углами. Поскольку \(∠A=∠A\) и \(∠B=∠B\), мы знаем, что внутренние углы \(∠A+∠B+∠C\) также должны быть равны \(180°\).
Q
Может ли треугольник быть 180 градусов?
A
Угол, равный \(180°\), считается прямым углом или прямой линией. Сумма внутренних углов треугольника должна быть равна \(180°\), а это означает, что ни один из углов не может быть равен \(180°\) по отдельности.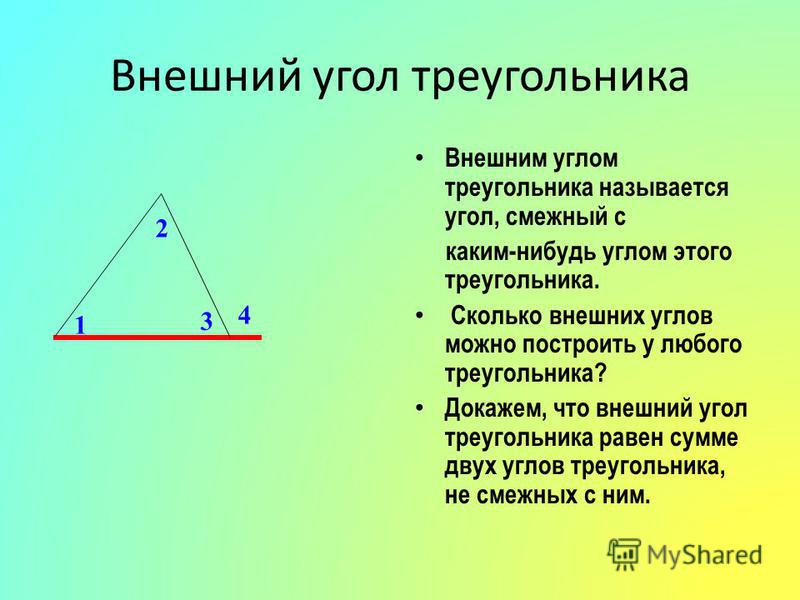
Q
Почему треугольник не может иметь угол 180 градусов?
A
Сумма трех внутренних углов треугольника всегда равна \(180°\). Треугольник не может иметь индивидуальную угловую меру \(180°\), потому что тогда не существовало бы двух других углов \((180°+0°+0°)\). Три угла треугольника нужно объединить в \(180°\).
Q
Чему равна сумма углов треугольника?
A
Сумма углов треугольника всегда будет равна \(180°\). Сумма углов четырехугольника равна \(360°\), а треугольник можно создать, разрезав четырехугольник пополам от угла к углу. Поскольку треугольник по существу является половиной четырехугольника, его угловая мера также должна быть равна половине. Половина \(360°\) равна \(180°\).
Например, сумма углов четырехугольника ниже равна \(360°\), потому что он состоит из четырех \(90°\) углов. Розовый треугольник составляет половину этого треугольника, поэтому сумма его углов также должна быть равна половине \((180°)\).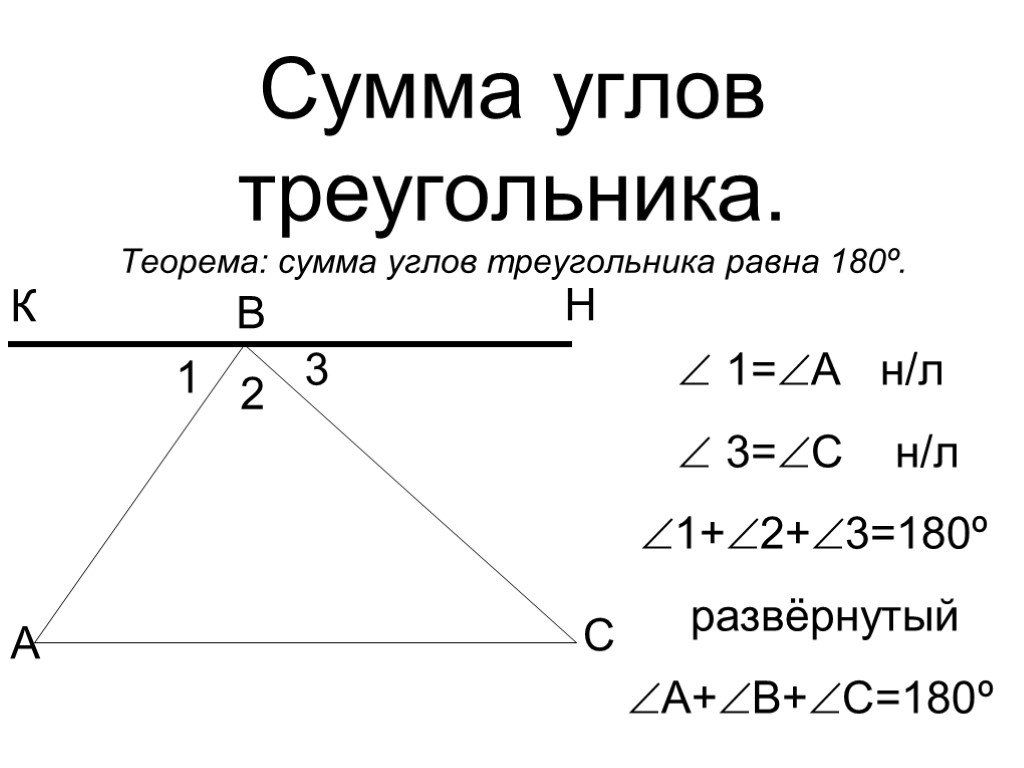
Q
Какой угол равен 180 градусам?
A
Угол \(180°\) всегда образует прямую линию. Эта линия также называется прямым углом. Один из способов доказать, что прямой угол равен \(180°\), состоит в том, чтобы сложить два прямых угла вместе. Два угла \(90°\) образуют угол \(180°\) или прямую линию.
Вернуться к видео по геометрии
687591
Почему треугольник имеет 180 градусов?
Вы знаете, что сумма углов треугольника всегда равна 180 0 ? Почему это? В конце концов, 180 0 это угол, который простирается от одной стороны прямой линии до другой, поэтому довольно странно, что это количество градусов в углах треугольника.
Какое отношение имеет треугольник к одной прямой? Как оказалось, довольно много. И треугольники также имеют много общего с прямоугольниками, пятиугольниками, шестиугольниками и целым семейством многогранных фигур, известных как многоугольники.
Через несколько недель мы увидим, что именно я имею в виду. Но сегодня мы начнем с выяснения, почему именно сумма углов треугольника всегда равна 180 0 . Или вы так думали… потому что мы также увидим, что иногда это не так.
Во-первых, обзор: типы треугольников
Краткое напоминание: существует три различных типа основных треугольников. Они равносторонние, равнобедренные и разносторонние.
- Равносторонний треугольник имеет три стороны одинаковой длины
- У равнобедренного треугольника две стороны одинаковой длины и одна сторона разной длины
- Разносторонний треугольник имеет три стороны разной длины
Длина стороны треугольника напрямую влияет на его углы.
СВЯЗАННЫЕ: открывается в новом окнеЧто такое треугольник Паскаля?
Внутренние и внешние углы
Прежде чем мы углубимся в нашу историю о треугольниках и общем количестве градусов в их трех углах, мы должны поговорить об одном небольшом геометрическом словаре. И в этом разница между внутренним и внешним углом.
И в этом разница между внутренним и внешним углом.
Проще всего описать разницу между этими двумя вещами на примере. Поскольку сегодняшняя тема — треугольник, давайте поговорим о внутренних и внешних углах треугольника. Короче говоря, внутренних углов — это все углы в пределах границ треугольника. Другими словами, это те углы, о которых мы говорили все это время.
внешних углов треугольника — это все углы между одной стороной треугольника и линией, полученной продолжением соседней стороны вне границ треугольника. Если вы подумаете об этом, вы увидите, что если вы прибавите любой внутренний угол треугольника к соседнему с ним внешнему углу, вы всегда получите 180 0 — прямую линию.
Почему треугольники имеют 180 градусов?
Что подводит нас к главному вопросу на сегодня: почему сумма внутренних углов треугольника всегда равна 180 0 ? Как оказалось, это можно понять, подумав о внутренних и внешних углах треугольника. Чтобы понять, что я имею в виду, включите свое воображение или лист бумаги, потому что пришло время для небольшого математического проекта по рисованию декоративно-прикладного искусства.
Чтобы понять, что я имею в виду, включите свое воображение или лист бумаги, потому что пришло время для небольшого математического проекта по рисованию декоративно-прикладного искусства.
Начните с рисования прямоугольного треугольника с одним горизонтальным катетом, одним вертикальным катетом и гипотенузой, идущей из верхнего левого угла в нижний правый. Теперь сделайте копию этого треугольника, поверните его вокруг 180 0 и прижмите его гипотенузой к гипотенузе с оригиналом (точно так же, как мы делали, когда выясняли, как найти площадь треугольника). Наконец, сделайте еще одну копию исходного треугольника и сдвиньте ее вправо так, чтобы она располагалась рядом с только что сформированным прямоугольником. Со мной до сих пор? Если это так, ваша картинка должна выглядеть так:
К чему эта картинка? Взгляните на внутренний угол в правом нижнем углу исходного треугольника (тот, что помечен буквой «А»). Теперь взгляните на два угла, которые составляют внешний угол для этого угла треугольника (обозначены буквами «В» и «С»). Как мы знаем, если сложить внутренний и внешний углы одного угла треугольника, мы всегда получим 180 0 . И наш маленький рисунок показывает, что рассматриваемый внешний угол равен сумме двух других углов треугольника. Другими словами, два других угла треугольника (те, которые в сумме образуют внешний угол) должны соединиться с углом в правом нижнем углу, чтобы получить угол 180 9 .0218 0 угол.
Как мы знаем, если сложить внутренний и внешний углы одного угла треугольника, мы всегда получим 180 0 . И наш маленький рисунок показывает, что рассматриваемый внешний угол равен сумме двух других углов треугольника. Другими словами, два других угла треугольника (те, которые в сумме образуют внешний угол) должны соединиться с углом в правом нижнем углу, чтобы получить угол 180 9 .0218 0 угол.
СВЯЗАННЫЕ: открывается в новом окнеМир тригонометрии
Для простоты мы сделали наш рисунок, используя прямоугольный треугольник. Но оказывается, что вы можете сделать точно такой же рисунок, используя любой треугольник, который вам нравится, и вы всегда будете приходить к одному и тому же выводу. Попробуйте сделать несколько рисунков, начиная с разных треугольников по вашему выбору, чтобы увидеть это своими глазами. В качестве примера, вот еще один, который я сделал:
Неизбежным выводом из этой игры является то, что сумма внутренних углов треугольника всегда должна составлять 180 0 . Наш милый и изящный маленький рисунок доказывает, что так и должно быть.
Наш милый и изящный маленький рисунок доказывает, что так и должно быть.
Или нет?
Могут ли треугольники иметь более 180 градусов?
Может быть, у нашего рисунка есть какие-то ограничения, которые не позволяют нам увидеть какую-то другую, более экзотическую возможность? Вам есть над чем подумать или попробовать. Возьмите ненадутый воздушный шар, положите его на плоскую поверхность и нарисуйте на нем как можно более совершенный треугольник. Если у вас есть под рукой транспортир, было бы здорово измерить и сложить внутренние углы треугольника и убедиться, что они довольно близки к 180 9 .0218 0 .
Теперь надуйте шарик и посмотрите на свой треугольник. Что с ним случилось? Если у вас есть этот транспортир, попробуйте еще раз просуммировать его внутренние углы. Что случилось с этой суммой? Вы все еще получаете 180
К счастью, у меня есть ответ.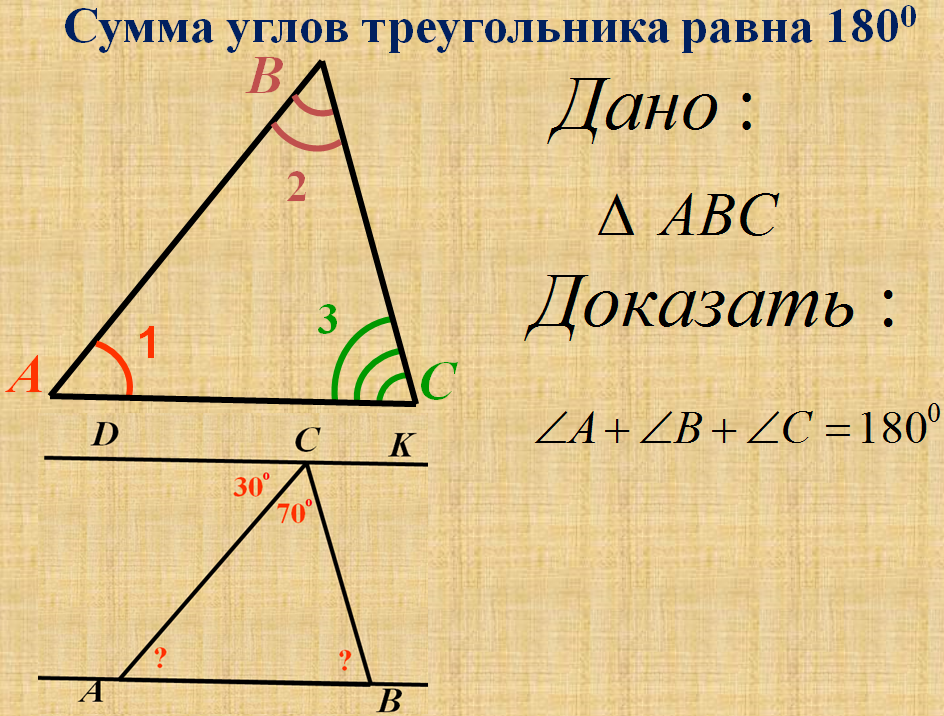

Leave A Comment