Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Масса бурого медведя 3/4 массы.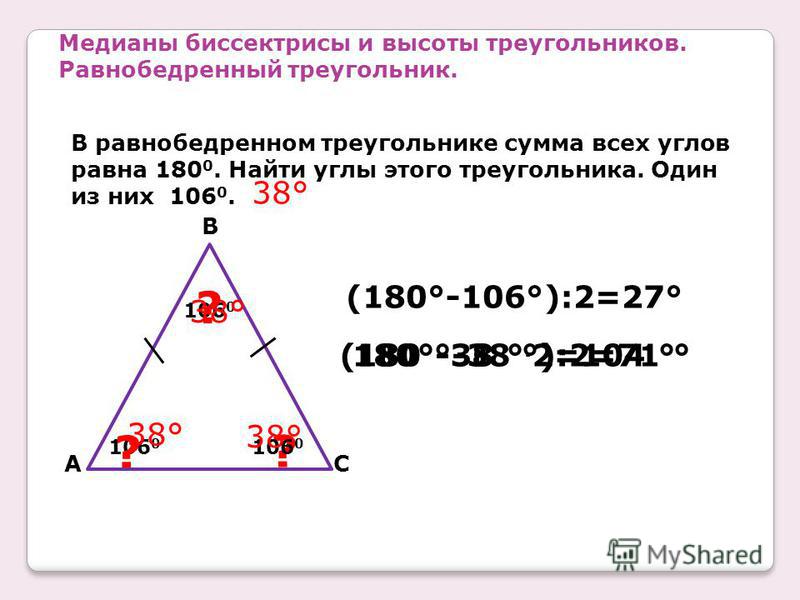 ..
..
первый отрезок на 8 см. длиннее второго,а третий на 4см. короче второго,на сколько см. первый отрезок длиннее третьего?
Решено
Высота конуса равна 6 см, угол при вершин осевого сечения равен 120 градусов. Найдите 1) площадь сечения конуса плоскостью проходящей через две…
Решено
Расстояние между городом и зимовкой…
Решено
В корзине лежат 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик ,а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?
Пользуйтесь нашим приложением
Сумма двух внешних углов треугольника равна 240 градусов. Найдите внутренний угол треугольника не смежный с этими внешними углами. — Знания.site
Геометрия
24 минут назад
Геометрия 7 классГеометрия
42 минут назад
Помогите пожалуйста срочно нужно
Геометрия
45 минут назад
помогите пж срочно
45 минут назад
Геометрия за 9 класс. Срочно нужно решить!!!!!!!!!!!!!!!!
Срочно нужно решить!!!!!!!!!!!!!!!!Геометрия
1 час назад
ПООГИТЕ ДАЮ 50БАЛОВ СРОЧНОГеометрия
2 часа назад
Помогите пожалуйста срочно нужноГеометрия
2 часа назад
З точки А, яка не належить площині, до площини α проведено перпендикуляр АС та похилу АВ . Знайти відстань до площини α, якщо довжина похилої 26см, а проекція похилої до площини дорівнює 24 см.Геометрия
3 часа назад
Помогите решить задачу по геометрии, пожалуйста.
Геометрия
3 часа назад
ПОМОГИТЕ С АЛГЕБРОЙ!Геометрия
3 часа назад
Вопрос про лежащую на прямой точкуГеометрия
4 часа назад
Молю, срочно помогитеГеометрия
4 часа назад
Помогите пожалуйста с геометрией!!!! Нужно дано и решение!!!! Только математичкими выражениями!!!!Геометрия
4 часа назад
Помогите пожалуйста с домашкойГеометрия
4 часа назад
ПОМОГИТЕ ПОЖАЛУЙСТА С ГЕОМЕТРИЕЙ!!!! Нужно дано и решение, без словГеометрия
4 часа назад
Як зміниться площа прямо- кутника, якщо одну з його СTOPiH: a) збільшити в 3 рази; б) зменшити в 4 рази; в) збільшити на 50% ?
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Свойства треугольника — типы и формулы [Видео и практика]
7 минут чтения
В этой статье мы узнаем о простейшей форме многоугольника, треугольника . Все многоугольники можно разбить на треугольники, или другими словами, они образуются путем объединения двух или более треугольников. Таким образом, понимание основных свойств треугольника и его типов имеет важное значение.
Все многоугольники можно разбить на треугольники, или другими словами, они образуются путем объединения двух или более треугольников. Таким образом, понимание основных свойств треугольника и его типов имеет важное значение.
Всего существует шесть типов треугольников – равнобедренный, разносторонний, равносторонний, косой, остроугольный и прямоугольный. Исходя из классификации по внутренним углам, различают три типа – равнобедренные, равнобедренные и разносторонние. Принимая во внимание, что типы треугольника, которые классифицируются в зависимости от длины его стороны, являются прямоугольным, остроугольным и косоугольным. Вот типы треугольников:
| Based on the Angle | Based on the Sides |
| Acute Angled Triangle | Equilateral Triangle |
| Oblique angled Triangle | Scalene Triangle |
| Right Angle Triangle | Равнобедренный треугольник |
Посмотрите это видео, чтобы узнать основные свойства треугольника:
youtube.com/embed/J_IYLtYw3dc?rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Вот краткое описание тем, которые мы рассмотрим в этой статье:
[скрыть]
Что такое треугольник?
Как следует из названия, треугольник представляет собой многоугольник с тремя углами. Итак, когда замкнутая фигура имеет три угла?
Когда он состоит из трех сегментов линии, соединенных встык.
Таким образом, можно сказать, что треугольник — это многоугольник, у которого три стороны, три угла, три вершины, а сумма всех трех углов любого треугольника равна 180°.
Свойства треугольника
Свойства треугольника:
- Треугольник имеет три стороны, три угла и три вершины.
- Сумма всех внутренних углов треугольника всегда равна 180 °. Это называется свойством суммы углов треугольника.

- Сумма длин любых двух сторон треугольника больше длины третьей стороны.
- Сторона, лежащая напротив наибольшего угла треугольника, является наибольшей стороной.
- Любой внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.
Типы треугольников
Треугольники можно классифицировать двумя основными способами:
- Классификация по внутренним углам (Прямой, Острый, Косой)
- Классификация по длине сторон (Равносторонний, Равнобедренный, Разносторонний)
Рассмотрим подробно шесть типов треугольников:
- Остроугольный треугольник
- Прямоугольный треугольник
- Косоугольный треугольник
- Разноугольный треугольник
- Равнобедренный угловой треугольник
- Равнобедренный угловой треугольник
Остроугольный треугольник
Треугольник, у которого все три угла меньше 90 °, является остроугольным треугольником.
- Итак, все углы остроугольного треугольника называются острыми углами
Ниже приведен пример остроугольного треугольника.
Прямоугольный треугольник
Треугольник, у которого один угол равен 92
Это известно как Теорема Пифагора
И наоборот, мы можем сказать, что если треугольник удовлетворяет условию Пифагора, то это прямоугольный треугольник.
Тупоугольный/косоугольный треугольник
Треугольник, у которого один угол больше 90 °, является тупоугольным треугольником.
Ниже приведен пример треугольника с тупым/косым углом.
Вопросы о треугольниках очень часто задают на GMAT. Ace GMAT Quant, подписавшись на нашу бесплатную пробную версию и получив доступ к более чем 400 вопросам. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2400 отзывами на GMATClub.
Сэкономьте более 60 часов подготовки к GMAT, составив четкий план обучения всего за 3 шага:
youtube.com/embed/5ftgtAl_3C0? rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Разносторонний треугольник
Треугольник, у которого все три стороны разной длины — это разносторонний треугольник.
- Поскольку все три стороны имеют разную длину, три угла также будут разными.
Ниже приведен пример разностороннего треугольника
Равнобедренный треугольник
Треугольник, у которого две стороны одинаковой длины, а третья сторона разной длины , является равнобедренным треугольником.
- Углы, противоположные равным сторонам, имеют одинаковую меру.
Ниже приведен пример равнобедренного треугольника.
Равносторонний треугольник
Треугольник, у которого все три стороны имеют одинаковую длину , является равносторонним треугольником.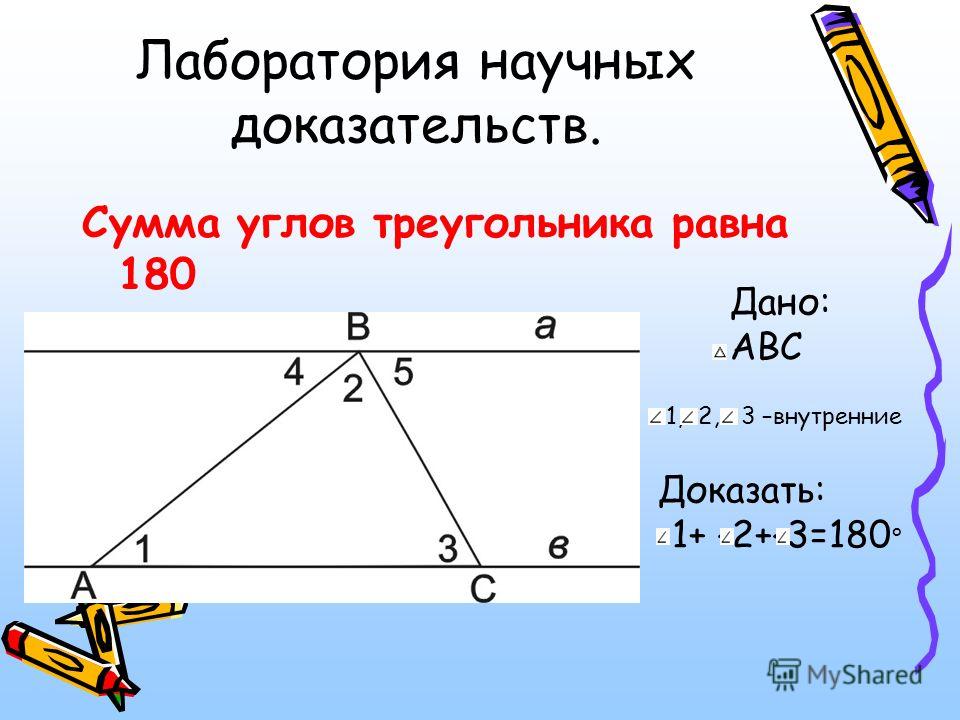
- Поскольку все три стороны имеют одинаковую длину, все три угла также будут равны.
- Каждый внутренний угол равностороннего треугольника = 60° треугольник,
- Два угла равны 45°, а третий угол прямой.
- Стороны этого треугольника будут в соотношении – 1:1:√2 соответственно.
- Этот треугольник также называется равнобедренным прямоугольным треугольником , так как два угла равны.
30-60-90 треугольник
В этом треугольнике
- Это прямоугольный треугольник, так как один угол = 90°
- Углы этого треугольника находятся в соотношении – 1:2:3, и
- Стороны , противоположные этим углам , будут в отношении – 1: √3: 2 соответственно
- Это разносторонний прямоугольный треугольник , так как все три угла разные.
Площадь треугольника
- Площадь любого треугольника = ½ * основание * высота
- Площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон Подытожим некоторые важные свойства треугольника.

- Сумма всех внутренних углов любого треугольника равна 180 °
- Сумма всех внешних углов любого треугольника равна 360 °
- Внешний угол треугольника равен сумме двух его внутренних противоположных углов
- Сумма длины любых двух сторон треугольника всегда больше длины третьей стороны
- Аналогично, разность длин любых двух сторон треугольника всегда меньше длины третьей стороны
- Сторона, противоположная наименьшему внутреннему углу, является самой короткой стороной, и наоборот.
- Точно так же сторона, противоположная наибольшему внутреннему углу, является самой длинной стороной, и наоборот.
- В случае прямоугольного треугольника эта сторона называется гипотенузой
- Высота треугольника равна длине перпендикуляра, опущенного из вершины на противоположную ему сторону, и эта сторона равна считается базовым
Если вам понравилась эта статья, вы также можете прочитать следующие статьи продвинутого уровня о треугольниках
- Геометрические понятия и формулы GMAT для треугольников (часть 1)
- Свойства треугольников: практические вопросы (часть 2)
- Особые свойства треугольников (часть 3)
Начинаете подготовку к GMAT? Вот пятиэтапный план подготовки к GMAT:
youtube.com/embed/7T9zeh-8XrY? rel=0″ title=»YouTube video player» frameborder=»0″ allow=»accelerometer rel=0; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Свойства треугольника: практический вопрос
Вопрос: 1
В равнобедренном треугольнике DEF, если внутренний угол ∠D = 100°, то какова величина ∠F?
- 20 °
- 40 °
- 60 °
- 80 °
- 100 °
Раствор
Шаг 1: дано
- oref ASOSF IS AOSTEF IS ASOSF IS ASOSF IS AOSTEF IS AOSTEF IS AOSTEF IS AOSTEF IS AOSTEF IS AOSTEF ASOSC.
Шаг 2: Найти
- Значение ∠F
Шаг 3: Подход и расчет
- Мы знаем, что сумма всех внутренних углов треугольника = 180°
- Отсюда следует, что ∠D + ∠E + ∠F = 180° = 80°
- Поскольку треугольник ∆DEF равнобедренный; два его угла должны быть равны.

- И единственная возможность ∠E = ∠F
- Следовательно, 2∠F = 80°
- Подразумевает, ∠F = 40°
Отсюда правильный ответ Вариант Б.
- 0004 В прямоугольном треугольнике ∆ABC, BC = 26 единиц и AB = 10 единиц. Если ВС — самая длинная сторона треугольника, то какова площадь ∆ABC?
- 120
- 130
- 240
- 260
- 312
Решение
Шаг 1: дано
- ∆Abc is rought-ant-ant-ant-
- ВС = 26 шт.
- АВ = 10 шт.
- до н.э. — самая длинная сторона треугольника .
Шаг 2: Нахождение
- Площадь треугольника ∆ABC
Шаг 3: Подход и вычисление hypotenuse
Thus, according to Pythagoras rule:
- BC 2 = AB 2 + AC 2
- 26 2 = 10 2 + AC 2
- AC 2 = 676 – 100 = 576
- Следовательно, AC = 24 единицы
- Мы знаем, что площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон = ½ * AB * AC = ½ * 10 * 24 = 120 квадратных единиц
Следовательно, правильный ответ: Вариант А .
Вот еще несколько статей, которые вы можете прочитать:
- Свойства четырехугольника
- Свойства чисел: четные/нечетные, простые, HCF и LCM
- Свойства круга
- Свойства линий и углов
Если вы планируете сдавать GMAT, мы можем помочь вам составить индивидуальный план обучения и предоставить доступ к качественному онлайн-контенту для подготовки. Напишите нам по адресу [email protected]. Мы являемся самой популярной компанией по подготовке к GMAT в gmatclub с более чем 2400 отзывами и единственной компанией по подготовке, которая набрала более 700+ баллов, чем любой другой партнер клуба GMAT . Почему бы вам не воспользоваться бесплатной пробной версией и не судить самостоятельно?
Знаете ли вы, что участники e-GMAT набрали больше 700 баллов, чем когда-либо прежде в истории GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг этого рекордного результата, инвестируя и внедряя инновации с единственной целью — создать платформу, которая позволяет учащимся достигать и показывать свои лучшие результаты.
FAQ – Свойства треугольника
Что такое треугольник и его свойства?
Треугольник – замкнутая фигура с тремя сторонами, тремя вершинами, тремя углами и суммой внутренних углов 180°
Какие бывают типы треугольников?
Треугольники можно классифицировать двумя способами: по внутренним углам и по длине сторон. По внутреннему углу треугольники бывают трех типов: остроугольные, прямоугольные и тупоугольные. В зависимости от длины сторон треугольники можно разделить на 3 категории: разносторонние, равнобедренные и равнобедренные.
Что такое разносторонний треугольник?
Треугольник, у которого все три стороны разной длины, является разносторонним треугольником.
Что такое равнобедренный треугольник?
Треугольник, у которого две стороны одинаковой длины, а третья сторона разной длины, является равнобедренным треугольником.
Что такое равносторонний треугольник?
Треугольник, у которого все три стороны имеют одинаковую длину, является равносторонним треугольником.
Внутренние углы многоугольника
Quick Definitions
Давайте рассмотрим несколько ключевых слов, чтобы мы все были на одной странице. Помните, что 9Многоугольник 0016 представляет собой двумерную фигуру, стороны которой нарисованы прямыми линиями (без кривых), которые вместе образуют замкнутую область. Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренних углов многоугольника. Квадрат, например, имеет четыре внутренних угла, каждый из которых по 90 градусов. Если квадрат представляет ваш класс, то внутренние углы — это четыре угла комнаты.
Если квадрат представляет ваш класс, то внутренние углы — это четыре угла комнаты.
Сумма внутренних углов
В дальнейшем, если многоугольник имеет x сторон, сумма S градусных мер этих x внутренних сторон определяется по формуле S = (х — 2)(180) .
Например, треугольник имеет 3 угла, сумма которых составляет 180 градусов. У квадрата 4 угла, сумма которых составляет 360 градусов. Для каждой дополнительной стороны, которую вы добавляете, вы должны добавить еще 180 градусов к общей сумме.
{включить ad_line.html %}
Давайте поговорим о диагонали на минуту. Что такое диагональ вообще? Диагональ — это отрезок, соединяющий две непоследовательных вершин многоугольника. Это все линии между точками многоугольника, если не считать тех, которые также являются сторонами многоугольника. На картинке ниже BD — это диагональ. Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов этих треугольников (180+180=360) равна сумме всех углов прямоугольника (360).
Сумма углов этих треугольников (180+180=360) равна сумме всех углов прямоугольника (360).
Пример 1
Четырехугольник ABCD имеет четыре угла. Эти четыре угла находятся в соотношении 2:3:3:4. Найдите градусную меру наибольшего угла четырехугольника ABCD.
Что мы знаем?
У нас есть четыре неизвестных ракурса, но информация об их отношении друг к другу. Поскольку мы знаем, что сумма всех четырех углов должна быть равной 360 градусам, нам просто нужно выражение, которое складывает наши четыре неизвестных угла и устанавливает их равными 360. Поскольку они находятся в отношении, они должны иметь какой-то общий множитель, который нам нужен. найти, называется х.
Шаги:
- Добавьте члены 2x + 3x + 3x + 4x
- Приравнять сумму слагаемых к 360
- Найти x
- Определите величину угла в градусах.
Решить
2x + 3x + 3x + 4x = 360
12х = 360
х = 360/12
x = 30
Хотя мы знаем, что x = 30, мы еще не закончили.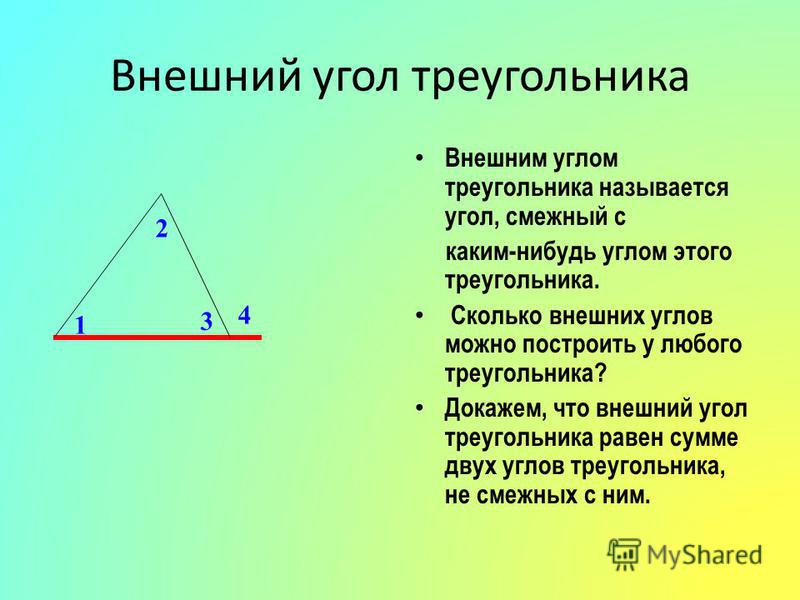 Умножаем 30 на 4, чтобы найти наибольший угол. Поскольку 30 умножить на 4 = 120, самый большой угол равен 120 градусам. Аналогично, остальные углы равны 9.0016 3 *30=90, 3 *30=90 и 2 *30 = 60.
Умножаем 30 на 4, чтобы найти наибольший угол. Поскольку 30 умножить на 4 = 120, самый большой угол равен 120 градусам. Аналогично, остальные углы равны 9.0016 3 *30=90, 3 *30=90 и 2 *30 = 60.
Правильные многоугольники
Правильный многоугольник равноугольный. Все его углы имеют одинаковую меру. Он также равносторонний. Все его стороны имеют одинаковую длину. Квадрат — это правильный многоугольник, и хотя квадрат — это тип прямоугольника, прямоугольники, состоящие из , а не квадратов, не будут правильными многоугольниками.
Пример 2
Найдите сумму градусных мер углов шестиугольника. Предполагая, что шестиугольник равен обычный , найдите градусную меру каждого внутреннего угла.
Что мы знаем?
Мы можем использовать формулу S = (x — 2)(180) для суммирования степенной меры любого многоугольника.
У шестиугольника 6 сторон, поэтому x=6.
Решите
Пусть x = 6 в формуле и упростите:
S = (6 — 2)(180)
S = 4(180)
S = 720
Правильный многоугольник равен равноугольному , что означает, что все углы имеют одинаковую меру.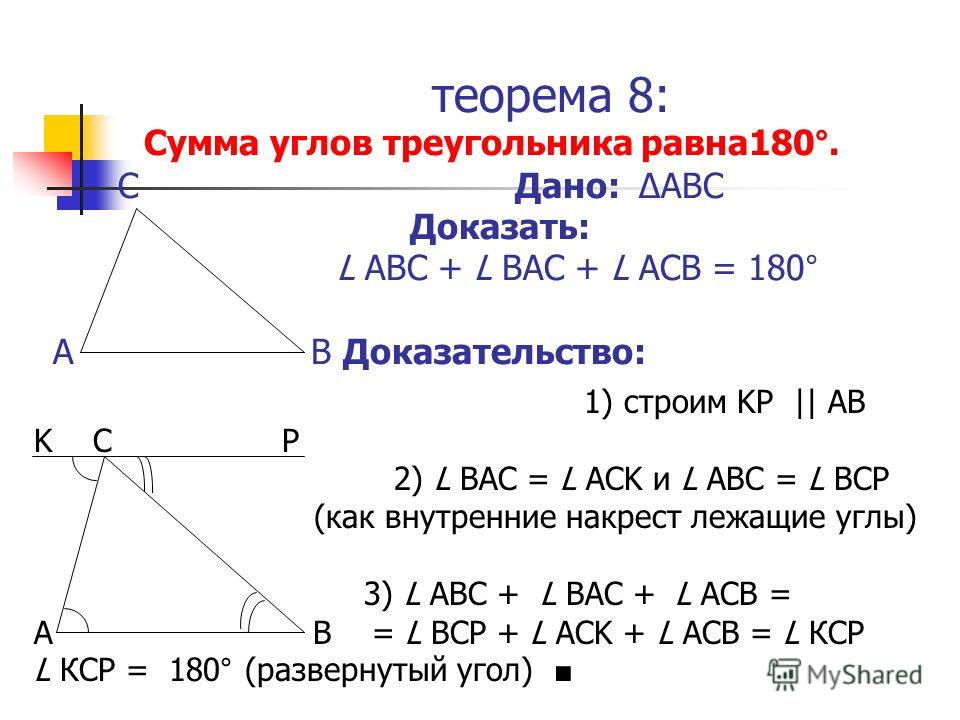 В случае правильного шестиугольника сумма 720 градусов будет равномерно распределена между шестью сторонами.
В случае правильного шестиугольника сумма 720 градусов будет равномерно распределена между шестью сторонами.
Итак, 720/6 = 120. В правильном шестиугольнике шесть углов, каждый по 120 градусов.
Пример 3
Если сумма углов многоугольника равна 3600 градусов, найдите количество сторон многоугольника.
Обращение формулы
Опять же, мы можем использовать формулу S = (x — 2)(180), но на этот раз мы вычисляем x вместо S. Ничего страшного!
Решите
В этой задаче пусть S = 3600 и решите x.
3600 = (х — 2)(180)
3600 = 180х — 360
3600 + 360 = 180х
3960 = 180x
3960/180 = х
22 = x
Многоугольник с 22 сторонами имеет 22 угла, сумма которых равна 3600 градусов.
Внешние углы многоугольника
В каждой вершине многоугольника внешний угол может быть образован путем удлинения одной стороны многоугольника так, чтобы внутренний и внешний углы в этой вершине были дополнительными (в сумме до 180). На рисунке ниже углы a, b c и d являются внешними, а сумма их градусных мер равна 360.
На рисунке ниже углы a, b c и d являются внешними, а сумма их градусных мер равна 360.
Если правильный многоугольник имеет x сторон, то градусная мера каждого внешнего угла равна 360, деленному на x.
Давайте рассмотрим два примера вопросов.
Пример 4
Найдите градусную меру каждого внутреннего и внешнего угла правильного шестиугольника.
Помните формулу суммы внутренних углов S=(x-2)*180. Шестиугольник имеет 6 сторон. Поскольку x = 6, сумму S можно найти, используя S = (x — 2)(180)
S = (10 -6)(180)
С = 4(180)
S = 720
В шестиугольнике шесть углов, а в правильном шестиугольнике все они равны. Каждый равен 720/6, или 120 градусов. Теперь мы знаем, что внутренний и внешний углы составляют дополнительных (в сумме 180) в каждой вершине, поэтому мера каждого внешнего угла равна 180 — 120 = 60.
Пример 5
Если мера каждого внутреннего угла правильный многоугольник равен 150, найдите количество сторон многоугольника.

 02.15
02.15 Срочно нужно решить!!!!!!!!!!!!!!!!
Срочно нужно решить!!!!!!!!!!!!!!!!



Leave A Comment