Сумма двух углов треугольника и внешнего угла к третьему равна 40: Вопросы»сумма двух углов треугольника и внешнего угла к третьему / найдите площадь параллелограмма|Поступи в ВУЗ

Теорема ⭐ о сумме углов треугольника: определение, доказательство, следствие

Формулировка теоремы о сумме углов треугольника

Треугольник может иметь различные углы — острые, прямой, тупой, — но сумма их величин не может превышать 180 градусов. Эта закономерность отражена в теореме, доказательство которой имеет несколько вариантов.

Теорема 

Сумма углов в треугольнике всегда равна .

Данная теорема является одной из основных, рассматриваемых на уроках геометрии.

Рассмотрим рисунок с треугольником ABC:

Источник: izamorfix.ru

Треугольник имеет углы: A, B, C. Это углы внутренние. Складывая их величины, неизменно получаем 180о. При этом не имеет значения, данный треугольник равнобедренный, равносторонний или прямоугольный.

Исходя из такого свойства, треугольник не может иметь два тупых угла, поскольку их сумма будет более 180о.

Смысл теоремы о сумме углов треугольника был известен еще в Древнем Египте, его установили эмпирическим путем, т. е. путем наблюдения. Однако вероятно, что в то время отсутствовало доказательство этого утверждения. Его можно обнаружить в трудах Прокла, когда он давал комментарии к «началам» Евклида.

В книге № 1 евклидовских «Начал» приведено иное доказательство данной теоремы, чем принято сейчас. Оно опирается на соответствующий чертеж.

Примечание 1

Рассматриваемая теорем приписывается не только Евклиду, но и Пифагору. Она много раз подвергалась сомнению в неевклидовой геометрии.

Доказательство теоремы

Продолжим рассмотрение треугольника ABC из предыдущего раздела.

Для доказательства теоремы проведем дополнительную прямую линию так, чтобы она была параллельна стороне AC и проходила через вершину треугольника B (угол 2).

Источник: izamorfix.ru

Таким образом, в районе угла B образовалось три угла (№№ 4, 2, 5). Из рисунка видно, что их сумма равняется 180о.

На данном рисунке имеются накрест лежащие углы: №1 и №4. Их образование произошло при пересечении прямой AB двух параллельных прямых AC и α. Углы №3 и №5 — также накрест лежащие. Только образованы они при пересечении прямой BC двух параллельных прямых AC и α.

Углы №1 и №4, а также №3 и №5 попарно равны.

Поскольку сумма углов №№ 4, 2, 5 равна 180о, а углы №4 можно заменить №1, а №5 — №3, сумма углов №№ 1, 2, 3 также равна 180о.

Такое доказательство опирается на свойства углов, образованных при пересечении двух параллельных прямых третьей.

Следствие из теоремы

Формулировка теоремы о сумме углов треугольника имеет несколько следствий. Среди них:

1. Если в треугольнике один из углов прямой, то сумма прочих двух углов равна 90о. Свойство вытекает из обычного алгебраического действия. Обозначим углы прямоугольного треугольника A, B, C. Допустим, что C=90о. Тогда (A+B)=180о+90о.
2. Для равнобедренного прямоугольного треугольника характерно, что каждый из его острых углов равен 45о.
3. Треугольник, у которого равны длины всех трех сторон, имеет равные углы — 60о.
4. Углы любого треугольника либо все являются острыми, либо острых два, а третий равен 90о либо больше 90о (тупой).
5. Сумма двух внутренних углов, которые не смежны с внешним, равна величине этого внешнего угла.

Классификация треугольников по видам углов

Рассматривая треугольники, как многоугольники с тремя вершинами, в геометрии выделяют их следующие разновидности:

1. Остроугольный треугольник (все три вершины представляют собой острые углы).
2. Прямоугольный (одна из вершин составляет 90о). Стороны, которые образуют данный угол, — катеты, а сторона, противолежащая углу в 90о, — гипотенуза.
3. Тупоугольный (одна из вершин представлена тупым углом, а две другие — острыми).

В зависимости от особых характеристик сторон треугольника, существует еще одна классификация:

1. Треугольник с тремя равными сторонам — равносторонний.
2. Треугольник с двумя равными сторонами — равнобедренный.

Приведенная классификация подразумевает существование определенных признаков у каждой из названных групп. Эти признаки приходят на помощь в решении задач, когда нужно доказать особенности каких-либо геометрических фигур.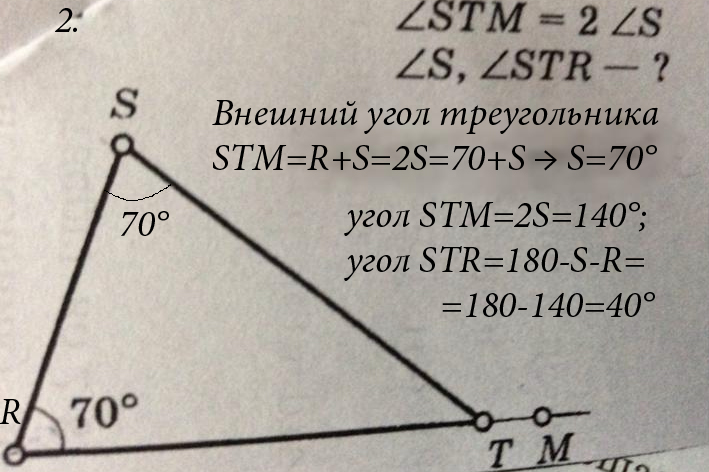 Так:

1. Больший угол всегда расположен напротив большей стороны.
2. Равные углы всегда расположены так, что напротив них — равные стороны.
3. Любой треугольник (равносторонний, равнобедренный, тупоугольный, прямоугольный и т. п.) имеет 2 острых угла.
4. Любой внешний угол всегда по размеру превышает внутренний и равен сумме прочих, не смежных с ним, углов.

Для прямоугольного треугольника существуют еще несколько свойств, вытекающих из его определения и изложенных в учебниках по геометрии:

1. Напротив катетов всегда расположены острые углы.
2. Гипотенуза всегда превышает по своей длине любой из катетов, однако меньше их суммы.
3. Тот катет, напротив которого находится острый угол величиной 30о, равен половине длины гипотенузы.
4. Сумма квадратов катетов равна квадрату гипотенузы. Данное свойство доказывается теоремой Пифагора.

Примечание 2

Существуют отдельные свойства для равнобедренного треугольника. Его высота, проведенная в направлении основания, совпадает с медианой и биссектрисой того угла, который расположен между равными сторонами. Кроме того, она совпадает с осью симметрии треугольника, проведенной по основанию.

Пояснение на примерах

Рассмотрим особенности треугольников, приведенные выше, на примерах.

Упражнение 1

Сколько градусов составляет один из углов треугольника, если величины других 25о и 42о?

Решение:

Исходя из теоремы о сумме углов в треугольнике, производим следующие вычисление:

180о-(25о+42о)=113о.

Следовательно, данный треугольник тупоугольный.

Упражнение 2

Известно, что в треугольнике один из углов равен сумме двух других. К какому виду треугольников относится данная геометрическая фигура?

Решение:

Обозначим угол, равный сумме двух других углов, за X. Тогда X+2X/2=180 Путем математических действий приходим к уравнению следующего вида: 2X=180, откуда X=90о.

Ответ: данный треугольник имеет прямой угол, поэтому является прямоугольным.

Упражнение 3

Дан треугольник ABC. В нем угол C на 15о больше, чем угол A, а угол B — на 30о его меньше. Найти величину каждого из углов.

Решение:

Обозначим X величину угла A. Тогда угол C=X+15, B=X-30

 

Источник: wiki.eduvdom.com

Используем свойство суммы углов треугольника и составляем уравнение:

X+(X+15)+(X-30)=180

3X-15=180

3X=195

X=65

Ответ: угол A=65о, угол B=65-30=35о, угол C=65+15=80о.

Для проверки можно сложить величины полученных результатов: 65+35+80=180о. Следовательно, задача решена верно. 

Упражнение 4

Про треугольник ABC известно, что угол A составляет 60о, угол B — 80о. Из угла A на сторону BC опущена биссектриса, образовав треугольник ACD. Каких величин углы имеет данный треугольник?

Источник: wiki.eduvdom.com

Решение:

Исходя из определения биссектрисы, мы знаем, что это луч, который начинаясь в вершине угла треугольника и деля его на два равных угла, пересекает противоположную сторону в определенной точке.

Поскольку биссектриса делит угол A пополам, образованный  угол DAB равен 30о, а угол ADC=30+80=110о (поскольку это внешний угол треугольника).

Исходя из правила, что сумма углов в треугольнике равна 180о, проводим математическое действие:

Угол C=180-(110+30)=40о

Ответ: Угол C равен 40о.

Упражнение 5

В треугольнике ABC известна величина одного угла: A = 40о. Известно, что также что угол, смежный с углом B, составляет 70о. Определить величины всех углов.

Решение:

Источник: multiurok.ru

Решение задания заключается в уравнении. Обозначим величину угла C за X. Тогда

(X+40o+(180o-70o))=180o

X+150o=180o

X=30o

Данный вариант решения основан на том свойстве, что если сумма смежных углов равна 180о (а именно это мы видим на рисунке относительно угла B), то величина каждого из них равна 180о минус величина смежного угла.

Ответ: Величина угла C = 30о, угла B — 110о.

Проверочным действием является операция сложения всех известных и найденных величин углов: 110о+30о+40о=180о.

Упражнение 6

В треугольнике ABC известен угол A (40о). Кроме того, по условию этот треугольник равносторонний (AC=BC). Найти величины двух оставшихся углов.

Решение:

Источник: multiurok.ru

Известно утверждение, что в равностороннем треугольнике величины углов прилегающих к этим сторонам, равны. Следовательно, углы B и A равны. Используя теорему о сумме углов в треугольнике, принимая величину угла C за X, составляем равенство:

2*40о+X=180о

X=100о

Ответ: Величина угла B равна 40о, угла C — 100о. Следовательно, треугольник является тупоугольным.

Входная диагностика по геометрии | Методическая разработка по геометрии (8 класс):

Входная диагностика по геометрии.    8 класс

Вариант 1

1) В треугольнике ABC угол A равен 750, АС=ВС. Найдите угол C.

3) В треугольнике ABC  АС=ВС. Внешний угол при вершине B равен 1530. Найдите угол C.

4) В треугольнике ABC АС=ВС, AD — высота, угол BAD равен 340. Найдите угол C.

5) Один из внешних углов треугольника равен 360. Углы, не смежные с данным внешним углом, относятся как 1 : 2. Найдите наибольший из них.

6) Сумма двух углов треугольника и внешнего угла к третьему равна 260. Найдите этот третий угол.

7) В треугольнике ABC угол A равен 350, угол C равен 400. На продолжении стороны AB отложен отрезок ВD=ВС. Найдите угол D треугольника BCD.

8) В треугольнике ABC угол A равен 200, угол B равен 280, CH — высота. Найдите разность углов ACH иBCH.

9) Какие из следующих утверждений верны?

    1) В треугольнике АВС, для которого АВ=4, ВС=5 , АС=6, угол В — наибольший.

    2) Внешний угол треугольника больше каждого внутреннего угла.

    3) Треугольник со сторонами 1, 2, 3 не существует.

    4) В треугольнике против меньшего угла лежит меньшая сторона.

10) Луч ВК – биссектриса угла ABD, луч ВС – биссектриса угла ABК. Угол АВС = 23°. Найти угол АВD.

11) В прямоугольном треугольнике АВС, угол С = 900. Внешний угол при вершине В равен 1500. АВ+АС=12 см. Найдите АС.

12) На отрезке AB взяты точки M и N. Известно, что АВ = 12см, АМ= 8 см, BN = 10 см.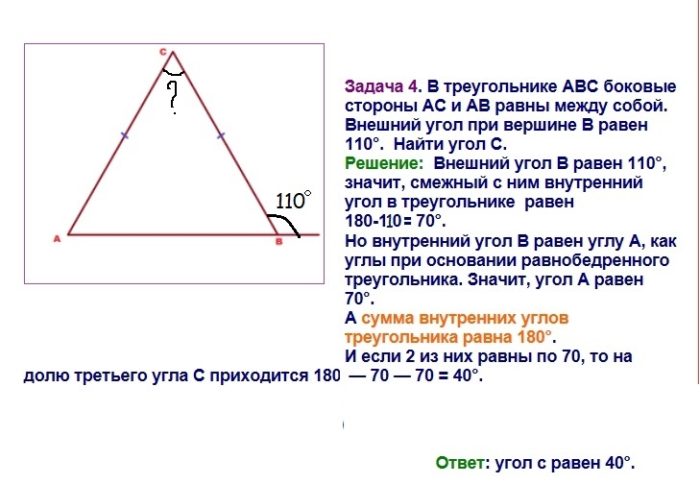 Найдите длину отрезка MN.

13) В прямоугольном АВС угол С=900. АС=ВС. Высота СD, опущенная на сторону АВ  равна 4. Найдите АВ

14) Периметр равностороннего треугольника 24 см. На его стороне, как на основании, построен равнобедренный треугольник, периметр которого 36 см. Найти боковую сторону этого треугольника.

15)

∠1 = ∠ 2 = 35°

∠ 3 = 42°

Найти ∠4

Вариант 2

1) В треугольнике ABC угол C равен 200, АС=ВС. Найдите угол A.

3) В треугольнике ABC  АС=ВС, угол C равен 720. Найдите внешний угол при вершине В.

4) В треугольнике ABC АС=ВС, AD — высота, угол BAD равен 260. Найдите угол C.

5) Один из внешних углов треугольника равен 840. Углы, не смежные с данным внешним углом, относятся как 2 : 5. Найдите наибольший из них.

6) Сумма двух углов треугольника и внешнего угла к третьему равна 740. Найдите этот третий угол.

7) В треугольнике ABC угол A равен 200, угол C равен 530. На продолжении стороны AB отложен отрезок ВD=ВС. Найдите угол D треугольника BCD.

 8) В треугольнике ABC угол A равен 170, угол B равен 790, CH — высота. Найдите разность углов ACH и BCH.

9) Какие из следующих утверждений верны?

      1) Если один из углов равнобедренного треугольника равен 300, то один из его оставшихся углов равен 1200.

      2) Если два угла треугольника равны 400 и 700 , то третий угол равен 700.

      3) В треугольнике АВС, для которого угол А = 500, угол В = 600, угол С=700, сторона АВ наибольшая.

     4) Треугольник со сторонами 2, 3, 4 не существует.

10) Луч ВК – биссектриса угла ABD, луч ВС – биссектриса угла ABК. Угол АВС = 19°. Найти угол АВD.

11)      В прямоугольном треугольнике АВС угол С=900. Внешний угол при вершине А равен 1200. АВ больше АС на 32 см. Найдите АВ.

12) На отрезке АВ длиной 12 см взята точка С так, что АС = 10 см, и точка D так, что CD = 5 см. Найдите длину отрезка BD.

13)  В прямоугольном АВС угол С=900. АС=ВС. Высота СD, опущенная на сторону АВ  равна 6. Найдите АВ

14) Периметр равнобедренного треугольника 40 см. На его боковой стороне построили равносторонний треугольник, периметр которого 45см. Найти основание равнобедренного треугольника.

15)

∠1 = 470

∠ 2 = 133°

∠ 3 = 108°

Найти ∠4

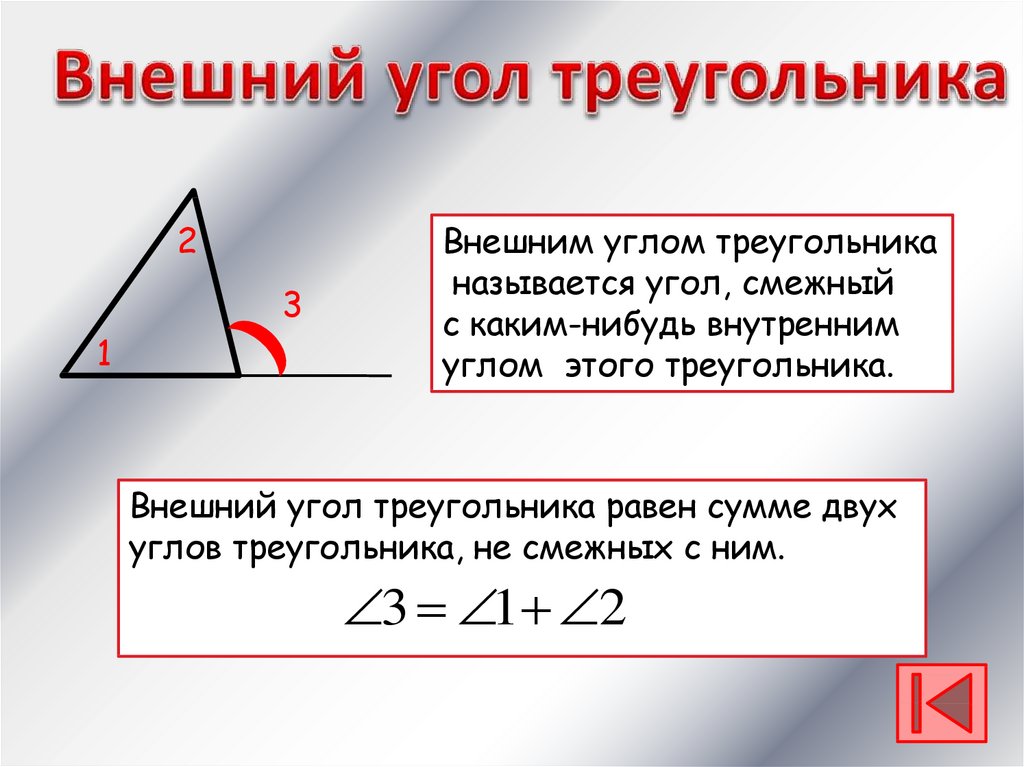
Теорема о внешнем угле – определение, доказательство, примеры

Теорема о внешнем угле утверждает, что при удлинении стороны треугольника образующийся результирующий внешний угол равен сумме мер двух противоположных внутренних углов треугольника. Теорема может быть использована для нахождения меры неизвестного угла в треугольнике. Чтобы применить теорему, нам сначала нужно определить внешний угол, а затем два связанных с ним удаленных внутренних угла треугольника.

1.	Что такое Теорема о внешнем угле?
2.	Доказательство теоремы о внешнем угле
3.	Теорема о неравенстве внешних углов
4.	Часто задаваемые вопросы по теореме о внешнем угле

Что такое Теорема о внешнем угле?

Теорема о внешнем угле утверждает, что мера внешнего угла равна сумме мер двух противоположных (дальних) внутренних углов треугольника. Давайте вспомним несколько общих свойств углов треугольника: Треугольник имеет 3 внутренних угла, сумма которых всегда равна 180 градусам. У него 6 внешних углов, и эта теорема применяется к каждому из внешних углов. Обратите внимание, что внешний угол является дополнительным к смежному с ним внутреннему углу, поскольку они образуют линейную пару углов. Внешние углы определяются как углы, образованные между стороной многоугольника и расширенной смежной стороной многоугольника.

Теорему о внешнем угле можно проверить, зная свойства треугольника. Рассмотрим Δ ABC.

Три угла a + b + c = 180 (свойство суммы углов треугольника) —— Уравнение 1

c= 180 — (a+b) —— Уравнение 2 (переписывая уравнение 1)

e = 180 — c—— Уравнение 3 (линейная пара углов)

Подставляя значение c в уравнение 3, получаем

e = 180 — [180 — (a + b)]

е = 180 — 180 + (а + б)

e = a + b

Следовательно проверено.

Доказательство теоремы о внешнем угле

Рассмотрим ΔABC. a, b и c — образуемые углы. Продлите сторону BC к D. Теперь образован внешний угол ∠ACD. Проведите прямую СЕ параллельно АВ. Теперь x и y — образованные углы, где ∠ACD = ∠x + ∠y

Утверждение	Причина
∠а = ∠х	Пара альтернативных углов. (Поскольку ВА параллельна СЕ, а АС трансверсальна).
∠б = ∠у	Пара соответствующих уголков. (Поскольку ВА параллельна СЕ, а BD — трансверсальна).
∠а + ∠б = ∠х + ∠у	Из приведенных выше заявлений
∠ACD = ∠x + ∠y	Из конструкции CE
∠а + ∠б = ∠АСД	Из приведенных выше утверждений

Отсюда доказано, что внешний угол треугольника равен сумме двух противоположных внутренних углов.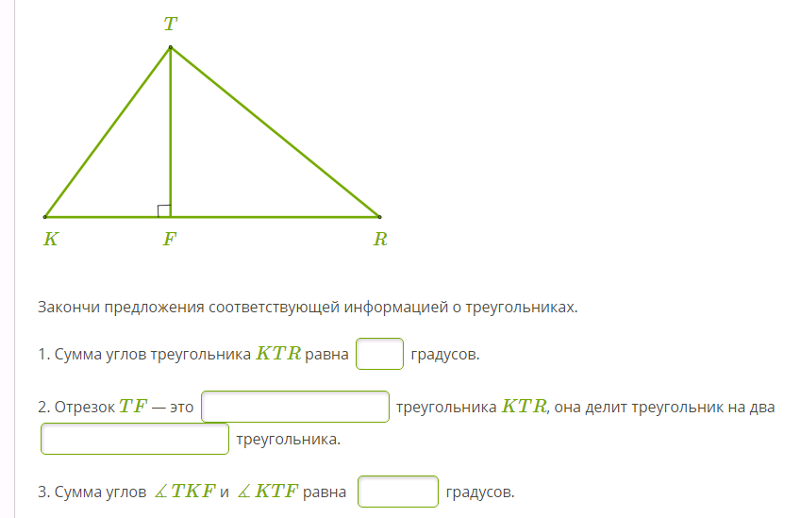

Теорема о неравенстве внешних углов

Теорема о неравенстве внешних углов утверждает, что мера любого внешнего угла треугольника больше любого из противоположных внутренних углов. Этому условию удовлетворяют все шесть внешних углов треугольника.

Статьи по теме

Ознакомьтесь с несколькими интересными статьями, связанными с теоремой о внешнем угле.

• Формула внешнего угла
• Теорема о внешнем угле Рабочие листы
• Альтернативные внешние углы
• Как найти величину каждого внешнего угла правильного пятиугольника?
• Свойства треугольника
• Внутренние и внешние углы Рабочие листы
• Сумма внешних углов Формула

Важные примечания

• Теорема о внешнем угле утверждает, что мера внешнего угла равна сумме мер двух удаленных друг от друга внутренних углов треугольника.
• Теорема о неравенстве внешних углов утверждает, что мера любого внешнего угла треугольника больше любого из противоположных внутренних углов.
• Внешний угол и примыкающий к нему внутренний угол являются дополнительными. Сумма всех внешних углов треугольника равна 360º.

 

Примеры теоремы о внешнем угле

1. Пример 1: Найдите значения x и y, используя теорему о внешнем угле треугольника.

   Решение:

   ∠x — внешний угол.

   ∠x + 92 = 180º (линейная пара углов)

   ∠x = 180 — 92 = 88º

   Применяя теорему о внешнем угле, получаем, ∠y + 41 = 88 47º

   Следовательно, значения x и y равны 88º и 47º соответственно.

2. Пример 2: Найдите ∠BAC и ∠ABC.

   Решение:

   160º — внешний угол Δ ABC. Таким образом, используя теорему о внешнем угле, мы имеем 3xº = 120º

3. Пример 3: Найдите ∠ BAC, если ∠CAD = ∠ADC

   Решение:

   Решив линейную пару в вершине D, получим ∠ADC + ∠ADE = 180º

   ∠ADC = 180º — 150º = 30º

   , используя свойство суммы углов ΔΔ 3

   ∠ADC + ∠ACD + ∠CAD = 180°

   ∠ACD = 180 — ∠CAD -∠ADC

   180° — ∠ADC -∠ADC (данные ∠CAD= ∠ADC)

   900 2 180° 02 180º — 2 × 30º

   ∠ACD = 180º — 60º = 120º

   ∠ACD – внешний угол ∠ABC

   Используя теорему о внешнем угле, для Δ ABC, ∠ACD = ∠ABC + ∠BAC

   120º = 60º + ∠ВАС

   Следовательно, ∠ВАС = 120º — 60º = 60º.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.

Записаться на бесплатный пробный урок

Практические вопросы по теореме о внешнем угле

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по теореме о внешнем угле

Что такое Теорема о внешнем угле?

Теорема о внешнем угле утверждает, что мера внешнего угла равна сумме мер двух удаленных друг от друга внутренних углов треугольника. Удаленные внутренние углы также называются противоположными внутренними углами.

Как вы используете теорему о внешнем угле?

Чтобы использовать теорему о внешнем угле в треугольнике, нам сначала нужно определить внешний угол, а затем два связанных с ним удаленных внутренних угла треугольника.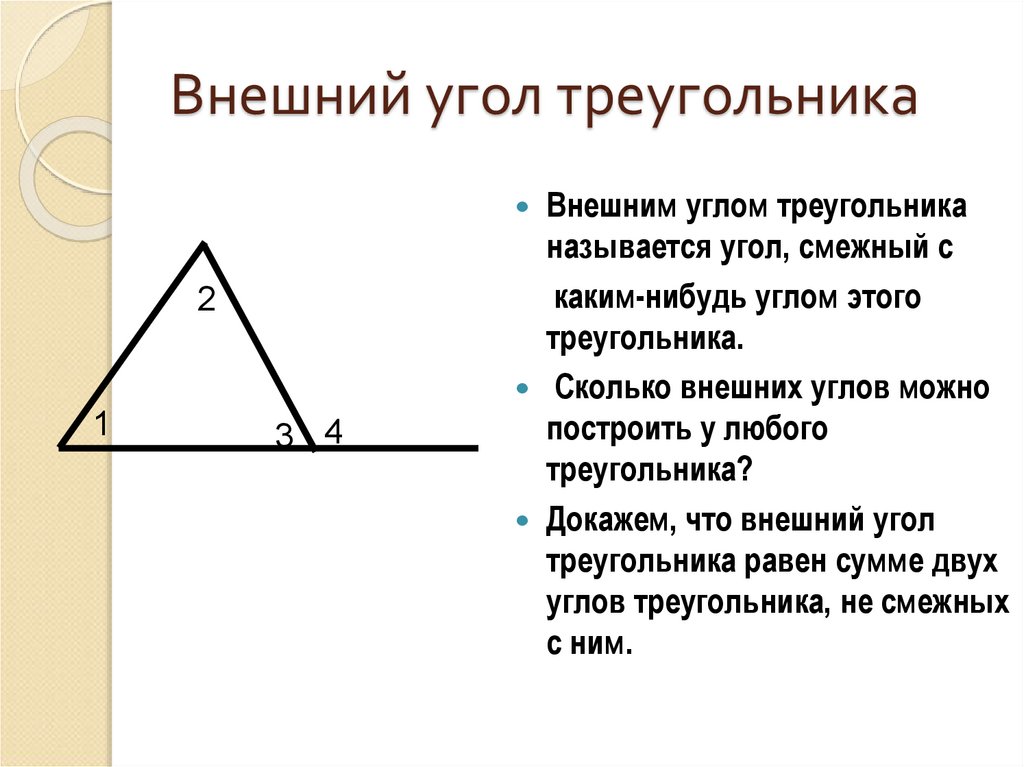 Следует избегать распространенной ошибки, связанной с рассмотрением смежного внутреннего угла. После определения внешних углов и связанных с ними внутренних углов мы можем применить формулу, чтобы найти недостающие углы или установить связь между сторонами и углами в треугольнике.

Что такое внешние углы?

Внешний угол треугольника образуется при удлинении любой стороны треугольника. У треугольника 6 внешних углов, так как каждая из 3 сторон может быть продолжена в обе стороны и получается 6 таких внешних углов.

Что такое Теорема о неравенстве внешних углов?

Внешний угол треугольника всегда больше, чем любой из противоположных внутренних углов треугольника.

Что такое свойство внешнего угла?

Внешний угол треугольника равен сумме двух его противоположных несмежных внутренних углов. Сумма внешнего угла и прилежащего к нему внутреннего угла, не противолежащего, равна 180º.

Что такое формула теоремы о внешнем угле?

Сумма внешнего угла = сумма двух несмежных внутренних противоположных углов.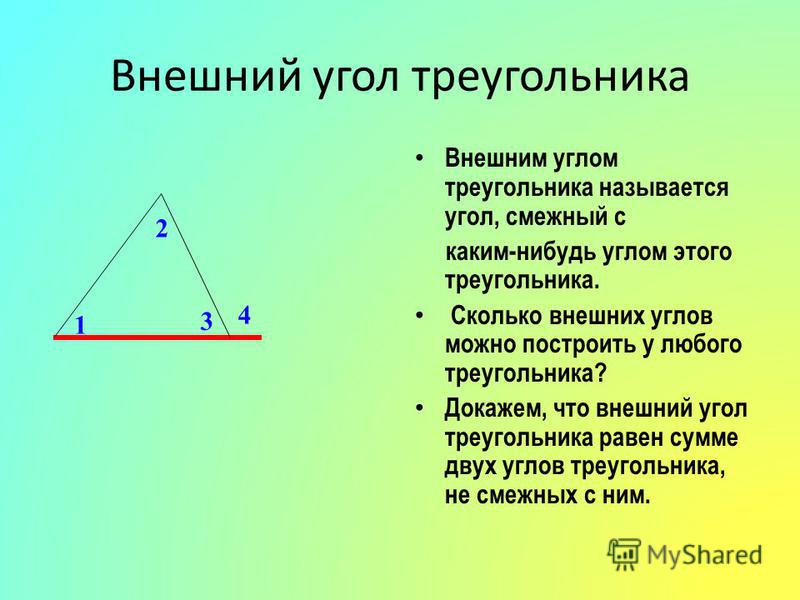 Внешний угол треугольника равен сумме двух его противоположных несмежных внутренних углов.

Где следует использовать теорему о внешнем угле?

Теорему о внешнем угле можно использовать для определения величин неизвестных внутренних и внешних углов треугольника.

Все ли внешние углы полигонов в сумме составляют 360?

Внешние углы многоугольника образуются при удлинении стороны многоугольника. Сумма внешних углов всех многоугольников равна 360º.

Скачать БЕСПЛАТНЫЕ учебные материалы

Скачать рабочие листы по геометрии

Внешний угол треугольника

Определение внешнего угла

В каждой вершине треугольника внешний угол треугольника может быть образован продолжением ОДНОЙ СТОРОНЫ треугольника. См. рисунок ниже.

Вычисление углов

Мы можем использовать уравнения для представления мер углов, описанных выше. Одно уравнение может сказать нам сумму углов треугольника. Например,

x + y + z = 180

Мы знаем, что это правда, потому что сумма углов внутри треугольника всегда равна 180 градусам.

Что такое ш? Мы еще не знаем. Но мы можем заметить, что мера угла w плюс мера угла z = 180 градусов, потому что они являются парой дополнительных углов. Обратите внимание, как Z и W вместе образуют прямую линию? Это 180 градусов. Итак, мы можем составить новое уравнение:

w + z = 180

Затем, если мы объединим два приведенных выше уравнения, мы сможем определить, что мера угла w = x + y. Вот как это сделать:

x + y + z = 180 (это первое уравнение)
w + z = 180 (это второе уравнение)

Теперь перепишите второе уравнение как z = 180 — w и подставьте это вместо z в первое уравнение:

x + y + (180 — w) = 180
х + у — ш = 0
x + y = w

Интересно. Это говорит нам о том, что мера внешнего угла равна сумме двух других 90 314 внутренних 90 315 углов. На самом деле, существует теорема, называемая теоремой о внешнем угле, которая дополнительно исследует эту связь:

Теорема о внешнем угле

Мера внешнего угла (нашего w) треугольника равна сумме мер двух удаленных друг от друга внутренних углов (наших x и y) треугольника.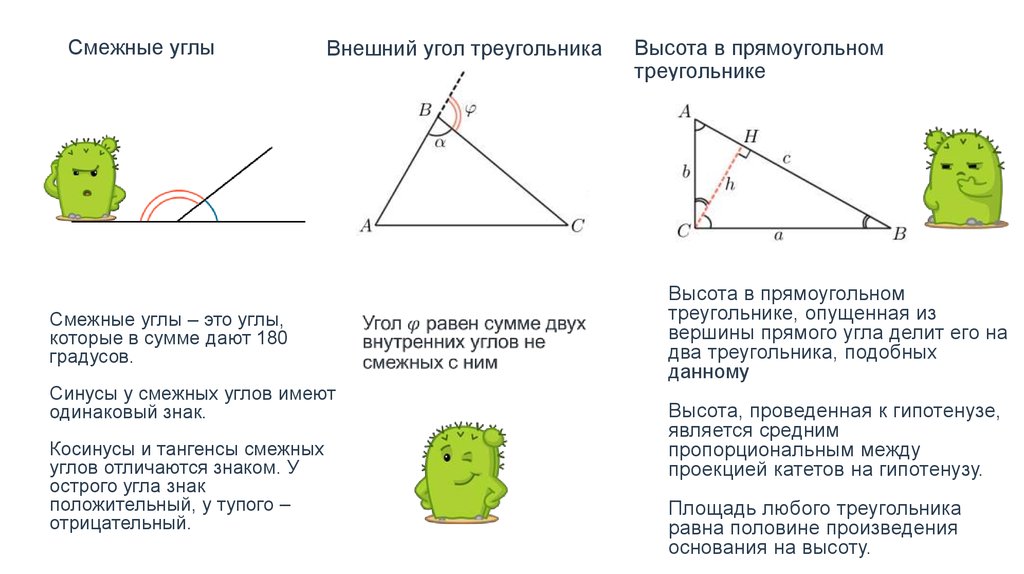

Давайте попробуем решить две задачи.

Пример A:

Если мера внешнего угла равна (3x — 10) градусов, а мера двух удаленных друг от друга внутренних углов составляет 25 градусов и (x + 15) градусов, найдите x.

Чтобы решить, мы используем тот факт, что W = X + Y. Обратите внимание, что здесь я имею в виду углы W, X и Y, как показано на первом изображении этого урока. Их имена не важны. Важно то, что внешний угол равен сумме удаленных внутренних углов.

Приравниваем и находим x.

внешний угол = внутренний угол + другой внутренний угол

$$ (3x — 10) = (25) + (x + 15) $$ $$ 3x — 10 = x + 40 $$ $$ 3x = x + 50 $$ $$ 2x = 50 $$ $$ х = 25 $$

Помните, что «x» здесь не является ответом. Нам нужны сами углы, которые вычисляются как (3x-10), 25 и (x+15). Тогда углы равны 65, 25 и 40 градусов.

Пример B

Внешний угол равен 110 градусам. Два отдаленных внутренних угла имеют размеры 50 и (2x + 30).