Сумма двух углов ромба равна найдите меньший угол ромба: Сумма двух углов ромба равна 120

Трапеция: свойства, признаки, площадь, средняя линия

Углы при параллельных прямых и секущей

Пусть прямая пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.

Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы 3 и 5 (а также 1 и 7, 2 и 8, 4 и 6) — накрест лежащие.

Накрест лежащие углы равны.

Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна , то есть

Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и 8) называются соответственными.

Соответственные углы равны, то есть

Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач по геометрии, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть две параллельных прямые и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это – один из шагов, из которых и состоит решение.

В этой статье – полезные теоремы и примеры решения задач ЕГЭ и ОГЭ по теме «Углы при параллельных прямых и секущей».

Этот материал можно использовать для проектов по геометрии, в работе на уроке и самостоятельно.

Теорема 1.

Углы с соответственно параллельными сторонами равны, если они оба острые или тупые.

Доказательство:

Дано два острых угла: и Известно, что их стороны параллельны: и

Докажем, что

Пусть

Тогда как соответственные углы при параллельных прямых CA и NF и секущей CB.

как соответственные углы при параллельных прямых CB и NM и секущей NF.

Отсюда следует, что что и требовалось доказать.

Аналогично и для тупых углов.

Теорема 2.

Углы с соответственно параллельными сторонами в сумме составляют если один из них острый, а другой тупой.

Доказательство:

Дано: – острый, а – тупой. Известно, что их стороны параллельны: и

Докажем, что сумма углов и равна

Пусть Продолжим луч NM за точку N и получим прямую MK.

Получили два острых угла, и с параллельными сторонами. Согласно теореме 1, они равны, т. е.

как смежные. Значит,

Теорема доказана.

Теорема 3.

Если накрест лежащие углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей AB накрест лежащие углы равны:

Докажем, что Если углы 1 и 2 прямые, то прямые и перпендикулярны к прямой AB и, следовательно, параллельны.

Рассмотрим случай, когда углы 1 и 2 не прямые.

Из середины О отрезка АВ проведем перпендикуляр OH к прямой

На прямой от точки В отложим отрезок равный отрезку AH

по двум сторонам и углу между ними, поэтому и Из равенства следует, что точка лежит на продолжении луча OH, т. е. точки H, O и лежат на одной прямой, а из равенства следует, что угол 6 – прямой (так как угол 5 – прямой). Итак, прямые и перпендикулярны к прямой поэтому они параллельны. Теорема доказана.

Теорема 4.

Если соответственные углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей соответственные углы равны, например

Так как углы 2 и 3 – вертикальные, то Из этих двух равенств следует, что . Но углы 1 и 3 – накрест лежащие, поэтому прямые и параллельны. Теорема доказана.

Теорема 5.

Если сумма односторонних углов равна 180 градусов, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей сумма односторонних углов равна например

Так как углы 3 и 4 – смежные, то Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые и параллельны. Теорема доказана

И самое главное. Подборка примеров заданий ОГЭ и ЕГЭ по темам: углы при параллельных прямых и секущей, внешние накрест лежащие и внутренние накрест лежащие углы, односторонние углы.

Задачи ОГЭ по теме: Свойства параллельных прямых и секущей, углы при пересечении параллельных прямых секущей

Задача 1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.

Решение:

Стороны BC и AD параллелограмма параллельны, АК – секущая. Углы и равны как накрест лежащие.

– равнобедренный треугольник.

Мы доказали важное утверждение.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

AB=BK=5.

Ответ: 48.

Задача 2. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F.

Найдите AB, если AF=24, BF=10.

Решение:

Основания трапеции АD и ВС параллельны, поэтому углы BAD и АВС – односторонние при параллельных прямых АD и ВС и секущей АВ.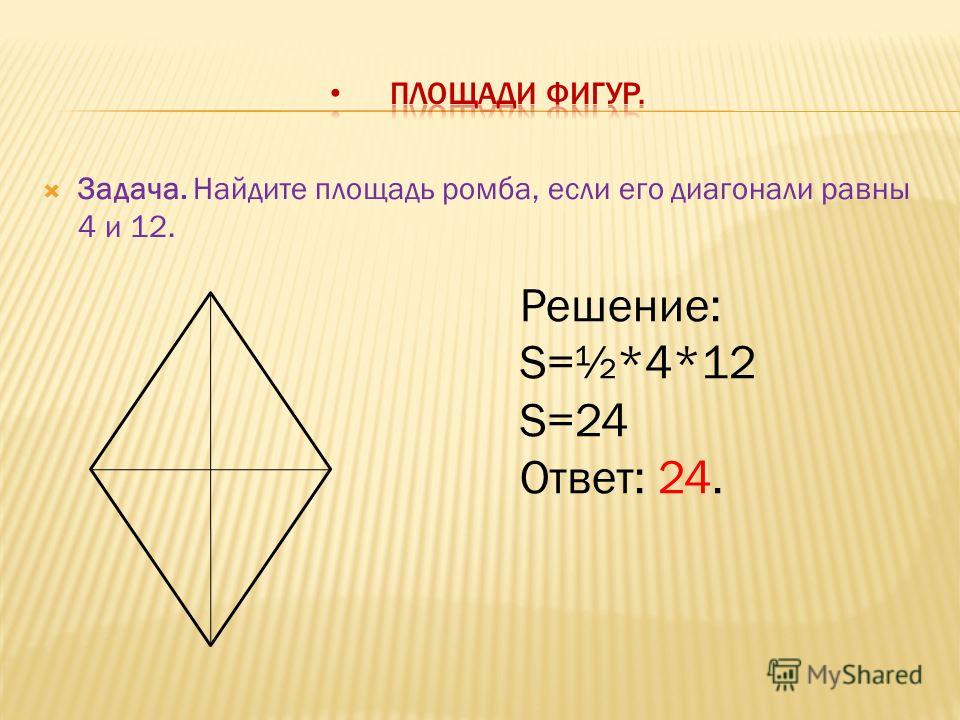 Сумма односторонних углов равна

Сумма углов, прилежащих к боковой стороне трапеции, равна

Мы получили, что

AF — биссектриса угла А,

BF — биссектриса угла В, поэтому

тогда

Из треугольника AFB получим, что

Мы доказали теорему:

Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AFB – прямоугольный.

По теореме Пифагора,

Ответ: 26.

Задача 3. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=16, MN=12. Найдите AM.

Решение:

Пусть М – середина АВ, N – середина ВС. Тогда MN – средняя линия треугольника АВС,

Значит, как односторонние углы при параллельных прямых и и секущей АВ.

по двум углам.

Отсюда ;

Ответ: 21.

Задача 4. Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 108 Найдите угол B этой трапеции. Ответ дайте в градусах.

Решение:

ABCD – трапеция, – основания, AB – секущая.

Значит, и – внутренние односторонне углы.

Отсюда

Ответ:

Задача 5. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.

Решение:

Сумма углов, прилежащих к боковой стороне параллелограмма, равна

Это значит, что

AК — биссектриса угла А,

BК — биссектриса угла В, поэтому

тогда

Из треугольника AKB получим, что

Мы доказали теорему:

Биссектрисы углов параллелограмма, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AKB – прямоугольный.

Расстояние от точки K до стороны AB – это длина перпендикуляра, проведенного из точки на прямую АВ, т.е.

по гипотенузе и острому углу

Аналогично, по гипотенузе и острому углу

Получили:

Тогда ;

Ответ: 56.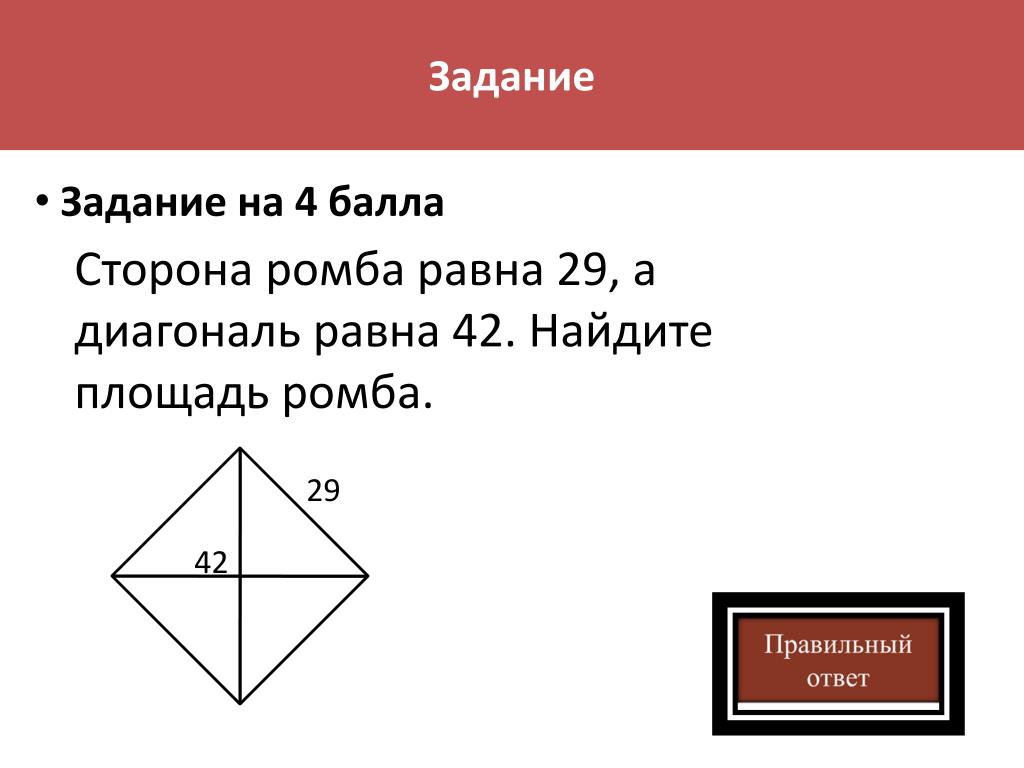

Задача 6. На плоскости даны четыре прямые. Известно, что Найдите Ответ дайте в градусах.

Решение:

и – это внутренние односторонние углы,

Отсюда следует, что прямые параллельны, т.е.

Рассмотрим углы при параллельных прямых и секущей d.

и – это односторонние углы, а значит, они равны:

Ответ:

Задача 7. Прямые m и n параллельны. Найдите если Ответ дайте в градусах.

Решение:

как односторонние углы.

Сумма углов треугольника равна

Для треугольника на рисунке:

Ответ: 86.

Задача 8. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30 и 45 Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение:

и – это внутренние односторонние углы при параллельных прямых.

и секущей АВ, их сумма равна

Тогда

Это и есть наибольший угол параллелограмма.

Ответ: 105.

Задача 9.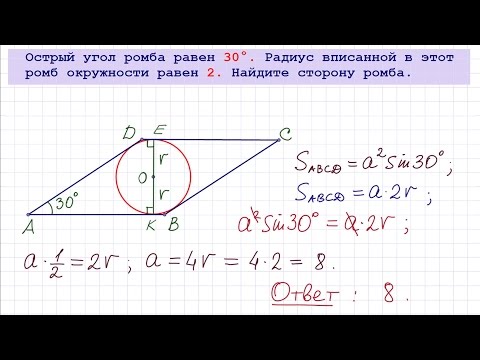 Найдите величину тупого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15 Ответ дайте в градусах.

Решение:

AK – биссектриса угла А параллелограмма ABCD,

и – внутренние односторонние углы при параллельных прямых.

и секущей АВ. Их сумма равна значит,

Ответ: 150.

Задача 10. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение: тогда – равнобедренный, в нем Значит,

Ответ: 5,5.

Задачи ЕГЭ по теме: Углы при параллельных прямых и секущей

Задача 1, ЕГЭ. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Решение:

Напомним, что биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.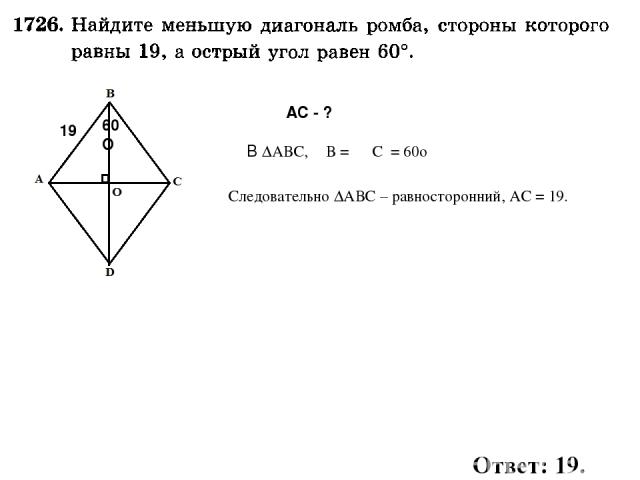

Пусть BM – биссектриса тупого угла B. По условию, отрезки MD и AB равны 3x и 4x соответственно.

Рассмотрим углы CBM и BMA. Поскольку AD и BC параллельны, BM – секущая, углы CBM и BMA являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник ABM – равнобедренный, следовательно, AB = AM = 4x.

Периметр параллелограмма – это сумма всех его сторон, то есть

7x+7x+4x+4x=88.

Отсюда

Ответ: 28.

Задача 2, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Решение:

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на рисунок. По условию, то есть

Углы и – односторонние при параллельных прямых и секущей, следовательно,

по свойству односторонних углов.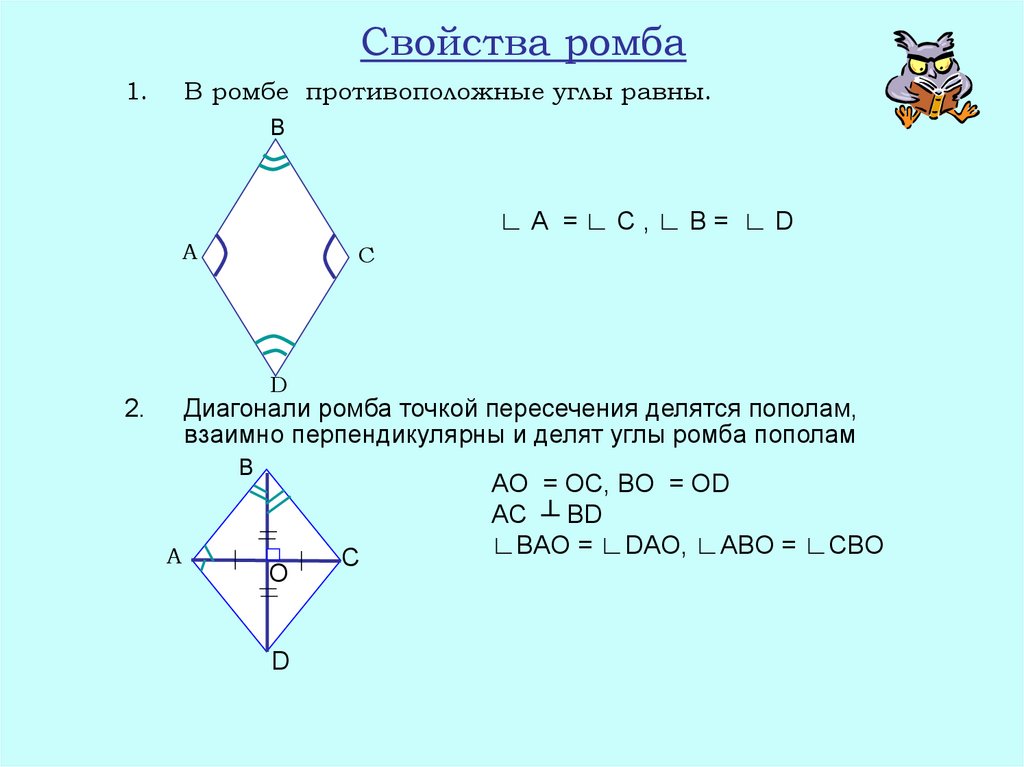

Итак,

тогда

Ответ: 115.

Задача 3, ЕГЭ. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Решение:

и – внутренние односторонние углы и при параллельных прямых

и и секущей BC; их сумма равна

BE – биссектриса угла В, значит как накрест лежащие углы при и секущей BE. Тогда – равнобедренный,

Аналогично, CE – биссектриса угла С, значит как накрест лежащие углы при и секущей CE. Тогда – равнобедренный и

Значит

Ответ : 10.

Задача 4, ЕГЭ. В ромбе ABCD угол ABC равен 122 Найдите угол ACD. Ответ дайте в градусах.

Решение:

и – это внутренние односторонние углы при параллельных прямых.

и секущей BC, их сумма равна

Значит,

– ромб, диагонали ромба делят его углы пополам.

Тогда

Ответ: 29.

Задача 5, ЕГЭ. Угол между стороной и диагональю ромба равен Найдите острый угол ромба.

Решение:

Диагональ ромба делит его угол пополам, то есть является биссектрисой угла ромба. Поэтому один из углов ромба равен градусов, и это тупой угол ромба. Тогда острый угол ромба равен

Ответ: 72.

Задача 6, ЕГЭ. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 Найдите площадь трапеции.

Решение:

Пусть

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними при и секущей BC. Их сумма равна

Тогда Построим высоту из вершины Получим прямоугольный треугольник с острым углом в 30

Высота трапеции DH – это катет, лежащий напротив угла в и равный половине гипотенузы, т. е.

Отсюда

Ответ: 42.

Задача 7, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.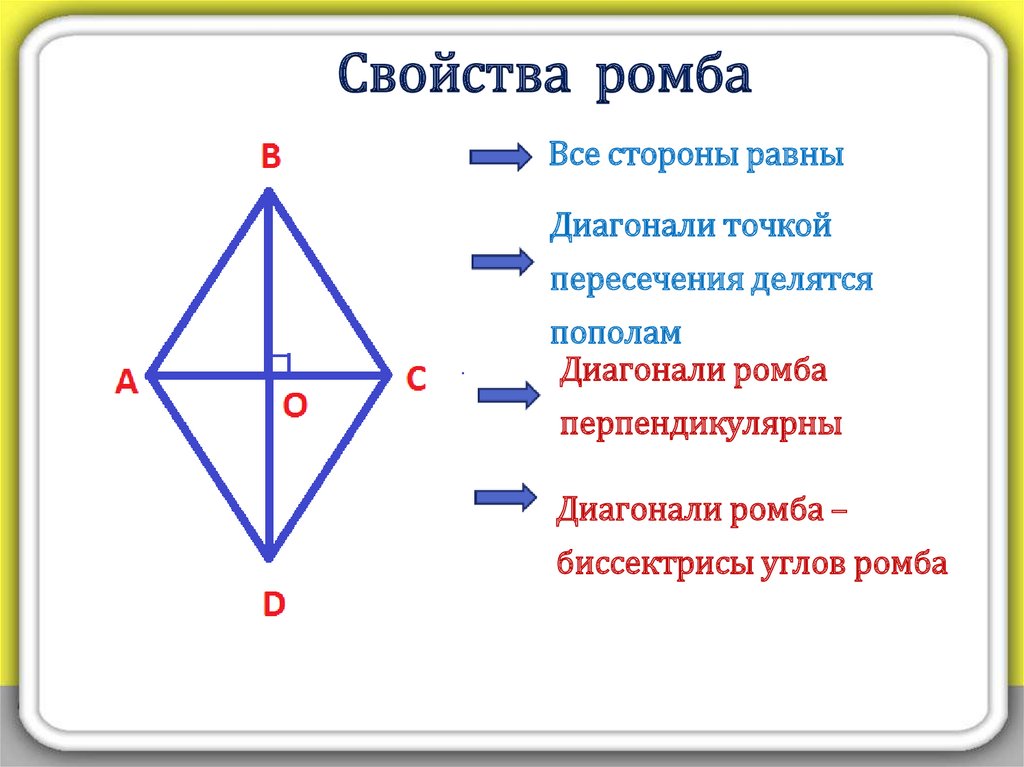

Решение:

У равнобедренной трапеции углы при основании равны т.е.

По условию,

и прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых
и и секущей BC. Их сумма равна

Получили:

Сложив два уравнения, получим: тогда

Ответ: 115.

Задания ЕГЭ Базового уровня, геометрия. Свойства углов при параллельных прямых и секущей.

Задание 1. Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол Найдите площадь трапеции.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных основаниях трапеции и секущей. Их сумма равна Значит, острый угол трапеции равен 30 Построив высоту, мы увидим, что она лежит против прямого угла в прямоугольном треугольнике. Значит, высота равна половине боковой стороны, т.е.

Отсюда

Ответ: 60.

Задание 2. В прямоугольной трапеции основания равны 4 и 7, а один из углов равен Найдите меньшую боковую сторону.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна Значит, острый угол равен

Вторая высота отсекает равнобедренный прямоугольный треугольник с катетом, равным разности оснований. Значит, высота равна: 7–4=3.

Отсюда

Ответ: 16,5.

Задание 3. В трапеции ABCD известно, что AB = CD, и Найдите угол ABD. Ответ дайте в градусах.

Решение:

Нам дана трапеция, в которой Очевидно, что это боковые стороны, и трапеция равнобедренная с основаниями и .

и параллельны, BD секущая, тогда

Ответ: 70.

Задание 4.

В параллелограмме ABCD проведена биссектриса угла A, пересекающая сторону BC в точке K. Найдите KC, если AB = 4, а периметр параллелограмма равен 20.

Решение:

ABCD – параллелограмм, тогда AB = DC = 4.

AK – биссектриса угла А, значит,

как накрест лежащие углы при параллельных прямых и и секущей AK.

Получили, что – равнобедренный и

значит

Ответ: 2.

Задание 5. Прямые m и n параллельны (см. рисунок). Найдите если Ответ дайте в градусах.

Решение:

(как накрест лежащие углы).

(развернутый угол).

Тогда

Ответ: 39.

Задание 6. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение:

Пусть диагонали пересекаются в точке О, т.е.

и параллельны, АС – секущая,

– равнобедренный, отсюда угол между диагоналями равен:

Ответ: 38.

Если вам понравился наш материал на тему «Углы при параллельных прямых и секущей» — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 07.02.2023

Сумма двух углов ромба равна 142 градусам. Найдите меньший угол ромба. Дайте ответ в градусах — Знания.site

Последние вопросы

Математика
5 минут назад
Помогите пожалуйста математика 6 класс уравнения

Математика
10 минут назад
4 2/5+ 2 3/5 вычислить
Математика
10 минут назад
Ө 2. Запиши уравнение по условию задачи. Реши задачу с помощью уравнения. За 7 карандашей заплатили 490 тенге. Сколько стоит 1 карандаш? Пусть x-цена карандаша.x / 7 = 70
Математика
10 минут назад
2. Запиши уравнение по условию задачи. Реши зада помощью уравнения. За 7 карандашей заплатили 490 тенге. Сколько стоит 1 карандаш? Пусть x — цена карандаша. x / 7 = 70
Математика
15 минут назад
Помогите дам 50 балов
Математика
20 минут назад
школьниками? Попробуй решить 10 Подумай и ответь. ТЫ ИССЛЕДОВАТЕЛЬ

Математика
20 минут назад
Линия, огибающая шляпку гриба, представляет собой параболу. Найди формулу, которой задана эта парабола
Математика
20 минут назад
А там где написано ап-в это всего апельсинов?
Математика
20 минут назад
Помогите пожалуйста, даю 15б
Математика
36 минут назад
в фермерском хозяйстве 6 свиней и 8 коров всем свиньям отпускают ежедневно 84 кг разных кормов для коровы требуется в 2 раза больше кормов чем для свиньи сколько кг кормов получают все коровы ежедневно
Математика
55 минут назад
срочно помогите с решением!!!
Математика
55 минут назад
даны три точки лежащие на одной прямой А(3;7), В(√129;7) и С(13;7)
Математика
1 час назад
В супермаркете Фрунзе продаются 6 видов ручек и 5 видов карандашей и 3 вида линеек сколькими различными способами можно составить набор из двух разных предметов
Математика
1 час назад
На шахматной доске на клетке а1 стоит король , которому необходимо попасть на клетку h8, не попадая на клетки c3,c6,f3,f6. Король может двигаться только вверх или вправо на одну клетку . Сколькими способами можно это сделать?
Математика
1 час назад
В супермаркете Фрунзе продаются 6 видов ручек, 5 видов карандашей и 3 вида линеек. Сколькими способами можно выбрать набор, состоящий из двух разных предметов? ?????

Все предметы

English

United States

Polski

Polska

Bahasa Indonesia

Indonesia

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Português

Brasil

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Как найти угол в ромбе

Все ресурсы по геометрии среднего уровня

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

Intermediate Geometry Help » Плоская геометрия » Четырехугольники » ромбы » Как найти угол в ромбе

Ромб имеет два внутренних угла, измеряемых в градусах. Чему равен каждый из двух других внутренних углов?

Возможные ответы:

Оба оставшихся угла равны градусам.

Недостаточно информации для решения этой проблемы.

Один угол равен градусам, а другой угол должен быть равен градусам.

Все внутренние углы ромба равны градусам.

Правильный ответ:

Оба оставшихся угла равны градусам.

Пояснение:

Четыре внутренних угла любого ромба должны иметь сумму градусов. Противоположные внутренние углы должны быть равны, а сумма смежных углов равна градусам.

Таким образом, если ромб имеет два внутренних угла в градусах, должны быть также два равных угла:

Проверить:

Сообщить об ошибке

Используя приведенную выше сумму углов ромба, и

Возможные ответы:

Правильный ответ:

Пояснение:

Четыре внутренних угла любого ромба должны иметь сумму градусов.

Противоположные внутренние углы должны быть равны, а сумма смежных углов должна составлять градусы.

С тех пор

Сообщить об ошибке

В приведенном выше ромбе угол градусы. Найдите сумму углов и

Возможные ответы:

Правильный ответ:

Пояснение:

Поскольку ,

Итак,

Сообщить об ошибке

В ромбе, показанном выше, угол измеряется в градусах. Найдите измерение угла .

Возможные ответы:

Правильный ответ:

Пояснение:

Четыре внутренних угла любого ромба должны иметь сумму градусов.

Противоположные внутренние углы должны быть равны, а сумма смежных углов должна составлять градусы.

Так как угол примыкает к углу, они должны иметь сумму градусов.

Решение:

Сообщить об ошибке

В показанном выше ромбе угол измеряется в градусах. Найдите сумму углов и Пояснение:

Четыре внутренних угла любого ромба должны иметь сумму градусов.

Противоположные внутренние углы должны быть равны, а смежные углы должны иметь сумму градусов.

Углы и являются противоположными внутренними углами, поэтому они должны иметь одинаковые размеры.

Сумма:

Сообщить об ошибке

Угол измеряется в градусах. Найдите сумму углов и Объяснение:

Четыре внутренних угла любого ромба должны иметь сумму градусов.

Противоположные внутренние углы должны быть равны, а сумма смежных углов должна составлять градусы.

Поскольку оба угла и прилегают к углу , найдите величину одного из этих двух углов по формуле: .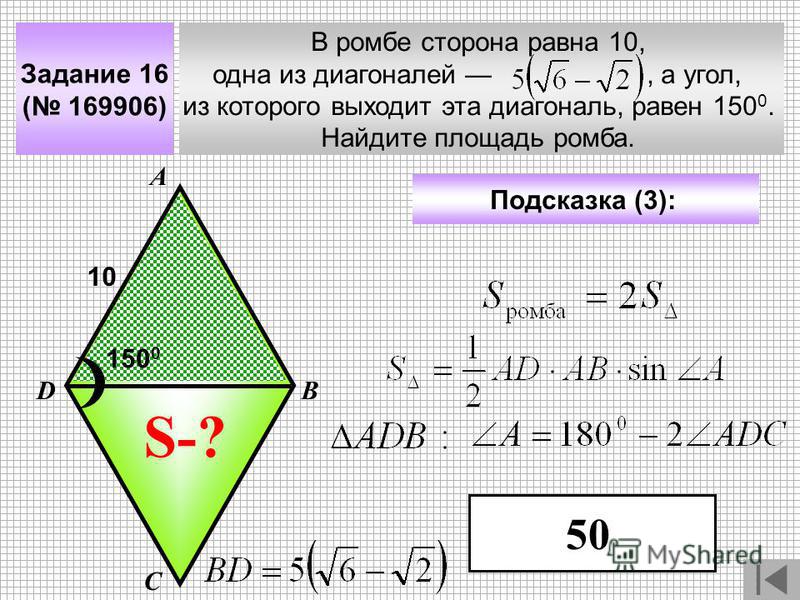

Угол и угол должны быть равны градусам. Итак, сумма углов и градусов.

Сообщить об ошибке

Дано: Параллелограмм такой, что .

Верно или неверно: параллелограмм не может быть ромбом.

Возможные ответы:

Верно

Неверно

Правильный ответ:

Неверно

Пояснение:

Ромб определяется как параллелограмм с четырьмя конгруэнтными сторонами; нет никаких ограничений относительно размеров углов. Следовательно, ромб может иметь углы любой меры. Правильный выбор — «ложь».

Сообщить об ошибке

Дано: ромб с диагоналями, пересекающимися в одной точке.

Правда или ложь: угол должен быть прямым.

Возможные ответы:

Неверно

Верно

Правильный ответ:

Верно

Пояснение:

Одной из характеристик ромба является то, что его диагонали перпендикулярны.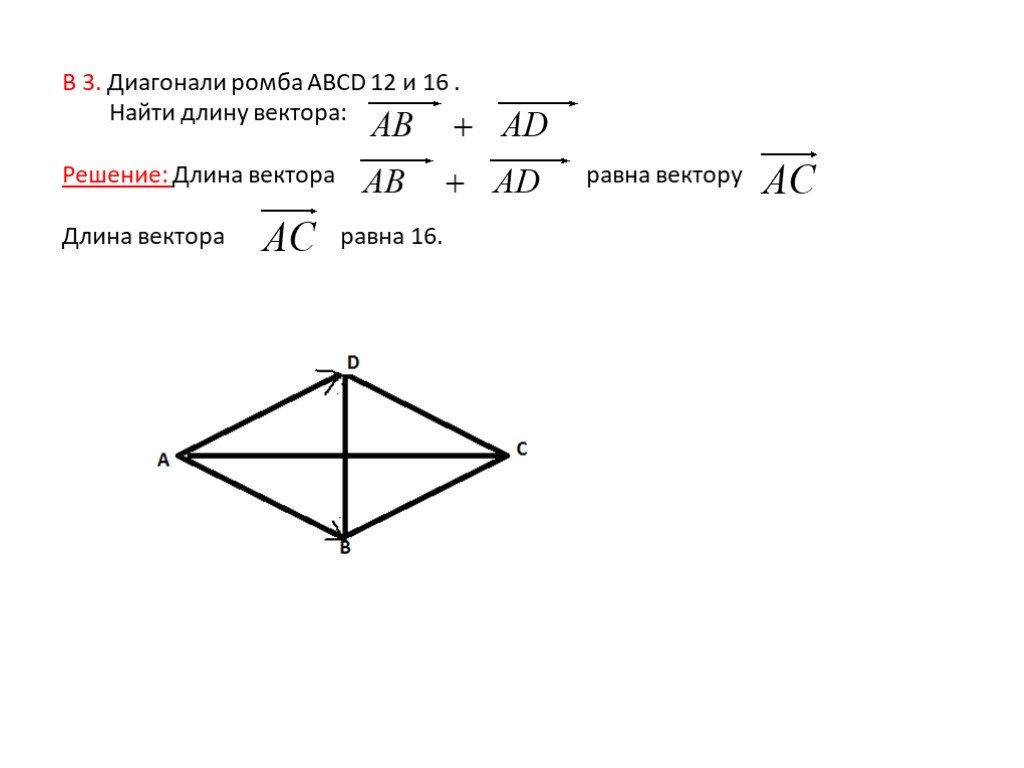 Отсюда следует, что угол должен быть прямым.

Сообщить об ошибке

Даны ромб и диагональ.

Возможные ответы:

Правильный ответ:

Объяснение:

Ниже указан ромб:

Поскольку ромб является параллелограммом, его углы и углы являются дополнительными, то есть

Установить и решить:

Диагональ ромба делит углы в его концах пополам, поэтому, в частности, делит пополам. Следовательно,

Сообщить об ошибке

Уведомление об авторских правах

Все промежуточные ресурсы по геометрии

8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept

Как найти угол в ромбе

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущий 1 2 Далее →

ACT Math Help » Геометрия » Плоская геометрия » Четырехугольники » ромбы » Как найти угол ромба

Сумма двух острых углов ромба равна . Какова мера одного тупых углов ромба?

Возможные ответы:

Правильный ответ:

Пояснение:

Здесь важно знать, что у ромба две пары равных углов. Другими словами, два острых угла ромба равны и два тупых угла равны.

В этой задаче, поскольку сумма двух острых углов равна и они оба должны быть равными, каждый из острых углов должен быть .

Также важно знать, что четыре угла ромба в сумме составляют . Если сумма двух острых углов равна , то это означает, что сумма двух тупых углов должна составлять или .

Наконец, поскольку сумма тупых углов равна и они должны быть равны, каждый из тупых углов должен быть равен .

Сообщить об ошибке

Ромб имеет два внутренних угла, каждый из которых имеет размер . Найдите измерение одного из двух оставшихся углов.

Возможные ответы:

Правильный ответ:

Пояснение:

Во-первых, учтите, что сумма четырех внутренних углов любого ромба должна быть равна . Кроме того, ромб должен иметь два набора эквивалентных противоположных внутренних углов, а ромб должен иметь два набора смежных внутренних углов. Смежные внутренние углы должны быть дополнительными, то есть их сумма равна .

Один из способов решить эту проблему — понять, что каждый из оставшихся двух углов должен иметь одинаковое измерение и что каждый из них будет дополнительным углом с . Найдите разницу между и и найдите решение.

Правильный ответ:

Сообщить об ошибке

У ромба внутренний угол равен . Найдите измерение для одного из углов, которые смежны с углом, у которого есть измерение.

Возможные ответы:

Правильный ответ:

Пояснение:

Ромб должен иметь два набора эквивалентных противоположных внутренних углов, а ромб должен иметь два набора смежных внутренних углов. Смежные внутренние углы должны быть дополнительными, то есть их сумма равна .

Если внутренний угол ромба имеет размерность , смежный угол должен быть равен:

Сообщить об ошибке

У ромба есть два противоположных внутренних угла, сумма которых равна . Найдите сумму оставшихся двух углов.

Возможные ответы:

Правильный ответ:

Объяснение:

Сумма четырех внутренних углов любого ромба должна быть равна . Кроме того, ромб должен иметь два набора эквивалентных противоположных внутренних углов, а ромб должен иметь два набора смежных внутренних углов. Смежные внутренние углы должны быть дополнительными, то есть их сумма равна .

Поскольку сумма двух противоположных внутренних углов в этом ромбе равна , сумма двух оставшихся углов должна быть равна:

равно ).

Сообщить об ошибке

Используя ромб, показанный выше, найдите значение угла .

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку в этой задаче используются дополнительные углы, решение будет следующим:

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Пояснение:

Один из способов решить эту проблему — понять, что каждый из оставшихся двух углов должен иметь одинаковое измерение и что каждый из них будет дополнительным углом с .

Найдите разницу между и , чтобы найти решение.

Сообщить об ошибке

Ромб имеет два внутренних угла, каждый из которых имеет размер . Найдите сумму оставшихся двух углов.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы решить эту задачу, учтите, что сумма четырех внутренних углов любого ромба должна быть равна . Кроме того, ромб должен иметь два набора эквивалентных противоположных внутренних углов, а ромб должен иметь два набора смежных внутренних углов. Смежные внутренние углы должны быть дополнительными, то есть их сумма равна .

Так как эта задача обеспечивает измерение двух внутренних углов, найдите сумму этих двух углов. Затем вычтите эту сумму из , чтобы найти сумму двух оставшихся внутренних углов.

Решение:

Сообщить об ошибке

Ромб имеет два внутренних угла, каждый из которых имеет размер . Найдите сумму оставшихся двух углов.

Возможные ответы:

Правильный ответ:

Пояснение:

Поскольку эта задача обеспечивает измерение двух внутренних углов, найдите сумму этих двух углов. Затем вычтите эту сумму из , чтобы найти сумму двух оставшихся внутренних углов.

Решение:

Сообщить об ошибке

Внутренний угол ромба имеет размер . Найдите измерение одного из углов, смежных с углом, у которого есть измерение .

Возможные ответы:

Правильный ответ:

Пояснение:

Таким образом, если внутренний угол ромба имеет величину , то прилежащий угол должен быть равен:

Сообщить об ошибке

Используя ромб, показанный выше, найдите величину угла .

Трапеция: свойства, признаки, площадь, средняя линия

Сумма двух углов ромба равна 142 градусам. Найдите меньший угол ромба. Дайте ответ в градусах — Знания.site