Сторона сд параллелограмма авсд вдвое больше стороны вс: Сторона CD параллелограмма ABCD вдвое больше стороны AD. Точка Р — середина стороны CD. Докажите, что АР

Разбор 24 задания ОГЭ

Основания ВС и AD трапеции ABCD равны соответственно 3 и 12, BD = 6. Докажите, что треугольники CBD и BDA подобны.

Решение.

Так как ABCD трапеция, то ее основания  , следовательно, равны и углы   как накрест лежащие при параллельных BC, AD и секущей BD. Рассмотрим треугольники CBD и BDA, у которых имеем следующие пропорции:

 и  .

Следовательно, треугольники CBD и BDA подобны друг другу по двум пропорциональным сторонам и равным углам, заключенными между этими сторонами.

Точка К – середина боковой стороны СD трапеции АВСD. Докажите, что площадь треугольника АВК равна сумме площадей треугольников ВСК и АКD.

Точка K — середина боковой стороны CD трапеции ABCD. Докажите, что площадь треугольника KAB равна половине площади трапеции.

Решение.

Продолжим BK до пересечения с прямой AD в точке F. Заметим, что в треугольниках FDK и BCK стороны CK и DK равны по условию, углы при вершине K равны как вертикальные, а углы KDF и KCB равны как накрест лежащие. Значит, треугольники FDK и BCK равны.

Следовательно, их площади равны, то есть площадь трапеции равна площади треугольника ABF. Но из равенства треугольников также вытекает, что FK = BK, то есть AK — медиана в треугольнике ABF. Тогда треугольник KAB по площади составит половину треугольника FAB, а значит, и данной трапеции.

В треугольнике ABC с тупым углом ACB проведены высоты AA₁ и BB₁. Докажите, что треугольники A₁CB₁ и ACB подобны.

Решение.

Поскольку угол ACB тупой, основания высот A₁ и B₁ будут лежать на продолжениях сторон BC и AC соответственно. Диагонали четырёхугольника AA₁B₁B пересекаются, поэтому он выпуклый. Поскольку ∠AA₁B = ∠AB₁B = 90°, каждый из прямоугольных треугольников AA₁B и AB₁B вписан в окружность с диаметром AB. Это означает, что все вершины четырёхугольника AA₁B₁B лежат на одной окружности. Тогда углы ∠AB₁A₁ и ∠ABA₁ равны как вписанные углы, опирающиеся на дугу A₁A.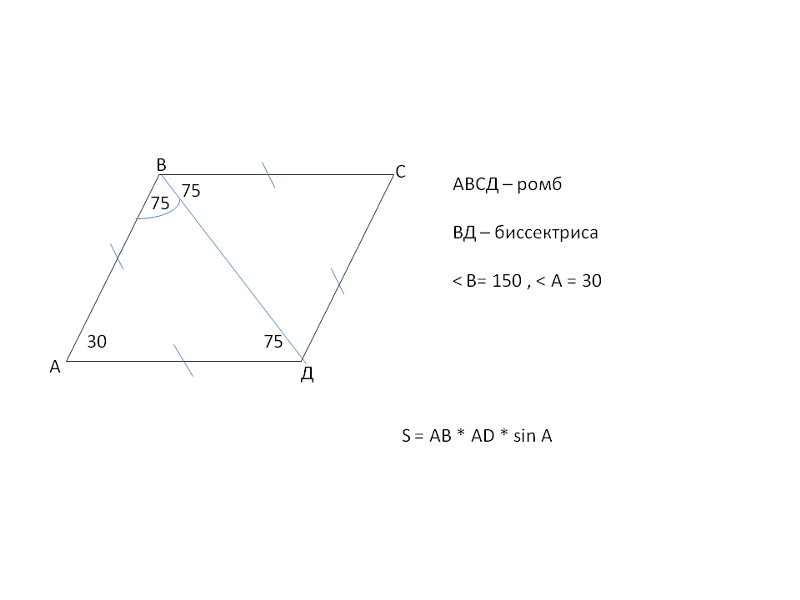 Аналогично, ∠BA₁B₁ = ∠BAB₁. Значит, указанные треугольники подобны по двум углам.

 

Укажем общую теорему.

Основания двух высот треугольника (остроугольного или тупоугольного) и одна из его вершин образуют треугольник, подобный исходному; коэффициент подобия равен модулю косинуса их общего угла.

 В треугольнике ABC с тупым углом АСВ проведены высоты АА1 и ВВ1. Докажите, что треугольники A1CB1 и АСВ подобны.

Решение.

Рассмотрим сначала два прямоугольных треугольника AA1C и BB1C, которые подобны по двум углам (один угол у них прямой, а углы   как вертикальные). У подобных треугольников AA1C и BB1C сторона A1C пропорциональна стороне B1C, а сторона AC пропорциональна стороне BC.

Рассмотрим теперь треугольники A1CB1 и ACB, у которых пропорциональны стороны AC, CB и A1C, B1C и равны углы  между этими сторонами как вертикальные. По второму признаку подобия два треугольника подобны, если стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника и углы, заключенные между этими сторонами, равны. То есть треугольники A1CB1 и ACB подобны друг другу. Утверждение доказано.

Сторона АВ параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны АВ. Докажите, что DK — биссектриса угла ADC.

Решение.

Проведём FK параллельно AD (см. рисунок). Тогда AD = AK = KB. Следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD делит угол ADC пополам.

Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники KAB и KCD подобны.

Решение.

Если вокруг четырехугольника можно описать окружность, то суммы его противоположных углов равны по 180 градусов, то есть  . Если положить угол  , тогда угол  , и, учитывая, что углы   и   смежные, то угол

то есть он равен углу  . Таким образом, треугольники KAB и KDC подобны по двум углам (угол K – общий). Утверждение доказано.

В остроугольном треугольнике ABC проведены высоты BB1 и CC1 Докажите, что углы BB1C1 и ВСC1 равны.

Решение.

1. Из рисунка видно, что треугольники BOC1 и CB1O подобны по двум углам (углы  , так как CC1 и BB1 – высоты, а углы   как вертикальные углы). В подобных треугольниках соответственные стороны пропорциональны, то есть можно написать соотношение

.

2. Треугольники C1OB1 и BOC подобны по двум пропорциональным сторонам и углам между ними (углы   – вертикальные).

3. Из подобия треугольников следует равенство углов:

,

а, значит, равны и углы

.

В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.

Решение.

Запишем площадь треугольника ABO в виде:

,

где   — площадь треугольника ABC;   — площадь треугольника BOC. То есть площадь треугольника ABO можно представить как:

.  (1)

Аналогично запишем площадь треугольника DCO, имеем:

Так как  , то последнее выражение можно переписать в виде:

.  (2)

Выражения (1) и (2) идентичны между собой и описывают площади треугольников ABO и DCO, то есть площади этих треугольников равны. Утверждение доказано.

Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.

Решение.

Треугольник CEF равен треугольнику DEF по трем сторонам, т.к. CE=DE (как радиусы одной окружности), EF – общая сторона (см. рисунок ниже). Тогда углы  .

Рассмотрим треугольник CED – равнобедренный, EF – биссектриса угла E, следовательно, EF – высота и 

Биссектрисы углов B и C трапеции ABCD пересекаются в точке О, лежащей на стороне AD. Докажите, что точка О равноудалена от прямых АВ, ВС и CD.

Решение.

По условию задачи ABCD – трапеция с основаниями BC и AD и биссектрисами BO и CO, то есть углы   и  . Из точки O проведем три перпендикуляра   (по сути они будут являться расстояниями от точки O до прямых AB, BC и CD).

Теперь заметим, что треугольники BMO=BNO равны как прямоугольные по гипотенузе и острому углу: BO – общая гипотенуза;  , так как BO – биссектриса. Из равенства треугольников следует, что OM=ON.

Аналогично для треугольников CNO=CKO, которые равны как прямоугольные по гипотенузе и острому углу: CO – общая гипотенуза;  , так как CO – биссектриса. Следовательно, ON=OK.

Таким образом, имеем, что MO=NO=KO, а значит, точка O равноудалена от прямых AB, BC и CD.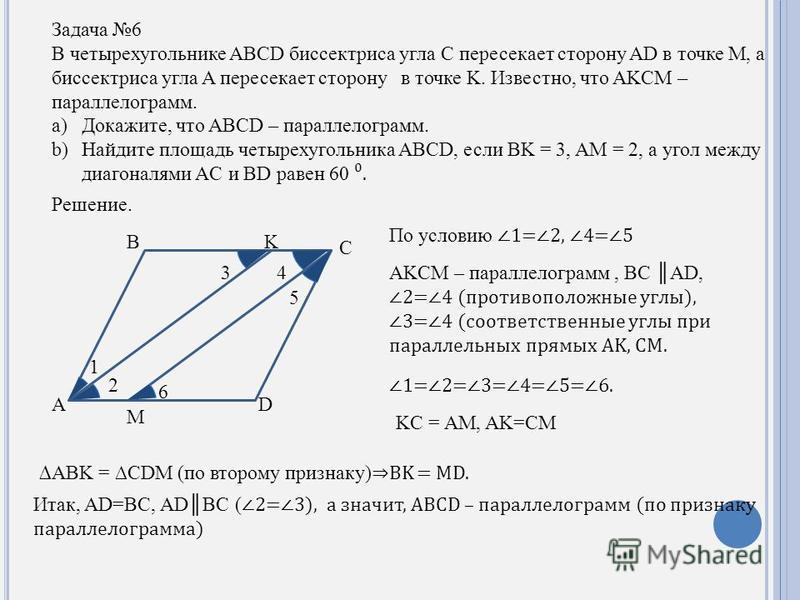 Положение доказано.

Внутри параллелограмма ABCD выбрали произвольную точку Е. Докажите, что сумма площадей треугольников АЕВ и CED равна половине площади параллелограмма.

Решение.

Проведем в параллелограмме ABCD высоту MN, равную h, и проходящую через точку E. Пусть расстояние ME=x, тогда NE=h-x. Площадь параллелограмма можно вычислить как

,

а площади треугольников как

Так как в параллелограмме противоположные стороны равны, то AB=CD и сумма площадей треугольников равна

,

что в точности равно половине площади параллелограмма ABCD. Утверждение доказано.

Окружности с центрами в точках I и J не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n.

Решение.

По условию задачи прямые IP:JP=m:n, а MN – касательная к окружностям в точках M и N, следовательно,   и  . Рассмотрим два прямоугольных треугольника IPM и JPN, которые подобны по двум углам: один угол у них прямой, а два других   как вертикальные углы. Для подобных треугольников можно записать соотношение:

,

но по условию  , следовательно,

или, что эквивалентно, в виде

,

где   — диаметры соответствующих окружностей. Утверждение доказано.

Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке М стороны AD. Докажите, что М — середина AD.

Решение.

Так как ABCD – параллелограмм, то стороны   и  . Из этого положения следует равенство углов   и  . Так как BM – биссектриса, то равны и углы  . Из равенства двух углов при основании BM следует, что треугольник ABM – равнобедренный, с равными сторонами AB=AM. Аналогично для треугольника CMD, у которого углы при основании MC равны, следовательно, он равнобедренный и CD=MD. Учитывая, что ABCD – параллелограмм, у которого стороны AB=CD, то автоматически следует, что и AM=MD, то есть точка M – середина отрезка AD. Положение доказано.

На средней линии трапеции ABCD с основаниями AD и ВС выбрали произвольную точку Е. Докажите, что сумма площадей треугольников АЕВ и CED равна половине площади трапеции.

Решение.

Доказательство проведем от обратного. Докажем сначала, что сумма площадей треугольников BEC и AED составляет половину площади трапеции. Это же автоматические будет означать, что оставшаяся площадь (сумма площадей треугольников AEB и CED) также будет равна половине площади трапеции.

По условию задачи точка E лежит на отрезке MN – средней линии трапеции. Проведем через эту точку высоту HL трапеции. Тогда по определению средней линии, отрезки EH=EL=1/2∙HL. Используя данные обозначения, выразим площади треугольников BEC и AED следующим образом:

Соответственно, сумма этих площадей составит величину, равную

но так как   — это площадь всей трапеции, то получаем, что

.

Положение доказано.

 В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

Решение.

Проведем в четырехугольнике диагонали AC и BD и отметим точку E на их пересечении. Рассмотрим треугольники ABE и DEC, у которых равны углы   по условию задачи, а также равны углы   как вертикальные. Таким образом, треугольники ABE и DEC подобные по двум углам с пропорциональными сторонами BE и CE, а также AE и DE. Рассмотрим теперь треугольники AED и BEC, у которых сторона AE пропорциональна стороне DE, а сторона BE пропорциональна стороне CE, кроме того, равны углы   как вертикальные. Отсюда следует, что треугольники AED и BEC подобны по двум соответствующим пропорциональным сторонам и углу между ними. Так как у подобных треугольников соответствующие углы равны, то угол  . Утверждение доказано.

Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны АВ и CD в точках Р и Т соответственно. Докажите, что BP = DT.

Решение.

У параллелограмма диагонали BD и AC делятся в точке пересечения O пополам, то есть BO=OD. Кроме того, в параллелограмме противоположные стороны параллельны, то есть   и, следовательно,   — как накрест лежащие при параллельных прямых и секущей BD. Углы   — как вертикальные углы. В результате имеем, что треугольники BOP и DOT равны по стороне и двум прилежащим к ней углам, а, следовательно, равны и стороны BP=DT.

Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка L — середина стороны BC. Докажите, что DL — биссектриса угла CDA. — Знания.site

Ответы 1

……………………..

Знаешь ответ? Добавь его сюда!

Последние вопросы

• Математика

  1 час назад

  Для строительства детской площадки рабочие проводили измерительные работы. Они подготовили две площадки квадратной формы. Найди их периметр, если известно, что величина периметра каждого из них меньше 90 м. Если цифры в записи одного периметра поменять местами, то получится периметр второго участка. Как записать решение?

• Математика

  9 часов назад

  Запишите решение в столбик и ответ.

• Русский язык

  10 часов назад

  Рус.яз 9 класс

• Физика

  10 часов назад

  Металлический шар массой 880 грамм падает на земл с высоты 3м. Какую работу при этом совершает сила тяжести

• Физика

  10 часов назад

  Процесс появление электрической дуги, ее физическое явление, способы гашения дуги

• Математика

  10 часов назад

  Нужна формула расчета

• Русский язык

  10 часов назад

  Русский язык 8 класс

• Русский язык

  10 часов назад

  Вставте пропущенные буквы в словах

• Геометрия

  10 часов назад

  Задача по геометрии

• Биология

  11 часов назад

  Биология дз срочно

• Химия

  11 часов назад

  1. Назовите групповой реагент и перечислите катионы, входящие в IV группу. 2. Укажите цвет гидроксидов катионов IV

• История

  11 часов назад

  Что произошло в риме после смерти Цезаря

• География

  11 часов назад

  Расположите регионы России в той последовательности, в которой их жители встречают Новый год.

• Русский язык

  11 часов назад

  Подскажите пожалуйста с заданием по русскому языку, дать характеристику предложению

• География

  11 часов назад

  Расположите регионы россии в порядке уменьшения среднегодового количества осадков.

How much to ban the user?

1 hour 1 day 100 years

Видео-вопрос: нахождение площади параллелограмма с помощью тригонометрической формулы площади треугольников

𝐴𝐵𝐶𝐷 — параллелограмм, где 𝐴𝐵 = 41 см, 𝐵𝐶 = 27 см и 𝑚∠𝐵 = 159°. Найдите площадь 𝐴𝐵𝐶𝐷, давая ответ с точностью до ближайшего квадратного сантиметра.

Video Transcript

𝐴𝐵𝐶𝐷 — параллелограмм, где 𝐴𝐵 равно 41 сантиметру, 𝐵𝐶 равно 27 сантиметрам, а мера угла 𝐵 159градусов. Найдите площадь 𝐴𝐵𝐶𝐷, давая ответ с точностью до ближайшего квадратного сантиметра.

Давайте начнем с наброска этого параллелограмм. Нам дана мера одного угол, угол 𝐵, который равен 159 градусам. И нам даны длины две стороны параллелограмма, заключающие этот угол.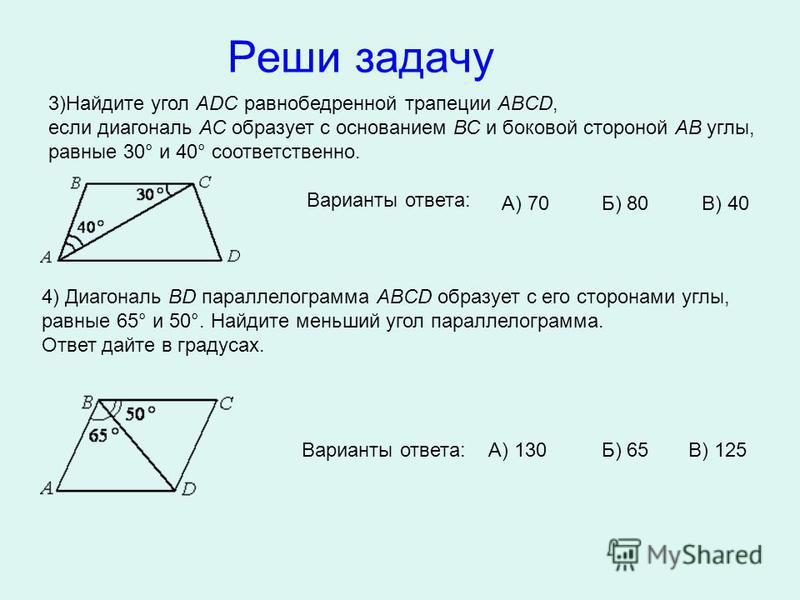 Итак, эта часть параллелограмма будет выглядеть так. Конечно, две другие стороны каждый параллелограмм параллелен одной из сторон, которые мы уже нарисовали. И они такой же длины, как их противоположная сторона. Таким образом, мы можем завершить параллелограмм.

Теперь нас просят найти площадь этого параллелограмма. Обычно мы использовали формулу основание, умноженное на перпендикулярную высоту. Но нам не дали перпендикулярная высота этого параллелограмма. Мы могли бы решить это, используя тригонометрия, но есть и другой метод, который мы можем использовать. Напомним, что диагонали параллелограмма каждая делит параллелограмм на две конгруэнтные треугольники. Если мы хотим, мы можем доказать это, используя условие конгруэнтности сторона-сторона-сторона или SSS.

В треугольниках 𝐴𝐵𝐶 и 𝐴𝐷𝐶 стороны 𝐴𝐵 и 𝐶𝐷 имеют одинаковую длину, потому что они являются противоположными сторонами в Оригинальный параллелограмм. По той же причине стороны 𝐴𝐷 и 𝐶𝐵 также имеют одинаковую длину. 𝐴𝐶 — это общая сторона двух треугольники. Итак, мы показали, что два треугольники равны по условию сторона-сторона-сторона. Так как два треугольника равны, их площади равны. И, следовательно, площадь параллелограмм в два раза больше площади каждого треугольника.

Затем мы вспоминаем тригонометрический формула площади треугольника. В треугольнике 𝐴𝐵𝐶, где прописные буквы 𝐴, 𝐵 и 𝐶 обозначают меры трех углов в треугольник и строчные буквы 𝑎, 𝑏 и 𝑐 обозначают длины трех противоположные стороны, то тригонометрическая формула площади треугольника равна половине 𝑎𝑏 грех 𝐶. Здесь 𝑎 и 𝑏 представляют длины любых двух сторон треугольника, а 𝐶 представляет собой меру их включенный угол. Это угол между двумя стороны, длину которых мы используем.

Если мы рассмотрим треугольник 𝐴𝐵𝐶 в наша фигура тогда, мы знаем длины двух сторон 𝐴𝐵 и 𝐵𝐶. Им 41 и 27 сантиметров, соответственно. И мы знаем меру их включенный угол; это 159 градусов. Таким образом, заменив 41 и 27 на две длины сторон в тригонометрической формуле и 159 градусов для меры их угол между ними, мы имеем, что площадь треугольника 𝐴𝐵𝐶 равна половине умножения на 41 умножить на 27 умножить на грех 159градусов.

Как мы уже говорили, площадь параллелограмм 𝐴𝐵𝐶𝐷 в два раза больше площади отдельных треугольников. Итак, у нас есть два умножить на половину умножить на 41 умножить на 27 умножить на грех 159 градусов. Но, конечно, фактор два и множитель половины компенсирует друг друга, в результате чего 41 умножается на 27. умножить на грех 159 градусов.

Теперь мы можем оценить это на калькулятор, убедившись, что калькулятор находится в режиме градусов. И это дает 396.713 продолжение. Вопрос просит нас дать наше ответ с точностью до ближайшего квадратного сантиметра. Таким образом, это значение округляется до ближайшее целое число равно 397.

Таким образом, если вспомнить, что диагонали параллелограмма разделить на два равных треугольника, а затем применить по тригонометрической формуле площади треугольника мы нашли, что площадь параллелограмм 𝐴𝐵𝐶𝐷 с точностью до ближайшего квадратного сантиметра равен 397 квадрат сантиметры.

Как найти периметр параллелограмма

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы » Как найти периметр параллелограмма

Ниже показан параллелограмм с размерами в см.

Чему равен периметр параллелограмма в см?

Возможные ответы:

Правильный ответ:

Объяснение:

Треугольник в левой части рисунка имеет угол a и . Поскольку сумма всех углов треугольника должна быть равна , мы можем найти угловую меру третьего угла:

Наш третий угол равен , и у нас есть треугольник.

Стороны треугольника находятся в соответствующем отношении . В этом случае сторона, противоположная нашему углу, равна , поэтому

Теперь мы также знаем, что

Теперь мы знаем длины всех недостающих сторон. Правая и левая стороны параллелограмма будут равны . Нижний и верхний будут каждый . Объединим их, чтобы найти периметр:

 

Сообщить об ошибке

Примечание: Рисунок выполнен НЕ в масштабе.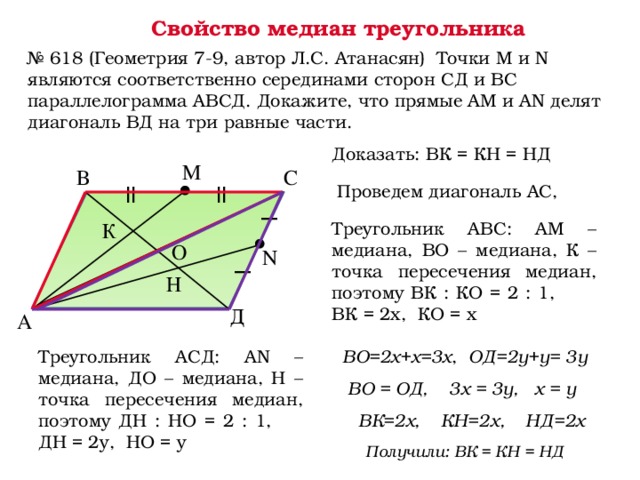

Укажите периметр параллелограмма на приведенном выше рисунке.

Возможные ответы:

Правильный ответ:

Объяснение:

По теореме 30-60-90 длина короткого катета равна длине длинного катета, деленному на , поэтому

Гипотенуза в два раза длиннее короткого катета, поэтому

Периметр параллелограмма равен

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе.

Укажите периметр параллелограмма на приведенной выше диаграмме.

Возможные ответы:

Правильный ответ:

Объяснение:

По теореме 45-45-90 длины катетов равны, поэтому

Его гипотенуза имеет меру общей меры его катетов, так что

Периметр параллелограмма равен

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе.

С точностью до десятых укажите периметр параллелограмма на приведенной выше диаграмме.

Возможные ответы:

Правильный ответ:

Объяснение:

 

 

Периметр параллелограмма равен

Сообщить об ошибке

900 Параграф выше,

3 имеет площадь 100. Чему равен его периметр с точностью до десятых?

Возможные ответы:

Правильный ответ:

Объяснение:

По теореме 45-45-90, . Так как  и  являются его основанием и высотой:

Также по теореме 45-45-90

Периметр параллелограмма равен

003

Сообщить об ошибке

На приведенном выше рисунке Параллелограмм имеет площадь 100.