Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Осевое сечение цилиндра — квадрат, площадь основания цилиндра равна 16П см^2. Найдите площадь полной поверхности цилиндра.
Найдите площадь полной поверхности цилиндра.
Осевое сечение цилиндра –квадрат, диагональ которого равна 4 см. Найти площадь полной поверхности цилиндра.
Радиус основания конуса равен 6см, а образующая наклонена к плоскости основания под углом 30 градусов. Найдите: а)площадь сечения конуса плоскостью,
Решено
Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведённого параллельно оси цилиндра на расстоянии 4 см от неё
Сумма длин всех рёбер прямоугольного параллелепипеда равна 80 см, а два его измерения – 10 см и 4 см. Найдите третье измерение параллелепипеда.
Пользуйтесь нашим приложением
Контрольно-оценочный материал по геометрии 8 класс
Контрольные работы по геометрии 8 класса
(к УМК А.Г. Мерзляк, В. Б. Полонский, М.С. Якир)
Б. Полонский, М.С. Якир)
Контрольная работа № 1
Тема. Параллелограмм и его виды
Вариант 1
Одна из сторон параллелограмма на 6 см больше другой, а его периметр равен 48 см. Найдите стороны параллелограмма.
В прямоугольнике АВСD диагонали пересекаются в точке О, АВ=9 см, АС=16 см. Найдите периметр треугольника СОD.
Один из углов ромба равен 72°. Найдите углы, которые образует сторона ромба с его диагоналями.
На диагонали ВD параллелограмма АВСD отметили точки Е и F так, что ∠ВСЕ = ∠DАF (точка Е лежит между точками В и F). Докажите, что СЕ=АF.
В параллелограмме АВСD бисссектриса угла А пересекает сторону ВС в точке Е. Отрезок ВЕ больше отрезка ЕС в 3 раза. Найдите периметр параллелограмма, если ВС = 12 см.
Найдите периметр параллелограмма, если ВС = 12 см.
Прямая проходит через середину диагонали АС параллелограмма АВСD и пересекает стороны ВС и АD в точках М и К соответственно. Докажите, что четырехугольник АМСК – параллелограмм.
Вариант 2
Одна из сторон параллелограмма в 5 раз больше другой, а его периметр равен 36 см. Найдите стороны параллелограмма.
В прямоугольнике АВСD диагонали пересекаются в точке О, АD=14 см, ВD=18 см. Найдите периметр треугольника ВОС.
Сторона ромба образует с одной из его диагоналей угол 68°. Найдите углы ромба.
На диагонали АС параллелограмма АВСD отметили точки Р и К так, что АР= СК (точка Р лежит между точками А и К). Докажите, что ∠АDР=∠СВК.
В параллелограмме АВСD бисссектриса угла D пересекает сторону АВ в точке Р. Отрезок АР меньше отрезка ВР в 6 раз. Найдите периметр параллелограмма, если АВ = 14 см.
Отрезок АР меньше отрезка ВР в 6 раз. Найдите периметр параллелограмма, если АВ = 14 см.
Прямая, пересекающая диагональ ВD параллелограмма АВСD в точке Е, пересекает его стороны АВ и СD в точках М и К соответственно, причем МЕ=КЕ. Докажите, что четырехугольник ВКDМ – параллелограмм.
Контрольная работа № 2
Тема. Средняя линия треугольника. Трапеция.
Вписанные и описанные четырехугольники.
Вариант 1
Найдите периметр треугольника, если его средние равны 6 см, 9 см и 10 см.
Основания трапеции относятся как 3:5, а средняя линия равна 32 см. Найдите основания трапеции.
Боковые стороны трапеции равны 7 см и 12 см. Чему равен периметр трапеции, если в нее можно вписать окружность?
Основания равнобокой трапеции равны 3 см и 7 см, а диагональ делит тупой угол трапеции пополам. Найдите периметр трапеции.
Найдите периметр трапеции.
Найдите углы четырехугольника АВСD, вписанного в окружность, если ∠АDВ= 43°, ∠АСD= 37°, ∠САD= 22°.
Высота равнобокой трапеции равна 9 см, а её диагонали перпендикулярны. Найдите периметр трапеции, если её боковая сторона равна 12 см.
Вариант 2
Стороны треугольника равны 10 см, 12 см и 14 см. Найдите периметр треугольника, вершины которого – середины сторон данного треугольника.
Основания трапеции относятся как 4:7, а средняя линия равна 44 см. Найдите основания трапеции.
Основания трапеции равны 6 см и 12 см. Чему равен периметр трапеции, если в нее можно вписать окружность?
Основания равнобокой трапеции равны 8 см и 10 см, а диагональ делит острый угол трапеции пополам. Найдите периметр трапеции.
Найдите углы четырехугольника АВСD, вписанного в окружность, если ∠СDВ= 48°, ∠АСD= 34°, ∠ВDС= 64°.
Высота равнобокой трапеции равна 109 см, а её диагонали перпендикулярны. Найдите боковую сторону трапеции, если её периметр равен 48 см.
Контрольная работа № 3
Тема. Теорема Фалеса. Подобие треугольников.
Вариант 1
Стороны угла М пересекают параллельные прямые АВ и CD, (точка А между М и С) MA=12 см, А С=4 см, BD=6 см. Найдите отрезок МВ.
Треугольники АВС и А1 В1 С1 подобны, причем сторонам АВ и ВС соответствуют стороны А1 В1 и В1 С1. Найдите неизвестные стороны этих треугольников, если АВ=8 см, ВС=10 см, А1 В1 =4 см, А1 С1=6 см.
Отрезок АК – биссектриса треугольника АВС, АВ=12 см, ВК=8 см, СК=18 см. Найдите сторону АС.
На стороне ВС треугольника АВС отметили точку М так, что ВМ : МС= 2:9. Через точку М провели прямую, которая параллельна стороне АС треугольника и пересекает сторону АВ в точке К. Найдите сторону АС, если МК =18 см.
В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке О, ВС : АD = 3:5, ВD=24 см. Найдите отрезки ВО и ОD.
Через точку М, находящуюся на расстоянии 15 см от центра окружности радиусом 17 см, проведена хорда, которая делится точкой М на отрезки, длины которых относятся как 1:4. Найдите длину этой хорды.
Вариант 2
Стороны угла О пересекают параллельные прямые PK и NM, (точка P между O и N), NP=20 см, PO=8 см, MK=15 см. Найдите отрезок KO.
Найдите отрезок KO.
2. Треугольники АВС и А1 В1 С1 подобны, причем сторонам АВ и ВС соответствуют стороны А1 В1 и В1 С1. Найдите неизвестные стороны этих треугольников, если ВС=5 см, АВ=6 см, В1 С1=15 см, А1 С1=21 см.
3. Отрезок CD – биссектриса треугольника АВС, АС=12 см, ВС=18 см, AD=10 см. Найдите отрезок BD.
4. На стороне АВ треугольника АВС отметили точку Е так, что АЕ : ВЕ= 3:4. Через точку Е провели прямую, которая параллельна стороне АС треугольника и пересекает сторону ВС в точке F. Найдите отрезок EF, если АС =28 см.
5. В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке О, ВО : ОD = 2:3, АС=25 см. Найдите отрезки АО и ОС.
6. Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см. Найдите расстояние от точки Р до центра окружности, если её радиус равен 6 см.
Контрольная работа № 4
Тема. Метрические соотношения в прямоугольном треугольнике.
Теорема Пифагора.
Вариант 1
Высота прямоугольного треугольника, проведенная к гипотенузе, делит её на отрезки длиной 9 см и 16 см. Найдите меньший катет треугольника.
В прямоугольном треугольнике гипотенуза равна 13 см, а один из катетов – 12 см. Найдите периметр треугольника.
Диагонали ромба равны 12 см и 16 см. Найдите сторону ромба.
Найдите сторону ромба.
Высота ВМ равнобедренного треугольника АВС (АВ=АС) делит сторону АС на отрезки АМ=15 см и СМ=2 см. Найдите основание треугольника АВС.
Из точки к прямой проведены две наклонные, проекции которых на прямую равны 9 см и 16 см. Найдите расстояние от точки до прямой, если одна из наклонных на 5 см больше другой.
Окружность, вписанная в прямоугольную трапецию, делит точкой касания большую боковую сторону на отрезки длиной 4 см и 25 см. Найдите высоту трапеции.
Вариант 2
Катет прямоугольного треугольника равен 30 см, а его проекция на гипотенузу – 18 см. Найдите гипотенузу треугольника.
В прямоугольном треугольнике катеты равны 8 см и 15 см. Найдите периметр треугольника.
Сторона ромба равна 10 см, а одна из диагоналей – 16 см. Найдите вторую диагональ ромба.
Высота АК равнобедренного треугольника АВС (АВ=ВС) равна 12 см, а КВ= 9 см. Найдите основание треугольника АВС.
Найдите основание треугольника АВС.
Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найдите расстояние от точки до прямой, если разность проекций наклонных на эту прямую равна 4 см.
Окружность, вписанная в равнобокую трапецию, делит точкой касания боковую сторону на отрезки длиной 2 см и 32 см. Найдите высоту трапеции.
Контрольная работа № 5
Тема. Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников.
Вариант 1
В треугольнике АВС известно, что ∠С= 90°, АВ= 25 см, ВС= 20 см. Найдите:
1) cos B; 2) tg A.
2. В прямоугольном треугольнике АВС (∠С= 90°) известно, что АВ= 15 см,
sin A = 0,6. Найдите катет ВС.
3. Найдите значение выражения sin216° + cos216° — sin260°.
4. Основание равнобедренного треугольника равно 12 см, а высота, проведенная к основанию , 8 см. Найдите синус, косинус, тангенс и котангенс угла при основании треугольника.
5. Высота ВD треугольника АВС делит сторону АС на отрезки АD и СD, ВС=6 см, ∠А= 30°, ∠С ВD=45°. Найдите отрезок АD.
6. Диагональ равнобокой трапеции перпендикулярна боковой стороне и образует с основанием трапеции угол α. Найдите высоту трапеции, если радиус окружности, описанной около трапеции равен R.
Вариант 2
В треугольнике АВС известно, что ∠С= 90°, АС= 8 см, ВС= 6 см. Найдите:
ctg B; 2) sin A.
В прямоугольном треугольнике АВС (∠С= 90°) известно, что АС= 12 см,
tg A = 0,8. Найдите катет ВС.
Найдите значение выражения cos230°+sin252° + cos252°.
Основание равнобедренного треугольника равно 10 см, а , боковая сторона 13 см. Найдите синус, косинус, тангенс и котангенс угла между боковой стороной треугольника и высотой, проведенной к его основанию.
Высота ВD треугольника АВС делит сторону АС на отрезки АD и СD, АВ=6 см, ∠А= 60°, ∠С ВD=30°. Найдите отрезок СD.
Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между боковой стороной и большим основанием трапеции равен α. Найдите радиус окружности, описанной около трапеции, если её высота равна h.
Контрольная работа № 6
Тема. Многоугольники. Площадь многоугольника.
Вариант 1
Чему равна сумма углов выпуклого четырнадцатиугольника?
Площадь параллелограмма равна 84 см2, а одна из его сторон – 12 см. Найдите высоту параллелограмма, проведенную к этой стороне.
Найдите высоту параллелограмма, проведенную к этой стороне.
Боковая сторона равнобедренного треугольника равна 15 см, а высота, проведенная к основанию, – 9 см. Найдите площадь треугольника.
Найдите площадь ромба, сторона которого равна 26 см, а одна из его диагоналей на 28 см больше другой.
Боковая сторона равнобокой трапеции равна 10√2 см и образует с основанием угол 45°. Найдите площадь трапеции, если в нее можно вписать окружность.
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной15 см и 20 см. Найдите площадь треугольника.
Вариант 2
Чему равна сумма углов выпуклого восемнадцатиугольника?
Площадь параллелограмма равна 98 см2, а одна из его высот – 14 см. Найдите сторону параллелограмма, к которой проведена эта высота.
Основание равнобедренного треугольника равно 16 см, а боковая сторона – 17 см. Найдите площадь треугольника.
Найдите площадь ромба, сторона которого равна 50 см, а разность диагоналей – 20 см.
Боковая сторона равнобокой трапеции образует с основанием угол 60°, а высота трапеции равна 6√3 см. Найдите площадь трапеции, если в нее можно вписать окружность.
Биссектриса острого угла прямоугольного треугольника делит катет на отрезки длиной 6 см и 10 см. Найдите площадь треугольника.
Контрольная работа № 7
Тема. Обобщение и систематизация знаний
учащихся за курс 8 класса.
Вариант 1
Найдите углы параллелограмма, если один из них на 26° больше другого.
Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке М. Меньшее основание ВС равно 5 см, ВМ = 6 см, АВ = 12 см. Найдите большее основание трапеции.
Высота АМ треугольника АВС делит его сторону ВС на отрезки ВМ и МС. Найдите сторону АС, если АВ= 10√2 см, МС = 24 см, ∠В=45°.
Найдите сторону АС, если АВ= 10√2 см, МС = 24 см, ∠В=45°.
Основания равнобокой трапеции равны 12 см и 20 см, а диагональ является биссектрисой её тупого угла. Найдите площадь трапеции.
Перпендикуляр, опущенный из точки окружности на её диаметр, делит его на два отрезка, один из которых на 27 см больше другого. Найдите радиус окружности, если длина данного перпендикуляра равна 18 см.
Вариант 2
Найдите углы параллелограмма, если один из них на 32° меньше другого.
Продолжения боковых сторон АВ и СD трапеции АВСD пересекаются в точке Е. Большее основание АD равно 12 см, DЕ = 16 см, СD = 102 см. Найдите меньшее основание трапеции.
Высота DЕ треугольника СDF делит его сторону CF на отрезки CE и EF. Найдите сторону СD, если EF= 8 см, DF = 17 см, ∠C=60°.
Основания равнобокой трапеции равны 12 см и 18 см, а диагональ является биссектрисой её острого угла. Найдите площадь трапеции.
Найдите площадь трапеции.
Перпендикуляр, опущенный из точки окружности на её диаметр, делит его на два отрезка, разность которых равна 21 см. Найдите радиус окружности, если длина данного перпендикуляра равна 10 см.
Каждая сторона ромба имеет длину 10 см, а одна из его диагоналей равна 16 см. Найдите длину другой…
Перейти к
- Четырехугольники Упражнение 10А
- Четырехугольники Упражнение 10B
- Четырехугольники Упражнение 10C
- Системы счисления
- Полиномы
- Факторизация многочленов
- Линейные уравнения с двумя переменными
- Координатная геометрия
- Введение в геометрию Евклида
- Линии и углы
- Треугольники
- Конгруэнтность треугольников и неравенства в треугольнике
- Четырехугольники
- Площади параллелограммов и треугольников
- Круги
- Геометрические построения
- Площади треугольников и четырехугольников
- Объем и площадь поверхности твердых тел
- Средняя медиана и режим разгруппированных данных
- Вероятность
Главная > Решения RS Aggarwal Класс 9 Математика > Глава 10 — Четырехугольники > Четырехугольники Упражнение 10B > Вопрос 12
Вопрос 12 Четырехугольники Упражнение 10B
Каждая сторона ромба имеет длину 10 см, а одна из его диагоналей равна 16 см.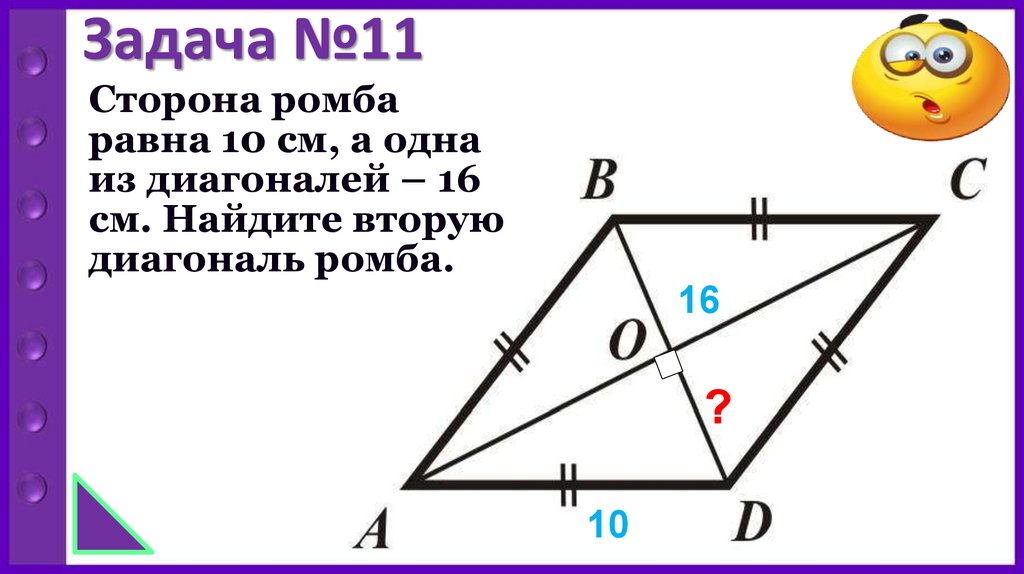 Найдите длину другой диагонали и, следовательно, площадь ромба.
Найдите длину другой диагонали и, следовательно, площадь ромба.
Ответ:
Мы знаем, что диагонали ромба делятся пополам под прямым углом. 8 см
Рассмотрим △ AOB
Используя теорему Пифагора 92.
Связанные вопросы
На соседнем рисунке ABCD — параллелограмм, в котором ∠ A = 72. Вычислите ∠ B, ∠ C и ∠ D.
На соседнем рисунке ABCD представляет собой параллелограмм, в котором ∠ DAB = 80 и ∠ DBC = 60. Вычислите ∠CDB …
На соседнем рисунке M — середина стороны BC параллелограмма ABCD, такого что ∠ BAM = ∠ DA…
На соседнем рисунке ABCD — параллелограмм, в котором ∠ A = 60o. Если биссектрисы ∠ A и ∠ B…
Если биссектрисы ∠ A и ∠ B…
На соседнем рисунке ABCD представляет собой параллелограмм, в котором ∠ BAO = 35, ∠ DAO = 40 и ∠ COD = 105. Кал…
В параллелограмме ABCD, если ∠ A = (2x + 25) o и ∠ B = (3x — 5) o, найдите значение x и меру…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Четырехугольники Упражнение 10A
Четырехугольники Упражнение 10B
Четырехугольники Упражнение 10C
Главы
Системы счисления
Многочлены
Факторизация многочленов
Линейные уравнения с двумя переменными
Координатная геометрия
Введение в геометрию Евклида
Прямые и углы
Треугольники углы и неравенства в треугольнике
четырехугольники
площади Параллелограммы и треугольники
Окружности
Геометрические построения
Площади треугольников и четырехугольников
Объем и площадь поверхности твердых тел
Средняя медиана и мода разгруппированных данных
Вероятность
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Площадь ромба 143 м 2 .
Правильный ответ:
d 1 = 11 мПошаговое объяснение:
A=143 м2 d2=26 м A = 2d1⋅ d2 d1=2⋅ A =2⋅ 143/26=11 м
Нашли ошибку или неточность? Не стесняйтесь
написать нам. Спасибо!
Для решения этой словесной задачи по математике необходимо знать следующие знания:
- алгебра
- выражение переменной из формулы
- контуры
- площадь фигуры
- ромб
- диагональ
Единицы физических величин:
- площадь 1
- практика для детей 12 лет
- практика для 13 лет годовалые
04
Предлагаем вам посмотреть обучающее видео по этой математической задаче: видео1 видео2
- Ромб
Один угол ромба равен 136°, а его меньшая диагональ равна 8 см. Найдите длину большей диагонали и сторону ромба.
Найдите длину большей диагонали и сторону ромба. - Ромб
Внутренние углы ромба относятся как 2:3. Во сколько раз меньшая диагональ длиннее стороны ромба? - Один из
Один из внутренних углов ромба равен 120°, а длина меньшей диагонали 3,4 метра. Найдите периметр ромба. - Ромб 2
Рассчитайте площадь ромба с высотой v=48 мм и меньшей диагональю u = 60 мм. - Ромб
У ромба площадью 137 одна диагональ длиннее второй на 5. Вычислите длины диагоналей и сторон ромба. - Диагональ ромба
Площадь ромба равна 224. Одна диагональ равна 33. Найдите длину второй диагонали. - Диагонали ромба
Одна из диагоналей ромба вдвое больше другой. Найдите площадь ромба, если сумма длин диагоналей равна 24. - Ромб
Найдите длину другой диагонали и площадь ромба. Периметр ромба равен 40 см, а длина одной из диагоналей 10 см. - Алмаз
Найдите сторону ромба, если его площадь S = 490 см² и одна диагональ u 2 = 39 см.
- Ромб
Стороны ромба имеют длину 10 см, а угол между двумя соседними сторонами составляет 76 градусов. Найдите длину большей диагонали ромба. - Две диагонали
Диагонали ромба EFGH имеют длины в соотношении 1:2. Какова длина окружности ромба, если его большая диагональ равна 8 см? - Стороны треугольника
Треугольник имеет длину окружности 42 см. Сторона а в два раза короче стороны b, а сторона с на 2 см длиннее стороны а. Найдите размеры сторон треугольника. - Прямоугольный 4184
Прямоугольный участок со сторонами 20м и 28м. Подсчитайте содержание корневища и узнайте, какой длины должна быть длинная сторона участка с тем же содержимым, если меньшая сторона имеет длину 16 метров. Кроме того, рассчитайте длину забора вокруг EAC - Станок
Станок производит стальные стержни нормально распределенной длины, средняя длина и стандартное отклонение которых равны 50,0 см и 0,5 см соответственно. Стержни не соответствуют стандартам безопасности, если они короче 49.

 01.21
01.21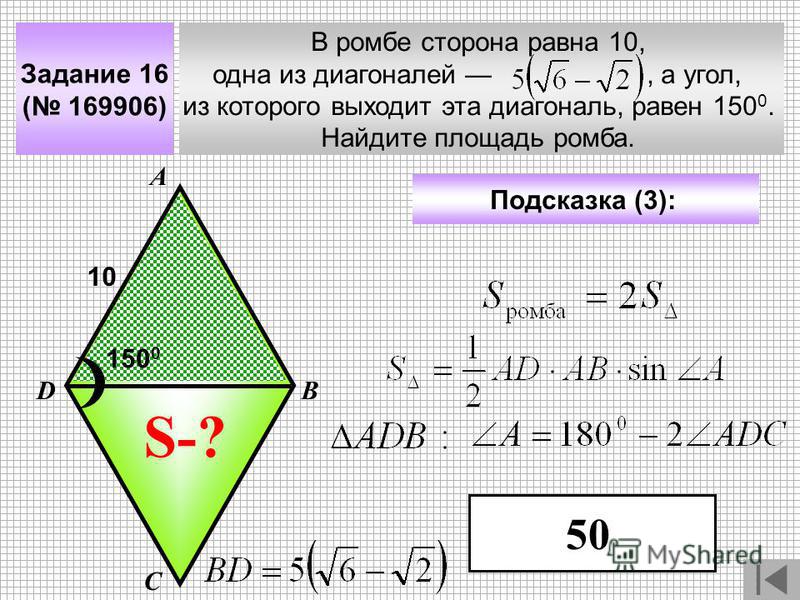 Найдите длину большей диагонали и сторону ромба.
Найдите длину большей диагонали и сторону ромба.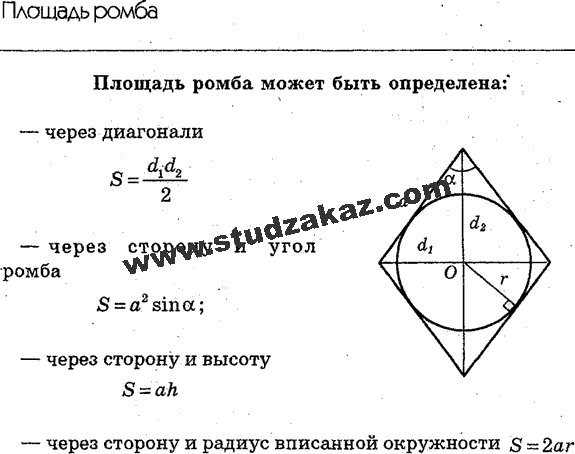

Leave A Comment